The electrical double layer at the ionic liquid/Au and Pt electrode interface

Abstract

The role of the electrode material on the interfacial double layer structure of a series of ionic liquids 1-butyl-3-methylimidazolium hexafluorophosphate ([C₄MIM][PF₆]), 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([C₄MIM][Tf₂N]) and 1-butyl-3-methylimidazolium tetrafluoroborate ([C₄MIM][BF₄]) was investigated on gold (Au) and platinum (Pt) electrodes. The aim of this work is to contribute with experimental data to complement theoretical models that are currently under discussion in order to describe the structure of the double layer formed at the interface electrode/ionic liquid. There is still a controversy about the general shape that differential capacitance curves should present and researchers still continue making efforts to correlate the nature of the electrode/ionic liquid with the shape of the curves. Differential capacitance curves at the Au and Pt interface shows that the values of capacity follow the same order C [C₄MIM][PF₆] < C [C₄MIM][Tf₂N] < C [C₄MIM][BF₄]. However, the values of C are considerably lower for Pt when compared with Au for all three liquids studied. The alkyl chain length effect on the differential capacity curves was also studied at the Pt/[C_nMIM][Tf₂N] interface (where n = 2, 4 and 6). The results follow an expected trend except for the liquid [C₆MIM][Tf₂N] that shows a value of capacity near to that obtained for [C₂MIM][Tf₂N]. Since ionic liquids have great applicability in energy storage devices and capacitors it is of great importance to evaluate the dependence of differential capacitance as function of temperature. The results indicate that the capacity increases with increasing temperature for all systems studied in this work.

---

Introduction

Room temperature ionic liquids (RTILs) are salts with a melting point below 100 °C which have been subject of intense research partially due to their potential as an environmentally friendly alternative to traditional organic solvents.¹ Unlike high-temperature molten salts, typical RTILs consist of bulky and often unsymmetrical organic cations of complex shape and inorganic anions with their charges typically delocalized among many atoms.^2,3

Albeit the large number of RTILs, research has been focused on 1,3-dialkylimidazolium salts.⁴ The bulk phase of some of these 1,3-dialkylimidazolium based liquids shows some spatial nanoscale structural organization, created by the existence of nonpolar regions comprised of segregated alkyl chains and polar regions formed by the anions and cationic groups.^5,6 Changes in the alkyl side chain length have been reported to cause changes in physicochemical properties of RTILs.⁷

Many of the ILs has wide electrochemical windows which combined to their very low vapour pressure and high thermal stability are considered to be advantageous in many electrochemical applications.^8,9 The understanding of the RTILs electrochemical interface at solid and liquid electrodes at a molecular level is of great importance to explain heterogeneous electron transfer processes present in a number of applications such as solar cells,¹⁰ supercapacitors,¹¹ sensors,¹² batteries¹³ or electrodeposition of metals.^14,15

The conformation of alkyl side chain attached to the imidazolium cation is also known to be important for the understanding of their structures and physicochemical properties.^16,17

Despite of its relevance and in contrast with the fast growing number of studies on the bulk properties of RTILs, little is known about the interfacial structure of interfaces of RTILs with solids or liquids, in particular the structure of electrochemical interfaces.

The most extensively studied macroscopic property of the Electric Double Layer (EDL) in RTILs is their differential capacitance.^18–22 The differential capacitance curves, C(E), vary considerably with the nature of the metal surface with three different types of trends. Whereas concave U-shape^23–25 capacitance-electrode potential C(E) curves were observed in many experiments, bell-shaped and camel-like C(E) curves¹⁹ have also been reported. Furthermore and similarly to what was observed for inorganic high temperature melts the so called anomalous temperature effect on the capacitance have been reported.²⁶

The existing classical theories can not satisfactorily explain the diverse and contrasting experimental observations. Recently, Kornyshev²⁷ and Oldham²⁸ presented models to describe the EDLs in ILs. For example, bell-shaped and camel-like C(E) curves can be explained by the EDL models proposed by Kornyshev and Oldham. Molecular dynamics simulation at solid electrodes suggests that the EDL structure is still strongly affected by short-range IL–IL and IL–electrode interactions.²⁹ Similar conclusions have also been reached for the EDLs in high-temperature molten salts.³⁰

Simplified models of the interface have been proposed as an attempt to accommodate the capacitance dependence on the alkyl chain length and the potential induced orientation of the cation assessed by spectroelectrochemical techniques.³¹ The orientation of the imidazolium ring has been found to be either parallel or perpendicular to the surface and seems to be dependent on the anion.^32,33 A simple Helmholtz layer thickness controlled by the length of the alkyl side chain length has been proposed leading to an average thickness of the interface of 3–6 Å.^34,20

The paper describes the effects on the differential capacity of Au and Pt electrodes in contact with a series of alkyl-methylimidazolium liquids aiming at understanding the role of alkyl side chain length and nature of the anions on the structure of the electrode/ionic liquid interface.

Experimental

The issue of purity is very important particularly in the context of studying ideally polarisable electrochemical interface.³⁵ In the literature there are references to purification/cleaning protocol and test procedure to detect the presence of particular impurities in ILs.³⁶ Apparently the contaminants in ILs have as main source the original synthetic materials.³⁷ In the absence of an accepted protocol for purification a combined process involving washing hydrophobic ILs with ultrapure water, separation and drying under reduced pressure at 60 °C for 72 hours was followed. The aim is to reduce water and the volatile contaminants. Besides the test procedure to detect the presence of halides the operational criteria was to obtain stable and reproducible voltammograms without any indication for the presence of electroactive impurities. The liquids were purchased from two different companies, Iolitec and Merck, with the highest purity available. With the exception of the hydrophilic [C₄MIM][BF₄], the liquids were washed with ultrapure water at room temperature and dried under vacuum allowing the removal of the halides and other water soluble impurities. [C₄MIM][BF₄] was washed at a temperature below 5 °C and a two immiscible phase system was formed. The immiscible liquid phase was separated and dried as the other liquids. The water content, according to Karl-Fisher titration (831 KF coulometer Metrohm) was below 30 ppm.

Since any oxidation and reduction reactions that may occur at the limits of potential window could introduce surface or solution contaminants, the potential excursion during impedance measurements was maintained within limits for which no Faradaic process occurring was electrochemically detected.

For solid electrodes the surface preparation is also a crucial step to obtain meaningful results. The procedure followed was: clean Au (0.0314 cm²) and Pt (0.0314 cm²) disc electrode embedded on a Teflon holder by mechanical polishing with Al₂O₃ paste (Buehler, micropolish 0.3 μm); after ultrasonication and washing, the electrodes were subjected to oxidation and reduction cycles in HClO₄ solutions until reproducible I–E profile was obtained. The electrode was afterwards dried with nitrogen and transferred to the cell containing the RTIL and subject to continuous cycling within the potential interval for which no Faradaic process was detected. Impedance spectra acquisition was only carried out after a stable CV was obtained.

Electrochemical measurements

Electrochemical experiments were performed in a three electrode cell. A spiral platinum wire was used as a counter electrode and a silver wire was used as a pseudo-reference electrode. The cell was water jacketed and thermostated by pumping water from a thermostated bath.

All the experiments were carried out inside a glove box under vacuum conditions. Before each experiment dry nitrogen was bubbled through the RTIL solution for about 45 minutes and a constant flow of dry nitrogen was kept over the solution during the measurements.

Cyclic voltammetry and electrochemical impedance spectroscopy (EIS) were carried out with an Autolab potentiostat model PGSTAT 20 (Ecochimie) equipped with a frequency response analyser module. Cyclic voltammetry (50 mV s⁻¹) was used to verify cleanness and reproducibility of the system and to define the double layer region. This technique was always performed before and after the impedance measurements to control the stability of the systems. Impedance spectra were obtained in the frequency range 25 KHz to 5 Hz (with 20 frequencies per decade) with an alternating signal of 10 mV (rms) within the potential window corresponding to the double layer as indicated by cyclic voltammetry. Potential was scanned from negative to positive direction with 50 mV steps allowing for a delay time of 150 s before the acquisition of each impedance spectra. Fixed frequency measurements (215 Hz and 1005 Hz) were also carried out and data converted to capacitance values. During these measurements the potential was scanned linearly at 20 mV steps.

Differential capacitance from impedance measurements

To obtain values of the double layer capacitance (C) from impedance data, a model is required relating the capacity to the equivalent circuit used to describe the data. Different capacitance extract procedures have been suggested.^38,39

When the impedance can be fitted to the equivalent circuit composed by a series combination of a resistance, R_s and a CPE (Y₀, n) the following relation proposed by Sluyters et al.⁴⁰ may be used to calculate the value of the capacitance from the CPE parameter through eqn (1)

The fitting of the experimental data is usually demonstrated on Z′′(ω) vs. Z′(ω) Nyquist plot. However, such plots do not clearly reveal the existence of deviations at high frequencies, which are known to occur in very resistive media or in the presence of impurities.⁴¹ By contrast the Z′′(ω) vs. Z′(ω) Nyquist plots are very sensitive to the influence of noise in the low frequency region. There are other representations of impedance data, which allow easy visualization of deviations and identification of frequency domain of dominant capacitive or resistive character. The normalized plots ωZ′′ vs. ωZ′ or Y′′/ω vs. Y′/ω can be very capacitance-sensitive.⁴¹ Since most commercial software allows to obtain a variety of plots an ensemble of plots were used to assist the judgement of best fits and to assess which frequency region should be selected to improve the fitting.

The Nyquist plots of the impedance measurements are nearly straight lines with potential dependent slopes. Fig. 1a shows the data plotted in the admittance form (Y′′/Y′) which is more sensitive to the capacitive behaviour of the interface. Fig. 1b) is the corresponding Bode plot (log |Z|/ϕ) which shows the existence of a single time constant confirming the absence of any Faradaic process within the potential window and nearly pure capacitive behaviour (ϕ ≈ 90°).

Fig. 1 Plots for the representation of experimental data for the Pt/[C₄MIM][BF₄] interface, 20 °C and at 0 V vs. Ag (wire). Full line: fitting to an R-CPE equivalent circuit: (a) admittance, (b) Bode plot.

The impedance plots were fitted to a simple equivalent circuit using only a series association of resistance and constant phase element to account for the frequency dispersion. The goodness of the fit was judged visually using different types of the plots of the impedance data, evaluating χ² (usually lower than 10⁻³) and assessing the effect on χ² of increasing the number of elements in the equivalent circuit.

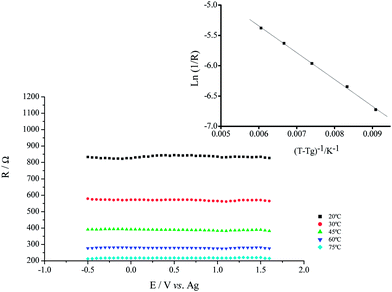
The resistance values of the ionic liquid were found to be invariant with the applied potential but showed expected marked temperature dependence (R_s decrease with increasing temperature). Using a modified version of the VTF type equation⁴²

where E_a is the activation energy for electrical conduction, σ_∞ is the maximum electrical conductivity, k_B is the Boltzmann constant and T_g the glass transition temperature.

Good linear relations were obtained plotting ln(1/R) vs. 1/[T − T_g] as represented in the insert of Fig. 2.

Fig. 2 Dependence of R_s obtained after fitting the impedance data to a R-CPE circuit as a function of the applied potential at different temperatures measured at Pt/[C₄MIM][Tf₂N] interface. Insert – plot of the Vogel–Tammann–Fulcher (VTF) type representation.

The temperature dependence of resistance allows to estimate the activation energy (E_a) for the electrical conduction.⁴² From the slope of the straight lines adjusted the values of E_a were calculated and are given in Table 1.

Table 1 Values of T_g/K and E_a/kJ mol⁻¹ of the RTILs studied

RTIL	Tg/K	Electrode	Ea/kJ mol^−1
[C4MIM][BF4]	188	Pt	3.83
		Au	4.26
[C4MIM][PF6]	191	Pt	4.34
		Au	4.52
[C4MIM][Tf2N]	186	Pt	3.50
		Au	3.70
[C2MIM][Tf2N]	186	Pt	2.84
[C6MIM][Tf2N]	192	Pt	3.55

---

A long alkyl chain difficults the movement of the cations and so the ILs with longer chains contribute to a lower electrical conductivity⁴² which results in higher activation energy. The E_a follow the following trend: E_a [C₂MIM][Tf₂N] < E_a [C₄MIM][Tf₂N] < E_a [C₆MIM][Tf₂N].

The values of CPE parameters (Y₀, n), n being the fractional exponent of CPE and Y₀ the CPE coefficient (F cm⁻² s⁻ⁿ) were obtained at each potential. An example of the variation of Y₀ and n with the electrode potential for Au/[C₄MIM][PF₆] interface is represented in Fig. 3.

Fig. 3 Differential capacitance–potential curves measured at different temperatures of Au/[C₄MIM][PF₆] interface. Insert: effect of temperature on n values.

It is clear that the value of n lies between 0.95 and 0.97 for both Au and Pt electrodes. These are high values pointing to a nearly pure capacitive behaviour. Lower values of n have been associated to the roughness of the surface.⁴³ Important is to notice the potential dependence of n that mirrors Y₀, similarly to what was reported by Motheo⁴⁴ for Au/aqueous electrolyte solution and recently by Kolb et al.⁴⁵ for Au/ionic liquid interface. Motheo suggests that the potential dependence of n mirroring that of Y₀ may be associated with an adsorption phenomenon. The average values of n are nearly independent of temperature for both electrodes. Comparing Y₀ and n data for Au polycrystalline and Au (111) data reported by Kolb, our values of n are much higher indicating a capacitive behaviour. The contrast between both surfaces is striking and cause doubts of any strong influence of roughness on the values of n since the surface used by Kolb et al. are certainly of high quality.

Results

Cyclic voltammetry

Such as remarked by Kolb et al.⁴⁵ flat CVs on a wide potential range for Au/ionic liquids interface can only be obtained using rather insensitive current scale. The CVs in Fig. 4 registered in normal current scales, indicate the absence of Faradaic processes measured at Au/[C₄MIM][PF₆] and Au/[C₄MIM][Tf₂N] interfaces.

Fig. 4 Cyclic voltammogram measured at Au/imidazolium ionic liquids interface at 303.15 K.

By contrast to [C₄MIM][PF₆] and [C₄MIM][Tf₂N], the CVs measured at Au/[C₄MIM][BF₄] show a small pair of peaks possible due to the presence of impurities which were not removed because the liquid could not be washed. However, the presence of these impurities seems not to be detected in the capacitance curves. Cyclic voltammograms and C(E) curves did not show significant differences when the electrode material or the batch of the ionic liquid under study was changed. The electrochemical windows considered on C(E) measurements were determinated at an arbitrary current density of 15 μA cm⁻². Similar electrochemical windows were used by Kolb et al.⁴⁵ The resulting potential window is considerably different from the interval o potentials reported by Su et al.⁴⁶ (−0.4 V to −2.0 V vs. Pt wire).

The anion effect on the cyclic voltammograms were also studied at Pt interfaces and are shown in Fig. 5.

Fig. 5 Cyclic voltammogram measured at Pt/imidazolium ionic liquids interface at 303.15 K.

It is clear that the capacitive current of Pt electrode increase when [PF₆]⁻ is replaced by [BF₄]⁻ and is highest in the presence of [Tf₂N]⁻.

There is little variation in the cathodic potential limit which depends on the identity of the cation. Once the cation is common to all three liquid, as expected, similar cathodic limits were obtained. Relatively to the anodic limit, it increases in order [Tf₂N]⁻ < [PF₆]⁻ < [BF₄]⁻.

Differential capacitance curves

The capacitance curve for Au/[C₄MIM][PF₆] interface is shown on Fig. 6.

Fig. 6 Differential capacitance curves measured at Au/imidazolium ionic liquids interface at 303.15 K.

The capacitance is nearly constant with potential (6–7 μF cm⁻²) showing an apparent increase at the extreme of the potential window. In the literature there are studies concerning the interface Au (111)/[C₄MIM][PF₆] reported by Kolb et al.⁴⁵ The authors argue that it is impossible to calculate capacitance for CPEs and propose a new equivalent circuit from which a so called high frequency capacitance, C_hf, can be obtained. It may be a coincidence but it is remarkable since the values of C_hf reported by Kolb et al. are practically coincident with the values obtained with our measurements using eqn (1) to extract the capacitance. It may also be mentioned that our values of n obtained from the fitting are much higher than those given by these authors. Su et al.⁴⁶ studied the interface between the Au (100) and [C₄MIM][BF₄] and [C₄MIM][PF₆]. The authors report that the capacitance has a bell-shape form. The curve reported in Fig. 6 does not have any specific feature which could be related to a bell-shape, U-shape or camel shape form within the potential range assessed.

Fig. 6 also shows that the C(E) curve for Au/[C₄MIM][BF₄] contrast with [PF₆]⁻ curve. Indeed not only the values of capacitance in the presence of [BF₄]⁻ are much higher than those obtained for [PF₆]⁻ but the nearly flat curve registered for potentials values more negative than 0.0 V are followed by a capacitive peak with maximum at 0.7 V. The curve obtained at fixed frequency has a similar potential dependence but with expectedly different values of capacitance. This curve is very similar to that reported by Alam et al.⁴⁷ The curve reported by Su et al.⁴⁶ for Au (100) show similar features but the position of the capacitance peak is shifted towards more negative potentials which may be caused by a difference on the pzc of the surface and/or of the reference electrode used.

Replacing the inorganic anions by a large organic anion, [Tf₂N]⁻, a capacitance curve with a nearly bell shape was obtained and without any regions of nearly potential independent capacitance.

Fig. 7 shows a comparison of our data for [C₄MIM][BF₄] on polycrystalline gold and the data of Su et al.⁴⁶ on Au (100).

Fig. 7 Comparison of differential capacitance data obtained by Gomes et al. for [C₄MIM][BF₄] on polycrystalline gold with Su et al. data on Au (100) with the same liquid.⁴⁶

The curves shape are similar to that reported for Au (100) by Su et al.⁴⁶ The curves have been shifted to allow coincidence of the peak potential for easier comparison.

The value of the capacitance at negative potentials for Au (polycrystalline) is higher than reported for Au (100). A simple explanation may be derived from the STM observations which indicates the formation of an organized monolayer of [C₄MIM]⁺ cation on Au (100). Furthermore, the authors indicate that such monolayer only exist on Au (100) and do not occur on other orientations. Such higher capacities may be taken as indication of disordered and consequently more polarisable layer of [C₄MIM]⁺ cation. Difference in the value of capacitance may occur by small reorientation of the cation induced by crystallographic constraints such those on Au (100) stabilized also by the interactions with the anions. The final arrangement is the net result with the nanoscale segregation of the ionic species reported for the bulk probably also occurring at the charged interface.⁴⁸

Direct surface force measurements obtained by Gebbie et al.⁴⁹ reveal a more effectively electrostatical screening of the polycrystalline gold surfaces by the enriched [C₄MIM]⁺ cations layers than [Tf₂N]⁻ anions enriched layers. This may be due to the fact of [C₄MIM]⁺ cations are largely planar, containing a well-defined polar and nonpolar regions, simultaneously exhibiting a lower degree of conformational flexibility when compared with the [Tf₂N]⁻ anions.

The use of polycrystalline electrodes adds complexity to the analysis and interpretation of data, making it difficult to theoretical modelling. Although, the study of polycrystalline planar electrodes have a fundamental importance in understanding the electrical double layer structure involving ionic liquids.

In Fig. 8 the differential capacitance curves measured at Pt/imidazolium ionic liquids interface are represented.

Fig. 8 Differential capacitance curves measured at Pt/imidazolium ionic liquids interface at 303.15 K.

The use of Pt as electrode material introduces significant modifications on the C(E) curve when compared to those obtained for Au. The values of C are considerably lower than those obtained for Au in all three liquids. This trend may also be noticed in data previously reported by other authors.¹⁹ Practically all curves are nearly flat with potential; only for [BF₄]⁻ a small maximum is visible around 0.0 V vs. Ag. Since the differences between Au and Pt are visible for all liquids it may be suggested that the interaction of the IL constituents with the metallic surface strongly affects the capacitive behaviour of the interface.

The results obtained at Pt electrode contrast the behaviour of [C₄MIM][BF₄] and [C₄MIM][PF₆] on Au (polycrystalline). It should be pointed out that structural alterations of the surface such as potential induced reconstruction did not cause significant modifications on the capacitance micelle-like structure adsorption of [C₄MIM]⁺ at negatively charged surface. Through columbic forces including π interactions, lead to parallel orientations of the imidazolium rings which may suffer crystallographic reorientations (only visible on Au (100)). An analogous study involving the effect of changing the electrode potential on the EDL of [BMIM][NO₃] ionic liquids at planar electrodes reveal that the NO₃⁻ ion dominates the response under both positive and negative electrode polarization.³⁰ This suggestion may be extrapolated to these results and it may be further suggested that, for each electrode material, the major contribution for the potential dependence of the C(E) at least positive potentials is made by the anion and its interactions with the cation. This hypothesis is corroborated by the data obtained for C(E) curves of liquid containing the same anion but varying the alkyl side chain of the imidazolium cation. Fig. 9 summarizes the potential dependence of the alkyl side of the imidazolium cation on C(E) curves.

Fig. 9 Capacitance curves measured at Pt/[Tf₂N] imidazolium ionic liquids interface.

The results follow an expected trend except for the liquid [C₆MIM][Tf₂N] that shows a value of capacity close to that obtained for [C₂MIM][Tf₂N]. Similar trend is observed at gold electrodes (results not shown).

Scanning tunneling microscopy (STM) measurements indicate that [C₄MIM]⁺ are persistently adsorbed on the electrode, particularly at negative charge. The adsorption of [C₄MIM]⁺ at positive charge is attributed to the overcoming of unfavourable electroactive interactions, by the short range van der Waals interactions with the electrode.⁵⁰

It is not easy to rationalize the data in terms of the size of the imidazolium side chain because the possible conformation and hydrophobic interactions of the chain on interface.

Alam et al.⁵¹ reported that capacitance decreases with increasing the length of the alkyl group attributed to the smaller value of ε with increasing the length of alkyl group in [C_nMIM][BF₄] n = 2, 4 and 8.

Lockett el al.¹⁹ studied the effect of the alkyl chain length on the differential capacitance curves for liquids with the same imidazolium cations with the chloride anion on GC surfaces. The results follow the trend C [C₂MIM]⁺ > C [C₄MIM]⁺ > C [C₆MIM]⁺.

Recently, molecular dynamics simulation of the interfacial structure at the liquid/vacuum interface of [C_nMIM][PF₆] on a graphite electrode was performed by Dou et al.⁵² The results showed that:

- [C₄MIM]⁺ ionic liquids follow a monolayer ordering arrangement;

- The imidazolium rings tend to be parallel and packed closely increasing the charge at the surface, and consequently increasing the differential capacitance values.

AFM force curves as function of potential performed by Zhang et al.⁵³ have demonstrated the existence of charged interior layers and neutral exterior layers involving a total of three to four layering structures at the Au (111)/[C₄MIM][PF₆] ionic liquid interfaces. The EDL structure is restricted within the interior layers, corroborating the theoretical results obtained by Dou et al.⁵²

The force – separation profiles measured by AFM suggest a multilayered arrangement at the Au (111)/IL interface dependent on the applied potential.⁵⁴

Despite the lack of direct structural studies focusing the interface between an electrode and ionic liquids, the ion densities profiles obtained in several experimental studies point to a pronounced oscillatory ionic structure with a multilayered arrangement at charged flat surfaces.^55,56

The role of the anion, cation alkyl chain length and electrode surface on the C(E) curves obtained in this work highlights the importance of the strong correlation effects that arises from the coulombic and short-range ion–ion interactions. It is also crucial to take into account the electrode structural effects on ions orientation, being all these interactions modulated by the applied potential. AFM measurements also evidenced the dependence of the surface nanostructuring of the ionic liquid with the magnitude of the applied potential.⁵⁴

The C(E) curves also confirm that ionic liquids electrostatically screen the charged surfaces through the strong ion–surface interactions inducing ion ordering leading to an alternating cation–anion multistructure layering.^57,58 In addition, the ionic liquid's molecular structure and the impact in their surface-induced orientation should also include the complex interplay of coulomb, van der Waals, dipole, hydrogen bonding, and steric interactions.⁵⁹

Conclusions

In summary, in this work the effect of the electrode material on the EDL capacitance of a series of RTILs electrolytes was studied. The flat curves of the differential capacitance as function of the electrode potential obtained are in contrast with the U-, bell-, or the camel shaped curves observed in many theoretical, simulation, and experimental studies of RTILs.

The shape of the curves obtained at the Au interfaces differs from C(E) curves obtained at Pt interfaces pointing to the important role that the surface play in shaping the EDL structure.

Besides the substrate effect, it is also interesting to examine the effect of the cations and anions structure at the IL/electrode interface on the differential capacitance curve shape assessment. The results demonstrate that the increase in the alkyl chain length do not affect the general shape of the differential capacitance curve, however, the absolute value does not vary in a systematic way probably due to constraints on the conformation of the chain in the interface. The results obtained do not follow entirely the trend found in the literature for IL constituted by the same imidazolium cation but with smaller anions such Cl⁻ and [BF₄]⁻. Changing the anion to [Tf₂N]⁻, non-spherical, multidendate species, further complicates the differential capacitance vs. alkyl chain length dependence.

The path towards a model that accurately describe the structure of the double layer will remains a multidisciplinary field where experimental studies meet the theoretical simulations and predictions.

Acknowledgements

This research was carried out with the financial support of FCT-CIQUP-Line 4 (PEst-C/QUI/UI0081/2013) and Renata Costa acknowledges a Post-Doc scholarship awarded by FCT (SFRH/BPD/89752/2012).

Notes and references

1. L. Barrosse-Antle, A. Bond, R. Compton, A. O. Mahony, E. Rogers and D. Silvester, Chem.–Asian J., 2010, 5, 202.
2. A. Fernandes, M. Rocha, M. Freire, I. Marrucho, J. Coutinho and L. Santos, J. Phys. Chem. B, 2011, 115, 4033.
3. R. Seoane, S. Corderí, E. Gómez, N. Calvar, E. González, E. Macedo and A. Domínguez, Ind. Eng. Chem. Res., 2012, 51, 2492.
4. S. Aparicio, M. Atilhan and F. Karadas, Ind. Eng. Chem. Res., 2010, 49, 9580.
5. J. Lopes and A. Pádua, Ind. Eng. Chem. Res., 2010, 49, 9580.
6. A. Pádua, M. Gomes and J. Lopes, Acc. Chem. Res., 2007, 40, 1087.
7. W. Zheng, A. Mohammed, L. Hines, J. Xiao, O. Martinez, R. Bartsch, S. Simon, O. Russina, A. Triolo and E. Quitevis, J. Phys. Chem. B, 2011, 115, 6572.
8. H. Ohno, Electrochemical aspects of ionic liquids, J. Wiley, 2005.
9. M. Buzzeo, R. Evans and R. Compton, ChemPhysChem, 2004, 5, 1106.
10. R. Kawanoa, H. Matsuib, C. Matsuyamaa, A. Satoa, Md. Susan, N. Tanabeb and M. Watanabe, J. Photochem. Photobiol., A, 2004, 164, 87.
11. G. Feng, D. Jiang and P. Cummings, J. Chem. Theory Comput., 2012, 8, 1058.
12. D. Wei and A. Ivaska, Anal. Chim. Acta, 2008, 607, 126.
13. V. Borgela, E. Markevicha, D. Aurbacha, G. Semraub and M. Schmidt, J. Power Sources, 2009, 189, 331.
14. A. Abbott and K. McKenzie, Phys. Chem. Chem. Phys., 2006, 8, 4265.
15. Y. Su, Y. Fu, Y. Wei, J. Yan and B. Mao, ChemPhysChem, 2010, 11, 2764.
16. J. Lopes and A. Pádua, J. Phys. Chem. B, 2006, 110, 7485.
17. E. Bodo, L. Gontrani, R. Caminiti, N. Plechkova, K. Seddon and A. Triolo, J. Phys. Chem. B, 2010, 114, 16398.
18. M. Alam, J. Masud, Md. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2011, 115, 19797.
19. V. Lockett, M. Horne, R. Sedev, T. Rodopoulos and J. Ralstona, Phys. Chem. Chem. Phys., 2010, 12, 12499.
20. R. Costa, C. Pereira and F. Silva, Phys. Chem. Chem. Phys., 2010, 12, 11125.
21. V. Lockett, R. Sedev, J. Ralston, M. Horne and T. Rodopoulos, J. Phys. Chem. C, 2008, 112, 7486.
22. X. Ge, C. Fuab and S. Chan, Phys. Chem. Chem. Phys., 2011, 13, 15134.
23. M. Alam, M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2008, 112, 16600.
24. M. Islam, M. Alam and T. Ohsaka, J. Phys. Chem. C, 2008, 112, 16568.
25. M. M. Islam, M. T. Alam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2009, 113, 3386.
26. D. Caprio, M. Valiskó, M. Holovko and D. boda, Mol. Phys., 2006, 104, 3777.
27. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545.
28. K. Oldham, J. Electroanal. Chem., 2008, 613, 131.
29. R. Bell, M. Pópolo, T. Youngs, J. Kohanoff, C. Hanke, J. Harper and C. Pinilla, Acc. Chem. Res., 2007, 40, 1138.
30. G. Feng, J. Zhang and R. Qiao, J. Phys. Chem. C, 2009, 113, 4549.
31. S. Baldelli, J. Phys. Chem. B, 2005, 109, 13049.
32. S. Rubero and S. Baldelli, J. Phys. Chem. B, 2004, 108, 15133.
33. S. Baldelli, Acc. Chem. Res., 2008, 41, 421.
34. C. Romero and S. Baldelli, J. Phys. Chem. B, 2006, 110, 6213.
35. L. Cammarata, S. G. Kazarian, P. A. Salter and T. Welton, Phys. Chem. Chem. Phys., 2001, 3, 5192.
36. K. Seddon, A. Stark and M. Torres, Pure Appl. Chem., 2000, 72, 2275.
37. M. Earle, C. Gordon, N. Plechkova, K. Seddon and T. Welton, Anal. Chem., 2007, 79, 758.
38. B. Boukamp, Tech. Mess., 2004, 71, 454.
39. G. Brug, A. Eeden, M. Rehbach and J. Sluyters, J. Electroanal. Chem., 1984, 176, 275.
40. M. Sluyters-Rehbach, Pure Appl. Chem., 1994, 66, 1831.
41. M. Orazem, P. Shukula and M. Membrino, Electrochim. Acta, 2002, 47, 2027.
42. J. Vila, L. Varela and O. Cabeza, Electrochim. Acta, 2007, 52, 7413.
43. R. Levie, Electrochim. Acta, 1965, 10, 113.
44. A. Motheo, A. Sadkowski and R. Neves, J. Electroanal. Chem., 1997, 430, 253.
45. M. Gnahm, T. Pajkossy and D. Kolb, Electrochim. Acta, 2010, 55, 6212.
46. Y. Su, Y. Fu, J. Yan, Z. Chen and B. Mao, Angew. Chem., 2009, 121, 5250.
47. M. Alam, M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2007, 111, 18326.
48. K. Shimizu, C. Bernardes, A. Triolo and J. Lopes, Phys. Chem. Chem. Phys., 2013, 15, 16256.
49. M. Gebbie, M. Valtiner, X. Banquy, E. Fox, W. Henderson and J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 9674.
50. H. Tokuda, K. Hayamizu, K. Ishii, M. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103.
51. M. Alam, J. Masud, Md. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2011, 115, 19797.
52. Q. Dou, M. Sha and G. Wu, J. Phys.: Condens. Matter, 2011, 23, 175001.
53. X. Zhang, Y. Zhong, J. Yan, Y. Su, M. Zhang and B. Mao, Chem. Commun., 2012, 48, 582.
54. R. Hayes, N. Borisenko, M. Tam, P. Howlett, F. Endres and R. Atkin, J. Phys. Chem. C, 2011, 115, 6855.
55. M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schröder, V. Honkimäki, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424.
56. R. Atkin and G. Warr, J. Phys. Chem. C, 2007, 111, 5162.
57. I. Malham and L. Bureau, Soft Matter, 2010, 6, 4062.
58. R. Hayes, G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2010, 12, 1709.
59. E. Castner, J. Wishart and H. Shirota, Acc. Chem. Res., 2007, 40, 1217.

---