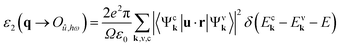Electronic and optical properties of silicene nanomeshes

Abstract

We have investigated the electronic and optical properties of silicene nanomeshes (SNMs) using first-principle calculations. The emerging information indicates that the resulting properties are sensitive to the width (W) of the silicon chains between neighboring holes. Our results show that the bandgaps of SNMs with an odd W value remain closed. On the contrary, bandgaps are opened in SNMs with an even W value at the Γ points. Most importantly, SNMs possess a broad frequency photoresponse ranging from far infrared (0 eV) to ultraviolet (10 eV) and the optical properties of SNMs can be tuned by varying the value of W. Our results reveal that SNMs, as silicon-based materials, have a significant potential for electronic, photonic, and photovoltaic applications.

---

1 Introduction

Graphene, one of the most promising carbon-based materials with numerous potential applications, has been extensively studied since it was first obtained by Novoselov et al.,^1,2 but cannot be used in transistor architectures because it is a semimetal with a closed bandgap.^3–6 As a consequence, currently there is a surge in attempts to open the bandgap to make semimetallic graphene suitable for electronic applications, e.g. by being cut into nanoribbons,^7–9 by applying a transverse electric field^10–13 and by absorbing atoms in a regular pattern,^14–19 and these methods meet particular nanotechnology challenges. Recently, graphene antidot lattices (i.e. graphene nanomeshes) have been first proposed by Pedersen et al.²⁰ as a strategy to open the bandgap of graphene around the Fermi level. Since then, graphene nanomeshes have been extensively explored.^{3–6,20–30} Previous results show that the opened gap is associated with the size, shape, and symmetry of the nanomeshes.^{5,20–25,31,32} Exhilaratingly, essential experimental progresses in graphene nanomeshes have been achieved. Graphene nanomeshes have been successfully fabricated via electron beam lithography, block copolymer lithography, and self-assembly of mono-disperse colloidal microspheres.^4,33–37

Notably, Si, as a fundamental material, has played a key role in modern electronics industries. However, in photovoltaic industries, Si with an indirect bandgap of 1.1 eV (ref. 38) cannot make use of the energy below the gap.³⁹ In addition, the carrier mobilities of Si are not balanced. The electron mobility (1400 cm² v⁻¹ s⁻¹) is much larger than the hole mobility (450 cm² v⁻¹ s⁻¹).^40,41 The unbalanced charge-transport property results in hole accumulation⁴² in Si solar cell devices. Consequently, it reduces the photon to current conversion efficiency.⁴³ Recently, silicene, the silicon-based counterpart of graphene with a linear dispersion of the band structure at the Fermi level, has been investigated quite intensively. Its extremely high carrier mobility makes it an ideal material, especially for electronic devices.^44–50 It is useful for photovoltaic materials that the mobilities of the holes and electrons of silicene are in one order of magnitude (10⁵ cm² v⁻¹ s⁻¹).⁵¹ The more balanced transport of holes and electrons results in a better device performance.⁴³ However, the pristine silicene is similar to graphene in that it lacks a band gap, which would be necessary for its use in transistor architectures.^3–6,28,52

Therefore, in this work we introduce periodic holes in silicene to form silicene nanomeshes (SNMs) by first-principle calculations. Furthermore, we explore the electronic and optical properties of the SNMs via density functional theory.

2 Model and methods

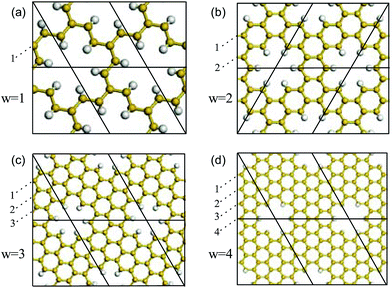
The SNMs with periodically removed hexagonal silicon chains are shown in Fig. 1. The rhombus represents the super cell of the SNMs. W indicates the width of the silicon chains between the neighbouring holes. Each type of SNM is defined as {1,W}, with one removed hexagonal silicon chain (1) and the width (W) of the silicon chains between the neighboring holes.²¹ The dangling bonds are passivated by hydrogen. In the structures, the yellow and gray atoms represent silicon and hydrogen, respectively. The structural optimizations, band structures and optical spectra were calculated by first-principle calculations via the CASTEP code^53–57 under periodic boundary conditions. The generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional⁵⁸ is employed to describe the exchange and correlation potentials. The Vanderbilt ultrasoft pseudopotential⁵⁹ is used in the reciprocal space. The energy cutoff for the plane-wave expansion is set to 260 eV and 400 eV for the band structure and optical spectra calculations, respectively. The Monkhorst–Pack k-point mesh⁶⁰ of 21 × 21 × 1 is set to provide sufficient accuracy in the Brillouin zone integration. SNM planes are separated by the vacuum of 16 Å in our calculations to avoid the effect of layers.

Fig. 1 Structures of silicene nanomeshes (SNMs) with a varying width, W, in the silicon chains between the neighbouring holes, labeled as {1,1} (a), {1,2} (b), {1,3} (c), and {1,4} (d). The 1 in {1,W} represents a removed hexagonal silicon chain in the SNMs. In the structures, the yellow and gray atoms represent silicon and hydrogen, respectively. The numbers of the dashed lines illustrate the values of W.

In the CASTEP calculations, the local field is not considered and therefore excitonic effects are not taken into account.^53–57 The imaginary part of the dielectric constant can be expressed as:

where q is the wave-number vector of electromagnetic radiation. The (q → 0_û,hω), Ω defines the long wavelength limit. ψ and E are the eigenstate and eigenvalue of electron, respectively. δ is the Kronecker delta. Ω and ε₀ are the volume of the super cell and the dielectric constant of the free space, respectively. c and υ represent the conduction band and the valence band, respectively. u and r indicate the polarization direction of the electric field and the position vector, respectively. The sum over k samples the whole region of the Brillouin zone (BZ) in the k space. ε₂(ω) is calculated by summing all transitions between the occupied and unoccupied electronic states in the Brillouin zone.^61,62 Since the real and imaginary parts are linked by a Kramers–Kronig transform, the real part of the dielectric function, ε₁(ω), can be obtained from ε₂(ω). Actually, as long as these two quantities, ε₁(ω) and ε₂(ω), are obtained, the absorption coefficient, η, can be evaluated via the formula, , where c is the speed of light and κ is the imaginary part of the refractive index, . In this work, we calculate the optical properties under unpolarized (U) and polarized (P) light conditions. E_‖ polarization is defined if the electric field is parallel to the SNMs and the E_⊥ polarization is defined if the electric field is perpendicular to the SNMs.^63–65 We have only calculated the in-plane absorption since the SNMs are two-dimensional materials which are discontinuous in the perpendicular direction.⁶⁵

3 Results and discussion

Fig. 2 illustrates the band structures of the SNMs calculated by the CASTEP code.^53–57 After introducing the holes into silicene, the symmetry of the unit cell of the SNMs with an odd W value is reduced from P-3M1 (silicene) to P-3. However, the space group of the SNMs with an even W value changes from P-3M1 (silicene) to P-31M. But they still belong to the hexagonal group. Therefore, the area surrounded by the Γ–M–K–Γ path is the irreducible Brillouin zone of the two dimensional SNMs. As expected, the ones with an even W value have open bandgaps (0.64 eV and 0.32 eV for the {1,2} and {1,4} SNMs, respectively) around the Fermi level at the Γ points, as shown in Fig. 2(b) and (d). As far as we know, hydrogen passivation has a significant influence on the defects of silicene,⁶⁶ but Pedersen et al. have proven that the antidot lattice, with regular holes in the graphene sheet, has important features as the size of the gap can be tuned via the antidot lattice parameters and the periodic perturbation turns the semimetal into a semiconductor.²⁰ Compared to the SNMs with an odd value of W, it is found that SNMs with an even W value have a partially broken translational symmetry and the Dirac points are hybridized by the perforation and the passivated hydrogen,^4,28,66–68 which lead to gaps.^{5,20–25,31,32,69,70} Hence, the energy gap opened in the SNMs results from the combination of quantum confinement and the periodic perturbation potential.^{22,25–28,69,70} Consequently, SNMs have a significant potential to be used as a transistor in logic applications and the small bandgap may be exploited to make new photonic devices for far infrared light detection. On the contrary, the SNMs with an odd W value remain semimetallic with Dirac cones in the Brillouin zone as shown in Fig. 2(a) and (c). Ouyang et al. have discussed that the closed bandgap at the k-point is related to the topological connection (bonding) between the carbon atoms in the graphene nanomeshes.²¹ In addition, the modulation behavior of the band gap, as a function of W in the SNMs, is similar to that in the graphene nanomeshes.²¹ Furthermore, we note that silicene has a linearly dispersing electronic band structure at the Fermi level, which contributes to its high carrier mobility.⁵¹ Though the introduced nanomeshes in silicene would reduce the mobilities of silicene, the valence band and the conduction band still preserve the symmetry and the linear dispersion around the Fermi level, as shown in Fig. 2. In this case, the high mobilities will still preserve well in the SNMs. Moreover, materials with higher mobilities can extremely improve the device performance.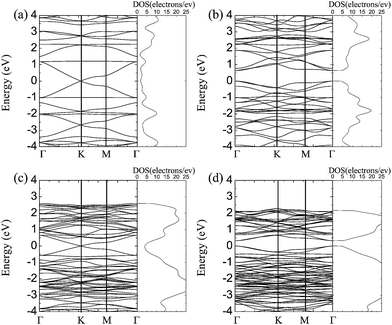

Fig. 2 Band structures and density of states (DOS) of the {1,1} (a), {1,2} (b), {1,3} (c), and {1,4} (d) SNMs.

Fig. 3 shows the imaginary part of the dielectric function, ε₂(ω), of the SNMs. A striking difference between the optical spectra of the SNMs and Si is that, not only for the polarized light but also for the non-polarized light, ε₂ of the SNMs has a nonzero value from a frequency of 0 eV, compared to that of Si which has a nonzero value from a frequency of 1.1 eV, which is the threshold for direct optical transitions between the valence band maximum and the conduction band minimum.⁷¹ In Fig. 3(a) and (b) the maximum values of ε₂(ω) for the four types of SNMs lie within the visible to infrared part of the spectrum (<l eV) and the peak positions do not noticeably change for the unpolarized and the E_‖ polarized light. But for the E_‖ polarization, the height of the maximum values of ε₂(ω) doubled compared to the non-polarization. However, a strong anisotropy in the imaginary part of the dielectric function is observed under E_‖ and E_⊥ polarization conditions. In the case of the E_⊥ polarization for the four types of SNMs, the maximum values of ε₂(ω) shift to a very high frequency region (∼8 eV).

Fig. 3 Imaginary part of the dielectric function ε₂(ω) of the SNMs for unpolarized (U) (a) and E_‖ (b) and E_⊥ (c) polarized (P) light. The black, red, green, and blue lines correspond to {1,1}, {1,2}, {1,3}, and {1,4}, respectively.

The real part of the dielectric function, ε₁(ω), is shown in Fig. 4. It is found that Fig. 4(a) and (b) also show the same change tendency of ε₁(ω) ranging from 0 eV to 6 eV, but the values of ε₁(ω) in Fig. 4(b) are higher than the ones in Fig. 4(a) under polarized conditions. One important quantity of ε₁(ω) is the zero frequency limit, ε₁(0), which represents the dielectric response to the static electric field. Fig. 4(a) and (b) show the inverse relationship between the band gap and ε₁(0). A smaller energy gap yields a larger ε₁(0) value.^71,72 This can be understood based on the equation .^71,72 In Fig. 4(b), ε₁(0) describes the varying values ranging from 4.56 to 14.81 for the four types of SNMs under the polarized condition. A higher value in the static dielectric constants leads to larger available free charge carriers.⁶¹ For example, in Fig. 4(b) under E_‖ polarization conditions the two types of SNMs ({1,1} and {1,3}) with Dirac points have higher values of 11.51 and 14.81, respectively. However, the SNM with W = 2 is a semiconductor with a larger bandgap about 0.64 eV and a lower corresponding ε₁(0) value of 4.56 for the E_‖ polarized light.

Fig. 4 Real part of the dielectric function, ε₁(ω), of the SNMs for unpolarized (U) (a) and E_‖ (b) and E_⊥ (c) polarized light. The black, red, green, and blue lines correspond to {1,1}, {1,2}, {1,3}, and {1,4}, respectively.

Fig. 5 describes the absorption spectra, which indicate the fraction of the energy lost by the light wave when it passes through the material.⁵⁷ It is clearly found that the absorption coefficients of the four types of SNMs have nonzero values from 0 eV under E_‖ polarized and unpolarized light conditions. They absorb light of different frequencies as W varies. It is obvious that the absorption spectra below 1 eV more intuitively correspond to the band structure of the four types of the SNMs around the Fermi level. SNMs with an odd W value reserve the Dirac cones, but their Dirac cones with larger W values become more flat, as shown in Fig. 2(a) and (c). The bandgap of the SNMs decreases as the value of the even W values increases. Therefore, a red shift appears in the absorption spectra of the SNM with W = 3 compared to the one with W = 1, and in the spectra of the one with W = 4 compared to the one with W = 2. In Fig. 5(a), under unpolarized light conditions, the four types of SMNs have three prominent peaks around 2 eV, 4.5 eV, and 8 eV, respectively. The first peak of the four types moves from the far infrared zone to the visible light zone, and the peak values locate from 1 eV to 2 eV as the corresponding W value varies from 1 to 4. In Fig. 5(b), under E_‖ polarization light conditions, the four types of SNMs lack the third peak as shown in Fig. 5(a). However, under E_⊥ polarization conditions, the four types of SNMs only preserve the third prominent peak around 8 eV. In Fig. 5(a)–(c) it can be easily seen that the absorption spectra are enhanced under polarization conditions compared to under non-polarization conditions. But the SNMs prefer to absorb the E_‖ polarized light below 6 eV, while the SNMs only absorb the E_⊥ polarized light around 8 eV.

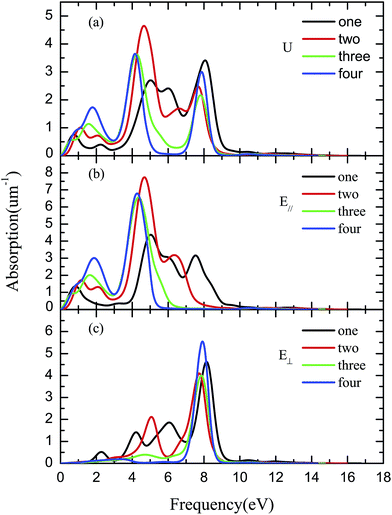Fig. 5 Absorption coefficients of the SNMs for unpolarized (a) and E_‖ (b) and E_⊥ (c) polarized light. The black, red, green, and blue lines correspond to {1,1}, {1,2}, {1,3}, and {1,4}, respectively.

Moreover, Fig. 3–5 all reveal that the optical properties of the SNMs are sensitive to the value of W. Our results show that the SNMs possess a broad frequency photoresponse ranging from 0 eV to 10 eV. We note that a limitation of Si is that it has a band gap of 1.1 eV, which means that photons with an energy below the bandgap are lost.^39,73 Nevertheless, the SNMs can make full use of the solar energy below 1.1 eV. If an SNM-based solar cell can be developed, the utilization of sunlight will be extremely improved. Furthermore, SNMs can be exploited to make new photonic devices for far infrared light detection with an absorption from 0 eV.⁶⁵ In addition, a strong anisotropy in the optical properties is also observed, which is in contrast to the fact that Si is optically isotropic. Polarized dependent optical spectra would make the SNMs more versatile than Si in potential applications.

4 Conclusions

In summary, we have investigated the electronic and optical properties of SNMs. Our results show that the electronic and optical properties of SNMs are extremely sensitive to the W value of the silicon chains between the neighboring holes. The bandgap of the SMNs with an odd W value remains closed. On the contrary, substantial bandgaps are opened in SMNs with an even W value around the Fermi level. Hence, SNMs have a significant potential for applications in electronics, and the SNMs with an even W value, which are semiconductors, can be used for effective field-effect transistors operating at room temperature. SNMs also can be exploited to make new photonic devices for far infrared light detection with an absorption from 0 eV. In addition, our results show that the optical properties of the SNMs are anisotropic under E_‖ and E_⊥ polarized conditions. Furthermore, the optical properties of the SNMs can be tuned by varying W. SNMs, possessing a broad frequency photoresponse ranging from 0 eV to the ultra-violet region 10 eV, can be used for solar energy. Since photovoltaics can make a considerable contribution to solving the energy problem that our society faces,³⁹ SNMs may pave a possible way towards solar cell materials.

Acknowledgements

Zhi-Gang Shao acknowledges the support by the National Natural Science Foundation of China (Grant no. 11105054 and 11274124), PCSIRT (Grant no. IRT1243), China Scholarship Council, and by the high-performance computing platform of South China Normal University. Hongbo Zhao acknowledges the support by the National Natural Science Foundation of China (Grant no. 91026005). Lei Yang acknowledges the support by the “Strategic Priority Research Program” of the Chinese Academy of Sciences (Grant no. XDA03030100). Cang-Long Wang acknowledges the support by the National Natural Science Foundation of China (Grant no. 11304324).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Frisov, Science, 2004, 306, 666–669.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Frisov, Nature, 2005, 438, 197.
3. R. Martinazzo, S. Casolo and G. F. Tantardini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245420.
4. J. Bai, X. Zhong, S. Jiang, Y. Huang and X. Duan, Nat. Nanotechnol., 2010, 5, 190–194.
5. R. Petersen, T. G. Pedersen and A.-P. Jauho, ACS Nano, 2011, 5, 523–529.
6. S. Yuan, R. Roldán, A.-P. Jauho and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085430.
7. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
8. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
9. L. Brey and H. A. Fertig, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235411.
10. E. V. Castro, K. S. Novoselov, S. V. Morozov, N. M. R. Peres, J. M. B. L. dos Santos, J. Nilsson, F. Guinea, A. K. Geim and A. H. C. Neto, Phys. Rev. Lett., 2007, 99, 216802.
11. E. McCann, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 161403.
12. A. Deshpande, W. Bao, Z. Zhao, C. N. Lau and B. J. LeRoy, Appl. Phys. Lett., 2009, 95, 243502.
13. Z. Ni, Q. Liu, K. Tang, J. Zheng, J. Zhou, R. Qin, Z. Gao, D. Yu and J. Lu, Nano Lett., 2012, 12, 113–118.
14. R. Balog, B. Jorgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Laegsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekaer, Nat. Mater., 2010, 9, 315–319.
15. J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401.
16. L. Liu and Z. Shen, Appl. Phys. Lett., 2009, 95, 252104.
17. X.-L. Wei, H. Fang, R.-Z. Wang, Y.-P. Chen and J.-X. Zhong, Appl. Phys. Lett., 2011, 99, 012107.
18. X. Liu, Y. Wen, Z. Chen, H. Lin, R. Chen, K. Cho and B. Shan, AIP Adv., 2013, 3, 052126.
19. R. Wang, X. Pi, Z. Ni, Y. Liu, S. Lin, M. Xu and D. Yang, Sci. Rep., 2013, 3, 1–6.
20. T. G. Pedersen, C. Flindt, J. Pedersen, N. A. Mortensen, A.-P. Jauho and K. Pedersen, Phys. Rev. Lett., 2008, 100, 136804.
21. F. Ouyang, S. Peng, Z. Liu and Z. Liu, ACS Nano, 2011, 5, 4023–4030.
22. J. Lee, A. K. Roy, J. L. Wohlwend, V. Varshney, J. B. Ferguson, W. C. Mitchel and B. L. Farmer, Appl. Phys. Lett., 2013, 102, 203107.
23. F. Ouyang, Z. Yang, S. Peng, X. Zheng and X. Xiong, Phys. E, 2014, 56, 222–226.
24. X. Y. Cui, R. K. Zheng, Z. W. Liu, L. Li, B. Delley, C. Stampfl and S. P. Ringer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125410.
25. H. Jippo, M. Ohfuchi and C. Kaneta, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075467.
26. M. H. Schultz, A. P. Jauho and T. G. Pedersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045428.
27. C.-H. Park, L. Yang, Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2008, 101, 126804.
28. K. Lopata, R. Thorpe, S. Pistinner, X. Duan and D. Neuhauser, Chem. Phys. Lett., 2010, 498, 334–337.
29. W. Oswald and Z. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115431.
30. H. Şahin and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035452.
31. J. A. Fürst, T. G. Pedersen, M. Brandbyge and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115117.
32. H. Y. He, Y. Zhang and B. C. Pan, J. Appl. Phys., 2010, 107, 114322.
33. M. Kim, N. S. Safron, E. Han, M. S. Arnold and P. Gopalan, Nano Lett., 2010, 10, 1125–1131.
34. X. Liang, Y.-S. Jung, S. Wu, A. Ismach, D. L. Olynick, S. Cabrini and J. Bokor, Nano Lett., 2010, 10, 2454–2460.
35. T. Shen, Y. Q. Wu, M. A. Capano, L. P. Rokhinson, L. W. Engel and P. D. Ye, Appl. Phys. Lett., 2008, 93, 122102.
36. S. Heydrich, M. Hirmer, C. Preis, T. Korn, J. Eroms, D. Weiss and C. Schüller, Appl. Phys. Lett., 2010, 97, 043113.
37. A. Sinitskii and J. M. Tour, J. Am. Chem. Soc., 2010, 132, 14730–14732.
38. J. D. Holmes, K. P. Johnston, R. C. Doty and B. A. Korgel, Science, 2000, 287, 1471–1473.
39. H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213.
40. G. W. Ludwig and R. L. Watters, Phys. Rev., 1956, 101, 1699–1701.
41. M. B. Prince, Phys. Rev., 1954, 93, 1204–1206.
42. C. Melzer, E. J. Koop, V. D. Mihailetchi and P. W. M. Blom, Adv. Funct. Mater., 2004, 14, 865–870.
43. G. Li, V. Shrotriya, J. Huang, Y. Yao, T. Moriarty, K. Emery and Y. Yang, Nat. Mater., 2005, 4, 864–868.
44. P. De Padova, C. Quaresima, C. Ottaviani, P. M. Sheverdyaeva, P. Moras, C. Carbone, D. Topwal, B. Olivieri, A. Kara, H. Oughaddou, B. Aufray and G. Le Lay, Appl. Phys. Lett., 2010, 96, 261905.
45. B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109.
46. S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
47. C.-C. Liu, W. Feng and Y. Yao, Phys. Rev. Lett., 2011, 107, 076802.
48. G. G. Guzmán-Verri and L. C. Lew Yan Voon, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075131.
49. F.-B. Zheng, C.-W. Zhang, P.-J. Wang and S.-S. Li, J. Appl. Phys., 2013, 113, 154302.
50. T. P. Kaloni, Y. C. Cheng and U. Schwingenschlögl, J. Appl. Phys., 2013, 113, 104305.
51. Z.-G. Shao, X.-S. Ye, L. Yang and C.-L. Wang, J. Appl. Phys., 2013, 114, 093712.
52. M. L. Trolle, U. S. Møller and T. G. Pedersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 195418.
53. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
54. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
55. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
56. M. C. Payne, M. P. Teter, D. C. Allan, T. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
57. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristallogr., 2005, 220, 567–570.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
60. J. D. Monkhorst and H. J. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
61. S. Kumar Jain and P. Srivastava, J. Appl. Phys., 2013, 114, 073514.
62. N. Singh, T. P. Kaloni and U. Schwingenschlögl, Appl. Phys. Lett., 2013, 102, 023101.
63. J. Kang, J. Li, F. Wu, S.-S. Li and J.-B. Xia, J. Phys. Chem. C, 2011, 115, 20466–20470.
64. Y. Liu, H. Shu, P. Liang, D. Cao, X. Chen and W. Lu, J. Appl. Phys., 2013, 114, 20466–20470.
65. L. Matthes, P. Gori, O. Pulci and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035438.
66. J. Gao, J. Zhang, H. Liu, Q. Zhang and J. Zhao, Nanoscale, 2013, 5, 9785–9792.
67. T. H. Osborn, A. A. Farajian, O. V. Pupysheva, R. S. Aga and L. L. Y. Voon, Chem. Phys. Lett., 2011, 511, 101–105.
68. E. Bekaroglu, M. Topsakal, S. Cahangirov and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075433.
69. C.-L. Lin, R. Arafune, K. Kawahara, M. Kanno, N. Tsukahara, E. Minamitani, Y. Kim, M. Kawai and N. Takagi, Phys. Rev. Lett., 2013, 110, 076801.
70. Y.-L. Song, Y. Zhang, J.-M. Zhang, D.-B. Lu and K.-W. Xu, J. Mol. Struct., 2011, 990, 75–78.
71. L. Guo, S. Zhang, W. Feng, G. Hu and W. Li, J. Alloys Compd., 2013, 579, 583–593.
72. D. R. Penn, Phys. Rev., 1962, 128, 2093–2097.
73. C. Solanki and G. Beaucarne, Energy Sustainable Dev., 2007, 11, 17–23.

---