The dynamics of the conformational changes in the hexopyranose ring: a transition path sampling approach†
Abstract
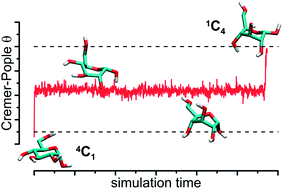
The ring conformation of the hexopyranose-based carbohydrate molecules is one of the central issues in glycobiology. We report the results of the transition path sampling simulations aimed at the detailed description of the dynamic features of these conformational changes. We focused on the α-D- and β-D-glucopyranose molecules (GlcA and GlcB, respectively), treated as model systems. A large number of unbiased dynamic trajectories leading from the 4C1 conformation to the 1C4 one has been collected and subjected to analysis. The results allowed for: (i) identifying the distinct local minima of the free energy corresponding to the states intermediate for the 4C1 → 1C4 transitions; (ii) assigning the time-characteristics to these transitions and intermediate states; (iii) searching for the optimal reaction coordinate based on the Peters–Trout approach (likelihood maximization, LM). Additionally, the structures corresponding to the 4C1 → 1C4 transition states (TS) have been found; surprisingly, in the case of GlcA, the water dynamics has very little influence on the probability of the TS evolution either to 4C1 or to 1C4. The differing result obtained for GlcB (large influence of water dynamics on the behavior of TS as well as the poor applicability of the LM approach for calculation of the reaction coordinate) speaks for slightly different mechanisms of the 4C1 → 1C4 puckering in the molecules of GlcB and GlcA.

 Please wait while we load your content...
Please wait while we load your content...