Power-law rheology characterization of biological cell properties under AFM indentation measurement
Abstract
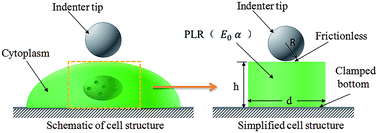
Using finite element modeling, the mechanical properties of biological cells are investigated based on the power-law rheology (PLR) model under atomic force microscopy (AFM) indentation testing. Three different loading modes, including relaxation tests, quasi-static indentation and dynamic indentation are considered. After correcting the effects of the Hertz contact radius and substrate stiffening, the parameters of E0 and α in the PLR model can be accurately determined from all three loading modes under AFM indentation. In addition, for all the three indentation loading modes, the aforementioned two effects are not sensitive to the material model used for the cell (e.g., the values of α and E0) but only depend upon the ratio of the indentation depth to the cell thickness. Because the parameters determined from various loading modes can be validated among each other, the AFM indentation will be a very effective route to accurately determine the cell mechanical properties based on the PLR model.

 Please wait while we load your content...
Please wait while we load your content...