Evolution of transient cluster/droplet size distribution in a heterogeneous nucleation process
Wei Xu,
Zhong Lan,
Benli Peng,
Rongfu Wen and
Xuehu Ma*
Department of Chemical Engineering, Dalian University of Technology, Dalian, China. E-mail: xuehuma@dlut.edu.cn; Fax: +86 411 84986159; Tel: +86 411 84986159
First published on 23rd June 2014
Abstract
The transient nucleation size distribution model was introduced into a water vapor condensation system to investigate the kinetics of the initial condensation stage. It was proven that the growth/decay of clusters was significantly affected by cluster size and contact angles of the condensation surface. As the cluster size increased, the cluster surface area exposed to vapor was also increased, and the attachment/detachment frequencies increased accordingly. As the contact angle decreased to a certain value, the attachment frequency became larger than the detachment frequency, which is beneficial for the growth of clusters. The evolution of cluster/droplet size distribution was also investigated. The results indicated that the transient cluster size distribution of the heterogeneous process translates from a monotonic decreasing to a unimodal distribution with time. Peak value of cluster/droplet population can be observed for a sufficiently long time, and the size distribution curve is found to be close to a lognormal distribution, which is distinctly different from the homogeneous equilibrium distribution. The peak value in the size distribution curve shifts to larger cluster sizes with time, and the absolute value decreases accordingly. It is very similar to the reported experimental results of micron scale droplets, revealing that the subsequent experimental phenomenon at macroscopic scale was the direct result of the further development of the initial cluster/droplet size distribution. The present study investigated the effect of contact angle on the growth/decay of clusters and analyzed the mechanism of the evolution of the cluster/droplet size distribution from the viewpoint of kinetics.
1. Introduction
Nucleation processes can be found in a wide range of applications such as crystallization, metal–organic chemical vapor deposition, frosting, dew formation, nucleate boiling and vapor condensation. The nucleation rate and the size distribution of the newly-formed phase (bubbles, droplets) have drawn significant attention from both academic and practical perspectives. In general, nucleation is treated as a continuous process of cluster growth, where a nucleation free energy barrier is introduced to evaluate the reversible work required to form an initial nucleus. Several theoretical investigations have been conducted to better predict the nucleation rate, amongst the three classic approaches, including the Kelvin model,1,2 the classic kinetic theory,3–5 and density functional method.6–8 The Kelvin equation was used to relate the critical nucleus radius and supersaturation for almost all the nucleation theories, and can also be used to determine the evaporation rates for clusters of a noncritical size.1,2 The classic nucleation theory (CNT) and the modified self-consistent classical model (SCC), on the other hand, are based on capillarity approximation, where the free energy of the critical nucleus was calculated by treating it as a macroscopic droplet with bulk and surface free energies relative to the background vapor.7 Although the specific approach and selected parameters may differ from each other, the theories proposed above were capable to give usable expressions for equilibrium cluster distribution and nucleation rates for condensation and crystallization processes.9–11Meanwhile, it can be easily noticed that the nucleation process can be considerably affected by the presence of solid substrates such as rough surfaces, solid particles, colloidal solids, etc. Indeed, most of the practical nucleation processes occur on solid surfaces, which are referred to as heterogeneous nucleation. It was proven that the contact angle, size and density of the adsorbed foreign particles play a crucial role in controlling the nucleation barrier and growth kinetics of crystal growth.12 The investigation on the cloud condensation nuclei activity of soot aerosols indicated that extremely hydrophobic soot is only expected to act as condensation nuclei under highly supersaturated conditions.13 To theoretically evaluate the effect of solid surface on the nucleation process, the solid–liquid interfacial energy was introduced into the calculation of nucleation free energy, and the heterogeneous nucleation rates can be obtained from the CNT model.14–17 These modified CNT models provide a good prediction of the transient nucleation rates of certain heterogeneous nucleation processes. On the other hand, Monte Carlo (MC) and molecular dynamics (MD) simulation methods have been rapidly developed in recent years, and the assumptions and results in CNT model are supported.18–20 Instead of using the phenomenological capillary approach as adopted in the CNT model, direct molecule–molecule interaction forces are used in MC and MD simulations. According to Oh and Zeng's21 MC simulation, the CNT model may underestimate the critical nuclei size at temperatures close to the triple point. However, the MD results proposed by Diemand22 indicated that the predicted critical sizes match the values from the nucleation theorem quiet well at low temperatures. The MC and MD simulation results are highly affected by the choice of molecular interaction potential model, as suggested by Merikanto et al.23 On the contrary, the CNT model is based on a phenomenological capillary approach, and the related parameters are readily available with sufficient accuracy.
In addition to the widely investigated nucleation rate, the evolution of transient cluster size distribution is also important for nucleation processes. Against this background, Z. Kožíšek et al.24,25 proposed a transient nucleation model to study the nucleation kinetics of different molecules on active sites such as the formation of diamond clusters on Si-substrates,26 the initial crystallization of polymers,27 and the transient nucleation of ethanol28,29 and ethanol–hexanol systems.30 In this model, the transient attachment/detachment frequencies of single molecules to/from the cluster surface were used to describe the growth/decay of cluster size, and then the evolution of cluster size distribution was obtained without any parameter fitting. The transient nucleation model was reasonable to describe the nucleation process from the first principle. It also provided a new method to investigate the mechanism of cluster growth and nuclei formation from the perspective of kinetics rather than the thermodynamic equilibrium theory.
The initial stage of water vapor condensation is a typical heterogeneous nucleation process. In general, the dropwise condensation (DWC) process can be divided into four sequential sub-stages, namely, nucleation, growth by direct condensation, growth by coalescence, and droplet departure because of gravitational force. In the initial nucleation stage, the steam molecules first aggregate in the form of clusters and randomly deposit on the condensing surface acting as the initial nuclei.31,32 The clusters that reach up to the thermodynamic equilibrium critical size can grow even further by direct condensation and coalescence until they reach the departure diameter. Based on the DWC theory, the heat transfer performance of DWC can be considerably affected by the size distribution of the condensate droplets. In addition, the discussion on droplet size distribution has become a very interesting and important topic. For small droplets that grow mainly by direct condensation, size distribution can be obtained by a population balance method, as proposed by Wu,33 Mousa34 and Vemuri.35 For larger droplets that grow mainly by coalescence, a semi-empirical correlation was proposed by Rose.36 In addition, experimental results,37,38 computer simulation methods,39–42 and theoretical models43,44 have also been provided progressively on the size distributions of droplets from the thermodynamic equilibrium critical size to the departure size. However, the size distribution of initial nuclei and its evolution has not been explicitly reported. In addition, the kinetic process of initial nuclei formation is not clear. For nucleation processes, the macroscopic droplets are developed from the sub-critical ones. The size distribution of sub-critical clusters has a significant effect on the development of macroscopic droplets. A better understanding regarding the size distribution of sub-critical droplets can be very helpful in understanding the underlying mechanism of how the macroscopic droplets size distribution is developed, which is an important investigation topic for nucleation processes, including deposition, condensation and crystallization.
In this paper, the transient nucleation size distribution model was introduced into a water vapor condensation system. A series of kinetic equations describing the transient nucleation of water vapor on active sites were solved to obtain the cluster/droplet size distribution. The effect of contact angle on the growth/decay of cluster size was analyzed from the viewpoint of kinetics. The evolution of cluster size distribution and the mechanism of the initial condensation stage were also investigated.
2. Model and computational methodology
The following assumptions were adopted during the development of the mathematical model: (1) the nucleation of initial droplets could only occur at the nucleation sites, and the number of nucleation sites is finite,25 (2) the physical properties of the clusters can be described on the basis of the classic capillarity approximation,45 and the interaction between the surface and the depositing cluster can be evaluated via surface free energy analysis; (3) in the range of low to intermediate densities, the volume occupied by the clusters is negligible as well as cluster–cluster interactions because of the short range of the intermolecular forces.46 The growth of clusters can be treated as a binary reaction between the n-sized cluster (defined as a cluster composed of n molecules) and monomer,42,47 as indicated by eqn (1):
 | (1) |
Based on the abovementioned assumptions, the evolution of cluster distribution can be written as follows:28,48,49
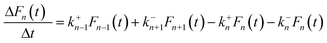 | (2) |
Based on the kinetic molecular theory, k+n can be calculated as follows:25
 | (3) |
Sn is the surface area that was exposed to the vapor phase for an n-sized cluster. It is necessary to note that depending on the considered shape, the heterogeneously formed cluster may have different spatial interfaces and surface areas. Typically, there are three possible shapes of the clusters, namely cap-shaped, lens-shaped and disk-shaped.48 Based on the classic capillarity approximation,45 the shape of a cluster can be approximated as a spherical cap for a water vapor condensation system. Sn can then be calculated as follows:
 | (4) |
 | (5) |
Activation energy E is an important parameter for the calculation of molecular attachment frequencies. The lack of E information has imposed restrictions on the application of the present model in various condensation systems. Fortunately, the wide spread use of molecular dynamics simulation (MD) has provided an effective route to measure these physico-chemical properties on the molecular scale. Based on a MD simulation method, Tsuruta50 reported that the activation energy E for water can be expressed as follows:
| E = [(4 − β)/2(2 − β) − 1]kBTv | (6) |
| B = 2(vl/vg)1/3 | (7) |
k−n can then be calculated by the local equilibrium principle:25,51
 | (8) |
Feqn = Ns![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Wn/kBTc), (n > 1) exp(−Wn/kBTc), (n > 1)
| (9) |
For homogeneous nucleation processes, Wn can be expressed based on the classic capillarity approximation as follows:45,49
Wn = −nkBTc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S + σlvSn S + σlvSn
| (10) |
For a heterogeneous nucleation process, the interaction between the surface material and clusters should also be included. That gives us the following expression:
Wn = −nkBTc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S + σlvSn + (σsl − σsv)S′n S + σlvSn + (σsl − σsv)S′n
| (11) |
 | (12) |
The model system described by eqn (2) constitutes thousands of coupled ordinary differential equations (ODEs). The direct Euler method was implemented in a C-language program to solve the ODEs and obtain the transient cluster size distribution. The system was initialized with an initial condition of F1(0) = Ns and Fn(0) = 0 (n > 1). k+n and k−n were then calculated according to eqn (3) and (8), respectively. An appropriate time interval Δt was chosen to determine the variation of n-sized cluster number densities, and the cluster size distribution Fn(t) was reassigned after each time step by the formula of F′n(t) = Fn(t) + ΔFn(t).
3. Results and discussion
Parameters adopted in the following simulations were: P = 101.3 kPa, S = 1.67, Tv = 373.2 K, Tc = 359.4 K, Ns = 5 × 109 m−2, and α = 25° unless otherwise noted. σc and ρl were determined at temperature Tc. The interface activation energy E was calculated by eqn (6) and (7) under temperature Tv, which is 2.4 × 10−22 J. The maximum cluster size under consideration is 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
3.1 The effect of condensation surface on the growth/decay of clusters
As discussed in the theoretical model section, the growth/decay of the n-sized cluster was decided by the corresponding attachment/detachment frequencies, namely k+n and k−n+1. To understand k+n and k−n+1 more thoroughly, eqn (3) and (8) were rearranged into formulas combining two or three product terms, namely the kinetic part (the first term in eqn (13) and (14)), the surface area part, and the thermodynamic part (the third term in eqn (14)):
 | (13) |
 | (14) |
The kinetic part is mainly governed by vapor pressure, which is deduced from the kinetic molecular theory, representing the intensity of the molecular motion in the bulk vapor phase. The surface area part denotes the surface area of the cluster–vapor interface. According to the surface free energy of the condensation surface, the clusters that are deposited on the surface can spread to a certain degree, yielding different cluster–vapor interface areas (see Fig. 1, Sn increases as α decreases). The thermodynamic part only appears in the calculation of k−n, representing the stability of the clusters. As indicated by eqn (12), the thermodynamic part is directly connected with the contact angle of the condensation surface (see Fig. 2). As the surface free energy of the condensation surface increases (α decreases), the interaction between the surface and cluster becomes more intense, and the re-evaporation probability of the molecules from the cluster surface becomes restricted.
The relationships between k+n, k−n and α are shown in Fig. 3. For k+n, there was only one surface area part connected with α. Hence, it can be predicted that the k+n curve will be identical to the Sn curve. The relationship between k−n and α is more complicated because of the presence of a thermodynamic part. As shown in Fig. 1 and 2, the surface area part was increasing, while the thermodynamic part was decreasing with decreasing α. As a result, k−n first decrease with α until reaching a minimum value, and then start increasing as α further increases.
An intersection point can be observed between the k+n and k−n curves with the same cluster size. Meanwhile, as the cluster size increases, the intersection point shifts to larger contact angles. Finally, no intersection point can be found on the k+n–k−n curves when the cluster size reaches a certain value (n = 1000, for example). Critical size was usually adopted to evaluate the stability of the clusters. Once a cluster achieves the critical size, the addition of another molecule causes a decrease in energy, and the cluster reaches a more stable energy level. This implies that there is a high probability that it will grow to a macroscopic size, and the clusters of critical size can be regarded as condensation nuclei. The critical size can be calculated from thermodynamic equilibrium analysis, and can also be directly observed from the intersection points, as shown in the k+n–k−n curves. The attachment frequency is equal to the detachment frequency at the critical size. For n = 1000 curve, k+n is larger than k−n for all the contact angles, indicating that a cluster of this size is stable even for homogeneous condensation conditions. According to the thermodynamic analysis, critical size is calculated as n* = 407 for a homogeneous nucleation process under the investigated condensation conditions. For n = 10 and n = 100 cases, the correlation between k+n and k−n are different with different contact angles. Because the cluster sizes are smaller than 407, the clusters are thermodynamically unstable for homogeneous and larger contact angle conditions, and k−n is therefore larger than k+n within a larger α range. It is interesting to notice that a smaller contact angle can change the correlation between k+n and k−n curves for the n = 10 and n = 100 cases. As α decreases to a certain value, k+n becomes larger than k−n, indicating that the cluster reaches a more stable energy level. As a result, the critical size can be reduced on a condensation surface with a relatively small contact angle. Considering that a higher k+n is preferred for the growth of clusters, a smaller α is favorable for the nucleation process.
3.2 Evolution of cluster/droplet size distribution during a heterogeneous nucleation process
The evolution of cluster/droplet size distribution Fn(t) is shown in Fig. 4. It was found that F1(t) rapidly decreases with t (see Fig. 4b, n = 1), indicating that active nucleation sites were gradually occupied by the clusters of different sizes. Interestingly, the variation of other Fn(t) were distinctly different from F1(t). For an n-sized cluster, Fn(t) first increases with t until reaching a maximum value, and then decreases rapidly after that. As expressed by eqn (2), the increment of Fn(t) after each time step can be divided into four parts. For F2(t), at shorter time, F1(t) is large enough, and ΔF2(t) was positive, which increased F2(t) accordingly. However, as t increased, F1(t) decreased gradually with F2(t) increasing conversely, and ΔF2(t) decreases accordingly. As t increased even further, ΔF2(t) decreased to zero, and a maximum value of F2(t) appeared. After that, ΔF2(t) decreased even further to negative values, and F2(t) started to decrease. The abovementioned discussion was also applicable to other Fn(t) ∼ t cases. The difference was that, as cluster size n increased, the maximum value of Fn(t) would appear at a relatively longer time.The Fn(t) ∼ n relationship at different simulation times are shown in Fig. 4c. It can be found that the relationship between Fn(t) and n was also t-related. At a short simulation time, Fn(t) monotonously decreased with n, and the maximum value of the Fn(t) ∼ n curve was obtained at F1(t). However, as t increased, the maximum value of the Fn(t) ∼ n curve shifted from F1(t) to larger cluster sizes, and the Fn(t) ∼ n curve translated from a monotonic decreasing to a unimodal distribution. For a relatively long simulation time, Fn(t) first increased with n until a maximum value achieved, and then Fn(t) decreased afterwards. The nucleation sites were finite in the heterogeneous process, the distribution of smaller clusters was therefore suppressed, and finally, the cluster size distribution of the heterogeneous process translated to a unimodal distribution.
In the classical condensation heat transfer theory, the size of the condensate liquid was usually considered by its radius, instead of the number of molecules it contained. Cluster/droplet size n can be converted to the curvature radius r by the following equation:
 | (15) |
The curvature radius may be preferred in the thermodynamic calculations. However, it cannot be directly detected in experiments. The detectable radius was therefore used in the following discussion, where rdet was defined as the projected radius of the cluster/droplet. rdet is equal to r when the contact angle is larger than 90°. Otherwise, the relationship between rdet and r can be expressed based on the following geometric relationship:
rdet = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α
| (16) |
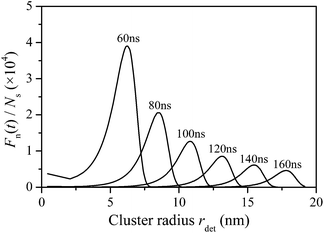
Cluster/droplet size n was converted to rdet by eqn (15) and (16), and the results are shown in Fig. 5. Again, peak values can be observed in the obtained curves. It was also interesting to observe that the radius distribution is similar to a lognormal distribution, which is in accordance with the results reported by Song et al.31 Based on the experimental images of steam condensation on magnesium surface, Song found that the primary initial droplets with a radius of several nanometers have a lognormal distribution feature. The obtained results show good agreement with the literature.
At 60 ns, the peak value appears at rdet = 6.23 nm, where the corresponding curvature radius is 14.75 nm. The critical cluster size calculated by thermodynamic equilibrium theory is 1.45 nm under simulated conditions. Beyond this limit, clusters can remain stable and translate into micro droplets. Consequently, most nucleation sites were already occupied by stable initial droplets at that time. It only took about several nanoseconds or less to complete the entire nucleation process under the simulated conditions. The widely adopted assumption39,42 that nucleation sites were instantaneously occupied by initial droplets of critical size is therefore acceptable. However, it may be appropriate to neglect the waiting time for one cluster to grow up to a critical droplet, the initial droplet size distribution cannot be ignored. By now, multiple scale simulations on dropwise condensation start from the same initial condition–initial droplet of the same critical size. Based on the abovementioned simulation results, this assumption appears questionable. Instead of uniform critical size, the size distribution of the initial cluster/droplet is similar to a lognormal distribution.
It can also be observed that the peak value of the Fn(t) ∼ rdet curve shifts to a larger radius as the simulation continues, while the absolute value decreases accordingly. This phenomenon has been observed in experiments by different researchers, although the results reported were usually restricted within the micron scale. Kumomi and Shi52 observed that the controlled solid-phase crystallization of a-Si thin films results in a log-normal crystallite size distribution (CSD), and the CSD shifts and broadens with time reducing its peak height. The condensation of moist air on a copper surface was reported by Ma et al.,32 and a series of droplet size distributions were obtained, which are redrawn in Fig. 6. The similar trend of size distribution evolution can be found between Fig. 5 and 6. The simulation results were thus proven to be reasonable. Most importantly, the physical significance of the experimental phenomenon within the micro scale was revealed by the abovementioned simulation results. The approximate lognormal distributions already exist in the cluster/droplet size distributions when nucleation occurs. In addition, the subsequent experimental phenomenon was a direct result of the further development of the cluster/droplet size distribution.
A more detailed discussion of Fig. 5 is as follows. At 140 ns, the peak value appears at rdet = 15.47 nm. 20 ns later, the peak value shifts to 17.80 nm. The radius of the majority of droplets grows up to 2.33 nm within 20 ns. The simulation results can be compared with that calculated by the heat transfer theory. Based on heat transfer resistance analysis,34,35 the growth rate of droplet radius can be expressed as follows:
 | (17) |
According to eqn (17), the projected radius of a droplet with a radius of 15.47 nm will increase up to 16.04 nm within 20 ns under the simulated conditions. The calculated result was clearly lower than the simulated result. As the heat transfer resistance for a hemispherical droplet is not considered in the simulation process, the obtained droplet growth rate is therefore greater than the calculated growth rate. In other words, the heat transfer resistances come into play when the droplet size gets large enough, which makes it inappropriate to extend the simulation process to even greater droplet sizes. One possible solution to this problem is to integrate the transient size distribution model with the heat transfer resistance analysis process. The cluster/droplet size distribution at the initial condensation stage can be first obtained by the kinetic model and then the simulation process can be switched to a macroscopic heat transfer model to investigate the subsequent evolution of the droplet size distribution. More detailed simulations based on this idea will be conducted in the future.
4. Conclusions
The transient cluster size distribution model was introduced into a water vapor condensation system to study the kinetics of the initial condensation stage. The attachment/detachment frequencies of molecules to/from the cluster surface for the homogeneous/heterogeneous nucleation processes were compared, and the evolution of the cluster/droplet size distribution was investigated.The growth/decay of the clusters was significantly affected by the surface free energy of the condensation surface. When an n-sized cluster deposited on a surface with a relatively small contact angle, the cluster surface area exposed to vapor was considerably increased, yielding a higher attachment frequency of steam molecules. Meanwhile, as the interaction between the surface and cluster became more intense, the re-evaporation of the molecules from the cluster surface was restricted as compared with a homogeneous process. Consequently, as the contact angle decreased to a certain value, the attachment frequency became larger than the detachment frequency.
The transient cluster/droplet size distribution of heterogeneous nucleation was time dependent. At a short simulation time, Fn(t) monotonously decreased with n. As t increased, the maximum value of the Fn(t) ∼ n curve shifted to larger cluster sizes, and Fn(t) ∼ n curve translated from a monotonic decreasing to a unimodal distribution. The Fn(t) curve at a sufficiently long time was close to lognormal distribution, which was distinctly different from the homogeneous equilibrium distribution. A similar evolution trend of the radius distribution can be found between simulated nanoscale clusters/droplets and experimental results of micron scale droplets, which revealed that the subsequent experimental phenomenon was the direct result of the further development of the initial cluster/droplet size distribution.
Acknowledgements
The authors greatly appreciate the financial support from the National Natural Science Foundation of China (no.51236002).Notes and references
- J. L. Katz, Pure Appl. Chem., 1992, 64, 1661–1666 CrossRef CAS.
- G. Wilemski, J. Chem. Phys., 1995, 103, 1119–1126 CrossRef CAS PubMed.
- A. Dillmann and G. E. A. Meier, Chem. Phys. Lett., 1989, 160, 71–74 CrossRef CAS.
- A. Laaksonen, I. J. Ford and M. Kulmala, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5517–5524 CrossRef CAS.
- X. M. Bai and M. Li, J. Chem. Phys., 2006, 124, 124707 CrossRef PubMed.
- D. W. Oxtoby and D. Kashchiev, J. Chem. Phys., 1994, 100, 7665–7671 CrossRef CAS PubMed.
- X. C. Zeng, J. Chem. Phys., 1996, 104, 2699–2704 CrossRef CAS PubMed.
- Y. Men and X. Zhang, J. Chem. Phys., 2012, 136, 124704 CrossRef PubMed.
- P. R. ten Wolde and D. Frenkel, Phys. Chem. Chem. Phys., 1999, 1, 2191–2196 RSC.
- P. G. Vekilov, Nanoscale, 2010, 2, 2346–2357 RSC.
- T. Li, D. Donadio, G. Russo and G. Galli, Phys. Chem. Chem. Phys., 2011, 13, 19807–19813 RSC.
- X. Y. Liu, K. Maiwa and K. Tsukamoto, J. Chem. Phys., 1997, 106, 1870–1879 CrossRef CAS PubMed.
- K. A. Koehler, P. J. DeMott, S. M. Kreidenweis, O. B. Popovicheva, M. D. Perrers, C. M. Carrico, E. D. Kireeva, T. D. Khokhlova and N. K. Shonija, Phys. Chem. Chem. Phys., 2009, 11, 7906–7920 RSC.
- M. Qian, Acta Mater., 2007, 55, 943–953 CrossRef CAS PubMed.
- K. K. Varanasi, M. Hsu, N. Bhate, W. Yang and T. Deng, Appl. Phys. Lett., 2009, 95, 094101 CrossRef PubMed.
- M. Qian and J. Ma, J. Chem. Phys., 2009, 130, 214709 CrossRef PubMed.
- M. Qian and J. Ma, J. Cryst. Growth, 2012, 355, 73–77 CrossRef CAS PubMed.
- S. Toxvaerd, J. Chem. Phys., 2002, 117, 10303–10310 CrossRef CAS PubMed.
- S. Toxvaerd, J. Chem. Phys., 2003, 119, 10764–10770 CrossRef CAS PubMed.
- X. M.Bai and M. Li, J. Chem. Phys., 2005, 122, 224510 CrossRef PubMed.
- K. J. Oh and X. C. Zeng, J. Chem. Phys., 1999, 110, 4471–4476 CrossRef CAS PubMed.
- J. Diemand, R. Angélil, K. K. Tanaka and H. Tanaka, J. Chem. Phys., 2013, 139, 074309 CrossRef PubMed.
- J. Merikanto, H. Vehkamäki and E. Zapadinsky, J. Chem. Phys., 2004, 121, 914–924 CrossRef CAS PubMed.
- Z. Kožíšek, P. Demo and M. Nesladek, J. Chem. Phys., 1998, 108, 9835–9838 CrossRef PubMed.
- Z. Kožíšek, P. Demo and K. Sato, J. Cryst. Growth, 2000, 209, 198–202 CrossRef.
- P. Demo, Z. Kožíšek, M. Vanéček, J. Rosa, K. Meykens, M. Nesladek, C. Quaeyhaegens, G. Knuyt and L. M. Stals, Diamond Relat. Mater., 1997, 6, 1092–1096 CrossRef CAS.
- Z. Kožíšek, M. Hikosaka, P. Demo and A. M. Sveshnikov, J. Cryst. Growth, 2005, 275, 79–83 CrossRef PubMed.
- Z. Kožíšek and P. Demo, J. Aerosol Sci., 2009, 40, 44–54 CrossRef PubMed.
- Z. Kožíšek and P. Demo, J. Aerosol Sci., 2009, 40, 802–806 CrossRef PubMed.
- Z. Kožíšek and P. Demo, J. Cryst. Growth, 1998, 194, 239–246 CrossRef.
- T. Y. Song, Z. Lan, X. H. Ma and T. Bai, Int. J. Therm. Sci., 2009, 48, 2228–2236 CrossRef CAS PubMed.
- X. H. Ma, T. Y. Song, Z. Lan and T. Bai, Int. J. Therm. Sci., 2010, 49, 1517–1526 CrossRef CAS PubMed.
- W. H. Wu and J. R. Maa, Chem. Eng. J., 1976, 12, 225–231 CrossRef CAS.
- A. O. Mousa, Int. J. Heat Mass Transfer, 1998, 41, 81–87 CrossRef.
- S. Vemuri and K. J. Kim, Int. J. Heat Mass Transfer, 2006, 49, 649–657 CrossRef CAS PubMed.
- J. W. Rose and L. R. Glicksman, Int. J. Heat Mass Transfer, 1973, 16, 411–425 CrossRef CAS.
- C. Graham and P. Griffith, Int. J. Heat Mass Transfer, 1973, 16, 337–346 CrossRef CAS.
- H. Tanaka, J. Heat Transfer, 1975, 75, 341–346 CrossRef.
- B. M. Burnside and H. A. Hadi, Int. J. Heat Mass Transfer, 1999, 42, 3137–3146 CrossRef CAS.
- R. N. Leach and F. Stevens, Langmuir, 2006, 22, 8864–8872 CrossRef CAS PubMed.
- M. Mei, B. Yu, M. Zou and L. Luo, Int. J. Heat Mass Transfer, 2011, 54, 2004–2013 CrossRef PubMed.
- B. S. Sikarwar, N. K. Battoo, S. Khandekar and K. Muralidhar, J. Heat Transfer, 2011, 133, 021501 CrossRef.
- Y. Wu, C. Yang and X. Yuan, Int. J. Heat Mass Transfer, 2001, 44, 4455–4464 CrossRef CAS.
- M. Mei, B. Yu, J. Cai and L. Luo, Int. J. Heat Mass Transfer, 2009, 52, 4823–4828 CrossRef CAS PubMed.
- M. Volmer and A. Weber, Z. Phys. Chem., 1926, 119, 277 CAS.
- A. Dillmann and G. E. A. Meier, J. Chem. Phys., 1991, 94, 3872–3884 CrossRef CAS PubMed.
- C. F. Delale and G. E. A. Meier, J. Chem. Phys., 1993, 98, 9850–9858 CrossRef CAS PubMed.
- D. Kashchiev, Nucleation: Basic Theory with Applications, Butterworth-Heinemann, Burlington, MA, 2000, ch. 3, pp. 32–33 Search PubMed; D. Kashchiev, Nucleation: Basic Theory with Applications, Butterworth-Heinemann, Burlington, MA, 2000, ch. 9, pp. 124–125 Search PubMed.
- V. Holten and M. E. H. van Dongen, J. Chem. Phys., 2009, 130, 014102 CrossRef CAS PubMed.
- T. Tsuruta and G. Nagayama, Energy, 2005, 30, 795–805 CrossRef CAS PubMed.
- V. G. Dubrovskii and M. V. Nazarenko, J. Chem. Phys., 2010, 132, 114507 CrossRef CAS PubMed.
- H. Kumomi and F. G. Shi, Phys. Rev. Lett., 1999, 82, 2717–2720 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |