Mechanism of pressure propagation and weakly compressible homogeneous and heterogeneous thixotropic gel breakage to study flow restart
Lalit Kumar*a,
Chris Lawrence†
b and
Johan Sjöbloma
aDepartment of Chemical Engineering, Norwegian University of Science and Technology (NTNU), N-7491 Trondheim, Norway. E-mail: lalitk@nt.ntnu.no; lalit181@yahoo.com
bInstitutt for Energiteknikk (IFE), Kjeller, Norway
First published on 12th May 2014
Abstract
Pressure propagation in the soft gels is commonly considered either in terms of acoustic waves or gel degradation. However, in a complete description, acoustic, viscous and gel degradation effects should all be considered simultaneously. Here a creep model is discussed with a suitable time scale. The model predicts a specific mechanism of pressure propagation, indicating that gel behaves like a creeping fluid rather than a fluid shearing only above a critical yield stress. The characteristics of pressure propagation can be used to distinguish between creeping and yield stress fluid. The presented results provide a new physical interpretation of recent experimental data. It is also shown that heterogeneity in the gel can cause center-core cohesive failure, as opposed to the near-wall failure which occurs in homogeneous gels.
1 Introduction
Complex fluids are ubiquitous in industry as well as in nature e.g. polymers, colloids and biological materials. Gelled waxy crude oil is one of the colloidal systems that show thixotropic behaviors under stress.1 Waxy crude oil comprises nearly 20% of the world oil reserves.2,3 Increasing consumer demand for petroleum products has resulted in exploration of waxy crude oil fields. Transportation and processing of waxy crude oils in cold weather conditions are challenging due to ubiquitous gelling and deposition phenomena. Gelling processes derive from the formation of percolating crystal structures in which a volume-spanning network of solid crystals occludes the remaining liquid. The rheological properties of the crude oil are modulated by gel structure formation.4,5 During maintenance and emergency shutdowns, significant temperature changes occur in the crude oil inside the pipeline, as a result of environmental heat loss. Dissolved paraffin waxes precipitate below the wax appearance temperature.6 Further reduction in the temperature drives the formation of a significant solid fraction, resulting in gel formation and non-Newtonian (thixotropic fluid with creep) behavior. Creep is inevitable for a system with non-uniform gel network strength.7 The rheological behavior of waxy crude gels resembles other glassy/jamming systems,8–10 and the present analysis is equally valid for glassy/jamming systems where the time scale of aging is much larger than the rejuvenation time scale.Pressure propagation in a gelled pipeline has been investigated for more than four decades. Two different approaches have been considered. The first approach assumes that the pressure propagation speed is the same as the acoustic speed.11,12 The other approach is based on a Bingham rheology, and considers gel breakdown propagation.13–15 On the one hand, in a realistic scenario, the pressure propagation mechanism has been experimentally reported to be a two step process.3 In the first step, the pressure propagates in the gel and develops an axial pressure gradient. In the second stage, the gel breaks slowly in the presence of the pressure gradient. However, a part of the explanation which has been provided previously is arguably insufficient, since high viscosity effects have not been taken into consideration for explaining a non-linear pressure profile and so-called delayed restart. The gel breakage phenomenon has been thought to be responsible for the non-linear pressure profile appearing in the first step. In the current work, the analysis shows that for low compressibility, the initial non-linearity is due to viscous dissipation, whereas gel breakage is a slow process, which only becomes significant after a long time compared to pressure propagation time. Furthermore, time delay in restart3 confirms no significant gel breakage by pressure propagation, especially for low compressible gel. The actual pressure front moves faster than the yield front, but slower than the acoustic speed.3,16 This is contrary to the prediction given by the Bingham approach. On the other hand, to avoid an excessively complex scenario, experimental researchers commonly consider an artificial scheme in which fresh fluid is slowly injected to maintain a linear pressure profile.4,17 The complete understanding of pressure propagation will on the one hand help to understand experimental results and on the other hand it will encourage researchers to do more realistic experiments.
In a recent theoretical study, different pressure propagation regimes for homogeneous gels were discussed for different parameter values, within a scheme where the velocity divergence in the momentum equations was neglected.16 The velocity divergence in the momentum equations has additional dissipation effects. Although the time scale can be chosen to resolve inertial pressure propagation and run simulations faster, the choice of time scale in previous works have rendered interpretation of the results unclear; mainly because different compressibility values give very different restart times in dimensionless units (as well as in physical units). In the present work, the mechanism of pressure propagation for homogeneous and heterogeneous gels is explored using a new characteristic time scale and complete model. Furthermore, key aspects of cohesive failure4,18 are explained for the first time in a theoretical study. The existence of center-core cohesive failure is interesting due to the fact that shear stress always remains high near the wall.
2 Theory
Flow re-start requires the application of a substantial axial pressure for an extended period to rupture the waxy gel. The rheology plays a crucial role in the prediction of the flow re-start dynamics. A thixotropic waxy gel ruptures within a small range of strain or applied stress values. Therefore, obtaining the rheological behavior precisely is an important and much debated topic in the literature.19–22 The most common rheological models used for waxy gels are those of Bingham, viscoelastic models, and shear thinning models. Alternatively, understanding of the pressure propagation mechanism can yield the right choice of rheology. Furthermore, the distribution of energy associated with the applied pressure may lead to the discovery of an appropriate mechanism for pressure evolution and gel rupture. Under applied pressure, the gel near the inlet undergoes compressional deformation. However, in the absence of immediate adhesive failure at the wall, gel deformation results in shearing, as seen from Fig. 1a. While the pressure propagates further downstream, the gel in the upstream region continues to deform. The continuous gel deformation may lead to creeping flow, as well as gel breakage near the wall; see Fig. 1b. Due to viscous dissipation, energy is also required to maintain the flow.Deformation of the gel can also be described as an elastic phenomenon, or by the combined effects of elasticity and viscosity. The induced deformation can lead to gel breakage. Therefore, both (i) viscoelastic and (ii) shear thinning thixotropic rheology with creep can explain the deformation and subsequent gel breakages. The gel network breakage can be interpreted as a result of either (i) stored elastic energy dissipation (stretching and breakage of the wax crystal network) or (ii) shearing dissipation (Van der Waals contact breakage within the crystal network). The Bingham rheology can be considered to be one extreme of these two rheologies, where all gel networks break simultaneously. In the current study, a shear thinning rheology is used, where the viscosity decreases exponentially with the strain.8,23 Such behaviour is known as first-order structural decay, which has characteristics similar to 3rd-order decay24 at the low and high strain limits. For a thixotropic fluid, a shear thinning rheology has been recommended by other researchers as well, for more detail see ref. 20 and 25. Furthermore, the failure of the gel structure should be a function of strain instead of strain rate for the case where the time scale for gel network breakage is much larger than the time scale for stress relaxation.
A horizontal pipe of radius R and length L, filled with either weakly compressible homogeneous or heterogeneous waxy crude oil gel at time (t = 0+) is considered. The density ρ is related to the pipeline pressure p at temperature Θ, with an isothermal compressibility given by χΘ = (1/ρ)(∂pρ)Θ. Total viscosity (gel strength) μ can be represented as a sum of the liquid part viscosity μ0 and the crystal part viscosity μg of the gel as
| μ = μ0 + μg(γ), | (1) |
Since the crystal microstructure breaks due to shearing, gel viscosity is considered as a function of shear history (absolute strain). The extent of microstructure breakage has been defined in the literature26,27 using structure parameter λ. The crystal part of the viscosity can be represented in terms of the structure parameter as follows:
| μ = μ0 + μg(γ → 0)λ(γ), | (2) |
| μ = μ0 (1 + μrλ(γ)), | (3) |
The 1st-order decay of the structure parameter with time26–28 can be given as
 | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = dγ/dt (in material frame of reference), the above differential equation can be rearranged in term of absolute strain24 γ. After integrating eqn (4) the value of λ can be written as a function of the absolute strain (γ). The strain dependent thixotropic rheology model has an advantage over the conventional time dependent thixotropic model,2,11,27 especially for compressible fluids. Strain contains implicit information about gel compressibility, time, and applied stress, which is useful for the simulation of pressure propagation in a weakly compressible gel.
= dγ/dt (in material frame of reference), the above differential equation can be rearranged in term of absolute strain24 γ. After integrating eqn (4) the value of λ can be written as a function of the absolute strain (γ). The strain dependent thixotropic rheology model has an advantage over the conventional time dependent thixotropic model,2,11,27 especially for compressible fluids. Strain contains implicit information about gel compressibility, time, and applied stress, which is useful for the simulation of pressure propagation in a weakly compressible gel.| (λ − λe) = k exp(−m0γ) | (5) |
| μ = μ0(1 + μr exp(−m0γ)), | (6) |
The exponential function is a fast decaying function at intermediate and high values of γ compared to reported gel degradation, therefore the following form of viscosity is chosen.
| μ = μ0(1 + k(1 − e−m0γ)/γ), | (7) |
From the Taylor expansion, we can analyze that the above equation replicates first order exponential decay for small values of γ and for large values of γ it decays slowly. In the limit of small values of γ, the Taylor expansion is given by
 | (8) |
In typical pipeline conditions with non-uniform cooling across different radial positions, the temperature history is most favorable for gelling near the wall, and least favorable at the center of the pipeline. Therefore, a heterogeneous gel that is strong near the wall and weaker at the center of the pipeline is also considered here.
3 Non-dimensional scheme and solution algorithm
For flow through high-aspect ratio pipelines, dimensionless quantities are defined in terms of the radial velocity u = ûεWs and the axial velocity w = ŵWs, with Ws ≔ Rτs/2μ0 and ε ≔ R/Ls, where τs is the typical yield stress value used for scaling (enabling a direct comparison with the Bingham approach) and Ls ≔ PR/(2τs) defines the limiting pipeline restart length for an incompressible Bingham fluid with yield stress τs for applied pressure difference P, with the compressibility number δ ≔ χΘP and the scaled Reynolds number is given by
with the compressibility number δ ≔ χΘP and the scaled Reynolds number is given by 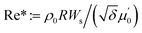 , where μ′0 = μ0P/τs and
, where μ′0 = μ0P/τs and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = μ/μ0′. Other important dimensional numbers are the viscosity ratio μr = μ(γ → 0)/μ0, the Bingham number α ≔ L/Ls, the steady state Reynolds number Ress ≔ ρ0wmaxR/μ0, where wmax is maximum velocity at steady state flow conditions, the pressure p =
= μ/μ0′. Other important dimensional numbers are the viscosity ratio μr = μ(γ → 0)/μ0, the Bingham number α ≔ L/Ls, the steady state Reynolds number Ress ≔ ρ0wmaxR/μ0, where wmax is maximum velocity at steady state flow conditions, the pressure p = ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) P; and the radial and axial coordinates r =
P; and the radial and axial coordinates r = ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) R and z = ẑL. The resulting model equation set is given by
R and z = ẑL. The resulting model equation set is given by
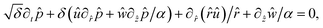 | (9) |
 | (10) |
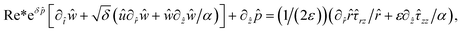 | (11) |
 | (12) |
 , and
, and  , where the secondary viscosity ξ is negligible for restart, and d is the strain tensor. The boundary conditions are as follows: at the pipeline inlet, Dirichlet conditions are prescribed as p = pinlet, γ = γinlet, u = τzz = 0. At the pipeline outlet, a combination of Dirichlet conditions (u = p = τzz = 0) and Neumann conditions (∂zγ = ∂zw = 0) are used. At the wall, no slip and no penetration conditions are implemented. Axisymmetric conditions have been assumed for the radial velocity, the shear stress and the strain at the pipeline center. The initial conditions are given by no flow, pristine gel inside the pipeline (γ = 0), and the pressure inside the pipeline equal to the outlet pressure.
, where the secondary viscosity ξ is negligible for restart, and d is the strain tensor. The boundary conditions are as follows: at the pipeline inlet, Dirichlet conditions are prescribed as p = pinlet, γ = γinlet, u = τzz = 0. At the pipeline outlet, a combination of Dirichlet conditions (u = p = τzz = 0) and Neumann conditions (∂zγ = ∂zw = 0) are used. At the wall, no slip and no penetration conditions are implemented. Axisymmetric conditions have been assumed for the radial velocity, the shear stress and the strain at the pipeline center. The initial conditions are given by no flow, pristine gel inside the pipeline (γ = 0), and the pressure inside the pipeline equal to the outlet pressure.
3.1 Numerical algorithm for compressible non-isothermal flow
The numerical algorithm is given in the following paragraph.Step (1) First initialize Û0, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 0,
0, ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) 0
0
Step (2) Time loop t = kΔt, k ≥ 1
* Initialize Ûk+10 = Ûk+1, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) k+10 =
k+10 = ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) k,
k, ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) k+10 =
k+10 = ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) k
k
* Predictor step – solve the Navier–Stokes problem using variables from the previous step.
* Solve the mass balance equation to find the new pressure.
* Corrector step – solve the Navier–Stokes problem using the solution from the predictor step.
* Solve the mass balance equation to find the new pressure.
* If solution converges go to step 2 with k = k + 1, otherwise
* Go to step 2 with k = k and in the first step initialize variables with updated values instead of previous time step values
* Obtained data (Û, p,…)
The detail of the finite volume method discretization scheme on a staggered grid is given in the Appendix.
4 Results and discussion
Eqn (9)–(12) are solved using a finite volume method on a staggered grid. A predictor–corrector solution algorithm with iteration is used for every time step, as discussed in the previous section. For the case of weakly compressible gels, the compressional front moves at acoustic speeds in an inviscid fluid. Furthermore, for a high applied pressure, the compressional front speed in the upstream region remains close to the acoustic speed for high viscosity gels, as reported.16 Therefore, for a numerical description of the pressure propagation in a weakly compressible gel, a proper time scale is needed to account for the acoustic speed. Here we choose a time scale that is proportional to the square root of the compressibility number to account for acoustic wave propagation. Hence, the new time scale is better for low gel strength where the compressional front speed is close to the acoustic speed.4.1 Pressure propagation in homogenous gel
To explore the important mechanism for the pressure propagation in the weakly compressible thixotropic gel, first we considered the case of a homogenous gel filling the pipeline. The advantages of the proposed time scale for a strong gel are shown in Fig. 2a and b. The prediction of a similar order of dimensionless restart times for different compressibility values justifies the choice of timescale. Furthermore, the gel strength (viscosity) distribution in the pipeline (Fig. 2c) shows a small reduction of viscosity as the pressure propagates in the gel. The compressional deformation causes breakage of the weak gel network as soon as the pressure signal passes through a given section of the pipeline. Behind the compressional front, additional reduction in viscosity near the wall is observed as a result of deformation due to shearing. Fig. 2d shows that significant viscosity reduction (gel breakage) is only observed after a long time delay, again pointing to the pipeline restart being a two-step process.To examine the effects of the gel strength on the pressure propagation, different μr-values are analyzed whilst keeping δ = 4 × 10−4, Ress = 818 and α = 1.1 constant. From the results it is clear that in a weak gel (μr = 20, Fig. 3a) the pressure propagates with the acoustic speed and the nature of the pressure propagation is inertial, since the speed of propagation remains constant. It is to be noted that compressional front speed will slow down with increasing pipeline length as a result of viscous attenuation. For larger gel strength (μr = 200, Fig. 3b), the pressure propagation appears to be controlled by inertial effects only at early times near the entrance of the pipeline. As the pressure propagates downstream, the speed is reduced quickly due to strong viscous attenuation. Higher gel strength causes faster viscous attenuation of the inertial effect. At very high gel strengths, μr = 2000 (Fig. 3c) and μr = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (Fig. 3d), the compressional front speed is severely dampened by viscous effects. At high gel strength, the pressure decays exponentially with position, as opposed to the spatially increasing pressure seen for low gel strength.
000 (Fig. 3d), the compressional front speed is severely dampened by viscous effects. At high gel strength, the pressure decays exponentially with position, as opposed to the spatially increasing pressure seen for low gel strength.
The inertial propagation and viscous propagation regimes can be distinguished by the following facts: in the inertial propagation regime, the main source of the pressure gradient at the compressional front is the compressional storage of energy. The pressure gradient behind the compressional front is due to viscous dissipation, which is much smaller (Fig. 3a and b) for weak gels. For pressure evolution in a strong gel, the supplied energy is used for viscous dissipation along with compressional storage. Therefore, a significant pressure gradient is observed behind the compressional front (Fig. 3c and d). Fig. 3e shows the inertial nature of the pressure evolution at high compressibility δ = 4 × 10−2 and low μr = 2 × 102. For high compressibility values, δ = 4 × 10−2 together with μr = 2 × 104, the deformations instantaneously become large enough to break the gel network (Fig. 3f), reducing the gel viscosity. Therefore, even for high gel strength (high initial viscosity), no viscous dissipation effects are observed on the pressure profile behind the compressional front. For high compressibility, the nature of the pressure evolution can be termed gel breakage. In the case of a highly compressible gel, large deformation ensures gel breakage before the compression front moves further downstream in the pipeline.
4.2 Qualitative comparison with experimental results
We can qualitatively compare our results for low compressibility and high gel strength (Fig. 3c) with the experimental results reported by El-Gendy et al. (see Fig. 9 (ref. 3)). We further assume a polynomial fitting for results presented by El-Gendy et al. instead of piecewise linear fitting. With polynomial fitting, the nature of pressure evolution will appear to be similar to our results. Moreover, the inlet and outlet flow rates are shown in Fig. 4 corresponding to the parameter used for the pressure profile presented in Fig. 3c. The outlet flow rate in Fig. 4 can be directly compared with the downstream pressure profile shown by El-Gendy et al. (Fig. 11 (ref. 3), pressure valve P7). In the experiment of El-Gendy et al., the fluid present in the pipeline after valve 7 is Newtonian in nature. For a Newtonian fluid, the pressure drop in a section of the pipeline is directly proportional to the outlet flow rate. By considering the outlet flow rate in Fig. 4 and the pressure evolution profile shown by El-Gendy et al., it is clear that pressure evolution at the outlet is a strong function of time. First, pressure propagates to the outlet, and then slowly the gel breaks. This results in an increase in flow rate in our case and an increase in pressure in El-Gendy et al.’s results. The increase in flow rate confirms breakage of the gel and reduction in flow resistance by the gel. Finally both the inlet and outlet flow rates should reach a steady state value similar to the pressure profile shown by El-Gendy et al. However, the gel breakage is a very slow process, especially for a low compressibility gel. Calculation of the outlet flow rate to the steady state by our simulation is a time consuming process. This is due to the fact that our time scaling resolves the fastest moving inertial wave as well.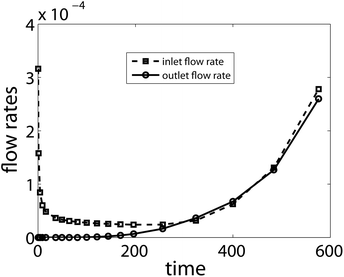 | ||
| Fig. 4 Inlet and outlet flow rate as a function of time for parameter values δ = 4 × 10−4, Ress = 818, α = 1.1 and μr = 2 × 104. | ||
4.3 Finger-like propagation of fresh crude oil
In the case when the pipeline is filled with highly compressible (δ = 4 × 10−2) waxy crude oil gel, the penetration of fresh crude oil in a homogeneous gel appears to be similar to fingering, see Fig. 5a and b at time![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 20 and
= 20 and ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 75. The dark red color represents incoming fresh crude oil and the light red color represents gelled crude oil inside the pipeline. The values of other parameters used for computation are Ress = 818, α = 1.1 and μ = 2 × 104. The theoretical prediction of low viscosity fluid penetration in the highly viscous fluid is similar to the experimental observation of fingering in the Bingham fluid. For more detail, see Lindner et al.32,33 The difference between our thixotropic rheology model and Bingham rheology is associated with the initial response of the material to applied stress, which itself is a debatable topic.19–22
= 75. The dark red color represents incoming fresh crude oil and the light red color represents gelled crude oil inside the pipeline. The values of other parameters used for computation are Ress = 818, α = 1.1 and μ = 2 × 104. The theoretical prediction of low viscosity fluid penetration in the highly viscous fluid is similar to the experimental observation of fingering in the Bingham fluid. For more detail, see Lindner et al.32,33 The difference between our thixotropic rheology model and Bingham rheology is associated with the initial response of the material to applied stress, which itself is a debatable topic.19–22
 | ||
Fig. 5 Penetration of fresh crude oil in the gelled pipeline for δ = 4 × 10−2, Ress = 818, α = 1.1 and μr = 2 × 104 at time (a) ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 20 (b) = 20 (b) ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 75. = 75. | ||
4.4 A brief summary of the nature of pressure propagation
We have shown the effect of gel strength and compressibility number on pressure propagation in an earlier section. However, there are other parameters that can influence the nature of pressure propagation (e.g. length of the pipe (aspect ratio), Ress). Here, the dimensionless number Ress is representative of the inertial force that causes gel breakdown. Gel breakage is a slow process, hence time is an important parameter. This makes the length of the pipeline an important factor in the determination of the overall mechanism of pressure propagation. In a longer pipeline, pressure will take more time to propagate. Hence the gel present downstream in the pipeline will be under applied stress for a longer period of time. This will lead to more gel breakage upstream, affecting the viscous attenuation of pressure upstream. Less viscous attenuation upstream helps further pressure propagation downstream. A brief summary of the nature of pressure propagation is given in Table 1.| L/R | δ | μr | Low Ress | High Ress |
|---|---|---|---|---|
| High | — | — | GD | GD |
| Intermediate | H | H | GD | GD |
| Intermediate | L | H | V/GD | I/V/GD |
| Intermediate | H | L | I/V/GD | I |
| Intermediate | L | L | I/V | I |
| Low | — | — | I/V | I |
In Table 1, we have presented only the main phenomena that are responsible for the overall nature of pressure propagation in a particular scenario. In reality, the inertial effect will always be present near the pipe inlet before it is attenuated by viscous effects. Furthermore, viscous effects lead to gel degradation, making it difficult to separate these two effects. In certain cases, the gel breaks by the time pressure propagates downstream. In such cases, the compression front speed becomes very slow and significant gel degradation causes drastic reduction in the gel strength before the viscous wave propagates further downstream. Therefore, gel degradation is cited as the key phenomenon responsible for pressure propagation in such a case. Furthermore, we would like to mention that the summary presented in Table 1 is valid in a typical scenario. There are always some exceptions to the typical scenario e.g. in the rheometer length scale, if high void fractions exist in the gel (high compressibility) pressure will propagate as gel breakage instead of an inertial wave. However, the results in Table 1 represent the only common scenario found in the industrial application and does not focus on possible extreme cases.
4.5 Pressure propagation in heterogeneous gel
In an industrial application, heat losses to the environment can result in non-uniform cooling. Hence, a radially heterogeneous gel has been considered, where the inner gel is assumed to be 100 to 1000 times weaker than the gel in the outer annulus. Furthermore, a step-like change in the gel strength is unlikely; therefore, the gel strength is a smooth function of the radial position, as seen from Fig. 6a. The time evolution of the pressure profile for the heterogeneous gel is presented in Fig. 6b, using the parameter values Ress = 818, α = 1.1 and δ = 4 × 10−4. The evolution of pressure profiles reveals that the speed of the compressional front speed is higher than for the case where the pipeline is filled with a homogeneous gel having a strength corresponding to the outer annulus gel. However, the propagation speed is slower than for the case of a homogeneous gel strength similar to the gel in the inner pipeline. Surprisingly, the evolution characteristics are closer to the pressure evolution for the case of stronger gels than the near wall gel. It appears that for weak gels at the pipe center, the high strength gels acts like a virtual wall. The weak gel cohesively breaks at its interface with the strong gel. If the pressure propagation is assumed to be carried via the inner section of the pipeline, then the flow parameters need to be recalculated based on the inner pipeline section where the weak gel resides. Since Ress ∝ R3, in the presence of the same applied pressure Ress becomes 10 times lower for the inner pipeline region. The low value of Ress results in a greater viscous attenuation and slower pressure propagation. Therefore, at low Ress = 81, a viscous dominated pressure profile is observed where the compressional front moves faster than in a corresponding strong homogeneous gel but slower than in a weak homogeneous gel.The strain evolution contours shown in Fig. 6c and d reveal center-core failure in the pipeline. This constitutes the first direct and detailed computation of center-core failure, to the best of the author's knowledge. To describe the effects of pressure propagation on gel deformation, the logarithm of the strain is represented by the contour plot in Fig. 6c and d. A high strain value has been assigned as the initial condition for the weak gel. Therefore, in order to clearly observe the failure in the gel, the initial value of the strain is subtracted from the current value in the plot. The failure is measured as the change in the strain value. Fig. 6c and d clearly indicate a center-core failure, as opposed to near wall failure observed in the case of a homogeneous gel.
5 Conclusion
In conclusion, we have proposed a suitable time scale to analyze the pressure propagation. The inertial, viscous and gel degradation effects on the pressure propagation have been discussed. In our simulations, we predict a propagation speed which is consistent with recent experimental results,3 and which is much faster than the gel degradation speed, as given by the Bingham rheology scheme. Yielding fluid (Bingham rheology) can be presented by infinite viscosity at applied stress below the yield stress,22 therefore the yielding fluid will act like a sink for shear development below the yield value. This indicates that waxy crude gel should be modelled in terms of creeping flow rheology, rather than with a yield stress description. Furthermore, the way in which the pressure propagates can be used to distinguish between creeping and yield stress fluid. It is also found that heterogeneity in the gel can lead to center-core cohesive failure. A theoretical understanding of pressure propagation and gel breakdown phenomena in gels will provide an appropriate interpretation of both past and future experimental studies to determine the nature of non-Newtonian fluids and the mechanisms involved in pipeline restart.Appendix
Assuming the velocity field at the node to be prevalent in the entire control volume, the integral in the control volume can be estimated as follows;
 | (13) |
To perform time integration of the terms that do not contain a time derivative, a weighting parameter ϕ between 0 and 1 can be used.
 | (14) |
The value of ϕ determines the scheme of the solution for the unsteady problem. For the explicit scheme ϕ = 0, for the Crank Nicholson scheme  (semi-implicit) and for the fully implicit scheme ϕ = 0 is used. In this study the fully implicit technique has been used. The fully implicit scheme involves unknown new data from the current time step. Hence, discretized non-linear governing equations are solved iteratively.
(semi-implicit) and for the fully implicit scheme ϕ = 0 is used. In this study the fully implicit technique has been used. The fully implicit scheme involves unknown new data from the current time step. Hence, discretized non-linear governing equations are solved iteratively.
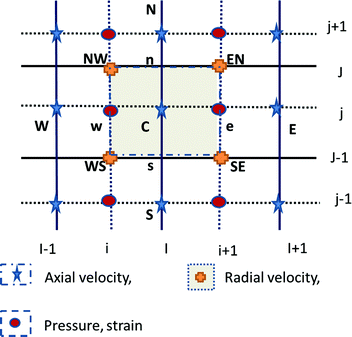
Discretization of mass balance equation at cell center control volume (see Fig. 7) is performed as follows;
 | (15) |
 | (16) |
 | (17) |
 | (18) |
Final discretized mass balance equation becomes as follows;
 | (19) |
![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) = w(I,j) + w(I − 1,j).
= w(I,j) + w(I − 1,j).
Discretization of axial momentum balance equation around its control volume (see Fig. 8) is performed as follows;
 | (20) |
Further integration of stress term can be written as follows;
 | (21) |
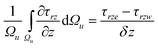 | (22) |
 and
and  .
.
For the velocity derivatives associated with the stress tensor, the following discretization scheme is used:
Discretization of axial momentum balance equation around its control volume (see Fig. 9) is performed as follows;
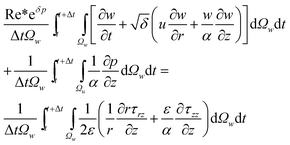 | (23) |
 | (24) |
 | (25) |
 . Velocity derivatives associated with the stress tensor can be further discretized using the following discretization scheme:
. Velocity derivatives associated with the stress tensor can be further discretized using the following discretization scheme:Strain evolution equation (scalar transport equation):
 | (26) |
Acknowledgements
Authors would like to acknowledge Petronas, Petrobras, Statoil ASA, Champion Technologies, BASF, Research Council of Norway for their financial support and Olaf Skjraasen from the Institute for Energy Technology Kjeller for critically reading this manuscript.References
- H. Petter Ronningsen, J. Pet. Sci. Eng., 1992, 7, 177–213 CrossRef.
- G. Vinay, A. Wachs and I. Frigaard, J. Non-Newtonian Fluid Mech., 2007, 143, 141–156 CrossRef CAS PubMed.
- H. El-Gendy, M. Alcoutlabi, M. Jemmett, M. Deo, J. Magda, R. Venkatesan and A. Montesi, AIChE J., 2012, 58, 302–311 CrossRef CAS.
- H. S. Lee, P. Singh, W. H. Thomason and H. S. Fogler, Energy Fuels, 2008, 22, 480–487 CrossRef CAS.
- R. F. Visintin, R. Lapasin, E. Vignati, P. D'Antona and T. P. Lockhart, Langmuir, 2005, 21, 6240–6249 CrossRef CAS PubMed.
- K. S. Pedersen and H. P. Rønningsen, Energy Fuels, 2003, 17, 321–328 CrossRef CAS.
- S. Pradhan, A. Hansen and B. K. Chakrabarti, Rev. Mod. Phys., 2010, 82, 499 CrossRef.
- C. J. Dimitriou, G. H. McKinley and R. Venkatesan, Energy Fuels, 2011, 25, 3040–3052 CrossRef CAS.
- C. Eisenmann, C. Kim, J. Mattsson and D. A. Weitz, Phys. Rev. Lett., 2010, 104, 035502 CrossRef.
- A. J. Liu and S. R. Nagel, Nature, 1998, 396, 21–22 CrossRef CAS PubMed.
- C. Chang, Q. D. Nguyen and H. P. Rønningsen, J. Non-Newtonian Fluid Mech., 1999, 87, 127–154 CrossRef CAS.
- T. Perkins and J. Turner, JPT, J. Pet. Technol., 1971, 23, 301–308 Search PubMed.
- M. R. Davidson, Q. Dzuy Nguyen, C. Chang and H. P. Rønningsen, J. Non-Newtonian Fluid Mech., 2004, 123, 269–280 CrossRef CAS PubMed.
- G. Vinay, A. Wachs and J.-F. Agassant, J. Non-Newtonian Fluid Mech., 2006, 136, 93–105 CrossRef CAS PubMed.
- G. M. Oliveira, C. O. Negrão and A. T. Franco, J. Non-Newtonian Fluid Mech., 2012, 169, 121–125 CrossRef PubMed.
- L. Kumar, C. Lawrence, Y. Zhao, K. Paso, B. A. Grime and J. Sjöblom, Numerical study of pipeline restarts of weakly compressible thixotropy waxy crude oil, AIChE J. Search PubMed , under review.
- G.-P. Borghi, S. Correra, M. Merlini and C. Carniani, International Symposium on Oilfield Chemistry, 2003.
- M. R. Jemmett, J. J. Magda and M. D. Deo, Energy Fuels, 2012, 27, 1762–1771 CrossRef.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1997, 70, 1–33 CrossRef CAS.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1999, 81, 133–178 CrossRef CAS.
- P. Moller, A. Fall, V. Chikkadi, D. Derks and D. Bonn, Philos. Trans. R. Soc. London, Ser. A, 2009, 367, 5139–5155 CrossRef PubMed.
- P. Møller, A. Fall and D. Bonn, Europhys. Lett., 2009, 87, 38004 CrossRef.
- S. Jones and J. Tyson, J. Colloid Sci., 1952, 7, 272–283 CrossRef CAS.
- Y. Zhao, L. Kumar, K. Paso, H. Ali, J. Safieva and J. Sjoblom, Ind. Eng. Chem. Res., 2012, 51, 8123–8133 CrossRef CAS.
- P. C. Møller, J. Mewis and D. Bonn, Soft Matter, 2006, 2, 274–283 RSC.
- F. Moore, Trans. Br. Ceram. Soc., 1959, 58, 470–494 CAS.
- M. Houska, Faculty of Mechanical Engineering, Czech Technical University of Prague, 1981 Search PubMed.
- D. De Kee, R. Code and G. Turcotte, J. Rheol., 1983, 27, 581 CrossRef.
- K. Paso, T. Kompalla, H. J. Oschmann and J. Sjöblom, J. Dispersion Sci. Technol., 2009, 30, 472–480 CrossRef CAS.
- D. A. Phillips, I. N. Forsdyke, I. R. McCracken and P. D. Ravenscroft, J. Pet. Sci. Eng., 2011, 77, 286–304 CrossRef CAS PubMed.
- Y. Zhao, L. Kumar, K. Paso, J. Safieva, M. Z. B. Sariman and J. Sjoblom, Energy Fuels, 2012, 26, 6323–6331 CrossRef CAS.
- A. Lindner, D. Bonn, E. C. Poiré, M. B. Amar and J. Meunier, J. Fluid Mech., 2002, 469, 237–256 Search PubMed.
- A. Lindner, P. Coussot and D. Bonn, Phys. Rev. Lett., 2000, 85, 314 CrossRef CAS.
Footnote |
| † Present address, SPT Group, N-2027 Kjeller, Norway. |
| This journal is © The Royal Society of Chemistry 2014 |