Predicting the mixture effects of three pesticides by integrating molecular simulation with concentration addition modeling

Abstract

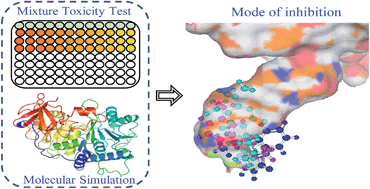
It is a tricky but fundamental problem in risk assessment to predict the combined toxicity of several chemicals by methods other than by experiment, especially for binary mixtures, in order to save time and experimental costs. Though several models have been developed, making a choice among them is difficult owing to the variation in mode of inhibition (MOI). To choose a reference model appropriately, we propose an in silico procedure which employs molecular simulation techniques to identify MOI, and which highlights the binding pattern of a small molecule to a biomacromolecule. Specifically, the method is verified by experimental study and shows that 15 binary mixtures of three pesticides, baygon, metacrate, and velpar, inhibit firefly luciferase bioluminescence. The results reveal that the pesticides share the same binding site at the bottom of the luciferin pocket, and combined toxicities could be predicted by the concentration addition model, which enables us to identify the MOI using molecular simulation techniques. In addition, there is a linear relationship between the binding free energy of the mixture (ΔG_mix) calculated from the ΔGs of the components and the median effective concentrations (EC₅₀) of the mixture.

---

Introduction

It is impractical to test the toxicity of every mixture in the environment. Therefore, several prediction models had been proposed, among which are two widely used models, the concentration addition model (CA) and the independent action model (IA).^1–3 The CA⁴ is optimal for mixtures where the components have similar mechanisms of action (MOA), whereas the IA⁵ is suitable for the combined toxicity generated by components having dissimilar MOAs. However, in practice, obtaining MOA information for a chemical against various biological targets is difficult even experimentally, which means it is a dilemma to put the models into practice.^6,7 To obtain MOA information, an existing feasible solution is the quantitative structure–activity relationship (QSAR) model which can discriminate different MOAs using the structure descriptors of chemicals.^8,9 Nonetheless, limitations of the model, derived from the limited applicability domain and small training set, restrain the utilization of QSAR. Obviously, a more feasible method is essential. Based on the viewpoint presented by some researchers that chemicals having different MOAs are toxic in different ways due to different interactions at the biomolecular level,^8,10 we attempted to introduce a computer simulation study into the process where a visible 3D pattern of small chemical molecules bound to the specific protein molecular target is simulated.

Firefly luciferase extracted from Photinus pyralis is a widespread bioluminescence indicator used in PubChem.^11,12 In biochemical assays, firefly luciferase catalyzes the oxidation of D-luciferin (LH₂) in the presence of oxygen, ATP, and Mg²⁺ to form oxyluciferin and yield light simultaneously.¹³ The luciferase inhibitors have been divided into two primary competition categories, the luciferin and adenylate competitive inhibitors, according to previous research focusing on the structure–activity relationships of luciferase inhibitors,^14,15 which further verifies the existence of two binding pockets in luciferase protein.^15,16 Later, some cocrystal structures of ligands bound to luciferase resolved by experiments and modeling confirmed the pockets.^12,17 Modeling results for substrate competitive inhibitors, quinoline and benzothiazole, exposed to Japanese firefly luciferase, revealed that quinoline occupies approximately the same space where the purine of AMP is located, whereas benzothiazole occupies an almost identical site to luciferin.¹⁶ In addition, the substitution of each extends into other binding regions despite the major binding pocket.¹⁶ Auld et al.¹⁸ first explored the X-ray cocrystal structure of luciferase bound to Ataluren (PTC124, an analogue of luciferin) and substrate ATP, which was determined to 2.0 Å resolution (PDB: 3IES), which makes it possible to gain a deeper insight into the inhibition mechanism.

The purposes of this paper were (1) to analyse the mode of inhibition (MOI) of three pesticides (baygon, metacrate, and velpar) to luciferase by molecular simulation; (2) to determine the toxicities of the three single pesticides and 15 binary mixtures experimentally; (3) to choose an appropriate reference model to predict the toxicities of binary mixtures according to the results of (1). Specifically, to achieve (1), four steps were included, molecular docking, molecular dynamics simulation (MD), Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) energy calculations, and MM/GBSA free energy decomposition analysis.¹⁹ To achieve (2), microplate toxicity analysis (MTA)²⁰ was chosen, following the procedures for design of the mixture composition, concentration–response data sampling, and CA model validation. The results from (1) and (2) indicated that the toxicities of the mixtures could be well predicted by the CA model in situations where the pesticide components share the same binding pattern as luciferase.

Methods

Structure of firefly luciferase

Generally, the structure of firefly luciferase consists of a large N-terminal domain (residues 1–436), a small C-terminal (residues 440–551) and a short hinge including three flexible peptides (residues 437–439).²¹ The active site of luciferase is mainly located in the N-terminal domain near the hinge region.^11,22 In our molecular simulation system, we employed the 2.0 Å resolution cocrystal structure from PDB (enter code of 3IES) to fit the structure of luciferase. 3IES is a complex of PTC124-AMP bound to the Photinus pyralis luciferase. The structure of luciferase, which is called LUC in what follows, in the 3IES complex only contains the 436 residues in the N-terminal. LUC has two active binding pockets: one is called the ATP pocket where hydrogen bonds form between AMP and Gly339, Gly316, Thr343, His245, Asp422 separately, and the other one is called the LH₂ pocket surrounded by Ala222, Phe227, Phe247, Ala313, Ala348, and Ile351 where there is no hydrogen bond but only hydrophobic interactions between PTC124 and LUC.¹⁸ The two important binding pockets, the ATP pocket and LH₂ pocket,²³ are shown in Fig. 1 drawn by PyMol 0.99rc6 (ref. 24) and LigPlot+.²⁵

Fig. 1 (a) The binding pocket of firefly luciferase in 3IES. (b) Hydrogen bond interaction patterns and hydrophobic contacts between PTC124-AMP and the side chain and backbone of binding residues in 3IES, where the hydrogen bond contact is expressed by green lines and hydrophobic contact groups are expressed by eyelash shaped curves.

Molecular docking and molecular dynamics simulation

The receptor structure for molecular docking was obtained by removing all water molecules as well as the ligand from 3IES in which the missing residues were constructed using Discovery Studio 2.5 (Accelrys Software, Inc., San Diego, CA).²⁶ The ligand files for pesticides were read in PyRx 0.8, all of the hydrogens and Gasteiger²⁷ charges were added, and non-polar hydrogens were merged. The structure of pesticide–LUC was obtained using a semi-flexible docking approach with AutoDockVina.²⁸ LUC was used as the receptor, and considered as if it was fully rigid. The pesticide ligand was flexible. For the docking calculations, a box of size 13.44 × 17.60 × 17.68 Å was used, centered at the geometric center of the PTC124–AMP structure. The exhaustiveness value (exhaustiveness of finding the global minimum) was changed to 25 (default is 8), and the program was allowed to generate 10 binding modes (default is 9).²⁹ An explicit random seed was used for the Genetic Algorithm. The maximum energy difference between the best binding mode and the worst one displayed was 3 kcal mol⁻¹. The docking pose with the lowest negative score value (highest binding affinity) was chosen as the initial conformation for MD.

MD was performed using the AMBER 12 software package.³⁰ Three pesticide–LUC complexes (the generalized AMBER force field (GAFF)³¹ for pesticide ligand and the ff99SB force field³² for LUC protein) were solvated by the TIP3P waters, with a minimum distance of 8.5 Å from the complex surface.³³ All MDs were conducted using the standard procedure, which is comprised of energy-minimization, gradual heating of the systems, and isothermal isobaric ensemble (NPT) molecular dynamics.^34,35 The ptraj module in AMBER was used to analyze the root mean-square displacements (RMSD) and root mean-square fluctuation (RMSF). All systems were equilibrated at 4 ns, and the MDs were prolonged for another 4 ns. One hundred snapshots of the simulated structures were sampled within the last 1 ns with a step of 10 ps. More details for molecular docking and MD are given in the ESI.†

Binding free energy and its components

The binding free energies (ΔG_is) of pesticides with LUC were calculated using the 100 snapshots of each complex (every 10 ps) generated from the last 1 ns MD trajectories. The enthalpy (ΔH) was calculated using the MM/GBSA procedure^19,36 in AMBER 12. The conformational entropy (translation, rotation, and vibration) upon ligand binding, TΔS, was calculated using normal-mode analysis³⁷ with the nmode program in AMBER 12. More details are given in the ESI.†

Furthermore, ΔG was decomposed to a single residue using the MM/GBSA method. This decomposition was only performed for molecular mechanics and solvation energies and not for entropies.³⁸ The MM/GBSA free energy decomposition³⁹ procedure was used to calculate the pesticide–residue pair energy (ΔG_r) between each pesticide and each individual residue.⁴⁰

ΔG_mix of a mixture was calculated from the ΔG_is of the pesticide components and the p_i of the components in the mixture,

where p_i is defined as the ratio of concentration of the ith component in the mixture to the mixture concentration; ΔG_mix is the assumed binding free energy of a mixture.

Determination of toxicity

The chemicals included ATP–Na₂ (Sigma-Aldrich, St. Louis, MO, ≥98.0% purity), QuantiLum recombinant luciferase (Promega, Madison, WI, ≥95% purity), endotoxin-free D-luciferin (Promega, Madison, WI, ≥98.5% purity), which were separately stored in glycylglycine buffer (pH 7.8, consisting of 50 mmol L⁻¹ glycylglycine, 1 mmol L⁻¹ MgSO₄, 0.5 mmol L⁻¹ EDTA, and 10 mmol L⁻¹ DTT). The final optimal conditions used in our luciferase luminescence inhibition toxicity test were as follows: luciferase concentration of 1 × 10⁻⁸ mol L⁻¹, luciferin concentration of 1.6 × 10⁻⁵ mol L⁻¹, ATP concentration of 1 × 10⁻⁵ mol L⁻¹, pH 7.8, and 15 min exposures at 22 ± 1 °C.

Baygon (BAY) and metacrate (MET) are methyl carbamate insecticides, and velpar (VEL) is a triazine herbicide. The concentration–response data for the single pesticides and mixtures were determined by the MTA.²⁰ The relative light unit (RLU) was determined on a Synergy™ 2 multi-mode microplate reader (BioTek Instruments Inc., USA) with a 96-well white flat-bottomed microplate (Corning, USA).

All pesticides were dissolved in 1% (v/v) DMSO and stored at room temperature. Twelve concentration series of pesticides and their mixtures in three repeats and 12 controls were arranged in a microplate. First, 100 μL of 1% (v/v) DMSO was added to 12 wells in the first row of the microplate as controls. Then, 100 μL solutions of pesticide or their mixtures of 12 gradient concentrations derived by dilution factors f were added to 12 column wells from the second to fourth row as treatments. Then, 50 μL of ATP solution, 50 μL of luciferin solution, and 50 μL of luciferase solution were successively added to each well to make a final test volume of 250 μL. The RLUs of various treatments and controls were determined after exposure for 15 min. Each microplate test was repeated at least twice.

The toxicity was expressed as a percentage inhibition (E or x) and the observed concentration–response data were fitted to a Weibull function, called concentration–response curve fitting (CRC). As a quantitative measure of the uncertainty, the 95% observation-based confidence intervals (OCIs) were also determined.⁴¹ From the OCIs, the uncertainty of some concentration such as EC₅₀ was also determined by linear interpolation. More details for the toxicity testing procedure are given in the ESI.†

Mixture design and additivity validation

The direct equipartition ray design (EquRay) procedure⁴² was employed to rationally design the concentration ranges of pesticides in some representative binary mixtures. Based on the EC₅₀ of a signal pesticide (Table S1†), 15 binary mixture rays were designed by EquRay. The p_is of various pesticides in the mixtures are listed in Table 1.

Table 1 Mixture ratios (p_i), model parameters (α and β), statistics (RMSE and R²), EC₅₀ (10⁻³ mol L⁻¹), lower and upper limits of 95% confidence intervals of EC₅₀, and binding free energy values (ΔG_mix, kcal mol⁻¹) of binary mixture rays

Ray	p1	α	β	RMSE	R^2	EC50 (lower, upper)	ΔGmix	EC50^a
a The values of the EC50s estimated from linear models (eqn (3)–(5)).
BAY-MET system (p1 = pBAY)
R1	0.731	6.25	2.36	0.010	0.999	1.572 (1.461, 1.723)	−11.0	1.653
R2	0.521	5.56	2.18	0.013	0.997	1.911 (1.718, 2.171)	−9.50	1.901
R3	0.353	5.66	2.23	0.022	0.993	1.984 (1.679, 2.409)	−8.27	2.123
R4	0.214	5.36	2.16	0.012	0.998	2.232 (2.041, 2.498)	−7.26	2.322
R5	0.098	4.97	2.08	0.016	0.996	2.718 (2.369, 3.172)	−6.41	2.502
MET-VEL system (p1 = pMET)
R1	0.328	7.39	2.74	0.019	0.997	1.476 (1.314, 1.676)	−14.2	1.487
R2	0.550	6.43	2.47	0.023	0.994	1.771 (1.512, 2.099)	−11.4	1.808
R3	0.710	6.43	2.54	0.015	0.997	2.109 (1.908, 2.359)	−9.38	2.081
R4	0.830	5.22	2.12	0.009	0.999	2.316 (2.171, 2.516)	−7.85	2.311
R5	0.920	4.91	2.03	0.013	0.998	2.516 (2.276, 2.830)	−6.66	2.522
VEL-BAY system (p1 = pVEL)
R1	0.790	7.63	2.75	0.029	0.992	1.238 (1.019, 1.490)	−17.2	1.209
R2	0.600	6.79	2.47	0.029	0.990	1.267 (1.030, 1.569)	−16.2	1.272
R3	0.429	6.67	2.46	0.021	0.995	1.379 (1.194, 1.607)	−15.3	1.332
R4	0.273	6.25	2.31	0.018	0.996	1.368 (1.199, 1.581)	−14.4	1.394
R5	0.131	6.28	2.34	0.019	0.995	1.446 (1.265, 1.688)	−13.7	1.443

---

The CA model^1,43 was employed to predict the combined toxicity based on the dose addition assumption. If the observed toxicity is consistent with that predicted, then the combined toxicity shows additivity or non-interaction. The CA can be written as follows:^1,43

where EC_x,mix is the concentration of the mixture that causes x combined toxicity, n is the number of mixture components, EC_x,i is the concentration of the ith component causing x toxicity when applied individually, and p_i is the concentration ratio of the ith component in the mixture.

Results and discussion

Pesticide binding pattern in active LUC

As a result of docking, for each pesticide, a set of 10 plausible ligand poses was attained and they are shown in Fig. S1.† According to the scores, the best eight poses of BAY are located at the bottom of the LH₂ pocket (score = −5.9), while the other two poses are at the entrance (score = −5.1). For MET, all poses are at the bottom. Almost every pose of VEL is located at the bottom (the best score = −8.5) apart from one at the entrance (score = −6.1). In other words, all clusters of poses have an obvious inclination that all three pesticides tend to bind at the bottom of the LH₂ pocket. The best scoring pose was chosen as the initial configuration for MD.

Molecular dynamics simulations for pesticide–LUC were run and equilibrated after a 4 ns equilibrium phase according to the convergences of RMSD between the trajectory structures and the first snapshot structure in the 1 ns trajectory (Fig. S2†). The RMSD of the protein backbone of BAY–LUC stabilized around 1.29 Å from 5 to 8 ns, and the standard deviation was 0.07 Å. The convergence of RMSD was 1.56 ± 0.09 Å for MET–LUC and 1.58 ± 0.09 Å for VEL–LUC. For each complex, the lowest potential energy conformation taken from the 100 snapshots of the last 1 ns simulation was treated as the binding pattern of pesticide with LUC. The crucial residues surrounding the pesticides are shown in Fig. S3.†

The hydrogen bonds were calculated according to the following two criteria: (1) a proton donor–acceptor distance ≤ 3.5 Å, and (2) a donor–H–acceptor bond angle ≥ 120°. For BAY and MET, a hydrogen bond between the –COO– group of the pesticide and the –NH₂ group of Arg218 was observed in the lowest energy conformation. For VEL, the NH group of Arg218 donates an H to the O of the carbonyl group of VEL forming a stable hydrogen bond (3.50 Å), and another strong hydrogen bond (2.70 Å) forms between another carbonyl group of VEL and the H atom of the NH group of Arg337.

Interaction mechanism of pesticide–LUC systems

The calculated ΔG_is and their components are presented in Table S2.† The higher absolute values of ΔE or ΔG (negative value) mean stronger binding affinity.

If the polar solvation free energy ΔG_ele,sol is taken into consideration, the value of polar interaction contributions (ΔG_ELE = ΔE_ele + ΔG_ele,sol) turns out to be an unfavorable factor for binding three pesticides (9.0, 6.9, and 4.7 kcal mol⁻¹ for BAY-, MET-, and VEL–LUC, respectively), which is to a large extent determined by the desolvation energy.⁴⁴ A similar phenomenon where the contribution from ligand–protein polar interactions could not compensate for the large desolvation penalty has been found in other research.^40,45 Furthermore, ΔE_vdw is found to have a similar favorable contribution in all systems, and the nonpolar energy (ΔG_VMD = ΔE_vdw + ΔG_nonpolar,sol) term considering the nonpolar solvation term shows a more favorable contribution (−42.0, −30.6, and −44.2 kcal mol⁻¹ for BAY-, MET-, and VEL–LUC, respectively).

Considering the summation of the energy components, the calculated ΔH_is are −33.1, −23.7, and −39.5 kcal mol⁻¹ for BAY–LUC, MET–LUC, and VEL–LUC, respectively. After introduction of TΔS, the ΔG_is for BAY–LUC, MET–LUC and VEL–LUC become −13.0, −5.7 and −18.4 kcal mol⁻¹, respectively. The thermodynamic parameters (ΔH and ΔS) are the main evidence confirming the binding force.^46,47 Ross and Subramanian⁴⁸ have summed up the thermodynamic laws to determine the types of binding with various interactions. In this study, ΔH < 0 and ΔS < 0 mean that van der Waals (vDW) and hydrogen bond interactions play the main roles in the binding reaction. On the one hand, for each pesticide, either the van der Waals interaction or the nonpolar part of solvation play a crucial role in binding affinity. On the other hand, it is more convincing that the hydrogen bond interaction is responsible for providing directional constraints on binding progress.

Per pesticide-residue interactions

The ΔG_rs of 25 residues which have the highest energy contributions for each pesticide are summarized in Fig. S4.†

In addition, the three series of ΔG_ELE and ΔG_VDW energy terms of each residue are also shown in Fig. 3.

Among the three systems, there is no significant distinction in energy contributions for His221, Phe227, Gly228, Leu286, Ser347, and Val366, respectively. However, for Arg337, the energy contribution is much larger in VEL–LUC than in the other two systems (Fig. S4†), which is a consequence of a strong hydrogen bond formed between the O atom of VEL and the H atom of Arg337 (Fig. 2).

Fig. 2 Schematic view of pesticide–LUC interactions of the lowest energy conformation, where the residues enclosed by red circles and ellipses appear at least twice in three systems.

Fig. 3 (a) The binding free energy ΔG_r of the residues located in the top 25 high-energy contributions in all systems, (b) Energy contribution of ΔG_VDW (ΔE_vdw + ΔG_nonpolar,sol), and (c) Energy contribution of ΔG_ELE (ΔE_ele + ΔG_ele,sol) interaction terms for the residues of LUC with the pesticides where refers to BAY–LUC, to MET–LUC, and to VEL–LUC.

Experimental validation of additivity

Alignment of BAY–LUC, MET–LUC, and VEL–LUC shows that the three pesticides occupy the same binding site that is located at the bottom of the luciferin pocket (Fig. S3†). The hydrophobic pocket enclosed by Asn229, Phe247, Thr251, Ala313 and Ile351 offers favourable van der Waals contacts. In addition, the off-centered parallel displaced π–π stacking interactions between the aromatic rings of BAY and Arg218, VEL and Arg218, as well as MET and Arg337, lead to a high contribution of vdW energy. From the analysis of binding free energy decomposition, Arg218 and Arg337 are the crucial residues for the three pesticides bound to LUC.

Therefore, an important hypothesis was proposed that if mixture components bind to the same target site and exhibit the same binding pattern, they are supposed to have the same MOI, and the combined toxicity could be predicted by the CA model. The hypothesis was sufficiently verified by the following mixture toxicity testing. The CRC information on BAY, MET, VEL, and the 15 binary mixtures determined by the MTA are shown in Tables S1† and 1. The corresponding CRC values are shown in Fig. 4.

Fig. 4 The concentration–response curves (CRCs) for the three chemicals and 15 mixture rays where the scattered points, solid lines, short dashed lines (in red), and dash dot lines (in black) represent the experimental values, CRCs fitted, CRCs predicted by CA models, and the 95% confidence intervals of the observed effect, respectively.

The toxicities of the 15 binary mixtures follow the CA model perfectly over the entire concentration–response curves. All CRCs predicted by the CA models are located in the 95% confidence intervals, which indicates that there is no interaction between mixture components and thus, the CA is suitable to predict the mixture toxicity.

Predicting combined toxicity from ΔG_mix of a mixture

In other research, a linear relationship was reported between ΔG and the toxicity of individual pesticides.^49,50 Taking the EC₅₀ value as a toxicity index (a lower value of EC₅₀ indicating higher toxicity), the toxicity order in this study is VEL > BAY > MET (Table S1†), which is consistent with ΔG_i. In addition, a linear relationship was observed between the ΔG_i values of the three pesticide–LUC and the inhibition toxicity (lg(EC₅₀)) (Table S2†).

More importantly, among the mixture with specific p_i, we also found a linear relationship between ΔG_mix and lgEC₅₀. Taking eqn (1) into consideration, all the lgEC₅₀s of the pesticides and their mixtures with five series p_i can be expressed as a linear function of the ΔG_i of a single pesticide to LUC,

where n is the number of toxicity experiments. The high coefficient of determination (R²) indicates that the models can be applied to predict the lgEC₅₀ value of various mixtures based only on ΔG_mix obtained from eqn (1). From Fig. 5, all of the points were rather uniformly distributed around the regression line of lgEC₅₀ vs. ΔG.

Fig. 5 Plot of experimental toxicity (lgEC₅₀) vs. binding free energies from MM/GBSA using AMBER where ■ (in red) refers to the single pesticide and ● (in black) to the binary mixtures.

Conclusions

We have presented an in silico method to identify the MOI based on ligand–receptor interactions between specific pesticide molecules and the luciferase biomacromolecule. The toxicity test results show that all of the toxicities of the mixtures combined from the three pesticides, which are classified into the same MOI model with the same binding sites, can be predicted perfectly using the CA model. In addition, linear models based on ΔG_mix are developed to predict the EC₅₀s of the 15 binary mixtures composed of different p_i values.

Acknowledgements

The authors are especially grateful to the National Natural Science Foundation of China (21377097) and the Specialized Research Fund for the Doctoral Program of Higher Education (no. 20120072110052) for their financial support.

References

1. T. Backhaus and M. Faust, Environ. Sci. Technol., 2012, 46, 2564–2573.
2. N. Cedergreen, A. M. Christensen, A. Kamper, P. Kudsk, S. K. Mathiassen, J. C. Streibig and H. Sorensen, Environ. Toxicol. Chem., 2008, 27, 1621–1632.
3. C. A. Laetz, D. H. Baldwin, T. K. Collier, V. Hebert, J. D. Stark and N. L. Scholz, Environ. Health Perspect., 2009, 117, 348–353.
4. S. Loewe and H. Muischnek, Naunyn-Schmiedebergs Arch. Exp. Pathol. Pharmakol., 1926, 114, 313–326.
5. C. I. Bliss, Ann. Appl. Biol., 1939, 26, 585–615.
6. L.-T. Qin, S.-S. Liu, J. Zhang and Q.-F. Xiao, Toxicology, 2011, 280, 164–172.
7. N. Dom, M. Penninck, D. Knapen and R. Blust, Chemosphere, 2012, 87, 742–749.
8. P. L. Piotrowski, B. G. Sumpter, H. V. Malling, J. S. Wassom, P. Y. Lu, R. A. Brothers, G. A. Sega, S. A. Martin and M. Parang, J. Chem. Inf. Model., 2007, 47, 676–685.
9. S. Spycher, E. Pellegrini and J. Gasteiger, J. Chem. Inf. Model., 2005, 45, 200–208.
10. S. Brosche and T. Backhaus, Aquat. Toxicol., 2010, 99, 457–465.
11. N. Thorne, J. Inglese and D. S. Auld, Chem. Biol., 2010, 17, 646–657.
12. N. Thorne, M. Shen, W. A. Lea, A. Simeonov, S. Lovell, D. S. Auld and J. Inglese, Chem. Biol., 2012, 19, 1060–1072.
13. L. P. da Silva and J. da Silva, ChemPhysChem, 2012, 13, 2257–2262.
14. D. S. Auld, N. Thorne, D.-T. Nguyen and J. Inglese, ACS Chem. Biol., 2008, 3, 463–470.
15. D. S. Auld, Y.-Q. Zhang, N. T. Southall, G. Rai, M. Landsman, J. MacLure, D. Langevin, C. J. Thomas, C. P. Austin and J. Inglese, J. Med. Chem., 2009, 52, 1450–1458.
16. D. S. Auld, N. T. Southall, A. Jadhav, R. L. Johnson, D. J. Diller, A. Simeonov, C. P. Austin and J. Inglese, J. Med. Chem., 2008, 51, 2372–2386.
17. P. G. Cruz, D. S. Auld, P. J. Schultz, S. Lovell, K. P. Battaile, R. MacArthur, M. Shen, G. Tamayo-Castillo, J. Inglese and D. H. Sherman, Chem. Biol., 2011, 18, 1442–1452.
18. D. S. Auld, S. Lovell, N. Thorne, W. A. Lea, D. J. Maloney, M. Shen, G. Rai, K. P. Battaile, C. J. Thomas, A. Simeonov, R. P. Hanzlik and J. Inglese, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4878–4883.
19. G. Rastelli, A. Del Rio, G. Degliesposti and M. Sgobba, J. Comput. Chem., 2010, 31, 797–810.
20. H.-L. Ge, S.-S. Liu, X.-W. Zhu, H.-L. Liu and L.-J. Wang, Environ. Sci. Technol., 2011, 45, 1623–1629.
21. E. Conti, N. P. Franks and P. Brick, Structure, 1996, 4, 287–298.
22. Y. Mao, Protein Eng., Des. Sel., 2011, 24, 341–349.
23. A. Szarecka, Y. Xu and P. Tang, Biophys. J., 2007, 93, 1895–1905.
24. A. T. Brunger, P. D. Adams, G. M. Clore, W. L. DeLano, P. Gros, R. W. Grosse-Kunstleve, J. S. Jiang, J. Kuszewski, M. Nilges, N. S. Pannu, R. J. Read, L. M. Rice, T. Simonson and G. L. Warren, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1998, 54, 905–921.
25. R. A. Laskowski and M. B. Swindells, J. Chem. Inf. Model., 2011, 51, 2778–2786.
26. S. Shanmugasundararaj, S. Lehle, H. I. Yamodo, S. S. Husain, C. Tseng, K. Nguyen, G. H. Addona and K. W. Miller, PLoS One, 2012, 7, e29854.
27. J. Gasteiger and M. Marsili, Tetrahedron, 1980, 36, 3219–3228.
28. O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461.
29. L. K. Wolf, Chem. Eng. News, 2009, 87(28), 31.
30. R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210.
31. J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
32. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725.
33. E. Pauwels, D. Claeys, J. C. Martins, M. Waroquier, G. Bifulco, V. Van Speybroeck and A. Madder, RSC Adv., 2013, 3, 3925–3938.
34. D. Zanuy, B. Teixeira-Dias, L. J. del Valle, J. Poater, M. Sola and C. Aleman, RSC Adv., 2013, 3, 2639–2649.
35. F. Chen, S. S. Liu and X. T. Duan, Acta Chim. Sin., 2013, 71, 1035–1040.
36. P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. H. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case and T. E. Cheatham, Acc. Chem. Res., 2000, 33, 889–897.
37. J. Kottalam and D. A. Case, Biopolymers, 1990, 29, 1409–1421.
38. Y. Yang, J. Qin, H. Liu and X. Yao, J. Chem. Inf. Model., 2011, 51, 680–692.
39. V. Zoete, M. Meuwly and M. Karplus, Proteins: Struct., Funct., Bioinf., 2005, 61, 79–93.
40. Y.-X. Shao, P. Zhao, Z. Li, M. Liu, P. Liu, M. Huang and H.-B. Luo, Eur. Biophys. J. Biophys. Lett., 2012, 41, 297–306.
41. X. W. Zhu, S. S. Liu, H. L. Ge and Y. Liu, Water Res., 2009, 43, 1731–1739.
42. R.-N. Dou, S.-S. Liu, L.-Y. Mo, H.-L. Liu and F.-C. Deng, Environ. Sci. Pollut. Res., 2011, 18, 734–742.
43. E. Silva, N. Rajapakse, M. Scholze, T. Backhaus, S. Ermler and A. Kortenkamp, Toxicol. Sci., 2011, 122, 383–394.
44. W. Khuntawee, T. Rungrotmongkol and S. Hannongbua, J. Chem. Inf. Model., 2012, 52, 76–83.
45. J. Guo, X. Wang, H. Sun, H. Liu and X. Yao, J. Mol. Model., 2012, 18, 1421–1430.
46. X. Y. Xie, W. J. Lu and X. G. Chen, J. Hazard. Mater., 2013, 248, 347–354.
47. Y. Teng, R. T. Liu, C. Li, Q. Xia and P. J. Zhang, J. Hazard. Mater., 2011, 190, 574–581.
48. P. D. Ross and S. Subramanian, Biochemistry, 1981, 20, 3096–3102.
49. D. Liang, J. Gao, Y. Cheng, W. Cui, H. Zhang and M. Ji, Bioorg. Med. Chem. Lett., 2011, 21, 6630–6635.
50. H. Zhang, Y. Yao, H. Yang, X. Wang, Z. Kang, Y. Li, G. Li and Y. Wang, Insect Biochem. Mol. Biol., 2012, 42, 583–595.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra02698e

---