Fe₂MnSi_xGe_1−x: influence thermoelectric properties of varying the germanium content

Abstract

The semi-classical Boltzmann theory, as implemented in the BoltzTraP code, was used to study the influence of varying the germanium content on the thermoelectric properties of the Heusler compounds, Fe₂MnSi and Fe₂MnGe. The electrical conductivity (σ/τ), the Seebeck coefficient (S), the electronic power factor (S²σ), the electronic thermal conductivity (κ_e), the electronic heat capacity c_el(T_el), and the Hall coefficient (R_H), as a function of temperature at certain values of chemical potential (μ) with constant relaxation time (τ), were evaluated on the basis of the calculated band structure using the standard Boltzmann kinetic transport theory and the rigid band approach. The increase/reduction in the electrical conductivity (σ = neμ) of Fe₂MnSi_xGe_1−x alloys is attributed to the density of charge carriers (n) and their mobility (μ = eτ/m_e). The S for Fe₂MnGe is negative over the entire temperature range, which represents the n-type concentration. Whereas Fe₂MnSi shows a positive S up to 250 K and then drops to negative values, which confirms the existence of the p-type concentration between 100–250 K. Fe₂MnSi_0.25Ge_0.75/Fe₂MnSi_0.5Ge_0.5/Fe₂MnSi_0.75Ge_0.25 possess positive S up to 270/230/320 K and then drop to negative values. The power factor of Fe₂MnGe rapidly increases with increasing temperature, while for Fe₂MnSi it is zero up to 300 K, and then rapidly increases with increasing temperature. The S²σ of Fe₂MnSi_0.25Ge_0.75 is zero between 250–350 K, whereas Fe₂MnSi_0.5Ge_0.5 possesses a zero S²σ of up to 320 K. Fe₂MnSi_0.75Ge_0.25 has a zero S²σ between 200 and 500 K. The electronic thermal conductivity (κ_e) and the electronic heat capacity c_el(T_el) increases with increasing temperature. The parent compounds (Fe₂MnGe and Fe₂MnSi) show the highest positive value of the Hall coefficient R_H at 100 K, and then drop to negative values at 260 K. On the other hand, the R_H for Fe₂MnSi_0.25Ge_0.75, Fe₂MnSi_0.5Ge_0.5 and Fe₂MnSi_0.75Ge_0.25 alloys exhibit negative R_H along the temperature scale. The behavior of R_H is attributed to the concentration of the charge carriers and their mobility.

---

1. Introduction

Half metallic compounds have received a significant amount of attention^1–13 because of the spin degree of freedom in electronics.^14–17 Significant effort has been paid to understanding the mechanism behind half-metallic magnetism and to study its implications on various physical properties.^18,19 The field of spin-based electronics (spintronics) aims to exploit a large class of emerging materials, such as ferromagnetic semiconductors,^20,21 high temperature superconductors,²² organic ferromagnets,^23,24 organic semiconductors,²⁵ and carbon nanotubes^26,27 based devices to bring novel functionalities to traditional devices. In other areas within spintronics, as high as possible a degree of spin polarisation is required, for which half metals are considered the best options. Half-metallic compounds behave as metals in one spin direction, and behave as semiconductors or insulators in the opposite spin direction.

In 1983, De Groot et al.^28,29 discovered the half-metallic ferromagnetic (HMF). Ever since this discovery, extensive studies have been carried out and many HMF compounds have been theoretically predicted, and some of them experimentally confirmed.^30–32 It is well known that the most important candidates for 100% spin polarization are semi-Heusler alloys,^{19,28,29,33–35} zinc-blende structured materials,^36,37 semi-metallic magnetic oxides CrO₂ and Fe₃O₄,^11,38,39 and full Heusler alloys.^9,40 Fe₂MnSi_1−xGe_x alloys are considered as very interesting HMF materials.^41–43 Fe₂MnSi_1−xGe_x alloys can be successfully applied to highly efficient spin injection and detection through Schottky tunnel barriers in group-IV semiconductor devices.

Epitaxial Fe₂MnSi thin films have a Curie temperature of about 210 K, which is much lower than room temperature;⁴⁴ however, only limited experimental work has been done on these materials. Zhang et al. have studied Fe₂MnSi_1−xGe_x alloys and found there is no significant change in the Curie temperature and the spontaneous magnetization, with change the Ge content in the single-phase L2₁ compounds. There is no field-induced transition and the magneto-caloric effect is rather small throughout the Fe₂MnSi_1−xGe_x series.⁴⁵ In addition, in the L2₁-type structure, both Fe₂MnGe and Fe₂MnSi have a Curie temperature of around 250 K.⁴⁵ Therefore, it is worth studying the transport properties of Fe₂MnSi_xGe_1−x alloys by varying the germanium content between 0.0 and 1.0, in steps of 0.25 atoms.

The rest of the paper is organized as; the structural aspects and the computational details are presented in Section 2. The results and discussion are demonstrated in Section 3. Section 4 summarizes the results.

2. Structural aspects and computational details

To study the influence of varying the germanium content on the thermoelectric properties of the Heusler compounds Fe₂MnSi and Fe₂MnGe, the semi-classical Boltzmann theory as implemented in the BoltzTraP code⁴⁶ was used. The thermoelectric transport tensors can be evaluated on the basis of the calculated band structure using the standard Boltzmann kinetic transport theory and the rigid band approach.⁴⁷ The electrical conductivity σ_αβ, the Seebeck coefficient S_αβ, and the electronic thermal conductivity k⁰_αβ tensors are the main transport properties.

In this work, the germanium content in Fe₂MnSi_xGe_1−x alloys was varied between 0.0 and 1.0, in steps of 0.25 atoms. The parent compounds crystallize in the L2₁ structure, which consists of four face-centered cubic sublattices with space Fm3̄m. The L2₁ phase is a cubic superstructure of four interpenetrating fcc sublattices, A, B, C, and D, centered at (0 0 0), (1/4 1/4 1/4), (1/2 1/2 1/2), and (3/4 3/4 3/4). Each A atom is at the center of a cube of four B atoms and four D atoms (Fig. 1). To trace the variation in the composition, we employed the supercell approach. The electronic structure was calculated using the full potential linear augmented plane wave, plus the local orbitals method, as implemented in WIEN2k code⁴⁸ with the Engel–Vosko generalized gradient approximation for the exchange–correlation potential. The structures were fully relaxed by minimizing the forces acting on each atom. A mesh of 5000 k-points in the irreducible Brillouin zone (IBZ) for binary, as well as for ternary alloys, was used for calculating the thermoelectric properties. The K_max was set at 9.0/R_MT and made the expansion up to l = 10 in the muffin tins spheres. The convergence of the total energy in the self-consistent calculations was taken with respect to the total charge of the system with a tolerance 0.0001 electron charges.

Fig. 1 Structure of the unit cell of Fe₂MnSi_xGe_1−x (x = 0.0, 0.25, 0.5, 0.75 and 1.0) alloys.

3. Results and discussion

3.1. Salient features of the electronic band structures

The calculated electronic band structure of Fe₂MnSi_xGe_1−x (x = 0.0, 0.25, 0.5, 0.75, 1.0) alloys along the high symmetry point in the first BZ are represented in Fig. 2a–e. These figures suggest that the investigated alloys are metallic, as it is clear that there exists some bands that controlled the overlapping around the Fermi energy (E_F). The density of states at E_F is determined by the overlap between the valence and conduction bands. This overlap is strong enough, indicating a metallic origin with different values of DOS at E_F, N(E_F) (Table 1). The electronic specific heat coefficient (γ), which is function of the density of states, can be calculated using the expression,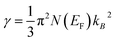 , where N(E_F) is the density of states at E_F, and k_B is the Boltzmann constant. The calculated density of states at the Fermi energy N(E_F) enables us to calculate the bare electronic specific heat coefficient (Table 1). It is clear that substituting 0.25 Ge atoms by Si atoms leads to increasing the metallic nature of Fe₂MnSi_0.25Ge_0.75 by 3.7% with respect to Fe₂MnGe, while substituting 0.5 Ge atoms by Si atoms causes an increase in the metallic nature of Fe₂MnSi_0.5Ge_0.5 by 1.9% with respect to Fe₂MnGe. Further increasing the continent of Si atoms leads to increasing the metallic nature of Fe₂MnSi_0.75Ge_0.25 by 3% with respect to Fe₂MnGe, and finally substituting Ge by Si causes a reduction of the metallic nature of Fe₂MnSi by 0.9% with respect to Fe₂MnGe. The same trends were observed for the electronic specific heat coefficient (γ).

Fig. 2 (a–e) Calculated electronic band structure of Fe₂MnSi_xGe_1−x (x = 0.0, 0.25, 0.5, 0.75 and 1.0) alloys.

Table 1 Density of states at Fermi energy N(E_F) states per eV cell and bare electronic specific heat coefficient γ (mJ mol⁻¹ K⁻²) of Fe₂MnSi_xGe_1−x (x = 0.0, 0.25, 0.5, 0.75, 1.0) alloys

	Fe2MnGe	Fe2MnSi0.25Ge0.75	Fe2MnSi0.5Ge0.5	Fe2MnSi0.75Ge0.25	Fe2MnSi
N(EF)states per eV cell	17.11	65.0	33.93	58.15	16.07
γ (mJ mol^−1 K^−2)	2.96	11.27	5.88	10.08	2.78

---

3.2. Transport properties

Fig. 3a illustrates the influence of substituting Ge by Si (in steps of 0.25 atoms) on the electrical conductivity (σ/τ) of the Heusler compounds Fe₂MnGe and Fe₂MnSi. In all cases, we notice that σ/τ increases with temperature, and it is clear that the increasing rate is dependent on the concentration of Ge and Si atoms. The end compounds (Fe₂MnGe and Fe₂MnSi) show the highest value for Fe₂MnSi of about 1.49 × 10²⁰ (Ω ms)⁻¹ at 100 K and 1.9 × 10²⁰ (Ω ms)⁻¹ at 800 K; while for Fe₂MnGe, it is 1.4 × 10²⁰ (Ω ms)⁻¹ at 100 K and 1.82 × 10²⁰ (Ω ms)⁻¹ at 800 K. With substituting 0.25 Ge by Si (Fe₂MnSi_0.25Ge_0.75), we notice that the value of σ/τ drops to the lowest values along the whole temperature range. Then, increasing the content of Si atoms to be equal to Ge atoms (Fe₂MnSi_0.5Ge_0.5) causes an increase in the electrical conductivity to its maximum value of about 1.1 × 10²⁰ (Ω ms)⁻¹ at 100 K and 1.4 × 10²⁰ (Ω ms)⁻¹ at 800 K. Further increasing the content of Si atoms (Fe₂MnSi_0.75Ge_0.25) leads to a reduction in the electrical conductivity to 0.9 × 10²⁰ (Ω ms)⁻¹ at 100 K and 1.3 × 10²⁰ (Ω ms)⁻¹ at 800 K. From above, we can conclude that the increase/reduction in the electrical conductivity of Fe₂MnSi_xGe_1−x alloys is attributed to the density of charge carriers (n) and their mobility (μ = eτ/m_e), since the electrical conductivity (σ = neμ) is related to the density of charge carriers and their mobility.

Fig. 3 (a) Calculated electrical conductivity; (b) calculated Seebeck coefficient; (c) calculated power factor; (d) calculated electronic thermal conductivity; (e) calculated electronic heat capacity; (f) calculated Hall coefficient.

The Seebeck coefficient S_αβ and the electrical conductivity σ_αβ tensors can be written as:^47,49

From the above formulas, it is clear that the Seebeck coefficient is inversely proportional to the electrical conductivity, and that these quantities are functions of temperature (T) and chemical potential (μ).^47,49

Fig. 3b illustrates the Seebeck coefficient (S) as a function of temperature at certain values of chemical potential (μ). Following Fig. 3b, one can see that the S for Fe₂MnGe is negative over the entire temperature range, which represents the n-type concentration. It is clear that S reduces rapidly with increasing the temperature, and it possesses a maximum value at 100 K (−0.2 × 10⁻⁵ V K⁻¹) and the lowest value at 800 K. Whereas, Fe₂MnSi shows positive S up to 250 K, and then drop to negative values, which confirms the existence of the p-type concentration between 100 K and 250 K. When we substitute 0.25 Ge atoms by Si (Fe₂MnSi_0.25Ge_0.75), we notice that the Seebeck coefficient shows the maximum positive value at 100 K (0.9 × 10⁻⁵ V K⁻¹), and then reduces with increasing the temperature up to 270 K. Above this temperature, S drops to negative values, to reach the lower value of about (−0.7 × 10⁻⁵ V K⁻¹) at 800 K.

With substituting half the content of Ge atoms by the same content of Si atoms (Fe₂MnSi_0.5Ge_0.5), we notice that the Seebeck coefficient reduced, to show a maximum value at 100 K of about (0.2 × 10⁻⁵ V K⁻¹), and then drops to negative values at 230 K to reach −0.8 × 10⁻⁵ V K⁻¹ at 800 K. In further increasing the Si content at the cost of the Ge content (Fe₂MnSi_0.75Ge_0.25), the value of the Seebeck coefficient at 100 K increases to 0.6 × 10⁻⁵ V K⁻¹ with respect to the value of S obtained for Fe₂MnSi_0.5Ge_0.5, and then drops to negative values at 320 K.

Fig. 3c shows the electronic power factor (S²σ) verses the temperature at certain values of chemical potential (μ) and constant relaxation time (τ). We notice that the power factor of Fe₂MnGe rapidly increases with increasing the temperature, to reach the maximum value (9 × 10¹⁰ W m⁻¹ K⁻² s⁻¹) at 800 K. While for Fe₂MnSi, the power factor is zero up to 300 K, and then rapidly increases with increasing temperature to reach the maximum value (3.9 × 10¹⁰ W m⁻¹ K⁻² s⁻¹) at 800 K. With replacing 0.25 Ge atoms by Si (Fe₂MnSi_0.25Ge_0.75), the power factor increases with respect to all other concentrations, and shows its maximum value of about (0.8 × 10¹⁰ W m⁻¹ K⁻² s⁻¹) at 100 K, and then reduces with increasing temperature to reach a zero value of S²σ between 250 K and 350 K. Above this temperature range, S²σ increases with increasing temperature, to reach 0.2 × 10¹⁰ W m⁻¹ K⁻² s⁻¹ at 800 K. Substituting 0.5 of Ge atoms by Si (Fe₂MnSi_0.5Ge_0.5) causes the power factor to drop to zero up to 320 K. Then above 350 K, the power factor increases with increasing temperature, to reach 1.0 × 10¹⁰ W m⁻¹ K⁻² s⁻¹ at 800 K. In the last case (Fe₂MnSi_0.75Ge_0.25), when we reduced the content of Ge to 0.25, the power factor became 0.4 × 10¹⁰ W m⁻¹ K⁻² s⁻¹ at 100 K, and then dropped to zero between 200 K and 500 K, while above 500 K, the Seebeck coefficient showed an insignificant increase to reach 0.2 × 10¹⁰ W m⁻¹ K⁻² s⁻¹ at 800 K.

The electronic thermal conductivity (κ_e) can be estimated from the electrical conductivity (σ) using Wiedemann–Franz's law. Fig. 3d illustrate κ_e for Fe₂MnSi_xGe_1−x alloys as a function of temperature at certain values of chemical potential. We notice that for all Fe₂MnSi_xGe_1−x alloys, κ_e increases rapidly with increasing temperature. The end compound Fe₂MnSi shows the highest value of κ_e between 100 K and 800 K. While κ_e for Fe₂MnGe lies directly below that of Fe₂MnSi exhibiting the same trend. When we replace a quarter of the Ge atoms by Si (Fe₂MnSi_0.25Ge_0.75), the thermal conductivity drops down to the lowest value along the temperature scale. With increasing the content of Si atoms to be equal to that of Ge atoms (Fe₂MnSi_0.5Ge_0.5), we can see that the κ_e values increases along the temperature scale. Substituting more Ge atoms by Si atoms (Fe₂MnSi_0.75Ge_0.25) leads to a reduction in the values of the electronic thermal conductivity with respect to that of Fe₂MnSi_0.5Ge_0.5. Following Fig. 3d, we can conclude that the electronic thermal conductivity is very sensitive to the density of the charge carriers and their mobility. The thermal conductivity has contributions from the lattice and electrons, but BoltzTraP calculates only the electronic part. In the absence of any calculations or measurements of the lattice thermal conductivity, it is difficult to confirm which alloy will have the largest figure of merit (FOM).

The electronic heat capacities c_el(T_el) for Fe₂MnSi_xGe_1−x alloys as a function of temperature at certain values of chemical potential with constant relaxation time are plotted in Fig. 3e. Here, we consider only the electronic contribution to the specific heat, because there is a linear relationship between the electronic specific heat and temperature i.e., c_el(T_el) = γT_el, where γ = the Sommerfeld coefficient.^50,51 The electrons are excited to the upper empty space and there is a smearing of Fermi below the Fermi level, which together contribute to the heat capacity. From Fig. 3e, we can see that the heat capacity for the end compounds (Fe₂MnGe and Fe₂MnSi) slowly increases with temperature up to 500 K, and then reach saturation up to 800 K. Fe₂MnSi_0.25Ge_0.75 alloy shows higher values of c_el(T_el) compared to the parents. Increasing the Si content (Fe₂MnSi_0.5Ge_0.5) causes a reduction in the c_el(T_el) lower than that of Fe₂MnSi_0.25Ge_0.75 but higher than that of the parents. Further increasing the Si content (Fe₂MnSi_0.75Ge_0.25) causes an increase in c_el(T_el), showing the highest value among the others. It is clear from Fig. 3e that the electronic heat capacity of Fe₂MnSi_xGe_1−x alloys obey the Debye approximation (T³), also called the “anharmonic approximation”.⁵²

Fig. 3f presents the Hall coefficient R_H as a function of temperature; its value depends on the type, number, and properties of the charge carriers that constitute the current. It is clear that the parents compounds (Fe₂MnGe and Fe₂MnSi) show the highest positive value of R_H at 100 K, which then rapidly reduces with increasing temperature to cross the zero line and then reach negative values at 260 K. Above 360 K, the R_H for the parents compounds is almost saturated. The R_H for Fe₂MnSi_0.25Ge_0.75, Fe₂MnSi_0.5Ge_0.5 and Fe₂MnSi_0.75Ge_0.25 alloys exhibits negative R_H along the temperature scale, which is attributed to the concentration of the charge carriers and their mobility.

To the best of our knowledge, there are no previous experimental data or theoretical results for the thermoelectric properties of the investigated materials available in literature to make a meaningful comparison. We would like to mention here that in our previous works^53–59 we calculated the band gap, bond lengths, bond angles, and linear and nonlinear optical susceptibilities using the FPLAPW method on several systems whose energy band gap, bond lengths, bond angles, and linear and nonlinear optical susceptibilities are known experimentally. We achieved very good agreement with the experimental data. Thus, we believe that our calculations reported in this paper could produce very accurate and reliable results, which therefore confirms the accuracy of the method used.

4. Conclusions

The full potential linear augmented plane wave plus local orbitals method, as implemented in WIEN2k code with the Engel–Vosko generalized gradient approximation for the exchange–correlation potential, were used to calculated band structure for Fe₂MnSi_xGe_1−x (x = 0.0, 0.25, 0.5, 0.75 and 1.0) alloys. Based on the calculated band structure, the semi-classical Boltzmann theory as implemented in the BoltzTraP code was used to study the influence of varying the germanium content on the thermoelectric properties of Fe₂MnSi_xGe_1−x alloys as a function of temperature at certain values of chemical potential (μ) with a constant relaxation time (τ). The increase/reduction in the electrical conductivity (σ = neμ) of Fe₂MnSi_xGe_1−x alloys is attributed to the density of charge carriers (n) and their mobility (μ = eτ/m_e). The parent Fe₂MnGe compound exhibits negative S over the entire temperature range, which confirms the existence of an n-type carrier. While Fe₂MnSi shows positive S up to 250 K, and then drops to negative values, to represent the p-type charge carrier between 100 K and 250 K. The alloys Fe₂MnSi_0.25Ge_0.75/Fe₂MnSi_0.5Ge_0.5/Fe₂MnSi_0.75Ge_0.25 all possess positive S up to 270/230/320 K. Above these temperatures, the Seebeck coefficient exhibits negative values. The power factor of Fe₂MnGe rapidly increases with increasing temperature, while for Fe₂MnSi it is zero up to 300 K, and then rapidly increases with increasing temperature. Fe₂MnSi_0.25Ge_0.75 has a zero power factor between 250 K and 350 K. While Fe₂MnSi_0.5Ge_0.5 shows a zero power factor up to 320 K. The Fe₂MnSi_0.75Ge_0.25 alloy shows a zero power factor between 200 K and 500 K. The electronic thermal conductivity (κ_e) and the electronic heat capacity c_el(T_el) increase with increasing temperature. The parent compounds show the highest positive value of R_H at 100 K, and then drop to negative values at 260 K. The alloys Fe₂MnSi_0.25Ge_0.75, Fe₂MnSi_0.5Ge_0.5 and Fe₂MnSi_0.75Ge_0.25 alloys exhibit negative R_H along the temperature scale. The positive and negative behavior of R_H is attributed to the concentration of the charge carriers and their mobility.

Acknowledgements

The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI program. Computational resources were provided by MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures.

References

1. K. E. H. M. Hanssen, P. E. Mijnarends, L. P. L. M. Rabou and K. H. J. Buschow, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1533.
2. H. Kino, F. Aryasetiawanx, I. Solovyer, T. Miyake, T. Ohno and K. Terakura, Phys. B, 2003, 329, 858.
3. R. A. de Groot, Phys. B, 1991, 172, 45.
4. J. H. Wijngaard, C. haas and R. A. de Groot, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 9318.
5. S. Chadov, J. Minar, H. Ebert, A. Perlov, L. Chioncel, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 140411.
6. B. I. Min, T. Oguchi, H. J. F. Jansen and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 324.
7. G. A. de Wijs and R. A. de Groot, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 020402.
8. E. Kisker, C. Carbone, C. F. Flipse and E. F. Wassermann, J. Magn. Magn. Mater., 1987, 70, 21.
9. I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429.
10. K. Nagao, M. Shirai and Y. Miura, J. Phys.: Condens. Matter, 2004, 16, 5725.
11. K. Schwarz, J. Phys. F: Met. Phys., 1986, 16, 211.
12. I. I. Mazin, D. J. Singh and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 411.
13. G. L. Zhao, J. Callaway and M. Hayashibara, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 15781.
14. G. A. Prinz, Science, 1998, 282, 1660.
15. S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488.
16. I. Zutic, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323.
17. D. D. Awschalom and M. E. Flatte, Nat. Phys., 2007, 3, 153.
18. T. Akimoto, Y. Moritomo, A. Nakamura and N. Furukawa, Phys. Rev. Lett., 2000, 85, 3914.
19. C. M. Fang, G. A. de Wijs and R. A. de Groot, J. Appl. Phys., 2002, 91, 8340.
20. H. Ohno, Science, 1998, 281, 951.
21. S. J. Pearton, C. R. Abernathy, M. E. Overberg, G. T. Thaler, D. P. Norton, N. Theodoropoulou, A. F. Hebard, Y. D. Park, F. Ren, J. Kim and L. A. Boatner, J. Appl. Phys., 2003, 93, 1.
22. A. M. Goldman, V. Vasko, P. Kraus, K. Nikolaev and V. A. Larkin, J. Magn. Magn. Mater., 1999, 200, 69.
23. V. Dediu, M. Murgia, F. C. Matacotta, C. Taliani and S. Barbanera, Solid State Commun., 2002, 122, 181.
24. A. J. Epstein, MRS Bull., 2003, 28, 492.
25. D. A. Pejakovic, C. Kitamura, J. S. Miller and A. J. Epstein, Phys. Rev. Lett., 2002, 88, 057202.
26. B. Zhao, I. Monch, H. Vinzelberg, T. Muhl and C. M. Schneider, Appl. Phys. Lett., 2002, 80, 3144.
27. K. Tsukagoshi, B. W. Alphenaar and H. Ago, Nature, 1999, 401, 572.
28. R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024.
29. R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, J. Appl. Phys., 1984, 55, 2151.
30. J. W. Dong, L. C. Chen, J. C. Palmstom, R. D. James and S. Mckernan, Appl. Phys. Lett., 1999, 75, 1443.
31. S. M. Watta, S. Wirth, S. Von Molnar, A. Barry and J. M. D. Coey, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9621.
32. F. J. Jedema, A. T. Filip and B. van Wees, Nature, 2001, 410, 345.
33. J. Kubler, Phys. B, 1984, 127, 257.
34. K. E. H. M. Hanssen and P. E. Mijnarends, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5009.
35. I. Galanakis, S. Ostanin, M. Alouani, H. Dreysse and J. M. Wills, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 4093.
36. B. G. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 172411.
37. I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 012406.
38. S. P. Lewis, P. B. Allen and T. Sasaki, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10253.
39. R. A. de Groot and K. H. J. Buschow, J. Magn. Magn. Mater., 1986, 54, 1377.
40. I. Galanakis, J. Phys.: Condens. Matter, 2002, 14, 6329.
41. S. Fujii, S. Ishida and S. Asano, J. Phys. Soc. Jpn., 1995, 64, 185.
42. L. Hongzhi, Z. Zhiyong, M. Li, X. Shifeng, L. Heyan, Q. Jingping, L. Yangxian and W. Guangheng, J. Phys. D: Appl. Phys., 2007, 40, 7121.
43. B. Hamad, J. Khalifeh, I. Adu Aljarayesh, C. Demangeat, H.-B. Luo and Q.-M. Hu, J. Appl. Phys., 2010, 107, 09311.
44. K. Ueda, K. Hamaya, K. Yamamoto, Y. Ando, T. Sadoh, Y. Maeda and M. Miyao, Appl. Phys. Lett., 2008, 93, 112108.
45. L. Zhang, E. Bruck, O. Tegus, H. H. J. Buschow and F. R. de Boer, Phys. B, 2003, 328, 295.
46. G. K. H. Madsen and D. J. Singh, cond-mat.mtrl-sci., 8 February 2006.
47. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
48. P. Blaha, K. Schwarz, G. Madsen, D. Kvasnika and K. Luitz, WIEN2k, Technical Universität Wien, Austria, 2001, ISBN 3-9501031-1-2.
49. P. Hua, W. C. Lei, L. J. Chao, Z. Rui-Zhi, W. Hong-Chao and S. Y. Chin, Phys. B, 2011, 20(4), 046103.
50. N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston, New York, 1976.
51. Z. Zhang, Nano/Microscale Heat Transfer, McGraw-Hill, New York, 2007.
52. C. Dong, et al., Chin. Phys. B DOI:1674-1056/2009/18(02)/0738-06.
53. A. H. Reshak, S. Auluck and I. V. Kityk, J. Phys.: Condens. Matter, 2008, 20, 145209.
54. A. H. Reshak, S. Auluck and I. V. Kityk, J. Solid State Chem., 2008, 181, 789–795.
55. A. H. Reshak, J. Chem. Phys., 2006, 124, 104707.
56. A. H. Reshak, Eur. Phys. J. B, 2005, 47, 503–508.
57. A. H. Reshak, I. V. Kityk and S. Auluck, J. Phys. Chem. B, 2010, 114, 16705–16712.
58. A. H. Reshak, S. Auluck, D. Stys, I. V. Kityk, H. Kamarudin, J. Berdowski and Z. Tylczynskif, J. Mater. Chem., 2011, 21, 17219.
59. A. H. Reshak, M. Piasecki, S. Auluck, I. V. Kityk, R. Khenata, B. Andriyevsky, C. Cobet, N. Esser, A. Majchrowski, M. S'wirkowicz, R. Diduszko and W. Szyrski, J. Phys. Chem. B, 2009, 113(46), 15237.

---