Carbon nanotubes adsorb U atoms differently in their inner and outer surfaces

Abstract

Effective clean up of radioactive waste remains one of the fundamental challenges in nuclear sciences due to the ever growing concern on the safety of nuclear power. Carbon nanotubes have recently shown encouraging promise in their potential capability of U atom adsorption and removal. In this paper, we used first-principles density functional theory (DFT) to illustrate the adsorption and interactions between U atoms and the inner/outer surfaces of a single-walled carbon nanotube. Our DFT calculations showed that when U atoms were adsorbed on each of the CNT surfaces, the ground electronic states were all quintet. However, U atoms showed differential adsorption modes depending on the surface, binding to bridge sites on the inner surface, and to hole sites on the outer surface. The interior adsorption was more stable with an interaction energy of about 1 eV greater than that of the external one, which is explained by their different ground state electronic structures. The electronic states were largely influenced by the ferromagnetic coupling between the U atoms and the net spintronics of the CNT only for the internal adsorption case, with the external adsorption mainly determined by the U atoms. Orbital and charge analysis show that compared to the external adsorption, there were about 1.0e more charge transfers between the internally adsorbed U atom and the CNT, which facilitated stronger donor–acceptor interactions. Further analysis on the density of states indicated that the internal adsorption had a larger bonding area between the U atoms and CNT, supporting the stronger internal adsorption.

---

Introduction

While, the active chemical properties and distinctive electronic structures of actinide elements have been used to advance nuclear energy and fuel efforts,^1,2 the issue of radioactive waste management still remains a major challenge.³ Recent advances in nanoscience and nanotechnology related to carbon-based nanomaterials^4,5 have led to promising applications of carbon nanotubes (CNTs) and graphene for waste treatment and extraction of actinide materials.^6–11 These exciting uses are possible due to the unique nature of the interaction between 5f electrons of actinides (such as U element) and p electrons of carbon materials, which is important and challenging in fundamental science.^12,13 Similarly to other carbon-based nano-materials, CNTs are known to possess remarkable physico-chemical properties such as quantum effects, electron conduction and absorption capacity, causing them to enhance the electrical properties of composite materials and production of many adsorption materials, including those for waste treatment.^14–21 Until recently, CNT has mainly been used in the laboratory as an adsorbent to remove trace contaminants in water.^19,20 Essentially, these applications should attribute to a fundamental quantum mechanism of the interaction between actinide and carbon-based systems, and it is also important and challenging to study this.

Being a typical carbon nanomaterial that can be extended infinitely in one dimension,^22,23 CNTs exhibit distinct structural and dynamic characteristics on the interaction with the substances internally confined or adsorbed on its outer surface. This can be utilized with great potential in applications such as confinement of water, transport of gas molecules,^24,25 and adjustment of the electronic structure of CNT.^26,27 Experimental and theoretical studies have shown that CNT can adsorb the uranyl formed by actinides,^9,28 and some of the adsorption is reversible.^11,29 However, compared to the zero-dimensional fullerene carbon material, there is little understanding of the basic physical and chemical interactions mechanism between the one-dimensional carbon material CNT and actinide metal particles.

Recent results from various experimental and theoretical studies have provided valuable insight into the interaction mechanism of some typical embedded metal fullerenes (EMFs) such as U@C₂₈, U@C₈₂, U₂@C₆₀, Gd@C₆₀, Gd@C₈₂, etc., which consist of actinide or lanthanide with embedded 5f or 4f valence orbital and fullerenes.^{12,13,30–35} Some attempts have also been applied to the functionalization and practical applications of the corresponding derivatives (such as Gd@C₈₂OH₂₂, U₂@C₆₁).^36–38 The studies of structural characteristics of these EMFs have helped explain the effect (closed-shell electron configuration, CSEC) of the coupling between the sp² hybrid orbital of the zero-dimensional carbon material and the f valence electrons of the metals, which enable the materials to play an important role in nuclear energy, magnetic, emission characteristics, tumor treatment and pharmaceutical fields. This has also inspired us to investigate the adsorption of the actinide U atoms onto the inner/outer surfaces of the CNT to gain a deeper understanding of the interactions between the one-dimensional CNT and actinide materials.

Due to the radioactivity of nuclear substances, rigorous experimental conditions are required through the whole process from nuclear material extraction to waste treatment making it very difficult and expensive for lab experiments. Alternatively, theoretical simulation can be used to show the potential adverse effects a priori. First principle density functional theory (DFT) has been widely used in actinide stoichiometry studies. With the inclusion of the relativistic effects, DFT method is the only viable way to study molecules systems like actinide containing tens or more atoms.³⁹ In this work, we applied the DFT method and systematically studied the adsorption between the internal or external surfaces of the CNT and the typical actinide U atoms. A (5,5) CNT was chosen since its diameter resembles the size of a C₆₀ nano-particle. We found that when the U atoms adsorbed on the internal and external surfaces of CNT, the ground-state electronic structures were different with dissimilar electron spin coupling characteristics, which showed a decisive influence on the stability adsorption sites of the U atom and the interaction intensity. Our studies may provide a practical reference for new devices designed to handle nuclear waste treatment based on the CNT carbon materials (nuclear effluent treatment, environmental remediation of contaminated locations, as backfill material for the final disposal of solid waste etc.).⁹

Methodology and calculation details

Since the relativistic effects of actinides – with non-full and relatively diffuse 5f and 6d shells – cannot be ignored, it is essential to include both the relativistic and electron correlation effects when applying quantum first principles theoretical calculations to actinides. DFT method takes electron correlation into account without too much increase of the computation requirements, so it is reliable and widely used in actinide studies.^40–46 Different scalar relativistic theories have also been reported for actinide systems.^47,48 Compared to the conventional large core effective central potential (LC-ECP) method, the small core effective central potential (SC-ECP) method can generate more reliable results.³⁹ Considering the consumption of resources and computational accuracy, the generalized gradient approximation (GGA) method in DFT is currently recognized as the basic choice for actinide systems containing dozens of atoms.³⁹ Both BP86 and PBE functionals have been applied to deal with the complexes formed by actinides and short period light elements.⁴⁹ In this paper, the BP86 functional was used to accomplish all the calculations, and the PBE function was used for verification.

A pseudopotential method was applied to deal with the relativistic effects: the (14s13p10d8f6g)/[10s9p5d4f3g] valence basis set and the corresponding small core (60 nuclear electrons) effective central potential were considered for the uranium atoms. We chose the 6-31G(d) as the basis functions for C and H atoms in the system,⁵⁰ as previously reported in literature.^12,33 The minimum energy structure and frequencies were obtained through geometry optimization calculations starting from different initial structures. We used 3-21 G for C and H atoms to performed the Mulliken charge analysis,^51–53 which has been proved to be reliable for similar system.³⁶ All calculations were conducted in the Gaussian 09 program.⁵⁴

The armchair CNT is a typical CNT with metallicity, which is more active than other CNTs with helicity.²³ To avoid edge effects, a (5,5) type single-walled carbon nanotube containing 5 six-membered rings with H saturation at the ends (12.4 Å) was used to adsorb a U atom in the middle position of the inner and exterior surfaces of the nano-structure, respectively. To ensure the reliability of the model, we also studied the system containing 8 six-membered rings (19.8 Å), and obtained similar results (see ESI†). In each case, the lowest energy structure was obtained by optimizing three conformations with the top, bridge and hole adsorption sites of the U atoms, including a variety of possible electronic state structures (see Part 1 of ESI†). We then analyzed the corresponding electronic structures as well as other aspects of the bonding characteristics.

Results and discussion

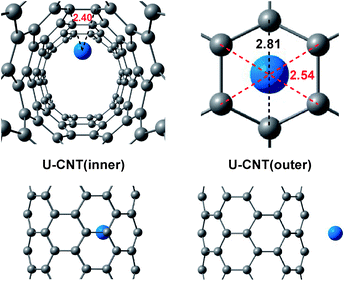
After optimization, we obtained the stable system structures shown in Fig. 1. The various electronic states and corresponding relative energies are given in Table S1 of the ESI.† For internal adsorption, the U atom adsorbed on the bridge site is the most stable, and its quintet energy is minimum (U–CNT(inner)). The distance between the U atom and two C atoms adsorbing it on the C–C bond is 2.40 Å. While for the case of external adsorption, the U atom adsorbed on the hole is the most stable, and the ground state is quintet (U–CNT(outer)). The distances between the U atom and six C atoms on the six-membered ring adsorbed are 2.81 and 2.54 Å.

Fig. 1 Optimized structures of U–CNT(inner) (left) and U–CNT(outer) (right).

To compare the interactions of these systems, we also calculated the interaction energy E_int, defined as E_int = E(U–CNT) − E(U) − E(CNT), where E(U–CNT) is the total energy of the U–CNT system, while E(U) and E(CNT) denote the total energies of the U fragment and the CNT fragment, respectively, with both the U atom and CNT being in the same atomic configurations as in the relaxed U–CNT system. The basis set superposition errors (BSSE) corrections were considered during these E_int calculations. The E_int of the inner and outer U atoms are −3.09 eV and −2.25 eV, suggesting that the U–CNT(inner) system is more stable than U–CNT(outer) system.

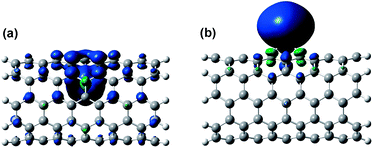
For both U atoms adsorbed on the CNT interior and exterior, the ground states are quintet. The specific contributions to the system electronic states can be obtained through spin density analysis. Fig. 2 shows the ground state spin density of the two systems respectively.

Fig. 2 Spin density distributions in the ground state of U–CNT(inner) and U–CNT(outer) systems. The blue area represents the net spin-up electrons, and the green area indicates the net spin-down electrons. Isovalue = 0.001.

Fig. 2(a) shows that, for the U–CNT(inner) system, the quintet spin state can be attributed to the ferromagnetic coupling (blue region) between the net spin electrons of the inner U atom and external CNT, with the U atom contributing more significantly. Further analysis on the spin density indicates that the number of net spin electrons on the U atom is +3.08e, whereas on CNT it is +0.92e. That is, from the six spin-up electrons on the U atom, three are donated to the CNT, among which two spin up, and one spins down. After ferromagnetic coupling of the two parts of the unpaired-electrons, the total net spin electrons number of the system is +4e, resulting in the quintet ground electronic state. For the U–CNT(outer) system, shown in Fig. 2(b), the formation of ground state quintet is mostly from the contribution of the U atom. Spin density analysis indicates that there are +4.07e single electrons on the U atom, but the CNT has nearly no net spin electrons (−0.07e). It is hypothesized then that the U atom donates two electrons to the CNT, which are arranged in opposite spins, resulting a net spin of almost zero on the CNT.

The charge transfer between the U atom and CNT is a key factor to reflect the structural stability. In previous studies about the system of U atoms encapsulated within the C material, such as endohedral metallofullerenes U@C₂₈, U₂@C₆₀, U@C₈₂ and others, the U atom usually donates electrons to the external C cage and exhibits cationic properties.^{12,13,30–33} For the two adsorption systems in this study, we performed Mulliken charge analysis and natural population analysis (NPA) which have been widely used for similar systems.^36,55–57

As shown in Table 1, the Mulliken charge analysis shows that the net charge on U is +2.44e for the system of U–CNT(inner). That is, U transfers charge to the CNT, which mainly distributes on the C atoms near the U atom, indicating a strong electrostatic attraction between the U atom and inner wall of the CNT. This effect has been observed in some other actinide adsorption systems as the donor–acceptor interaction,^58,59 which reflects the interaction nature of the electrostatic attraction. For the U–CNT(outer) system, the net charge on U is +1.39e, which is about 1.05e less than that of the interior adsorption. Table 1 also shows that, from natural population analysis, the net charge on U is +1.18e for U–CNT(inner), and +1.13e for U–CNT(outer), with a small difference of only 0.05e. The charges from both analysis methods are consistent in general trend, but NPA gives smaller numbers quantitatively. These results indicate that the effect of electrostatic attraction between the U atom and CNT in U–CNT (outer) is somewhat weaker than that in U–CNT(inner), which is consistent with the above adsorption energies – the external adsorbed U atom has lower absorption energy than that of the internal adsorbed one. These findings indicate that the electrostatic attraction plays an important role in the interaction between the U atom and CNT. The charge transfer results also comply with the observations of the spin electron density (Fig. 2).

Table 1 The calculated net charge on U atoms using Mulliken charge analysis and NPA

Charge (e)	U–CNT(inner)	U–CNT(outer)
Mulliken	+2.44	+1.39
NPA	+1.18	+1.13

---

From the electron density distribution shown in Fig. 3(a) and (b), it can be seen that for the U–CNT(inner) system, there is a significant electron accumulation between the U atom and two C atoms on the adsorbed C–C bond, which indicates the presence of valence interactions. On the other hand, for the U–CNT(outer) system, the electron accumulation between the U atom and CNT is not evident; therefore, there is almost no covalent interaction. This conclusion is supported by the following analysis on the molecular orbital characteristics.

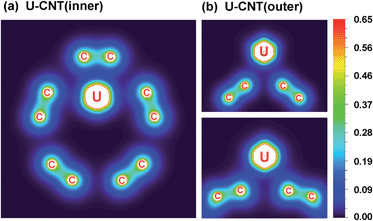Fig. 3 Electron density distributions of U–CNT(inner) and U–CNT(outer) systems. The section of (a) is through the U atom and its adsorbed C–C bond; (b) there are two cases of U–CNT(outer) section, the top shows two C atoms that have larger distance among its adsorbed six-ring through U atom, the bottom shows two opposite C atoms among four close atoms in the adsorbed six-ring through U atom (see Fig. 1). The white region in the figure indicates where the electron density is beyond the upper limit of the scale 0.65.

To further understand the formation of the electronic states, we analyzed the characteristics of the orbitals, shown in Fig. 4(a) and (b) and Table 2. Since there are 4 unpaired electrons in both systems, we focused on the single occupied frontier molecular orbitals.

Fig. 4 Frontier molecular orbitals of U–CNT(inner) and U–CNT(outer) systems, in accordance with the order of α electron. In (a), the highest occupied orbital of α electron HOMO−α is the HOMO of the system, and the highest occupied orbital of β electron HOMO-β is the HOMO−4; in (b), the highest occupied molecular orbital of α electron HOMO-α is the HOMO of the system, and the highest occupied orbital of β electron HOMO-β is the HOMO−5. Isovalue = 0.035.

Table 2 Contribution of U atomic orbitals to the frontier molecular orbitals of the U adsorption systems. As the contribution of U is mainly from its 5f and 6d electrons, only the contribution of electrons on these two shells of U is listed. In the case that the 5f and 6d electrons' contribution is relatively small, the largest contributor to the orbital is presented and marked with superscripts

Orbital composition (%)		HOMO	HOMO−1	HOMO−2	HOMO−3	HOMO−4	HOMO−5
U–CNT(inner)	Total	17.84	92.61	62.52	74.67	46.13	3.46
	5f	17.02	92.20	58.12	74.44	43.81	2.03
	6d	0.82	0.11	4.38	0.22	1.74	1.35
U–CNT(outer)	Total	95.37	89.39	92.19	98.40	1.41	28.72
	5f	94.79	79.07	29.45	79.64	0.23	15.48
	6d	0.53	2.57	52.23^7s	15.63^7s	1.12	11.24

---

The ground states of both systems are quintet, with four unpaired electrons. In the U–CNT(inner) system, the orbitals HOMO–HOMO−3 are single occupied. In the HOMO orbital, the U atom's contribution is about 17.84%, and the majority comes from the contribution of CNT. In the HOMO−1 orbital, the contribution mainly comes from the 5f electrons of the U atom, which is approximately 92.61%. In the HOMO−2 and HOMO−3 orbitals, the contributions of the U atom are 62.52% and 74.67% respectively, mainly exhibit on the orbital hybridization between the U atom and adjacent C atoms, indicating strong covalent interactions between the U atom and CNT wall, and is consistent with the previous results about spin and charge distribution. In the U–CNT(outer) system, the single occupied molecular orbitals are HOMO–HOMO−3. According to the analysis of orbital component, these four orbitals are mostly from the U atom's contribution (about 89–99%) while the CNT contribute is not significant. This suggested that there is no covalent interaction but electrostatic attraction between the U and CNT wall.

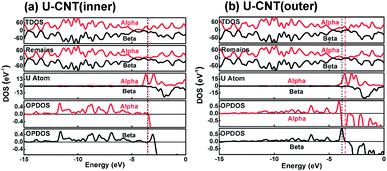
The electronic state characteristics of the system can be reflected through the density of state distribution. Fig. 5 shows the electronic density of states of both U–CNT(inner) and U–CNT(outer) systems. According to the analysis of total DOS and PDOS of the U atom, the peaks near the red and black dash lines exhibit the significant characteristics of the U atom's contribution. Consistent with the orbital analysis (Fig. 4), the frontier molecular orbital of the two systems are mainly contributed by the U atoms. As can be seen in Fig. 5, for the U–CNT(inner) system, the highest occupied molecular orbital of alpha and beta electron (HOMO-α and HOMO-β correspond to the HOMO and HOMO−4, respectively) are from the contributions of both CNT and U atom; for the U–CNT(outer) system, the HOMO-α (corresponding to the HOMO) is contributed mostly by the U atom, and the HOMO-β (corresponding to the HOMO−5) is mainly contributed by the CNT. These results are in good accordance with the previous orbital analysis. As shown in the “Remains” part of Fig. 5, the difference between alpha and beta of the U–CNT(inner) system is larger than that of U–CNT(outer). This indicated that in the internal adsorption system, the CNT is more affected by the U atom, even with changed energy level, resulting in a strong bonding effect between them. The interaction between the U atoms and CNT can be directly observed on the OPDOS curve, where the positive values represent the bonding interaction, the negative values indicate the anti-bonding interaction, and 0 is the non-bonding interaction. In the figure, the HOMO-α of U–CNT(inner) system and HOMO-β of both systems are the bonding orbitals, HOMO-α of U–CNT(outer) system is the lone-electron orbital, which coincide well with the orbital chart. It is also noted that, the difference between HOMO-α and HOMO-β in U–CNT(inner) is as small as 0.01 eV, but in U–CNT(outer) it is 0.30 eV. This difference can be explained by the orbital. The HOMO-α and HOMO-β of the U–CNT(inner) system are contributed by both the CNT and U atom, and the U atom's contribution is from the 5f electrons. As comparison, for the U–CNT(outer) system, the HOMO-α is from the contribution of the U atom's 5f electrons, while the HOMO-β is mainly from the contribution of CNT, and the U atom contribution is from its 5f electrons.

Fig. 5 Distributions of the electronic state density in the U–CNT(inner) and U–CNT(outer) systems. The red dash dotted line represents the HOMO-α position, and the black dashed line indicates the HOMO-β position. FWHM = 0.01.

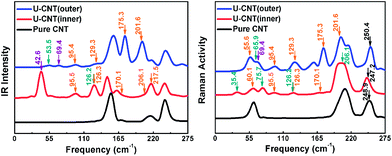
The system vibrational characteristics can be studied by the infrared and Raman spectra, in which the interactions between the U atom and CNT are exhibited by the relative vibrations. We calculated the infrared and Raman spectra of both U–CNT(inner) and U–CNT(outer) systems, as shown in Fig. 6. Since the vibrational modes of carbon material with the participation of the U atoms are generally less than 300 cm⁻¹,^33,36 the spectra with a range of 0–275 cm⁻¹ are presented here (full spectrum is included in the ESI†). Compared with the pure CNT, both the U–CNT(inner) and U–CNT(outer) structures retain the characteristic vibrational mode of the CNT (no involvement of U), but the adsorption of the U atom on different positions of the CNT causes different degrees of shift of the vibrational mode. It is well known that, there are three distinct vibrational modes of pure carbon nanotube: radial mode, breathing mode and tangential mode. According to our calculation for the (5,5) pure carbon nanotubes using BP86/6-31G*, the radial mode (marked by black arrows in the figure) has a frequency of 248.9 cm⁻¹, and the frequencies of the breathing mode and tangential mode are 337.3 cm⁻¹ and 1564.7 cm⁻¹ respectively. In the U–CNT(inner) system, these three vibrational modes are switched to 247.2 cm⁻¹, 344.0 cm⁻¹, 1538.2 cm⁻¹, and in the U–CNT(outer) structure they are 250.4 cm⁻¹, 337.8 cm⁻¹, 1552.8 cm⁻¹. In both U adsorption systems, the special vibrational modes maintain the characteristics of the CNT itself, but different degrees of shift occurred due to the different adsorption positions. We also notice that, when the U atom is adsorbed on the surface of CNT, all the vibrational modes of pure CNT are retained, meanwhile some of them include the participation of uranium atoms (the vibrational mode at 60.9 cm⁻¹ is shown in the ESI†).

Fig. 6 Infrared and Raman spectra of U–CNT(inner) and U–CNT(outer) systems. The black arrows mark the radial vibrational mode of CNT itself, the purple arrows mark the radial vibration of U atom relative to the CNT, the green arrows mark the tangential vibration of U atom relative to the CNT, and the yellow arrows mark the vibration of U atom toward the axis of CNT.

In addition, for both U–CNT(inner) and U–CNT(outer) structures, the adsorption of the U atom generates some special vibrational modes including the radial vibration of U atom relative to the CNT (purple arrow), the tangential vibration of U atom relative to the CNT (green arrow), and the vibration of U atom toward the CNT axis (yellow arrow). These vibrational modes of the U atom relative to the CNT indicate the strong interaction between them.

The surface curvature can be another important factor affecting the adsorption nature of carbon-based nanomaterials,⁶⁰ and our current results indicate the internal surface of (5,5)-CNTs is more advantageous for adsorption of U atoms. Therefore, we also studied the adsorption of U atoms on the internal surfaces of CNTs with different diameters, and found some interesting results (see Part 6 of ESI†). For (5,5)-, (6,6)-CNTs, the most stable site is the bridge site on the internal surface. By contrast, the most stable site changed to the hole site starting from (7,7)-CNT. As the curvature continues to decrease, the most stable adsorption site remained at the hole site, such as (8,8)-CNT. Moreover, with the decrease in curvature of the CNTs, the strength of interaction weakens gradually, and the difference with the outer surface also diminishes. It should be noted though the ground electronic states of the adsorption systems remain as quintet for all these single-walled CNTs.

Conclusions

In summary, two different adsorption modes of U atoms exist on carbon nanotubes, one inside the CNT (U–CNT(inner)) and one outside the CNT (U–CNT(outer)). By using DFT theory, stable structures of both adsorption systems were obtained: for the U–CNT(inner), the U atom occupied a bridge position; while for U–CNT(outer), the U atom occupied a hole position. The U–CNT(inner) system is more stable than the U–CNT(outer) system. The comparison of the electronic structures of both systems shows that the ground states are both quintet, however, with different electronic configuration. For the U–CNT(inner) system, the quintet resulted from the ferromagnetic coupling between three net spin electrons on the inner U atom and one net spin electron on the CNT. On the other hand, the quintet of the U–CNT(outer) system is entirely from the contribution of four net spin unpaired electrons on the U atom. Further analysis of the electronic properties shows that, for the U–CNT(inner) structure, there are mixed effects of electrostatic attraction and covalent interaction between the U atom and the CNT. But for the U–CNT(outer) structure, electrostatic attraction is the main interaction between U and the CNT surface.

Previous studies have shown that the structures of endohedral metallofullerene (EMFs) as actinides or lanthanides formed inside the fullerene rely on the Coulomb attraction and strong bonding of closed cage formed by the external carbon–carbon bond.^{12,13,30–35} So, the synthesis of the EMF structure is relatively difficult. CNT have significant advantages on structural stability, spatial scalability, and ease to form physical or chemical adsorption.^18,22,23 The current finding that U atoms confined inside CNTs are more stable might provide important insights for CNT-based embedded structure designs and potential practical applications such as extraction of actinide materials from the environment,^9,19,20 and nuclear waste cleanup.

Acknowledgements

We thank the support of the National Science Foundation of China under grant no. 11374221, 11034003 and 11374004. Z. W. acknowledges the Fok Ying Tung Education Foundation (142001) and High Performance Computing Center (HPCC) of Jilin University.

Notes and references

1. W. Shi, Y. Zhao and Z. Chai, Prog. Chem., 2011, 23, 1478–1484.
2. S. V. Krivovichev, P. C. Burns, I. G. Tananaev and B. F. Myasoedov, J. Alloys Compd., 2007, 444, 457–463.
3. J. M. Haschke and J. L. Stakebake, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein, J. Fuger and J. J. Katz, Springer, Dordrecht, The Netherlands, 3rd edn, 2006, vol. 5, pp. 3199–3272.
4. S. Iijima, Nature, 1991, 354, 56–58.
5. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
6. G. X. Zhao, T. Wen, X. Yang, S. B. Yang, J. L. Liao, J. Hu, D. D. Zhao and X. K. Wang, Dalton Trans., 2012, 41, 6182–6188.
7. Z. Li, F. Chen, L. Yuan, Y. Liu, Y. Zhao, Z. Chai and W. Shi, Chem. Eng. J., 2012, 210, 539–546.
8. A. K. S. Deb, P. Ilaiyaraja, D. Ponraju and B. Venkatraman, J. Radioanal. Nucl. Chem., 2012, 291, 877–883.
9. F. Belloni, C. Kütahyali, V. V. Rondinella, P. Carbol, T. Wiss and A. Mangione, Environ. Sci. Technol., 2009, 43, 1250–1255.
10. X. K. Wang, C. L. Chen, W. P. Hu, A. P. Ding, D. Xu and X. Zhou, Environ. Sci. Technol., 2005, 39, 2856–2860.
11. C. L. Chen, X. L. Li, D. L. Zhao, X. L. Tan and X. K. Wang, Colloids Surf., A, 2007, 302, 449–454.
12. X. Liu, L. Li, B. Liu, D. Q. Wang, Y. L. Zhao and X. F. Gao, J. Phys. Chem. A, 2012, 116, 11651–11655.
13. I. Infante, L. Gagliardi and G. E. Scuseria, J. Am. Chem. Soc., 2008, 130, 7459–7465.
14. X. L. Tan, D. Xu, C. L. Chen, X. K. Wang and W. P. Hu, Radiochim. Acta, 2008, 96, 23–29.
15. R. Martel, V. Derycke, C. Lavoie, J. Appenzeller, K. K. Chan, J. Tersoff and P. Avouris, Phys. Rev. Lett., 2001, 87, 256805.
16. A. Akturk, N. Goldsman, G. Pennington and A. Wickenden, Phys. Rev. Lett., 2007, 98, 166803.
17. A. K. Manna and S. K. Pati, Nanoscale, 2010, 2, 1190–1195.
18. D. Tasis, N. Tagmatarchis, A. Bianco and M. Prato, Chem. Rev., 2006, 106, 1105–1136.
19. A. Stafiej and K. Pyrzynska, Sep. Purif. Technol., 2007, 58, 49–52.
20. Y. H. Li, S. G. Wang, J. Q. Wei, X. F. Zhang, C. L. Xu, Z. K. Luan, D. H. Wu and B. Q. Wei, Chem. Phys. Lett., 2002, 357, 263–266.
21. S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area, and Porosity, Academic Press, New York, 2nd edn, 1982.
22. T. W. Ebbesen, H. J. Lezec, H. Hiura, J. W. Bennett, H. F. Ghaemi and T. Thio, Nature, 1996, 382, 54–56.
23. P. M. Ajayan, Chem. Rev., 1999, 99, 1787–1799.
24. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190.
25. B. Arash and Q. Wang, Sci. Rep., 2013, 3, 1782.
26. M. S. Xin, F. T. Wang, Y. Meng, C. J. Tian, M. X. Jin, Z. G. Wang and R. Q. Zhang, J. Phys. Chem. C, 2011, 116, 292–297.
27. P. O. Lehtinen, A. S. Foster, A. Ayuela, T. T. Vehviläinen and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155422.
28. M. Sundararajan and S. K. Ghosh, J. Phys. Chem. A, 2011, 115, 6732–6737.
29. C. L. Chen, X. L. Li and X. K. Wang, Radiochim. Acta, 2007, 95, 261–266.
30. T. Guo, M. D. Diener, Y. Chai, M. J. Alford, R. E. Haufler, S. M. McClure, T. Ohno, J. H. Weaver, G. E. Scuseria and R. E. Smalley, Science, 1992, 257, 1661–1664.
31. M. D. Diener, C. A. Smith and D. K. Veirs, Chem. Mater., 1997, 9, 1773–1777.
32. K. Akiyama, Y. L. Zhao, K. Sueki, K. Tsukada, H. Haba, Y. Nagame, T. Kodama, S. Suzuki, T. Ohtsuki, M. Sakaguchi, K. Kikuchi, M. Katada and H. Nakahara, J. Am. Chem. Soc., 2001, 123, 181–182.
33. X. Wu and X. Lu, J. Am. Chem. Soc., 2007, 129, 2171–2177.
34. J. Lu, W. N. Mei, Y. Gao, X. Zeng, M. Jing, G. Li, R. Sabirianov, Z. Gao, L. You, J. Xu, D. Yu and H. Ye, Chem. Phys. Lett., 2006, 425, 82–84.
35. A. Sebetci and M. Richter, J. Phys. Chem. C, 2009, 114, 15–19.
36. X. Dai, C. Cheng, W. Zhang, M. S. Xin, P. Huai, R. Q. Zhang and Z. G. Wang, Sci. Rep., 2013, 3, 1341.
37. S. G. Kang, T. Huynh and R. Zhou, Nanoscale, 2013, 5, 2703–2712.
38. S. G. Kang, G. Zhou, P. Yang, Y. Liu, B. Sun, T. Huynh, H. Meng, L. Zhao, G. Xing, C. Chen, Y. Zhao and R. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15431–15436.
39. G. Schreckenbach and G. A. Shamov, Acc. Chem. Res., 2010, 43, 19–29.
40. A. L. Kutepov, J. Alloys Compd., 2007, 444/445, 174–176.
41. K. I. M. Ingram, N. Kaltsoyannis, A. J. Gaunt and M. P. Neu, J. Alloys Compd., 2007, 444/445, 369–375.
42. K. I. M. Ingram, M. J. Tassell, A. J. Gaunt and N. Kaltsoyannis, Inorg. Chem., 2008, 47, 7824–7833.
43. P. Whlin, C. Danilo, V. Vallet, F. Réal, J. P. Flament and U. Wahlgren, J. Chem. Theory Comput., 2008, 4, 569–577.
44. L. Andrews, B. Liang, J. Li and B. E. Bursten, J. Am. Chem. Soc., 2003, 125, 3126–3139.
45. J. T. Lyon, H. S. Hu, L. Andrews and J. Li, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18919–18924.
46. J. Li, H. S. Hu, J. T. Lyon and L. Andrews, Angew. Chem., Int. Ed., 2007, 46, 9045–9049.
47. N. Iché-Tarrat and C. J. Marsden, J. Phys. Chem. A, 2008, 112, 7632–7642.
48. S. O. Odoh and G. Schreckenbach, J. Phys. Chem. A, 2010, 114, 1957–1963.
49. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
50. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
51. Y. Cong, Z. Z. Yang, C. S. Wang, X. C. Liu and X. H. Bao, Chem. Phys. Lett., 2002, 357, 59–64.
52. M. S. Xin, X. Dai, B. L. Huang, Y. Meng, W. Feng, M. X. Jin, Z. G. Wang and R. Q. Zhang, Chem. Phys. Lett., 2013, 585, 107–111.
53. J. S. Binkley, J. A. Pople and J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2013.
55. D. Manna and T. K. Ghanty, J. Phys. Chem. C, 2013, 117, 17859–17869.
56. L. Maron, O. Eisenstein and R. A. Andersen, Organometallics, 2009, 28, 3629–3635.
57. J. Han, X. Dai, C. Cheng, M. S. Xin, Z. G. Wang, P. Huai and R. Q. Zhang, J. Phys. Chem. C, 2013, 117, 26849–26857.
58. H. A. Bent, Chem. Rev., 1968, 68, 587–648.
59. I. López-Corral, E. Germán, A. Juan, M. A. Volpe and G. P. Brizuela, Int. J. Hydrogen Energy, 2012, 37, 6653–6665.
60. G. Zuo, X. Zhou, Q. Huang, H. P. Fang and R. H. Zhou, J. Phys. Chem. C, 2011, 115, 23323–23328.

---

Footnote

† Electronic supplementary information (ESI) available: Electronic state as well as the corresponding relative energy of U–CNT(inner) and U–CNT(outer) system; calculation for the U adsorption system on the (5,5) type single-walled carbon nanotube containing 8 six-membered rings with 3-21 G; infrared and Raman spectra of U–CNT(inner) and U–CNT(outer) systems; the same vibrational mode of pure CNT, U–CNT(inner) and U–CNT(outer); isogram of electronic density distribution of the U–CNT(inner) and U–CNT(outer) systems; curvature effect on the interaction between U atoms and the internal surface of CNTs; coordinates of the ground state structures. See DOI: 10.1039/c4ra02662d

---