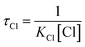Degradation of methyl salicylate through Cl initiated atmospheric oxidation – a theoretical study†
A. Mano Priya and
L. Senthilkumar*
Department of Physics, Bharathiar University, Maruthamalai Road, Coimbatore-641046, Tamil Nadu, India. E-mail: lsenthilkumar@buc.edu.in
First published on 7th May 2014
Abstract
In the present study, a possible reaction mechanism for the degradation through Cl initiated atmospheric oxidation of methyl salicylate (MeSA) was studied using density functional theory at B3LYP and M06-2X levels of theory with 6-311++G(d,p) basis set. The degradation occurred through an abstraction process at the meta position of MeSA along the entire reaction path. The barrier height values indicated that the reaction of the benzoate radical of MeSA and NO was a favourable route for degradation, which was thermodynamically exothermic and exergonic in nature. The lifetime calculations indicated a short life span for MeSA at 1.14 days. The rate constant values displayed good Arrhenius character with respect to temperature. The activation hardness predicted a rapid reaction between MeSA and NO. The HOMO and LUMO values along with their plot indicated that the NO radical and benzene ring in the MeSA were highly reactive. Topological analysis revealed that during the reaction the interaction between reactants was covalent in nature.
Introduction
Anthropogenic and biogenic volatile organic compounds (VOCs) are regularly emitted into the atmosphere.1–3 Many of these compounds are aromatic hydrocarbons, esters, ethers, aldehydes, and ketones, which play an important role in the chemistry of pollutants.4 These compounds undergo a series of chemical reactions that lead to their removal from the troposphere or transformation into other compounds. VOCs play a central role in these processes, generating both urban photochemical smog and tropospheric ozone. Presently, a great interest is being shown in the atmospheric chemistry of VOCs because these compounds play a significant role in the formation of secondary organic aerosols, which are harmful to human health.5,6Methyl salicylate (MeSA), a green leaf semi-volatile (GLV), is known to be one of the aromatic compounds that is emitted in significant amounts by plants such as tea.1,7–9 It is widely used in the flavor industry to create aromas such as strawberry, raspberry, banana, tomato, cocoa, mint, cherry, fig, peach, and tea. Due to its sweet smelling aroma (candy-like), it is attractive to small children and is a frequent cause of poisoning.10–13 MeSA is a frequent constituent of insect-induced plant volatiles detected in the headspace of many insect-infested plants such as lima bean,14 Arabidopsis,15 tomato,16 and soybean.17 GLVs undergo chemical reactions with atmospheric oxidants, yielding compounds that contribute to the formation of secondary organic aerosols (SOAs), which are harmful to human health and ecosystem. Therefore, information regarding the possible products of the oxidation of MeSA in the atmosphere, and their environmental implications is important.
Halogen atoms and oxides are highly reactive and can profoundly affect atmospheric compositions. Like all halogens, chlorine also has a high reactivity towards numerous organic and inorganic molecules. Molecular chlorine in the atmosphere is photo-dissociated by either visible or ultraviolet light that results in the chlorine radical. This chlorine radical is capable of reacting with either ozone or organics in the atmosphere. Several sources emit molecular chlorine in the atmosphere, and certain anthropogenic sources release large amounts of chlorine and chlorine atom precursors.18 Some of these sources include petroleum refineries, chlor-alkali facilities, chlorinated chemical manufacturing operations, and other industrial facilities. The average global concentration of Cl was estimated to be about 104 atoms per cm3.19 In atmospheric chemistry, chlorine atom is particularly important since it competes with the hydroxyl radical (OH*) in photochemical reactions. This in particular results in the faster atmospheric removal rates of VOCs. Further, chlorine atoms can decrease the lifetimes of gaseous elemental mercury20 and hydrocarbons such as the greenhouse gas methane.21 Chlorine atoms also influence reaction cycles that catalytically destroy or produce tropospheric ozone,22 a greenhouse gas which is potentially toxic to plant and animal life. Stolarski and Cicerone23 emphasized the importance of chlorine species in atmospheric chemistry.24 These abovementioned observations of a large amount of reactive chlorine, its role in the atmosphere and its ability to remove VOCs make it an efficient source for MeSA degradation, particularly in the marine boundary layer, polar and coastal air environments.25–27
During literature search regarding MeSA degradation we found only one experimental study28 on the reaction of methyl salicylate with Cl radical, which explains the kinetics involved. The limited availability of experimental results makes it essential to provide a detailed theoretical study of MeSA with Cl radical to understand the reaction mechanism and to project secondary reaction pathways. Hence, the objective of this work was to elucidate the reaction pathways for the degradation of MeSA by Cl radical and to understand the kinetics involved in the most favourable reactions using density functional theory and variational transition state theory (VTST),29 respectively. For the abovementioned objective, the full potential energy surface of MeSA with Cl radical was mapped carefully to understand the degradation processes. Furthermore, the H-atom abstraction from the aromatic ring, which resulted in the formation of peroxy radical, and subsequent secondary reaction was fully analysed.
Computational details
The geometries of all reactants, transition states and products of MeSA with Cl radical were optimized using density functional theory methods at B3LYP30,31 and M06-2X32 levels of theory with 6-311++G(d,p) basis set. The corresponding frequencies of the optimized geometries at the these levels of theory showed that the characters of the transition states have one imaginary frequency, thus confirming their location as maxima in one reaction coordinate and the stationary points without any imaginary frequency. Using the intrinsic reaction coordinate (IRC) calculations at B3LYP and M06-2X levels of theory, the connection of transition state structure with designated reactant and product in each case was ascertained. The verification of reaction paths was performed by following the Gonzalez–Schlegel steepest descent path in mass-weighted internal coordinates.33,34 Thermodynamic correction to the potential energy surface at the temperature of 298.15 K and pressure of 1 atm was included in the calculation of enthalpy, height of barrier reaction, and Gibbs free energy. Rate constants of the most favourable reactions involved in this study estimated using canonical VTST Quantum tunneling effects were performed using small curvature tunneling (SCT)35,36 method. The potential energy surface, gradients, and Hessians obtained from M06-2X/6-311++G(d,p) level electronic structures are more reliable and were directly used to calculate rate constants. Further, for the initial reaction, we calculated the values of ΔE, ΔH and ΔG using BMK37 and MPW1K38 functionals to check the accuracy of M06-2X functional.Through canonical variational transition state theory (CVT),39–41 the rate constant at temperature T was given by
 | (1) |
 | (2) |
The equilibrium constant (Kc in concentration units) for the reactions at equilibrium was evaluated using the standard formulae42
| Kc = Kp(R′T)−Δn | (3) |
RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kp = −ΔGT0 Kp = −ΔGT0
| (4) |
Reactivity parameters
The frontier molecular orbitals are important descriptors for understanding chemical interactions, clarifying key features in the chemistry of complexes and solids such as reactivity and stability. K. Fukui from Japan47 has proposed a useful molecular orbital model named as the fragment molecular orbital (FMO) for analysing reactions. Frontier molecular orbital approach is based on the assumption that bonds are formed by a flow of electrons from the highest occupied molecular orbital (HOMO) of one reactant or participating bond to the lowest unoccupied molecular orbital (LUMO) of another reactant or bond. In terms of chemical reactivity, the HOMO is the orbital that donates electrons, and the ionization potential (I) is a reasonable measure of its energy. Electron affinity (A) is the energy describing the acceptance of electrons, and the corresponding orbital is LUMO. In simple terms, HOMO energy characterizes the ability to donate an electron and LUMO energy characterizes the ability to accept an electron. The HOMO and LUMO energies are expressed by Koopmans theorem48 in terms of ionization potential (I) and electron affinity (A) as| I = −HOMO | (5) |
| A = −LUMO | (6) |
 | (7) |
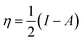 | (8) |
 | (9) |
Using the abovementioned definitions for reactivity parameters, Zhou and Parr50 introduced the concept of activation hardness Δη* for aromatic electrophilic substitution. With the activation hardness suitably defined, the smaller the activation hardness is, the faster is the reaction. The activation hardness can be calculated using molecular orbital theory and is expressed as Δη* (ref. 50)
| Δη* = ηR − ηT | (10) |
To explore and define the reactive attacking site of molecules involved in the reaction, an available important parameter is the Fukui function.51,52 For a molecule with N electron system, the Fukui function is defined as
 | (11) |
| f+k = qk(N + 1) − qk(N) for nucleophilic attack | (12) |
| f−k = qk(N) − qk(N − 1) for electrophilic attack | (13) |
 | (14) |
 | (15) |
 | (16) |
Eqn (15) is the nucleophilic Fukui function to characterize a nucleophilic attack on the reagent. Eqn (16) is the electrophilic Fukui function to characterize an electrophilic attack on the reagent. All the abovementioned reactive parameters have been calculated only at M06-2X/6-311++G(d,p) level of theory because recent studies32,65,66 have concluded that M06-2X functional performs well in predicting ionization potential, proton affinity, electron affinity and nucleophilic substitution.
Results and discussion
Reaction mechanism and reaction paths
The reaction is initiated in three different ways, i.e. Cl abstraction of H-atom from the phenol group, the methyl group and the aromatic ring. In the abovementioned initial reactions, the H-atom abstraction from the aromatic ring is possible at two meta positions (i.e. 3rd and 5th hydrogen atom); however, the 3rd meta position (1.99 kcal mol−1) appears to be more favourable than the 5th meta position (84.39 kcal mol−1) because of its lower barrier height. Hence, all secondary reactions occur at the 3rd meta position.The reaction mechanism of MeSA with Cl radical has been studied under five pathways. The reactants, products, intermediates, and transition states are labelled as R, P, I and TS, respectively. Fig. 1 shows the proposed reaction scheme for the reaction of MeSA with Cl radical. The structures of the stationary state in the ground state potential energy surface (PES) of the reaction optimized at M06-2X/6-311++G(d,p), are shown in Fig. S1 and S2 (in ESI†). The structures of the pre-reactive complexes, I1 + O2, I2 + HO2, I2 + NO2, I2 + NO and I3 + O2 are shown in Fig. S1 and S2 (in ESI†). A schematic of the potential energy surface of all the reactions obtained at M06-2X/6-311++G(d,p) level of theory is shown in Fig. 2 and 3. The thermodynamic properties, such as enthalpy of reaction (ΔH), relative energy barrier (ΔE), and Gibbs free energy of reaction (ΔG), of the reactive species were calculated at room temperature and atmospheric pressure at B3LYP/6-311++G(d,p) and M06-2X/6-311++G(d,p) levels of theory, and their results are summarized in Table 1. It can be noted from Table 1 that for a few systems, the B3LYP thermodynamic values are marginally larger in magnitude, especially for TS1 ΔH = 1.91 and 10.38 at M06-2X and B3LYP, respectively. This may be due to a self-interaction error (non-physical interaction of an electron with itself) in local DFT.67,68 However, the thermodynamic values obtained from M06-2X are comparable with the values obtained from BMK and MPW1K functionals for TS1. The thermodynamic values obtained at only M06-2X/6-311++G(d,p) level of theory are used for further discussion. Further, the optimized geometrical parameters of the favourable reaction path calculated at M06-2X/6-311++G(d,p) level of theory are shown in Table S1 in ESI.†
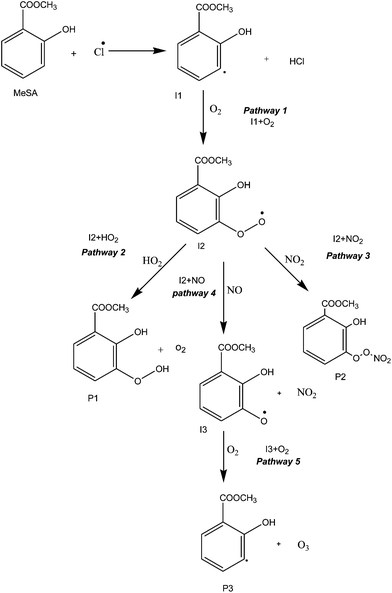 | ||
| Fig. 1 Reaction scheme for the initial H-atom abstraction reactions from the aromatic ring group of methyl salicylate by Cl radical and their subsequent reactions. | ||
 | ||
| Fig. 2 Relative energy profile corresponding to the formation of peroxy radical from Cl-initiated reaction of methyl salicylate calculated at M06-2X/6-311++G(d,p) level of theory. | ||
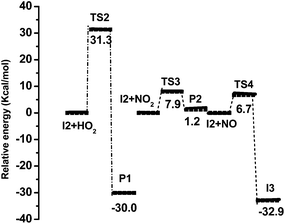 | ||
| Fig. 3 Relative energy profile corresponding to the reactions of peroxy radical with HO2, NO2, and NO calculated at M06-2X/6-311++G(d,p) level of theory. | ||
| Stationary point | B3LYP/6-311++G(d,p) | M06-2X/6-311++G(d,p) | ||||
|---|---|---|---|---|---|---|
| ΔE | ΔH | ΔG | ΔE | ΔH | ΔG | |
| a Indicates structure not converged.b Values in parenthesis were calculated using BMK/6-311++G(d,p).c Values in parenthesis were calculated using MPW1K/6-311++G(d,p). | ||||||
| MeSA + Cl | 0 | 0 | 0 | 0 | 0 | 0 |
| TS1 | 3.14 | 10.38 | 11.32 | 1.99 | 1.91 | 3.95 |
| (5.21)b (2.14)c | (4.75)b (1.90)c | (5.60)b (3.38)c | ||||
| I1 | −23.20 | −19.27 | −13.62 | −15.15 | −12.21 | −11.87 |
| (−16.75)b (−18.35)c | (−13.66)b (−15.67)c | (−13.09)b (−14.69)c | ||||
| I1 + O2 | 0 | 0 | 0 | 0 | 0 | 0 |
| I2 | −39.80 | −37.23 | −28.86 | −42.66 | −40.27 | −34.93 |
| I2 + HO2 | 0 | 0 | 0 | 0 | 0 | 0 |
| TS2 | 35.31 | 31.74 | 32.34 | 31.35 | 28.00 | 30.73 |
| P1 | −11.45 | −12.63 | −16.01 | −30.09 | −31.04 | −32.72 |
| I2 + NO2 | 0 | 0 | 0 | 0 | 0 | 0 |
| TS3 | 8.25 | 7.65 | 8.36 | 7.97 | 7.47 | 6.36 |
| P2 | 1.11 | 1.14 | 0.59 | 1.21 | 1.15 | 0.88 |
| I2 + NO | 0 | 0 | 0 | 0 | 0 | 0 |
| TS4 | 5.89 | 5.37 | 6.23 | 6.70 | 6.32 | 7.32 |
| I3 | −33.02 | −31.28 | −30.36 | −32.90 | −31.27 | −30.51 |
| I3 + O2 | 0 | 0 | 0 | 0 | 0 | 0 |
| TS5 | a | a | a | a | a | a |
| P3 | a | −114.24 | −114.42 | a | −121.43 | −122.21 |
To assess the structural changes in the chemical species during the course of reaction, the geometrical parameters obtained at M06-2X/6-311++G(d,p) level of theory are summarized in Table S1 (in ESI†). In the initial reaction, the bond distance between carbon atom (C3) and hydrogen atom (H16) in the reactant was 1.082 Å, whereas the bond distance of the same atoms was 1.083 Å in the transition state and 6.640 Å in the intermediate I1. The hydrogen atom (H16) abstracted by chlorine atom (Cl20) has a bond distance of 3.775 Å in the reactant. The same bond distance was reduced in the transition state and intermediate I1 to 3.772 Å and 1.296 Å, respectively. The corresponding bond angle θ (C3–H16–Cl20) was 85.3° in the reactant, whereas in the transition state because of the abstraction of H by Cl radical it was decreased to 70.7° and linear (167.8°) in the intermediate I1 at M06-2X/6-311++G(d,p) level of theory.
Kinetics of the reaction
In recent studies, the M06-2X functional has been shown to give reliable barrier heights and rate constant values, which agree well with experimental results.76,77 Hence, in the present study, rate constant calculation was performed using M06-2X functional. The rate coefficients were calculated only for the most favourable pathways CVT with small curvature tunnelling (SCT) correction method over the temperature range of 278–350 K. The rate constant for hydrogen abstraction channel (I1), peroxy radical intermediate channel (I2) and the aryloxy intermediate channel (I3) are designated as KI1, KI2 and KI3 respectively. The rate constants of initial reaction (MeSA + Cl) listed in Table 2 vary from 7.23 × 10−11 to 2.09 × 10−10 cm3 per molecule per s over the temperature range 278 to 350 K. The calculated forward rate constant for hydrogen abstraction in the initial reaction (MeSA + Cl) was 1.01 × 10−10 cm3 per molecule per s at 298 K. The calculated reverse rate constant for this reaction was 3.74 × 10−17 cm3 per molecule per s. According to these values, the forward reaction was more favourable than the reverse reaction. The equilibrium constant Kc of the initial reaction (MeSA + Cl) was 2.71 × 106 with a transmission coefficient of 1.027 at 298 K, which shows that the tunneling effect was significant in H-atom abstraction step. The calculated initial reaction rate constant is comparable to the experimental value determined for MeSA with Cl (2.8 × 10−12 cm3 per molecule per s) by C. E. Canosa-Mas et al.28 However, we see a difference of two orders between the theory and the experiment, which is justifiable, as an earlier study78 showed that an error of 2 kcal mol−1 in the energy barrier will lead to an error in the calculated rate constant by one order of magnitude. In addition, Wang et al.79 calculated the rate constant for phenol with OH abstraction by DFT method, which shows that the theoretical rate constant value is two order of magnitude higher than the experimental value. In pathway 1, the intermediate peroxy radical (methyl 3-peroxy-2-hydroxybenzoate) (I2) was formed without any potential barrier under the loose transition state. In this reaction, only the forward reaction was possible with a rate constant of 2.98 × 10−4 cm3 per molecule per s at 298 K. Due to the formation of barrierless reaction, the tunneling factor was negligible for this reaction. It is evident from Table 1 that pathway 4 (I2 + NO), was the most favourable path with a small energy barrier of 1.21 kcal mol−1. The calculated forward rate constant of the reaction at 298 K was 3.75 × 10−13 cm3 per molecule per s while the reverse rate constant was 4.90 × 10−35 cm3 per molecule per s. The equilibrium constant Kc for the formation and decomposition of this reaction channel was 7.65 × 1021 with a transmission coefficient of 1.018, indicating a significant tunneling effect. Further, for pathway 4, the forward reaction was faster than the reverse reaction, which makes it important near the tropopause or in highly polluted areas.80,81 Fig. 4 shows the kinetic scheme of the most favourable pathways of the reaction between MeSA and Cl radical. Similarly, Fig. 5 shows the plots of the computed rate coefficients of the most favourable pathways over the temperature range of 278 to 350 K, which exhibit typical Arrhenius behaviour. The rate constant values in this temperature range can be useful for atmospheric modelling calculations that can help in assessing the atmospheric lifetimes of MeSA.| Temperature (K) | KI1 | KI2 | KI3 |
|---|---|---|---|
| a Indicates experimental value. | |||
| 278 | 7.23 × 10−11 | 2.15 × 10−2 | 1.97 × 10−13 |
| 288 | 8.61 × 10−11 | 2.35 × 10−3 | 2.75 × 10−13 |
| 298 | 1.01 × 10−10 (2.8 × 10−12)a | 2.98 × 10−4 | 3.75 × 10−13 |
| 308 | 1.19 × 10−10 | 4.31 × 10−5 | 5.01 × 10−13 |
| 318 | 1.38 × 10−10 | 7.07 × 10−6 | 6.60 × 10−13 |
| 328 | 1.58 × 10−10 | 1.29 × 10−6 | 8.56 × 10−13 |
| 338 | 1.80 × 10−10 | 2.62 × 10−7 | 10.94 × 10−13 |
| 348 | 2.04 × 10−10 | 5.81 × 10−8 | 13.79 × 10−13 |
| 350 | 2.09 × 10−10 | 4.34 × 10−8 | 14.42 × 10−13 |
 | ||
| Fig. 4 Kinetic scheme of the most favourable pathways of methyl salicylate abstraction by Cl radical calculated at 298 K. | ||
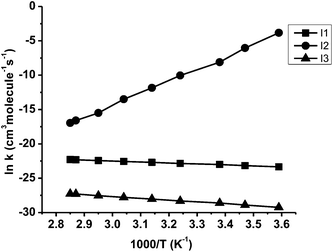 | ||
| Fig. 5 Arrhenius plot for the rate constants for the initial H-atom abstraction I1, peroxy radical I2 and aryloxy radical I3. | ||
Atmospheric lifetime
In general, VOCs are chemically removed from the troposphere mainly by their reaction with free radicals such as Cl, OH, NO3 and O3. Among these free radicals, the reaction with chlorine is important in the marine boundary layer and coastal areas. The atmospheric lifetime of MeSA with respect to its reaction with Cl was estimated by the following equation,where KCl is the rate coefficient of the title reaction taken as 1.01 × 10−10 cm3 per molecule per s at 298 K. A Cl concentration of 1 × 105 molecule per cm3 (ref. 27) was used to evaluate the tropospheric lifetime of MeSA. The tropospheric lifetime of MeSA was computed to be 1.14 days, which is short because the same was reported to be 40 days by experiments. Therefore, it appears that the reaction with Cl atoms provides an efficient route for the removal of MeSA from the atmosphere in coastal areas. The discrepancy in the lifetimes between the calculated and experimental value could be attributed to the accuracy of the calculated rate constants.
Chemical reactivity parameters
Tables S2 and S3 (in ESI†) present the frontier molecular orbital-based chemical reactivity parameters: HOMO, LUMO, HOMO–LUMO gap, chemical hardness, chemical softness, electrophilicity and activation hardness. The chemical hardness values of all the reactants indicate their higher stability compared with the corresponding transition states and intermediates. The activation hardness values predicted that the reaction of NO with I2 would proceed faster than other reactions because of a low activation hardness value. Based on the softness values of the transition state structures TS1, TS2, TS3, and TS4, it was found that TS2 was more reactive with a marginally higher softness value and a smaller HOMO–LUMO gap. In the case of the intermediates obtained (I1, I2, I3), I3 was the most reactive intermediate with a marginally larger softness and was the least stable. Of the products P1, P2, and P3, P3 was the most reactive with a large softness value and possessed a higher stability because of a large HOMO–LUMO gap. Hence, product P3 has a larger chemical softness than P1 and P2. The abovementioned results suggest that the reaction with NO was the most favourable for MeSA degradation.The global electrophilicity index measures the stabilization energy when a system acquires an additional charge from its environment, which is a useful quantity to classify the electrophilicity of the reactants, intermediate and transition state. Electrophilicity values listed in Table S2 (in ESI†) indicate that the reactants were highly nucleophilic, and were expected to interact preferentially with electrophiles. On the contrary, all the transition states and intermediates I2 and I3 were highly electrophilic. The product P3 was highly electrophilic when compared to the products P2 and P1. Among all the radicals, O2 has a minimum HOMO–LUMO gap value of 6.114 eV (given in Table S3†), which indicate a high reactivity.
During a reaction, the electrons are redistributed as bonds form and break. The redistribution of electrons followed by the change in molecular orbitals when two reactants react can often be understood by considering the interaction between the highest energy of occupied MO and the lowest energy of unoccupied MO. For the present study, the energy of HOMO and LUMO of the favourable reaction pathways  are discussed with the contour value of 0.05 a.u, and the plots are shown in Fig. S3 and S4 (in ESI†). Colours denote bonding and anti-bonding combinations between different orbitals. The red region indicates the positive lobe and the blue region represents the negative lobe.
are discussed with the contour value of 0.05 a.u, and the plots are shown in Fig. S3 and S4 (in ESI†). Colours denote bonding and anti-bonding combinations between different orbitals. The red region indicates the positive lobe and the blue region represents the negative lobe.
From the frontier molecular orbital analysis plots of the structures MeSA, TS1, I1, I2, TS4, and I3, HOMO was found to occupy the majority of the benzene ring (along the bonds C1–C2, C2–C3, C4–C5 and C5–C6) with π character due to p orbitals. In addition, a small contribution to HOMO was noted, arising from the lone pairs of oxygen atom in C2–O15 bond. In the I2 and TS4 structures, HOMO received additional contribution from the lone pairs of the oxygen atoms in O16–O20 bond due to their interaction. In the structure I3, HOMO spread to C3–C4 bond sustaining π character along the benzene ring. Similar to the abovementioned structure, the lone pair of the p orbitals of the oxygen atom in C3–O16 bond also contributed to HOMO.
The LUMO distribution in the structures of MeSA, TS1, I1, I2, TS4 and I3 significantly differed from the HOMO distribution. The large contributors to the LUMO were C1–C7 and C3–C2 bonds while a small contribution was from the vacant p orbitals of carbon (C4 and C6) with π* anti-bonding character. Similar to carbon, O8, O9, and O15 oxygen atoms also contributed to LUMO through their vacant p orbitals. This trend is consistent throughout the reaction path. In addition to the abovementioned contributions to LUMO, contributions from the lone pairs of oxygen in O16–O20 bond were observed in TS4. Unlike HOMO, a small evolution in the form of decrease in LUMO was visible along C5–C6 and C6–H19 bonds.
In the entire reaction path, the abstraction and addition of reactants occured only at the meta position of the MeSA, i.e. at C3–H16 bond. However, the contribution of H16 to neither HOMO nor LUMO was minimal, similar to the other hydrogens in MeSA. One of the interesting observations along the entire reaction path was that the methyl group was not involved in the contribution to HOMO and LUMO. This suggests that the benzene ring of the MeSA is more reactive than the methyl group.
Natural Orbital Fukui Function (NOFF)
To understand and interpret the reactivity of chemical bond involved in the abstraction reactions of MeSA by Cl radical, NOFFs were calculated using eqn (15) and (16). The NOFFs for the bond in MeSA along with the Cl radical of the initial reaction, peroxy radical with their reactivities calculated at M06-2X/6-311++G(d,p) level of theory are listed in Tables S4 and S5 (in ESI†). The NOFFs of peroxy radical with HO2, NO2, and NO radicals and their corresponding intermediates, transition state and products with their reactivities are tabulated in Table S5 (ESI†). A positive f+nbo suggests that the orbital can accept electrons when attacked by a nucleophile. However, a negative f+nbo value indicates a substantial orbital relaxation, and occurs when the additional electron does not contribute to the NBO but shields it from the nucleus, raising its energy and reducing its population. Similarly, a positive f−nbo suggests that the orbital can donate electrons when attacked by an electrophile. A negative f−nbo value is indicative of orbital relaxation and occurs when removing an electron, which causes other electrons to be deshielded and their orbitals to contract towards the nucleus in a manner that increases the shielding of the electron.The description of the abovementioned analysis was carried out only for the favourable pathways  . From the results of f−nbo for the reactant MeSA, its bonding orbitals, i.e. BD(C3–H16), BD(C3–C2), and BD(C3–C4) were prone to electrophilic attack. In the same manner, the anti-bonding orbitals of MeSA, i.e. BD*(C3–H16), BD*(C3–C2), and BD*(C3–C4) were also reactive to electrophiles. Among the f−nbo values for anti-bonding orbitals, BD*(C3–H16) bond has the smallest value when compared with BD*(C3–C4) and BD*(C3–C4) bonds. This indicates that the C3–H16 anti-bonding orbital was more positive than C3–C2 and C3–C4 bonds, and therefore the electronegative chlorine atom with a lone pair was able to attract C3–H16 bond and abstract the hydrogen atom. On the contrary, both bonding and anti-bonding orbitals in transition state TS1, i.e. BD(C3–H16), BD(C3–C2), BD(C3–C4), BD*(C3–H16), BD*(C3–C2), and BD*(C3–C4) were nucleophilic in nature (ability to accept electrons). Both bonding and anti-bonding orbitals in the intermediate I1, i.e. BD(C3–C2), BD(C3–C4), BD*(C3–C2), and BD*(C3–C4) were also nucleophilic in nature, and thus reacted spontaneously.
. From the results of f−nbo for the reactant MeSA, its bonding orbitals, i.e. BD(C3–H16), BD(C3–C2), and BD(C3–C4) were prone to electrophilic attack. In the same manner, the anti-bonding orbitals of MeSA, i.e. BD*(C3–H16), BD*(C3–C2), and BD*(C3–C4) were also reactive to electrophiles. Among the f−nbo values for anti-bonding orbitals, BD*(C3–H16) bond has the smallest value when compared with BD*(C3–C4) and BD*(C3–C4) bonds. This indicates that the C3–H16 anti-bonding orbital was more positive than C3–C2 and C3–C4 bonds, and therefore the electronegative chlorine atom with a lone pair was able to attract C3–H16 bond and abstract the hydrogen atom. On the contrary, both bonding and anti-bonding orbitals in transition state TS1, i.e. BD(C3–H16), BD(C3–C2), BD(C3–C4), BD*(C3–H16), BD*(C3–C2), and BD*(C3–C4) were nucleophilic in nature (ability to accept electrons). Both bonding and anti-bonding orbitals in the intermediate I1, i.e. BD(C3–C2), BD(C3–C4), BD*(C3–C2), and BD*(C3–C4) were also nucleophilic in nature, and thus reacted spontaneously.
In the pathway (I1 + O2), the bonding orbital BD(O16–O20) in the reactant O2 was electrophilic, while the anti-bonding orbital was found to be inactive but still bonded with C3–O16. The bonding orbitals for intermediate I2 were BD(C3–C2), BD(C3–C4), BD(C3–O16), and BD(O16–O20) and anti-bonding orbitals were BD*(C3–C2), BD*(C3–C4), BD*(C3–O16), and BD*(O16–O20), all of which were nucleophilic in nature, i.e. were able to accept electrons. The intermediate I2 reacted with NO, which was inactive but it was able to form NO2 by abstracting an oxygen atom from I2. Due to the abstraction of oxygen, the resultant bonding and anti-bonding orbitals, i.e. BD(C3–C2), BD(C3–C4), BD(C3–O16), BD(O16–O20), BD*(C3–C2), BD*(C3–C4), BD*(C3–O16), and BD*(O16–O20) in TS4 were electrophilic in nature. In the intermediate I3, the bonding orbitals of BD(C3–C2), BD(C3–C4), and BD(C3–O16) and the anti-bonding orbitals of BD*(C3–C2), BD*(C3–C4), and BD*(C3–O16) were nucleophilic in nature. In the same manner, pathways with HO2, and NO2 showed that the bonding and anti-bonding orbitals of P3 were nucleophilic in nature, while the bonding and anti-bonding orbitals of all the bonds in TS2, TS3, P1 and P3 were electrophilic in nature. In conclusion, the results of the Fukui functions were able to predict reactive sites, and correlate the reactive nature of the reactants.
Atoms in molecule analysis
The atom in molecules theory (AIM) is a useful tool to understand the nature of the bonds in detail.82 AIM topological analysis helps in the extraction of electronic charge density over atomic basins (up to 0.001 a.u level) as well as electron density, ρ(r), Laplacian of electron density, ∇2ρ(r), and bond ellipticity, at BCP where λ1, λ2, λ3 are the eigen values of the hessian matrix of the electron density. The BCP refers to the two negative and one positive eigen values at a critical point (3, −1). If a critical point has two positive and one negative eigen value, then it is called (3, +1) or the ring critical point (RCP), which indicates that a ring structure exists. The strength and the characteristic of the bond were described from the topological analysis of wave function, electron density ρ(r), and Laplacian of electron density ∇2ρ(r). The positive value of Laplacian indicates a weak interaction or an ionic bond; however, the negative value of Laplacian shows a strong covalent bond between the atoms. The energetic topological parameters and the Laplacian at BCP is given as:
at BCP where λ1, λ2, λ3 are the eigen values of the hessian matrix of the electron density. The BCP refers to the two negative and one positive eigen values at a critical point (3, −1). If a critical point has two positive and one negative eigen value, then it is called (3, +1) or the ring critical point (RCP), which indicates that a ring structure exists. The strength and the characteristic of the bond were described from the topological analysis of wave function, electron density ρ(r), and Laplacian of electron density ∇2ρ(r). The positive value of Laplacian indicates a weak interaction or an ionic bond; however, the negative value of Laplacian shows a strong covalent bond between the atoms. The energetic topological parameters and the Laplacian at BCP is given as:In addition,
| HBCP = G(rBCP) + V(rBCP) | (17) |
The reaction begins with the abstraction of a hydrogen atom from C3–H16 bond in MeSA by a chlorine atom. In the reactant MeSA, the essential BCP between C3–H16 has an electron density value ρ(r) of 0.2802 a.u., ∇2ρ(r) of −0.9620 a.u and a low ellipticity of 0.0205 to indicate that the bond had a strong sigma character and little distortion. In TS1, the electron density between C3–H16 increased marginally than the reactant (ρ(r) = 0.2806 a.u.) due to the interaction of chlorine atom. Correspondingly, the decrease of ∇2ρ(r) (−0.9655 a.u.) in TS1 indicates an electronic charge concentration along the bond path and the covalent nature of C3–H16 bond. The increase in electron density ρ(r) in C3–H16 from its corresponding reactant state led to the redistribution of electron density in the adjacent C–C bonds in the same region. In particular, the electron density of C3–C2 bond decreased by 0.0011 a.u., whereas in C3–C4 bond it increased feebly by 0.0005 a.u., in comparison to the reactant state. The ellipticity values of the C3–H16 bond in the reactant and TS1 were 0.0205 a.u. and 0.0187 a.u., respectively. Thus, the decrease in ellipticity value for C3–H16 bond in MeSA from reactant to TS1 ascertained an increase in the sigma bond character and a decrease in anisotropy while transforming from reactant to the TS1 state. The total energy density H(r) was negative for C3–H16 bond in both reactant and the TS1 state, confirming covalent character. The H(r) values of C3–C2 and C3–C4 bond indicated a strong covalent character compared to C3–H16 bond.
Continuing in the reaction path, TS1 transformed into I1, which formed I2 through the reaction with O2. From Table S6 (in ESI†) we could see that the ρ(r) values for both C3–C2 and C3–C4 bonds increased considerably from that of TS1. This increase was due to the redistribution of electron density associated with hydrogen atom abstraction by chlorine atom. Similarly, the ∇2ρ(r) value has a negative increase, suggesting shared or covalent interactions. The ellipticity values of C3–C2 and C3–C4 bonds in I1 decreased from TS1 state, indicating lesser distortion of electron density and a strong sigma bond character. The H(r) values of C3–C2 and C3–C4 bonds indicated a strong covalent character.
Further, in the reaction path, the intermediate structure (I1) reacted with O2 molecule leading to the formation of I2. This reaction proceeded through the bonding of O2 molecule with C3 atom in I1. From Table S6 (in ESI†), the reactant O2 (O16–O20) gave ρ(r) of 0.5614 a.u. and ∇2ρ(r) of −0.8980 a.u. along the bond critical path. In addition, a low ellipticity value indicated minimal distortion along with a strong covalent character due to a large H(r) value. In the intermediate structure (I2) for O16–O20 bond the value of ρ(r) decreased to 0.4045 a.u. but the ∇2ρ(r) increased to −0.2978 a.u. The decrease in electron density of the bond implies the bonding with C3 atom, while the increase in Laplacian of electron density indicates the covalent character of the bond due to the electronic charge concentration between the nuclei of O16 and O20 atoms. The ellipticity value of O16–O20 in intermediate (I2) was 0.0219 a.u., which implied that the distortion of electron density in O16–O20 decreased from the reactant state to the intermediate (I2) state, but still maintained the sigma character with a negative H(r) value. The binding of O2 with C3 atom resulted in I2 due to the C3–O16 bond. This C3–O16 bond has a ρ(r) of 0.2656, and ∇2ρ(r) of −0.3308 at bond critical path, and the values were comparatively lower than other bonds in the I2 structure, suggesting a weak bond formation. Nevertheless, the ellipticity value (0.0474 a.u.) indicates low distortion with sigma bond character, and the negative H(r) implies shared or covalent interaction between the C and O atoms.
The intermediate I2 further reacted with NO via the transition state TS4, resulting in I3. From Table S6 (in ESI†), the reactant NO (N21–O22 bond) has a ρ(r) of 0.5727 a.u. and ∇2ρ(r) of −1.8902 a.u. along the bond critical path. Notably, the NO bond in the reactant has a strong covalent character with a large magnitude for ∇2ρ(r) and H(r) (−1.0563) of all bonds. In TS4, the ρ(r) and ∇2ρ(r) of N21–O22 bond increased, while the ellipticity and H(r) values decreased from the reactant state due to the interaction with O20 atom. In contrast, all the topological parameters (ρ(r), ∇2ρ(r), ε, and H(r)) were low for N21–O20 bond as the bond was weak. In TS4, the electron density and H(r) increased for the C3–O16 bond, while Laplacian of electron density and ellipticity decreased from I2 state, which implies that covalent character of the bond remained unchanged. Further, the C3–C2 and C3–C4 bonds showed a small change in their topological parameters from the I2 state.
The NO molecule abstracted an O atom from the O16–O20 bond in TS4, resulting in C3–O16 bond that led to the formation of I3. From Table S6 (in ESI†), for C3–O16 in I3 along the bond critical path, the electron density ρ(r) of 0.2864 a.u. and ∇2ρ(r) of −0.6068 a.u. increased from the values found in the intermediate I2 and TS4. This shows that C3–O16 was stronger in I3 than in the intermediate I2. The large negative Laplacian of electron density and H(r) value denoted an increase in covalent character in I3 when compared to I2. The ellipticity value was also found to decrease compared to I2, which implies a strengthening of sigma character. Similar to C3–O16 bond, the electron density, Laplacian of electron density and H(r) value increased in C3–C2 and C3–C4 bonds (ρ(r) = 0.3125, 0.3222 a.u, ∇2ρ(r) = −0.9250, −0.9681a.u., and H(r) = −0.3210, −0.3433 for C3–C2 and C3–C4, respectively) than in I2. These observations clearly confirmed I3 as the favourable product. This increase in the electron density of the bond C3–O16 revealed that the bond became stronger, and a large negative value of Laplacian of electron density indicated that the electronic charge between the bonds was more covalent in nature than in the intermediate I2.
On observing the electron density ρ(r) and Laplacian of electron density ∇2ρ(r) of all the bonds in the remaining structures in other pathways such as TS2, P1, P2, and P3 were practically covalent in nature, whereas in TS3 a positive value of the Laplacian of electron density was observed in O16–O20 bond. This positive value for ∇2ρ(r) in TS3 indicated a locally depleted electron density between O16–O20 bond because of non-covalent or weak interactions. However, the total energy densities H(r) were uniformly negative in all the structures pointing to a covalent nature. Overall, electron density values predicted that the bonds formed were strong, and the corresponding Laplacian of electron density along with energy density show that the interactions were covalent in nature. Ellipticity values differentiated between sigma and π characters observed in C–H and C–C bonds, respectively.
Conclusion
The potential energy surface, reaction mechanisms and kinetics for the reaction of MeSA with Cl were investigated at B3LYP/M06-2X levels of theory with 6-311++G(d,p) basis set, and the kinetics of the reaction were studied using SCT. Analysis of the results provided the following main conclusions. The study elucidated the reaction pathways for the atmospheric oxidation of methyl salicylate initiated by Cl radical.(1) The reaction of Cl radical with MeSA proceeded mainly by hydrogen atom abstraction from the aromatic group of MeSA, resulting in the formation of an alkyl radical, and the subsequent reaction of this alkyl radical with O2 yielded a methyl 3-peroxy-2-hydroxy benzoate radical intermediate via a barrierless reaction.
(2) The secondary reaction occurred with other atmospheric species, i.e. HO2, NO2 and NO. The reaction between methyl 2-hydroxy-3-phenoxybenzoate radical and NO resulted in the formation of a peroxy radical, and it was one of the most favourable reactions with an energy barrier of 6.70 kcal mol−1.
(3) The rate constant of the initial H-atom abstraction was 1.017 × 10−10 cm3 per molecule per s at 298 K with an energy barrier of 1.99 kcal mol−1. Furthermore, the plot between the rate constant and temperature showed an Arrhenius nature.
(4) The HOMO and LUMO values indicated that the NO radical was more reactive than other radicals. Furthermore, the HOMO and LUMO plots suggested that the benzene ring in MeSA was more reactive than the methyl group. The chemical reactivity parameter and the activation hardness value augmented the favourable degradation path of MeSA with NO radical.
(5) From AIM analysis, the topological parameters of electron density values indicated that strong bonds were formed during the reactions between reactants, and the total energy density value showed that the interactions involved were covalent-dominant.
References
- R. P. Wayne, Chemistry of Atmospheres, Oxford University Press, third edn, 2000 Search PubMed.
- R. Atkinson and J. Arey, Chem. Rev., 2003, 103, 4605–4638 CrossRef CAS.
- J.-Q. Ni, W. P. Robarge, C. Xiao and A. J. Heber, Chemosphere, 2012, 89, 769–788 CrossRef CAS.
- B. J. Finlayson-Pitts and J. N. Pitts, Jr, Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications, Wiley, New York, 2000 Search PubMed.
- E. Grosjean and D. Grosjean, J. Atmos. Chem., 1999, 32, 205–232 CrossRef CAS.
- A. Mellouki, G. LeBras and H. Sidebottom, Chem. Rev., 2003, 103, 5077–5096 CrossRef CAS.
- A. Gulati, S. D. Ravindranath and A. K. Gupta, Mycol. Res., 1999, 103, 1380–1384 CrossRef.
- K. Kumazawa, H. Masuda, O. Nishimura and T. Kato, J. Jpn. Soc. Food Sci., 1998, 45, 728–734 CrossRef CAS.
- M. Nishikitani, D. Wang, K. Kubota, A. Kobayashi and F. Sugawara, Biosci. Biotechnol. Biochem., 1999, 63, 1631–1633 CrossRef CAS.
- E. L. Liebel and M. W. Shannon, Pediatr. Emerg. Care, 1993, 9, 292–297 CrossRef.
- D. L. Howrie, R. Moriarity and R. Breit, Pediatrics, 1985, 75, 869–871 CAS.
- J. L. Kloss and C. R. Boeckman, Ohio State Med. J., 1967, 63, 1064–1065 CAS.
- M. A. Halle and P. J. Collipp, J. Med., 1969, 69, 1788–1789 CAS.
- G. Arimura, R. Ozawa, T. Nishioka, W. Boland, T. Koch, F. Kuhnemann and J. Takabayashi, Plant J., 2002, 29, 87–98 CrossRef CAS.
- F. Chen, J. C. D'Auria, D. Tholl, J. R. Ross, J. Gershenzon, J. P. Noel and E. Pichersky, Plant J., 2003, 36, 577–588 CrossRef CAS.
- K. Ament, M. R. Kant, M. W. Sabelis, M. A. Haring and R. C. Schuurink, Plant Physiol., 2004, 135, 2025–2037 CrossRef CAS.
- J. Zhu and K. C. Park, J. Chem. Ecol., 2005, 31, 1733–1746 CrossRef CAS.
- W. Allan, H. Struthers and D. C. Lowe, J. Geophys. Res. D, 2007, 112, D04306 CrossRef.
- O. W. Wingenter, M. K. Kubo, N. J. Blake, T. W. Smith, D. R. Blake and F. S. Rowland, J. Geophys. Res., 1996, 101, 4331–4340 CrossRef CAS.
- D. L. Donohoue, D. Bauer and A. J. Hynes, J. Phys. Chem. A, 2005, 109, 7732–7741 CrossRef CAS.
- U. Platt, W. Allan and D. Lowe, Atmos. Chem. Phys., 2004, 4, 2393–2399 CrossRef CAS.
- E. M. Knipping and D. Dabdub, Environ. Sci. Technol., 2003, 37, 275–284 CrossRef CAS.
- R. S. Stolarski and R. J. Cicerone, Can. J. Chem., 1974, 52, 1610–1615 CrossRef CAS.
- P. Dalmasso, R. Taccone, J. Nieto, M. Teruel and S. Lane, Atmos. Environ., 2006, 40, 7298–7307 CrossRef CAS.
- J. P. Kercher, T. P. Riedel and J. A. Thornton, Atmos. Meas. Tech., 2009, 2, 193–204 CrossRef CAS.
- K. W. Oum, M. J. Lakin, D. O. Dehaan, T. Brauers and B. J. Finlayson-Pitts, Science, 1998, 279, 74–76 CrossRef CAS.
- C. W. Spicer, E. G. Chapman, B. J. Finlayson-Pitts, R. A. Plastridge, J. M. Hubbe, J. D. Fast and C. M. Berkowitz, Nature, 1998, 394, 353–356 CrossRef CAS.
- C. E. Canosa-Mas, J. M. Duffy, M. D. King, K. C. Thompson and R. P. Wayne, Atmos. Environ., 2002, 36, 2201–2205 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1990, 94, 5523–5527 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- D. H. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y. P. Liu, B. C. Grarrett, R. Steckler, A. D. Issacson, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, POLYRATE 4: A new version of a computer program for the calculation of chemical reaction rates for polyatomics., Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS.
- B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811–4815 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Am. Chem. Soc., 1979, 101, 4534–4548 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730–1748 CrossRef CAS.
- S. W. Benson, Thermochemical Kinetics, Wiley & Sons, New York, 1976, p. 8 Search PubMed.
- J. Zheng, S. Zhang, J. C. Corchado, Y. Y. Chuang, E. L. Coitino, B. A. Ellingson and D. G. Truhlar, GAUSSRATE version, 2009 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
- J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y. Y. Chaung, P. L. Fast, W. P. Hu, Y. P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Villa, I. Rossi, E. L. Coitino, J. Pu and T. V. Albu, POLYRATE version, 2010 Search PubMed.
- P.L.A. Popelier, MORPHY 98, A Topological analysis program written by P.L.A. Popelier with a contribution from RGA Bone, (UMIST, Engl, EU), University of Manchester UK, 1998.
- K. Fukui, Y. Yonezawa and H. A. Shingu, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, UK 1989 Search PubMed.
- Z. Zhou and R. G. Parr, J. Am. Chem. Soc., 1990, 112, 5720–5724 CrossRef CAS.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- V. Yang and W. J. Mortier, J. Am. Chem. Soc., 1986, 108, 5708–5711 CrossRef.
- L. T. Nguyen, F. D. Proft, A. K. Chandra, T. Uchimaru, M. T. Nguyen and P. Geerlings, J. Org. Chem., 2001, 66, 6096–6103 CrossRef CAS.
- M. T. Nguyen, A. K. Chandra, S. Sakai and K. Morokuma, J. Org. Chem., 1999, 64, 65–69 CrossRef CAS.
- P. Lopez and F. Mendez, Org. Lett., 2004, 6, 1781–1783 CrossRef CAS.
- Y. L. Lin, Y. M. Lee and C. Lim, J. Am. Chem. Soc., 2005, 127, 11336–11347 CrossRef CAS.
- J. Melin, P. W. Ayers and J. V. Ortiz, J. Phys. Chem. A, 2007, 111, 10017–10019 CrossRef CAS.
- T. Sato, K. Tokunaga and K. Tanaka, J. Phys. Chem. A, 2008, 112, 758–767 CrossRef CAS.
- R. E. Estrada-Salas and A. A. Valladares, J. Phys. Chem. A, 2009, 113, 10299–10305 CrossRef CAS.
- H. L. Chen and W. C. Chao, J. Phys. Chem. A, 2011, 115, 1133–1142 CrossRef CAS.
- P. Zhou, P. W. Ayers, S. Liu and T. Li, Phys. Chem. Chem. Phys., 2012, 14, 9890–9896 RSC.
- R. K. Roy, K. Hirao, S. Krishnamurty and S. Pal, J. Chem. Phys., 2001, 115, 2901–2907 CrossRef.
- R. K. Roy, K. Hirao and S. Pal, J. Chem. Phys., 2000, 113, 1372–1379 CrossRef.
- R. K. Roy, S. Pal and K. Hirao, J. Chem. Phys., 1999, 110, 8236–8245 CrossRef CAS.
- D. Glossman-Mitnik, Procedia. Comput. Sci., 2013, 18, 816–825 CrossRef.
- D. Glossman-Mitnik, Chem. Cent. J., 2013, 7, 155 CrossRef.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41(2), 157–167 CrossRef CAS.
- A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Chem. Rev., 2012, 112(1), 289–320 CrossRef CAS.
- I. Barnes, J. Hjorth and N. Mihalopoulos, Chem. Rev., 2006, 106, 940–975 CrossRef CAS.
- Z. Li, P. Nguyen, M. F. Leon, J. H. Wang, K. Han and G. Z. He, J. Phys. Chem. A, 2006, 110, 2698–2708 CrossRef CAS.
- M. B. Williams, P. Campuzano-Jost, B. M. Cossairt, A. J. Hynes and A. J. Pounds, J. Phys. Chem. A, 2007, 111, 89–104 CrossRef CAS.
- S. B. Barone, A. A. Turnipshed and A. R. Ravishankara, J. Phys. Chem., 1996, 100, 14694–14702 CrossRef CAS.
- C. O. Zavala and A. Galano, J. Chem. Theory Comput., 2009, 5, 1295–1303 CrossRef.
- G. D. Silva, M. R. Hamdan and J. W. Bozzelli, J. Chem. Theory Comput., 2009, 5, 3185–3194 CrossRef.
- L. Sandhiya, P. Kolandaivel and K. Senthilkumar, Struct. Chem., 2012, 23, 1475–1488 CrossRef CAS.
- G. da Silva, J. Phys. Chem. A, 2012, 116, 5317–5324 CrossRef CAS.
- A. Perez de la Luz, C. Iuga, J. R. Alvarez-Idaboy, E. Ortiz and A. Vicier-Bunge, Int. J. Quantum. Chem., 2012, 112, 3525–3534 CrossRef.
- S. Raoult, M. T. Rayez, J. C. Rayez and R. Lesclaux, Phys. Chem. Chem. Phys., 2004, 6, 2245–2253 RSC.
- C. Xu and L. Wang, J. Phys. Chem. A, 2013, 117, 2358–2364 CrossRef CAS.
- I. Hermans, J. F. Müller, T. L. Nguyen, P. A. Jacobs and J. Peeters, J. Phys. Chem. A, 2005, 109, 4303–4311 CrossRef CAS.
- I. Hermans, T. L. Nguyen, P. A. Jacobs and J. Peeters, J. Am. Chem. Soc., 2004, 126, 9908–9909 CrossRef CAS.
- R. F. W. Bader, Atoms in molecules: a quantum theory, Oxford University Press, Oxford 1990 Search PubMed.
- W. D. Arnold and E. Oldfied, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- Y. X. Lu, J. W. Zou, Y. H. Wang, Y. J. Jiang and Q. S. Yu, J. Phys. Chem. A, 2007, 111, 10781–10788 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The selected geometrical parameters (bond length R in Å, bond angle θ and dihedral angle ϕ in degrees) on the potential energy surface of the favourable reaction path calculated at M06-2X/6-311++G(d,p) level of theory are given in Table S1. The global reactivity parameters, hardness (η), softness 1/η, electrophilicity index (ω), activation hardness (Δn*), HOMO, LUMO, energy gap (ΔE) (in eV) calculated at M06-2X/6-311++G(d,p) level of theory are summarized in Tables S2 and S3. NOFFs (in electrons) of methyl salicylate with the Cl radical of the initial reaction and peroxy radical with HO2, NO2, and NO radicals calculated at M06-2X/6-311++G(d,p) level of theory are shown in Tables S4 and S5. Topological analysis of reactants, transition states, intermediates and products of methyl salicylate with Cl radical calculated at M06-2X/6-311++G(d,p) level of theory is shown in Table S6. The optimized structures of the reactive species corresponding to the formation of the peroxy radical I2 from the Cl-initiated reaction of MeSA at M06-2X/6-311++G(d,p) level of theory is shown in Fig. S1. The optimized structures of the reactive species corresponding to the reactions of peroxy radical I2 with HO2, NO2 and NO at M06-2X/6-311++G(d,p) level of theory are shown in Fig. S2. The density plot of the highest occupied molecular orbital (HOMOs) and the lowest unoccupied molecular orbital (LUMOs) of the most favourable reaction pathway calculated at M06-2X/6-311++G(d,p) level of theory is shown in Fig. S3 and S4. See DOI: 10.1039/c4ra02398f |
| This journal is © The Royal Society of Chemistry 2014 |