DOI:
10.1039/C4RA02246G
(Paper)
RSC Adv., 2014,
4, 22911-22925
Dual mode of extraction for Cs+ and Na+ ions with dicyclohexano-18-crown-6 and bis(2-propyloxy)calix[4]crown-6 in ionic liquids: density functional theoretical investigation†
Received
14th March 2014
, Accepted 6th May 2014
First published on 7th May 2014
Abstract
The unusually high selectivity of the Cs+ ion over the Na+ ion with bis(2-propyloxy)calix[4]crown-6 (BPC6) compared to dicyclohexano-18-crown-6 (DCH18C6) has been investigated using generalized gradient approximated (GGA) BP86, hybrid B3LYP and meta hybrid TPSSH density functionals, employing split valence plus polarization (SVP) and triple zeta valence plus polarization (TZVP) basis sets in conjunction with the COSMO (conductor like screening model) solvation approach. The calculated theoretical selectivity of the Cs+ ion over the Na+ ion was found to be in accordance with the experimental selectivity obtained using solvent extraction experiments in ionic liquids (IL) and octanol. The distribution constant of the Cs+ ion, DCs with DCH18C6 in the 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide (BMIMTF2N) IL phase was found to be significantly large than that in octanol. The experimentally measured DCs value was found to be very large compared to the value of DNa in the IL phase. The presence of the BMIM cation in the recorded UV-visible spectra of the raffinate phase with and without DCH18C6 indicates the BMIM cation exchange with Cs+ and Na+ ions, thus supporting the dual mode of extraction. The dual mode of metal ion extraction observed in the experimental study was complemented by density functional theoretical study. The calculated free energy of extraction, ΔGext, for the metal ion was found to be higher in IL compared to octanol. Further, preferential selectivity of the Cs+ ion over the Na+ ion was established from the free energy difference, ΔΔGext, between the two competing metal ions. The unusually high selectivity of Cs+ over the Na+ ion by BPC6 in IL compared to DCH18C6 is also demonstrated by the free energy difference, ΔΔΔGext, between the two competing ligands which was shown to be free from the complicated metal ion solvation energy.
Introduction
Ionic liquids (ILs) are generally salts of organic cations (such as imidazolium, pyridinium, etc.) and inorganic anions (such as (CF3)2SO3−, PF6−) and exist in liquid state at relatively low temperatures. The unique properties of ILs are essentially zero vapor pressure, non-flammability, high thermal stability, relatively low viscosity, high ionic conductivity and sustainment as liquid over a wide range of temperature. Due to these unique characteristics, ILs have drawn widespread attention in chemistry,1–7 chemical engineering,8–15 and materials research.16–21 Therefore, continuous efforts are being devoted for the promising application of ionic liquid in the field of separations, in particular, on the service of these materials as the next generation diluents in the extraction of metal ions22–30 using solvent extraction principle. The extraction mechanism associated with these hydrophobic ionic solvents is generally believed to involve the conventional complexation of metal ions via an extractant along with the exchange of aqueous metal ions with the cation of the ILs.31
In view of these novel characteristics of ILs, it is worthwhile to explore its applicability as diluents in spent nuclear fuel reprocessing. One of the most interesting and difficult challenge in spent nuclear fuel reprocessing is the recovery and separation of the Cs+/Na+ ions pair, as reprocessing of spent nuclear fuel leads to a large volume of solutions with a low content of radioactive Cs and a high content of Na.32,33 For this cause, a huge effort has been devoted to find ways to extract Cs+ from acidic solutions resulting from the reprocessing of nuclear fuel.34–39 The intention of various extraction processes used in nuclear technologies is the selective partitioning and concentrating of metal ions with least environmental infectivity. Macrocyclic crown ether40 and calix[n]arene compounds41 are being practiced for the removal of Cs+ ion from nuclear waste solution. Alkyl substituted or phenyl/cyclohexyl derivatives of 18-crown-6 (18C6) show very poor selectivity as clear from the reported separation factor (βCs/Na = 0.3–4.57).42,43 However, modest separation factor (βCs/Na = 210 for ditertiarybutyl-di-benzo-18C6 (DTBDB18C6)) was observed42 when alkyl substituents are attached in the phenyl or cyclohexyl derivatives of 18C6. It has been reported that calix itself has very puny affinity for metal ions until it is functionalized with some substituent.44 The solvent extraction of univalent cations into nitrobenzene using calix[4]arene-bis(t-octylbenzo-18-crown-6) and 1,3-alternate-25,27-bis(1-octyloxy)calix[4]arene-crown-6 were studied including DFT calculations.45–52There is a significant increase in the selectivity (βCs/Na = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) when a hybrid calix-crown compound was used by functionalizing the calix[4]arene in the 1, 3 alternate conformation resulting to the formation of 18C6 like cavity.53
000) when a hybrid calix-crown compound was used by functionalizing the calix[4]arene in the 1, 3 alternate conformation resulting to the formation of 18C6 like cavity.53
The use of ILs as an extracting agent for heavy metal ions has been reported earlier.54 Extraction of various metal ions has been studied with imidazolium based ILs.55,56 In most of the studies, extraction of metal ions into the hydrophobic ILs phase was found to be insignificant because metal ions which are to be extracted from the aqueous phase are strongly hydrated. Thus, an extractant should be used, which generally forms hydrophobic complexes with the metal ions and subsequently facilitates their transfer from aqueous to the ILs phase. Luo et al.57 have reported very high values of distribution constant for Sr2+ and Cs+ ion in protic amide-based ILs employing DCH18C6 as an extractant. They have further shown that BOBCalix6 (calix[4]arene-bis(tert-octylbenzo-crown-6)) is an efficient extractant for Cs+ ion in ILs compared to simple organic solvents like 1,2-dichloroethane and chloroform.58 It is worthwhile to mention that even in the absence of extractant molecules, some partitioning of Cs+ ion was observed in ILs, but no such partitioning was noticed in conventional organic molecular solvents.59 It was also reported that the extraction mechanism for transfer of metal ions from aqueous phase to the ILs phase is different than that of in molecular organic solvent. It is generally believed that the exchange of aqueous phase metal ions with the cation of ILs occurs without co-extraction of the counter anions when a neutral extractant is used, whereas, the transfer of metal ions from aqueous solution is generally accompanied with the co-anions in the common molecular organic solvents. The mechanism and radiation effect on the extraction of Cs+ ion using calix-crown ether in ILs has also been reported earlier.21 The extraction ability of calix-crown was found to be considerably higher than that of only crown ether ligands.60,61
This rather remarkable and interesting affair should be explored by means of further experimental and theoretical studies. Numerous works have been reported on the metal ion extraction in ILs using solvent extraction techniques.22–31 Theoretical studies concerning only thermo-physical properties of ILs62–68 or metal ion-crown ligand/calix-crown ligands69–75 have been reported. But, theoretical studies involving ILs and metal ion–ligand together are rather scarce. Among theoretical studies, sole MD simulation has been performed by Wipff et al.76 on Cs+/Na+ extraction in BMIMTF2N. They have shown that the metal ion is exchanged with the BMIM cation of IL. To the best of our knowledge, no quantum computational study has been reported so far to understand the dual exchange mode of ion transfer from aqueous phase to the ILs phase.
Hence, our endeavor here is to investigate the dual mode of ion transfer employing quantum electronic structure calculation in conjunction with COSMO solvation approach. Solvent extraction technique is used to estimate the distribution constant, whereas quantum electronic structure calculation with implicit and explicit solvation model is used to calculate the free energy of extraction, ΔGext of the metal ions with DCH18C6 and BPC6 ligands. The structures, energetic and thermodynamic parameters for the metal ion–ligand systems were computed using DFT. The solvent effect for water, organic solvent and ILs was taken into account through COSMO approach. Attempt has been made to correlate the experimentally measured separations factors to the computed extraction free energy ΔGext, the metal–ligand interaction which governs the selectivity has further been investigated by molecular orbital population analysis. The experimental and theoretical details are presented in the following section.
Experimental and computational studies
Reagents
All reagents used in the solvent extraction experiments were of AR grade. DCH18C6 was procured from Aldrich and was used without further purification. BMIMTF2N (Sigma Aldrich make) and octanol (SD fine chemicals, India) were used as diluents for the solvent extraction experiment. The Aldrich make metal salts of CsNO3, NaNO3, CsCl and NaCl were used for the preparation of aqueous solution using Millipore water (conductivity – 0.054 μS cm−1) which was used as aqueous phase. The stock solution of DCH18C6 of 0.05 M was prepared in BMIMTF2N and octanol solvents which were used as water immiscible phase.
Distribution studies
Equal volumes (3 ml) of aqueous phase containing either Cs (1.1413 × 10−3 M) or Na (4.3096 × 10−4 M) ions and organic phase (IL or octanol) were taken in a glass bottle for equilibration in a thermostatted water bath. The bottles were equilibrated at constant temperature (25 ± 0.1 °C) for 30 min to attain equilibrium. The two phases were then centrifuged and assayed by taking suitable aliquots from both the phases. The concentration of Cs and Na ions in the feed as well as in the raffinate was estimated using the flame atomic absorption spectrophotometer instrument (GVC Model no. Avanta PM3000). Analysis results were typically reproducible within ±5%.
Computational methodology
Density functional theory (DFT), which had been used extensively for the calculations of various molecular properties was used here for the optimization of structure of free crown ethers, calix-crowns and their Cs+ and Na+ ion complexes using generalized gradient approximated (GGA) BP86, hybrid B3LYP and meta hybrid TPSSH density functional with split valence plus polarization (SVP)77 and triple zeta valence plus polarization basis set (TZVP)77 as implemented in the Turbomole suite of program.77,78 For Cs, ECP with 46 core electrons was used.79 BP86 functional consists of Becke's exchange functional80 and Perdew's correlation functional81 and was found to be reliable in predicting the molecular properties of metal ion–ligand system. B3LYP functional consists of Becke's three-parameter nonlocal hybrid exchange correlation functional82 and Lee–Yang–Parr correlation functional83 whereas TPSSH functional consists of Tao–Perdew–Staroverov–Scuseria exchange functional.84 Geometry optimization was carried out at BP86, B3LYP and TPSSH level of theories using both SVP and TZVP basis sets without arresting any symmetry restriction. The equilibrium structure was established by the absence of any imaginary frequency in the vibrational modes obtained through aoforce and NumForce module of Turbomole package. The optimized coordinates were further used for the single point energy calculation with MP2 level of calculations85 to check the accuracy and reliability of the various density functional. Further, the non-covalent interactions were accounted for by using the M06 suite of density functionals86 with TZ2P basis set as implemented in ADF package.87 The thermodynamic parameters were calculated using freeh module of Turbomole program. Implicit and explicit solvation effect on the interaction and selectivity was performed using COSMO88 approach. Structural parameters and geometry was viewed by Molden graphics program.89 Aqueous solubility and partition coefficients of free crown ether and calix-crown in aqueous–organic bi-phasic system were calculated using COSMOtherm package.90 The free energy, ΔG of the metal ion–ligand complexation (considering 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (M
1 (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) stoichiometry for both Cs+ and Na+ ion) is computed using the following basic complexation reaction:
L) stoichiometry for both Cs+ and Na+ ion) is computed using the following basic complexation reaction:| |
 | (1) |
Here, L stands for DCH18C6 and BPC6 ligand. The molecular interactions which dictates the ion selectivity was further investigated by analyzing different molecular orbital population analysis, topological parameters using atom in molecule (AIM) approach and second order stabilization energy using NBO program.
Results and discussions
Distribution studies
The solvent extraction studies were carried out for the extraction of Cs+ and Na+ ion from the aqueous solution of chloride and nitrate salts by DCH18C6 extractant either in BMIMTF2N or octanol solvent phase. The distribution constant, DCs and DNa in solvent extraction experiments were calculated by the concentration ratio of each metal ion, representing the total analytical concentration in the non-aqueous solvent phase (extract) to its analytical concentration in the aqueous phase (raffinate) and is expressed as:| | |
D = [M+]non-aq/[M+]aq, [M+ = Cs or Na]
| (2) |
here, [M+]non-aq and [M+]aq is the total metal ion concentration in the non-aqueous and aqueous phase respectively. The separation factor (SF) can be calculated as the ratio of the respective distribution ratio of the two extractable metal ions measured in the same identical conditions as follows:| | |
Separation factor (SFCs/Na) = DCs/DNa
| (3) |
The estimated values of distribution constant for Cs+ or Na+ ions are presented in Table 1. From the table it is seen that the extraction of Cs+ ion with common organic diluents such as octanol (DCs = 0.15 and 0.13 in case of chloride and nitrate salts respectively) is negligible whereas Cs+ extraction is significantly high with DCH18C6 in BMIMTF2N IL (DCs = 100 and 91 for chloride and nitrate salts respectively). The distribution constant of Cs+ ion was found to be slightly more in chloride than nitrate solution. On the other hand, DCH18C6 in IL extracts Na+ ion in smaller extent than Cs+ ion as revealed from the value of distribution constant (DNa = 19.2 and 16.5 in case of chloride and nitrate salts respectively; see also Fig. 1a and b). Further, the extraction of Na+ ion with DCH18C6 in BMIMTF2N phase is higher compared to octanol. The separation factor, SF(Cs/Na) was shown to be increased slightly from octanol (∼4) to ILs media (∼5.3). However, it is interesting to note that the while the partitioning of Cs+ ion is increased in IL in presence of DCH18C6, the partitioning of Na+ was slightly reduced as the anion is changed from chloride to nitrate, which was not observed in the conventional solvents.55 The distribution constant of Cs+ and Na+ ions for both chloride and nitrate solution without ligand in ILs were also measured and presented in Table 1 (also see Fig. S1†). Though the distribution constant of Cs+ ion is higher than that of Na+ ion (D < 1), but not large enough to be used in the large scale separation process. Nevertheless cationic partitioning was observed in ILs without the addition of ligands which attributed to the ion exchange of the BMIM cation with the inorganic ions. The UV-visible spectra of BMIMTF2N with and without DCH18C6 also capture the exchange of the BMIM cation with the metal ion. The BMIM cation gets exchanged with Cs+ or Na+ ion in water (raffinate phase) as reflected from the recorded UV-visible spectra (see Fig. 2). The water phase UV-spectra after mixing BMIMTF2N with water does not show maxima peak at 211 nm (characteristics peak of IL) suggesting that BMIMTF2N is not soluble in water. Xu et al.21 earlier reported that Cs+ extraction with calix crown ether in BMIMTF2N shows dual cation extraction.
Table 1 Distribution constant, D of Cs+ and Na+ ions using chloride and nitrate solution with DCH18C6 and BPC6 extractant in octanol and BMIMTF2N
| |
Chloride solution |
Nitrate solution |
| Extractant/diluents |
DCs |
DNa |
SFCs/Na |
DCs |
DNa |
SFCs/Na |
| Ref. 99. Ref. 21. |
| DCH18C6 in octanol |
0.15 |
0.04 |
3.75 |
0.13 |
0.03 |
4.33 |
| DCH18C6 in BMIMTF2N |
100 |
19.2 |
5.2 |
91 |
16.50 |
5.51 |
| BMIMTF2N |
0.25 |
0.05 |
5.0 |
0.32 |
0.02 |
16.0 |
| BPC6 in octanol |
— |
— |
— |
9.78a |
0.01a |
978 |
| BPC6 in BMIMTF2N |
— |
— |
— |
>1000b |
— |
— |
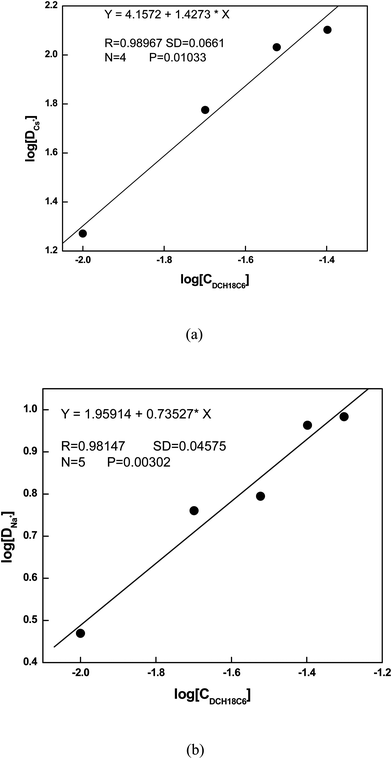 |
| | Fig. 1 Plot of D vs. concentration (C) of crown ether in BMIMTF2N. (a) Cs+ ion (b) Na+ ion. | |
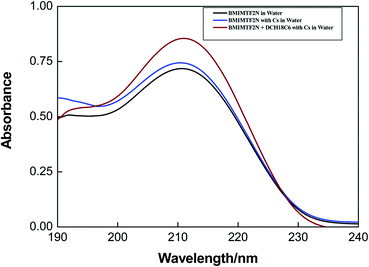 |
| | Fig. 2 UV-vis spectra of [BMIM]+ in the aqueous phase before and after the extraction of Cs+ with DCH18C6, [Cs+] = 10 mmol L−1. | |
Hence, the extraction of metal ion with DCH18C6 in BMIMTF2N can also be considered to be occurred via dual extraction mode as one through complexation with ligand
| | |
M+(aq) + BMIM(org) + L(org) → M+L(org) + BMIM(aq), (M = Cs/Na)
| (4) |
and another direct ion exchange with BMIM cation of ILs as
| | |
M+(aq) + BMIM(org) → M+(org) + BMIM(aq)
| (5) |
It is worth mentioning that though the distribution constant of Cs+ ion is very high with DCH18C6 in ILs media, the distribution constant of Na+ ion is also considerable. So, the use of DCH18C6 as selective extractant for Cs+ ion is not workable as high level nuclear waste contains large volume of Na+ ion. So, an alternative extractant has to be worked out with which the distribution constant of Cs+ ion will be very high whereas negligible for Na+ ion. It has been reported that the calix-crown ligand can plays the wonder here. Experimentally21–60 it has been shown that the distribution of Cs+ ion is enhanced many folds whereas the distribution constant for Na+ ion is reduced significantly. From the solvent extraction experiment of Cs+ and Na+ ion with DCH18C6 in ILs and octanol, it was observed that the extraction of metal ion in ILs is different than that of in octanol. The metal ion extraction in ILs occurs via cation exchange mechanism. In order to understand the dual cation extraction mechanism, free energy of extraction for the metal ion is calculated using DFT calculation which is described in the next section.
In order to model the metal–ligand complexation reaction, the correct stoichiometry of the metal–ligand (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) complex is required. But, there is lack of data on stoichiometry of M
L) complex is required. But, there is lack of data on stoichiometry of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L complexes for both Cs and Na ions with DCH18C6 in ILs. In order to find out the stoichiometry of the complexes, the distribution constant of the Cs and Na metal ions were estimated using different concentration of ligand and the distribution constants were plotted against the concentration of the ligand which is displayed in Fig. 1. From the plot the slope are found to be ∼1 for both Cs and Na ions which indicates 1
L complexes for both Cs and Na ions with DCH18C6 in ILs. In order to find out the stoichiometry of the complexes, the distribution constant of the Cs and Na metal ions were estimated using different concentration of ligand and the distribution constants were plotted against the concentration of the ligand which is displayed in Fig. 1. From the plot the slope are found to be ∼1 for both Cs and Na ions which indicates 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 M
1 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L complexes for both the metal ions.
L complexes for both the metal ions.
Computational results
Structure of ligand and metal ion–ligand complexes
The optimized minimum energy structures of free crown and calix-crown ligands and their complexes of Cs+ and Na+ ions are displayed in Fig. 3. All the structures were optimized using three different DFT functional (BP, B3LYP and TPSSH) and two different basis sets (SVP and TZVP) to study the effect of functional and basis set on the structure of free crown as well as complex. From the figures and structural parameters (ESI Fig. S2–S14 and Tables S1–S6†) it is seen that the structures of free DCH18C6 and BPC6 obtained from different level of DFT and basis set are very close. From the table, it is seen that the difference in structural parameters obtained using different level of functional and basis set combinations is negligible and hence one might use the cost effective BP86 functional for geometry optimization instead of time consuming B3LYP and TPSSH functional. The cavity size (after subtracting the dia of O atom of 2.644 Å from the centre to centre O–O distance) of the DCH18C6 was found to be 3.13 Å at BP/SVP level of theory, which is very close to the reported experimentally observed cavity (3.20 Å). Whereas in the case of BPC6 the cavity size was found to be 4.07 Å, higher than the cavity of DCH18C6 by 0.94 Å. Hence, Cs+ ion (dia: 3.38 Å)91 sits at the top of the DCH18C6 but nicely fits in the cavity of calix-crown moiety as seen in the Fig. 3. The Cs–O bond distance in the case DCH18C6 was found to be varied from 3.12–3.28 Å and was very close to the reported crystallographic value of 3.20–3.23 in DTBDB18C6 ether.92 The optimized structure of Na+ ion complex with DCH18C6 and BPC6 are also displayed in Fig. 3. Due to smaller ionic diameter (value) compared to Cs+ ion, Na+ is completely encapsulated within the cavity of DCH18C6. Four O donor atoms of DCH18C6 are leading to four equivalent Na–O distance (2.41–2.58 Å) and remaining two leads to higher Na–O bond length (2.60–2.71 Å), resulting in overall six coordination. The Cs+–O distance with BPC6 is 3.25–3.49 Å which was found to be in good agreement with the reported experimental values of 3.10–3.47 Å (ref. 91) as shown in Table 2. In case of Na metal ion-complex with calix-crown ether, the metal ion is coordinated to only three O atoms of the crown ring as seen from the Fig. 3 and the Table 2 (two O atoms from phenolic ring and one from polyether bridge).
 |
| | Fig. 3 Optimized minimum energy structure of free (I) DCH18C6 and (II) BPC at BP/SVP level of theory. a and b represents complexes with Cs+ and Na+ ions respectively. Green, red, grey, yellow and cyan sphere represent the C, O, H, Cs and Na atom respectively. | |
Table 2 Calculated structural parameters of DCH18C6, BPC6 and their complexes with Cs+ and Na+ ions at BP/SVP level of theory
| Method |
C–C (Å) |
C–O (Å) |
O–O (Å) |
M–O (Å) |
| DCH18C6 |
1.521, 1.521, 1.517, 1.517 |
1.412, 1.420, 1.421, 1.416, 1.412, 1.413, 1.412, 1.412, 1.415, 1.412, 1.410, 1.410 |
5.461, 6.062, 5.805 |
|
| BPC6 |
1.523, 1.521, 1.530, 1.521, 1.519 |
1.378, 1.387, 1.425, 1.423, 1.411, 1.412, 1.413, 1.412, 1.415, 1.416, 1.413, 1.415 |
6.998, 6.422, 6.729 |
|
| DCH18C6–Cs+ |
1.516, 1.517, 1.518, 1.518 |
1.439, 1.438, 1.428, 1.430, 1.423, 1.422, 1.422, 1.424, 1.423, 1.422, 1.423, 1.422 |
4.704, 5.886, 5.937 |
3.138, 3.138, 3.126, 3.287, 3.218, 3.120 |
| DCH18C6–Na+ |
1.512, 1.508, 1.513, 1.523 |
1.444, 1.439, 1.430, 1.438, 1.424, 1.427, 1.425, 1.430, 1.427, 1.423, 1.423, 1.425 |
4.872, 5.023, 4.796 |
2.510, 2.581, 2.710, 2.420, 2.608, 2.411 |
| BPC6–Cs+ |
1.514, 1.514, 1.523, 1.518, 1.518 |
1.400, 1.394, 1.438, 1.420, 1.422, 1.420, 1.420, 1.421, 1.421, 1.419, 1.419, 1.437 |
6.459, 6.597, 6.291 |
3.256, 3.261, 3.327, 3.445, 3.497, 3.264 |
| BPC6–Na+ |
1.515, 1.517, 1.525, 1.516, 1.518 |
1.404, 1.408, 1.446, 1.428, 1.434, 1.415, 1.424, 1.414, 1.415, 1.423, 1.448, 1.414 |
5.798. 6.967, 5.123 |
2.382, 2.424, 2.468, 3.980, 5.013, 4.265 |
There is a possibility that the gas phase conformation of DCH18C6, BPC6 and their complexes with Cs+ and Na+ ion can be changed in octanol organic solvent. In order to study the effect of solvent on gas phase conformation the structures of DCH18C6, BPC6 and their complexes with Cs+ and Na+ ion was further optimized in COSMO solvent of dielectric constant, ε = 10.3 at BP/SVP level of theory. The computed structural parameters are presented in Table 3. From the table it is seen that the solvent phase structural parameters is almost identical as that of in gas phase structures. Hence, single point energy calculation was done in solvent phase using coordinates of gas phase optimized structures. The effect of solvent phase structure on the thermodynamic parameters is discussed in subsequent section.
Table 3 Calculated structural parameters of DCH18C6 and BPC6 in octanol solvent at BP/SVP level of theory
| System |
C–C (Å) |
C–O (Å) |
O–O (Å) |
| DCH18C6 |
1.517, 1.517, 1.519, 1.519 |
1.423, 1.425, 1.424, 1.419, 1.415, 1.415, 1.415, 1.416, 1.414, 1.414, 1.412, 1.412 |
5.438, 6.009, 5.789 |
| BPC6 |
1.523, 1.520, 1.529, 1.521, 1.519 |
1.386, 1.376, 1.427, 1.425, 1.413, 1.414, 1.416, 1.415, 1.417, 1.415, 1.416, 1.415 |
7.004, 6.420, 6.770 |
Binding energy
One of the most important parameter in modeling the metal ion–ligand complexation reaction in liquid–liquid extraction is the binding energy (BE, ΔE) of the metal ion (Cs+/Na+) with the ligand (L). The metal ion–ligand complexation reaction is modeled as the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric reaction. The BE (ΔE) of the Cs+/Na+ ions for the following 1
1 stoichiometric reaction. The BE (ΔE) of the Cs+/Na+ ions for the following 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation reaction
1 complexation reaction| | |
M+ + L = M+ − L, (M+ = Cs or Na)
| (6) |
can be written as:| | |
ΔE = EM–L − (EM + EL).
| (7) |
where, EM–L, EM and EL refer to the energy of M–L complex, M ion and the free ligand, L, respectively. The calculated values of binding energy in gas phase for both Cs+ and Na+ ions with DCH18C6 are presented in Table 4. From the table it is seen that the calculated binding energy of Cs+ metal ion with DCH18C6 using B3LYP and TPSSH functional are almost equivalent with both SVP and TZVP basis sets, whereas the calculated binding energy using BP86 functional is smaller by ∼3 kcal mol−1 than the value predicted from B3LYP and TPSSH functional with SVP basis set and is smaller by 1.5 kcal mol−1 with TZVP basis set. The basis set effect on the Cs+ ion binding energy is not considerable. The calculated binding energy for Na+ ion with DCH18C6 is also presented in the same table. There is a strong basis set effect in the binding energy of the Na+ ion as the binding energy predicted using SVP basis set is smaller by 25–26 kcal mol−1 than that of using TZVP basis set for all the DFT functional considered here. The calculated binding energy at BP86 level of theory is smaller by 5–7 kcal mol−1 compared to the value predicted from B3LYP and TPSSH level of density functional, whereas the BE is smaller by 4–5 kcal mol−1 using TZVP basis set than that of B3LYP and TPSSH functional. The accuracy of the various DFT functional (BP86, B3LYP and TPSSH) using different basis set (SVP and TZVP) was further tested using single point energy calculation at the second order Moller–Plesset (MP2) level of theory using TZVP basis set. The calculated binding energy with MP2 level of theory using the optimized coordinates obtained from various DFT-basis set combinations are also presented in the same table. The calculated BE at MP2/TZVP level of theory was found to be higher by 10–11 kcal mol−1 using coordinates from SVP basis set whereas it is higher by 11–13 kcal mol−1 using optimized coordinates from TZVP basis set. The BE calculated at MP2 level of theory using optimized coordinates from BP86, B3LYP and TPSSH density functional with TZVP basis set are found to be very close in value to each other. Similar is the case for Na+ ion also. The calculated BE for Na+ ion at MP2/TZVP level of theory was found to be higher by 29–36 kcal mol−1 using optimized coordinates from SVP basis set whereas it is higher by 7–12 kcal mol−1 using coordinates from TZVP basis set. The gas phase BE for Na+ ion is always higher than the Cs+ ion by 28–32 kcal mol−1 for all the DFT functional basis set combinations indicating the higher selectivity for Na+ ion compared to Cs+ ion.
Table 4 Calculated values of binding energy of Cs+ and Na+ ion with DCH18C6 at different DFT functional and basis seta
| System |
BE (kcal mol−1) |
| SVP |
TZVP |
| BP86 |
B3LYP |
TPSSH |
BP86 |
B3LYP |
TPSSH |
| Values in the parentheses are obtained using MP2 level single point energy at TZVP level of theory using optimized geometry at the respective functional and basis set. |
| Cs |
−52.52 (−62.91) |
−55.83 (−67.26) |
−55.92 (−67.32) |
−54.26 (−67.64) |
−55.83 (−67.26) |
−55.91 (−67.34) |
| Na |
−56.19 (−92.13) |
−62.98 (−96.48) |
−61.87 (−96.64) |
−82.87 (−95.52) |
−88.42 (−95.88) |
−87.22 (−95.88) |
Next, we will deal with the BE of Cs+ and Na+ ions with BPC6 as the extraction ability of calix-crown (BPC6) was reported to be remarkably high than that of DCH18C6. The calculated BE for both Cs+ and Na+ ions with BPC6 are presented in Table 5. From the table it is seen that the calculated binding energy of Cs+ metal ion with BPC6 using B3LYP and TPSSH functional are almost equivalent with both SVP and TZVP basis sets, whereas the calculated binding energy using BP86 functional is smaller by ∼2.9 kcal mol−1 than the value predicted from B3LYP and TPSSH functional with SVP basis set and is smaller by 1.4–1.8 kcal mol−1 with TZVP basis set. The basis set effect on the Cs+ ion binding energy is negligible as was observed with DCH18C6. The calculated binding energy for Na+ ion with BPC6 is also presented in the same table. There is a strong basis set effect in the binding energy of the Na+ ion as the binding energy predicted using SVP basis set is smaller by 28–29 kcal mol−1 than that of using TZVP basis set for all the DFT functional studied here. The calculated binding energy at BP86 level of theory is smaller by 4.1–4.5 kcal mol−1 compared to the value predicted from B3LYP and TPSSH level of density functional, whereas the BE is smaller by 3.7 kcal mol−1 using TZVP basis set than that of B3LYP and TPSSH functional. It is interesting to note that the BE predicted using SVP basis set for Na+ ion is smaller than that of Cs+ ion with BPC6 for all the DFT functional studied here, whereas with DCH18C6 ligand it was higher for Na+ ion over Cs+ ion. The BE for Na+ with BPC6 using TZVP basis set is higher than Cs+ ion by 21–23 kcal mol−1 indicating the higher selectivity of Na+ ion over Cs+ ion. Thus for BE calculations SVP basis set is not sufficient and may lead to wrong interpretations. So for BE calculations TZVP basis set is required. Further, the BE for Cs+ ion with BPC6 is higher by 2.3–2.8 kcal mol−1 than that of with DCH18C6. It is interesting to note that the BE for Na+ ion with BPC6 is smaller by 4.8–6.6 kcal mol−1 than that of DCH18C6.
Table 5 Calculated values of binding energy of Cs+ and Na+ ion with BPC6 at different DFT functional and basis seta
| System |
BE (kcal mol−1) |
| SVP |
TZVP |
| BP86 |
B3LYP |
TPSSH |
BP86 |
B3LYP |
TPSSH |
| Values in the parentheses are obtained using MP2 level single point energy at TZVP level of theory using optimized geometry at the respective functional and basis set. |
| Cs |
−55.93 (−76.18) |
−58.88 (−75.91) |
−58.80 (−75.69) |
−56.83 (−76.99) |
−58.63 (−76.43) |
−58.27 (−77.14) |
| Na |
−48.99 (−96.34) |
−53.56 (−96.39) |
−53.16 (−96.06) |
−77.98 (−96.21) |
−81.77 (−96.09) |
−81.75 (−96.52) |
Further, the BE of Cs+ and Na+ ions with BPC6 ligand was also calculated at MP2 level of theory using the optimized coordinates originated from various DFT-basis set combinations and the values are presented in the same table. The calculated BE for Cs+ ion at MP2/TZVP level was found to be higher by 16.8–20.2 kcal mol−1 using optimized coordinates from SVP basis set whereas it is higher by 17.8–20.1 kcal mol−1 when optimized coordinates from TZVP basis set are used. The BE, calculated at MP2 level of theory using optimized coordinates from BP86, B3LYP and TPSSH density functional with TZVP basis set are found to be very close to each other. The calculated BE for Na+ ion at MP2/TZVP level was found to be higher by 42.8–47.3 kcal mol−1 using optimized coordinates from SVP basis set whereas it is higher by 14.3–18.2 kcal mol−1 when optimized coordinates from TZVP basis set are used. The gas phase BE for Na+ ion at MP2/TZVP level of theory is always found to be higher than the Cs+ ion by 19.2–19.6 kcal mol−1 for all the DFT functional basis set combinations indicating the higher selectivity for Na+ ion compared to Cs+ ion. This behavior is expected as solvent effect was not considered here which play a profound role in dictating the selectivity. It is interesting to note that the BE at MP2/TZVP level of theory with BPC6 for Cs+ ion is higher by 9.1–9.8 kcal mol−1 than that of with DCH18C6, whereas the BE for Na+ ion is higher by only 0.2–0.6 kcal mol−1. In order to account for the non-covalent interaction in the binding energy, further single point energy calculation was performed using M06 suite of density functionals (metaGGA M06-L, meta hybrid GGA M06 and M06-2X) employing TZ2P basis set as implemented in ADF package (ESI Table S7†). From the above binding energy analysis using different combination of DFT functional and basis sets it is found that the BP86/TZVP level of calculation leads to very close value to that of B3LYP and TPSSH level of calculation. Also it is observed that the BE of Na+ ion is found to more compared to Cs+ ion in the gas phase with either DCH18C6 or BPC6. The reason for this is explained using population analysis, second order interaction energy and topological parameters in subsequent sections.
The selectivity of Cs+ ion over Na+ ion with BPC6 and DCH18C6 was addressed in the free energy section at BP86/TZVP level of theory including both implicit and explicit solvation models.
Population analysis
The higher gas phase binding energy of Na+ ion compared to Cs+ ion with DCH18C6 can be well correlated with the residual charge on metal ion from Mulliken and natural population analysis.93,94 The calculated values of charge are presented in Table 6. The transfer of charge is found to be higher for Na+ compared to Cs+ as evident from the value shown in the table from Mulliken and natural population analysis suggesting the higher binding energy for Na+ ion compared to Cs+ ion in gas phase.
Table 6 Calculated values of charge using Mulliken population and NPA of Cs+ and Na+ ion with DCH18C6 and BPC6 at B3LYP/TZVP level of theory
| System |
Mulliken |
NPA |
| Cs+ |
Na+ |
Cs+ |
Na+ |
| DCH18C6 |
0.78 |
0.57 |
0.94 |
0.89 |
| BPC |
0.80 |
0.60 |
0.91 |
0.88 |
Similarly, the higher gas phase binding energy of Na+ ion compared to Cs+ ion with BPC6 is also well correlated with the transfer of charge on metal ion from Mulliken and natural population analysis.93,94 The calculated values of charge are presented in Table 6. From the table it is seen that the transfer of charge for Na+ ion is higher than Cs+ which in turn leads to the higher binding energy for Na+ ion than that of Cs+ ion in gas phase.
Second order interaction energy
The selectivity of metal ion with various ligands is further investigated using natural bond order (NBO) analysis program NBO 5.0 (ref. 95) as implemented in ADF package.87 We have performed NBO analysis to understand the nature of coordinated interaction between metal ions and the ligands at B3LYP/TZ2P level of theory. In this analysis the values of second order interaction energies E(2)ij are used as measure of the strength of the coordinated interactions. The stability of a metal ion complex is related to the stabilization energy E(2)ij. The larger the stabilization energy higher is the stability which in turn enhances the selectivity of the metal ion by the ligand. The stabilization energy E(2)ij is nothing but the intermolecular delocalization (2e-stabilization) i → j for each donor NBO (i) and acceptor NBO (j) orbital and is expressed as| | |
E(2)ij = qi × F(ij)2/(εi − εj)
| (8) |
where, qi is the donor orbital occupancy, εi and εj are diagonal elements (orbital energies), and F(ij)2 is the off-diagonal NBO Fock matrix element. The stabilization energy is related to the strength of charge transfer interaction between Lewis type NBOs (donor) and non-Lewis NBOs (acceptor). The stronger the donor–acceptor interaction, larger the stabilization energies. The calculated values of E(2)ij is presented in Table 7 (details are presented in ESI†). There are three types of dominating charge transfer interaction from NBO donor to NBO acceptor. First, six lone pair of oxygen atom, LP(O), second, from the bonding orbital of C–H bond, BD (C–H) and third is from the bonding orbital of C–O, BD (C–O). The anti bonding vacant orbital of Cs/Na metal ion is the NBO acceptor, LP*(Cs/Na). The average stabilization energy from the six lone pair of O atoms in case of DCH18C6 is highest with Na ion (3.56 kcal mol−1) and is lowest with Cs ion (0.69 kcal mol−1). The stabilization energy follows the selectivity order in gas phase i.e. Na+ ion which has the highest gas phase binding energy has the highest stabilization energy and Cs+ has the lowest second order stabilization energy.
Table 7 Calculated values of average second order stabilization energies E(2)ij using NBO analysis as implemented in ADF Package at B3LYP/TZ2P level of theory
| System |
Donor NBO |
Acceptor NBO |
E2 (kcal mol−1) |
| DCH18C6–Cs+ |
LP (1) O |
LP (1) Cs63 |
0.69 |
| DCH18C6–Na+ |
LP (1) O |
LP (1) Na27 |
3.56 |
Atom in molecule (AIM) topological parameters
The topology of electron density is used in AIM theory to describe the bond critical point (BCP) in a molecule.96 Two most important topological parameters are electron density (ρ) and the Laplacian of electron density (∇2ρ) which are calculated here using AIM theory as implemented in GUI version of ADF2012 package.87 The strength of a chemical bond is reflected in the electron density at BCP (ρ). The larger the value of ρ, the stronger the corresponding chemical bond. It has been shown that binding energy for several types of bonding interaction are strongly correlated with the ρ. Similarly, the Laplacian at the BCP is the measure of covalent, ionic or covalent interaction. In covalent bonding, ∇2ρ < 0 and in closed-shell bonding, for example ionic, coordination, hydrogen-bonding or van der Walls interactions, ∇2ρ > 0. The ellipticity (ε) of the bond measures the extent to which density is preferentially accumulated in a given plane containing the bond path.
The calculated various topological parameters ρ, ∇2ρ and ellipticity (ε) are tabulated in Table 8 (details are submitted in the ESI, Table S5†). From the table it is seen that in the case of Cs+ and Na+ complex of DCH18C6, the value of ρ is positive and same. Similarly, ∇2ρ was found to be positive indicating the closed shell interaction between donor atoms and metal ions and the value was found to be higher with Na+ ion complex (0.075) compared to Cs+ ion complex (0.044) indicating more ionic character for Na+ ion complex. The value of ellipticity is quite large (0.091 and 0.056) indicating considerable ionic character.
Table 8 Calculated values of average electron density and Laplacian of electron density and ellipsity at B3LYP/TZ2P level of theory using Bader's AIM calculation as implemented in ADF package
| Complex |
BCP |
ρ |
∇2ρ |
ε = (λ1/λ2) − 1 |
| DCH18C6–Cs+ |
Cs–O |
0.0115 |
0.044 |
0.091 |
| DCH18C6–Na+ |
Na–O |
0.0116 |
0.075 |
0.056 |
| BPC6–Cs+ |
Cs–O |
0.0078 |
0.029 |
0.160 |
| BPC6–Na+ |
Na–O |
0.0144 |
0.090 |
0.110 |
In case of Cs+ and Na+ complex of BPC6, the value of ρ is found to be positive but quite high for Na+ ion (0.0144 e au−3) compared to Cs+ ion (0.0078 e au−3). Interesting to note that incase of Cs+–BPC6 complex, there were six BCP whereas only three BCP were observed in Na+–BPC6 complex. This might be the reason for very small increase in interaction energy (<2 kcal mol−1) for Na ion with BPC6 compared to DCH18C6, whereas the increment for Cs+ ion was >12 kcal mol−1. Similarly, ∇2ρ was found to be positive indicating the closed shell interaction between donor atoms and metal ions. Further, the value of ellipticity with BPC6 is found to higher than that of observed with DCH18C6 indicating strong ionic bonding with BPC6 than DCH18C6.
Free energy of extraction
In the gas phase binding energy analysis it has been observed that the Na+ ion selectivity is higher than that of Cs+ ion for both DCH18C6 and BPC6 which is contradictory to the experimentally observed selectivity. This is be due to non consideration of solvent effect in the metal ion hydration energy and metal ion–ligand complexation energy. Here, in next section the solvent effect is considered. The free energy of extraction, ΔGext for the complexation reaction in aqueous and organic bi-phasic system can be modeled either using implicit or explicit solvation of the metal ions considered here.
Implicit solvation model
In implicit solvation model the metal ion is directly immersed in the dielectric continuum of the solvent media. The solvent effect was incorporated using conductor like screening model (COSMO) developed by Klamt et al.88 The complexation reaction using implicit solvation model can be written as| | |
M+(aq) + L(org) → M+L(org)
| (9) |
here, the metal ion, M+ (Cs/Na) is considered to be initially in the aqueous phase and the ligand, L (DCH18C6/BPC6) is considered to be in the organic solvent phase or ILs phase. The free energy of extraction for the above complexation reaction can be written as| |
 | (10) |
where, EM+–L(org), 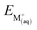 and EL(org) is the energy of the metal ion–ligand complex in organic phase, energy of the metal ion in aqueous phase and energy of the ligand in the organic phase respectively. The dielectric constant of the water and organic solvent (octanol) were taken as 80 and 10.3 respectively. R is universal gas constant and T is the temperature. SM+–L(gas),
and EL(org) is the energy of the metal ion–ligand complex in organic phase, energy of the metal ion in aqueous phase and energy of the ligand in the organic phase respectively. The dielectric constant of the water and organic solvent (octanol) were taken as 80 and 10.3 respectively. R is universal gas constant and T is the temperature. SM+–L(gas),  and SL(gas) is the entropy of the metal ion–ligand complex, metal ion and the ligand in the gas phase respectively. The calculated value for the free energy of extraction for both the Cs+ and Na+ metal ion with DCH18C6 and BPC6 is presented in the Table 9 and Fig. 4 The free energy of extraction, ΔGext can be computed to calculate the ΔΔGext (ΔΔG = ΔGCs+ − ΔGNa+) corresponding to the selectivity of the Cs+ ion over Na+ ion for a particular ligand [separation factor = βCs/Na = ∼exp(−ΔΔGext/RT)]. The value of ΔGext is found to be positive for both the metal ion with DCH18C6 in octanol but is less positive for Na metal ion which contradicts the experimentally observed selectivity (positive value of ΔΔGext, 6.2 kcal mol−1), whereas though the value of ΔGext is positive for both the metal ion with BPC6, it is less positive for Cs metal ion and hence predicts the experimentally observed selectivity as seen from the negative value of ΔΔGext (−3.85 kcal mol−1). The implicit solvation of the metal ion seems to be inadequate to capture the correct experimental selectivity because of its simple bare metal ion hydration mechanism. In real system, the metal ion remains strongly hydrated in the aqueous environment and during complexation it undergoes dehydration leading to release of water molecules which play a decisive role in the selectivity of metal ion. Hence, next the explicit solvation model for the hydration of metal ion is considered.
and SL(gas) is the entropy of the metal ion–ligand complex, metal ion and the ligand in the gas phase respectively. The calculated value for the free energy of extraction for both the Cs+ and Na+ metal ion with DCH18C6 and BPC6 is presented in the Table 9 and Fig. 4 The free energy of extraction, ΔGext can be computed to calculate the ΔΔGext (ΔΔG = ΔGCs+ − ΔGNa+) corresponding to the selectivity of the Cs+ ion over Na+ ion for a particular ligand [separation factor = βCs/Na = ∼exp(−ΔΔGext/RT)]. The value of ΔGext is found to be positive for both the metal ion with DCH18C6 in octanol but is less positive for Na metal ion which contradicts the experimentally observed selectivity (positive value of ΔΔGext, 6.2 kcal mol−1), whereas though the value of ΔGext is positive for both the metal ion with BPC6, it is less positive for Cs metal ion and hence predicts the experimentally observed selectivity as seen from the negative value of ΔΔGext (−3.85 kcal mol−1). The implicit solvation of the metal ion seems to be inadequate to capture the correct experimental selectivity because of its simple bare metal ion hydration mechanism. In real system, the metal ion remains strongly hydrated in the aqueous environment and during complexation it undergoes dehydration leading to release of water molecules which play a decisive role in the selectivity of metal ion. Hence, next the explicit solvation model for the hydration of metal ion is considered.
Table 9 Calculated values of free energy of extraction for Cs+ and Na+ ion using implicit and explicit solvation model in BMIM ionic liquid and octanola
| Diluents |
Ligand |
ΔGext (kcal mol−1) |
ΔΔGext (kcal mol−1) |
ΔΔΔGext (kcal mol−1) |
| Values in the parentheses are calculated using cluster of water molecules. |
| BMIMTF2N |
| |
|
Cs+ |
Na+ |
|
|
| Implicit |
DCH18C6 |
2.56 |
−3.58 |
6.15 |
−10.00 |
| BPC6 |
0.25 |
4.10 |
−3.85 |
|
| Explicit |
DCH18C6 |
−56.04 (−10.33) |
−48.05 (−2.34) |
−7.99 |
−10.00 |
| BPC6 |
−58.35 (−12.64) |
−40.37 (5.33) |
−17.98 |
|
| |
| Octanol |
| Implicit |
DCH18C6 |
8.31 |
2.12 |
6.19 |
−10.03 |
| BPC6 |
5.80 |
9.63 |
−3.83 |
|
| Explicit |
DCH18C6 |
−50.28 (−4.58) |
−42.34 (3.35) |
−7.94 |
−10.03 |
| BPC6 |
−52.80 (−7.10) |
−34.83 (10.87) |
−17.97 |
|
 |
| | Fig. 4 Free energy of extraction, ΔGext of Cs+ and Na+ ions (a) DCH18C6 in IL and octanol (b) BPC6 in IL and octanol. | |
Explicit solvation model
In explicit solvation model, the metal ion with its first solvation shell was considered for the complexation reaction in the aqueous phase. Similarly, metal–ligand complexation reaction can be written using explicit solvation model in two schemes.| | |
M+(H2O)6(aq) + L(org) → M+L(org) + 6H2O(aq)
| (11) |
Scheme 1. The free energy of extraction for the above complexation reaction can be written as:| |
 | (12) |
here, EH2O(aq) is the energy of the single water molecule in the aqueous phase and SH2O(gas) is the entropy of the single water molecule.The calculated value of ΔGext is displayed in Table 9. Now, the value of ΔGext are found to be negative for both Cs+ and Na+ ions with DCH18C6 and is more negative for Cs+ ion (−56.21 kcal mol−1) compared to Na+ ion (−48.22 kcal mol−1) indicating the high selectivity of Cs+ ion over Na+ ion as revealed from the large negative value of ΔΔGext (−7.99 kcal mol−1). The selectivity between two metal ions towards a ligand (here L1, DCH18C6 and L2, BPC6) using the following exchange reaction
| | |
L1Na+(org) + Cs+(aq) → L1Cs+(org) + Na+(aq)
| (13) |
| | |
L2Na+(org) + Cs+(aq) → L2Cs+(org) + Na+(aq)
| (14) |
The value of ΔΔGext is found to be quite high with BPC6 (−17.98 kcal mol−1) compared to DCH18C6 (−7.99 kcal mol−1) which indicates that the selectivity of Cs+ over Na+ ion with BPC6 is very high than that of DCH18C6 as observed in the experiments (see Table 1: SFCs/Na = 4.33 in DCH18C6 and SFCs/Na = 978 in BPC6). The complicated solvation model can be avoided if one considers the selectivity between two metal ions towards different ligands (here DCH18C6 and BPC6) using the following exchange reaction:
| | |
L1Cs+(org) + L2Na+(org) → L1Na+(org) + L2Cs+(org)
| (15) |
The free energy of extraction, ΔGext can be used to calculate the ΔΔΔGext (ΔΔΔGext = ΔΔG[L2] − ΔΔG[L1]) corresponding to the selectivity difference between two ligands (L1, DCH18C6 and L2, BPC6). From the table it is seen that the value of ΔΔΔGext is independent (same value for implicit and explicit solvation model) of the complicated metal ion hydration free energy.
Scheme 2. In the Scheme 1, the free energy was calculated by considering the energy of the monomer water unit. But, the released water molecules may form cluster during complexation reaction of metal ion with the ligand due to strong hydrogen bonding affinity among the water molecules. In view of this event, free energy of extraction, ΔGext was also calculated using the energy of water cluster97 and the calculated values are presented in Table 9.| | |
M+(H2O)6(aq) + L(org) → M+L(org) + (H2O)6(aq)
| (16) |
The free energy of extraction for the above complexation reaction can be written as:
| |
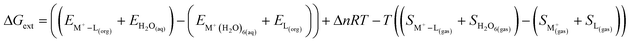 | (17) |
here,
E(H2O)6(aq) is the energy of the water cluster in the aqueous phase and
S(H2O)6(gas) is the entropy of the water cluster.
The value of ΔGext computed from cluster approach was found to be less exothermic compared to the explicit model as the favorable positive entropy becomes less positive due to cluster formation from monomer water unit. The value of ΔGext has become positive for the Na+–ligand complexation reaction. Though the value of ΔGext was changed, the selectivity of Cs+ over Na+ ion for both DCH18C6 and BPC6 in octanol remains unaffected as the value of ΔΔGext and ΔΔΔGext was unchanged. This is due to the absence of water cluster in the calculation of ΔΔGext and ΔΔΔGext (see eqn (13)–(15)).
Free energy of extraction in ILs medium
It has been discussed in the introduction that the ILs show greater extraction efficiency compared to volatile organic solvent of comparable dielectric constant. It has been proposed that the cation of the ILs get transfer to the aqueous phase from the IL phase due to cation exchange between aqueous and IL phase, which is absent in the common organic solvent and in turn, increases the extraction efficiency of the metal ion from aqueous phase to the IL phase. This cation exchange can be modeled using the following proposed reaction:| | |
M+(aq) + IL+(org) → M+(org) + IL+(aq)
| (18) |
here, IL+ is the cation (BMIM) of the ionic liquid. The dielectric constant of the BMIMTF2N is taken as 11.6.100 The exchange free energy, ΔGexc for the above reaction is found to be 4.66 and 7.31 kcal mol−1 for Cs+ and Na+ cation respectively. From the positive value of ΔGexc it seems that the exchange reaction is not feasible using implicit hydration of the metal cation. Next, the explicit solvation of the metal ion is considered using the following reaction:| | |
M+(H2O)6(aq) + IL+(org) → M+(org) + IL+(aq) + 6H2O(aq)
| (19) |
Interesting to note that the value of exchange free energy, ΔGexc becomes negative after inclusion of the first solvation shell. This might be due to the positive entropy contribution from the released single water molecules. The value of ΔGexc for the above reaction is found to be −43.31 and −38.39 kcal mol−1 for Cs+ and Na+ ion respectively. The value is found to be unreasonably high nevertheless it captures the exchange extraction of the metal ion with the cation of the ILs. Next, the complexation reaction along with the ligand in IL is modeled using implicit solvation of the metal ion as per the following reaction:
| | |
M+(aq) + IL+(org) + L(org) → M+L(org) + IL+(aq)
| (20) |
The calculated value of ΔGext is presented in Table 9. The value of ΔGext is found to be positive which stress the inadequacy of the implicit solvation model. But point to be noted that the value of ΔGext is less positive than that of octanol means ILs media has better extraction ability than that of octanol. Next, the explicit solvation of the metal ion is considered using the following reaction:
| | |
M+(H2O)6(aq) + IL+(org) + L(org) → M+L(org) + IL+(aq) + 6H2O(aq)
| (21) |
The calculated value of ΔGext is presented in Table 9. From the table it is seen that the calculated value of ΔGext has now become negative and also higher than that of observed in octanol for the Cs+ and Na+ metal ions. The value of ΔGext is higher for Cs+ than that of Na+ by 7.99 kcal mol−1 with DCH18C6 and by 17.98 kcal mol−1 with BPC6. The same trend was observed in the experiment also as seen from the Fig. 4. The high value of ΔGext (−56.04 in IL and −50.28 kcal mol−1 in octanol with DCH18C6) is due to the approximate explicit monomer water solvation model, which overestimates the entropy contribution as the released water molecules is found to be free during complexation reaction. In real solution system, the water remains to be hydrogen bonded cluster, which in turn reduces the entropy. Hence, the value of ΔGext was found to be small for cluster solvation model (−10.33 kcal mol−1 in IL and −4.58 kcal mol−1 in octanol with DCH18C6). Further, the theoretically calculated free energy of extraction for Cs+ ion in octanol medium using monomer water model (ΔGext = −50.28 kcal mol−1) is found to be comparable to the value obtained in IL medium (ΔGext = −56.04 kcal mol−1), though, the experimental distribution constant for Cs+ ion (DCs = 0.15) in octanol is found to be much smaller than that of in IL medium (DCs = 100). Since, we are interested in the preferential selectivity of Cs+ ion in IL over octanol, we can estimate the free energy difference between IL and octanol using the approximated relation, ΔΔG = –RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[DCs(IL)/DCs(octanol)], leading to a value of −3.85 kcal mol−1, which was found to be in qualitative agreement with the theoretical ΔΔG value of −5.75 kcal mol−1 (ΔΔG = ΔGIL − ΔGoctanol). In case of cluster water model, though the value of ΔG has been reduced considerably compared to monomer model, still the value is quite large [−10.33 and −4.58 kcal mol−1]. But, here also the value of ΔΔG (−5.75 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.85 kcal mol−1. Similarly, for Na+ ion, the estimated value of ΔΔG (−3.65 kcal mol−1) using distribution constant of Na+ ion (DNa = 19.2 in IL and DNa = 0.04 in octanol) was found to be in qualitative agreement with the theoretically predicted ΔΔG value of −5.71 kcal mol−1 (ΔGIL = −48.05 and ΔGoctanol = −42.34 kcal mol−1). In case of cluster water model, not only, the value of ΔG has been reduced considerably compared to monomer model but has become positive [−2.34 and 3.35 kcal mol−1]. But, here also the value of ΔΔG (−5.69 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.65 kcal mol−1. It is really interesting to mention that the value of experimental ΔΔG for Cs+ ion is higher than Na+ ion by 0.2 kcal mol, whereas the theoretically calculated value was shown to be higher by 0.05 kcal mol−1. Keeping in mind the complexity of the metal ion complexation in solvent phase, the predicted theoretical results and trend are found to be modest. The same explanation holds for BPC6 also. Further, the optimized geometries obtained in COSMO solvent phase was used for single point energy calculation at BP86/TZVP level of theory and subsequently thermodynamic parameters were evaluated. The calculated thermodynamic parameters are displayed in Table S11.† The values of thermodynamic parameters obtained using coordinates of optimized geometries in gas phase (see Table 9) are found to be very close to the values of thermodynamic parameters obtained using coordinates of optimized geometries in COSMO solvent phase (Table S11, ESI†).
ln[DCs(IL)/DCs(octanol)], leading to a value of −3.85 kcal mol−1, which was found to be in qualitative agreement with the theoretical ΔΔG value of −5.75 kcal mol−1 (ΔΔG = ΔGIL − ΔGoctanol). In case of cluster water model, though the value of ΔG has been reduced considerably compared to monomer model, still the value is quite large [−10.33 and −4.58 kcal mol−1]. But, here also the value of ΔΔG (−5.75 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.85 kcal mol−1. Similarly, for Na+ ion, the estimated value of ΔΔG (−3.65 kcal mol−1) using distribution constant of Na+ ion (DNa = 19.2 in IL and DNa = 0.04 in octanol) was found to be in qualitative agreement with the theoretically predicted ΔΔG value of −5.71 kcal mol−1 (ΔGIL = −48.05 and ΔGoctanol = −42.34 kcal mol−1). In case of cluster water model, not only, the value of ΔG has been reduced considerably compared to monomer model but has become positive [−2.34 and 3.35 kcal mol−1]. But, here also the value of ΔΔG (−5.69 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.65 kcal mol−1. It is really interesting to mention that the value of experimental ΔΔG for Cs+ ion is higher than Na+ ion by 0.2 kcal mol, whereas the theoretically calculated value was shown to be higher by 0.05 kcal mol−1. Keeping in mind the complexity of the metal ion complexation in solvent phase, the predicted theoretical results and trend are found to be modest. The same explanation holds for BPC6 also. Further, the optimized geometries obtained in COSMO solvent phase was used for single point energy calculation at BP86/TZVP level of theory and subsequently thermodynamic parameters were evaluated. The calculated thermodynamic parameters are displayed in Table S11.† The values of thermodynamic parameters obtained using coordinates of optimized geometries in gas phase (see Table 9) are found to be very close to the values of thermodynamic parameters obtained using coordinates of optimized geometries in COSMO solvent phase (Table S11, ESI†).
From the table it is also seen that the value of ΔΔΔGext is equal in both the octanol and ILs solvent indicating that the selectivity of Cs+ over Na+ cation between DCH18C6 and BPC6 is independent of the aqueous solvent transfer media. The selectivity of Cs+ ion over Na+ ion with BPC6 is increased many folds over DCH18C6 as revealed from the calculated value of ΔΔΔGext (=−10 kcal mol−1). Earlier, a large separation factor (SF) of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 for Cs+ (D = 19.5) over Na+ (D = 2 × 10−3) ion with BPC6 in 1,2 nitrophenyl hexy ether was reported39 which is much higher than that of with DCH18C6 (∼4). The calculated value of ΔΔG is found to be slightly higher with IL compared to octanol as observed in the experiments. Further, the value of ΔΔΔG is also found to be slightly different in IL and octanol as expected in the experiment. Point to be noted, that the value of ΔΔG and ΔΔΔG is found to be very close for both IL and octanol is due to the cancellation of effect of IL cation because of identical exchange and close dielectric constant for both octanol (10.3) and IL (11.6). This limitation can be addressed using MD simulation, where the explicit structure of octanol and IL can be incorporated (detailed exchange reaction is given in the ESI†).
500 for Cs+ (D = 19.5) over Na+ (D = 2 × 10−3) ion with BPC6 in 1,2 nitrophenyl hexy ether was reported39 which is much higher than that of with DCH18C6 (∼4). The calculated value of ΔΔG is found to be slightly higher with IL compared to octanol as observed in the experiments. Further, the value of ΔΔΔG is also found to be slightly different in IL and octanol as expected in the experiment. Point to be noted, that the value of ΔΔG and ΔΔΔG is found to be very close for both IL and octanol is due to the cancellation of effect of IL cation because of identical exchange and close dielectric constant for both octanol (10.3) and IL (11.6). This limitation can be addressed using MD simulation, where the explicit structure of octanol and IL can be incorporated (detailed exchange reaction is given in the ESI†).
It is of importance to study whether the metal ion after reaching to the ILs phase undergoes complexation with the ligand in the organic phase as per the following reaction given below.
| | |
M+(org) + L(org) → M+L(org)
| (22) |
The free energy of the above complexation reaction is found to be positive. Hence, one might conclude that the complexation of the metal ion with the ligand in the ILs phase is improbable. Hence, from the above free energy analysis it is clear that the extraction of metal ion occurs via dual exchange mechanism, one is the direct cation exchange and other is the ligand assisted transfer which resulted in the high extraction efficiency of the cation in the ILs media.
So far, the binding/free energy was calculated by considering the energy of the monomer water unit. But, the released water molecules may form cluster during complexation reaction of metal ion with the ligand due to strong hydrogen bonding affinity among the water molecules. In view of this event, free energy of extraction, ΔGext was also calculated using the energy of water cluster97 (as Scheme 2) and the calculated values are presented in Table 9. The value of ΔGext computed from cluster approach was found to be less exothermic compared to the explicit model as the favorable positive entropy becomes less positive due to cluster formation from monomer water unit. Even, the value of ΔGext has become positive for the Na+–ligand complexation reaction. Though the value of ΔGext was changed, the selectivity of Cs+ over Na+ ion for both DCH18C6 and BPC6 in ionic liquid unaffected as the value of ΔΔGext and ΔΔΔGext was unchanged.
In any solvent extraction experiment, two most important parameters are solubility loss of the ligands in water and partition coefficients of the ligands in water–diluents biphasic system. The ligands having zero solubility in water and high partition coefficient are highly desirable. Hence, the solubility of the ligands in water and partition coefficient in water–organic biphasic system are calculated because screening of the extractant based on the solubility in water and partition coefficients of the extractant in water–diluents bi-phasic system can be judiciously used for the selection of the extractant/diluents systems in the practical solvent extraction application. The solubility and partition coefficients of DCH18C6 and BPC6 are calculated adopting the methodology given elsewhere.68 DCH18C6 has some solubility (4.2 × 10−7 g cm−3) in water whereas it is zero for BPC6 indicating the high hydrophobicity of BPC6. Also, the calculated partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of DCH18C6 (log
P) of DCH18C6 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 2.91) is much lower than that of BPC6 (log
P = 2.91) is much lower than that of BPC6 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 7.98) in BMIMTF2N. The high hydrophobicity and high partition coefficient in ILs media might also be the reason for high distribution constant of the metal ion with BPC6 in ILs media.
P = 7.98) in BMIMTF2N. The high hydrophobicity and high partition coefficient in ILs media might also be the reason for high distribution constant of the metal ion with BPC6 in ILs media.
There is a possibility that DCH18C6 and BPC6 can interact with the cation of IL and play a role in the ion exchange reaction. It would be quite important to investigate the interaction of DCH18C6 and BPC6 with the BMIM cation. In order to test the affinity of DCH18C6 and BPC6 for IL cation, the structures of BMIM–DCH18C6 and BMIM–BPC6 were optimized in the gas phase and the optimized structures are presented in the Fig. 5. The interaction energy between DCH18C6 and BPC6 with BMIM cation was found to be −12.81 and −13.04 kcal mol−1 respectively, which is much lower than the interaction energy of Cs+ and Na+ with DCH18C6 and BPC6 suggesting that ion complex formation with inorganic ion is stronger than the organic BMIM cation.
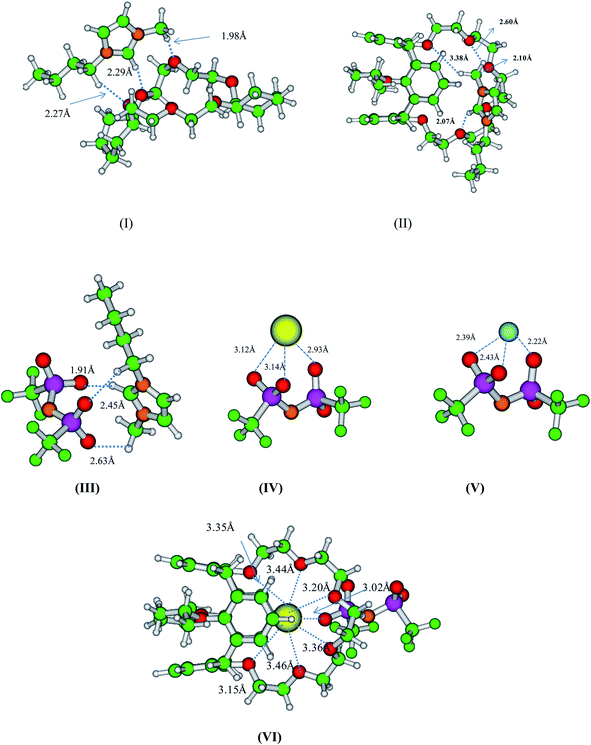 |
| | Fig. 5 Optimized structure of (I) BMIM–DCH18C6, (II) BMIM–BPC6, (III) BMIM–TF2N, (IV) Cs+–TF2N, (V) Na+–TF2N and (VI) BPC6–Cs+–TF2N complexes. | |
Further, the interaction energy between BMIM and TF2N anion (optimized structure is presented in Fig. 5) was computed which was found to be −72.45 kcal mol−1 indicating their preference to remain as an ion pair instead of complexation with DCH18C6. Further, there is a possibility that Cs+ ion and Na+ can interact with the anion of IL and facilitate the ion exchange complexation. Hence, it would be worthwhile to include the interaction of Cs+ ion and Na+ with the TF2N anion. In order to test the affinity of Cs+ ion and Na+ for IL anion, the structures of Cs+–TF2N and Na+–TF2N were optimized in the gas phase and the optimized structures are presented in the Fig. 5. The interaction energy between Cs+ ion and Na+ with TF2N was found to be −86.12 and −111.31 kcal mol−1 respectively, which is higher than the interaction energy of BMIM–TF2N pair. Recently,98 good extraction ability of BPC6 for Cs+ ion has been proven by predicting a complex structure between deficient metal extractant complex of BPC6–Cs+ and anion of the IL, TF2N by X-ray diffraction study. Hence, in order to study the stability of the coordinating complex, the structure of BPC6–Cs+–TF2N was also optimized. The computed structure is presented in Fig. 5. The Cs+ ion was found to coordinate to six O atoms of calix-crown and one O atom of the sulfonyl group of TF2N anion as observed in the X-ray diffraction study. The stability of the coordinating complex was confirmed by calculating the interaction energy which was found to be considerable (−51.32 kcal mol−1).
Conclusion
From solvent experiment data it has been shown that the distribution constant of Cs+ ion is much higher than Na+ ion in IL in presence or absence of ligand and in octanol in the presence of ligand. Further, the distribution constant is found to be almost independent of the nature of the anion. The high distribution constant of Cs+/Na+ ion in ILs solvent may attributed to dual cationic exchange of the BMIM cation of ILs with the aqueous phase metal ions in the presence of DCH18C6 ligand. The dual cationic exchange has also been established from the DFT calculation of free energy of transfer of the metal ion from aqueous phase to the non-aqueous ILs solvent phase. It is also established that the implicit COSMO solvation model is inadequate to capture the experimentally observed metal ion transfer from aqueous phase to the non-aqueous phase whereas explicit solvation model successfully predicts the transfer of the metal ions. The higher extraction of metal ions in IL is successfully modeled by the exchange of the metal ion with the cation of the IL. The remarkably high extraction capacity of BPC6 over DCH18C6 is also demonstrated by free energy difference, ΔΔΔGext between two competing ligands which was shown to be free from the complex metal ion hydration effect. One interesting point to be noted is that though the gas phase binding energy for both Cs+ and Na+ ions is found to be increased with BPC6 compared to DCH18C6, the free energy of extraction, ΔGext which determines the transfer of metal ion from aqueous phase to the solvent phase is increased for Cs+ ion with BPC6 but is decreased for Na+ which in turn enhance the selectivity of Cs+ ion with BPC6. The stability of the complex of crown ligand with inorganic ion was found to be stronger than the organic BMIM cation. The higher gas phase interaction energy of Na+ ion over Cs+ ion was found to be well correlated to the different bonding analysis parameters. The present work will thus help in the elucidation of dual extraction mechanism of cation in ILs medium and hence in the future design of ligand/IL systems for efficient and selective separation of metal ions.
Acknowledgements
Computer Division, BARC is acknowledged for providing the Anupam supercomputing facility.
References
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS PubMed.
- T. Koddermann, C. Wertz, A. Heintz and R. Ludwig, Angew. Chem., Int. Ed., 2006, 45, 3697–3702 CrossRef PubMed.
- M. J. Earle, U. Hakala, C. Hardacre, J. Karkkainen, B. J. McAuley, D. W. Rooney, K. R. Seddon, J. M. Thompson and K. Wahala, Chem. Commun., 2005, 903–905 RSC.
- J. Y. Weng, C. M. Wang, H. R. Li and Y. Wang, Green Chem., 2006, 8, 96–99 RSC.
- H. M. Luo, G. A. Baker, J. S. Lee, R. M. Pagni and S. Dai, J. Phys. Chem. B, 2009, 113, 4181–4183 CrossRef CAS PubMed.
- A. J. Heintz, J. Chem. Thermodyn., 2005, 37, 525–535 CrossRef CAS PubMed.
- J. F. Huang, H. M. Luo, C. D. Liang, I. W. Sun, W. A. Baker and S. Dai, J. Am. Chem. Soc., 2005, 127, 12784–12785 CrossRef CAS PubMed.
- A. Arce, M. J. Earle, H. Rodriguez, K. R. Seddon and A. Soto, Green Chem., 2009, 11, 365–372 RSC.
- L. P. N. Rebelo, J. N. C. Lopes, J. Esperanca, H. J. R. Guedes, J. Lachwa, V. Najdanovic-Visak and J. P. Visak, Acc. Chem. Res., 2007, 40, 1114–1121 CrossRef CAS PubMed.
- C. M. Wang, L. P. Guo, H. R. Li, Y. Wang, J. Y. Weng and L. H. Wu, Green Chem., 2006, 8, 603–607 RSC.
- X. Han and D. W. Armstrong, Acc. Chem. Res., 2007, 40, 1079–1086 CrossRef CAS PubMed.
- A. Arce, M. J. Earle, H. Rodriguez and K. R. Seddon, J. Phys. Chem. B, 2007, 111, 4732–4736 CrossRef CAS PubMed.
- J. L. Anderson, J. Ding, T. Welton and D. W. Armstrong, J. Am. Chem. Soc., 2002, 124, 14247–14254 CrossRef CAS PubMed.
- J. L. Anderson, D. W. Armstrong and G. T. Wei, Anal. Chem., 2006, 78, 2892–2902 CrossRef.
- D. W. Armstrong, L. F. He and Y. S. Liu, Anal. Chem., 1999, 71, 3873–3876 CrossRef CAS.
- J. S. Lee, X. Q. Wang, H. M. Luo, G. A. Baker and S. Dai, J. Am. Chem. Soc., 2009, 131, 4596–4597 CrossRef CAS PubMed.
- J. F. Huang, H. M. Luo, C. D. Liang, D. E. Jiang and S. Dai, Ind. Eng. Chem. Res., 2008, 47, 881–888 CrossRef CAS.
- B. Lee, H. M. Luo, C. Y. Yuan, J. S. Lin and S. Dai, Chem. Commun., 2004, 240–241 RSC.
- P. S. Sharma, T. Payagala, E. Wanigasekara, A. B. Wijeratne, J. M. Huang and D. W. Armstrong, Chem. Mater., 2008, 20, 4182–4184 CrossRef CAS.
- D. W. Armstrong, L. K. Zhang, L. F. He and M. L. Gross, Anal. Chem., 2001, 73, 3679–3686 CrossRef CAS.
- C. Xu, L. Yuan, X. Shen and M. Zhai, Dalton Trans., 2010, 3897–3902 RSC.
- V. A. Cocalia, K. E. Gutowski and R. D. Rogers, Coord. Chem. Rev., 2006, 250, 755–764 CrossRef CAS PubMed.
- M. J. Earle and K.
R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CrossRef CAS.
- M. L. Dietz, Sep. Sci. Technol., 2006, 41, 2047–2063 CrossRef CAS.
- M. P. Jensen, J. Neuefeind, J. V. Beitz, S. Skanthakumar and L. Soderholm, J. Am. Chem. Soc., 2003, 125, 15466–15473 CrossRef CAS PubMed.
- S. I. Nikitenko, C. Cannes, C. Le Naour, P. Moisy and D. Trubert, Inorg. Chem., 2005, 44, 9497–9505 CrossRef CAS PubMed.
- P. Wormald and R. E. Morris, Nature, 2004, 430, 1012–1016 CrossRef PubMed.
- A. E. Visser and R. D. Rogers, J. Solid State Chem., 2003, 171, 109–113 CrossRef CAS.
- K. Nakashima, F. Kubota, T. Maruyama and M. Goto, Anal. Sci., 2003, 19, 1097–1098 CrossRef CAS.
- K. Nakashima, F. Kubota, T. Maruyama and M. Goto, Ind. Eng. Chem. Res., 2005, 44, 4368–4372 CrossRef CAS.
- M. L. Dietz and J. A. Dzielawa, Chem. Commun., 2001, 2124–2125 RSC.
- P. V. Bonnesen, L. H. Delman, B. A. Moyer and G. Lumetta, Solvent Extr. Ion Exch., 2003, 21, 141 CrossRef CAS PubMed.
- R. S. Herbst, J. D. Law and T. A. Todd, Solvent Extr. Ion Exch., 2002, 20, 429 CrossRef CAS PubMed.
- R. Joseph and C. Pulla Rao, Chem. Rev., 2011, 111, 4658 CrossRef CAS PubMed.
- Z. Asfari, C. Bressot, J. Vicens, C. Hlll, J. F. Dozol, H. Rouquette, S. Eymard, V. Lamare and B. Toumois, Anal. Chem., 1995, 67, 3133–3139 CrossRef CAS.
- D. R. Raut, P. K. Mohapatra, S. A. Ansari and V. K. Manchanda, J. Membr. Sci., 2008, 310, 229 CrossRef CAS PubMed.
- D. R. Raut, P. K. Mohapatra, S. A. Ansari and V. K. Manchanda, Sep. Sci. Technol., 2009, 44, 3364 CrossRef.
- T. J. Haverlock, P. V. Bonnesen, R. A. Sachleben and B. A. Moyer, Radiochim. Acta, 1997, 76, 103 CAS.
- J. F. Dozol, N. Simon, V. Lamare, H. Rouquette, S. Eymard, B. Toumois, D. De Marc and R. M. Macias, Sep. Sci. Technol., 1999, 34, 877 CAS.
- C. J. Pederson, J. Am. Chem. Soc., 1967, 89, 7017 CrossRef.
- C. D. Gutsche, B. Dhawan, K. H. No and R. Muthukrishan, J. Am. Chem. Soc., 1981, 103, 3782 CrossRef CAS.
- V. V. Yakshin, O. M. Vilkova, N. A. Tsarenko, A. Y. Tsivadze, S. V. Demin and V. I. Zhilov, Radiochemistry, 2006, 48, 170 CrossRef CAS.
- Y. Takeda, A. Kawarabayashi, K. Endo, T. Yahata, Y. Kudo and S. Katsuta, Anal. Sci., 1998, 14, 215 CrossRef CAS.
- A. F. Danil de Namor, R. M. Cleverly and M. L. Zapata-Ormachea, Chem. Rev., 1998, 98, 2495 CrossRef PubMed.
- J. Dybal, E. Makrlík, P. Vaňura and J. Budka, Monatsh. Chem., 2008, 139, 1175–1178 CrossRef CAS.
- E. Makrlík, J. Dybal and P. Vaňura, J. Radioanal. Nucl. Chem., 2013, 295, 1299–1303 CrossRef PubMed.
- E. Makrlík, J. Dybal and P. Vaňura, J. Mol. Struct., 2013, 1042, 73–77 CrossRef PubMed.
- E. Makrlík, P. Selucký and P. Vaňura, J. Inclusion Phenom. Macrocyclic Chem., 2013, 76, 13–17 CrossRef.
- E. Makrlík, P. Toman, P. Vaňura and B. A. Moyer, J. Mol. Struct., 2013, 1033, 14–18 CrossRef PubMed.
- E. Makrlík, P. Toman and P. Vaňura, J. Radioanal. Nucl. Chem., 2013, 298, 429–434 CrossRef.
- E. Makrlík, P. Selucký, P. Vaňura and B. A. Moyer, J. Radioanal. Nucl. Chem., 2013, 295, 1015–1018 CrossRef.
- E. Makrlík, P. Selucký, P. Vaňura and B. A. Moyer, J. Radioanal. Nucl. Chem., 2013, 295, 2171–2174 CrossRef PubMed.
- R. A. Sachleben, P. V. Bonnesen, T. Descazeaud, T. J. Haverlock, A. Urvos and B. A. Moyer, Solvent Extr. Ion Exch., 1999, 17, 1445 CrossRef CAS.
- A. V. Mudring and S. Tang, Eur. J. Inorg. Chem., 2010, 2569–2581 CrossRef CAS.
- M. L. Dietz, S. Jakab, K. Yamato and R. A. Bartsch, Green Chem., 2008, 10, 174–176 RSC.
- Z. Kolarik, Solvent Extr. Ion Exch., 2013, 31, 24–60 CrossRef CAS.
- H. Luo, J. F. Huangb and S. Dai, Sep. Sci. Technol., 2010, 45, 1679–1688 CrossRef CAS.
- H. Luo, S. Dai, P. V. Bonnesen, A. C. Buchanan, J. D. Holbrey, N. J. Bridges and R. D. Rogers, Anal. Chem., 2004, 76, 3078 CrossRef CAS PubMed.
- H. Luo, S. Dai and P. V. Bonnesen, Anal. Chem., 2004, 76, 2773 CrossRef CAS PubMed.
- T. G. Levitskaia, D. M. Macdonald, J. D. Lamb and B. A. Moyer, Phys. Chem. Chem. Phys., 2000, 2, 1481–1491 RSC.
- J. Kriz, J. Dybal, E. Makrlik, P. Vanura and B. A. Moyer, J. Phys. Chem. B, 2011, 115, 7578–7586 CrossRef CAS PubMed.
- H. Li, M. Ibrahim, I. Agberemi and M. N. Kobrak, J. Chem. Phys., 2008, 129, 124507–124512 CrossRef PubMed.
- S. A. Katsyuba, E. E. Zvereva, A. Vidis and P. J. Dyson, J. Phys. Chem. A, 2007, 111, 352–370 CrossRef CAS PubMed.
- Z. Meng, A. Dolle and W. R. Carper, J. Mol. Struct.: THEOCHEM, 2002, 585, 119–128 CrossRef CAS.
- E. A. Turner, C. C. Pye and R. D. Singer, J. Phys. Chem. A, 2003, 107, 2277–2288 CrossRef CAS.
- K. Dong, S. Zhang, D. Wang and X. Yao, J. Phys. Chem. A, 2006, 110, 9775–9782 CrossRef CAS PubMed.
- H. Markusson, J. P. Belieres and P. Johansson, J. Phys. Chem. A, 2007, 111, 8717–8723 CrossRef CAS PubMed.
- A. Boda, S. K. M. Ali, M. R. K. Shenoi and S. K. Ghosh, Desalin. Water Treat., 2012, 38, 245–253 Search PubMed.
- B. P. Hay, J. B. Nicholas and D. Feller, J. Am. Chem. Soc., 2000, 122, 10083–10089 CrossRef CAS.
- R. A. Sachleben, J. C. Bryan, N. L. Engle, T. J. Haverlock, B. P. Hay, A. Urvos and B. A. Moyer, Eur. J. Org. Chem., 2003, 4862–4869 CrossRef CAS.
- L. I. Shamova, G.
A. Shamov, I. S. Antipin and A. I. Konovalov, J. Phys. Chem. A, 2009, 113, 5691–5699 CrossRef CAS PubMed.
- B. Boulet, L. Joubert, G. Cote, C. Bouvier-Capely, C. Cossonnet and C. Adamo, J. Phys. Chem. A, 2006, 110, 5782–5791 CrossRef CAS PubMed.
- K. Yang, K. D. Kang, Y. H. Park, I. S. Koo and I. Lee, Chem. Phys. Lett., 2003, 381, 239–243 CrossRef CAS PubMed.
- A. B. Rozhenko, W. W. Schoeller, W. C. Letzel, B. Decker, C. Agena and J. Mattay, J. Mol. Struct.: THEOCHEM, 2005, 732, 7–20 CrossRef CAS PubMed.
- A. Boda and S. K. M. Ali, J. Phys. Chem. A, 2012, 116, 8615–8623 CrossRef CAS PubMed.
- N. Sieffert and G. Wipff, J. Phys. Chem., 2006, 110, 19497–19506 CrossRef CAS PubMed.
- F. Weigend, M. Haser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- TURBOMOLE V6.0, 2009, A development of University of Karlsruhe and Forschungszentrum Karlsruhe, GmbH, 1989–2007, TURBOMOLE GmbH.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129 CrossRef CAS PubMed.
- C. Moller and M. S. Plesset, Phys. Rev. Lett., 1934, 46, 618 CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- ADF2012.01, SCM; Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2012, http://www.scm.com Search PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134 CrossRef CAS.
- F. Eckert and A. Klamt, COSMOtherm, version C2.1, Release01.08; COSMOlogic, GmbH & Co, KG, Leverkusen, Germany, 2008 Search PubMed.
- A. Casnati, A. Pochini, R. Ungaro, J. F. Ugozzoli, F. Arnaud, S. Fanni, M. Schwing, R. J. M. Egberink, F. Jong and D. N. Reinhoudt, J. Am. Chem. Soc., 1995, 117, 2767–2777 CrossRef CAS.
- M. R. Antonio, M. L. Dietz, M. P. Jensen, L. Soderholm and E. P. Horwitz, Inorg. Chim. Acta., 1997, 255, 13–20 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS PubMed , 1841–1846, 2338–2342, 2343–2346.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS PubMed.
- E. D. Glendening, O. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, TCI, University of Wisconsin, Madison, WI, 2001 Search PubMed.
- C. F. Matta and R. J. Boyd, An introduction to the Quantum Theory of Atoms in Molecules, ed. C. F. Matta and R. J. Boyd, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007, pp. 1–34 Search PubMed.
- J. Ciupka, X. Cao-Dolg, J. Wiebke and M. Dolg, Phys. Chem. Chem. Phys., 2010, 12, 13215–13233 RSC.
- T. T. Sun, Z. Wang and X. Shen, Inorg. Chim. Acta, 2012, 390, 8–11 CrossRef CAS PubMed.
- W. Jianchen, Z. Xiaowen and S. Chongli, Sep. Sci. Technol., 2005, 40, 3381–3392 CrossRef.
- T. Singh and A. Kumar, J. Phys. Chem. B, 2008, 112, 12968–12972 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra02246g |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) when a hybrid calix-crown compound was used by functionalizing the calix[4]arene in the 1, 3 alternate conformation resulting to the formation of 18C6 like cavity.53
000) when a hybrid calix-crown compound was used by functionalizing the calix[4]arene in the 1, 3 alternate conformation resulting to the formation of 18C6 like cavity.53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (M
1 (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) stoichiometry for both Cs+ and Na+ ion) is computed using the following basic complexation reaction:
L) stoichiometry for both Cs+ and Na+ ion) is computed using the following basic complexation reaction:

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) complex is required. But, there is lack of data on stoichiometry of M
L) complex is required. But, there is lack of data on stoichiometry of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L complexes for both Cs and Na ions with DCH18C6 in ILs. In order to find out the stoichiometry of the complexes, the distribution constant of the Cs and Na metal ions were estimated using different concentration of ligand and the distribution constants were plotted against the concentration of the ligand which is displayed in Fig. 1. From the plot the slope are found to be ∼1 for both Cs and Na ions which indicates 1
L complexes for both Cs and Na ions with DCH18C6 in ILs. In order to find out the stoichiometry of the complexes, the distribution constant of the Cs and Na metal ions were estimated using different concentration of ligand and the distribution constants were plotted against the concentration of the ligand which is displayed in Fig. 1. From the plot the slope are found to be ∼1 for both Cs and Na ions which indicates 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 M
1 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L complexes for both the metal ions.
L complexes for both the metal ions.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric reaction. The BE (ΔE) of the Cs+/Na+ ions for the following 1
1 stoichiometric reaction. The BE (ΔE) of the Cs+/Na+ ions for the following 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation reaction
1 complexation reaction
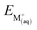 and EL(org) is the energy of the metal ion–ligand complex in organic phase, energy of the metal ion in aqueous phase and energy of the ligand in the organic phase respectively. The dielectric constant of the water and organic solvent (octanol) were taken as 80 and 10.3 respectively. R is universal gas constant and T is the temperature. SM+–L(gas),
and EL(org) is the energy of the metal ion–ligand complex in organic phase, energy of the metal ion in aqueous phase and energy of the ligand in the organic phase respectively. The dielectric constant of the water and organic solvent (octanol) were taken as 80 and 10.3 respectively. R is universal gas constant and T is the temperature. SM+–L(gas),  and SL(gas) is the entropy of the metal ion–ligand complex, metal ion and the ligand in the gas phase respectively. The calculated value for the free energy of extraction for both the Cs+ and Na+ metal ion with DCH18C6 and BPC6 is presented in the Table 9 and Fig. 4 The free energy of extraction, ΔGext can be computed to calculate the ΔΔGext (ΔΔG = ΔGCs+ − ΔGNa+) corresponding to the selectivity of the Cs+ ion over Na+ ion for a particular ligand [separation factor = βCs/Na = ∼exp(−ΔΔGext/RT)]. The value of ΔGext is found to be positive for both the metal ion with DCH18C6 in octanol but is less positive for Na metal ion which contradicts the experimentally observed selectivity (positive value of ΔΔGext, 6.2 kcal mol−1), whereas though the value of ΔGext is positive for both the metal ion with BPC6, it is less positive for Cs metal ion and hence predicts the experimentally observed selectivity as seen from the negative value of ΔΔGext (−3.85 kcal mol−1). The implicit solvation of the metal ion seems to be inadequate to capture the correct experimental selectivity because of its simple bare metal ion hydration mechanism. In real system, the metal ion remains strongly hydrated in the aqueous environment and during complexation it undergoes dehydration leading to release of water molecules which play a decisive role in the selectivity of metal ion. Hence, next the explicit solvation model for the hydration of metal ion is considered.
and SL(gas) is the entropy of the metal ion–ligand complex, metal ion and the ligand in the gas phase respectively. The calculated value for the free energy of extraction for both the Cs+ and Na+ metal ion with DCH18C6 and BPC6 is presented in the Table 9 and Fig. 4 The free energy of extraction, ΔGext can be computed to calculate the ΔΔGext (ΔΔG = ΔGCs+ − ΔGNa+) corresponding to the selectivity of the Cs+ ion over Na+ ion for a particular ligand [separation factor = βCs/Na = ∼exp(−ΔΔGext/RT)]. The value of ΔGext is found to be positive for both the metal ion with DCH18C6 in octanol but is less positive for Na metal ion which contradicts the experimentally observed selectivity (positive value of ΔΔGext, 6.2 kcal mol−1), whereas though the value of ΔGext is positive for both the metal ion with BPC6, it is less positive for Cs metal ion and hence predicts the experimentally observed selectivity as seen from the negative value of ΔΔGext (−3.85 kcal mol−1). The implicit solvation of the metal ion seems to be inadequate to capture the correct experimental selectivity because of its simple bare metal ion hydration mechanism. In real system, the metal ion remains strongly hydrated in the aqueous environment and during complexation it undergoes dehydration leading to release of water molecules which play a decisive role in the selectivity of metal ion. Hence, next the explicit solvation model for the hydration of metal ion is considered.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[DCs(IL)/DCs(octanol)], leading to a value of −3.85 kcal mol−1, which was found to be in qualitative agreement with the theoretical ΔΔG value of −5.75 kcal mol−1 (ΔΔG = ΔGIL − ΔGoctanol). In case of cluster water model, though the value of ΔG has been reduced considerably compared to monomer model, still the value is quite large [−10.33 and −4.58 kcal mol−1]. But, here also the value of ΔΔG (−5.75 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.85 kcal mol−1. Similarly, for Na+ ion, the estimated value of ΔΔG (−3.65 kcal mol−1) using distribution constant of Na+ ion (DNa = 19.2 in IL and DNa = 0.04 in octanol) was found to be in qualitative agreement with the theoretically predicted ΔΔG value of −5.71 kcal mol−1 (ΔGIL = −48.05 and ΔGoctanol = −42.34 kcal mol−1). In case of cluster water model, not only, the value of ΔG has been reduced considerably compared to monomer model but has become positive [−2.34 and 3.35 kcal mol−1]. But, here also the value of ΔΔG (−5.69 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.65 kcal mol−1. It is really interesting to mention that the value of experimental ΔΔG for Cs+ ion is higher than Na+ ion by 0.2 kcal mol, whereas the theoretically calculated value was shown to be higher by 0.05 kcal mol−1. Keeping in mind the complexity of the metal ion complexation in solvent phase, the predicted theoretical results and trend are found to be modest. The same explanation holds for BPC6 also. Further, the optimized geometries obtained in COSMO solvent phase was used for single point energy calculation at BP86/TZVP level of theory and subsequently thermodynamic parameters were evaluated. The calculated thermodynamic parameters are displayed in Table S11.† The values of thermodynamic parameters obtained using coordinates of optimized geometries in gas phase (see Table 9) are found to be very close to the values of thermodynamic parameters obtained using coordinates of optimized geometries in COSMO solvent phase (Table S11, ESI†).
ln[DCs(IL)/DCs(octanol)], leading to a value of −3.85 kcal mol−1, which was found to be in qualitative agreement with the theoretical ΔΔG value of −5.75 kcal mol−1 (ΔΔG = ΔGIL − ΔGoctanol). In case of cluster water model, though the value of ΔG has been reduced considerably compared to monomer model, still the value is quite large [−10.33 and −4.58 kcal mol−1]. But, here also the value of ΔΔG (−5.75 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.85 kcal mol−1. Similarly, for Na+ ion, the estimated value of ΔΔG (−3.65 kcal mol−1) using distribution constant of Na+ ion (DNa = 19.2 in IL and DNa = 0.04 in octanol) was found to be in qualitative agreement with the theoretically predicted ΔΔG value of −5.71 kcal mol−1 (ΔGIL = −48.05 and ΔGoctanol = −42.34 kcal mol−1). In case of cluster water model, not only, the value of ΔG has been reduced considerably compared to monomer model but has become positive [−2.34 and 3.35 kcal mol−1]. But, here also the value of ΔΔG (−5.69 kcal mol−1) was found to be very close to the experimentally obtained ΔΔG value of −3.65 kcal mol−1. It is really interesting to mention that the value of experimental ΔΔG for Cs+ ion is higher than Na+ ion by 0.2 kcal mol, whereas the theoretically calculated value was shown to be higher by 0.05 kcal mol−1. Keeping in mind the complexity of the metal ion complexation in solvent phase, the predicted theoretical results and trend are found to be modest. The same explanation holds for BPC6 also. Further, the optimized geometries obtained in COSMO solvent phase was used for single point energy calculation at BP86/TZVP level of theory and subsequently thermodynamic parameters were evaluated. The calculated thermodynamic parameters are displayed in Table S11.† The values of thermodynamic parameters obtained using coordinates of optimized geometries in gas phase (see Table 9) are found to be very close to the values of thermodynamic parameters obtained using coordinates of optimized geometries in COSMO solvent phase (Table S11, ESI†).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 for Cs+ (D = 19.5) over Na+ (D = 2 × 10−3) ion with BPC6 in 1,2 nitrophenyl hexy ether was reported39 which is much higher than that of with DCH18C6 (∼4). The calculated value of ΔΔG is found to be slightly higher with IL compared to octanol as observed in the experiments. Further, the value of ΔΔΔG is also found to be slightly different in IL and octanol as expected in the experiment. Point to be noted, that the value of ΔΔG and ΔΔΔG is found to be very close for both IL and octanol is due to the cancellation of effect of IL cation because of identical exchange and close dielectric constant for both octanol (10.3) and IL (11.6). This limitation can be addressed using MD simulation, where the explicit structure of octanol and IL can be incorporated (detailed exchange reaction is given in the ESI†).
500 for Cs+ (D = 19.5) over Na+ (D = 2 × 10−3) ion with BPC6 in 1,2 nitrophenyl hexy ether was reported39 which is much higher than that of with DCH18C6 (∼4). The calculated value of ΔΔG is found to be slightly higher with IL compared to octanol as observed in the experiments. Further, the value of ΔΔΔG is also found to be slightly different in IL and octanol as expected in the experiment. Point to be noted, that the value of ΔΔG and ΔΔΔG is found to be very close for both IL and octanol is due to the cancellation of effect of IL cation because of identical exchange and close dielectric constant for both octanol (10.3) and IL (11.6). This limitation can be addressed using MD simulation, where the explicit structure of octanol and IL can be incorporated (detailed exchange reaction is given in the ESI†).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of DCH18C6 (log
P) of DCH18C6 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 2.91) is much lower than that of BPC6 (log
P = 2.91) is much lower than that of BPC6 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 7.98) in BMIMTF2N. The high hydrophobicity and high partition coefficient in ILs media might also be the reason for high distribution constant of the metal ion with BPC6 in ILs media.
P = 7.98) in BMIMTF2N. The high hydrophobicity and high partition coefficient in ILs media might also be the reason for high distribution constant of the metal ion with BPC6 in ILs media.


