Nucleating effect of multi-walled carbon nanotubes and graphene on the crystallization kinetics and melting behavior of olefin block copolymers
Abstract
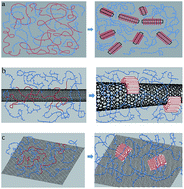
Crystallization is of primary importance to the properties of olefin block copolymers (OBCs). In the present work, multi-walled carbon nanotubes (MWCNTs) and graphene are used as nucleating agents for the crystallization of OBC. Thus nanocomposites of OBC filled with MWCNTs and graphene were prepared by solution blending. Differential scanning calorimetry (DSC) tests were carried out to study the effect of CNTs and graphene on isothermal crystallization of OBC; polarizing optical microscopy (POM), and wide-angle X-ray diffraction (WAXD) were used to study the morphology and crystal structure of OBC and its nanocomposites. It is found that both MWCNTs and graphene act as effective nucleating agents that significantly shorten the induction period of crystallization and increase the crystallization rate of OBC, exhibiting a remarkable decrease in the Avrami exponent n, surface folding energy σe and crystallization activation energy ΔE. These two carbon-based fillers both act as templates for hard block chains of OBC to form an ordered structure on the surface of nanoparticles during the induction period, bringing about some increase in equilibrium temperature. With the decrease in n, σe and ΔE not as remarkable as those of MWCNTs, graphene exhibited weaker nucleating ability than MWCNTs which might be due to strict lattice matching. The melting process of OBC and its nanocomposites are also studied; the nanocomposites exhibit two melting peaks at higher crystallization temperature which mainly refer to the melting of the crystals with different crystal sizes and perfection during heating, which is not observed for neat OBC.

 Please wait while we load your content...
Please wait while we load your content...