Molecular characterization of l-phenylalanine terminated poly(l-lactide) conjugates†
Abstract
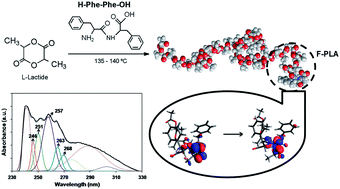
Peptide–polymer conjugates made of poly(L-lactide) and L-phenylalanine or L,L-diphenylalanine (F–PLA and FF–PLA, respectively) have been synthesized by the ring-opening polymerization of L-lactide using the peptide fragment as an initiator. The structure of the conjugates was confirmed by 1H NMR, FT-IR, GPC, UV-Vis and CD. Molecular dynamics simulations have been used to identify both the conformational preferences of the FF–PLA conjugate in solution and the potential intramolecular interactions between the peptide and polymer blocks, while TD-DFT calculations have been applied to model the electronic transitions observed by the UV-Vis absorption spectroscopy. Results show that the polymer fragment prefers a random coil or a mix of helix/strand while the peptide fragment tends to have folded and helical conformations. Although the degree of interaction between the two fragments is slightly higher than that reported for other peptide–polymer conjugates, it is small enough to suggest that FF–PLA is a potential candidate to aggregate forming peptide-guided organizations via self-assembly. On the other hand, quantum mechanical calculations have allowed us to identify the π → π* transition, which is typically observed in helical peptides and proteins, as well as the n → π* transition along the N–C–O backbone.

 Please wait while we load your content...
Please wait while we load your content...