DOI:
10.1039/C4RA01421A
(Paper)
RSC Adv., 2014,
4, 19746-19755
Polymer chain length, phosphoric acid doping and temperature dependence on structure and dynamics of an ABPBI [poly(2,5-benzimidazole)] polymer electrolyte membrane†
Received
12th March 2014
, Accepted 14th April 2014
First published on 15th April 2014
Abstract
An ABPBI [poly(2,5-benzimidazole)] membrane doped with phosphoric acid (PA) are promising electrolytes in high temperature fuel cells. In the present work, we employ Molecular Dynamics (MD) simulations to characterize the effect of polymer chain length using a dimer to hectamer. Results from our MD simulations (dimer to decamer) show the following trends: the inter-chain and intra-chain interactions in membrane are unaffected with polymer chain length and temperature, though a significant increase with PA doping is observed. The radius of gyration linearly increases with polymer chain length and remains unchanged with PA doping and temperature. However, the end-to-end distance deviates from linearity with polymer chain length which suggests increasing coiling of the membrane. The diffusion coefficient of PA increases with PA doping and temperature, but remains constant with polymer chain length. The activation energy of diffusion of PA decreases significantly with an increase in polymer chain length at low PA doping, but remains unaffected at higher PA doping. A comparison of the structural and dynamical properties of a decamer and a hectamer shows that the decamer represents the optimum polymer chain length beyond which no significant change in properties is observed.
1. Introduction
Polymer Electrolyte Membrane (PEM) fuel cells have attracted interest due to their ability to provide clean energy and high power density for a variety of stationary and mobile applications.1,2 The key requirements of a polymer membrane to serve as an electrolyte are: thermal and mechanical stability, chemical resistivity, inhibiting fuel cross-over across electrodes, reduction of CO poisoning of the catalyst, and high proton conduction under prolonged fuel cell operation.3–5 Several classes of polymer membranes like the perfluorosulfonic acid (PFSA) membranes,3–7 cross-linked sulfonated poly(1,3-cyclohexadiene)8,9 have been investigated as electrolytes. Among them, PFSA membranes like Dow, Aciplex and Nafion have been extensively investigated by experiments and theoretical methods.10–21 While, PFSA membranes offer high conductivity, their efficiency depend on the amount of humidification and fuel cell operating temperature. Hence, the use of PFSA membranes remains limited to 100 °C, due to their dependence on water for proton transport. Further, operation of fuel cells using the membranes as electrolytes at T > 100 °C leads to decrease in CO poisoning of the catalyst layer.
As an alternative to PFSA membranes, cost effective membranes such as poly(2,5-benzimidazole) (ABPBI) and poly[2,2-(m-phenylene)-5,5-bibenzimidazole] (PBI) membranes have been developed and tested up to 200 °C.22–27 These membranes can be doped with phosphoric acid (PA) which serve as replacement of water for transport of protons. ABPBI membrane have received recent attention due to equivalent or better electrochemical properties compared to PBI.28–38 Kim et al.28 showed that the ABPBI membrane can be easily synthesized from 3,4-diaminobenzoic acid (DABA). Asensio et al.29 employed Fourier transform infrared spectroscopy on PA doped ABPBI membranes and reported a maximum conductivity of 6.2 × 10−2 S cm−1 at 150 °C and 30% relative humidity. Diaz et al.39 investigated the role of temperature on PA uptake by the ABPBI membrane and found that low temperature casting results in higher uptake of PA due to less compact supra-molecular packing and large number of accessibility of sorption sites. Linares et al.40 characterized physico-chemical properties of ABPBI membranes at varying amount of PA doping. The authors observed suitable mechanical strength, low acid leaching rate, good electrochemical stability and excellent thermal stability even beyond 500 °C.
Li et al.41 characterized hydrogen bonding interactions using Molecular Dynamics (MD) simulations study on neat, hydrated and PA doped ABPBI and PBI membranes at 298 K. The authors concluded that compared to PBI, hydrogen bonding interactions are stronger between ABPBI and PA and also suggested that the structure of polymer membrane play a significant role in proton transport. Recently, Sunda et al.42 employed MD simulations and observed that the degree of hydration show a significant influence on structure and dynamics in various hydrated environments of PA doped ABPBI membrane. The authors observed that the number of PA molecules around the ABPBI polymer chain decrease significantly with hydration, and an inclusion of trifluoromethanesulfonic acid results in a decrease in water mobility. However, the effect of PA doping and temperature were not examined in non-humidified PA doped ABPBI membrane. Further, the hetero-aromatic nature of the polymer membrane which increases with polymer chain length can influence the structural properties of the polymer membrane. The objective of this work is to characterize the effect of polymer chain length, PA doping and temperature on various structural and dynamical properties of PA doped ABPBI membrane using MD simulations. In order to demonstrate the effect of polymer chain length for various PA doping and temperatures, we have chosen a dimer, trimer, tetramer, pentamer and decamer units of the ABPBI membrane. Sunda et al.42 demonstrated that increasing polymer chain length from decamer to icosamer results in negligible effect on structure and dynamics of hydrated PA doped ABPBI membrane. Based on their observations and to simulate a large polymeric system, we also perform simulations on a hectamer and compare the structural and dynamical properties obtained from a decamer. The input preparation of polymers of varying chain lengths with various PA doping, force-field parameters and details of MD simulations are described in computational details section. The structure and dynamical properties calculated from MD simulations are presented in the Results and discussion section. A summary of important results concludes the paper.
2. Computational details
The chemical structure of ABPBI membrane [“n” is a repeat unit of the membrane used for generation of polymers of varying chain length or molecular weight (MW)] and PA, with atom types (used for description of structural properties) is shown in Fig. 1. MD simulations were performed using the GROMACS43 4.5.4 program. The force-field parameters of the ABPBI membrane were taken from the OPLS-AA force-field database.44 Force-field parameters of PA were extracted from the work of Spieser et al.45 The input configurations of a dimer (n = 2, MW = 234), trimer (n = 3, MW = 350), tetramer (n = 4, MW = 466), pentamer (n = 5, MW = 582), decamer (n = 10, MW = 1162) and hectamer (n = 100, MW = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602) was generated using a molecular builder program.
602) was generated using a molecular builder program.
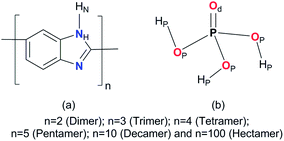 |
| | Fig. 1 Chemical structure with atom types of (a) ABPBI polymer membrane and (b) phosphoric acid (PA). | |
Each configuration (dimer, trimer, tetramer, pentamer and decamer) was energy-minimized using the steepest descent algorithm.46 The energy minimized configuration was replicated in three directions of a cubic box to create a large system containing N = 128 polymer replicas. In order to obtain a density close to an experimental density, a simulated annealing was performed on the replicated systems in the following manner: each system was heated from 300 K to 1000 K and cooled back to 300 K with an annealing time of 1.35 ns. The annealing procedure was repeated five times for a total annealing time of 6.75 ns and the final configuration used as an input for a 10 ns equilibration (isobaric–isothermal: NPT) at T = 300 K, 350 K, 400 K and 450 K. The calculated density (from the last 5 ns equilibration) of a decamer is (1.35 g cm−3, T = 300 K) is in good agreement with the experimental47 density (1.4 g cm−3, T = 298 K). The final configuration obtained from this equilibration was chosen as a template to create configurations which vary only in amount of PA doping. The amount of PA doping chosen in our present study is γ = 1.6, 3.0 and 3.7, where, γ denotes the number of PA molecules per monomer unit of ABPBI membrane. The choice of γ was based on the experimental work of Kim et al.28 and Asensio et al.29,30,32 on PA doped ABPBI membrane. Further, we have included only the neutral form of PA in this study due to the following reasons: (a) the Infrared spectroscopy measurements of Glipa et al.48 on PA doped PBI membranes show that the neutral form of PA is in equilibrium with its corresponding ionic species,49 and (b) the limitations of the classical force-field used in this study do not permit the dissociation of PA into phosphate ions. Nevertheless, the inclusion of neutral PA can offer a molecular level understanding of the interactions in neutral PA and with the polymer membrane.
For configuration (dimer, trimer, tetramer, pentamer and decamer) which contains 128 polymer replicas and various PA doping (γ = 1.6, 3.0 and 3.7), MD simulations were performed at T = 300, 350, 400 and 450 K. The cut-off for calculation of van der Waals and electrostatic interactions was chosen as 12 Å. The particle-mesh Ewald50,51 method was used for calculation of long-range electrostatic interactions. The leapfrog algorithm46 was used to integrate the equations of motion with a time-step of 1 fs. Each system was equilibrated for 10 ns using the NPT ensemble at a constant 1 bar isotropic pressure maintained by a Berendsen barostat.52 The velocity-rescale thermostat53 was chosen to keep the systems set at the target temperature. The number of PA molecules (calculated based on each polymer chain and γ), total number of atoms in the system and cubic box length are shown in Table 1. The instantaneous densities are shown in Fig. S1 (ESI†). The calculated densities from the last 5 ns of the equilibration run are shown in Table 2. As seen, density increases with polymer chain length. At 300 K and γ = 1.6, the density calculated for a dimer is 1.56 g cm−3, tetramer is 1.60 g cm−3 and pentamer is 1.61 g cm−3. Similar trends in density are also seen at γ = 3.0 and γ = 3.7, and T = 350 K, 400 K and 450 K. The final configuration from the equilibration run was chosen as an input for a 10 ns production run using the isochoric–isothermal (NVT) ensemble. A final snapshot from the production run in PA doped ABPBI membrane is shown in Fig. S2 (ESI†). Trajectories from the production run were recorded every 5 ps for calculation of various structural and dynamical properties. The results presented in Sections 3.1–3.6 are from ABPBI polymer membrane constructed from dimer to decamer in a single chain.
Table 1 The number of PA molecules, total number of atoms and cubic box length (after equilibration)
| Polymer chain length |
PA doping (γ) |
Number of PA molecules |
Total number of atoms |
Box length (Å) |
| 300 K |
450 K |
| Dimer (n = 2) |
1.6 |
410 |
6864 |
42.040 |
42.606 |
| 3.0 |
768 |
9728 |
47.153 |
47.974 |
| 3.7 |
947 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
49.432 |
50.162 |
| Trimer (n = 3) |
1.6 |
614 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
47.797 |
48.429 |
| 3.0 |
1152 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 464 |
53.742 |
54.540 |
| 3.7 |
1421 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 616 |
56.363 |
57.157 |
| Tetramer (n = 4) |
1.6 |
819 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 464 |
52.534 |
53.200 |
| 3.0 |
1536 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
59.106 |
59.895 |
| 3.7 |
1894 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 064 |
61.905 |
62.839 |
| Pentamer (n = 5) |
1.6 |
1024 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 768 |
56.415 |
57.194 |
| 3.0 |
1920 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936 936 |
63.629 |
64.451 |
| 3.7 |
2368 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
66.686 |
67.584 |
| Decamer (n = 10) |
1.6 |
2048 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280 |
71.316 |
71.739 |
| 3.0 |
3840 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 616 |
80.506 |
81.118 |
| 3.7 |
4736 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784 784 |
84.038 |
84.998 |
Table 2 Density (ρ) obtained from a 5 ns equilibration run
| Polymer chain length |
PA doping (γ) |
ρ (g cm−3) |
| 300 K |
350 K |
400 K |
450 K |
| Dimer (n = 2) |
1.6 |
1.56 |
1.55 |
1.53 |
1.50 |
| 3.0 |
1.66 |
1.64 |
1.62 |
1.58 |
| 3.7 |
1.68 |
1.66 |
1.64 |
1.61 |
| Trimer (n = 3) |
1.6 |
1.59 |
1.58 |
1.56 |
1.53 |
| 3.0 |
1.67 |
1.66 |
1.64 |
1.61 |
| 3.7 |
1.71 |
1.68 |
1.66 |
1.63 |
| Tetramer (n = 4) |
1.6 |
1.60 |
1.59 |
1.57 |
1.54 |
| 3.0 |
1.69 |
1.67 |
1.64 |
1.61 |
| 3.7 |
1.72 |
1.69 |
1.66 |
1.64 |
| Pentamer (n = 5) |
1.6 |
1.61 |
1.60 |
1.58 |
1.55 |
| 3.0 |
1.69 |
1.67 |
1.65 |
1.61 |
| 3.7 |
1.72 |
1.69 |
1.67 |
1.64 |
| Decamer (n = 10) |
1.6 |
1.59 |
1.59 |
1.58 |
1.57 |
| 3.0 |
1.67 |
1.66 |
1.65 |
1.63 |
| 3.7 |
1.71 |
1.70 |
1.68 |
1.65 |
In order to investigate the differences in structural and dynamical properties between a decamer and polymer chain lengths larger than the decamer (and to simulate a large polymeric system), we choose a hectamer (n = 100) of the ABPBI polymer membrane. The input configuration of the hectamer was created (constructed from 100 monomer units with a total of 1302 atoms in each chain), energy minimized and replicated in a cubic box to contain 16 polymer replicas. The replicated configuration was used as input for a simulated annealing procedure as described earlier. The final configuration from the annealing procedure was solvated with 2560 PA molecules (γ = 1.6). After energy minimization, the PA doped configuration was pre-equilibrated for 1 ns using the NPT ensemble, followed by a 10 ns NPT equilibration (at 300 K and 450 K). Equilibration was followed by a 20 ns production run using the NVT ensemble. Section 3.7 describes the structural and dynamical properties (calculated from the trajectories of the production run) of hectamer and its comparison with a decamer (γ = 1.6 and T = 300 K and 450 K).
3. Results and discussion
3.1. Intra and inter chain membrane interactions
The interactions in the polymer membrane can be seen from an examination of N–N, N–NH and N–HN Radial Distribution Functions (RDFs) (Fig. 2 and S3 of ESI†) and coordination numbers calculated at γ = 1.6, 3.0 and 3.7 (Fig. 2). All coordination numbers are calculated at the first minima of the RDFs. For each polymer chain length and PA doping, a first and second peak from the N–N RDFs (Fig. 2a and S3a and b†) appears at 4.8 Å and 6.1 Å which correspond to inter-chain and intra-chain interactions respectively. The peak positions resemble closely with work of Sunda et al.42 on hydrated PA doped ABPBI membrane. This suggests that exclusion of hydration does not impact the interactions in the membrane. The first peak of the N–NH RDFs at 3 Å (Fig. 2c and S3c and d†) shows inter-chain interactions, whereas intra-chain interactions are seen only at 6.1 Å, with a small peak at 5.2 Å (inset of Fig. 2c and S3c and d†) absent in a decamer. The peak of N–HN RDFs at 5.2 Å and 6.1 Å correspond to a separation of N–HN by six and seven bonds respectively.42 In a dimer, the intensity of N–HN intra-chain interactions at 5.2 Å is very low and increases with polymer chain length (inset of Fig. 2e and S3e and f†). The increase in intensity could be due to increasing possibility of free rotation around the C–C single bond which connect adjacent benzimidazole moieties. The coordination numbers from the N–N, N–NH and N–HN RDFs decrease with increase in PA doping. This is because more amount of PA can interact with the membrane matrix thereby reducing the interactions within the membrane. Further, a negligible effect of temperature on RDF profiles and coordination numbers is observed which illustrates the thermal stability of the membrane.
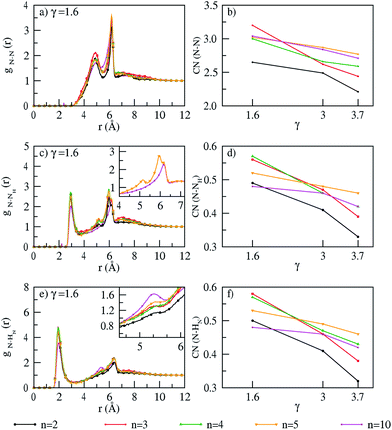 |
| | Fig. 2 RDFs (γ = 1.6) and coordination numbers (for all PA doping) of (a and b) N–N, (c and d) N–NH and (e and f) N–HN interactions at T = 300 K. | |
3.2. Phosphoric acid and membrane–phosphoric acid interactions
The various interactions in PA are seen from RDFs (Fig. 3 and S4 of ESI†) and coordination numbers calculated at γ = 1.6, 3.0 and 3.7 (Fig. 3). The variation in polymer chain length has no effect on all interactions. The interactions between PA molecules show the following features: the P–P RDFs show a first minimum at 6 Å, higher than the minimum at 5.5 Å reported on hydrated42 PA doped ABPBI membrane. This shows that unlike membrane interactions (as discussed in previous section), the solvation shell of PA is different in hydrated and dry environments. As expected, the coordination numbers from the P–P RDFs shows (see Fig. 3b) an increase with PA doping. The coordination numbers show that the interaction between the non-protonated oxygen atom (Od) and hydrogen atoms (HP) of PA show (see Fig. 3d) a slight increase with PA doping. This shows that the double bonded oxygen atom has less preference for hydrogen bonding with other PA molecules.
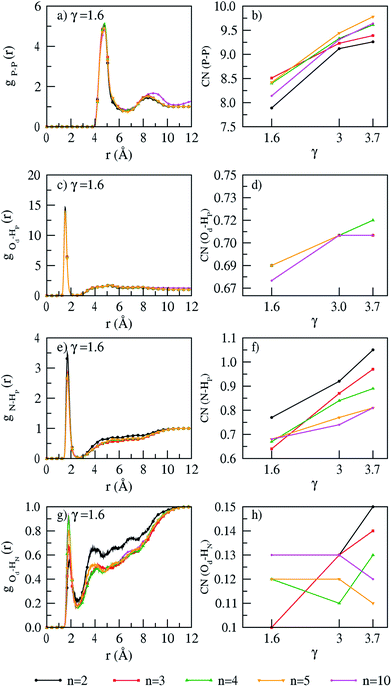 |
| | Fig. 3 RDFs (γ = 1.6) and coordination numbers (for all PA doping) of (a and b) P–P, (c and d) Od–Hp, (e and f) N–Hp, (g and h) Od–HN interactions at T = 300 K. | |
The membrane–phosphoric acid interactions elucidated from the coordination numbers show the following features: the interaction between the nitrogen atom (lone pair) of the benzimidazole moiety of the membrane and the hydrogen atom of PA (HP) shows an increase with PA doping (see Fig. 3f). This compensates the decreasing interactions seen within the membrane with increasing PA doping. The hydrogen bond interactions between the hydrogen atom of the imidazole moiety (HN) and the double bonded oxygen atom of PA (Od) slightly increases with PA doping (see Fig. 3h). This again shows that the double bonded oxygen atom has less inclination for interactions with the membrane. The variation in temperature shows no effect on RDF profiles and coordination numbers.
3.3. Radius of gyration and end-to-end distance
The radius of gyration, Rg, for each polymer chain is calculated as:| |
 | (1) |
where, Mi is the mass of atom i, Si is the position of atom i with respect to the center of mass of the ABPBI polymer chain. This is further illustrated by a normalized probability distribution plot of a time averaged radius of gyration (〈Rg〉t) and end-to-end distance (〈RE–E〉t) calculated for N = 128 polymer replicas at γ = 1.6 (see Fig. 4). The normalized probability plot shows a broad distribution of 〈Rg〉t and 〈RE–E〉t which increases with polymer chain length (from n = 2 to n = 10). For example, in the case of dimer, a sharp peak of Gaussian probability distribution is observed which diminishes in the decamer. Similar trends are seen at γ = 3.0 and γ = 3.7.
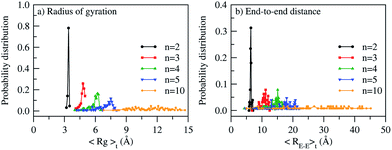 |
| | Fig. 4 Normalized probability distribution (for N = 128 polymer replicas) for various polymer chain length (n = 2, 3, 4, 5, 10) at γ = 1.6 using (a) time averaged radius of gyration (〈Rg〉t) and (b) time averaged end-to-end distance (〈RE–E〉t). | |
For each polymer chain length, PA doping and temperature, a time and system (N = 128) averaged radius of gyration (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g) and the end-to-end distance (
g) and the end-to-end distance (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E) is calculated. The effect of polymer chain length, PA doping and temperature on
E–E) is calculated. The effect of polymer chain length, PA doping and temperature on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E shows the following trends: at 300 K,
E–E shows the following trends: at 300 K, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g increases linearly with polymer chain length for all PA doping (Fig. 5a). Similar trends are seen at other temperatures. For each polymer chain length and temperature, the increase in PA doping shows no effect on
g increases linearly with polymer chain length for all PA doping (Fig. 5a). Similar trends are seen at other temperatures. For each polymer chain length and temperature, the increase in PA doping shows no effect on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g. For each polymer chain length and PA doping, the effect of temperature on
g. For each polymer chain length and PA doping, the effect of temperature on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g is insignificant (Fig. 5b). Similar to the trends seen in
g is insignificant (Fig. 5b). Similar to the trends seen in ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g,
g, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E remains invariant to change in PA doping and temperature.
E–E remains invariant to change in PA doping and temperature. ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E increases linearly from a dimer to tetramer (Fig. 6), though a deviation in linearity is seen in a pentamer and decamer. A deviation in linearity of
E–E increases linearly from a dimer to tetramer (Fig. 6), though a deviation in linearity is seen in a pentamer and decamer. A deviation in linearity of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E in a pentamer and decamer can be attributed to the flexibility of the membrane which arises from more unrestricted rotations around the C–C bond with an absence of aromatic ring current drive through the single bond which connects benzimidazole segments. Asensio et al.29 used thermal gravimetric analysis on PA doped ABPBI membrane and concluded that the glass transition temperature (Tg) of ABPBI is higher than the membrane degradation temperature (560 °C).54 Hence, our calculated
E–E in a pentamer and decamer can be attributed to the flexibility of the membrane which arises from more unrestricted rotations around the C–C bond with an absence of aromatic ring current drive through the single bond which connects benzimidazole segments. Asensio et al.29 used thermal gravimetric analysis on PA doped ABPBI membrane and concluded that the glass transition temperature (Tg) of ABPBI is higher than the membrane degradation temperature (560 °C).54 Hence, our calculated ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E suggest the stability of the membrane within the temperature range used in this present study.
E–E suggest the stability of the membrane within the temperature range used in this present study.
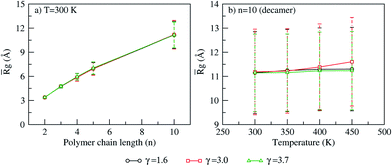 |
| | Fig. 5 Time and system averaged radius of gyration (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g) calculated at varying PA doping for (a) various polymer chain length (n = 2, 3, 4, 5, 10) at T = 300 K and (b) decamer (n = 10) at different temperatures. (Error bar are standard deviation of g) calculated at varying PA doping for (a) various polymer chain length (n = 2, 3, 4, 5, 10) at T = 300 K and (b) decamer (n = 10) at different temperatures. (Error bar are standard deviation of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g). g). | |
 |
| | Fig. 6 Time and system averaged end-to-end distance (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E) at varying PA doping for various polymer chain length (n = 2, 3, 4, 5, 10) at (a) T = 300 K and at (b) T = 450 K respectively. (Error bar represents standard deviation of E–E) at varying PA doping for various polymer chain length (n = 2, 3, 4, 5, 10) at (a) T = 300 K and at (b) T = 450 K respectively. (Error bar represents standard deviation of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E). E–E). | |
The error bar in Fig. 5 and 6 represents standard deviation of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g or
g or ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E. For all PA doping and temperature, the standard deviation in
E–E. For all PA doping and temperature, the standard deviation in ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E increases with polymer chain length. This trend is consistent with the broadening of probability distribution with increasing polymer chain length (see Fig. 4). The effect of PA doping on
E–E increases with polymer chain length. This trend is consistent with the broadening of probability distribution with increasing polymer chain length (see Fig. 4). The effect of PA doping on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E is examined by a calculation of scaling exponents (υ)55–57 at 300 K and 450 K. The scaling exponent can be expressed as:
E–E is examined by a calculation of scaling exponents (υ)55–57 at 300 K and 450 K. The scaling exponent can be expressed as:
where,
R is either
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g
g or
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E
E–E,
c is a constant and
n is “chain length”. The variation of
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g
g and
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E
E–E with polymer chain length (
n = 2, 3, 4, 5 and 10) is fitted using
eqn (2). For all
γ, the calculated
υ at 300 K and 450 K are shown in
Table 3. The
υ value for
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g
g is 0.73, which closely resembles a characteristic polymer chain behavior (
υ = 0.75)
58 where Self-Avoiding Walks (SAWs) of ABPBI polymer chains in PA are two-dimensional.
55–58 The
υ value for
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E
E–E is 0.9, which represents the SAWs of ABPBI polymer chains in PA are confined to one dimension. In conclusion, the effect of PA doping and temperature on scaling exponents is insignificant. Our calculations shows that the behavior of ABPBI membrane differ from the work of Wang
et al.59,60 on poly-ethylene terephthalate oligomers where authors found the
υ value of 0.59 to represent a three dimensional SAWs of polymer chains. A higher
υ value in ABPBI membrane (in this study) could be due to the compact packing of polymer chains in a highly dense PA environment.
Table 3 Scaling exponent (υ) calculated for radius of gyration (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g) and end-to-end chain (
g) and end-to-end chain (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E) distance at 300 and 450 K
E–E) distance at 300 and 450 K
| PA doping (γ) |
υ from ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g g |
υ from ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E E–E |
| 300 K |
450 K |
300 K |
450 K |
| 1.6 |
0.736 |
0.746 |
0.902 |
0.913 |
| 3.0 |
0.738 |
0.760 |
0.908 |
0.934 |
| 3.7 |
0.737 |
0.743 |
0.889 |
0.895 |
3.4. Cluster analysis
a. Interactions between benzimidazole moiety. A visual61 inspection of polymer chain (dimer to decamer) with the lowest Rg (skewed) and the highest Rg (extended) is shown in Fig. 7. To obtain further insights into inter-chain interactions and orientations of benzimidazole (BI) units, we choose only a skewed polymer chain as a reference polymer chain to characterize the interactions of other polymer chains around this reference polymer chain. To illustrate this, a cluster analysis is performed using the Gromos algorithm62 with a 12 Å distance (the cutoff used in MD simulations for non-bonding interactions) at γ = 1.6 and 300 K. A snapshot of polymer chains (of various Rg) around the skewed configuration of a dimer, trimer, tetramer and pentamer, respectively is shown in Fig. 8. We examine inter-chain interactions with respect to the center of mass of each BI unit of a skewed polymer chain with other polymer chains from the BIcom–BIcom RDFs. The details of calculation of the BIcom–BIcom RDFs are shown in ESI.† For each polymer chain length, a peak at ∼5.2 Å (Fig. 8) seen from the BIcom–BIcom RDFs show that the inter-chain BI distance (center of mass to center of mass) is higher than the geometrical criteria63 (3.4 to 3.8 Å) of π–π interaction. Hence, the peak distance from the BIcom–BIcom RDFs suggest that the nearest distance between any two inter-chain BI moiety can be only from N–NH inter-chain interactions which appears at a distance of 3 Å (see Fig. 2). Additionally, a low intensity peak from the BIcom–BIcom RDFs appears at ∼4.2 Å in a tetramer and pentamer. The presence of low intensity peaks could arise from van der Waals interactions or C–H/π interactions64–66 of aromatic ring in BI moieties which is difficult to distinguish from an all atom MD simulation performed in the present study.
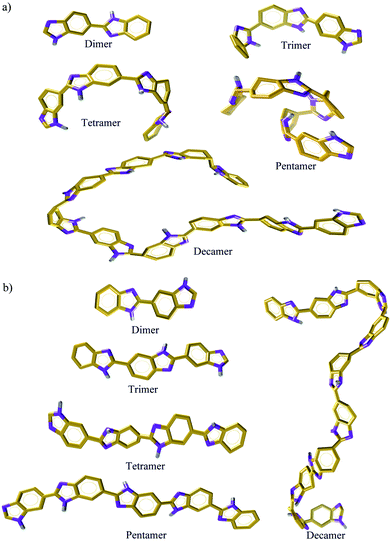 |
| | Fig. 7 Snapshots of (a) skewed and (b) extended ABPBI membrane for various polymer chain length [benzimidazole ring: orange, hydrogen: grey, nitrogen: violet (Licorice)] at 300 K. | |
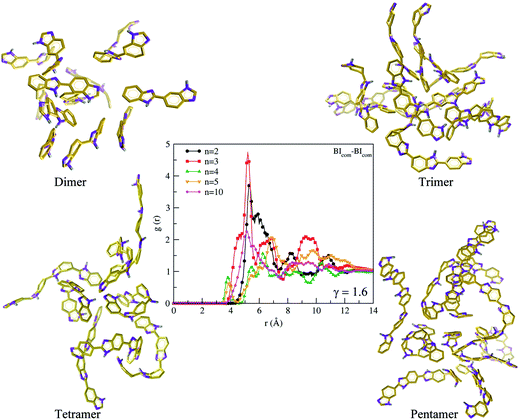 |
| | Fig. 8 Snapshots of ABPBI polymer chain clusters for dimer (top left), trimer (top right), tetramer (bottom left), pentamer (bottom right) and RDFs (at γ = 1.6) for center of mass to center of mass of any benzimidazole unit in ABPBI cluster (center) at 300 K [benzimidazole ring: orange, hydrogen: grey, nitrogen: violet (Licorice)]. | |
b. PA clusters around the polymer chain. For each polymer chain length, PA doping and temperature, we choose a skewed and an extended polymer configuration to calculate the number of PA molecules present in a cluster calculated using the criteria described earlier. The average number of PA molecules around the skewed and extended polymer chain at 300 K and 450 K is shown in Fig. 9. The number of PA molecules in a cluster shows no particular trend with variation in polymer chain length and PA doping. However, a significant effect of temperature is seen on the average number of PA molecules which forms a cluster. For example, compared to 300 K, a decrease of ∼25–30% in the number of PA molecules at 450 K is observed around the skewed or extended configuration with varying polymer chain length and PA doping.
 |
| | Fig. 9 Average number of PA molecules in a cluster around the skewed and extended ABPBI membrane at (a and b) T = 300 K and (c and d) T = 450 K. | |
3.5. Diffusion of PA
The mobility of PA is seen from the Mean Square Displacement (MSD) calculated using the Einstein equation46 as| |
 | (3) |
where, ri is the center of mass position of PA and DA represents the corresponding self-diffusion coefficient. The MSDs are shown in Fig. S5 of ESI† where a linear regime is observed from 2 ns to 8 ns. The diffusion coefficients (DA) of PA calculated from the linear regime are shown in Fig. 10 with the corresponding values in Table S1 (ESI†). The effect of polymer chain length on the diffusion coefficient of PA is insignificant, though diffusion coefficients are slightly lower in a decamer compared to dimer only at 450 K. For each polymer chain length and temperature, a significant effect of PA doping is seen on the diffusion coefficient of PA. For example, in a decamer, at 450 K, the diffusion coefficient of PA increase by a factor of ∼2.3 from γ = 1.6 to γ = 3.0. An increase from γ = 3.0 to γ = 3.7, results in an increase in the diffusion coefficient of PA by a factor of ∼1.2. For each polymer chain length and PA doping, an increase in temperature results in a significant increase in PA mobility. For e.g., in a decamer, at γ = 3.0, the diffusion coefficient of PA increases by a factor of ∼2.8 from 300 K to 350 K. Further, increase in temperature from 350 K to 400 K and 400 K to 450 K results in increase in diffusion coefficient of PA by a factor of ∼4.3 and ∼5.2, respectively.
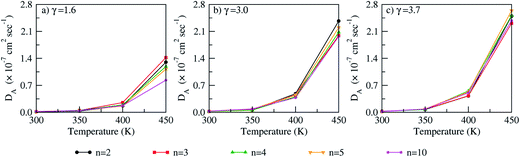 |
| | Fig. 10 Diffusion coefficients (DA) of PA using varying polymer chain lengths (n = 2, 3, 4, 5, 10) at (a) γ = 1.6, (b) γ = 3.0 and (c) γ = 3.7. | |
3.6. Activation energy of diffusion
The calculated diffusion coefficients of PA at 300 K, 350 K, 400 K and 450 K are used to calculate the activation energy of diffusion (EA) of PA using an Arrhenius equation:| |
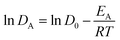 | (4) |
where, EA is calculated from the slope of linear fit. The calculated EA values are presented in Table 4. The variation in PA doping gives similarity in EA of PA at low polymer chain length (dimer and trimer). For example, the EA of PA for dimer is 33.29 kJ mol−1 (γ = 1.6) and 35.25 kJ mol−1 (γ = 3.7), and in trimer is 32.74 kJ mol−1 (γ = 1.6) and 35.06 kJ mol−1 (γ = 3.7). The EA of PA in decamer is 26.99 kJ mol−1 (γ = 1.6), 30.63 kJ mol−1 (γ = 3.0) and 34.25 kJ mol−1 (γ = 3.7) respectively. These trends in calculated EA values are in qualitatively agreement with the experiment EA of PA [27.4 kJ mol−1 (γ = 2.7) and 39.8 kJ mol−1 (γ = 3.0)] reported by Asensio et al.30 The difference in EA calculated from our work is due to the presence of water molecules in the experimental work of Asensio et al.30
Table 4 Activation energy of diffusion (EA) from a 10 ns production run
| Dimer (n = 2) |
1.6 |
33.29 |
| 3.0 |
35.25 |
| 3.7 |
33.45 |
| Trimer (n = 3) |
1.6 |
32.74 |
| 3.0 |
34.13 |
| 3.7 |
35.06 |
| Tetramer (n = 4) |
1.6 |
31.14 |
| 3.0 |
34.42 |
| 3.7 |
34.51 |
| Pentamer (n = 5) |
1.6 |
30.08 |
| 3.0 |
33.41 |
| 3.7 |
36.17 |
| Decamer (n = 10) |
1.6 |
26.99 |
| 3.0 |
30.63 |
| 3.7 |
34.25 |
3.7. Effect of long polymer chain lengths on structure and dynamics
The influence of long polymer chain length is examined by a comparison of structural and dynamical properties obtained from a decamer and hectamer. As seen (Table S2 of ESI†), the densities obtained from MD simulations using a decamer and hectamer resemble very closely. An examination of N–N, N–NH, and N–HN RDFs (Fig. S6 of ESI†) show that structural properties from a decamer and hectamer are similar. As expected, due to increasing chain length, the end-to-end polymer chain distance shows a difference between a decamer and hectamer. For e.g., the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E is 28.15 Å for a decamer and 48.66 Å for a hectamer (see Table S2 of ESI†). However, the radius of gyration shows a small change from a decamer to hectamer. For e.g., the
E–E is 28.15 Å for a decamer and 48.66 Å for a hectamer (see Table S2 of ESI†). However, the radius of gyration shows a small change from a decamer to hectamer. For e.g., the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g for decamer is 11.15 Å and 14.91 Å for a hectamer (γ = 1.6, T = 300 K). Similar trends are seen at T = 450 K. The dynamical properties of PA obtained from the MSDs (Fig. S7 of ESI†) and diffusion coefficients (Table S2 of ESI†) show similar behavior from a decamer and hectamer. A representative snapshot of a hectamer (extracted from the final snapshot of a production run) shown in Fig. 11 illustrates enhanced coiling of polymer chain compared to the decamer (see Fig. 7). Nevertheless, the similarity in properties between decamer and hectamer does indicate that the decamer can be an optimum chain length of ABPBI polymer electrolyte membrane.
g for decamer is 11.15 Å and 14.91 Å for a hectamer (γ = 1.6, T = 300 K). Similar trends are seen at T = 450 K. The dynamical properties of PA obtained from the MSDs (Fig. S7 of ESI†) and diffusion coefficients (Table S2 of ESI†) show similar behavior from a decamer and hectamer. A representative snapshot of a hectamer (extracted from the final snapshot of a production run) shown in Fig. 11 illustrates enhanced coiling of polymer chain compared to the decamer (see Fig. 7). Nevertheless, the similarity in properties between decamer and hectamer does indicate that the decamer can be an optimum chain length of ABPBI polymer electrolyte membrane.
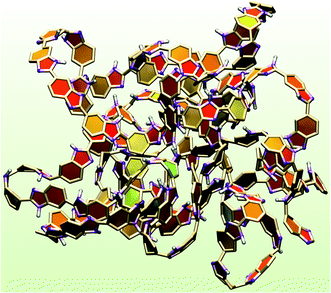 |
| | Fig. 11 Snapshot of a single polymer chain of hectamer (n = 100) of ABPBI membrane (γ = 1.6) at 300 K [benzimidazole ring: paperchain; hydrogen: white (CPK); nitrogen: violet (CPK)]. | |
4. Conclusions
A molecular investigation on structure and dynamics of PA doped ABPBI membrane is performed using varying polymer chain length, PA doping and temperature. An examination of properties calculated using polymer chain lengths from dimer to decamer shows the following trends: an increase in polymer chain length and PA doping show a more dense packing of polymer membrane, where the intra-chain hydrogen-bonding interaction (N–HN) increase significantly with polymer chain length. The variation in temperature does not affect the N–N, N–NH and N–HN interactions between sites in the membrane, within sites in PA and between the membrane and PA. The variation in polymer chain length and temperature has insignificant effect on interactions in PA, whereas interactions increase with PA doping. The radius of gyration and end-to-end distance of various polymer chains remains unaffected with PA doping and temperature which show the thermal stability of the PA doped ABPBI membrane. A scaling exponent of 0.73 for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and 0.9 for
g and 0.9 for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E suggest that the inclusion of PA shows the self-avoiding walk of ABPBI polymer chains in one or two dimensions.
E–E suggest that the inclusion of PA shows the self-avoiding walk of ABPBI polymer chains in one or two dimensions.
The interactions and orientations of benzimidazole units seen from the BIcom–BIcom RDFs and BI–BI clusters shows that inter-chain benzimidazole interactions are from N–HN hydrogen bonding. The random orientations of BI units and the presence of free rotation around the single bond which connects two monomeric BI segments lead to minimal possibility of π–π interactions. The number of PA molecules in a cluster around the polymer chain is invariant to polymer chain length and PA doping, though increasing temperature leads to reduced number of PA molecules. The effect of PA doping and temperature shows a significant impact on diffusion of PA, but remains unchanged with variation in polymer chain length. The activation energy of PA diffusion is unaffected by polymer chain length at higher doping (γ = 3.0 or γ = 3.7). The structural and dynamical properties using a decamer and hectamer exhibit identical characteristics. A molecular understanding of effect of polymer chain length, PA doping and temperature effects presented in this study can guide experimental efforts to deploy these membranes in fuel cell applications.
Acknowledgements
This work used the computing resources provided by Indian Institute of Science Education and Research, Pune (IISER Pune) and Center for Development of Advanced Computing, Pune. Minal acknowledges IISER Pune for graduate fellowship support. Anurag acknowledges the Jawaharlal Nehru Centre for Advanced Scientific Research for financial support. The authors thank the Department of Science and Technology, India (SB/S1/PC-015/2013) and Department of Science and Technology, Nanomission, India (SR/NM/NS-42/2009 and SR/NM/NS-15/2011) for support towards this work.
References
- M. S. Dresselhaus and I. L. Thomas, Nature, 2001, 414, 332–337 CrossRef CAS PubMed.
- B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS PubMed.
- K.-D. Kreuer, S. J. Paddison, E. Spohr and M. Schuster, Chem. Rev., 2004, 104, 4637–4678 CrossRef CAS.
- K. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535–4585 CrossRef CAS.
- M. A. Hickner, H. Ghassemi, Y. S. Kim, B. R. Einsla and J. E. McGrath, Chem. Rev., 2004, 104, 4587–4612 CrossRef CAS.
- K.-D. Kreuer, Solid State Ionics, 1997, 97, 1–15 CrossRef CAS.
- K.-D. Kreuer, J. Membr. Sci., 2001, 185, 29–39 CrossRef CAS.
-
(a) Q. Wang, D. J. Keffer, S. Deng and J. Mays, Polymer, 2012, 53, 1517–1528 CrossRef CAS PubMed;
(b) Q. Wang, D. J. Keffer, S. Deng and J. Mays, Polymer, 2013, 54, 2299–2307 CrossRef CAS PubMed;
(c) Q. Wang, D. J. Keffer, S. Deng and J. Mays, J. Phys. Chem. C, 2013, 117, 4901–4912 CrossRef CAS.
- Q. Wang, N. S. Suraweera, D. J. Keffer, S. Deng and J. Mays, Macromolecules, 2012, 45, 6669–6685 CrossRef CAS.
- S. J. Paddison and J. A. Elliott, J. Phys. Chem. A, 2005, 109, 7583–7593 CrossRef CAS PubMed.
- R. Paul and S. J. Paddison, J. Chem. Phys., 2005, 123, 224704 CrossRef PubMed.
- S. J. Paddison and J. A. Elliott, Solid State Ionics, 2006, 177, 2385–2390 CrossRef CAS PubMed.
- S. Cui, J. Liu, M. E. Selvan, D. J. Keffer, B. J. Edwards and W. V. Steele, J. Phys. Chem. B, 2007, 111, 2208–2218 CrossRef CAS PubMed.
-
(a) A. Venkatnathan, R. Devanathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 7234–7244 CrossRef CAS PubMed;
(b) R. Devanathan, A. Venkatnathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 8069–8079 CrossRef CAS PubMed;
(c) R. Devanathan, A. Venkatnathan and M. Dupuis, J. Phys. Chem. B, 2007, 111, 13006–13013 CrossRef CAS PubMed.
- D. Brandell, J. Karo and A. Liivat, J. Mol. Model., 2007, 13, 1039–1046 CrossRef CAS PubMed.
- S. Cui, J. Liu, M. E. Selvan, S. J. Paddison, D. J. Keffer and B. J. Edwards, J. Phys. Chem. B, 2008, 112, 13273–13284 CrossRef CAS PubMed.
- J. Karo, A. Aabloo, J. O. Thomas and D. Brandell, J. Phys. Chem. B, 2010, 114, 6056–6064 CrossRef CAS PubMed.
- J. Liu, N. Suraweera, D. J. Keffer, S. Cui and S. J. Paddison, J. Phys. Chem. C, 2010, 114, 11279–11292 CAS.
- R. Devanathan and M. Dupuis, Phys. Chem. Chem. Phys., 2012, 14, 11281–11295 RSC.
- J. K. Clark, II and S. J. Paddison, Solid State Ionics, 2012, 213, 83–91 CrossRef PubMed.
-
(a) A. P. Sunda and A. Venkatnathan, Soft Matter, 2012, 8, 10827–10836 RSC;
(b) A. P. Sunda and A. Venkatnathan, J. Mater. Chem. A, 2013, 1, 557–569 RSC.
- J. A. Asensio, S. Borros and P. Gómez-Romero, J. Polym. Sci., Part A: Polym. Chem., 2002, 40, 3703–3710 CrossRef CAS.
- Q. Li, R. He, J. O. Jensen and N. J. Bjerrum, Chem. Mater., 2003, 15, 4896–4915 CrossRef CAS.
- J. Zhang, Z. Xie, J. Zhang, Y. Tang, C. Song, T. Navessin, Z. Shi, D. Song, H. Wang, D. P. Wilkinson, Z. S. Liu and S. Holdcroft, J. Power Sources, 2006, 160, 872–891 CrossRef CAS PubMed.
- R. Devanathan, Energy Environ. Sci., 2008, 1, 101–119 CAS.
- E. Quartarone and P. Mustarelli, Energy Environ. Sci., 2012, 5, 6436–6444 CAS.
- H. Zhang and P. K. Shen, Chem. Rev., 2012, 112, 2780–2832 CrossRef CAS PubMed.
- H. J. Kim, S. Y. Cho, S. J. An, Y. C. Eun, J. Y. Kim, H. K. Yoon, H. J. Kweon and K. H. Yew, Macromol. Rapid Commun., 2004, 25, 894–897 CrossRef CAS.
- J. A. Asensio, S. Borros and P. Gómez-Romero, J. Electrochem. Soc., 2004, 151, A304–A310 CrossRef CAS PubMed.
- J. A. Asensio, S. Borros and P. Gómez-Romero, J. Membr. Sci., 2004, 241, 89–93 CrossRef CAS PubMed.
- J. A. Asensio, S. Borros and P. Gómez-Romero, Electrochim. Acta, 2004, 49, 4461–4466 CrossRef CAS PubMed.
- J. A. Asensio and P. Gómez-Romero, Fuel Cells, 2005, 5, 336–343 CrossRef CAS.
- P. Krishnan, J. S. Park and C. S. Kim, J. Power Sources, 2006, 159, 817–823 CrossRef CAS PubMed.
- V.-A. Glezakou, M. Dupuis and C. J. Mundy, Phys. Chem. Chem. Phys., 2007, 9, 5752–5760 RSC.
- Q. Li, J. O. Jensen, R. F. Savinell and N. J. Bjerrum, Prog. Polym. Sci., 2009, 34, 449–477 CrossRef CAS PubMed.
- C. Wannek, B. Kohnen, H.-F. Oetjen, H. Lippert and J. Mergel, Fuel Cells, 2008, 8, 87–95 CrossRef CAS.
- J. A. Asensio, E. M. Sánchezab and P. Gómez-Romero, Chem. Soc. Rev., 2010, 39, 3210–3239 RSC.
- M. S. Kondratenko, M. O. Gallyamov and A. R. Khokhlov, Int. J. Hydrogen Energy, 2012, 37, 2596–2602 CrossRef CAS PubMed.
- L. A. Diaz, G. C. Abuin and H. R. Corti, J. Power Sources, 2009, 188, 45–50 CrossRef CAS PubMed.
- J. J. Linares, C. Sanches, V. A. Paganin and E. R. González, J. Electrochem. Soc., 2012, 159, F194–F202 CrossRef CAS PubMed.
- S. Li, J. R. Fried, J. Colebrook and J. Burkhardt, Polymer, 2010, 51, 5640–5648 CrossRef CAS PubMed.
- A. P. Sunda, M. More and A. Venkatnathan, Soft Matter, 2013, 9, 1122–1133 RSC.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theor. Comput., 2008, 4, 435–447 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- S. A. H. Spieser, B. R. Leeflang, L. M. J. Kroon-Batenburg and J. Kroon, J. Phys. Chem. A, 2000, 104, 7333–7338 CrossRef CAS.
- M. P. Allen and D.
J. Tildesley, Computer Simulations of Liquids, Oxford Science Publications, New York, 1987 Search PubMed.
- W.-E. Hwang, D. R. Wife, C. Verschoore, G. E. Price, T. E. Helminiak and W. W. Adams, Polym. Eng. Sci., 1983, 23, 784–788 CAS.
- X. Glipa, B. Bonnet, B. Mula, D. J. Jones and J. Roziére, J. Mater. Chem., 1999, 9, 3045–3049 RSC.
- Y. L. Ma, J. S. Wainright, M. H. Litt and R. F. Savinell, J. Electrochem. Soc., 2004, 151, A8–A16 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8592 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S.-K. Kim, T. Ko, S.-W. Choi, J. O. Park, K.-H. Kim, C. Pak, H. Chang and J.-C. Lee, J. Mater. Chem., 2012, 22, 7194–7205 RSC.
- S. F. Edwards, Proc. Phys. Soc., 1966, 88, 265–280 CrossRef CAS.
- M. Daoud, J. P. Cotton, B. Farnoux, G. Jannink, G. Sarma, H. Benoit, R. Duplessix, C. Picot and P. G. de Gennes, Macromolecules, 1975, 8, 804–818 CrossRef CAS.
- P.-G. de Gennes, Scaling concepts in Polymer Physics, Cornell University Press, London, 1979 Search PubMed.
- M. Laso and N. C. Karayiannis, J. Chem. Phys., 2008, 128, 174901 CrossRef PubMed.
- Q. Wang, D. J. Keffer, S. Petrovan and J. B. Thomas, J. Phys. Chem. B, 2010, 114, 786–795 CrossRef CAS PubMed.
- Q. Wang, D. J. Keffer, D. M. Nicholson and J. B. Thomas, Macromolecules, 2010, 43, 10722–10734 CrossRef CAS.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed, 1999, 38, 236–240 CrossRef CAS.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- C. A. Sacksteder, S. L. Bender and B. A. Barry, J. Am. Chem. Soc., 2005, 127, 7879–7890 CrossRef CAS PubMed.
- M. J. Plevin, D. L. Bryce and J. Boisbouvier, Nat. Chem., 2010, 2, 466–471 CrossRef CAS PubMed.
- S. Tsuzuki, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2012, 108, 69–95 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra01421a |
| ‡ Equal contribution. |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602) was generated using a molecular builder program.
602) was generated using a molecular builder program.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160
160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160
160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464
464![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616
616![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464
464![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064
064![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768
768![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936
936![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520
520![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280
280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616
616![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784
784


![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g) and the end-to-end distance (
g) and the end-to-end distance (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E) is calculated. The effect of polymer chain length, PA doping and temperature on
E–E) is calculated. The effect of polymer chain length, PA doping and temperature on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E shows the following trends: at 300 K,
E–E shows the following trends: at 300 K, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g increases linearly with polymer chain length for all PA doping (Fig. 5a). Similar trends are seen at other temperatures. For each polymer chain length and temperature, the increase in PA doping shows no effect on
g increases linearly with polymer chain length for all PA doping (Fig. 5a). Similar trends are seen at other temperatures. For each polymer chain length and temperature, the increase in PA doping shows no effect on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g. For each polymer chain length and PA doping, the effect of temperature on
g. For each polymer chain length and PA doping, the effect of temperature on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g is insignificant (Fig. 5b). Similar to the trends seen in
g is insignificant (Fig. 5b). Similar to the trends seen in ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g,
g, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E remains invariant to change in PA doping and temperature.
E–E remains invariant to change in PA doping and temperature. ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E increases linearly from a dimer to tetramer (Fig. 6), though a deviation in linearity is seen in a pentamer and decamer. A deviation in linearity of
E–E increases linearly from a dimer to tetramer (Fig. 6), though a deviation in linearity is seen in a pentamer and decamer. A deviation in linearity of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E in a pentamer and decamer can be attributed to the flexibility of the membrane which arises from more unrestricted rotations around the C–C bond with an absence of aromatic ring current drive through the single bond which connects benzimidazole segments. Asensio et al.29 used thermal gravimetric analysis on PA doped ABPBI membrane and concluded that the glass transition temperature (Tg) of ABPBI is higher than the membrane degradation temperature (560 °C).54 Hence, our calculated
E–E in a pentamer and decamer can be attributed to the flexibility of the membrane which arises from more unrestricted rotations around the C–C bond with an absence of aromatic ring current drive through the single bond which connects benzimidazole segments. Asensio et al.29 used thermal gravimetric analysis on PA doped ABPBI membrane and concluded that the glass transition temperature (Tg) of ABPBI is higher than the membrane degradation temperature (560 °C).54 Hence, our calculated ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E suggest the stability of the membrane within the temperature range used in this present study.
E–E suggest the stability of the membrane within the temperature range used in this present study.![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g or
g or ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E. For all PA doping and temperature, the standard deviation in
E–E. For all PA doping and temperature, the standard deviation in ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E increases with polymer chain length. This trend is consistent with the broadening of probability distribution with increasing polymer chain length (see Fig. 4). The effect of PA doping on
E–E increases with polymer chain length. This trend is consistent with the broadening of probability distribution with increasing polymer chain length (see Fig. 4). The effect of PA doping on ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E is examined by a calculation of scaling exponents (υ)55–57 at 300 K and 450 K. The scaling exponent can be expressed as:
E–E is examined by a calculation of scaling exponents (υ)55–57 at 300 K and 450 K. The scaling exponent can be expressed as:![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g or
g or ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E, c is a constant and n is “chain length”. The variation of
E–E, c is a constant and n is “chain length”. The variation of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and
g and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E with polymer chain length (n = 2, 3, 4, 5 and 10) is fitted using eqn (2). For all γ, the calculated υ at 300 K and 450 K are shown in Table 3. The υ value for
E–E with polymer chain length (n = 2, 3, 4, 5 and 10) is fitted using eqn (2). For all γ, the calculated υ at 300 K and 450 K are shown in Table 3. The υ value for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g is 0.73, which closely resembles a characteristic polymer chain behavior (υ = 0.75)58 where Self-Avoiding Walks (SAWs) of ABPBI polymer chains in PA are two-dimensional.55–58 The υ value for
g is 0.73, which closely resembles a characteristic polymer chain behavior (υ = 0.75)58 where Self-Avoiding Walks (SAWs) of ABPBI polymer chains in PA are two-dimensional.55–58 The υ value for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E is 0.9, which represents the SAWs of ABPBI polymer chains in PA are confined to one dimension. In conclusion, the effect of PA doping and temperature on scaling exponents is insignificant. Our calculations shows that the behavior of ABPBI membrane differ from the work of Wang et al.59,60 on poly-ethylene terephthalate oligomers where authors found the υ value of 0.59 to represent a three dimensional SAWs of polymer chains. A higher υ value in ABPBI membrane (in this study) could be due to the compact packing of polymer chains in a highly dense PA environment.
E–E is 0.9, which represents the SAWs of ABPBI polymer chains in PA are confined to one dimension. In conclusion, the effect of PA doping and temperature on scaling exponents is insignificant. Our calculations shows that the behavior of ABPBI membrane differ from the work of Wang et al.59,60 on poly-ethylene terephthalate oligomers where authors found the υ value of 0.59 to represent a three dimensional SAWs of polymer chains. A higher υ value in ABPBI membrane (in this study) could be due to the compact packing of polymer chains in a highly dense PA environment.
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g) and end-to-end chain (
g) and end-to-end chain (![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E) distance at 300 and 450 K
E–E) distance at 300 and 450 K
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g
g![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E
E–E


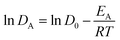
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E is 28.15 Å for a decamer and 48.66 Å for a hectamer (see Table S2 of ESI†). However, the radius of gyration shows a small change from a decamer to hectamer. For e.g., the
E–E is 28.15 Å for a decamer and 48.66 Å for a hectamer (see Table S2 of ESI†). However, the radius of gyration shows a small change from a decamer to hectamer. For e.g., the ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g for decamer is 11.15 Å and 14.91 Å for a hectamer (γ = 1.6, T = 300 K). Similar trends are seen at T = 450 K. The dynamical properties of PA obtained from the MSDs (Fig. S7 of ESI†) and diffusion coefficients (Table S2 of ESI†) show similar behavior from a decamer and hectamer. A representative snapshot of a hectamer (extracted from the final snapshot of a production run) shown in Fig. 11 illustrates enhanced coiling of polymer chain compared to the decamer (see Fig. 7). Nevertheless, the similarity in properties between decamer and hectamer does indicate that the decamer can be an optimum chain length of ABPBI polymer electrolyte membrane.
g for decamer is 11.15 Å and 14.91 Å for a hectamer (γ = 1.6, T = 300 K). Similar trends are seen at T = 450 K. The dynamical properties of PA obtained from the MSDs (Fig. S7 of ESI†) and diffusion coefficients (Table S2 of ESI†) show similar behavior from a decamer and hectamer. A representative snapshot of a hectamer (extracted from the final snapshot of a production run) shown in Fig. 11 illustrates enhanced coiling of polymer chain compared to the decamer (see Fig. 7). Nevertheless, the similarity in properties between decamer and hectamer does indicate that the decamer can be an optimum chain length of ABPBI polymer electrolyte membrane.

![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) g and 0.9 for
g and 0.9 for ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) E–E suggest that the inclusion of PA shows the self-avoiding walk of ABPBI polymer chains in one or two dimensions.
E–E suggest that the inclusion of PA shows the self-avoiding walk of ABPBI polymer chains in one or two dimensions.





