Characterization of structural, mechanical and nano-mechanical properties of electrospun PGS/PCL fibers

Abstract

Physical and mechanical studies of aligned nanofibers of poly (glycerol sebacate) (PGS)/poly (ε-caprolactone) (PCL) designed for application in cornea tissue engineering are investigated. The fibers were fabricated by electrospinning different weight ratios of PGS and PCL (1 : 1, 2 : 1, 3 : 1, and 4 : 1), and had diameters in the range of 300–550 nm. DSC and XRD measurements showed that the overall crystallinity decreased with increasing amount of amorphous PGS in the composition. Accordingly, the elastic modulus of the fibers was found to decrease with increasing PGS/PCL blend ratio. In contrast, the surface modulus of the nanofibers, measured by nanoindentation, exceeded the elastic modulus by two orders of magnitude and increased with weight ratio of PGS. It is assumed that this is caused by the increasing content of PGS forcing the fiber-forming PCL into confined and cross-linked domains near the fiber surface.

---

1. Introduction

Corneal diseases constitute the second leading cause for vision loss and affect more than 10 million people globally.¹ In most cases, cornea replacement forms a suitable remedy, and in 2000, approximately 33 000 transplants were performed in the United States alone.² An inherent problem is the great variation in the quality of donor graft material, however. As a consequence, transplantations have around an 18% failure rate mainly due to immunological rejection.³

In recent years, regenerative medicine has very much benefited from the progress in tissue engineering and scaffold development technology, which aims to mimic natural tissues in all their complexity.^4,5

In the context of a tissue-engineered substitute for corneal donor graft material, the technological concept has to understand the cornea as a transparent and avascular, multi-laminar structure. The thickness of human cornea is approximately 500 μm,⁶ and the stroma with its keratocytes and collagen lamellae is the main part of the cornea.⁷ Each collagen fibril with a diameter around 10–20 nm lies at a fixed distance from its neighbors (20 nm).^8,9 The collagen fibrils are packed in 300–500 parallel arrays (lamellae) which are naturally parallel to the corneal surface.¹⁰ The transmission and refraction of light through the cornea and also heterogeneous mechanical properties of the cornea (elastic modulus varied in the range 1–13 MPa) depend generally on this highly specialized ultrastructure. Dysfunction in any of these elements can cause a loss of transparency and function.^9,10

In their review of the corneal tissue engineering, Ruberti et al.¹⁰ suggest that the corneal stroma should be the current focus of investigators, as the corneal stroma is the most functional part of the corneal tissue. Mimicking the structure of the stroma with its nanoscale organization and its transparency, on the other hand, proved a very important interesting engineering challenge, and different ways have been tried recently to produce the suitable and similar structure to the native cornea.^11–15 In this framework, it is important to note that Wagner et al.¹⁶ reported that keratocytes, cultured on aligned scaffolds similar to the natural structure of aligned collagen nanofibrils of the corneal stroma, produced an organized matrix in vitro. Similar organized structures were not observed on scaffolds composed of randomly oriented fibers.

With regard to suitable material, poly(glycerol sebacate) (PGS) was introduced in the recent decade as a promising scaffold material for soft tissue engineering applications.^17–19 PGS is a FDA approved biocompatible and biodegradable elastomeric polymer.²⁰ In comparison to other kind of polyesters like poly(lactic-co-glycolic acid) (PLGA), the hydrophilic PGS showed a remarkable cellular response in biocompatibility studies.^20,21 Vascular endothelial or fibroblasts cells in contact with a PGS sample were viable and showed normal morphology with higher growth rate than the control, as tested by MTT assay. To the best of our knowledge, however, there is no report about investigating of corneal specific cells response to PGS as a biodegradable scaffolds. Given this background, it was the scope of a long-term study by the authors to prepare aligned and transparent nanofibrous scaffolds of PGS with the structure similar to the native stroma.²² Alignment of fibers was one of the main objectives in this approach.

Electro-spinning was chosen as an appropriate, yet simple method to fabricate aligned fibrous scaffolds. It was known from earlier work that the pure, low molecular weight PGS cannot be spun into nanofibers in this process, but a spinning solution with suitable viscosity could well be prepared by adding some spinnable polymer.^22–25 The concept chosen in the authors' approach was to blend PGS with poly(ε-caprolactone) (PCL). PCL is well established for straight-forward and reliable nanofiber production. In addition, the polymer is FDA approved and biodegradable. It should be noted on the other hand, that pure PCL fibers would not be feasible for the envisaged application. First, PCL is hydrophobic and, second, the mechanical properties differ significantly from natural tissue. Literature gives an elastic modulus of 237–300 MPa as compared to 1–1.2 MPa in case of natural corneal stroma.²⁶ Given this background, blending PGS with PCL is regarded as the most promising approach.

The first part of this long-term study, published in a recent paper,²² was focused on the development of the concept of scaffold fabrication by electro-spinning. Following optimization of spinning parameters, this allowed to produce unidirectional nanofibrous scaffolds with fibers diameters of the order of 300 to 550 nm as shown in Fig. 1. In order to produce aligned, parallel fibers, the electro-spinning setup was designed to employ a collector composed of parallel conductive bars positioned at a distance of 4 cm. The degradation properties of the PGS/PCL blend fibers, their chemical constitution of polymer (characterized by FTIR), and the transparency of the scaffolds indicated suitability for cornea tissue engineering.

Fig. 1 (a) SEM overview micrograph shows the alignment of fibers (b) transparent nanofibrous oriented scaffold.²²

The second part of the study summarized in the present paper is focused on characterizing the polymer structure and elastic properties of the actual nano-sized fibers. Nowadays it is well known that the nanometer-sized features of the substrates influence most of the cell behaviors by allowing the cells to attach to the diameters smaller than the cells size.²⁷ Electrospun nanofibers specifically have been shown to support cell attachment and proliferation of most of the cell types like smooth muscle cells, limbal epithelial cells and fibroblasts because of their high surface area.^15,28,29 Tissue cells feel and respond to the local stiffness of their substrate.³⁰ Cell adhesion to the scaffolds in molecular pathways is governed by adhesion complexes and the actin–myosin cytoskeleton. The local nanomechanical properties of substrates in contact with cytoskeleton have important implications for cell differentiation and regenerative functions.^30–32 From their study of the correlation of the endothelial cell area and substrate stiffness, King et al.³³ concluded that increasing the elasticity of the substrate results in higher cell area and higher cell spreading, which is also in agreement with another study of this group.³⁴ It has also been reported that increasing the stiffness of the substrate altered the morphology of mammary epithelial³⁵ and endothelial cells.^36,37 The same has been shown with regard to cornea, which means nanomechanical features of substrate influence cell contact acuity and alignment of corneal epithelial keratinocytes.³⁸ Discher et al.³⁰ also stated that tissue cells feel and respond to the local stiffness of their substrate, and the mechanical properties of the scaffolds in contact with the cell may further act as stimuli for cell functions. In connection with cornea regenerative therapeutic strategies involving innovative tailored biomaterials as cell substrates, it is important to evaluate, whether substrate elasticity modulates parameters of tissue homeostasis.

Basically, it is sensible to assume that, by blending a rather crystalline polymer (PCL) with an amorphous polymer (PGS), mechanical properties are affected by the blend ratio. At the same time, the increasing orientation of macromolecules (most probably of the PCL part) during fiber forming in the spinning process is of additional effect as is generally known from spinning processes. Given this background, the scope of the paper aims at the evaluation of these dependencies. Here, the important question was, whether the blend can be optimized to mimic the mechanical properties of the natural stroma in addition to the already proven orientation of the nanofibers. In the presented study, differential scanning calorimeter (DSC) and X-ray diffraction (XRD) are used to analyze polymer structure and crystallinity, which are then related to macro- and nano-mechanical properties measured by tensile testing and AFM-based nano-indentation.

We like to mention at this point that related cell cultivation experiments are presently undergoing and will be published in the near future. To indicate the potential of the nanofibrous PGS/PCL scaffold a first result of this study shall be presented here as a proof of concept. Immunostaining was performed to observe the cytoskeletal organization (beta-actin) of human cornea endothelial cells (HCECs) at day three on nanofibrous scaffolds by Phalloidin CF™543 and DAPI and visualized using a confocal fluorescent microscope. As can be taken from the micrograph shown in Fig. 2, it could be clearly shown that HCECs seeded on nanofibrous scaffolds were well growing after three days and aligned in the direction of fibers.

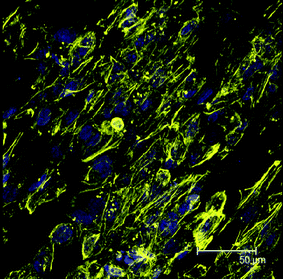Fig. 2 Stained HCECs with DAPI (blue, nuclei) and phalloidin (yellow, F-actin) after three days culturing on the aligned nanofibrous scaffolds.

2. Results and discussion

2.1 Thermal analysis

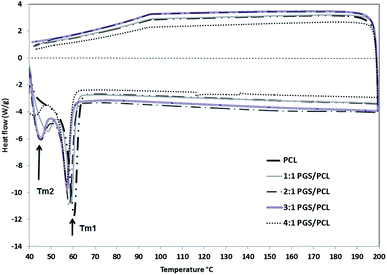
Structural stability and the crystallinity of the nanofiber scaffolds were analyzed by DSC. The relevant thermograms of the PGS/PCL nanofibers with different blend ratios are shown in Fig. 3. Basically the thermograms exhibit a main melting peak at around T_m1 = 55 to 60 °C, which represents the PCL component (cf. Table 1). A second melting peak T_m2 at around 45 °C occurs with increasing PGS/PCL blend ratio. This relates to the PGS, which has a reported melting temperature of 42.66 °C.³⁹ It should be noted that, as Liu et al.³⁹ reported, the melting temperature of PGS depends strongly on the composition. This relates well to own DSC analyses, which showed that the melting temperature of pure PGS depends on molar ratio of the sebacic acid and glycerol.⁴⁰

Fig. 3 DSC curves of the PGS/PCL blend nanofibrous scaffolds with different blend ratio.

Table 1 Thermal properties of the PGS/PCL blend nanofibers of different blend ratio

Samples	Tm1 (°C ± SD)	Tm2 (°C ± SD)	Enthalpy of fusion (J g^−1 ± SD)
0 : 1 PGS/PCL	60.25 ± 0.47	—	78.67 ± 0.11
1 : 1 PGS/PCL	58.56 ± 1.05	45.50 ± 2.34	39.55 ± 5.51
2 : 1 PGS/PCL	57.50 ± 1.16	42.60 ± 6.56	29.42 ± 1.89
3 : 1 PGS/PCL	56.50 ± 0.93	44.47 ± 1.15	25.98 ± 1.84
4 : 1 PGS/PCL	56.43 ± 0.003	43.17 ± 1.03	25.90 ± 5.90
PGS pre-polymer	—	42.67 ± 1	10.08

---

As can be seen in the graphs and also in Table 1, with increasing the blend ratio, the main melting peak has shifted slightly to lower temperature. In addition the overall enthalpy of fusion is also decreased. The value of the enthalpy of fusion relates to the crystallinity of the materials.⁴¹ In the case of a pure polymer, is given by the ratio of the measured enthalpy and the enthalpy of fusion of the full crystal (cf. eqn (1)), which is 139.5 J g⁻¹ for 100% crystalline PCL.⁴¹ According to this, the pure PCL fiber is semi-crystalline with a crystallinity α_DSC of approximately 56%. Obviously, the crystallinity of the blend fibers decreases with increasing PGS/PCL blend ratio. As confirmed by Wang et al.,²⁰ Jaafar et al.⁴² and also in the previous study of the authors,²² the PGS pre-polymer is fully amorphous above 35 °C. Thus, increasing the PGS content of the blend nanofiber causes a decrease in crystallinity of the fibers. It should be pointed out that the low crystallinity is extremely important for good elasticity and biodegradability of a potential implant material.³⁹

2.2 Phase composition (XRD)

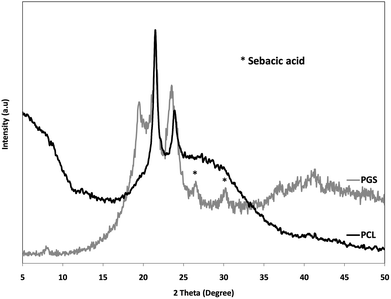
Since the PGS pre-polymer is fully amorphous, and, accordingly, no enthalpy of fusion is available for fully crystalline PGS, the degree of crystallinity of the blend fibers could not be determined by DSC. Therefore, XRD measurements were performed as alternative.

Before the analysis of the actual blend fibers, X-ray diffraction patterns were determined from the PGS-prepolymer and the PCL nanofibers. The relevant patterns are shown in Fig. 4. The XRD pattern of the PGS-prepolymer exhibits three peaks at 19°, 21°, and 23°. Although the signals are rather weak, this is quite remarkable as the pre-polymer is generally accepted as an amorphous polymer (cf. ref. 20 and 42). In the case of the PCL nanofibers, two peaks are observed at 21° and 23°. The clear pattern allows to calculate the crystallinity of the PCL nanofibers, and using eqn (2) one obtains α_XRD = 57%, which is in remarkable agreement with the value derived from DSC measurements.

Fig. 4 XRD pattern of PGS pre-polymer and PCL nanofibers.

The XRD patterns of the blend fibers are summarized in Fig. 5. The patterns exhibit three peaks, which constitute the major peaks of the PCL spectrum and a peak at 2θ = 19°, which can be assigned to the PGS portion. From the analysis of the peaks areas, the degrees of crystallinity of the PGS/PCL blend fibers were according to eqn (2). The relevant data are summarized in Table 2.

Fig. 5 XRD patterns of nanofibrous blend scaffolds. Note: for clarity, XRD diagrams of the different polymer blends are shifted along the y-axis.

Table 2 XRD-derived crystallinity of the PGS/PCL blend nanofibers

Samples	Crystallinity (%)
PCL	57
1 : 1 PGS/PCL	28.34
2 : 1 PGS/PCL	21.08
3 : 1 PGS/PCL	18.62
4 : 1 PGS/PCL	17.07

---

As expected, the crystallinity of the blend fibers decreases with increasing PGS content. This is in agreement with the DSC results. However, even at the highest PGS content, the fibers have a significant crystallinity. It is to be assumed that the electrical and mechanical forces acting during the spinning process effect a pronounced orientation of macromolecules, which is stabilized through solvent evaporation, i.e. fiber solidification.

2.3 Mechanical properties

2.3.1 Elastic properties. As was described in greater detail in the experimental section, the elastic properties of the nanofibers were characterized with the help of stress–strain measurements performed on 3 mm wide ensembles of nanofibers, which were cut from the scaffolds. From the elastic properties of these ensembles, namely the linear elastic modulus E_l, the specific modulus of individual fibers could be derived. The resulting values are shown in Table 3. In the case of fibers spun form PGS/PCL blends 2 : 1 to 4 : 1, the moduli decrease with increasing PGS content. This trend was basically to be expected from the crystallinity measurements. The value of 4 : 1 blend is also in good agreement with measurements of the Young's modulus of pure PGS by Chen et al., which was determined to be of the order of 1–1.2 MPa.⁴³ It is important to note that, with values of the order of 1 MPa, the elastic modulus of the nanofibers fits nicely in the range of the mechanical properties of the native stroma.¹⁰

Table 3 Elastic modulus (linear modulus) of the PGS/PCL blend nanofibers

Samples	Linear modulus [cN/tex]	Linear modulus [MPa]
2 : 1 PGS/PCL	14.3 ± 3.1	1.24 ± 0.27
3 : 1 PGS/PCL	11.7 ± 4.4	1.02 ± 0.38
4 : 1 PGS/PCL	9 ± 2.2	0.78 ± 0.19

---

It may be noted that no value for the 1 : 1 blend material is given in Table 3. In the experiment, serious handling problems were encountered, when the rectangular samples cut from these scaffolds were offered to the clamps of the tensile tester. The samples proved to be sticky and systematically decomposed to a certain degree during the preparation of the test. Therefore, it had to be concluded that not all fibers of the specimen contribute to the recorded stress–strain curves, and that the determined modulus was far too low as a result.

2.3.2 Nanoindentation. It is well-reported in literature that nano-mechanical features of the substrate influence cell contact acuity and alignment of corneal epithelial keratinocytes.³⁸ An important objective of the presented study, therefore, was to characterize structural properties of the very surface of the nanofibers, which could not be assessed by the bulk-sensitive analyses discussed before.

Atomic force microscopy (AFM) based nanoindentation was chosen as means to characterize the surface stiffness and derive the surface elastic modulus in dependence on the blending ratio of PGS and PCL.

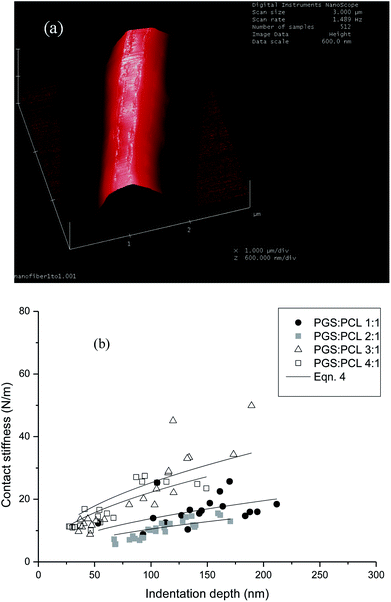
In the measurement, the mechanical contact stiffness, k, is determined as the slope of the initial elastic unloading curve. The modulus is then derived from the contact stiffness. Specimens were prepared by fixing separate nanofibers on silicon wafers with a thin layer of pre-coated epoxy. The measured local mechanical stiffnesses of the fiber surfaces are given in Fig. 6 for all blends as a function of indentation depth. Basically the data show large scatter, which is related to the general test procedure – e.g. due to inhomogeneous fixing of the nanofibers in the epoxy – and also inhomogeneities in the polymer blend structure. Also, systematic effects – the nanoindentation test could, e.g., be affected by surface viscoelastic creep – cannot be fully excluded. In spite of this, the trend that the apparent stiffness profile of the nanofiber surface shifts to overall much higher stiffness values for high PGS concentrations (3 : 1, 4 : 1) is clearly visible, suggesting a mechanically more rigid surface. By calculation of best-fit curves and using eqn (3) and (4), surface moduli of 0.26 GPa, 0.29 GPa, 0.12 GPa and 0.16 GPa can be determined for PGS/PCL weight ratios of 4 : 1, 3 : 1, 2 : 1, 1 : 1, respectively.

Fig. 6 (a) Three-dimensional AFM image of a PGS/PCL nanofiber on a silicon wafer. (b) Surface contact stiffness as a function of indentation depth for the nanoindentation of the surfaces of the PGS/PCL nanofibers.

The results of the nanoindentation tests are striking in two respects: first, the trend of surface moduli is opposite to what was found for the elastic modulus, i.e. the fibers manufactured from high blend ratios exhibit high surface moduli. Second, surface moduli are significantly higher than elastic moduli.

While not fully proven by the performed analyses, it is assumed that the increasing content of PGS forces the fiber-forming PCL into confined and cross-linked domains near the fiber surface, which are responsible for the observed dimension and behavior of the surface moduli. At the same time, the content of PCL in the fiber bulk is reduced with increasing PGS content, and crystallinity as well as elastic modulus decrease.

3. Experimental

3.1 Materials

The experimental procedure was in all respects in accordance to spinning solutions and geometry and conditions of the spinning derived from the experiments described in the previous study of the authors.²²

Briefly, the PGS pre-polymer (M_w 3884–7516) and poly(ε-caprolactone) (PCL, Sigma M_w 70 000–90 000) were solved at different weight ratios (4 : 1, 3 : 1, 2 : 1 and 1 : 1, respectively) in anhydrous chloroform–ethanol (9 : 1) mixture. Polymer concentrations were 13 wt% in case of the 1 : 1 PGS/PCL-blend, and 18 wt% for all others. Pure PCL scaffolds were also electro-spun using 10 wt% polymer solution.

In order to produce aligned, parallel fibers, the electro-spinning setup employed a collector composed of parallel conductive bars positioned at a distance of 4 cm. The distance between needle and collector was 12 cm, the applied voltage was 12.5 kV for 1 : 1, 18 kV for 2 : 1 and 3 : 1 and 20 kV for 4 : 1 blends, respectively. The spinning solution was supplied at a rate of 1 ml h⁻¹ through a 26 gauge (26 G) capillary. A Heinzinger PNC 30000-40 ump (Heinzinger, Germany) served as high-voltage power supply, and a model KDS 100 syringe pump (K.D. Scientific Inc., Holliston, MA, USA) for constant supply of the spinning solution.

3.2 Analytical methods

3.2.1 Thermal stability. The thermal behavior of the PGS pre-polymer, PCL and PGS/PCL-blend scaffolds were measured by Differential scanning calorimetry (DSC). DSC curves were obtained by a thermal analysis instrument (Q20, USA) in a scan range of 40–200 °C at a heating rate of 5 °C min⁻¹. In the case of the PCL nanofibers, the measured enthalpy of fusion ΔH served to calculate the crystallinity α_DSC according to eqn (1):⁴⁴where ΔH_∞ is the melt enthalpy of 100% crystalline polymer.

3.2.2 Phase composition. The crystallinity of blend scaffolds was determined via X-ray diffraction (XRD). XRD patterns were recorded using a XRD: D8 Advance (Bruker, Germany) (Cu K_α). The scan covered a range of 2θ = 5–50° at a rate of 0.05° s⁻¹. After background subtraction, the total area of crystalline peaks l_c and the total area under the diffraction curve (crystalline plus amorphous peaks) l_a were determined. The crystallinity α_XRD is then calculated according to eqn (2):⁴⁵

3.2.3 Mechanical analysis. The elastic properties of the nanofibers were characterized by stress–strain measurements. Due to size and thickness of the delicate samples a technique developed for single fiber measurements was adapted, and 3 mm wide ensembles representing an unknown number of fibers cut from the scaffolds measured in an automatic single fiber tester (model FAVIMAT, Textechno, Mönchengladbach, Germany). The rectangular specimens cut from the scaffolds were inserted into the clamps to give an initial sample length (at zero elongation) of 10 mm. Stress–strain-curves were recorded at a strain rate ε° = 25 mm min⁻¹. From these curves, the tensile strength (F_max) and maximum elongation (ε_max) at breakage were determined, and the linear elastic modulus of the fiber ensemble (E_l) calculated from the 0–5% strain region. Three samples were tested of each type of scaffold. Values were reported as mean ± SD. A special feature of the testing device was the possibility to determine the mass of the sample by a non-contacting vibrational analysis. With the given length (10 mm) and width (3 mm) of the samples, and the approximate density of the polymer blends, the cross-section of the samples could be calculated. This represents the sum of the cross-sections of all nanofibers constituting the 3 mm wide sample. This way, the elastic modulus of the individual fibers could be determined. All these measurements were performed with the help of the manufacturer of the testing device.

In addition, an atomic force microscope (AFM) (Digital Instruments D3100, USA) was used both as a surface imaging tool and for nanoindentation measurements to characterize the effects of blending ratio of PGS and PCL on nanomechanical behavior of nanofibers. The topography of samples was studied in tapping mode. The mechanical contact stiffness, k, is the slope of the initial elastic unloading curve was determined by the nanoindentation in the lateral direction of the nanofiber which allowed a precise continuous measurement of the load F and indentation depth h, as described in previous studies.^46,47 The single crystal diamond AFM probe (SCD14/AIBS, Mikro Masch, Estonia) has a spring constant of 9.6 N m⁻¹, a tip cone angle <20°, a tip radius, R = 5–10 nm and the Young modulus >1000 GPa to assure good imaging resolution and nanometer scale indents. A modified formalism based on equation of Sneddon⁴⁸ allows a quantitative evaluation of the contact stiffness and modulus of samples. The expression of contact stiffness and elastic modulus are given by eqn (3) and (4) respectively:

with

E_s ≈ E_r(1 − ν_s²) (4)

where ν_s is Poisson's ratio of the nanofiber which is taken to be 0.3.⁴⁹ The subscript s refers to the properties of the specimens. E_r is an effective reduced elastic modulus which includes contributions from both the specimen and the indenter. The equation used for the calculation of nanofiber modulus assumes that the fiber surface is flat since the tip radius is much smaller than the fiber radius. Specimens were prepared by fixing separate nanofibers on the silicon wafers with a thin layer of precoated epoxy. For all samples, about twenty measurements were made at different forces and locations along the length of the fiber to verify the reproducibility of the observed features.

4. Conclusions

DSC and XRD measurements showed that, with increasing amount of amorphous PGS in the composition, the overall crystallinity decreased. While both analyses indicated a crystallinity of 57% of pure PCL nanofibers, the crystallinity of the blend fibers dropped to values as low as 17%. In agreement with the decreasing crystallinity the elastic modulus of the fibers was found to decrease with increasing PGS/PCL blend ratio.

In this context, and for these blend nanofibers for the first time, nano mechanical properties were studied and nanoindentation analysis revealed that there is an increase in surface modulus with increasing content of PGS (contrary to elastic modulus), i.e. the highest surface modulus was found for the 4 : 1 blend fiber. Also, the surface moduli were higher by approximately two orders of magnitude than the relevant elastic moduli. It is assumed that the increasing content of PGS forces the fiber-forming PCL into confined and cross-linked domains near the fiber surface, which are responsible for the observed dimension and behavior of the surface moduli. Related cell cultivation experiments are presently undergoing (early data) and will be published in the near future.

Acknowledgements

The authors are indebted to the company Textechno of Mönchengladbach, Germany, who kindly supported the mechanical measurements and Prof. Matthias Epple and Mrs Olga Rotan of Universität Duisburg-Essen, who supported the X-ray diffraction measurements. The authors are also grateful for support by Isfahan University of Technology, Prof. Mohammadhossein Fathi and Saied Nouri Khorasani. Marta Czugala of Universitätsklinikum Düsseldorf and Klaus-Peter Steuhl of Universitätsklinikum Essen and Shaghayegh Haghjooy Javanmard of Isfahan University of Medical Sciences are acknowledged.

References

1. J. P. Whitcher, M. Srinivasan and M. P. Upadhyay, Bull. W. H. O., 2001, 79, 214.
2. P. Aiken-O'Neill and M. J. Mannis, Cornea, 2002, 21, 1.
3. R. W. Thompson Jr, M. O. Price, P. J. Bowers and F. W. Price Jr, Ophthalmology, 2003, 110, 1396.
4. H. Kenar, G. T. Kose, M. Toner, D. L. Kaplan and V. Hasirci, Biomaterials, 2011, 32, 5320.
5. B. M. Baker, A. M. Handorf, L. C. Ionescu, W. J. Li and R. L. Mauck, Expert Rev. Med. Devices, 2009, 6, 515.
6. A. J. Quantock and R. D. Young, Dev. Dyn., 2008, 237, 2607.
7. H. F. Edelhauser, Invest. Ophthalmol. Visual Sci., 2006, 47, 1754.
8. T. Ihanamaki, L. J. Pelliniemi and E. Vuorio, Prog. Retinal Eye Res., 2004, 23, 403.
9. Y. Qazi, G. Wong, B. Monson, J. Stringham and B. K. Ambati, Brain Res. Bull., 2010, 81, 198.
10. J. W. Ruberti and J. D. Zieske, Prog. Retinal Eye Res., 2008, 27, 549.
11. E. J. Orwin, M. L. Borene and A. Hubel, J. Biomech. Eng., 2003, 125, 439.
12. R. A. Crabb, E. P. Chau, M. C. Evans, V. H. Barocas and A. Hubel, Tissue Eng., 2006, 12, 1565.
13. Y. Liu, L. Gan, D. J. Carlsson, P. Fagerholm, N. Lagali, M. A. Watsky, R. Munger, W. G. Hodge, D. Priest and M. Griffith, Invest. Ophthalmol. Visual Sci., 2006, 47, 1869.
14. N. Builles, H. J. Manificat, M. Malbouyres, V. Justin, M. R. Rovère, G. Pellegrini, J. Torbet, D. J. S. Hulmes, C. Burillon, O. Damour and F. Ruggiero, Biomaterials, 2010, 31, 8313.
15. P. Deshpande, C. Ramachandran, F. Sefat, I. Mariappan, C. Johnson, R. McKean, M. Hannah, V. S. Sangwan, F. Claeyssens, A. J. Ryan and S. MacNeil, Biomaterials, 2013, 34, 5088.
16. J. Wu, Y. Du, S. C. Watkins, J. L. Funderburgh and W. R. Wagner, Biomaterials, 2012, 33, 1343.
17. J. Gao, P. Crapo, R. Nerern and Y. D. Wang, J. Biomed. Mater. Res., Part A, 2008, 85, 1120.
18. S. Redenti, W. L. Neeley, S. Rompani, S. Saigal, J. Yang, H. Klassen, R. Langer and M. J. Young, Biomaterials, 2009, 30, 3405.
19. C. A. Sundback, J. Y. Shyu, Y. D. Wang, W. C. Faquin, R. S. Langer, J. P. Vacanti and T. A. Hadlock, Biomaterials, 2005, 26, 5454.
20. Y. D. Wang, G. A. Ameer, B. J. Sheppard and R. Langer, Nat. Biotechnol., 2002, 20, 602.
21. E. J. Lee, G. V. Novakovic, Y. Wang and L. E. Niklason, Cell Transplant., 2009, 18, 731.
22. S. Salehi, M. H. Fathi, S. Haghjooy Javanmard, T. Bahners, J. S. Gutmann, S. Ergün, K. P. Steuhl and T. A. Fuchsluger, Macromol. Mater. Eng., 2013 DOI:10.1002/mame.201300187.
23. H. Kenar, G. T. Kose and V. Hasirci, J. Mater. Sci.: Mater. Med., 2010, 21, 989.
24. F. Yi and D. A. Lavan, Macromol. Biosci., 2008, 8, 803.
25. S. Sant, C. M. Hwang, S. H. Lee and A. Khademhosseini, J. Tissue Eng. Regener. Med., 2011, 5, 283.
26. S.-C. Wong, A. Baji and S. Leng, Polymer, 2008, 49, 4713.
27. M. M. Stevens and J. H. George, Science, 2005, 310, 1135.
28. R. el-Kenawy, J. M. Layman, J. R. Watkins, G. L. Bowlin, J. A. Matthews, D. G. Simpson and G. E. Wnek, Biomaterials, 2003, 24, 907.
29. C. Y. Xu, R. Inai, M. Kotaki and S. Ramakrishna, Biomaterials, 2004, 25, 877.
30. D. E. Discher, P. Janmey and Y. Wang, Science, 2005, 310, 1139.
31. V. Thomas, M. V. Jose, S. Chowdhury, J. F. Sullivan, D. R. Dean and Y. K. Vohra, J. Biomater. Sci., Polym. Ed., 2006, 17, 969.
32. L. E. Bilston, Neural Tissue Biomechanics, Springer, Randwick, Australia, 2011, vol. 3.
33. J. P. Califano and C. A. Reinhart-King, Cell. Mol. Bioeng., 2010, 3, 68.
34. B. N. Mason, A. Starchenko, R. M. Williams, L. J. Bonassar and C. A. Reinhart-King, Acta Biomater., 2013, 9, 4635.
35. M. J. Paszek, N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo, D. Boettiger, D. A. Hammer and V. M. Weaver, Cancer Cell, 2005, 8, 241.
36. F. J. Byfield, R. K. Reen, T. P. Shentu, I. Levitan and K. J. Gooch, J. Biomech., 2009, 42, 1114.
37. A. L. Sieminski, R. P. Hebbel and K. J. Gooch, Exp. Cell Res., 2004, 297(2), 574.
38. E. J. Tocce, V. K. Smirnov, D. S. Kibalov, S. J. Liliensiek, C. J. Murphy and P. F. Nealey, Biomaterials, 2010, 31, 4064.
39. Q. Liu, M. Tian, T. Ding, R. Shi and L. Zhang, J. Appl. Polym. Sci., 2005, 98, 2033.
40. S. Salehi, M. H. Fathi, S. Haghjooy Javanmard, T. Bahners, J. S. Gutmann, T. Mayer-Gall, M. Epple, O. Rotan, B. B. Singer and T. A. Fuchsluger, unpublished work.
41. X. Wang, H. Zhao, L. S. Turng and Q. Li, Ind. Eng. Chem. Res., 2013, 52, 4939.
42. I. H. Jaafar, M. M. Ammar, S. S. Jedlicka, R. A. Pearson and J. P. Coulter, J. Mater. Sci., 2010, 45, 2525.
43. Q. Z. Chen, A. Bismarck, U. Hansen, S. Junaid, M. Q. Tran, S. E. Harding, N. N. Ali and A. R. Boccaccini, Biomaterials, 2008, 29, 47.
44. M. Wei, X. Shuai and A. E. Tonelli, Biomacromolecules, 2003, 4, 783.
45. S. Kavesh and J. M. Schultz, Polym. Eng. Sci., 1969, 9, 331.
46. S. L. Gao, R. Häßler, E. Mäder and T. Bahners, Appl. Phys. B: Lasers Opt., 2005, 81, 681.
47. S. L. Gao, E. Mäder, A. Abdkader and P. Offermann, Langmuir, 2003, 19, 2496.
48. I. N. Sneddon, Int. J. Eng. Sci., 1965, 3, 47.
49. J. M. Kemppainen and S. J. Hollister, J. Biomed. Mater. Res., 2010, 94, 9.

---