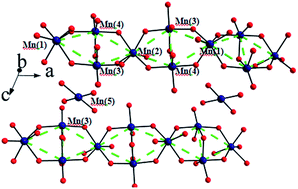
KNa3Mn7(PO4)6: 2D spin-frustrated magnetic material with a diamond-like chain structure

Abstract

The search for spin frustrated magnets has attracted great scientific interest. Here we report on the synthesis of a novel two dimensional spin-frustrated compound KNa₃Mn₇(PO₄)₆ with a diamond-like chain structure. Our results confirm spin freezing at T_c = 3.9(1) K with the Weiss constant θ = −64.1(2) K, showing a remarkable spin frustration effect in the system. The origin of spin frustration is also suggested.