Theoretical investigation of the adsorption, IR, and electron injection of hydroxamate anchor at the TiO₂ anatase (1 0 1) surface

Abstract

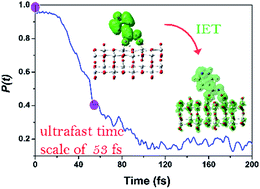
The adsorption of hydroxamate onto a TiO₂ anatase surface has been theoretically determined. We find that the doubly deprotonated configuration is the optimal adsorption mode in terms of energetic and dynamical stability, which is demonstrated by vibrational spectrum analysis. This configuration can also undergo the ultrafast electron transfer event, with a time-scale of 53 fs.

---

Among renewable energy solutions, dye-sensitized solar cells (DSSC) have attracted intensive attention as an alternative for light-to-electricity conversion.¹ In the DSSC system, light energy is harvested by dye molecules grafted onto the nanocrystalline semiconductor through the anchor group. The photo-excited electrons are then transferred, resulting in electron–hole separation at the dye/semiconductor interface. The highest conversion efficiency for DSSC has reached 12.3% in experiment,² but it is still low for large-scale implantation. The need for investigating the structure and electronic interaction of the adsorbate/substrate interface is urgent, as they are crucial in determining the time-scale of electron injection following photo-excitation of the dye. Meanwhile, the dye must anchor strongly onto the substrate to ensure the long-term stability of the cell. Carboxylic acid is the commonly used anchor group, as it appears to give good electronic coupling across the dye/TiO₂ interface. However, the dye bearing a carboxylic acid anchor may be affected by its limited stability in the presence of water and highly oxidizing conditions, which make it unsuitable for use in an artificial photosynthetic cell. Some other groups, i.e., phosphonic acid,³ biscarbodithiolic acid,⁴ and hydroxamic acid⁵ have also been reported to date. Among these, hydroxamic acid stands out for its long-term stability and efficient electron injection. Although there are a number of experimental works concerning the hydroxamate anchor,⁵ the preferred configuration of hydroxamate adsorbed on the titanium dioxide surface has not yet been unambiguously determined.

In this work, we systematically study the adsorption configurations of hydroxamic anchor on the TiO₂ anatase (1 0 1) surface. The geometry optimization was performed with the Vienna ab initio simulation package (VASP),⁶ using the generalized gradient approximation (GGA) of Perdewe–Wang 91 (PW91) exchange–correlation functional.⁷ The bulk anatase TiO₂ was relaxed with a k-point of (5, 5, 2) and an energy cutoff of 400 eV. A slab comprised of two layers (2 × 4) of titanium and oxygen atoms was used (Fig. S1†). This set of parameters gives a force convergence within 0.01 eV Å⁻¹. We choose the hydroxamic acid functionalized with pyridine as the anchor model to investigate the full DSSC system, since it provides an important stepping-stone from detailed studies of small molecules on metal oxide surfaces. Molecular dynamics simulations of various adsorbate/TiO₂ systems were also performed with VASP. In this calculation, a time step of 1 fs is used, producing the total time of 4 ps.

Among all of the initial-guess configurations (Fig. S2†), a few representative ones after optimizations are shown in Fig. 1. The relevant bond lengths and adsorption energies are listed in Table 1. As shown in Fig. 1, for configuration M1, the double bound oxygen is directly coordinated to a surface five-coordinated Ti_5c atom, allowing the hydroxyl group to form a hydrogen bond with a double-coordinated surface O_2c atom. The calculated adsorption energy for M1 is −0.89 eV. In configuration M2, the hydroxyl group donates a proton to the nearest surface O_2c atom at a different row, and then the deprotonated O atom is bonded to a Ti_5c atom. The double bound O atom is not bonded to a Ti_5c atom but forms a hydrogen bond with the dissociated proton. In regard to M3, the hydroxamate is bonded to the TiO₂ surface by the Ti–N bond. The dissociated proton is transferred to the neighboring double bound oxygen; thus two hydroxyl groups can exist in configuration M3. Furthermore, we find that the protons of two hydroxyl groups remain hydrogen-bonded to the surface O_2c atoms, with distances d(O_2c–H) of 1.582 Å and 1.752 Å, stabilizing the structure and producing an adsorption energy of −0.68 eV.

Fig. 1 The different adsorption configurations of the hydroxamate anchor.

Table 1 The calculated adsorption energies (in eV) and corresponding bond lengths (in Å)

	M1	M2	M3	B1	B2	B3
Eads	−0.89	−0.81	−0.68	−0.67	−0.53	−0.89
d(Ti–O)1	2.093	1.920	—	1.968	2.019	2.086
d(Ti–O)2	—	—	—	1.837	—	1.959
d(Ti–N)	—	—	2.284	—	2.160	—
d(O2c–H)1	1.729	1.509	1.752	—	2.373	—
d(O2c–H)2	—	—	1.582	—	—	—

---

Configuration B1 is a doubly deprotonated structure, with the double bound O atom and the deprotonated O atom coordinated to two different Ti_5c atoms, which leads to an adsorption energy of −0.67 eV. The dissociated protons in B1 are, respectively, placed on nearby O_2c atoms. Configuration B2 is also characterized by the dissociation of the N–H bond, with the dissociated proton placed on the nearest O_2c, which belongs to a different row. In configuration B2, the double bound O atom and the deprotonated N atom are coordinated to different Ti_5c atoms, forming the bidentate bridging geometry. For this case, d(O_2c–H) is about 2.4 Å, indicating that the hydroxyl is involved neither in the surface bonding to the Ti_5c atom nor in the formation of hydrogen bond to the surface O_2c atom. Also, since it provides the worst adsorption energy, −0.53 eV, we will not discuss this configuration in the following. As for the last configuration, B3, differently from the cases of B1 and B2, the dissociated proton comes from the hydroxyl group, with the double bound O atom and deprotonated O atom coordinated to different Ti_5c atoms; see Fig. 1. Its calculated adsorption energy is −0.89 eV.

In order to explore the dynamics stability for configurations M1, M2, M3, B1, and B3, molecular dynamics simulations of these configurations were performed at 300 K. We present the time evolution of anchor bond lengths for some representative configurations in Fig. 2. First we note that all the Ti–O bonds in M1, M2, and B1 are found to be stable, oscillating around their equilibrium values during the entire 4 ps trajectory. Conversely, the formed hydrogen bonds in M1 and M2 cannot maintain their stability during the trajectory. For example, in M1, the H–O bond vibrates around ∼1.8 Å with a small amplitude of approximately 0.3 Å during the first 1.9 ps, then the H atom moves with a large amplitude (about 2–4 Å) relative to the O atom at the later 2.1 ps. We also verified that the molecule rotates and bends largely in the M1 and M2 cases. A similar behaviour occurs for configuration M3, as shown in Fig. S3.† In the case of B3, one of its Ti–O bonds does not remain stable with respect to the other after the 3 ps time propagation. Overall, B1 is the most kinetically stable configuration concerning the hydroxamate anchoring on the TiO₂ surface.

Fig. 2 Evolution of anchoring bond lengths in configurations M1, M2, B1, and B3.

The vibrational spectra of the adsorbed (configuration B1) and free hydroxamic acid have been investigated at the DFT/B3LYP/6-31G(d) level of theory with the Gaussian 09.⁸ The corresponding results are listed in Fig. S4 and Table S1.† Previously, McQuillan et al. conducted an infrared spectroscopic study of acetohydroxamate acid adsorbed on titanium dioxide.⁹ Noting that only the anchor group is shared between the acetohydroxamate acid in McQuillan's study⁹ and the molecule of the present work, only those vibrations related to the anchor group have been considered. According to our calculated results, the DFT-calculated vibrational frequencies for configuration B1 generally agree with the experimental data, taking into account that discrepancies are expected due to differences between the substituent of hydroxamate, regarding theory (pyridine) and experiment (methyl). In particular, for the free anchor we observe a strong peak at about 1746 cm⁻¹, which can be assigned to the C=O stretching mode, although it is weakened and further redshifted to 1651 cm⁻¹ upon adsorption onto TiO₂ surface. This redshift is consistent with the experimental observation,⁹ indicating that carbonyl may be involved in the binding to surface Ti_5c. Secondly, as shown in Fig. S4c,† there is a prominent peak at 1425 cm⁻¹, which is ascribed to the N–H and O–H bending modes, and it is shifted to the lower wavenumber of 1355 cm⁻¹ upon adsorption, which can be assigned to the C–N and C=O as well as C–C stretching modes. Furthermore, a strong peak at around 823 cm⁻¹ is shown in Fig. S4b† but is almost absent for Fig. S4c.† This mode can be assigned to the O_2c–H bending, which is probably related to the dissociation of N–H and O–H bonds and the protons placed on the surface O_2c atoms during the adsorption process. This similar behaviour has also occurred in the experiment, although wavenumbers below 1000 cm⁻¹ are not reported.

The densities of states of the combined adsorbate/TiO₂ system were obtained by the semiempirical Extended-Hückel (EH) molecular orbital method. The detailed description of this methodology can be found in the ESI† and elsewhere.¹⁰ Fig. 3 presents the total and projected densities of states (DOS) of B1 calculated by the EH method, as compared to the DOS of the bare TiO₂ nanostructure. The EH method predicts a band gap of about 4 eV for the (TiO₂)₃₂ model, which is slightly larger than the experimental value of 3.4 eV for the 2.4 nm particle.^10a In general, the band gap for small TiO₂ clusters is overestimated with respect to the larger systems.^10b The filled red curve represents the projected DOS onto electronic states of the adsorbate. It is shown that there are several virtual orbitals of the adsorbate, such as LUMO, LUMO + 1, and LUMO + 2, positioned within the TiO₂ conduction band in the range from −11–−6 eV. These virtual molecular orbitals overlap in energy with electronic states of the TiO₂ conduction band, which is suitable for interfacial electron injection. We show, in Fig. S5,† some representative lowest unoccupied molecular orbitals. For comparison, the corresponding Kohn–Sham (KS) orbitals obtained at the DFT/B3LYP/6-31G(d) level are also included in Fig. S5.† The semi-empirical calculations for the molecular orbitals are in excellent agreement with the corresponding ab initio calculations. In addition, both LUMO and LUMO + 2 have significant electron populations on the hydroxamate anchor. Conversely, for the LUMO + 1, there is no electron occupation on the anchor group, which accounts for the slower interfacial electron injection from this orbital. Although several electronic states of adsorbate can be photo-excited, we concentrate our description on the LUMO orbital as the initial state for the following electron wavepacket propagation.

Fig. 3 Total and projected densities of states (DOS) calculated by the extended Hückel method for B1 and a bare TiO₂ nanostructure.

Next we analyse the interfacial electron transfer (IET) by means of quantum dynamics simulation. The quantum mechanical part of the method is based on a tight binding model Hamiltonian originating from the EH method. First of all, it has to be recognized that the presence of the hole influences the electron injection, since the electron–hole coupling could delay the electron transfer. But in most instances, the hole remains confined to the donor part of the adsorbate while the electron is injected. Therefore, for ultrafast interfacial electron transfer processes such as those studied herein, it is a good approximation to assume a static hole and just propagate the electronic wavepacket.^10b The Coulomb coupling of the photo-excited electron and hole pair is described within the time-dependent Hartree approximation. The procedure for quantum propagation of the photo-excited electron is summarized in the ESI.† P(t) is the survival probability for the photo-excited electron to be in the adsorbate molecule at time t after excitation of the system.

Fig. 4 shows the results for the survival probability P(t) for M1, M2, and B1. Starting from the LUMO, it can be seen that the electron gradually delocalizes and is injected into the semiconductor region within the 200 fs time scale. Specifically, for B1, the electron is located at the adsorbate at the initial time (t = 0), then it begins to be rapidly injected after around t = 22 fs and finally evolves into stable oscillations after t = 93 fs. We show the representative snapshots of the time-dependent charge distribution in Fig. S6.† The IET curve for B1 can be well fitted by a decaying exponential function: P(t) = 1.763 exp(−(t − 22)/30.125) + 0.153 for t ≥ 22 fs. For B1, we find that the electron undergoes an ultrafast electron transfer from the adsorbate LUMO to the TiO₂ conduction band within a time scale of 53 fs, with 31 fs decay time after a 22 fs delay. The ultrafast electron injection is more evident if we compare the electron density distribution for t = 0 fs with t = 53 fs, in Fig. S6†. Following the same analysis, we find that M1 has a similar IET time scale of 53 fs. Meanwhile, M2 has a slower electron injection time scale of 92 fs compared with B1 and M1, indicating that configurations B1 and M1 facilitate a faster electron injection process. In addition, the small survival population P(t) that remains for t > 100 fs can be ascribed to finite-size effects produced by the limited (TiO₂)₃₂ cluster model.

Fig. 4 Survival probability curves for electron injection starting from the adsorbate LUMO orbital of hydroxamate.

In conclusion, our theoretical results indicate that the bidentate bridging mode with the double-bonded O atom and deprotonated O atom coordinated to different Ti_5c atoms is the most dynamically stable configuration, and that the corresponding vibrational spectrum agrees with results of infrared spectroscopy experiment. Interfacial electron injection simulations suggest that this type of configuration yields an ultrafast electron injection, with a time scale of 53 fs. Overall, this work highlights the optimal adsorption mode for the hydroxamic anchor, which is expected to provide valuable hints into the design of an efficient anchor group for DSSC application.

Acknowledgements

This work was supported by the Natural Science Foundation of China (Grant no. 21003057, 21303068 and 21173096), the State Key Development Program for Basic Research of China (Grant no. 2013CB834801) and Specialized Research Fund for the Doctoral Program of Higher Education (Grant no. 20110061110018).

Notes and references

1. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737.
2. A. Yella, H. W. Lee, H. N. Tsao, C. Y. Yi and A. K. Chandiran, Science, 2011, 334, 1203.
3. (a) B. Bozic-Weber, E. C. Constable, S. O. Furer, C. E. Housecroft, L. J. Troxler and J. A. Zampese, Chem. Commun., 2013, 49, 7222; (b) K. R. Mulhern, A. Orchard, D. F. Watson and M. R. Detty, Langmuir, 2012, 28, 7071.
4. J. Warnan, L. Favereau, Y. Pellegrin, E. Blart, D. Jacquemin and F. A. Odobel, J. Photochem. Photobiol., A, 2011, 226, 9.
5. (a) T. P. Brewster, S. J. Konezny, S. W. Sheehan, L. A. Martini, C. A. Schmuttenmaer, V. S. Batista and R. H. Crabtree, Inorg. Chem., 2013, 52, 6752; (b) W. R. McNamara, R. L. Milot, H.-E. Song, R. C. Snoeberger III, V. S. Batista, C. A. Schmuttenmaer, G. W. Brudvig and R. H. Crabtree, Energy Environ. Sci., 2010, 3, 917.
6. (a) G. Kresse and J. Furthmüllerb, Comput. Mater. Sci., 1996, 6, 15; (b) G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251; (c) G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558; (d) G. Kresse and J. Furthmüllerb, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
7. (a) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671; (b) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978.
8. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2009.
9. J. Yang, P. J. Bremer, L. L. Lamout and A. J. McQuillan, Langmuir, 2006, 22, 10109.
10. (a) L. G. C. Rego and V. S. Batista, J. Am. Chem. Soc., 2003, 125, 7989; (b) D. A. Hoff, R. Silva and L. G. C Rego, J. Phys. Chem. C, 2011, 115, 15617.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures and table as well as relevant theoretical backgrounds for the simulation of quantum dynamics. See DOI: 10.1039/c4ra01116c

---