The mechanism of water–isopropanol exchange in cement pastes evidenced by NMR relaxometry

Abstract

¹H nuclear magnetic resonance (NMR) relaxometry shows that arresting the hydration of cement paste by isopropanol exchange does not involve simple replacement of the pore water with isopropanol. Isopropanol fills capillary voids. It removes and replaces the water in the calcium-silicate-hydrate (C-S-H) interhydrate pores. In the C-S-H gel pores, the isopropanol draws water out, but does not replace it to the same extent. The exchange has only a minor impact on C-S-H interlayer water. The connectivity of the interlayer-gel network and interhydrate pores and capillary voids is evidenced by proton–deuteron chemical exchange in the C-S-H pore structure which is observed experimentally for the first time. Isopropanol also reveals the presence of large capillary voids that are not detected in samples saturated with water.

---

1. Introduction

Arresting the growth of calcium-silicate-hydrate (C-S-H) and other hydration products both effectively and efficiently is a precursor to many studies seeking to understand the properties and morphology of cement pastes.^1,2 Removing the free water available for hydration processes is an important route for achieving this. Numerous studies have therefore addressed the structural and chemical changes which occur during different drying (e.g. oven, vacuum, freeze) and solvent exchange procedures.^3,4 They have been reviewed by Zhang and Scherer.² The method of exchanging water with organic solvents such as methanol, isopropanol and acetone has been found to be very effective and relatively quick in stopping hydration.⁵ However, the influence of the solvent on the physical and chemical properties of the paste can be substantial and may cause irreversible damage to the microstructure.^6–8 The predominant conclusion is that isopropanol causes the least damage as evidenced by measurable macroscopic shrinkage and therefore isopropanol exchange is often the method of choice for arresting the hydration of cement.^5,6,9,10

The drying of either water or solvent can modify the structure of even well matured pastes due to the loss of water from the different nano-scale pore reservoirs of the hydrate products.^3,4 Therefore, a key limitation of almost all the prior studies of solvent exchange is that the cement samples have been characterised not only after the water, but also the solvent, was removed.^4,8,11 The structure is not characterised in the presence of either the water or the solvent in “never-dried” conditions. Studying “as-prepared” samples is necessary to understand the influence of the exchange per se on the nano-scale morphology. However, there are only very limited reports of such experiments.^7,9 In the case of morphology, these experiments have been made at the macroscopic level by measurement of expansion/contraction and solvent diffusion (weight loss).

Nuclear Magnetic Resonance (NMR) relaxometry is one of the most powerful techniques to study porous materials.^12,13 By monitoring differences in the spin–spin, T₂, and spin–lattice, T₁, relaxation times of liquids within pores it is possible to obtain direct information about the pore size distribution and pore connectivity in porous media in general and cements and mortars in particular.^14–17 A key advantage of NMR relaxometry over alternative methods for the study of cements is that the pore water is itself the direct probe of the confining nanostructure. There is no requirement to dry or otherwise prepare the sample. In the case of cement pastes, ¹H NMR of water reveals the hierarchy of water combined in nano-crystallites (Ca(OH)₂ and ettringite in the approximate mass ratio 4 to 1 (ref. 18)), calcium-silicate-hydrate (C-S-H) interlayer space and gel pore water, interhydrate pore water and capillary pore reservoirs shown schematically in Fig. 1.

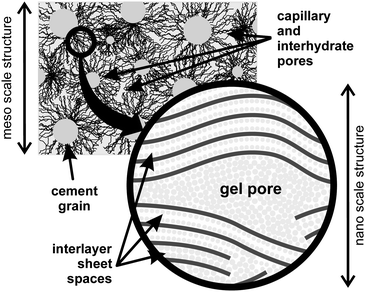Fig. 1 The schematic structure of the calcium-silicate-hydrate (C-S-H) on the meso- and nano-scale (white cement paste).

NMR has been used to study kinetics and microstructural consequences of the drying and rewetting of the cement pastes and mortars.^19–21 Isopropanol drying, that is isopropanol exchange followed by its removal by slow oven drying, has been used in conjunction with NMR to conclude that oven drying has significantly more destructive influence on mortar microstructure than isopropanol drying.²² The direct effect of the isopropanol on the microstructure, without solvent removal has not been investigated.

This contribution reports a study of the mechanism of isopropanol drying in cement pastes and of the changes to microstructure that it induces. The focus is an analysis of the filled porosity directly through the exchange solvent using ¹H relaxometry. Without drying the sample, the reversibility of the process is investigated. Measurements have been made on samples prepared with both H₂O and D₂O and exchanged with both isopropanol and partially deuterated isopropanol.

This study finds that isopropanol acts as a drying agent by removing and selectively replacing water molecules in the interhydrate and capillary network. It also draws out the gel pore water but does not fully replace it in these spaces. It has more minor impact on the C-S-H interlayer water. There is however contact between the highly confined water in the interlayers and the network of larger pores as evidenced by the observation of the proton–deuteron chemical exchange between the liquids.

2. Materials and methods

Cement pastes were prepared by mixing white Portland cement powder with distilled water in the water to cement (w/c) mass ratio 0.46 (except where stated otherwise) using an electric blender. The ratio was adjusted to 0.51 when the cement powder was mixed with deuterated water (Sigma-Aldrich) to account for the larger atomic mass of D₂O compared to H₂O. The mixing was carried out in cylindrical polyethylene beakers in three steps: (i) mixing for 3 minutes with the rotor speed 500 rpm, (ii) 2 minutes of resting and (iii) mixing for 2 minutes at 2000 rpm. Directly after mixing, the paste was transferred to polyethylene moulds 8 mm in diameter and 20 mm long. Special care was taken to avoid entrapping any air bubbles. The moulds were transferred to containers filled with lime water, air sealed and left to allow the cement paste to harden. After 24 h the cement paste cylinders were removed from the moulds and transferred to small glass bottles filled with lime water (ca. 1 part of lime water to 15 parts of sample) in order to continue curing underwater. In the case of deuterated samples, D₂O was used in all curing steps (>99.9% purity). Samples were cured for 50 days at 21 °C. Underwater curing caused the effective w/c ratio to increase to >0.5 as evidenced by recording the mass of selected samples dried above the 1000 °C.

Post-curing, some samples were crushed into millimetre sized granules and solvent exchange was carried out in glass bottles for 72 h. Reagent grade isopropanol (Sigma-Aldrich) was used as the primary exchange solvent. Exchange was performed over 3 wash cycles of 24 hours each using fresh solvent for each cycle. The solvent to sample volume ratio was at least 20 : 1. Bottles were constantly rolled to assure homogeneity of the exchange fluid. To test reversibility, a second exchange was carried out using deionised water (Sigma-Aldrich) following the same procedure. Further, to ensure that three washes was sufficient for full exchange, some measurements were carried out after as many as five washes. The results were substantially the same.

As well as regular isopropanol, (CH₃)₂CHOH, partially deuterated isopropanol with the composition (CH₃)₂CDOD was also used. The level of deuteration was greater than 98%. The specific isotopic substitution was chosen to negate the impact on ¹H NMR measurements of H–D exchange between the solvent and pastes prepared with D₂O. Isopropanol hydroxyl hydrogens are expected to exchange easily with deuterons in D₂O. A ¹H NMR spectrum of regular isopropanol (0.2%) in D₂O was acquired at 500 MHz in order to assess whether isopropanol methyl and, in particular, C2 hydrogens also exchange. The spectrum is shown in Fig. 2. The methyl doublet at 1.05 ppm has a total intensity 6 times that of the 7 line multiplet of the C2 hydrogen at 3.9 ppm. This implies that if hydrogen at these two sites exchange with deuterated water, then they exchange directly in proportion to their ¹H number density. The H₂O/HDO line at 4.7 ppm is 1.67 times as intense as that of the C2 hydrogen. One unit of this intensity arises from the exchanged OH–D₂O. The remaining 0.67 is attributed to hydrogen impurity in the D₂O. An intensity of 0.67 is less than would be expected based on the minimum stated purity of the D₂O (99.9%). This is strong evidence that no measurable fraction of methyl or C2 hydrogen exchanges. Therefore by using (CH₃)₂CDOD, we eliminate concern about D associated with water-of-mixing contaminating the isopropanol ¹H NMR signal. Of course, (CH₃)₂CHOD would have been equally useful, but was not available.

Fig. 2 The ¹H high resolution spectrum of 0.2% (CH₃)₂CHOH in D₂O.

Relaxation NMR measurements were performed using a ¹H NMR Kea benchtop spectrometer operating at 20 MHz (Magritek, New Zealand). The Carr–Purcell–Meiboom–Gill (CPMG) pulse sequence²³ was applied to record a train of logarithmically spaced echoes in the range of 26 μs to 1.5 s (typically 512 echoes, 32 points per echo with a sampling rate 1 MHz). The lower time limit was governed by duration of the pulse (P₉₀ = 5 μs) and dead time of the spectrometer (10 μs). Up to 1024 averages were acquired with a recycling time of 2.5 s.

The crystalline solid fraction of the distribution was measured using the solid (or quadrature) echo experiment.²⁴ Two 90° radio frequency pulses were applied to refocus static dipolar interactions. The signal was recorded as a function of the spacing, τ, between the pulses in the range 10 and 35 μs. The solid echo and mobile water amplitudes as a function of τ were back extrapolated to zero time thus providing a good estimate of the fraction of water combined in Ca(OH)₂ and ettringite as previously described.²⁵

In justification of these parameters, we note that the maximum pore water T₁ values encountered are of the order of 0.1 s, with the overwhelming majority of the pore water volume having T₁ less than 0.01 s. The T₁ of the crystalline solids is of the order of 1 s at high frequency, but less at frequencies comparable to that used here, 20 MHz.^26,27 We measured 290 ± 30 ms. The isopropanol T₁ in large pores is ≈300 to 400 ms; comparable to, and therefore hard to distinguish from, the solids. That the method is quantitative was previously demonstrated by cross checking against thermal gravimetric analysis and X-ray diffraction.¹⁸

Measurements were made on two sets of samples. The results were the same within experimental error. For the repeats, that are the samples reported here, the ignited mass of samples was additionally measured by controlled drying to temperatures in excess of 1000 °C so as to allow more quantitative comparison of results. Unfortunately, insufficient (CH₃)₂CDOD was available for one of the seven experimental repeats, so, for this case alone, normalisation was performed by cross reference to a measurement of normal paste.

The exponential decay of the CPMG echo train intensity provides an estimate of the T₂ relaxation time. This in turn relates to pore size through the fast diffusion model of relaxation.^28,29 Hence, inverse Laplace transform (ILT) of the decay yields the pore size distribution. The inverse Laplace transforms were carried out on echo train decays using the algorithm proposed by Venkataramanan et al.³⁰ In the case of deuterated samples, the signal to noise ratio of the data was sometimes insufficient to properly resolve all the distribution features. In these cases, multiple exponential fitting using the relaxation times known from protonated material was used instead.

There are three aspects to consider with respect to accuracy and reproducibility. The first relates to the ILT. The output of the ILT routine depends to a limited extent on the input parameters, specifically the regularisation parameter introduced by Venkataramanan et al.³⁰ If it is too small, then the output spectrum is highly broadened and individual peaks merge together. If it is too big then the spectrum breaks up into a very large number of individual peaks. Venkataramanan et al. provide a quantitative procedure for optimising this parameter that has been extensively tested on synthetic data. So long as the peaks have not merged the integral intensity (i.e. area) of peaks is essentially independent of the regularisation although the height and width measured separately do change. It is therefore the area that is used as “intensity” in this and our earlier¹⁸ work. A related effect is “pearling” whereby two closely neighbouring peaks in a spectrum tend to move towards each other leading to systematic error in the measured T₂.³¹ For this reason, far greater emphasis is placed on the peak intensities than on the T₂ values in the analysis.

In cases where multi-exponential fitting is used, fitting with both intensity and decay constants allowed to float is highly dependent on the initial guess values. This is not a problem when the decay constants are constrained, as here: the algorithm generates reproducible intensities. However, the intensities do depend of the T₂ constraints chosen. As stated, values obtained with ILT from fully protonated material analysis are used.

The second issue arises from measurement uncertainty in the echo data. We have previously made multiple repeats of the NMR measurement on the same sample. We have also analysed data to which synthetic noise has been added. In particular, in order to use the ILT we seek an NMR signal-to-noise ratio in excess of 400. Considering both analysis issues together, the standard deviation of multiple analyses is ±1% absolute in the peak intensities.

The third source of uncertainty is variability arising from different samples. Since the samples are necessarily small, they are affected by inhomogeneity of mixing, by slight differences in temperature during curing, and especially by surface drying during the short times that they are exposed to air. To mitigate against the first two of these, all but one of the samples reported are from the same batch of cement and were cured together. To mitigate against the last, the samples were exposed for as little time as possible.

The combined uncertainty from all sources is estimated from repeated measurements of the 6 pairs of duplicated samples, and, for protonated samples, direct comparison of ILT and multi-exponential fitting analyses. It is ±3% absolute in peak intensity in the worst cases.

3. Results and discussion

3.1 Protonated cement paste

Fig. 3a and the first line of Table 1 show the T₂ distribution in as prepared paste made with H₂O. The distribution shows the expected peaks corresponding to crystalline solid (Ca(OH)₂ and ettringite) from the quadrature echo experiment at 10 μs with a relative intensity of 24%; to C-S-H interlayer water at 90 μs, 21%; to gel pore water at 300 μs, 44%; to interhydrate pore water at 1.5 ms, 8%; and to capillary pore water at higher T₂ values totaling 3%. These intensities and T₂ values are consistent with previously reported results for a sample cured sealed with w/c = 0.48 (ref. 18) and a sample cured underwater with w/c = 0.40.³²

Fig. 3 The distribution graph of the T₂ relaxation times for cement paste. The as-prepared sample cured under H₂O, (a); exchanged with isopropanol (b); and exchanged back with H₂O (c).

Table 1 ¹H signal intensities recorded for water in different environments of as prepared and solvent exchanged pastes. The intensities are normalised to ignited sample mass and such that 100% is the total signal for the normal paste

Sample	Non-evaporable water	Evaporable water				Total signal intensity%
	Nano-crystalline solids	C-S-H interlayer	C-S-H gel pore	Interhydrate spaces	Capillary pores
As prepared paste	24	21	44	8	3	100
+ IPA	24	18	16	11	28	97
+ IPA + H2O	21	18	37	10	11	97
Paste prepared with D2O	1	1	3	0	2	7
+ H2O	21	18	40	9	10	98
+ IPA(D)	2	11		6	24	43
+ IPA	18	11	14	13	15	71

---

The distribution for an isopropanol exchanged sample, Fig. 3b and the second line of Table 1 is compared to the as prepared paste. The intensities are shown relative to it, per gram of anhydrous cement. The first observation is that the overall signal intensity is scarcely changed at 97%. At first site, this is unsurprising. The ¹H density of water and isopropanol are 0.111N_A and 0.105N_A cm⁻³ respectively. Hence, for an equal volume exchange of all the evaporable liquid (approximately 76% of the total water), one expects a 4.1% decrease in signal. However, a more careful examination of the data reveals that the fraction of capillary and interhydrate pore liquid has increased dramatically, from 11% of the total to 39% whereas the C-S-H interlayer and gel pore fraction has decreased from 65% of the total to 34% with most of this change being in the gel pore fraction. The signal from the crystalline solid is unchanged.

The easiest explanation is that isopropanol exchange damages the pore network resulting in an increase in the number of large pores and a decrease in the number of small pores. That this is unlikely to be a correct explanation is revealed by an experiment to investigate the reversibility of the isopropanol exchange.

The third line of Table 1 and Fig. 3c report results obtained when an as prepared sample is first exchanged with isopropanol and then exchanged back with water. Comparing line 3 of the table with lines 1 and 2, it is seen that the changes in line 2 are substantially reversed. The critical gel, interhydrate and capillary liquid signal intensities are all intermediate between the earlier values. We cannot explain why the T₂ associated with the interlayer component is slightly increased save that the ILT algorithm is known to be susceptible to “pearling”.

A better explanation leads to two conclusions. The first is that isopropanol invades large capillary pores that are inaccessible to water. There is considerable previous NMR¹⁸ and other³³ evidence that larger capillary pores are empty in as prepared material, even when the sample is cured underwater. The curing water cannot cross the very low permeability paste sufficiently quickly to maintain full saturation of the capillary porosity created by chemical shrinkage as hydration proceeds. The resultant reduced internal relative humidity of the paste ensures self desiccation of larger pores. For instance, the Kelvin–Laplace radius for water at 98% RH is 53 nm. That isopropanol can enter these larger pores is suggested by the very much smaller contact angle of isopropanol (at least with SiO₂) compared to water.³⁴ It might be considered that the large pores contain a mixture of isopropanol and water. However, it should be remembered that the exchange isopropanol is at least 20 times the sample volume, while the mobile water is only about 44% of the sample volume. Hence the dilution is less than 2.2%. Moreover the system is washed 3 times leading to further dilution: circa 10 ppm.

The combined interhydrate and capillary pore signal intensity of the exchanged sample is consistent with this explanation. If it is assumed that 0.38 g of water are required to hydrate 1 g of cement³⁵ then, given the w/c ratio at mixing (0.46), 0.08 cm³ of water are available for interhydrate and capillary pores at full hydration. Further, the sample undergoes chemical shrinkage of about 0.075 cm³ g⁻¹ of anhydrous cement.¹⁸ This creates voidage that is accessible to isopropanol. Hence, in an exchanged sample, the capillary liquid occupies 0.155 cm³, or 29% of the total liquid volume, at full hydration. At a more realistic value of degree of hydration (85% (ref. 18)) the expected capillary liquid fraction is 38%. A similar dilution argument applies for reverse exchange. However, in this case, what is now nearly pure water cannot enter large pores due to the Kelvin–Laplace law. They are once again left empty.

The second conclusion is that isopropanol dries gel pores by drawing water out of the C-S-H network, without fully invading and replacing it. The evidence is the hugely reduced gel pore signal in line 2 compared to line 1 in Table 1. This is presumably because the gel pore entrances are small, isopropanol has a larger molecular size than water and isopropanol is very hygroscopic. The interlayer signal is reduced to a much lesser extent in the isopropanol exchange sample compared to the as prepared material. This suggests that isopropanol does not replace water in the interlayer spaces. It seems unreasonable to assume that the isopropanol has exchanged these (smaller) sites if it cannot exchange the larger gel pores, an assumption verified in the experiments using deuterated cement paste discussed below.

A further observation of these first experiments is that the T₂ associated with the gel-pore liquid is somewhat greater in the exchanged sample than in the as prepared sample. There are two possible reasons for this. First, the surface relaxation time of isopropanol molecules in cement, that controls the pore liquid T₂, may be greater than that of water molecules. One reason is that the average distance of closest approach of an isopropanol ¹H may be greater than that of a water ¹H. A second reason may be that there is a distribution of gel pore sizes. They are all empty of water, but the isopropanol only re-invades the larger of them. Since the observed T₂ varies with pore size, the bias to larger pores increases the mean gel pore liquid T₂. The former explanation is preferred since a similar fractional increase is seen for the other mobile reservoirs.

3.2 Deuterated cement paste

The experiments so far reported cannot distinguish between water and isopropanol molecules. The fourth line of Table 1 shows that negligible signal is recorded from a paste made with, and cured under, D₂O. The signal that does appear is almost certainly due to H–D exchange occurring during the mixing and curing process.

If a deuterated sample is subsequently exchanged with H₂O, then all the original peaks occur as shown by line 5 of the table. The signals recorded for the crystalline solid, C-S-H interlayer and gel porosity are almost exactly as in line 1. In the case of the solid, this is somewhat surprising. It suggests that the solid is nanocrystalline with a very high specific surface area in close contact with the porosity. Otherwise, such H–D exchange would seem unlikely to occur. In the case of the interhydrate and capillary pores, the signal is somewhat larger than originally seen. There is no obvious reason for this. It has been reported elsewhere that cement mixed with D₂O hydrates more slowly than that cured with H₂O.³⁶ It is possible that this results in more numerous, smaller, pores that water can invade more easily. However, there is minimal evidence for this in the measured T₂ values, that, if anything are larger. It may be that a more slowly developing capillary porosity is less susceptible to self desiccation in under-deuterated-water cured paste and that subsequently the D₂O can readily exchange by H–D exchange, if not full molecular transport.

The sixth line of the table reports the results of a D₂O mixed and cured paste exchanged with partially deuterated isopropanol. Recall, that the isopropanol is deuterated at all sites likely to undergo H–D exchange with D₂O but is otherwise protonated so that a ¹H NMR signal can be measured from it. The first observation is that minimal signal is measured from the crystalline solid (2%). As expected, and unlike H₂O, there is no significant H–D exchange taking place from the deuterated isopropanol. The second observation is the modest signal from the C-S-H gel (11%). It is almost impossible to divide this 11% between C-S-H interlayer and gel pore signal. We surmise that it comes from isopropanol molecules able to invade the largest gel pores. This conclusion agrees with the interpretation of the data in line 2. If 11% is multiplied by 8/6 to account for the partial deuteration, then this becomes 15%, close to the corresponding entry in line 2, 16%. A third observation is that a large signal is seen from the capillary network, totaling 30%. Multiplying this by 8/6 yields a 40% signal associated with large pores compared to 39% in the regular paste exchanged with regular isopropanol.

Finally, we report in line seven, the results of exchanging the deuterated paste with regular isopropanol. There is now the opportunity for both isopropanol–water molecular exchange and H–D chemical exchange. We see evidence of both. There are strong signals from all environments including the solid and C-S-H interlayer (indicating chemical exchange) and all the pore reservoirs. However, overall, the signal intensities are consistently about 3/4 as intense as those observed in protonated paste exchanged with protonated isopropanol suggesting that perhaps the H–D exchange is not complete.

3.3 Time dependency of exchange

As a final note of caution, we present evidence that full equilibration of the exchange process is very slow in larger paste samples. The work presented so far was carried out on millimetre sized pieces of paste and exchange occurred in 1–3 days. Fig. 4 shows the change in signal fraction attributed to liquid in the interlayer and gel pores combined and the capillary pores during isopropanol exchange for a centimetre sized cylinder mixed at w/c ratio 0.4. The capillary component increases from about 3 to 20% of the water fraction showing that the capillary pores are not filled initially even though the sample is cured underwater.³³ The revealed capillary porosity is comparable to expectation. The combined interlayer and gel fraction decreases from about 70 to 27% showing as before water drawn out, but not replaced, in comparable fraction. The surprise is the time constants involved. Based on the dotted line exponential fits to the data, these are 1.5 days to draw water out from the gel, 4 days to fill the capillaries, and 25 days to equilibrate water in the interlayer spaces and on the gel surface that appears interlayer-like in partially dried material.³² It is evident that full equilibration takes of the order of 1 to 2 months.

Fig. 4 The decrease of the combined gel and interlayer pore signal (squares) and increase of the capillary pore signal (circles) during isopropanol exchange of a large sample. The dotted lines are exponential fits to the data, the upper one having two components.

4. Conclusions

The study shows that, during arrestation of hydration in cement pastes by isopropanol exchange, isopropanol invades empty capillary pores. Isopropanol draws water out of C-S-H gel pores and to a much lesser extent interlayer spaces. However, isopropanol does not enter the C-S-H to the same extent. It only invades the more accessible (larger?) gel pores.

The work also shows that water confined in the interlayer-gel network chemically exchanges deuterons and protons with liquid residing in the larger interhydrate and capillary pore network. This demonstrate experimentally for the first time the interconnectivity of interlayers and gel pores with large interhydrate pores and capillary voids.

Water–isopropanol exchange reveals the presence of large capillary pores which water is unable to fill but which are fully accessible to isopropanol. This confirms earlier explanations as to why NMR porosimetry with water is unable to detect large pores – they are empty.

Acknowledgements

We thank Goss Scientific Instruments Ltd. for providing the partially deuterated isopropanol; Aalborg Portland for providing white cement; and Patrik Galvosas for making available ILT software. This work was funded by the European Commission (grant no. FP7/2007-2013-264448) and the UK Engineering and Physical Sciences Research Council (grant no. EP/H033343/1).

Notes and references

1. J. W. Bullard, H. M. Jennings, R. A. Livingston, A. Nonat, G. W. Scherer, J. S. Schweitzer, K. L. Scrivener and J. J. Thomas, Cem. Concr. Res., 2011, 41, 1208–1223.
2. J. Zhang and G. W. Scherer, Cem. Concr. Res., 2011, 41, 1024–1036.
3. A. Korpa and R. Trettin, Cem. Concr. Res., 2006, 36, 634–649.
4. N. C. Collier, J. H. Sharp, N. B. Milestone, J. Hill and I. H. Godfrey, Cem. Concr. Res., 2008, 38, 737–744.
5. L. Konecny and S. J. Naqvi, Cem. Concr. Res., 1993, 23, 1223–1228.
6. J. J. Beaudoin, P. Gu, J. Marchand, B. Tamtsia, R. E. Myers and Z. Liu, Adv. Cem. Based Mater., 1998, 8, 56–65.
7. D. C. Hughes, Cem. Concr. Res., 1988, 18, 321–324.
8. R. F. Feldman and J. J. Beaudoin, Cem. Concr. Res., 1991, 21, 297–308.
9. J. J. Beaudoin, B. Tamtsia, J. Marchand and H. R. Myers, Cem. Concr. Res., 2000, 30, 359–370.
10. R. F. Feldman, Cem. Concr. Res., 1987, 17, 602–612.
11. E. Knapen, O. Cizer, K. Van Balen and D. Van Gemert, Construct. Build. Mater., 2009, 23, 3431–3438.
12. R. Kimmich, NMR: Tomography, Diffusometry, Relaxometry, Springer, 1st edn, 2001.
13. Y.-Q. Song, New J. Phys., 2012, 14, 055017.
14. R. Blinc, M. Burgar, G. Lahajnar, M. Rozmarin, V. Rutar, I. Kocuvan and J. Ursic, J. Am. Ceram. Soc., 1978, 61, 35–37.
15. K. S. Mendelson, W. P. Halperin, J.-Y. Jehng and Y.-Q. Song, Magn. Reson. Imaging, 1994, 12, 207–208.
16. P. J. McDonald, J. P. Korb, J. Mitchell and L. Monteilhet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011409.
17. R. Holly, E. J. Reardon, C. M. Hansson and H. Peemoeller, J. Am. Ceram. Soc., 2007, 90, 570–577.
18. A. C. A. Muller, K. L. Scrivener, A. M. Gajewicz and P. J. McDonald, J. Phys. Chem. C, 2013, 117, 403–412.
19. R. Valckenborg, L. Pel, K. Hazrati, K. Kopinga and J. Marchand, Mater. Struct., 2001, 34, 599–604.
20. S. D. Beyea, B. J. Balcom, T. W. Bremner, R. L. Armstrong and P. E. Grattan Bellew, J. Am. Ceram. Soc., 2003, 86, 800–805.
21. P. F. Faure, S. Caré, J. Magat and T. Chaussadent, Construct. Build. Mater., 2012, 29, 496–503.
22. L. Pel, K. Hazrati, K. Kopinga and J. Marchand, Magn. Reson. Imaging, 1998, 16, 525–528.
23. S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691.
24. J. G. Powles and J. H. Strange, Proc. Phys. Soc., London, 1963, 82, 6–15.
25. P. J. McDonald, V. Rodin and A. Valori, Cem. Concr. Res., 2010, 40, 1656–1663.
26. L. J. Schreiner, J. C. Mactavish, L. Miljkovic, M. M. Pintar, R. Blinc, G. Lahajnar, D. D. Lasic and L. W. Reeves, J. Am. Ceram. Soc., 1985, 68, 10–16.
27. J. P. Korb, Curr. Opin. Colloid Interface Sci., 2009, 14, 192–202.
28. K. R. Brownstein and C. E. Tarr, J. Magn. Reson., 1977, 26, 17–24.
29. F. D'Orazio, J. C. Tarczon, W. P. Halperin, K. Eguchi and T. Mizusaki, J. Appl. Phys., 1989, 65, 742.
30. L. Venkataramanan, Y.-Q. Song and M. D. Hurlimann, IEEE Trans. Signal Process., 2002, 50, 1017–1026.
31. P. T. Callagan, Translational Dynamics and Magnetic Resonance, Oxford University Press, 2011.
32. A. Muller, K. L. Scrivener, A. M. Gajewicz and P. J. McDonald, Microporous Mesoporous Mater., 2013, 178, 99–103.
33. H. Chen, M. Wyrzykowski, K. Scrivener and P. Lura, Modelling of internal relative humidity in cement pastes at early-ages in 2nd International Conference on Microstructural-related Durability of Cementitious Materials, eds. G. Ye, K. van Breugel, W. Sun and C. Miao, RILEM Publications SARL, 2012, 342–349.
34. H. J. Busscher, G. A. M. Kip, A. van Silfhout and J. Arends, J. Colloid Interface Sci., 1986, 114, 307–313.
35. H. F. W. Taylor, Cement Chemistry, Academic Press, 1990.
36. J. J. Thomas, H. M. Jennings and A. J. Allen, Cem. Concr. Res., 1998, 28, 897–905.

---