An experimental and theoretical study of the kinetics and mechanism of hydroxyl radical reaction with 2-aminopyrimidine†
Kavanal P. Prasanthkumar*a and
Juan Raul Alvarez-Idaboy*b
aDepartment of Chemistry, Government Engineering College, Thrissur 680009, India. E-mail: prasanthkumarkp@gmail.com
bDepartamento de Física y Química Teórica, Facultad de Química, Universidad Nacional Autónoma de México, México D. F., 04510, México. E-mail: jidaboy@unam.mx
First published on 7th March 2014
Abstract
Oxidation of 2-aminopyrimidine (2Apy) by hydroxyl radicals (˙OH) in aqueous medium has been studied using pulse radiolysis coupled to optical absorption and M05-2X/6-311++G(d,p) level DFT calculations aimed at elucidation of the reaction mechanism. The rate constant (k) 2.76 ± 0.06 × 109 M−1 s−1 determined by the pulse radiolysis method for the title reaction at neutral pH reflects a diffusion-controlled process. The maximum absorption wavelength (λmax 330 and 550 nm) of transient(s) remains intact in the pH range 10.5–7. Radical adduct formation (RAF) reactions with N1 (N3 is an identical site), C2, C4 (C6 is an identical site) and C5 as the target atoms, hydrogen transfer (HT) reaction with amino group and single electron transfer (SET) of 2Apy with ˙OH were modelled theoretically. Lowest Gibbs free energy of activation (ΔG≠) in solution, 1.72 kcal mol−1, was calculated for RAF at C5; the computed k value for this process is 2.0 × 109 M−1 s−1 using the transition state theory (TST). The relative yield (87%) of this major product predicted from the computed k value shows excellent agreement with the results of the pulse radiolysis redox titrations. Subsequently, the possibilities for other RAF reactions, HT and SET were ruled out. As an extension to the above work, we have carried out a theoretical survey of the reactivity of ˙OH with 4-aminopyrimidine (4Apy); wherein the RAF at C5 is proposed as the most probable mechanism with a ΔG≠ of 2.15 kcal mol−1.
Introduction
Structural analogues of nucleic acid bases with unusual photo-physical properties and their exploitation with appropriate spectroscopic techniques are very convincing for the study of structure, dynamics, and local conformations of nucleic acids and their interactions with proteins. For example, 2-aminopurine, the structural analogue of natural nucleic acid base adenine, has been extensively used as a fluorescent probe for the study of structural dynamics and charge transfer processes in DNA assemblies.1–4 However, the use of structural analogues for in vivo studies require a special attention mainly because of two reasons, first the photo probe is shined normally by means of high energy near-UV light and secondly such compounds are exposed to various endogenous reactive species such as ˙OH, HOO˙ etc. in living cell. It should be noted that, ˙OH is a prominent oxidizing radical produced either endogenously or by UV and ionizing radiations.Obviously, much intense attention has been devoted on the investigations of ˙OH induced DNA damage.5 However, an exceptional feature in the reaction of ˙OH with nucleic acid components especially for nucleobases are the diffusion controlled rate as demonstrated by in vitro studies; rate constants are typically of the order of 109 M−1 s−1.6 Furthermore, according to prior reports the additions of ˙OH to pyrimidines were observed with substantial regioselectivity.5 These two paradoxical behaviors viz. diffusion controlled rate and regioselectivity should perhaps make the assignment of exact transient ambiguous. Indeed, addressing such experimental behaviors using theoretical modeling with substantial accuracy is quite exigent.
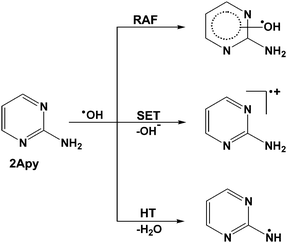
2-Aminopyrimidine (2Apy, Scheme 1) is an interesting pyrimidine derivative with unusual photo-physical properties with regard to natural pyrimidine nucleobases.7 However, the fluorescent properties of this compound have not been explored much for the study of structure and conformations of nucleic acids. 2Apy structural motifs are present in a number of biologically and pharmacologically important groups of compounds.8 2Apy has also been extensively used in synthetic organic/inorganic chemistry for the preparation of versatile compounds/inorganic complexes of manifold applications.9–18 The drug ‘imatinib’ used for the treatment of chronic myeloid leukaemia is a representative example of several marketed drugs which contains 2Apy structural unit.19 The ability of 2Apy and its functionalized compounds to form molecular architectures via strong intermolecular hydrogen bonds and π–π interactions make them suitable for designing supramolecular architectures.20–24
The present work is devoted to the study of the reactions of ˙OH with 2Apy in aqueous medium using pulse radiolysis with optical absorption detection. A trustworthy computational protocol by one author of this article and his co-worker25 designed recently for getting the accurate kinetic data for radical–molecule reactions in solution have been applied for identifying appropriate mechanism (from RAF, SET, and HT) operated in the experiment. Theoretical predictions have been extended further to decipher the reactions of ˙OH with 4-aminopyrimidine (4Apy) in solution.
Experimental and computational details
2-Aminopyrimidine and 2,2′-azinobis(3-ethylbenzthiazoline-6-sulfonate (ABTS2−)) were purchased from Sigma-Aldrich and used for experiments without further purification. All other chemicals used were of good quality available commercially; solutions were prepared using water purified with a Millipore-Milli-Q system.Pulse radiolysis
Pulse radiolysis experiments were carried out using a 7 MeV LINAC at National Centre for Free Radical Research, Pune. Radical reactions were initiated by irradiating high-energy electron pulses of 50 ns duration to sample solutions; more details of this pulse radiolysis with optical absorption detection set-up can be found in the literature.26 The assault of high energy electron radiation on water leads to the formation of highly reactive species viz. ˙OH, hydrated electron (eaq−) and hydrogen atom (H˙) (eqn (1)). The radiolytic yield (or G-value; in μmol J−1) of radical species derived from water radiolysis are also shown in eqn (1) as prefixes.27 An oxidizing environment with full of ˙OH is obtained by scavenging the hydrated electrons and hydrogen atoms by N2O saturation of water (eqn (2) and (3)).| H2O → 0.28 ˙OH, 0.28 eaq−, 0.06H˙ | (1) |
| N2O + eaq− + H2O → N2 + ˙OH + OH− | (2) |
| N2O + H˙ → N2 + ˙OH | (3) |
Thiocyanate dosimetry using N2O saturated aqueous solutions of KSCN (0.01 M) was used to determine the dose per pulse by monitoring the formation of (SCN)2˙− at 480 nm.28 Redox titration method has been used to estimate the quantitative yield of oxidizing transient formed in the reaction of ˙OH and 2Apy with the reductant ABTS2−, a low dose of 8.8 Gy per pulse was used and the formation of ABTS˙− was monitored at 650 nm.29 All reactions were carried out at 298 K.
Quantum chemical calculations
Geometry optimizations and harmonic vibrational frequency analyses of neutral and various open shell species were carried out by means of M05-2X/6-311++G(d,p) level DFT method using the Gaussian 09 suite of program.30 Unrestricted calculations were used for open-shell systems, the spin contamination values for the open shell systems were very close to zero with the expectation value (〈Ŝ2〉) of 0.75. The M05-2X is a hybrid meta exchange-correlation functional mainly used for the study of thermochemistry, kinetics and non-covalent interactions as proposed by its developers.31 This functional has been successfully used for kinetic calculations32–37 and is also the best performing functional for the determinations of reaction energies involving free radicals.38 The effects of aqueous environment in the calculations were considered using the solvation model density (SMD) method of Truhlar and coworkers39 implemented in the Gaussian program.The rate constants for RAF, SET, and HT reactions were calculated by using a quantum mechanics based methodology formulated by one of the author of this article and his co-worker.25 Relative energies were calculated with respect to the sum of separated reactants, also the thermodynamic corrections at 298.15 K were included in the calculations. Solvent cage effects have been incorporated into the calculations based on the corrections proposed by Okuno,40 taking into account of the free volume theory.41 In this work the expression used to correct the Gibbs free energy is
 | (4) |
The rate constants (k) are evaluated by using the classical transition state theory (TST) at 298.15 K and 1 M standard state as shown in eqn (5) wherein kB and h are the Boltzmann and Planck constants, T is the temperature (in K), and ΔG≠ is the Gibbs free energy of activation representing the free energy difference between transition states and reactants. As the computational program uses a reference state of 1 atm for ΔG≠ calculations it must be converted 1 M standards state, that corresponds to a correction factor −1.89 kcal mol−1 at 298.15 K. IRC calculations42 have been carried out when required to confirm that transition states are linked nicely to the proposed reactants and products.
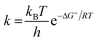 | (5) |
Actually, the ΔG≠ calculation is appropriate for RAF and HT reactions and is not reasonable in SET mechanism since it is not driven by any nuclear motions. Therefore, the Marcus theory43 has been used for the determination of activation free energy barrier (denoted as ΔGSET≠, eqn (6)) of SET, which comprise of two factors, one representing the free energy of reaction (ΔG0SET) and the other accounts for nuclear reorganization energy (λ).
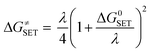 | (6) |
The λ can be calculated by using a simple approximation as shown in eqn (7) wherein ΔESET denotes the energy (non-adiabatic) difference between reactants and products, latter at the equilibrium geometry of the reactants.
| λ ≈ ΔESET − ΔG0SET | (7) |
When the reaction path degeneracy (σ) which accounts for the number of identical reaction paths and also the quantum mechanical tunneling corrections κ (meant for HT pathway) calculated using the zero curvature tunneling44 approach are taken into account, the rate constant expression assumes the expression as shown in eqn (8)
 | (8) |
In the case of k values close to the diffusion-limit, the rate constants cannot be directly obtained from TST calculations. Therefore, in the present work the Collins–Kimball theory45 is used for that purpose. Thus, the apparent rate constant (kapp) for each reaction channel in the diffusion-limit regime is given by,
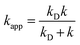 | (9) |
 | (10) |
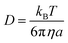 | (11) |
The overall rate constant (koverall) for the radical–molecule reaction is calculated as the sum of apparent rate constants of different reaction pathways (eqn (12)).
| koverall = kSET + kHT + kRAF | (12) |
The branching ratios (Γ) of the individual reactions provides an estimate of the yield of a particular product in the reaction are calculated using the expression given in eqn (13)
 | (13) |
Results and discussions
Spectra and kinetics of ˙OH reaction with 2Apy
The absorption spectrum of the transient(s) produced in the reaction of ˙OH with 2Apy at pH 7 is shown in Fig. 1. The spectrum is characterized by a strong peak with maximum absorption wavelength (λmax) 330 nm and a broad (500–600 nm) one centred at 550 nm. The time dependence of signal absorbance at 330 and 550 nm are shown in the inset of Fig. 1. Furthermore, the spectral shape and characteristic λmax were remains intact (except intensities of spectra) at higher time scales; demonstrating that there is no transformation of the initially formed transient(s) in the measured time period of our pulse radiolysis experiments. In other words, the transient species formed in the reaction of ˙OH with 2Apy does not undergo any secondary reactions but seems rather stable.The transient absorption at pH 10.5 is shown as Fig. S1 in the ESI.† As the reported pKa value of 2Apy is 3.54,50 it is the same molecular entity that reacts with ˙OH at pH 10.5 and 7. It has been found that, the spectral characteristics in terms of both λmax and absorbance are very similar at pH 10.5 and 7, concomitantly this behaviour is quite identical to the ˙OH reactions of some substituted 2-aminopyrimidines reported earlier51 but distinct from pyrimidine nucleobases and some other substituted pyrimidine systems.27 The spectral difference noted for those pyrimidine compounds at near neutral and basic pH (approximately 10.5) were mainly attributed to the acid–base equilibrium of the ˙OH adducts formed from them.
The second order rate constant (k) for the reaction of ˙OH with 2Apy (eqn (4)) was determined from the slope of the plot of apparent first order rate constant (kobs) against varying 2Apy concentrations at 330 nm (plot is given as Fig. S2 in ESI†). The k value for eqn (14) being deduced as 2.76 ± 0.06 × 109 M−1 s−1 at pH 7; this value signifies the diffusion controlled nature of ˙OH reaction in solution.
| 2Apy + ˙OH → Transient(s) | (14) |
A comparison has been made between the pulse radiolytically determined k values for ˙OH reactions of pyrimidine nucleobases6 and some substituted 2-aminopyrimidines51 with that of 2Apy (see Table 1), apparently the order of reactivity of all these pyrimidines with ˙OH are comparable. Accordingly, the reaction kinetics emphasizes the possibility of RAF reaction as the most appropriate mechanism in 2Apy similar to other pyrimidines exemplified in Table 1. Apart from RAF mechanism, ˙OH can induce oxidations by SET and HT pathways. For instance, about 10% of the transients formed in the reactions of ˙OH with thymine originated via HT reaction while the remaining 90% constitute RAF reactions;52 SET was cited as the preferred mechanism in the reactions of ˙OH with 2-thio and 4-thio uracils.53,54
The G(˙OH) available in the reaction ˙OH and 2Apy is calculated as 0.545 μmol J−1 by using an equation formulated by Schuler and co-workers.55 The yield of oxidizing radicals produced during the reaction of ˙OH with 2Apy was estimated by monitoring the electron transfer characteristics of the oxidizing transient(s) to ABTS2−. The yield of ABTS˙− which in turn corresponds to G (oxidizing transients) is calculated as 0.068 μmol J−1, which accounts for 12.5% ≈ 13% of total ˙OH produced. Therefore, the remaining 87% reaction of ˙OH with 2Apy produces reducing radicals. A generalization of redox titration method in the pulse radiolysis of pyrimidine systems is that, if the radical center is on C5 or an electron affinic hetero atom such as N, or O (via resonance) then the transient shows oxidizing properties while if the radical center is on C6 or totally on a C atom (other than C5) where hetero conjugation is not feasible then it is reducing.27 For instance, in the reactions of ˙OH with cytosine and uracil the RAF at C6 lead to the radical center on C5 and/or hetero atom and their yield constitute respectively 10% and 18% of total ˙OH reaction, while the RAF at C5 gave C centered radical and the yield of reducing transients were cited as 87% and 82% of total ˙OH reactions.52,56 However, for 2Apy the SET and HT pathways mostly would lead to radical center on N atom, but the RAF at different sites would lead to N-centered or C-centered radical not very easy to detect on the basis of experimental results alone. Another remarkable results of our redox titration is that, the yield of oxidizing radicals did not exhibit any dramatic change at higher pH as observed in the case of pyrimidine nucleobases.52,56
Because of the complexity of the free radical–molecule reactions and the variety of influencing factors such as solvent, substituent effect on substrate molecule etc. it is desirable to have a separate theoretical investigation to endorse the most suitable reaction mechanism applicable. In this context, we have undertaken a comprehensive DFT study and the results are detailed in the subsequent section.
Elucidation of mechanism by DFT calculations
Using DFT methods we have modelled three types of reactions of ˙OH with 2Apy viz. RAF, SET and HT as shown in Scheme 2. There are four RAF reactions, accounting the additions of ˙OH at N1 (N3 is identical to N1), C2, C4 (C6 is identical to C4) and C5 ring atoms of 2Apy.The optimized geometries of 2Apy and its transients with selected bond lengths are shown in Fig. 2. The dihedral angle τ(N1–C2–N7–H) ≈ 16° noted for 2Apy describes the pyramidalization of the amino group. The drift of lone pair electron from the amino group to the ring is evident from the short bond distance noted for C2–N7 (1.356 Å) while compared to a normal C–N single bond distance of 1.472 − 1.479 Å. The N1–C6 (which is identical with N3–C4) bond of 2Apy constitute a highly localized double bond in the ring; however other bond distances in the ring demonstrate more or less delocalized double bonds.
Substantial modifications of bond lengths in 2Apy have been observed upon SET pathway. The radical cation is characterized with a high degree of planarity and the observed τ(N1–C2–N7–H) ≈ 180°; N7 is noted as the charge center while the odd electron spin density is found maximum on C5 and N7 atoms. The radical species obtained via HT pathway is a perfectly planar structure with the unpaired spin localized mostly over N7 atom. The planarity of 2Apy ring gets disturbed in all RAF pathways with noticeable puckering at the ˙OH addition sites. In all the cases, the unpaired spin is mostly found at the ortho and para positions with respect to the ˙OH addition site while extensive spin dispersions are observed in the case of RAF at C2 and C5.
The thermodynamic parameters ΔG0 and ΔG≠ for the different reaction channels depicted in Scheme 2 with respect to the reactants 2Apy and ˙OH are summarized in Table 2. It can be seen from the table that, the minimal ΔG0 values are noted for RAFs at C-sites among the various possible pathways. The RAF at N1 or N3 has the maximum ΔG0 value much beyond the limit of a normal chemical reaction; which rule out the scope of this reaction. According to ΔG0 values, the SET pathway is endergonic in nature, while the HT pathway is exergonic in character. However, a more meaningful appraisal of reaction pathways can be done by considering the ΔG≠ values since it takes account of transition states. From the ΔG≠ values in Table 2, it seems that the most probable reaction of ˙OH with 2Apy is RAF at C5 followed by RAF at C4 or C6. Therefore, both the kinetic and thermodynamic factors are highly favourable for RAF of ˙OH at C5 position of 2Apy.
| Mechanism | ΔG0 | ΔG≠ | k(κ) | Γ |
|---|---|---|---|---|
| SET | 7.94 | 9.91 | 3.4 × 105 | 0.01 |
| HT | −3.59 | 9.08 | 1.8 × 108 (64.92) | 7.83 |
| RAF at N1 or N3 | 22.18 | — | 0 | 0.00 |
| C2 | −7.08 | 13.70 | 1.1 × 103 | 0.00 |
| C4 or C6 | −12.11 | 6.91 | 1.1 × 108 | 4.78 |
| C5 | −10.84 | 1.72 | 2.0 × 109 | 86.96 |
| koverall | 2.3 × 109 | |||
The computed rate constants of each reaction channels as well as the overall rate constant and the branching ratios (Γ) of individual reactions are presented in Table 2. It can be seen that, the calculated k value for RAF at C5 which typically represents a diffusion-limit value shows good quantitative agreement to the pulse radiolysis experimental k value (2.76 ± 0.06 × 109 M−1 s−1) within a few percent. The k values computed for HT and RAF at C4 or C6 channels are close to the diffusion-limit. Interestingly, the Γ value estimated for RAF at C5 is 86.96 ≈ 87%; already recognized with spin localization on C-centres, agree very well with experimental observation of 87% reducing radicals. Typically the radical formed through HT pathway can be considered as oxidizing in nature as the odd spin is localized on an electron affinic N7-atom. Also the RAF at C4 or C6 leads to C5 centred radical well comparable to oxidizing radicals produced in the RAF at C6 of pyrimidine nucleobases.27 Therefore, 13% of oxidizing radicals in the pulse radiolysis experiment can be considered as evolved from the close diffusion limit pathways namely HT (Γ = 7.83%) and RAF at C4 or C6 (Γ = 4.78%).
Therefore, the scrutiny of the different reaction pathways of ˙OH with 2Apy by DFT calculations has shown that RAF at C5 is responsible for the experimental observations.
DFT study on the reactions of ˙OH with 4-aminopyrimidine
We found that, the DFT calculations performed herein on 2Apy was quite successful to support the experimental results as well as to establish the reaction mechanism. Therefore, in this context a complete theoretical study has been carried out on the reactions of ˙OH with 4Apy and the results of the calculations are delineated below.The optimized geometries of 4Apy and its possible ˙OH reaction products are presented in Fig. 3. The structural features of pyrimidine ring was found to be fairly modified with the attachment of NH2 unit at 4-position with respect to 2Apy and considerable flattering of the amino group has been noted for 4Apy. Apparently, still shorter C–N (N from exo-cyclic amino group) bond distance noted for 4Apy in comparison to 2Apy (wherein C2–N7) point at better resonance effect of the amino group with the pyrimidine ring of the former. The radical cation of 4Apy obtained via SET mechanism retains the planarity of the ring system and spin values are found to be localized at C5 and N7 atoms. As in the case of 2Apy, the radical obtained through the HT pathway is a perfect planar entity with the unpaired spin localized mostly on N7 atom. We did not consider the RAFs at N1 and N3-positions due to the low paucity of ˙OH additions at these sites apparent from 2Apy molecule (ΔG0 > 20 kcal mol−1). Obviously fewer reports are available for ˙OH additions at hetero atoms of pyrimidine systems.57 Consequently, we have considered the RAFs at C2, C4, C5 and C6-atoms in 4Apy. Ring puckering has been observed at the ˙OH additions sites and also the unpaired spin is localized mostly on the ortho and para positions of addition sites.
Table 3 lists the ΔG0, ΔG≠, individual k values of each reaction channels, overall rate constant as well as Γ values of ˙OH reactions with 4Apy. The results of our calculations suggest that all of the RAFs and HT reactions are energetically favourable due to the exergonic (ΔG0 < 0) nature of these reactions. The SET process seems to be quite difficult as the estimated ΔG0 value is endergonic by 11.06 kcal mol−1. The calculated barrier heights of the different reaction pathways indicate that RAF at C5 possess the lowest ΔG≠ value and hence represents the kinetic product in the reactions of ˙OH with 4Apy. The k value for this RAF signifies a diffusion controlled reaction as depicted in the case of 2Apy. A quantitative estimate of different reaction pathways on the basis of calculated Γ values pointed out that about 71% of ˙OH reactions with 4Apy constitute RAF at C5-position and 28% occurs via HT pathway.
| Mechanism | ΔG0 | ΔG≠ | k(κ) | Γ |
|---|---|---|---|---|
| SET | 11.06 | 12.01 | 9.7 × 103 | 0.00 |
| HT | −16.52 | 9.28 | 7.9 × 108 (79.8) | 28.14 |
| RAF at C2 | −14.56 | 9.69 | 4.8 × 105 | 0.02 |
| C4 | −1.93 | 12.04 | 9.1 × 103 | 0.00 |
| C5 | −14.81 | 2.15 | 2.0 × 109 | 71.26 |
| C6 | −11.95 | 7.64 | 1.6 × 107 | 0.57 |
| koverall | 2.8 × 109 | |||
Conclusions
By using a combination of state-of-the-art experimental and computational techniques, we have gained new insight into the ˙OH initiated oxidation reactions of 2Apy. Pulse radiolysis studies have shown that the reaction of ˙OH with 2Apy occurs with diffusion controlled rates and envisaged the formation of approximately 13% oxidizing and 87% reducing radicals (by redox titration). The experimental spectrum characterized with λmax at 330 and 550 nm was ascertained as RAF at C5 using M05-2X/6-311++G(d,p) level theory calculations. The ΔG≠ = 1.72 kcal mol−1 calculated for this reaction is very low compared to other RAFs, SET and HT reactions. Subsequent theoretical k value determination for this RAF depicted a diffusion controlled behavior and the predicted figure quantitatively agrees with the experimental k value. A theoretical demonstration of ˙OH reaction with 4Apy has also been done wherein RAF at C5 possess the least ΔG≠ (2.15 kcal mol−1). About 71% of the reaction of ˙OH with 4Apy occurs by RAF at C5 and 28% constitute HT pathway. This work has also shown that, the M05-2X DFT method with SMD solvation model is an appropriate combination for the accurate determination of diffusion controlled rate constants in the oxidation reactions of ˙OH with pyrimidine heterocyclic systems.Acknowledgements
We are thankful to Prof. A. S. Kumbhar for giving us access to Pulse radiolysis facility at NCFRR, Pune.References
- C. Wan, T. Fiebig, O. Schiemann, J. K. Barton and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 14052 CrossRef CAS PubMed.
- T. Fiebig, C. Wan and A. H. Zewail, ChemPhysChem, 2002, 3, 781 CrossRef CAS.
- M. A. O'Neil, C. Dohno and J. K. Barton, J. Am. Chem. Soc., 2004, 126, 1316 CrossRef PubMed.
- M. F. Soulière, A. Haller, R. Rieder and R. Micura, J. Am. Chem. Soc., 2011, 133, 16161 CrossRef PubMed.
- T. Douki and J. Cadet, in Radiation Chemistry: From Basics to Applications in Material and Life Sciences, ed. M. Spotheim-Maurizot, M. Mostafavi, T. Douki and J. Belloni, EDP Sciences, Les Ulis Cedex A, 2008, pp. 177–189 Search PubMed.
- G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513 CrossRef CAS PubMed.
- V. Kleinwachter, J. Drobnik and L. Augenstein, Photochem. Photobiol., 1966, 5, 579 CrossRef CAS.
- I. M. Lagoja, Chem. Biodiversity, 2005, 2, 1 CAS.
- J. J. Hanthorn, L. Valgimigli and D. A. Pratt, J. Org. Chem., 2012, 77, 6908 CrossRef CAS PubMed.
- E. A. Lindsey, R. J. Worthington, C. Alcaraz and C. Melander, Org. Biomol. Chem., 2012, 10, 2552 CAS.
- N. Anand, P. Singh, A. Sharma, S. Tiwari, V. Singh, D. K. Singh, K. K. Srivastava, B. N. Singh and R. P. Tripathi, Bioorg. Med. Chem., 2012, 20, 5150 CrossRef CAS PubMed.
- K. Singh, H. Kaur, K. Chibale, J. Balzarini, S. Little and P. V. Bharatam, Eur. J. Med. Chem., 2012, 52, 82 CrossRef CAS PubMed.
- F. Xie, H. Zhao, D. Li, H. Chen, H. Quan, X. Shi, L. Lou and Y. Hu, J. Med. Chem., 2011, 54, 3200 CrossRef CAS PubMed.
- J. Lee, K. H. Kim and S. Jeong, Bioorg. Med. Chem. Lett., 2011, 21, 4203 CrossRef CAS PubMed.
- N. Singh, S. K. Pandey, N. Anand, R. Dwivedi, S. Singh, S. K. Sinha, V. Chaturvedi, N. Jaiswal, A. K. Srivastava, P. Shah, M. I. Siddiqui and R. P. Tripathi, Bioorg. Med. Chem. Lett., 2011, 21, 4404 CrossRef CAS PubMed.
- W.-J. Hao, B. Jiang, S.-J. Tu, X.-D. Cao, S.-S. Wu, S. Yan, X.-H. Zhang, Z.-G. Han and F. Shi, Org. Biomol. Chem., 2009, 7, 1410 CAS.
- L. P. Nitha, R. Aswathy, N. E. Mathews, B. S. Kumari and K. Mohanan, Spectrochim. Acta, Part A, 2014, 118, 154 CrossRef CAS PubMed.
- T. S. Balaban, R. Goddard, M. Linke-Schaetzel and J. M. Lehn, J. Am. Chem. Soc., 2003, 125, 4233 CrossRef CAS PubMed.
- R. Capdeville, E. Buchdunger, J. Zimmermann and A. Matter, Nat. Rev. Drug Discovery, 2002, 1, 493 CrossRef CAS PubMed.
- M. C. Etter and D. A. Adsmond, J. Chem. Soc., Chem. Commun., 1990, 589 RSC.
- M. Krische, J.-M. Lehn, N. Kyritsakas and J. Fischer, Helv. Chim. Acta, 1998, 81, 1909 CrossRef CAS.
- I. Stoll, R. Brodbeck, B. Neumann, H.-G. Stammler and J. Mattay, CrystEngComm, 2009, 11, 306 RSC.
- J. Eberhard, I. Stoll, R. Brockhinke, B. Neumann, H.-G. Stammler, A. Riefer, E. Rauls, W. G. Schmidt and J. Mattay, CrystEngComm, 2013, 15, 4225 RSC.
- L. Wang, L. Zhao, Y. Hu, W. Wang, R. Chena and Y. Yanga, CrystEngComm, 2013, 15, 2835 RSC.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430 CrossRef CAS PubMed.
- P. Gaikwad, K. I. Priyadarsini and B. S. M. Rao, Radiat. Phys. Chem., 2008, 77, 1124 CrossRef CAS PubMed.
- C. von Sonntag, Free Radical Induced DNA Damage and Its Repair: A Chemical Perspective, Springer-Verlag, Berlin, 2006 Search PubMed.
- G. V. Buxton and C. R. Stuart, J. Chem. Soc., Faraday Trans., 1995, 91, 279 RSC.
- S. L. Scott, W.-J. Chen, A. Bakac and J. H. Espenson, J. Phys. Chem., 1993, 97, 6710 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364 CrossRef.
- C. Zavala-Oseguera, J. R. Alvarez-Idaboy, G. Merino and A. Galano, J. Phys. Chem. A, 2009, 113, 13913 CrossRef CAS PubMed.
- E. Velez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971 CrossRef CAS.
- A. Galano and J. R. Alvarez-Idaboy, Org. Lett., 2009, 11, 5114 CrossRef CAS PubMed.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823 CrossRef CAS.
- A. Perez-Gonzalez and A. Galano, J. Phys. Chem. B, 2011, 115, 1306 CrossRef CAS PubMed.
- C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, J. Phys. Chem. A, 2011, 115, 5138 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- Y. Okuno, Chem. – Eur. J., 1997, 3, 212 CrossRef CAS PubMed.
- S. W. Benson, The Foundations of Chemical Kinetics, Krieger, Florida, 1982 Search PubMed.
- C. Gonzales and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef PubMed.
- J. C. Corchado, E. L. Coitino, Y.-Y. Chuang, P. L. Fast and D. G. Truhlar, J. Phys. Chem. A, 1998, 102, 2424 CrossRef CAS.
- D. G. Truhlar and A. Kuppermann, J. Am. Chem. Soc., 1971, 93, 1840 CrossRef.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425 CrossRef CAS.
- M. Smoluchowski, Z. Phys. Chem., 1917, 92, 129 Search PubMed.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- G. G. Stokes, Mathematical and Physical Papers, Cambridge University Press, Cambridge, 1903 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549 CrossRef CAS.
- A. Albert, R. Goldacre and J. Phillips, J. Chem. Soc., 1948, 2240 RSC.
- T. L. Luke, T. A. Jacob, H. Mohan, H. Destaillats, V. M. Manoj, P. Manoj, J. P. Mittal, M. R. Hoffmann and C. T. Aravindakumar, J. Phys. Chem. A, 2002, 106, 2497 CrossRef CAS.
- S. Fujita and S. Steenken, J. Am. Chem. Soc., 1981, 103, 2540 CrossRef CAS.
- K. P. Prasanthkumar, C. H. Suresh and C. T. Aravindakumar, J. Phys. Chem. A, 2012, 116, 10712 CrossRef CAS PubMed.
- K. P. Prasanthkumar, C. H. Suresh and C. T. Aravindakumar, J. Phys. Org. Chem., 2013, 26, 510 CrossRef CAS.
- R. H. Schuler, A. L. Hartzell and B. Behar, J. Phys. Chem., 1981, 85, 192 CrossRef CAS.
- D. K. Hazra and S. Steenken, J. Am. Chem. Soc., 1983, 105, 4380 CrossRef CAS.
- G. Pramod, K. P. Prasanthkumar, H. Mohan, V. M. Manoj, P. Manoj, C. H. Suresh and C. T. Aravindakumar, J. Phys. Chem. A, 2006, 110, 11517 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The transient absorption spectra obtained from the reaction of ˙OH with 2-aminopyrimidine at pH 10.5; a plot of kobs as a function of 2-aminopyrimidine concentration at 330 nm from its reactions with ˙OH at pH 7; and the cartesian coordinates as well as the thermodynamic parameters used for the calculations of rate constants of major reaction channels of ˙OH with 2-/4-aminopyrimidine are presented. See DOI: 10.1039/c4ra00811a |
| This journal is © The Royal Society of Chemistry 2014 |