Experimental connections between aqueous–aqueous and aqueous–ionic liquid biphasic systems†
Valérie Mazanab,
Isabelle Billard*ab and
Nicolas Papaiconomouc
aIPHC, CNRS/IN2P3, Université de Strasbourg, 23 rue du Loess, 67037 Strasbourg, France. E-mail: isabelle.billard@iphc.cnrs.fr
bCNRS, UMR7178, 67037 Strasbourg, France
cLEPMI, Université de Savoie, 1130 rue de la piscine, 38402 Saint-Martin d'Hères Cedex, France
First published on 26th February 2014
Abstract
Aqueous–ionic liquid (A–IL) biphasic systems containing deuterated water, deuterated nitric acid (10−2 M to 7 M) and either [C1C4im+][Tf2N−], [C1C10im+][Tf2N−] or [Me3BuN+][Tf2N−] have been examined in terms of water and acid solubilities in the IL-rich phase and in terms of IL cation and anion solubilities in the water-rich phase. Other experiments focused on the IL cation and anion solubility in the water-rich phase upon addition of either [C1C4im+][Cl−] or [Li+][Tf2N−]. The results evidence a complex interplay between all negatively and positively charged ions of the samples that could be described following the usual approach used for aqueous–aqueous (A–A) biphasic systems. Other examples from the literature are discussed and demonstrate that the frontier between A–A and A–IL systems is questionable. Predictions are made for the extraction of metallic ions by use of biphasic systems in this work that are successfully compared to literature data.
1. Introduction
Although aqueous–molecular solvent (A–Mol) biphasic systems are applied to a huge number of extraction processes with great success, they suffer from some drawbacks, in particular environmental concerns, mainly because of the toxicity and other safety hazards associated with molecular solvents such as toluene, chloroform, dodecane, etc. Even before the REACH regulation, this has prompted researchers to investigate two types of alternatives. The first idea is to replace the volatile organic solvent by a greener one. This is done in aqueous–ionic liquid (A–IL) biphasic systems because ionic liquids (ILs), a new class of solvents composed of ions and which melting temperature is below 100 °C,1,2 usually display interesting “green” properties, such as non-volatility and non-flammability. Examples of such systems can be found in recent review papers dedicated to the use of ILs for the extraction of metallic ions.3,4 Most of the time, ILs of the imidazolium family are favored, together with hydrophobic anions such as (CF3SO2)2N− (thereafter denoted as Tf2N−), but very different ILs can also be used, such as [(C6H13)3(C14H27)P+][Cl−].5 A second way to get rid of the problems encountered in classical A–Mol systems is the use of aqueous–aqueous (A–A) biphasic systems (also known as aqueous biphasic systems, ABS, or Aqueous Two Phase Systems, ATPS), where the mixing of two homogeneous aqueous solutions of “incompatible” salts, under some specific chemical conditions (concentration and temperature), leads to a biphasic system (i.e. a meniscus is clearly visible), where both the upper and lower phases are aqueous solutions. Several types of such A–A systems can be found: polymer–polymer, polymer–salt or even polyelectrolyte–salt,6 the most common polymers being from the polyethylene glycol family7–9 and the most popular salts being potassium phosphate or carbonate, ammonium sulfate, sodium or potassium citrate etc. Quite recently, some publications have investigated A–A biphasic systems in which one of the salts is indeed an ionic liquid.10–15The fact that ILs can be used either for A–IL or A–A biphasic systems appears quite surprising at first glance. We have thus performed a series of experiments aiming at evidencing the links between the two approaches. To this aim, we have studied biphasic mixtures of aqueous nitric acid solutions of various concentrations (from 0 to ca. 7.5 M) and of three ionic liquids, 1-methyl-3-butylimidazolium bis(trifluoromethylsulfonyl)imide [C1C4im+][Tf2N−], 1-methyl-3-decylimidazolium bis(trifluoromethylsulfonyl)imide [C1C10im+][Tf2N−] and trimethylbutylammonium bis(trifluoromethylsulfonyl)imide [Me3BuN+][Tf2N−]. Determination of the concentrations of various entities (H2O, H+, Tf2N−, C1C4im+, C1C10im+ and Me3BuN+) in the lower and/or upper phases gives some insights onto these systems, showing the border between A–A and A–IL is a rather vague notion. In this paper, discussion will be based on these new experiments but will also take advantage of several published data.
2. Experimentals
2.1 Definitions and notation for the samples
In this paper, the term “aqueous” refers either to D2O or H2O. All throughout this paper, the definition of an ionic liquid (IL) is an ionic compound which melting temperature is below 100 °C. The term “salt” will be indifferently used for ILs and “classical” ionic compounds with melting points above 100 °C. Molecular compounds will be noted without brackets, i.e. H2O or D2O, while salts will be denoted as [Cat+][Ani−], in order to highlight the ionic nature of the compound. In the case of multicharged salts, the stoichiometry will be indicated, e.g. [3Na+][cit3−] for sodium citrate.A user-friendly notation is required on a practical perspective, in view of facilitating description and preparation of the samples of this work. To this aim, we use the notation Mol&[Cat1+][Ani1−]&[Cat2+][Ani2−] to indicate the overall composition of a system made of a molecular compound, Mol (H2O, dichloroethane etc.), and of two salts. Depending on the usual state of each of the salts (i.e. solid or liquid), the concentration, the mass or the volume (or range thereof) will be indicated in parenthesis in the molar, gram or milliliter scales, respectively. The amount of the molecular (liquid) compound acting as a solvent for one of the salt is indicated as the quantum satis (qs) corresponding to the molar scale. Whenever the volume or molar scales are used, the temperature at which the samples have been prepared should be indicated but, for the samples of this work, the constant temperature of 19 °C will be omitted for the sake of simplicity. Extension of this notation to any number of salts is easily made, as is easily made the extension to non-aqueous systems. For example, H2O&[H+][NO3−] (0.1 M, qs 0.8 ml)&[C1C4im+][Tf2N−] (0.8 ml) indicates a sample composed of an aqueous solution of volume 0.8 ml, containing the salt [H+][NO3−] at concentration 0.1 M to which 0.8 ml of the salt [C1C4im+][Tf2N−] is added. This notation does not give any indication on the exact state of the system, either biphasic or monophasic, once all components have been introduced in a test tube and contacted by vigorous shaking.
Depending on the chemical conditions (concentration and temperature), systems under discussion may change from biphasic to monophasic state and vice versa. Therefore, as a complement to the notation Mol&[Cat1+][Ani1−]&[Cat2+][Ani2−] described above, we use the notation Mol, [Cati+], [Anij−]//[Cati′+], [Anij′−] to describe the final biphasic state. The sign // indicates phase separation, with left hand list describing all system components present in the upper phase in amounts over 50% of their initial quantity and the right hand list displaying components in the lower phase in amounts over 50% of their initial value. This notation is in line with that we used previously in various papers dealing with liquid–liquid extraction of metallic ions from aqueous liquid phases towards IL phases.16–18 This notation is easily extended to more than two salts. Should the system be in a monophasic state, the notation (Mol, [Cati−], [Cati+], [Anij−], [Anij−]) will be used. Conversely, this notation does not give any indication on the preparation step. Whenever known, the exact amounts of any of the compounds in the upper or lower phase could be indicated as previously explained but we would recommend using solely the mole scale for the sake of simplicity.
In the following, subscript “init” will indicate aqueous concentration values from the sample preparation step, prior to the mixing and subscript “eq” will indicate concentrations in the upper phase after equilibration.
2.2 Chemicals
All reagents used in this study were of analytical grade and needed no further purification. The ILs 1-methyl-3-butylimidazolium bis(trifluoromethylsulfonyl)imide [C1C4im+][Tf2N−], 1-methyl-3-butylimidazolium chloride [C1C4im−][Cl−], 1-methyl-3-decylimidazolium bis(trifluoromethylsulfonyl)imide [C1C10im+][Tf2N−], 1-methyl-3-decylimidazolium chloride [C1C10im+][Cl−], trimethylbutylammonium bis(trifluoromethylsulfonyl)imide [Me3BuN+][Tf2N−] and trimethylbutylammonium bromide [Me3BuN+][Br−] (see Scheme 1 for the cation chemical structures) were purchased from Solvionic (Toulouse, France). Purities are above 98%, except for [C1C10im+][Cl−] which purity is 95.5%. [Li+][Tf2N−] (Solvionic) has a purity of 99%. | ||
| Scheme 1 Chemical structures of the IL cations used in this work. (a) C1C4im+; (b) C1C10im+; (c) Me3BuN+. | ||
The standards used in 1H NMR were dihydrated sodium citrate and tetrahydrated sodium–potassium tartrate (Merck). The standard used in 19F NMR was sodium trifluoroacetate (Alfa Aesar). Their analytical grades were above 98%. Deuterated nitric acid of analytical grade was purchased from Sigma Aldrich. Deuterium oxide purity was 99%.
2.3 Sample preparation and experimental protocol
In view of the NMR measurements, for all aqueous samples, deuterated nitric acid, [D+][NO3−], was used in place of nitric acid [H+][NO3−] and was diluted accordingly in deuterated water, D2O. Similarly, the internal NMR standards were dissolved in D2O. All deuterated solutions were stored under nitrogen, to avoid hydrogen exchange with the atmosphere.19 The [Li+][Tf2N−], [Me3BuN+][Br−] and [C1C4im+][Cl−] powders were dried before dilution in the aqueous phases, while [C1C10im+][Cl−], a very viscous liquid, was used as received, owing to the difficulty of the drying procedure in this case. Its water content has been checked to be negligible. The ILs [C1C4im+][Tf2N−], [C1C10im+][Tf2N−] and [Me3BuN+][Tf2N−] (these salts are liquid at room temperature) were dried under vacuum following a previously published procedure20 prior to sample preparation. However, ILs unavoidably absorb H2O from the atmosphere and their average H2O content was ca. 200 ppm prior to mixing.Using the notation described in the above section, the individual samples of this work are of two types. Series 1 to 3 (S#1 to S#3) correspond to mixtures of D2O, [D+][NO3−] and one of the three ILs [C1C4im+][Tf2N−], [C1C10im+][Tf2N−] or [Me3BuN+][Tf2N−], while series 4 to 7 (S#4 to S#7) correspond to mixtures of D2O, [D+][NO3−], [C1C4im+][Tf2N−] and a third salt, either [Li+][Tf2N−] or [C1C4im+][Cl−] according to:
S#1: D2O&[D+][NO3−] (0.010–6.195 M, qs 0.8 ml)&[C1C4im+][Tf2N−] (0.8 ml)
S#2: D2O&[D+][NO3−] (0.012–6.368 M, qs 0.8 ml)&[C1C10im+][Tf2N−] (0.8 ml)
S#3: D2O&[D+][NO3−] (0.010–6.450 M, qs 0.8 ml)&[Me3BuN+][Tf2N−] (0.8 ml)
S#4: D2O&[D+][NO3−] (0.305 M – qs 0.8 ml)&[C1C4im+][Cl−] (0–0.0800 g)&[C1C4im+][Tf2N−] (0.8 ml)
S#5: D2O&[D+][NO3−] (2.221 M – qs 0.8 ml)&[C1C4im+][Cl−] (0–0.0837 g)&[C1C4im+][Tf2N−] (0.8 ml)
S#6: D2O&[D+][NO3−] (2.221 M – qs 0.8 ml)&[Li+][Tf2N−] (0–0.2169 g)&[C1C4im+][Tf2N−] (0.8 ml)
S#7: D2O&[D+][NO3−] (0.305 M – qs 0.8 ml)&[Li−][Tf2N−] (0–0.2264 g)&[C1C4im+][Tf2N−] (0.8 ml).
To prepare a given sample, all the chemical components were introduced in a small plastic tube of 2 ml and were mechanically shaken for 3 hours. The temperature was 19 ± 1 °C. Then, the samples were centrifuged at 4000 rpm during two minutes. All samples displayed a clear visible meniscus and the two phases were thus separated in view of NMR measurements. In all cases, the upper phase was a D2O-rich phase. No phase inversion could be observed in any of the sample of this work but for S#3 at [D+][NO3−] ≥ 6.3 M and these samples were not considered further, owing to the difficulty in measuring reliable D2O amounts in this case. Note that for samples similar to S#3 prepared with non deuterated compounds (H2O and [H+][NO3−]) no phase inversion could be observed up to 7.5 M of [H+][NO3−], a difference ascribed to the differences in densities of the ingredients. Samples of series S#7 have been independently prepared and measured twice and agreement between the two data sets is excellent (see Fig. 9 and 10).
2.4 Protocol for NMR measurements
Several techniques have been applied for the determination of IL solubility in aqueous phases. In pure water, obviously, ILs' cations and anions dissolve in identical amounts, to comply with electroneutrality of phases so measuring either the ILs' cation or anion gives access to the quantity of the other ILs' ion. UV-vis is quite efficient for the quantification of imidazolium moieties21 and is also valuable for Tf2N−.22 More specific techniques, such as chromatography23 or ICP-AES24 have been used for cations and Tf2N−, respectively. Recently, conductivity25 has been also successfully used for the joint measurement of cations and anions, taken as a whole. However, in the case of our samples that contain large amounts of nitric acid, ion exchange, either cationic or anionic, may be envisioned between the two phases in contact so that it is necessary to measure both IL ions independently. Under such conditions, conductivity is inaccurate, and so is UV-vis, owing to the large nitrate contribution to the conductivity and to the UV-vis absorption spectra.Therefore, we developed an experimental protocol using quantitative NMR for the determination of ILs' cations and anions solubilized in the aqueous phases of our work, based on the work of Bell and co-workers26 and taking into account the recommendations of the paper of Malet-Martino et al.27,28 for accurate measurements. Experimental details are presented in the ESI.†
2.5 Other analytical protocols
Deuterated acidic aqueous solutions (before and after contact with the IL phases) were titrated by [Na+][OH−]/H2O 0.01 M (Schott titrator). The uncertainty is equal to 0.5%. The D2O amount in the IL phases was titrated by the Karl Fisher method with a coulometer (Mettler Toledo DL32). The uncertainty is equal to 5%. For these two methods no particular caution was set concerning the use of D2O instead of H2O.3. Experimental results
3.1 Samples with two salts (S#1 to S#3)
Fig. 1 displays the amount of D2O at equilibrium in the lower phase for S#1, S#2 and S#3. For comparison purposes, our previously published data16 on H2O&[H+][NO3−]&[C1C4im+][Tf2N−] are presented in the ESI (Fig. S1†). There is a slight difference between the deuterated series and its non-deuterated equivalent, which tends to diminish at the highest acidities. This is ascribed to physico-chemical differences (density, for the main part) between D2O and H2O. Note that the value of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ppm of H2O dissolved in [C1C4im+][Tf2N−] displayed in Fig. S1† fits very well with the data published by another group, as 13
500 ppm of H2O dissolved in [C1C4im+][Tf2N−] displayed in Fig. S1† fits very well with the data published by another group, as 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ppm (at T = 20 °C).21
900 ppm (at T = 20 °C).21
 | ||
| Fig. 1 D2O amount in the lower phase for: (●) D2O&[D+][NO3−]&[Me3BuN+][Tf2N−]; (Δ) D2O&[D+][NO3−]&[C1C4im+][Tf2N−]; (♦) D2O&[D+][NO3−]&[C1C10im+][Tf2N−]. Solid lines are guide for the eye only. | ||
For the deuterated samples of this work, the trend and the values as shown in Fig. 1 are in line with previous determinations in various systems which were measured in non-deuterated solutions.29 Even in the absence of [D+][NO3−], the amount of D2O transferred to the lower phase is not negligible and the trend follows that of the hydrophilicity of the ILs' cations: C1C10im+ > C1C4im+ > Me3BuN+. Because ILs are composed of ions, interactions with dipolar water molecules are expected, and consequently, water transfers to IL phases with which it is contacted, as is the case in our experiments. This order is maintained as [D+][NO3−] is added, although the D2O amount is increasing significantly as [D+][NO3−]init is raised from 0 to 6 M for all samples. However, for the three series, the D2O transfer is more or less constant up to [D+][NO3−]init ∼ 3 M and then increases. This is ascribed to acid partial association above this value,30 assuming [D+][NO3−] and [H+][NO3−] behave similarly. D2O transfer to the lower phase, as evidenced in Fig. 1, implies a decrease in the volume of the upper phase. This volume change is almost negligible for S#2 ([C1C10im+][Tf2N−]), as it is less than 2.5% even at the maximum [D+][NO3−] value and is limited to ca. 4% for S#3 ([Me3BuN+][Tf2N−]) at [D+][NO3−]init = 6.45 M. Therefore, no correction to the experimental data has been made.
In addition to D2O transfer, [D+][NO3−] transfer to the lower phase also occurs, as previously mentioned in other publications.17,29,31,32 Fig. 2 shows the remaining [D+]eq values in the upper phase as a function of [D+][NO3−]init for S#1, S#2 and S#3. As compared to the volume change induced by D2O transfer, this is a second order effect, owing to the quantities involved. Considering the experimental uncertainties, only a slight difference can be acknowledged from one system to the other. Linear fits of the [D+]eq variations give very good regression coefficients (all above 0.997) and the three slopes are equal to 0.92 ([C1C4im+][Tf2N−] and [Me3BuN+][Tf2N−]) and 0.95 ([C1C10im+][Tf2N−]). These fits are displayed in Fig. 2 as lines. A slope value of 0.92 means that 92% of the initial [D+][NO3−] concentration remain in the upper phase after mixing. In our previous publication dealing with [H+][NO3−] transfer to [C1C4im+][Tf2N−], we indicated a slope of 0.90,18 but again, this slight difference may be ascribed to some variation in physico-chemical properties (density, mainly) as a consequence of the change from [D+][NO3−]/D2O to [H+][NO3−]/H2O for sample preparation.
For samples containing [C1C4im+][Tf2N−] or [Me3BuN+][Tf2N−], both IL ions could be accurately measured by NMR under any of the acidic conditions of this work. Fig. 3 presents the variations of [C1C4im+]eq and [Tf2N−]eq as a function of [D+][NO3−]init. Similarly, Fig. 4 presents the variations of [Me3BuN+]eq and [Tf2N−]eq as a function of [D+][NO3−]init. Again, because of the polarity of water and the presence of ions as IL components, there will be interactions between ions from the two phases, as mixing offers a better energetical balance. In both systems, the solubility of the cationic and anionic component of the IL increases as a function of [D+][NO3−]init, roughly in the same range, from ca. 15 mM in pure water up to ca. 90 mM for [D+][NO3−]init = 6 M. Values obtained in the absence of [D+][NO3−] compare well with previous published data: ca. 5 mM for [C1C6im+][Tf2N−] dissolved in H2O25 or 16 mM for [C1C4im+][Tf2N−] dissolved in H2O at T = 20 °C (ref. 33) or 16.5 mM at T = 298.2 K.22 In the absence of [D+][NO3−], to comply with electroneutrality, the amounts of IL cation and IL anion solubilized in the upper phase are equal, thus allowing to consider IL solubility as a whole. [Me3BuN+][Tf2N−] is slightly more soluble than [C1C4im+][Tf2N−] (16 mM and 22 mM respectively) in pure D2O. By contrast, values for [C1C10im+][Tf2N−] (3 mM) are close to the detection limits, evidencing a very low solubility of this IL in pure D2O as compared to the other two ILs, in agreement with the hydrophobicity of the C1C10im+ cation. In the presence of [D+][NO3−], the electroneutrality principle allows Tf2N− to be exchanged with NO3− and D+ to be exchanged with the IL cation. For [C1C4im+][Tf2N−] and [Me3BuN+][Tf2N−] there is a small but nevertheless significant difference between the IL cation and anion concentrations in the upper phase, the cation being more soluble, and this difference increases as a function of [D+][NO3−]init, reaching ca. 20 mM at the highest acidities of this work. By contrast, for the samples containing [C1C10im+][Tf2N−] (S#2), the IL cation concentration at equilibrium in the upper phase is too close to the detection limit, whatever the acid concentration and thus could not be reliably recorded so that only [Tf2N−]eq concentration is presented in Fig. 5. The low cation solubility is in line with the data obtained by another group,34 evidencing a C1C10im+ solubility in nitric acid phases in the range 0.4–1.5 mM from [H+][NO3−] = 0 to 4 M. As these authors did not measure the Tf2N− solubility, no further comparison with our work is possible. The [Tf2N−]eq values are low (Fig. 5), compared to those measured for the two other ILs, reaching ca. 45 mM at the highest acidity.
 | ||
| Fig. 3 Variations of [C1C4im+]eq (◊) and [Tf2N−]eq (●) as a function of [D+][NO3−]init for D2O&[D+][NO3−]&[C1C4im+][Tf2N−]. Solid lines are guide for the eye only. | ||
 | ||
| Fig. 4 Variations of [Me3BuN+]eq (Δ) and [Tf2N−]eq (●) as a function of [D+][NO3−]init for D2O&[D+][NO3−]&[Me3BuN+][Tf2N−]. | ||
 | ||
| Fig. 5 Variations of [Tf2N−]eq as a function of the [D+][NO3−]init value for D2O&[D+][NO3−]&[C1C10im+][Tf2N−]. Solid lines: linear fits below and above 3 M [D+][NO3−] (see text). | ||
The experimental data for S#1 and S#3 can be tentatively rationalized through the plots of the solubility products ks1, defined as ks1 = [C1C4im+]eqx[Tf2N−]eq, and ks3 = [Me3BuN+]eqx[Tf2N−]eq as a function of [D+][NO3−]init (Fig. 6). Interestingly, the variations can be divided in two linear ranges, below and above [D+][NO3−]init = 3 M (solid and dotted lines in Fig. 6), which would be in line with partial association of [D+][NO3−] above 3 M, as is known for [H+][NO3−]. Whatever the reasons, [C1C4im+][Tf2N−] and [Me3BuN+][Tf2N−] are more soluble in highly concentrated nitric acid solutions than in pure water. Our results show that the parameters controlling their solubility include ionic strength and composition of the sample. Understanding these effects at a molecular/ionic level would require a theoretical investigation out of the scope of this paper.
3.2 Samples with three salts (S#4–S#7)
Fig. 7 shows the amount of C1C4im+ in the upper phase as a function of [C1C4im+][Cl−]init for two different acidities (0.305 M and 2.221 M), while Fig. 8 presents the Tf2N− values under the same chemical conditions. As can be seen, most of the added cation remains in the upper phase, while [Tf2N−]eq is sharply decreasing. Similarly, Fig. 9 shows the amount of Tf2N− in the upper phase as a function of added [Li+][Tf2N−] under two different acidities (0.305 M and 2.221 M), while Fig. 10 displays the C1C4im+ variations. In this case, most of the added Tf2N− anion remains in the upper phase while C1C4im+ is expelled from the upper phase. The IL ion that was added to the aqueous phase (C1C4im+ or Tf2N−), is retained in the aqueous phase thanks to the hydrophilic counter-ion (Cl− or Li+) with which it is introduced. If the data are analyzed in terms of the solubility product defined as ks = [C1C4im+] × [Tf2N−], it is observed that: (i) ks is an increasing function of the added salt concentration; (ii) for a given acidity, ks does not depend on the type of salt added (see Fig. S2†). To the best of our knowledge, these results cannot be compared to any similar data in the literature. The closest study is that of Katsuta and co-workers, who studied the system H2O&[Na+][picrate−]&[Li+][Tf2N−]&[C1Cnim+][Tf2N−].22 The picrate and lithium salts were added in the mM range and there was no acid. Under such conditions, they observed a merely constant solubility product k = [Tf2N−] × [C1C4im+], a situation very different from ours. | ||
| Fig. 8 Variation of [Tf2N−]eq as a function of added [C1C4im+][Cl−] for [D+][NO3−] = 0.305 M (●) and [D+][NO3−] = 2.221 M (■). Solid lines: empirical fits; dotted lines: calculations. | ||
 | ||
| Fig. 9 Variation of [C1C4im+]eq as a function of added [Li+][Tf2N−] for [D+][NO3−] = 0.305 M (●, ○) and [D+][NO3−] = 2.221 M (■). Solid lines: empirical fits; dotted lines: calculations. | ||
 | ||
| Fig. 10 Variation of [Tf2N−]eq as a function of added [Li+][Tf2N−] for [D+][NO3−] = 0.305 M (● and ○) and [D+][NO3−] = 2.221 M (■). Solid lines: linear fits; dotted lines: calculations (see text). | ||
In order to go a step further than the descriptive approach above, we propose a quantitative basis of this phenomenon, under very simple assumptions. This model is briefly described here in the case of [Li+][Tf2N−] addition and can be easily adapted in case of [C1C4im+][Cl−] addition. First, as stated above, in the absence of any added [Li+][Tf2N−], the measured (experimental) values of C1C4im+ and Tf2N− are related through the solubility product as: ks = [C1C4im+]o × [Tf2N−]o, where superscript “o” denotes values in the absence of added [Li+][Tf2N−].
We consider this experimental solubility product value of [C1C4im+][Tf2N−] in water to be a constant at a given acidity value, whatever the other ions that may be present in the aqueous phase. This might not be the case under all chemical conditions, and especially at very high acidity values, where the ratio between water molecules and nitrate ions is low, but it is nevertheless a first attempt at describing the experimental data presented here. Upon addition of [Li+][Tf2N−] in excess, the mass balance for the equilibrium aqueous concentrations of C1C4im+, hereafter denoted as [C1C4im+]eq, should take into account the concentration of C1C4im+ which has transferred to the IL phase, denoted as y:
| [C1C4im+]eq = [C1C4im+]o − y |
Similarly:
| [Tf2N−]eq = [Tf2N−]o +[Tf2N−]ad − y |
| ([C1C4im+]o − y)([Tf2N−]o +[Tf2N−]ad − y) = ks |
In this last equation, y is the only unknown, which is the unique chemically acceptable solution of a degree 2 polynomial and is a function of the added quantity of [Li+][Tf2N−]. Under such a formalism, the expected values of [C1C4im+] and [Tf2N−] could be calculated for the samples of this work and the results are plotted in Fig. 7 to 10 as dotted lines. As can be seen, although this model is quite simple, the trend of the experimental data is very satisfactorily reproduced in case of [C1C4im+][Cl−] addition, whatever the acidity of the aqueous phase. This is an a posteriori justification of our assumptions under such chemical conditions. However, the agreement in case of [Li+][Tf2N−] addition is not so good, especially at low acidity (Fig. 8).
4. General comments on A–A and A–IL system similarities
In this section, we would like to put forward several arguments and facts in support of strong similarities between A–A and A–IL systems. To our opinion, the frontier between A–A and A–IL biphasic systems is rather thin. In this discussion, we will focus on samples containing two salts but most of the arguments can be easily extended to samples containing three or more salts.4.1 Similarities according to sample preparation
Using the notation of Section 2.1, the connection between A–A and A–IL biphasic systems is clear. As an illustration, let us consider the sample H2O&[H+][NO3−] (3.4 M, qs 0.8 ml)&[C1C4im+][Tf2N−] (0.8 ml), which contains identical amounts (in mole) of [H+][NO3−] and [C1C4im+][Tf2N−] (2.72 × 10−3 mole of each). On a practical perspective, i.e. for the exact chemical preparation of such a system, it is strictly identical to H2O&[H+][Tf2N−] (3.4 M, qs 0.8 ml)&[C1C4im+][NO3−] (2.72 × 10−3 mole). Both systems can be easily prepared because nitric and bis(trifluoromethanesulfonic)imide acids are commercially available and so is the IL [C1C4im+][Tf2N−], while the IL [C1C4im+][NO3−] can be synthesized according to published procedures.35 However, H2O&[H+][NO3−]&[C1C4im+][Tf2N−] could be considered as an A–IL biphasic system, because [C1C4im+][Tf2N−], which is a highly hydrophobic compound, is indeed an ionic liquid according to the definition based on melting points. Reversely, H2O&[H+][Tf2N−]&[C1C4im+][NO3−] could be classified as an A–A system, because [C1C4im+][NO3−] (which is also an IL, by the way) is highly soluble in water, and thus is also a “classical salt”.In the case of three or more salts, the possibilities for exchanging ions between the salts for the sake of preparation easiness are even extended and this reinforces the connections between A–A and A–IL discussed above. For example, H2O&[H+][NO3−]&[C1C4im+][Cl−]&[C1C4im+][Tf2N−], which contains two salts that are ILs, the latter being acknowledged as immiscible to water, is formally identical to the system H2O&[H+][Tf2N−]&[C1C4im+][Cl−]&[C1C4im+][NO3−] where the two salts are ILs highly soluble in water. An even more striking example of ion exchange from the preparation step is given by the sample H2O&[H+][NO3−] (6.8 M, qs 0.8 ml)&[C1C4im+][Tf2N−] (0.8 ml)&[Li+][Tf2N−] (2.72 × 10−3 mol) where the amount (in mole) of nitric acid is exactly twice as any of the two salts. Therefore, preparation can be done following H2O&[H+][Tf2N−] (6.8 M, qs 0.8 ml)&[C1C4im+][NO3−] (2.72 × 10−3 mol)&[Li+][NO3−] (2.72 × 10−3 mol). In the latter case, all salts used are common ones, independently highly soluble in water, while in the former case, one of the salts is an IL considered as not miscible to water. Finally, ion exchanges of this type can also be done using multicharged salts, such as the dicationic IL based on [C5(C10im)2]2+.36
4.2 Similarities in the biphasic state
Here, we will consider solely samples under a biphasic state at a fixed temperature, such as the samples of this study. Data in Fig. 1 clearly demonstrate that both the upper and lower phases of our samples contain water. Although the “solvent” is commonly the major fraction of a mixture, this is merely a question of definition and the lower phases of S#3, which contain up to 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm of water (for [D+][NO3−] = 7 M) (ca. 1.78 M of water, which corresponds to ca. a factor of 1.12 between D2O and IL number of moles) could be qualified “aqueous” provided the usual notion of solvent is extended, thus merging the A–A and A–IL definitions.
000 ppm of water (for [D+][NO3−] = 7 M) (ca. 1.78 M of water, which corresponds to ca. a factor of 1.12 between D2O and IL number of moles) could be qualified “aqueous” provided the usual notion of solvent is extended, thus merging the A–A and A–IL definitions.
Furthermore, in our study, ca. 5% of [D+] solubilizes in the lower phase (Fig. 2), while Cat+ and Ani− dissolve in the upper phase to different extents (Fig. 3 to 6, see Section 3.1). A difference between Cat+ and Ani− in the upper phase implies a difference between D+ and NO3− in the lower phase in order to comply with the electroneutrality rule. Therefore, the samples of this work, strictly speaking, once equilibrated, contain a small amount of [D+][Tf2N−] in the upper phase and a small amount of [Cat+][NO3−] in the lower phase. This actually corresponds to the exchange between ions as discussed above in Section 4.1 and is in line with what has been observed under the biphasic state of the A–A system H2O&[C1C4im+][Cl−]&[3K+][PO43−], for which any of the ions of the two salts distribute between the two phases.11
In the cases of S#4 to S#7, the salt added to the aqueous phase obviously influences the concentrations of the ions of the ionic liquids due to a limited solubility, as described in Section 3.2. For instance, considering the expression of ks for [C1C4im+][Tf2N−], addition of [C1C4im+][Cl−] in water in contact with [C1C4im+][Tf2N−] increases the concentration of IL cation, thus reducing the amount of [Tf2N−] anion in water. This makes as if introducing chloride anions in the system expels the Tf2N− from the upper phase (Fig. 8), while the added C1C4im+ ions are retained in the upper phase, whatever the [D+][NO3−]init value. Similarly, introduction of Li+ ions withdraw C1C4im+ from the upper phase. However, Tf2N− ions appear to be less soluble (being introduced as [Li+][Tf2N−] salt) at [D+][NO3−] = 2.221 M, as compared to [D+][NO3−] = 0.305 M. These experimental observations can be gathered under the phenomenological frame of salt-in/salt-out effects but again, a theoretical study would be required to understand the thermodynamic basis (at a molecular/ionic level) of this phenomenon. Anyway, the mixing of the various ions between the two phases evidenced in this work is typical of A–A systems, so that the barrier between A–IL and A–A is rather loose on this point.
4.3 Similarities in monophasic–biphasic transitions
Transitions from the monophasic to the biphasic state (or vice versa) may occur mainly under two different stimuli: change in concentration of the components or change in temperature. To our opinion, these are just two different ways of influencing the mutual solubilities of all components of the system. In the following, we will first discuss concentration effects and then temperature effects. Examples will be mainly taken from the literature.Typical studies on A–A systems include the determination of the binodal curve, which provides all information on the monophasic–biphasic state as a function of sample composition.7–10,13–15 In a large majority of cases, this binodal curve more or less resembles a monotonic decreasing curve, with two asymptotic ends, as schematically depicted in Fig. 11a. As a consequence, the monophasic state is obtained for rather limited ranges of concentrations of the two salts, when one of the salts is in low amount as compared to the other one. As schematically illustrated in Fig. 11a, starting from point A or A′ and following the arrows to B or to B′ i.e. increasing one salt concentration, keeping the other salt concentration constant, leads to changes from the monophasic to the biphasic state. Typical examples of such concentration ranges from the literature are for H2O&[C4C1im+][Cl−]&[3K+][PO43−] (ref. 10) where increasing the phosphate salt concentration from 1 mol kg−1 to 2.5 mol kg−1 for a constant 0.1 mass fraction of [C1C4im+][Cl−] modifies the system state from monophasic to biphasic. Similarly, for a fixed value of [K+][OH−] = 3 mol kg−1, increasing the [(C4H7)4N+][Cl−] IL concentration from 1 to 2 mol kg−1 turns the system from monophasic to biphasic.15 The fact that increasing the concentration of one salt, whatever the concentration of the other salt, leads to a change from monophasic to biphasic state has been often described as “incompatibility” of the two salts. However, this notion is purely qualitative and better reflects a personal feeling of the experimentalist than a quantitative notion. In a very limited number of cases, the binodal curve displays an unusual curvature,37 as schematically represented in Fig. 11b. In this case, the monophasic state can be obtained either for low or very high concentration of one of the salts (see points A and C in Fig. 11b) and therefore, the ‘incompatibility’ of the salts is a questionable concept.
 | ||
| Fig. 11 (a) Schematic representation of a ‘typical’ bimodal curve. (b) Schematic representation of an ‘atypical’ bimodal curve. | ||
Let us now consider the A–IL system: H2O&[H+][Tf2N−] (0–4 M, qs 0.8 ml)&[C1C4im+][Tf2N−] (0.8 ml). In a previous paper29 we have indicated that this system is biphasic at room temperature below 3 M of [H+][Tf2N−] and becomes monophasic above this value, therefore turning from H2O, [H+], [Tf2N−]//[C1C4im+], [Tf2N−] (biphasic state) to (H2O, [H+], [C1C4im+], [Tf2N−]), (monophasic state) according to the notation defined in Section 2.1. This phenomenon is well described under the frame of A–A systems, assuming the ‘atypical’ behavior as illustrated in Fig. 11b. The biphasic state observed would thus correspond to point B (the amount of [C1C4im+][Tf2N−] being on the x axis while that of [H+][Tf2N−] being on the y-axis). Above 3 M [H+][Tf2N−], the system turns to a monophasic state, from point B to C.
Another very interesting example from the literature of A–IL system can be well described under this A–A and binodal curve frame. One of our recent paper evidences Au(III) extraction from hydrochloric or hydrobromic aqueous phases by use of various pure IL phases.38 In particular, we have shown that the sample prepared as H2O&[H+][Cl−] (1.3 × 10−1 mol)&[K+][AuCl4−] (2.65 mM, qs 2 ml)&[C1C4im+][Cl−] (2.65 mM, qs 2 ml) instantaneously leads to a biphasic system upon mixing of the components, as H2O, [H+], [Cl−]//[C1C4im+], [AuCl4−]. A similar effect is obtained by use of [C1C4im+][Br−] and [H+][Br−] instead of [C1C4im+][Cl−] and [H+][Cl−] respectively and, in the case of [H+][Br−] and [C8pyr+][Br−], the biphasic system obtained is of the solid–liquid type. These results can be interpreted under different theoretical frames. One can consider that this illustrates a metathesis synthesis of an Au-based IL being not soluble in water, metathesis being a rather common way to exchange anions in view of IL synthesis.2 One can present the data as being liquid extraction of an unusual type, as we tentatively discussed in the cited paper, or one can acknowledge a case of A–A system involving a chloride salt being an IL, based on the melting point criterion.
Let us now turn to the discussion of temperature effects.
The small temperature variation allowed in our experiments (T = 19 ± 1)°C did not significantly influence IL and water mutual solubilities, as already observed for several systems,21,25 neither modify the biphasic status of the systems. However, larger changes in the temperature can lead to reversible switches from biphasic to monophasic state as already evidenced in various cases.7,12,39 In general, the higher the temperature, the higher are the salt and IL concentrations required for phase separation.40 As a consequence, this phenomenon can be applied to tune and control the mono/biphasic state of a system. This is illustrated in the paper of Zhou and co-workers,41 who investigated the system H2O&[Na+][Cl−] (8.5 × 10−3 mol)&[C1C6im+][PF6−] (45 μl, qs 10 ml) and showed that it is under a monophasic state above T = 70 °C, while it is biphasic at room temperature. Therefore, this typical A–IL system behaves as an A–A system does.
These examples are clear evidence that A–A and A–IL systems behave similarly, thus limiting the interest of classifying them differently.
5. Experimental implications for metal extraction
The experimental results of this study and in particular those depicted from S#4 to S#7 are of importance to the question of metal extraction by use of ILs and this is discussed below, with an attempt to make some predictions.5.1 Predictions of distribution ratio variation upon addition of IL cation or anion
Since the first papers by Dai and Visser,31,42 extraction of metallic ions from acidic aqueous phases has been investigated by use of various extractants, E, dissolved in IL phases instead of usual VOC (dodecane, chloroform, dichloroethane etc.). The reader is referred to some recent review papers on this topic.3,4,43,44 Liquid–liquid systems for such metallic ion extraction are basically A–IL systems very similar to the samples of this work because, most of the time, the metal and the extractant are in very limited amounts, so that the basic properties of the A–IL biphasic system are not significantly modified by these additives. As such, those liquid–liquid systems would in fact be A–IL systems composed of more than two salts, and, in view of sample preparation, could be noted as H2O&E&[Mm+][mX−]&[H+][X−]&[Cat+][Ani−], where [Mm+][mX−] is the metallic salt, [H+][X−] is the acid and E is the extracting agent. Their final stage (i.e. after extraction of the metal ion has been performed) would be noted as H2O, [H+], [X−]//E, [Mm+], [Cat+], [Ani−] according to the notation defined in Section 2.1.Based on several experimental evidences obtained by different groups, it is now acknowledged that metal extraction in A–IL systems proceeds mainly by ion exchange, either cationic or anionic, although extraction of neutral metallic species may also play a role.45–47 In a sense, ion exchange should be considered as of the same nature than the complex interplay between the three salts as evidenced for S#4 to S#7. In the following, we assume that the acid [H+][X−] is partly soluble in the IL phase, as shown here for [D+][NO3−] and evidenced for some other acids.29 Therefore, H+ is also present in non-negligible amounts (as compared to the maximum metal concentration) in the IL-rich phase. We will limit ourselves to the case of a neutral extracting agent not liable to protonation/deprotonation. Under this frame, the three possible extraction equilibria can be written as:
Cationic exchange:
 | (1) |
Ion pair extraction:
 | (2) |
Anionic exchange:
 | (3) |
According to eqn (1), addition of the salt [Cat+][Cl−] to the upper water-rich phase at a fixed [H+] value will lead to a decrease in the D values, as a consequence of [Cat+] increase, thus confirming a posteriori the cationic exchange mechanism (provided no by-side complexation occurs between Mm+ and Cl−). Similarly, according to eqn (3), addition of [Li+][Ani−] to the upper water-rich phase leads to an increase of [Ani−] and to the subsequent decrease in D value as a logical consequence of the anionic exchange mechanism. In the case of eqn (2), the distribution ratio should not be affected by addition of either [Cat+][Cl−] or [Li+][Ani−]. Actually, adding either [Cat+][Cl−] or [Li+][Ani−] in order to decipher the extraction mechanism has been a widely used method since its first use by Nakashima and co-workers,48 confirming a cationic or anionic exchange mechanism.16,26,49,50 However, our results show that addition of such salts leads to a rather complex composition of the upper water-rich phase. In particular, the addition of [Cat+][Cl−] is accompanied by a noticeable decrease of the Ani− concentration. This change in the Ani− concentration will result in an increase in D values according to eqn (3), as an indirect consequence of [C1C4im+][Cl−] addition. Conversely, adding [Li+][Ani−] in case of a cationic exchange ruled by eqn (1) should lead to a rise in the D values, because of the sharp decrease of Cat+ concentration, a phenomenon which would not be expected on the basis of eqn (1) alone.
In order to further investigate this aspect on a quantitative basis, we performed calculations taking advantage of the experimental data of this work for the eight possible cases: cationic or anionic exchange, addition of [C1C4im+][Cl−] or [Li+][Tf2N−], at two acidities [H+] = 0.305 M and [H+] = 2.22 M. The experimental C1C4im+ and Tf2N− variations displayed in Fig. 7 to 10 were first described with the help of empirical functions, which general forms are displayed in Table 1. Although we were able to reproduce the general trends of our experimental variation on a basis of a simple model (see Section 3.2), we prefer to use an empirical function, allowing a perfect recovery of the data for this part of the study. Solid lines in Fig. 7 to 10 represent the corresponding fitted variations. The form y = ax + b is the simplest way to take into account the solubility of the ions as displayed in Fig. 7 and 10. Note that the linear term added to the hyperbolic expression for the [C1C4im+] variation as a function of added [Tf2N−] was necessary to correctly recover the data at high anion loading: using a simple hyperbolic function in this case significantly degrades the χ2 values. Our data were acquired for a maximum [C1C4im+][Cl−] = 0.6 M, owing to difficulties in solubilization of this salt in highly acidic conditions, while the maximum of added [Li+][Tf2N−] was equal to 1 M. This difference in maximum ion loading from C1C4im+ to Tf2N− is most probably the reason for the difference in the empirical expressions needed for fitting and we are in favor of identical mathematical variations for both ions provided that the range of concentration is large enough. This point, however, could not be verified in the course of this work.
| Addition of [C1C4im+][Cl−] | Addition of [Li+][Tf2N−] | |||
|---|---|---|---|---|
| [C1C4im+] variation | [Tf2N−] variation | [C1C4im+] variation | [Tf2N−] variation | |
| [H+] = 0.3 M | y = ax + b | y = (ax + b)/(cx + d) | y = [(ax + b)/(cx + d)] + ex | y = ax + b |
| [H+] = 2.22 M | y = ax + b | y = (ax + b)/(cx + d) | y = [(ax + b)/(cx + d)] + ex | y = ax + b |
Then, we express the theoretical relation between the metal distribution ratio, D, the extraction equilibrium constant, K, and the aqueous concentrations of either Tf2N− or C1C4im+, according to eqn (1) or (3):
Cation exchange:
 | (4) |
Anion exchange:
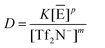 | (5) |
These two expressions have been obtained by neglecting the activity corrections and by assuming the concentrations of C1C4im+ and Tf2N− to be unity in the IL-rich phase. As a consequence, K is a conditional constant. In addition, the ratio of the [H+] quantities is constant, as illustrated in Fig. 2 and will thus be also included in the conditional constant K, together with the term [E]p. The other assumption underlying these two expressions is that the metallic entity is not liable to competitive complexation with the acid counter-anion of the system. By considering the empirical expressions displayed in Table 1, it is immediately understood that the plots ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D versus ln[C1C4im+] or versus Ln[Tf2N−] are not straight lines of slopes j (eqn (1)) or m (eqn (3)), as could be naively envisioned according to the traditional slope analysis method. In addition, the extend of deviation from linearity strongly depends on several factors: (i) the value of j, which is different from m, the charge of the metal ion, unless the number of exchanged H+ is zero, (ii) the acid concentration, (iii) the ion added, (iv) the nature of the ionic exchange actually occurring in the solution.
D versus ln[C1C4im+] or versus Ln[Tf2N−] are not straight lines of slopes j (eqn (1)) or m (eqn (3)), as could be naively envisioned according to the traditional slope analysis method. In addition, the extend of deviation from linearity strongly depends on several factors: (i) the value of j, which is different from m, the charge of the metal ion, unless the number of exchanged H+ is zero, (ii) the acid concentration, (iii) the ion added, (iv) the nature of the ionic exchange actually occurring in the solution.
As a third step of this quantitative part, we thus calculated the theoretical variations of D as a function of the initial concentration of the added salt, for the eight possible cases (two mechanisms, two acidities, two salts), assuming K = 1, as this is a conditional constant, and i = 0 in order to better compare j and m. In order to compare to typical literature cases whenever available, we supposed m = 1, 2 or 3 in case of cationic exchange, mimicking Cs+ (ref. 51) or Na+,52 UO22+ (ref. 16 and 17) or Eu3+.48,53 In case of anionic exchange, we supposed m = 1 or 2, as simulations for AuCl4− (ref. 38) or [Pu(NO3)6]2−.54
The results of these predictions are evaluated along two criteria. First, the D variation as a function of concentration of the added salt is qualified either “normal”, if D is monotonously decreasing as would be expected on the sole basis of eqn (1) or (3), or “abnormal”, in any other event. Second, in case of a “normal” behavior, the slope analysis method has been applied to the calculated D values, in order to derive japp, the apparent j value, to be compared to the charge of the metal entity, m. All the results are gathered in Table 2. The two different predicted abnormal D variations are displayed as ESI (Fig. S3 and S4†)
| Cation exchange | Anion exchange | |||
|---|---|---|---|---|
| [C1C4im+][Cl−] added | [Li+][Tf2N−] added | [C1C4im+][Cl−] added | [Li+][Tf2N−] added | |
| a n.a.: not applicable. | ||||
| [H+] = 0.3 M | Normal | Abnormal | Abnormal | Normal |
| m = 1; japp = 0.79 | n.a. | n.a. | m = 1; japp = 1.1 | |
| m = 2; japp = 1.59 | m = 2; japp = 2.2 | |||
| m = 3; japp = 2.39 | ||||
| [H+] = 2.2 M | Normal | Abnormal | Abnormal | Normal |
| m = 1; japp = 0.62 | n.a. | n.a. | m = 1; japp = 0.93 | |
| m = 2; japp = 1.25 | m = 2; japp = 1.86 | |||
| m = 3; japp = 1.87 | ||||
5.2 Discussion on the predicted variations and trends
We first make some general comments onto the results of our calculations.The first and possibly most important conclusion that can be drawn from a close examination of Table 2 is that, fortunately, it is impossible to misinterpret a mechanism. Adding the IL cation in case of a cationic exchange or adding the IL anion in case of an anionic exchange, whatever the acid value, always leads to a “normal” (i.e. expected) decrease of the D value, which is thus interpreted as the signature of the correct mechanism. However, in case of cation exchange/addition of IL cation, even without H+ exchange (i = 0 in eqn (1)) the derived japp value is quite different from m, which may be misinterpreted. For example, the non-integer value japp = 2.39 (cationic exchange, addition of [C1C4im+][Cl−], [H+] = 0.3 M, m = 3) may be ascribed to the joint extraction of +2 and +3 species instead of being due to distortion of the plot. By contrast, in case of anionic exchange/IL anion addition, the japp values are closer to the expected m ones. Similarly, adding the IL cation in case of anionic exchange, or adding the IL anion while a cationic exchange occurs leads to clear “abnormal” behaviors, thus the slope analysis method cannot be applied. As a first conclusion of practical interest, our results show that whatever the mechanism at work in the system under investigation and whatever the added salt, there is no risk to derive a wrong conclusion on the mechanism by adding a single salt. Consequently, we would suggest to add [Li+][Tf2N−] in any case, although it is quite expensive, because Li+ has very limited chance to be involved in any by-side reaction with the metallic ion, by contrast to Cl− arising from [C1C4im+][Cl−] addition, a weak complexing agent of several metallic ions. Another possibility in view of avoidance of by-side effects would be the use [C1C4im+][ClO4−].
5.3 Comparison to literature data
We now turn to the discussion of some experimental literature data concerning D variations of several metallic ions, upon addition of Cat+ or Ani− in the aqueous phase, at a fixed acidic concentration that can be put under the light of our predictions. In the followings, we thus assumed that our data, collected for deuterated solutions, can be readily used for comparison to data obtained in non-deuterated samples. We also assume that the presence of the extracting moiety, E, does not modify the experimental variations displayed in Fig. 7 to 10.“Normal” experimental results for IL cation addition that could be identified in the literature with chemical conditions closest to ours (i.e. acidic concentration close to 0.3 M or 2.2 M; [C1C4im+][Tf2N−] as the IL) have been published by ourselves and concern the system H2O&FILMA&[UO22+][2NO3−]&[H+][NO3−]&[C1C4im+][Tf2N−],16 where FILMA is a malonamide extracting agent. In this previous paper, we interpreted the decrease in D as [C1C4im+][Cl−] was added ([H+] = 0.3 M) as being the signature of a cation exchange between UO22+ and one C1C4im+ plus one H+. Re-considering the experimental variation under the light of this work, this conclusion is strongly supported by the excellent fit of the D values according to eqn (4), imposing j = 1 (see Fig. 12). For comparison purposes, the calculations for j = 2 are also displayed, showing the clear difference between the two trends and slopes. From the same work, we can also re-examine the experimental data obtained for [Li+][Tf2N−] addition at [H+][NO3−] = 4 M. The comparison is not as reliable as above, because of the difference in the acidic values. In our previous paper, we interpreted the decrease in D as a function of added [Li+][Tf2N−] salt as the signature of anionic exchange involving one Tf2N− anion and [UO2(NO3)3]−. Again, this interpretation is strongly supported by the excellent match between the experimental data and the fit according to eqn (5) (Fig. 13). Other examples of the literature concerning “normal” variations are more difficult to compare to our results because either the IL is not same or the acidity at which the salt has been added is rather different from those we fixed.48,53 We thus limit ourselves to mention the work of Rout et al., where addition of [Li+][Tf2N−] at [H+][NO3−] = 5 M, with or without extracting agent, leads to a clear decrease in the D values, with slope very close to one.54
 | ||
| Fig. 12 Variation of the U(VI) distribution ratio, D, as a function of added [C1C4im+][Cl−], at [H+][NO3−] = 0.3 M for the H2O&FILMA&[UO22+][2NO3−]&[H+][NO3−]&[C1C4im+][Tf2N−] system. Symbols: experimental data from ref. 16. Solid line: fit according to eqn (4), j = 1 and data of this work. Dotted line: calculation for j = 2 (see text). | ||
 | ||
| Fig. 13 Variation of the U(VI) distribution ratio, D, as a function of added [Li+][Tf2N−], [H+][NO3−] = 4 M for the H2O&FILMA&[UO22+][2NO3−]&[H+][NO3−]&[C1C4im+][Tf2N−] system. Symbols: experimental data from ref. 16. Solid line: fit according to eqn (5), m = 1 and data of this work. | ||
Of even larger interest is comparison with “abnormal” cases but such examples are scarce in the literature. We first identified the system H2O, H+, NO3−//DOA, Pu4+, C1C4im+, Tf2N−,54 where DOA is a new amide extracting agent. The authors added [Li+][Tf2N−] at [H+][NO3−] = 1 M, and observed an increase in D values. No interpretation is provided, and the authors indicate that “more studies are needed to understand the extraction behavior of Pu(IV) below 4 M nitric acid”. Under the classification of our work, such a variation is qualified as an abnormal case and would thus corresponds to a cationic exchange involving Pu(IV). This seems reasonable, because at 1 M nitric acid, the anionic plutonium complexes are probably not formed. In this paper, note that the authors performed addition of C1C4im+ at [H+][NO3−] = 1 M and also observed an increase in D, which would appear in contradiction with our results. However, the salt they used is [C1C4im+][NO3−] so that the counter-ion is a complexing agent of Pu(IV) that is certainly strongly interfering with the extraction mechanism, in particular because the maximum amount added is 1 M, thus modifying the Pu(IV)/NO3− speciation to a large extend, a situation which is not considered in our calculations. The second example from the literature comes from the system H2O&BPC6&[Cs+][Cl−]&[C1C2im+][Tf2N−],55 where BPC6 is a calix-crown extractant. Note that in this system, all aqueous solutions are at neutral pH. The authors demonstrate that the mechanism is cation exchange. Then, addition of C1C2im+ leads to a clear decrease in the extraction efficiency, as is expected, while addition of [Li+][Tf2N−] induces a large increase in the extraction efficiency, in perfect agreement with our predictions.
6. Conclusion
The strong similarities evidenced in this work between A–IL and A–A systems, in terms of preparation steps, ion exchange in the biphasic state and changes from mono to biphasic states under concentration or temperature stimuli are evidences that the distinction usually made between these system is rather artificial. Our work is also offering some prediction for specific experiments dedicated to the understanding of extraction mechanism of metallic ions that were successfully compared to data of the literature.It would be needed to go further than this more or less phenomenological step. Linking A–A and A–IL systems should be possible on a thermodynamical perspective. The usual description of A–IL (or A–Mol) systems used for metallic extraction by use of a set of chemical equilibria and subsequent mathematical treatment based on mass action law can be easily pursued by the determination of thermodynamical constants and quantities. The theoretical treatment of aqueous two phase systems6 and of imidazolium-based ILs56 that have appeared quite recently in the literature have set the theoretical basis for such an ambitious task, that will require more experimental and theoretical work, if possible performed in conjunction. Foreseen extensions could be the theoretical of third phase formation.
Acknowledgements
The help of Drs Lionel Allouche and Bruno Vincent for the NMR measurements of this work is greatly acknowledged. The comments of an unknown referee were of great help to improve the qualitative discussion of this work.References
- N. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123 RSC.
- P. Wasserscheid and T. Welton, Ionic liquids in synthesis, Wiley-VCH, Weinheim, 2008 Search PubMed.
- I. Billard, in Handbook on the Physics and Chemistry of Rare earth, ed. J. C. G. Bünzli and V. K. Percharsky, Elsevier, 2013, vol. 43 Search PubMed.
- A. Stojanovic and B. K. Keppler, Sep. Sci. Technol., 2012, 47, 189 CrossRef CAS.
- T. V. Hoogerstraete, S. Wellens, K. Verachtert and K. Binnemans, Green Chem., 2013, 15, 919 RSC.
- S. Naeem and G. Sadowski, Fluid Phase Equilib., 2011, 306, 67 CrossRef CAS PubMed.
- M. T. Zafarani-Moattar and A. A. Hamidi, J. Chem. Eng. Data, 2003, 48, 262 CAS.
- T. Murugesan and M. Perumalsamy, J. Chem. Eng. Data, 2005, 50, 1392 CAS.
- J. C. Merchuk, B. A. Andrews and J. A. Asenjo, J. Chromatogr. B: Biomed. Sci. Appl., 1998, 711, 285 CAS.
- M. T. Zafrani-Moattar and S. Hanzehzadeh, J. Chem. Eng. Data, 2010, 55, 1598 Search PubMed.
- K. E. Gutowski, G. A. Broker, H. D. Willauer, J. G. Huddleston, R. P. Swatloski, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2003, 125, 6632 CrossRef CAS PubMed.
- L. I. N. Tomé, F. R. Varanda, M. G. Freire, I. M. Marrucho and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 2815 CrossRef PubMed.
- S. P. M. Ventura, C. M. S. S. Neves, M. G. Freire, I. M. Marrucho, J. Oliveira and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 9304 CAS.
- Y. Deng, J. Chen and D. Zhang, J. Chem. Eng. Data, 2007, 52, 1332 CAS.
- N. J. Bridges, K. E. Gutowski and R. D. Rogers, Green Chem., 2007, 9, 177 RSC.
- M. Bonnaffé-Moity, A. Ouadi, V. Mazan, S. Miroshnichenko, D. Ternova, S. Georg, M. Sypula, C. Gaillard and I. Billard, Dalton Trans., 2012, 41, 7526 Search PubMed.
- I. Billard, A. Ouadi, E. Jobin, J. Champion, C. Gaillard and S. Georg, Solvent Extr. Ion Exch., 2011, 29, 577 CrossRef CAS.
- M. Sypula, A. Ouadi, C. Gaillard and I. Billard, RSC Adv., 2013, 3, 10736 CAS.
- F. A. Deeney and J. P. O'Leary, Eur. J. Phys., 2009, 30, 871 CrossRef CAS.
- I. Billard and S. Georg, Helv. Chim. Acta, 2009, 92, 2227 CAS.
- M. G. Freire, P. J. Carvalho, R. L. Gardas, I. M. Marrucho, L. M. N. B. F. Santos and J. A. P. Coutinho, J. Phys. Chem. B, 2008, 112, 1604 CrossRef CAS PubMed.
- S. Katsuta, K. Nakamura, Y. Kudo and Y. Takeda, J. Phys. Chem. B, 2012, 116, 852 CAS.
- M. J. Ruiz-Angel and A. Berthod, J. Chromatogr. A, 2006, 1113, 101 CrossRef CAS PubMed.
- A. N. Turanov, V. K. Karandashev and V. E. Baulin, Solvent Extr. Ion Exch., 2010, 28, 367 CrossRef CAS.
- K. Rehac, P. Moravek and M. Strejc, Fluid Phase Equilib., 2012, 316, 17 CrossRef PubMed.
- T. J. Bell and Y. Ikeda, Dalton Trans., 2011, 40, 10125 RSC.
- M. Malet-Martino, V. Gilard, F. Desmoulin and R. Martino, Clin. Chim. Acta, 2006, 366, 61 CAS.
- M. Malet-Martino and U. Holzgrabe, J. Pharm. Biomed. Anal., 2011, 55, 1 CrossRef CAS PubMed.
- C. Gaillard, V. Mazan, S. Georg, O. Klimchuk, M. Sypula, I. Billard, R. Schurhammer and G. Wipff, Phys. Chem. Chem. Phys., 2012, 14, 5187 CAS.
- A. Ruas, P. Pochon, J. P. Simonin and P. Moisy, Dalton Trans., 2010, 39, 10148 CAS.
- A. E. Visser, R. P. Swatloski, W. M. Reichert, S. T. Griffin and R. D. Rogers, Ind. Eng. Chem. Res., 2000, 39, 3596 CrossRef CAS.
- P. Giridhar, K. A. Venkatesan, T. G. Srinivasan and P. R. V. Rao, J. Radioanal. Nucl. Chem., 2005, 265, 31 CrossRef CAS.
- F. M. Maia, O. Rodriguez and E. A. Macedo, J. Chem. Thermodyn., 2012, 48, 221 CrossRef CAS PubMed.
- P. G. Rickert, D. C. Stepinski, D. J. Rausch, R. M. Bergeron, S. Jakab and M. L. Dietz, Talanta, 2007, 72, 315 CrossRef CAS PubMed.
- S. Georg, I. Billard, A. Ouadi, C. Gaillard, L. Petitjean, M. Picquet and V. Solov'ev, J. Phys. Chem. B, 2010, 114, 4276 CrossRef CAS PubMed.
- B. L. Bhargava and M. L. Klein, J. Phys. Chem. B, 2011, 115, 10439 CrossRef CAS PubMed.
- C. M. S. S. Neves, S. P. M. Ventura, M. G. Freire, I. M. Marrucho and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 5194 CrossRef CAS PubMed.
- N. Papaiconomou, G. Vite, N. Goujon, J. M. Levêque and I. Billard, Green Chem., 2012, 14, 2050 RSC.
- J. H. Olivier, F. Camerel and R. Ziessel, Chem.–Eur. J., 2011, 17, 9113 CrossRef CAS PubMed.
- R. Sadeghi, R. Golabiazar and H. Shekaari, J. Chem. Thermodyn., 2010, 42, 441 CrossRef CAS PubMed.
- Q. Zhou, H. Bai, G. Xie and J. Xiao, J. Chromatogr. A, 2008, 1177, 43 CrossRef CAS PubMed.
- S. Dai, Y. H. Yu and C. E. Barnes, J. Chem. Soc., Dalton Trans., 1999, 1201 RSC.
- K. Takao, T. J. Bell and Y. Ikeda, Inorg. Chem., 2013, 52, 3459 CrossRef CAS PubMed.
- K. Binnemans, Chem. Rev., 2007, 107, 2592 CrossRef CAS PubMed.
- M. N. Kobrak, Solvent Extr. Ion Exch., 2008, 26, 735 CrossRef CAS.
- I. Billard, A. Ouadi and C. Gaillard, Dalton Trans., 2013, 42, 6203 RSC.
- C. A. Hawkins, S. L. Garvey and M. L. Dietz, Sep. Purif. Technol., 2012, 89, 31 CrossRef CAS PubMed.
- K. Nakashima, F. Kubota, T. Maruyama and M. Goto, Ind. Eng. Chem. Res., 2005, 44, 4368 CrossRef CAS.
- F. Kubota, Y. Shimobori, Y. Baba, Y. Koyanagi, K. Shimojo, N. Kamiya and M. Goto, J. Chem. Eng. Jpn., 2011, 44, 307 CrossRef CAS.
- X. Sun, D. Wu, J. Chen and D. Li, J. Chem. Technol. Biotechnol., 2007, 82, 267 CrossRef CAS.
- H. Luo, S. Dai and P. V. Bonnesen, Anal. Chem., 2004, 76, 2773 CrossRef CAS PubMed.
- C. Xu, L. Yuan, X. Shen and M. Zhai, Dalton Trans., 2010, 39, 3897 RSC.
- K. Shimojo, K. Kurahasha and H. Naganawa, Dalton Trans., 2008, 5083 RSC.
- A. Rout, K. A.Venkatesan, T. G. Srinivasan and P. R. V. Rao, Sep. Purif. Technol., 2012, 97, 164 CrossRef CAS PubMed.
- T. X. Sun, X. H. Shen and Q. D. Chen, Sci. China: Chem., 2013, 56, 782 CrossRef CAS.
- X. Jin, C. Held and G. Sadowski, Fluid Phase Equilib., 2013, 335, 64 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra00645c |
| This journal is © The Royal Society of Chemistry 2014 |



