Chiral segregation of hockey-stick shaped particles in two dimensions
J. A. Martínez-González†
a,
R. Pablo-Pedro‡
a,
J. C. Armas-Pérez§
a,
G. A. Chapelab and
J. Quintana-H*a
aInstituto de Química, Universidad Nacional Autónoma de México, Apdo. Postal 70213, 04510, Coyoacán, México, D.F., Mexico. E-mail: jaq@unam.mx; Fax: +52 55 56224510; Tel: +52 55 56224510
bDepartamento de Física, División de Ciencias Básicas, Universidad Autónoma Metropolitana, Iztapalapa, México, D.F., Mexico
First published on 12th March 2014
Abstract
Chiral segregation and liquid crystalline aggregates in two dimensions are studied for a heterochiral mixture of oversimplified versions of so called hockey stick-shaped particles, made with two line segments that interact via an infinitely repulsive potential. The goal of this study is to explore the possibility of producing chiral segregation and finding liquid crystalline mesophases using this model which has an extreme level of idealization. In particular, by considering infinitely thin particles and infinite repulsions interacting exclusively side to side, the substrate does not act on the molecules. Since only infinite repulsions are considered, the phase behavior is ruled by entropic effects, where self-assembly takes place. Onsager theory and Monte Carlo simulations in the Gibbs and canonical ensembles were used to study several molecular conformations in order to delineate the mesophase diagram which includes the chiral segregation region and several liquid crystalline mesophases, most of them heterochiral. The enantiomerically pure phase is of the smectic kind and corresponds to the highest density regime. The heterochiral mesophases are nematic, smectic with antiferroelectric order and tetratic. The appearance of the different assemblies strongly depends on the molecular conformation defined by the angle between the segments and their lengths. To study the phase transitions, the molar concentration, the nematic and tetratic order parameters, as well as the distribution functions were calculated.
1 Introduction
Chirality is a phenomenon where symmetry plays an essential role. It has important consequences in several fields of natural sciences such as chemistry, biology and physics. Chirality at the molecular level gives rise to a pair of mirror-image molecules, called enantiomers. Although there are similarities between the enantiomeric pair components, such as identical physical or chemical properties, each of them may have very different or even opposite effects in living beings. This is the reason why the separation of enantiomeric mixtures is of fundamental interest in the food and pharmaceutical industries. At the same time, the presence of chirality in materials science may change the characteristics of materials opening diverse possibilities for their fabrication.In nature, the production of chiral components is asymmetrical, that is, the components of living beings, such as amino acids or sugars, have a specific chirality. On the other hand, in the laboratory, synthesis of chiral compounds produces heterochiral mixtures, unless special procedures are applied.1
Spontaneous separation of racemic mixtures (50% of each component) is not frequent, up today have been possible to separate less than 10% of the known racemic compounds.2 The first was discovered by Pasteur using a crystallization process in the bulk. However, in the laboratory, unless special procedures are applied, synthesis of chiral compounds results in a racemic mixture.1 In recent years, several experiments have shown that enantiomeric separation can be enhanced in situations that show some kind of constraint, for example, a reduction in the dimensionality of the system, creating a reduction in the spatial degrees of freedom and therefore a change of the symmetry rules. One of the consequences of this is that there are systems that in three dimensions are not chiral, but when they are confined to a bi-dimensional domain the structure can be considered chiral. Molecules with this feature are called pro-chiral3 and the molecular model considered in this paper is one example. Another condition that seems to be necessary is that this phenomenon occurs in high density regimes, for example, the molecular self-assembly that occurs in two dimensional domains.4 One of the earliest experiments reported is the spontaneous chiral separation of amphiphilic molecules in a monolayer by Nassoy et al.4 in a Langmuir balance. Chiral domains of small size are formed by reduction of the surface of the monolayer formed at the water/air interface. Some other experiments have been performed using the Langmuir–Blodgett device, where chiral segregation also occurs.5 In these cases, the substrate is a central part of the separation process. In general, in all these experiments, the common characteristic is that a considerable degree of molecular ordering, both positional and orientational, is present. However, Huang et al.6 found that the orientation may not be necessary.
Important efforts have been made in order to elucidate this complex phenomenon. From the theoretical point of view, Huckaby et al. were among the pioneers attacking this problem using lattice models. Since the 1980s they have published several papers in which the particles used were adsorbed onto a plane.7,8 More recently, they studied the chiral separation of the Andelman–de Gennes9 model using different kinds of interactions, including van der Waals and electrostatic.10 There are also several simulation studies on this topic.11,12 Despite the fact that there have been several attempts dedicated to analyzing this problem, the understanding of the molecular details that enhance the chiral separation is still incomplete.
The background behind this paper is that a similar system constructed from three segments, a zigzag model, interacting with infinitely repulsive potentials and confined to a 2D domain, was able to show chiral separation.13 In this case, since the system was athermal, the phase separation was controlled only by the density. Complementary studies of the zigzag model were devoted to investigating its liquid crystalline behavior. The first used a Monte Carlo isobaric ensemble,14 and a further study16 applied the Onsager theory.15
The general goal of this paper is to investigate the ability to produce chiral phase separation considering a modification of the zigzag system where the present model has only two segments. This oversimplified system, built with only two lines, is called a hockey-stick shaped particle.17 The molecular conformations used for this paper are those that create chiral structures, i.e. where the lengths of the two segments are unequal.
The paper is organized as follows; the introduction is found in Section 1, the definition of the model and the simulation details are in Section 2, Section 3 contains the results and their explanations, and finally the conclusions are in Section 4.
2 The model and Monte Carlo simulation details
A two-dimensional hard body model whose shape mimics hockey-stick (HSM) molecules is studied. Our model particle consists of two line segments of unequal length. The lengths of the segments are a and b, i.e. the total length of the model particle is L = a + b. The model is sketched in Fig. 1.Our previous study17 has been extended by examining the chiral segregation of HSMs with a = 0.11, 0.15, 0.18, 0.20, 0.22, 0.25, 0.30, 0.35, 0.40 and 0.45, for θ = π/4 and π/2. Note that the total length of the particle is L = 1, i.e. b = 1 − a. The total number of particles in the simulation was N = 1000.
The density is defined as ρ* = N/(L*x*L*y) where L*x and L*y are the simulation box lengths for the x and y axes, respectively, and L is used to make the lengths dimensionless (r* = r/L). The dimensionless pressure is defined as p* = pβL2 where β = 1/kBT, and kB is the Boltzmann constant and T is the temperature. Because the model is athermal the temperature has been set to kBT = 1.
For chiral segregation studies, Monte Carlo simulations in the Gibbs ensemble (GEMC) were performed. The use of this ensemble allows the simulation of the coexistence of two enantiomerically different phases. Despite the chiral separation process being reached at high densities, it is possible to use the Gibbs ensemble because of the thickness of the model considered. According to the standard methodology,18 three types of configurational changes were performed: (a) random displacements or orientation changes were performed for randomly selected particles, (b) changes in the area of the simulation boxes were made, and (c) randomly selected particles were transferred from one of the simulation boxes to the other. In this work, a Monte Carlo cycle (MCC) consisted of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 attempted displacements or orientation changes, 1 attempted area change and about 1000 attempted particle swaps. Approximately 4 × 106 MCCs were required for equilibration and a further 2 × 106 MCCs for obtaining statistics.
000 attempted displacements or orientation changes, 1 attempted area change and about 1000 attempted particle swaps. Approximately 4 × 106 MCCs were required for equilibration and a further 2 × 106 MCCs for obtaining statistics.
The acceptance criterion for these trial moves corresponds to the standard Metropolis algorithm for this ensemble. The maximum displacement, rotation angle and area change was adjusted during the simulation so that roughly 30% of these types of moves are accepted. The number of particles in each box at the beginning of the simulations was 500. In order to verify the lack of influence of the initial configuration on our results, we performed simulations where the initial composition of the two regions was either heterochiral or fully segregated (pure phases of each enantiomer in each region, see Section 3).
Finally, the order parameter that characterizes the phase transition that produces chiral separation is the configurational average of the molar fractions XS and XR of the simulation boxes, where the subscripts refer to right (R) and left (S) enantiomers. The criterion adopted is as follows:19 segregation is considered finished when in one of the boxes the molar fractions XS ≥ 0.85 and XR ≤ 0.15, while in the other box the opposite occurs.
The orientational order in the mesophases was quantified by means of the order parameter given by Sm = max〈cos[m(ϕ − ϕ0)]〉, where ϕ is the angle between the molecular axis of the particle and the axis of reference and ϕ0 defines the vector n = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0, sin
ϕ0, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0) which provides the natural coordinate system for orientationally ordered phases. When m = 2, Sm gives the nematic order parameter, while m = 4 provides the tetratic order parameter. Similarly, for nematic and tetratic order, the orientational correlation function is gm(r*) = 〈cos m(ϕ − ϕ0)〉r, where the average is taken over a pair of particles.
ϕ0) which provides the natural coordinate system for orientationally ordered phases. When m = 2, Sm gives the nematic order parameter, while m = 4 provides the tetratic order parameter. Similarly, for nematic and tetratic order, the orientational correlation function is gm(r*) = 〈cos m(ϕ − ϕ0)〉r, where the average is taken over a pair of particles.
Several studies in 2D indicate that the nematic and tetratic order parameters vanish in the thermodynamic limit and the orientational correlation functions g2 and g4 have a power law decay, which are indications of quasi-long range order (QLRO) for both mesophases.17,20–23 Because of the fact that g2 and g4 have an exponential decay in the isotropic phase, the change in their behavior is a consequence of a phase transition.
Canonical simulations were implemented to complement the GEMC simulations, in particular to compute the nematic (S2) and tetratic (S4) order parameters, as well as the radial correlation function (g(r*)) and the orientational correlation functions (g2(r*) and g4(r*)).
3 Results
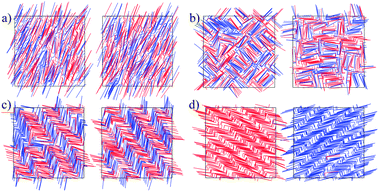
Since the model is athermal, the only thermodynamic variable that controls the phase transitions is the density ρ*. The Gibbs ensemble was simulated using a wide range of densities, several molecular conformations a = 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, and two molecular angles θ = π/2, π/4. In all cases, the initial configuration was heterochiral (racemic) for both boxes. For sufficiently low densities, an isotropic (I) structure was obtained. As the density was raised, orientational correlations started to appear, more explicitly, for enough anisotropic molecular conformations.For θ = π/2, a heterochiral nematic (N) phase was developed for a ≤ 0.15, while for 0.15 ≤ a ≤ 0.225 a heterochiral tetratic (T) phase was displayed for ρ* ≈ 20 (see Fig. 2b). The S2 and S4 order parameters for different a-values, as well as the orientational correlation functions g2 and g4 for a = 0.11 and a = 0.20, are plotted in Fig. 3 where the change in the decay for different values of the density can be appreciated. As can be observed, the nematic order parameter S2 is reported for a = 0.11, 0.15, while for the other values of a the tetratic order parameter S4 is shown. Only for a = 0.15 does the system present I–T, T–N and N–Sm phase transitions.
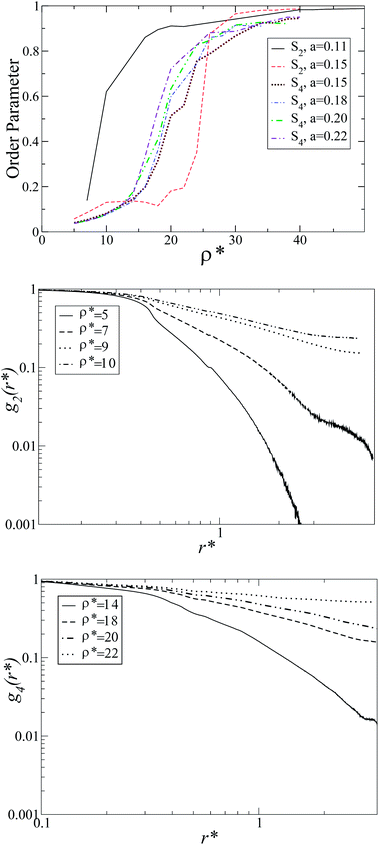 | ||
| Fig. 3 Nematic and tetratic order parameters (top), and the orientational correlation functions g2 and g4 on a log–log scale for a = 0.11 and a = 0.20 (centre and bottom, respectively). | ||
Positional correlations were developed for sufficiently high densities, that depend on the molecular anisotropy. For example, for a > 0.25 a racemic smectic order (SmR) was obtained; this structure is globally heterochiral in both boxes (see Fig. 2c). In this kind of smectic order the rows have both kinds of enantiomers which alternate with each other, producing heterochiral rows. Chiral segregation was obtained as two coexisting homochiral smectic phases, each one in a simulation box (see Fig. 2d). It should be noted that both phases are chiral, and this is represented by the asterisk in the notation (Sm*). For a ≤ 0.25 chiral separation is a result of a nematic–smectic phase transition, while for a > 0.25 it is a consequence of a smectic–smectic phase transition from a heterochiral smectic to a homochiral smectic. In all cases, the specific value of the density depends on the molecular conformation. A qualitative mesophase diagram is shown in Fig. 4.
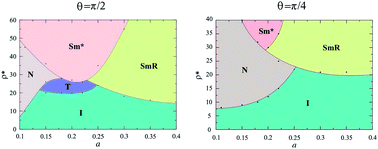 | ||
| Fig. 4 A mesophase diagram of density as a function of the molecular parameter a, for (a) θ = π/2 and (b) θ = π/4. The dots are the simulation results and the lines are to guide the eye. | ||
For θ = π/4, a tetratic order was not observed and higher densities were required to achieve chiral segregation, as can be observed from Fig. 4. Fig. 5 shows a comparison of the lowest densities for which segregation was obtained as a function of the parameter a of the model. It is possible to appreciate from the figure that a = 0.25 is the value that favors chiral segregation for both bent angles, and when a → 0.5 or a → 0 the density increases dramatically. Actually, chirality is lost in the banana limit (a = 0.5) and in the hard needles limit (a = 0), where the simulation results coincide with those previously reported for these cases.20,23 The difference in the homochiral case17,20 is that in heterochiral systems of HSMs there is a tetratic behavior for θ = π/2, and because of the effect of the excluded area between enantiomeric pairs, the smectic phase is obtained for higher densities in both cases (θ = π/2 and θ = π/4).
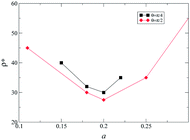 | ||
| Fig. 5 A graph of the lowest density in the simulations for which the system segregates as a function of the molecular parameter a. | ||
As mentioned, this model shows isotropic (I), nematic (N), heterochiral-smectic (SmR) and tetratic (T) behavior, this last one for θ = π/2, and the chiral segregation is given by two chiral smectic phases (Sm*); actually these smectics have an antiferroelectric order.
It is possible to explain the formation of all these structures by means of the second virial theory which has been successfully used to study the isotropic–nematic and the nematic–smectic phase transitions of banana and hockey-stick particles in two dimensions.16,17,20 In this work, we focus on showing what kind of smectic correlations (Sm* or SmR) are more favorable according to the values of a, θ and ρ*.
Because we consider only hard interactions, the formation of mesophases is controlled by entropic effects which are related to the excluded area. Based on the second virial theory, the free energy F can be written as the sum of an ideal energy Fid and an excess contribution Fex,
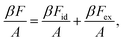 | (1) |
In processes where the density is continuously increased and the system shows a N–Sm* phase transition, just before the smectic phase is formed, the nematic phase is orientationally well ordered. As a result, in the study of the N–Sm* phase transition it is possible to assume that the nematic phase is formed by a mixture of perfectly aligned particles. The “species” of this mixture are the possible orientations of the particles and they are referred to as conformations. In the case of a nematic phase made from one component with polar geometry, there are two conformations (up and down), while in the case of two components (as happens in the heterochiral mixture) there are four conformations (each component can be up or down, see Fig. 6a). Therefore the ideal and the excess contributions of the free energy are given by
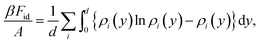 | (2) |
 | (3) |
First, an estimation of the free energy of a heterochiral smectic phase (SmR) is performed. In a perfectly aligned nematic phase, the local densities do not depend on the position and are identical, i.e. ρ1,2,3,4(y) = ρ/4, and Aiiexc = Ajjexc, Aijex = Ajiexc, A12exc = A34exc, A13exc = A24exc and A14exc = A23exc (see Fig. 6a). Therefore, the nematic free energy is then,
 | (4) |
From the snapshots of the simulation (see Fig. 2c), the particle assembly for the SmR phase is such that each layer of the smectic phase is formed by either conformations 1 and 4, or 2 and 3, as sketched in Fig. 6b. The periodicity of the layers in the weakly ordered smectic phase can be modeled by means of the first order Fourier representation of the local densities, given by  and
and  , where
, where  is the smectic wave number, ϕ* is the phase shift and ε is a parameter which goes to zero in the nematic limit. After substitution of these density dependencies, the ideal and excess parts of the free energy become
is the smectic wave number, ϕ* is the phase shift and ε is a parameter which goes to zero in the nematic limit. After substitution of these density dependencies, the ideal and excess parts of the free energy become
 | (5) |
 | (6) |
 | (7) |
The parameters ϕ* and q are such that  ; in the first case ϕ* = π, which means that the phase is always antiferroelectric and q satisfies
; in the first case ϕ* = π, which means that the phase is always antiferroelectric and q satisfies
| ∫dy12y12d11exc(y12)sin(qy12) + ∫dy12y12d14exc(y12)sin(qy12) − ∫dy12y12d12exc(y12)sin(qy12) − ∫dy12y12d13exc(y12)sin(qy12) = 0. | (8) |
With the values of ϕ* and q, it is possible to estimate the heterochiral-smectic free energy for different ε values. The coexistence density for the nematic-heterochiral smectic phase transition is given by the condition  , which is equivalent to the condition that the quadratic term in epsilon in eqn (7) must vanish. From eqn (9) it is found that
, which is equivalent to the condition that the quadratic term in epsilon in eqn (7) must vanish. From eqn (9) it is found that  . A similar procedure was done to estimate the free energy of the homochiral smectic (Sm*) phase, but in this case there are only two conformations such that the smectic layers are made either by conformations 1 and 2, or 3 and 4 (see Fig. 6c). As a result the free energy is
. A similar procedure was done to estimate the free energy of the homochiral smectic (Sm*) phase, but in this case there are only two conformations such that the smectic layers are made either by conformations 1 and 2, or 3 and 4 (see Fig. 6c). As a result the free energy is
 | (9) |
| ∫dy12y12d11exc(y12)sin(qy12) + ∫dy12y12d14exc(y12)sin(qy12) = 0, | (10) |
By equating eqn (7) with the smectic free energy of a homochiral system (the segregated case) it is possible to obtain an approximation of the densities for which such phases coexist and the intervals in which a given smectic (racemic or segregated) is more favorable, as shown in Fig. 7.
The theoretical estimations of the density for which chiral segregation is reached, ρ*c, are given in Fig. 8 for some values of the parameter a. For a ≤ 0.2 it is found that the heterochiral nematic phase is more favorable than the heterochiral and homochiral smectic phases at intermediate densities, while for densities larger than ρ*c the homochiral smectic phase becomes more favorable. For a ≥ 0.25, the heterochiral smectic phase is the more favorable phase for intermediate densities, and for higher densities the homochiral smectic phase is again more favorable, which is in agreement with the simulation results. Although the theory underestimates the N–Sm* and SmR–Sm coexistence densities, it captures the qualitative behavior obtained by the simulations.
4 Conclusions
An oversimplified version of a HSM made of 2-segment lines interacting with an infinitely hard potential that is geometrically chiral in 2D, is capable of producing chiral segregation and several liquid crystalline mesophases. As in many other cases, chiral segregation requires a high density regime and therefore molecular ordering is achieved. For lower densities, the system exhibits different heterochiral liquid crystalline phases. That is, depending on the value of the parameter a, as density decreases the model shows nematic or smectic structures. As expected, for small values of a, close to the hard needle limit, the nematic phase is preferred, while for large values of a, the smectic phase is generated; both are heterochiral. For the lowest densities considered, the heterochiral isotropic phase is present. These features are common to both values of the molecular angle θ studied; θ = π/2 and π/4. To complement the Monte Carlo simulation results, the second virial Onsager theory was used to predict some of the phase transitions provided by the simulations, in particular, N–Sm*, N–SmR, and SmR–Sm. To the best of our knowledge, this is the first time this kind of theory has been used to study chiral separation. This has been possible in this particle model, since chiral separation occurs along smectic correlations.It should be considered that the transition to the smectic phase (racemic or not) was done in the limit of parallel particles (perfectly nematic) and it is useful for the study of the N–Sm phase transition. This approximation was used for the whole range of the parameter a, even for some regions where the phases involved (from MC) were either I or T. Despite this approximation being rough, it is interesting to note that the qualitative behavior is captured. On the other hand, the estimation of the SmR–Sm coexistence density was performed by equating the free energies of both mesophases up to the second virial approximation and using the first order Fourier representation of the local densities. Although the coexistence densities are just approximations, the development of the theory was useful to find the parameters for which the smectic mesophases found are more favourable. The extension of the theory to include the isotropic-tetratic phase transition is also possible and it is part of a future work.
Acknowledgements
This research was financially funded by CONACYT grant 168001 and UNAM-DGAPA-PAPIIT. J.A. Martinez-Gonzalez and R. Pablo-Pedro are grateful for the support given by the CONACYT grant 168001; Julio C. Armas-Pérez is thankful to CONACYT for the Postdoctoral Fellowship no. 203840. We also gratefully acknowledge Martha Elena Buschbeck Alvarado for improving the English of the manuscript.References
- J. Jacques, A. Collet and S. H. Wilen, Enantiomers, Racemates and Resolutions, John Wiley & Sons, New York, 1981 Search PubMed.
- I. Paci, I. Szleifer and M. A. Ratner, J. Am. Chem. Soc., 2007, 12, 3545–3555 CrossRef PubMed.
- N. Richardson, Nat. Mater., 2006, 5, 91–92 CrossRef CAS PubMed.
- P. Nassoy, M. Goldmann, O. Bouloussa and F. Rondelez, Phys. Rev. Lett., 1995, 75, 457–460 CrossRef CAS.
- R. Viswanathan, J. Zasadzinski and D. Schwartz, Nature, 1994, 368, 440–443 CrossRef CAS.
- T. Huang, Z. Hu, A. Zhao, H. Wang, B. Wang, J. Yang and J. G. Hou, J. Am. Chem. Soc., 2007, 129, 3857–3862 CrossRef CAS PubMed.
- D. A. Huckaby, M. Ausloos and P. Clippe, J. Chem. Phys., 1985, 82, 5140–5145 CrossRef CAS PubMed.
- D. A. Huckaby, M. Shinmi, M. Ausloos and P. Clippe, J. Chem. Phys., 1986, 84, 5090–5094 CrossRef CAS PubMed.
- D. Andelman and P. G. de Gennes, C. R. Acad. Sci., 1988, 307, 233–237 CAS.
- I. Medved, A. Trnik, A. K. Belkasri and D. A. Huckaby, J. Chem. Phys., 2007, 126, 154512 CrossRef PubMed.
- I. Paci, J. Phys. Chem. C, 2010, 114, 19425–19432 CAS.
- P. Szabelski and D. S. Sholl, J. Chem. Phys., 2007, 126, 144709 CrossRef PubMed.
- R. A. Perusquia, J. Peon and J. Quintana, Phys. A, 2005, 345, 130–142 CrossRef CAS PubMed.
- J. Peon, J. Saucedo-Zugazagoitia, F. Pucheta-Mendez, R. A. Perusquia, G. Sutmann and J. Quintana-H, J. Chem. Phys., 2006, 125, 104908 CrossRef PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- S. Varga, P. Gurin, J. Armas-Pérez and J. Quintana-H, J. Chem. Phys., 2009, 131, 184901 CrossRef PubMed.
- J. Martínez-González, S. Varga, P. Gurin and J. Quintana-H, J. Mol. Liq., 2013, 185, 26–31 CrossRef PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2nd edn, 2002 Search PubMed.
- L. Gonzalez-Lee, J. Armas, J. Peon and J. Quintana, Phys. A, 2008, 387, 145–158 CrossRef PubMed.
- J. A. Martínez-González, S. Varga, P. Gurin and J. Quintana-H, Europhys. Lett., 2012, 97, 26004 CrossRef.
- A. Donev, J. Burton, F. H. Stillinger and S. Torquato, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 054109 CrossRef.
- D. A. Triplett and K. A. Fichthorn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011707 CrossRef.
- D. Frenkel and R. Eppenga, Phys. Rev. A, 1985, 31, 1776–1787 CrossRef CAS.
Footnotes |
| † Present address: Departamento de Física, División de Ciencias Básicas, Universidad Autónoma Metropolitana, Iztapalapa, México D.F., Mexico. |
| ‡ Present address: Department of Chemistry, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. |
| § Present address: Institute for Molecular Engineering, University of Chicago, Chicago, Illinois 60637, USA. |
| This journal is © The Royal Society of Chemistry 2014 |