Research on epoxy resin decomposition under microwave heating by using ReaxFF molecular dynamics simulations

Abstract

To investigate the effects of microwave heating on decomposing epoxy resin, ReaxFF molecular dynamics simulations are performed. As one of its special effects, the thermal runaway phenomenon is studied and compared under microwave heating and under conventional heating. This study shows that this phenomenon results from the enhancement of system absorption of microwave energy, which is caused by the increasing number of small size polar species generated during the pyrolysis of epoxy resin under microwave heating. Meanwhile, non-thermal effects are investigated under microwave heating. Simulations indicate that, at the early stage of decomposition, average generating rates of H₂O and H₂ obtained under microwave heating are always, or partly, lower than that obtained under conventional heating. To analyze the influence of microwave heating on reaction rates, collision theory is introduced. Further, several simplified collision models are constructed and formulated to study the effectiveness of collision orientations under microwave heating. Analyses illustrate that external microwave heating reduces the effectiveness of collision orientations between polar hydric fragments as well as hydroxyl radicals and polar hydric fragments, thus, decreasing relevant reaction rates.

---

1. Introduction

Today, there is an ever-increasing amount of waste electrical and electronic equipment (WEEE). Of this equipment, the waste printed circuit board (WPCB) is one of the most abundant elements. Thus, how to dispose of or recycle WPCBs attracts more and more attention and research. High temperature pyrolysis is a popular method of dealing with WPCBs.^1–4 Due to its characteristic high efficiency, strong penetrability, and selective heating,^5–8 microwave heating has been introduced into the decomposition process of WPCBs as a heating source in recent years.^9,10 As a main material, epoxy resin is selected as a model compound for WPCBs. When analyzing the pyrolysis stage of epoxy resin under microwave heating, efficient analytical methods are required. Since decomposition of epoxy resin is relatively complex, especially when microwave heating is applied to the reaction system, it is difficult to analyze interactions between microwave and chemical reactions through conventional methods. Although some conventional numerical simulations based on heat equations and electromagnetic equations, as well as equivalent dielectric coefficient equations, have been performed in recent years, they only focus on some substances under microwave heating, for example, microwave heating of infinitely dilute solutions or pure water.^11,12 The heating process involving complicated chemical reactions under a microwave environment has not been studied extensively.

Molecular dynamics simulation (MDS) is an efficient method to study non-equilibrium processes and chemical reactions. The use of MDS to investigate heating processes and special effects of some substances under microwave heating is ever increasing.^13–16 In recent decades, MDS employing Reactive Force Field (abbreviated as ReaxFF)¹⁷ has been widely used to simulate hydrocarbon oxidation, organic matter decomposition, and other complicated chemical reactions such as pyrolysis and oxidation of toluene,¹⁸ early maturation processes in coal,¹⁹ decomposition of nitromethane,²⁰ and so on.^21–24 With the computing cost of classical molecular dynamics, ReaxFF MDS can achieve the accuracy of quantum mechanical methods when simulating some large scale chemical reactions and is reliable in the investigation of reaction processes and products.

Here, ReaxFF MDS is used to analyze the cracking process of epoxy resin under microwave heating. As compared with the process under conventional heating, thermodynamic characteristics and effects after introducing microwave energy into the reaction system are studied in depth.

2. Simulation details

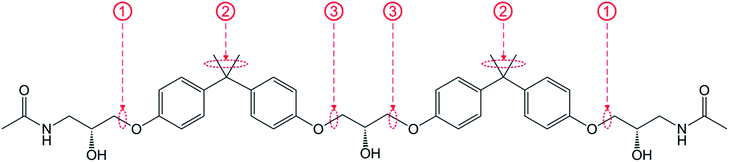
In this paper, a non-crosslinked structure is selected as the molecular model of epoxy resin, as shown in Fig. 1. A ReaxFF for the C/H/O/N system developed by Mattsson et al.²⁵ is employed to simulate decomposition of epoxy resin.

Fig. 1 Non-crosslinked structure of epoxy resin.

The simulation system of epoxy resin in this study consists of 15 epoxy resin molecules. Initial size and density of the system are 28.5 × 28.5 × 28.5 ų and 0.8 g cm⁻³, respectively. A series of relaxations are performed to make the system achieve equilibrium before carrying out the heating process. Energy minimization of the initial system is first evaluated. Then, a 20 ps NPT-MDS is performed at 300 K to optimize the system size. When the NPT-MDS is done, its size and density are 25.95 × 25.95 × 25.95 ų and 1.05 g cm⁻³. Subsequently, a 20 ps NVT-MDS is performed at a temperature of 300 K. Finally, the epoxy resin system achieves an equilibrium state and can be used in subsequent simulations of the heating stage.

The integration algorithm used in our simulations is the velocity Verlet algorithm. The time step is set to 0.1 fs during all simulations. When performing the NPT-MD simulation, the Nose–Hoover thermostat (damping constant is set to 2 fs) and barostat are adopted to adjust temperature and pressure, and the same thermostat is employed in the NVT-MD simulation. For conventional heating, we use a NVT ensemble with a rising temperature heat bath. For microwave heating, we employ a non-strict NVE ensemble, which allows simulation systems to absorb microwave energy.

Microwave energy involves an electric field and a magnetic field based on classical electromagnetic theory. Considering the reaction system is non-magnetic, the effect of the magnetic field in the system can be considered negligible. Therefore, microwave energy applied to the system can be expressed as

where E₀ and e⃑_x are the amplitude and direction of the electric field, respectively, and f is the operation frequency of the microwave energy. As the wavelength of microwaves below 300 GHz is much larger than the size of the simulation system when performing MD simulations, the instantaneous electric field of the system can be treated as a uniform distribution regardless of frequencies under this microwave range. On the other hand, an appreciable temperature rise and interaction between the microwave energy and reaction system should be captured in a reasonable MDS time. Thus, the operation frequency of the microwave energy is set to 100 GHz, based on research by English et al.¹⁴

3. Simulation results and analyses

The heating process is divided into two stages: the first stage is rapid heating, where a high intensity electric field is applied to make the system temperature rise rapidly and, thus, approach the full decomposition stage of the epoxy resin. The second is the continuous reacting stage, where the electric field intensity relative to the first stage is much smaller to ensure a smooth variation of temperature under continuous microwave heating. For the two stages, electric field amplitudes are set to 2.1 V Å⁻¹ and 0.2 V Å⁻¹, respectively.

We obtain a temperature curve against time after MD simulations of epoxy resin pyrolysis under microwave heating. Meanwhile, we perform a similar simulation, but under conventional heating, with the same process of temperature rising observed under microwave heating. The temperature curves, partial transition state species, and decomposition products of epoxy resin under microwave and conventional heating are shown in Fig. 2(a) and (b), respectively. In the following sections, results of the two heating modes are analyzed in detail.

Fig. 2 Time evolution of temperature, epoxy resin, H₂, H₂O, and total number of small size polar species obtained under (a) microwave heating and (b) conventional heating.

3.1 Analyses of temperature-rising characteristics

As mentioned above, all simulations in this section include two stages. The purpose of the first stage, namely the rapid heating stage, is to make the system temperature rise very quickly. The simulation duration is set from 0 to 10 ps. Fig. 2 shows that the system temperature under the two heating modes increases rapidly and identically from 300 K to 3000 K. The system temperature under conventional heating increases almost linearly, while it exhibits some fluctuations under microwave heating due to timed alternating of the amplitude of the electric field. Despite some discrepancies during the first 10 ps process, the system temperatures obtained under the two heating modes are almost identical at the end of the first stage, as expected. At the beginning of the second stage, the amplitude of the electric field is lowered to 0.2 V Å⁻¹. It is seen from Fig. 2 that at the time span from 10 ps to 70 ps, temperature curves obtained under the two heating modes are nearly the same, namely they increase linearly from 3000 K to 3600 K. However, beyond 70 ps, they exhibit an ever-increasing difference against time. The temperature rising rate under microwave heating increases non-linearly, while the rate obtained under conventional heating exhibits a gradual linear increase. This phenomenon is similar to thermal runaway, which is one of the special effects of microwave heating and often appears during practical applications of microwave heating. In most cases, thermal runaway under microwave heating is an undesired or even destructive phenomenon. Consequently, the phenomenon observed here needs to be further studied.

It is known that the temperature rise under microwave heating is related to the dielectric loss of substances in the electromagnetic field. The basic mechanism of microwave heating is that polar molecules or charged particles rotate and shift when microwave energy is applied. This causes the total kinetic energy of the system to rise, thereby, increasing the temperature of the overall system. Thus, statistical numbers of small size polar species, belonging to C₁–C₅ compounds obtained under two heating modes, are respectively evaluated, as shown in Fig. 3. The numbers of polar species obtained under the two heating modes increase suddenly at the beginning of the rapid heating stage and both cases approach a peak value at a time of 15 ps, then both decline. Starting from 50 ps, the numbers related to conventional heating remain constant with small fluctuations. However, the numbers under microwave heating generally increase and, subsequently exhibit a drastic increase after 120 ps.

Fig. 3 Time evolution of total number of small size polar species obtained under microwave heating and conventional heating.

Table 1 lists reference values of bond dissociation energies (BDEs) of C–C, C–O, and C–N bonds in organic compounds.²⁶ It is found that the BDEs of the oxygen bridge and C–C bonds that appear on the side chain of the benzene ring of non-crosslinked epoxy resin are much lower than the others. These are marked on the molecular structure shown in Fig. 4. Regardless of whether it is under microwave heating or conventional heating, when starting the first heating stage, bonds marked as ① and ③ in Fig. 4 break first, and then ② dissociates. This causes the numbers of C₁–C₅ compounds to rocket.

Table 1 Reference values of bond dissociation energies (BDEs) of C–C, C–O, and C–N bonds in organic compounds

The broken bonds	BDEs (kJ mol^−1)
C2H5–OC6H5	268.2
CH3–OC6H5	268.6 ± 7.1
CH3–C(CH3)(C6H5)2	290.8 ± 8.4
CH3–NHCH3	343.9 ± 10.5
C2H5–NH2	354.8 ± 6.3
HO–CH(CH3)(nC3H7)	400.4 ± 4.2
C6H5–OCH3	415.1 ± 5.9
CH3C(O)–NH2	417.1 ± 8.4
HC(O)–NH2	424.3 ± 8.4

---

Fig. 4 The low BDE bonds of non-crosslinked epoxy resin marked from ① to ③.

Based on research by Diao et al.,²⁷ partial small free radicals obtained during the early stage of epoxy resin decomposition combine into graphene. Acharya et al.²⁸ reported that fullerene fragments were detected during the decomposition of polycyclic aromatic compounds. According to the research by Harris,²⁹ high temperatures can increase the generation rate of fullerene when treating resin through glassy carbon technology. These indicate that at the early stage of the epoxy resin cracking process, small fragments formed during pyrolysis would combine into carbon clusters rapidly, which causes the number of C₁–C₅ compounds to decrease after the peak shown in Fig. 3, around 15 fs.

From the point of view of the heating mechanism, microwave heating transfers energy via dielectric loss caused by rotation and movement of polar molecules and charged particles, while the quantity of polar species has no direct effect on temperature when using conventional heating since conventional heating transfers energy via heat conduction. Hence, the quantity of polar molecules and charged particles of the system under microwave heating directly affects the temperature-rising rate. At the time span of 0 to 30 ps, the quantity of small size polar radicals rises quickly, and then declines as a result of radicals combining into clusters, obscuring the influence on temperature of these radicals. Thus, the temperature-rising rate of the system under microwave heating is linear as expected from 10 ps to 70 ps. When numbers of C₁–C₅ compounds are no longer falling and become stable, the contribution of these polar radicals to the absorption of microwave energy is ever apparent. Based on these analyses, we believe that the small size polar radicals generated during the decomposition process enhance the system's capacity to absorb microwave energy, leading to an increased temperature-rising rate of the system. The rapidly rising temperature further promotes more large size groups to crack into small ones, resulting in their numbers drastically increasing. Due to the interaction between system temperature and small size polar radicals, the thermal runaway phenomenon is found when performing MDS of decomposing epoxy resin under microwave heating.

3.2 Investigation of influence on reaction rates under microwave heating

For chemical reactions under microwave heating, both thermal and non-thermal effects are research focuses. It is noted that some special phenomena, which are difficult to investigate using actual experiments, can be readily captured based on the MDS method, for instance, the study of the influence of microwave heating on chemical reaction rate when not considering temperature effects.

To investigate the influence of microwave heating on reaction rates, yields of H₂ and H₂O (i.e., the main products of epoxy resin decomposition) are calculated under microwave heating and conventional heating as shown in Fig. 2. It is found that at the early heating stage, outputs of H₂O are always higher than those of H₂ for both cases. Along with the temperature rising, the production of H₂ has a rapidly increasing stage. This is consistent with research by Jie et al.³ on the pyrolysis of WPCBs in a tubular type oven. As shown in Fig. 2, yields of H₂ and H₂O show some noticeable disparity between the two heating modes. Here, we evaluate average generation rates (v_avg, defined as the ratio of total amount and time) of H₂O and H₂; the result is shown in Fig. 5. Since the temperature rising rate of the system under microwave heating goes up in the late period, we choose a time span from 0 to 70 ps to investigate the influence of microwave heating on reaction rates. Within this time span, temperature under the two heating modes is almost identical.

Fig. 5 Average generating rates (v_avg, number per ps) of (a) H₂O and (b) H₂ obtained under microwave and conventional heating.

It is seen from Fig. 5(a) that v_avg of H₂O obtained under microwave heating is always lower than that obtained under conventional heating from 10 ps to 70 ps. Also, v_avg of H₂ obtained under the two heating modes exhibits a similar result compared with that of H₂O. Moreover, the initial time to generate H₂O under microwave heating lags behind the time obtained under conventional heating. This indicates that, although the temperature curves obtained under the two heating modes are similar in the initial stage (i.e., from 10 to 70 ps) of pyrolysis, the generation rates of major products obtained under conventional heating are higher than those obtained under microwave heating on the whole. Therefore, this fact gives us an insight that the inhibition of microwave heating on reaction rates is a non-thermal effect.

Tanaka et al.¹⁵ reported that water dipoles align along the direction of the time-alternating electric field when performing MDS of microwave heating of water initially at 300 K. This indicates that rotation of the hydroxyl free radical, whose electric dipole moment is higher than that of water, can be well controlled under microwave heating initially at 300 K. The rotation performance of polar fragments during microwave heating at high temperatures needs to be analyzed. Here, water (H₂O), methane (CH₃OH) and anisole (CH₃OC₆H₅) molecules are selected as equivalent models of partial polar fragments, which correspond to some resin decomposition products. MDSs of microwave heating of water, methane and anisole systems are employed with the same initial temperature of 3000 K. Similarly, the amplitude and frequency of the employed microwave energy are 0.2 V Å⁻¹ and 100 GHz, respectively. The x component of the average electric dipole of the three molecule models under microwave heating initially at 3000 K are shown in Fig. 6. Table 2 lists the dipole energies of the three molecules and comparisons with thermal energy kT₃₀₀₀ at 3000 K, where P is the electric dipole moment and k is the Boltzmann constant. It indicates that the dipole energies of the three molecules are much less than the thermal energy at 3000 K.

Fig. 6 The x component (red with symbols) of the average electric dipole of (a) water, (b) methane and (c) anisole under microwave heating and the magnitude of the microwave electric field E_x(t) (black) initially at 3000 K.

Table 2 Electric dipole moments (P) and dipole energies (E₀P) of the three molecules, and comparisons with thermal energy at 3000 K

Molecule model	P (C·M)	E 0 P (eV)	E 0 P/kT3000
Water	6.17 × 10^−30	7.70 × 10^−2	0.298
Methane	5.64 × 10^−30	7.04 × 10^−2	0.272
Anisole	4.50 × 10^−30	5.62 × 10^−2	0.217

---

It can be observed from Fig. 6 that there is almost no phase lag between the temporal phase variations of the x component of the water electric dipole and the external electric field initially at 3000 K. Likewise, the phase transition of the methane dipole is similar. However, the existence of phase lag between the anisole dipole and the electric field is verified in Fig. 6(c), which shows the phase lag is over one-fourth of an electric field period. It can be inferred that the electric dipole directions of small size polar fragments, such as water and methane molecules, can be well controlled by the external electric field over 3000 K. However, for large size polar fragments (≥C₇), this is not true. This is also the reason that we selected C₁ ∼ C₅ polar fragments as analytic targets to investigate thermal run-away rather than larger size fragments in Fig. 2 and 3. It should be indicated that, although partial phase lag exists, the three molecule models rotate in one period of the external electric field.

As studied by Diao et al.,²⁷ during pyrolysis of epoxy resin, the main mechanisms to form H₂O and H₂ are hydroxyl free radical capture of hydrogen from other radicals and intermolecular dehydrogenation reactions, respectively. Thus, combined with discussions of Fig. 6, the generating processes of H₂ and H₂O can be equivalent to collisions of hydric radicals and collisions between hydroxyl free radicals and hydric radicals, respectively. Consequently, classical collision theory is introduced in our analyses to identify the interaction between microwave energy and reaction rates. Based on collision theory, the reaction-rate function can be expressed as

v = Z_AB × F × P (2)

where Z_AB is the amount of collisions per unit time, F is the energy factor, P is the orientation factor, and v is the reaction rate. Parameters Z_AB and F are defined as

F = e^−E_c/RT (4)

where πd_AB² is the collision cross section, μ is the reduced molar mass, and c_A and c_B are the concentrations of reactant fragments A and B, respectively. The energy factor F formulates that valid collision occurs only when kinetic energies of reactants reach a critical value E_c. It is noted that the influence of microwave energy on the energy factor F is tiny. The temperature, directly calculated from the kinetic energy of the system, is almost identical under the two heating modes.

Eqn (2) shows that the reaction rate v is proportional to the collision frequency Z_AB and orientation factor P. Considering the whole system, when neglecting thermal effects, the introduced microwave energy restrains movement of polar molecules and free radicals, thus, reducing the disorder degree of the system. As compared to conventional heating, when MDS is performed under microwave heating, entropy-reduction effects caused by suppression of the disorder degree results in a decline in total collisions per unit time of the overall system. Hence, collision probability between polar fragments, namely the collision frequency Z_AB, is decreased.

The orientation factor P indicates that whether a valid collision occurs or not also depends on the collision orientations. Here, we simplify the collision model and select generation reactions of H₂ as analysis models to study the effect of microwave energy on the factor P. Small polar fragments A and B obtained during the decomposition of epoxy resin are chosen as main reactants to form H₂ through intermolecular dehydrogenation. A simplified model A is composed by radical A₁ and hydrogen, while B consists of radical B₁ and hydrogen, as shown in Fig. 7. All collision orientations to generate H₂ between fragments A and B are shown in Fig. 8. It can be seen that only the orientation expressed by Fig. 7(a) is valid, which corresponds to hydrogen atoms of fragments A and B meeting face to face.

Fig. 7 Effectiveness of four collision orientations between polar fragments A and B, for generating H₂.

Fig. 8 Transformations of original valid collisions of polar hydric fragments before and after introducing microwave energy. Column (a) is the original valid collision orientation of polar fragments without microwave energy, (b) and (c) are the orientations after dipole moments polarized by electric field (marked as ) with different directions. Directions of dipole moments and electric field are both indicated by black arrows.

The external electric field is time varied, leading to rotation of the electric dipole moment of polar fragments over time. Therefore, the initial effective collision may become invalid because of the introduction of an electric field. Fig. 8 shows transformations of original valid collisions of polar hydric fragments before and after introducing microwave energy, where various directions of electric dipole moments (defined as D → A and D → B in Fig. 8) of the collision fragments are considered (there are four polar fragments H–A₁, H–B₁, H–A₂, and H–B₂). The directions of electric dipole moments of the four fragments H–A₁, H–B₁, H–A₂ and H–B₂ are defined as A₁ → H, H → B₁, H → A₂ and B₂ → H. For instance, models of free radicals (H–O˙), (˙CO–NH˙), (˙N–CH₂˙), and (˙CO–CH₂˙) obtained during epoxy resin cracking can be simplified as H–A₁, H–B₁, H–A₂, and H–B₂, respectively. In Fig. 8, the x-o-y plane is assumed as the collision plane, while the direction of the electric field is along the x-axis, that is, directed along the positive and negative x-axis due to the electric field alternating over time. It can be seen that after introducing an electric field, the four initial valid collision orientations shown in Fig. 8(a) are all affected, especially the orientations shown in the second and third rows in Fig. 8. They are all transformed into invalid orientations whether the direction of the electric field is positive or negative. The first and fourth rows are still valid collisions only when the direction of the electric field is specified.

Meanwhile, variations of original invalid orientations of polar fragments A and B, before and after introducing the external electric field, are also analyzed in Fig. 9. It illustrates that the influence of the electric field on the initial invalid collision orientations is finite. Only when the directions of the electric field and the electric dipole moments of fragments are both specified as the first and fourth rows, as depicted in Fig. 9 can the orientations be changed from invalid to valid. The invalid collision orientation shown in Fig. 9 is one of the three invalid orientations described in Fig. 7. In fact, analyses reveal that interactions between the other two invalid orientations and microwave energy are similar to the situation shown in Fig. 9.

Fig. 9 Transformations of original invalid collisions of polar hydric fragments before and after introducing microwave energy. Column (a) is the original invalid collision orientation of polar fragments without microwave energy, (b) and (c) are the orientations after dipole moments were polarized by electric fields with different directions.

With these analyses, we believe that the influence of microwave energy on polar fragments which are transformed from valid to invalid is significant. The convention rate is 75% in our ideal analysis model. However, the influence on the initial invalid orientations is finite, with an ideal convention rate of 25%. Compared with conventional heating, the orientation factor P declines when microwave heating is introduced. In short, the external microwave energy decreases both the collision frequency Z_AB and orientation factor P, thus, finally reducing the rate v. Similarly, replacing the fragment H–B₂ as radical O–H in Fig. 8 and 9, simplified collision models of H₂O generation can be constructed. Also, the results are analogous to H₂ formation. The rate characteristics of Z_AB and P are decreased, leading to a decreased reaction rate.

It should be noted here that, at the initiation of epoxy resin pyrolysis, the hydroxyl free radical also begins to be generated, while the formation process of H₂ starts at the intermolecular dehydrogenation between large size fragments, which are almost polar species. As illustrated in Fig. 6, for large size polar fragments, their rotations exhibit phase lag compared with the alternating of the external electric field. Hence, the influence of microwave heating on v_avg of H₂O is obvious when reactions begin, while v_avg of H₂ is not obvious until there are enough small size polar fragments. Thus, phenomena shown in Fig. 5 show that the disparity in v_avg of H₂O obtained under the two heating modes exists from the beginning of H₂O generation, while a significant disparity in H₂ generation appears after a short period of heating time.

Conclusions

The ReaxFF MDSs have been performed to investigate effects on decomposing epoxy resin (i.e., the model compound of WPCBs) under microwave heating. As one of its special effects, the thermal runaway phenomenon is investigated under microwave heating by comparing it with conventional heating. This phenomenon results from the enhancement of system absorption of microwave energy, caused by the increasing number of small size polar species generated during the pyrolysis under microwave heating.

On the other hand, non-thermal effects are also studied under microwave heating based on MDSs. At the early stage of decomposition, the average generation rate of H₂O and H₂ obtained under microwave heating are always, or partly, lower than that obtained under conventional heating when neglecting the influence of temperature. This phenomenon is explained by introducing collision theory and constructing simplified collision models. Compared with conventional heating, the introduced microwave energy restrains movement of polar fragments and reduces the entropy of the system, thus, finally causing a decline in the collision frequency Z_AB. Studies show that the influence of microwave heating on polar fragments transforming from valid to invalid is significant, whereas, the effect on the initial invalid orientation is finite, meaning that the orientation factor P is decreased by the polarization effect of the microwave energy. Therefore, the relative reaction rate under microwave heating is reduced due to the decrease of reaction-rate characteristics Z_AB and P compared with conventional heating.

Rotation time of some equivalent models of polar fragments formed during epoxy resin cracking have also been measured and compared to the phase change of the external electric field. It is found that small size polar fragments, such as water and methane, can be well controlled by an external electric field. However, for large size fragments (≥C₇), there exists a phase lag between the electric dipole and external electric field.

Acknowledgements

This work was supported in part by the Fundamental Research Funds for the Central Universities of China (ZYGX2011X009), by the Natural Science Foundation of China (61271025, 61101047, 61271027), and by the Program for New Century Excellent Talents in University NCET-12-0094.

Notes and references

1. F. Barontini, K. Marsanich, L. Petarca and V. Cozzani, Ind. Eng. Chem. Res., 2005, 44, 4186–4199.
2. K. Chen, H. Chen, C. Wu and Y. Chou, J. Environ. Eng., 1999, 125, 277–283.
3. G. Jie, Y. S. Li and M. X. Lu, J. Anal. Appl. Pyrolysis, 2008, 83, 185–189.
4. M. P. Luda, A. I. Balabanovich and G. Camino, J. Anal. Appl. Pyrolysis, 2002, 65, 25–40.
5. C. O. Kappe, Angew. Chem., Int. Ed., 2004, 43, 6250–6284.
6. E. Lester and S. Kingman, Energy Fuels, 2004, 18, 140–147.
7. K. G. Mayo, E. H. Nearhoof and J. J. Kiddle, Org. Lett., 2002, 4, 1567–1570.
8. M. Nuchter, B. Ondruschka, W. Bonrath and A. Gum, Green Chem., 2004, 6, 128–141.
9. J. Sun, W. Wang, Z. Liu and C. Ma, Ind. Eng. Chem. Res., 2011, 50, 11763–11769.
10. J. Sun, W. Wang, Z. Liu, Q. Ma, C. Zhao and C. Ma, Energies, 2012, 5, 3295–3306.
11. F. Torres and B. Jecko, IEEE Trans. Microwave Theory Tech., 1997, 45, 108–117.
12. X. Q. Yang and K. M. Huang, IEEE Trans. Geosci. Rem. Sens., 2005, 43, 315–320.
13. N. J. English, Mol. Phys., 2006, 104, 243–253.
14. N. J. English and J. MacElroy, J. Chem. Phys., 2003, 118, 1589.
15. M. Tanaka and M. Sato, J. Chem. Phys., 2007, 126, 034509.
16. M. Tanaka and M. Sato, J. Microwave Power, 2009, 42, 62.
17. A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
18. X. M. Cheng, Q. D. Wang, J. Q. Li, J. B. Wang and X. Y. Li, J. Phys. Chem. A, 2012, 116, 9811–9818.
19. E. Salmon, A. C. T. Van Duin, F. Lorant, P. M. Marquaire and W. A. Goddard Iii, Org. Geochem., 2009, 40, 1195–1209.
20. S. P. Han, A. C. T. Van Duin, W. A. Goddard and A. Strachan, J. Phys. Chem. B, 2011, 115, 6534–6540.
21. L. L. Huang, T. Bandosz, K. L. Joshi, A. C. T. van Duin and K. E. Gubbins, J. Chem. Phys., 2013, 138, 034102.
22. P. Valentini, T. E. Schwartzentruber and I. Cozmuta, J. Chem. Phys., 2010, 133, 084703.
23. L. L. Huang, K. L. Joshi, A. C. T. van Duin, T. J. Bandosz and K. E. Gubbins, Phys. Chem. Chem. Phys., 2012, 14, 11327–11332.
24. N. Lummen, Phys. Chem. Chem. Phys., 2010, 12, 7883–7893.
25. T. R. Mattsson, J. M. D. Lane, K. R. Cochrane, M. P. Desjarlais, A. P. Thompson, F. Pierce and G. S. Grest, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054103.
26. Y. R. Luo, Handbook of bond dissociation energies in organic compounds, CRC Press, Boca Raton, Fla., 2003.
27. Z. Diao, Y. Zhao, B. Chen and C. Duan, Acta Chim. Sin., 2012, 70, 2037–2044.
28. M. Acharya, M. S. Strano, J. P. Mathews, S. J. Billinge, V. Petkov, S. Subramoney and H. C. Foley, Philos. Mag. B, 1999, 79, 1499–1518.
29. P. Harris, Philos. Mag. B, 2004, 84, 3159–3167.

---