Quantitative and qualitative analysis of ionic solvation of individual ions of imidazolium based ionic liquids in significant solution systems by conductance and FT-IR spectroscopy†
Abstract
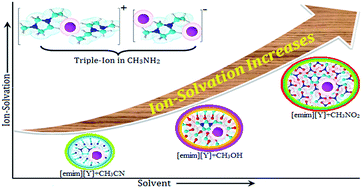
Quantitative analysis of molecular interactions by precise conductance (Λ) measurements and qualitative analysis by FT-IR spectroscopy have been reported for solution systems between some imidazolium-based ionic liquids ([emim]NO3, [emim]CH3SO3, [emim]Tos) and non-aqueous solvents (acetonitrile, methanol, nitromethane, methylamine solution) at 298.15 K. The Fuoss conductance equation (1978) and Fuoss–Kraus theory for ion-pair and triple-ion formations, respectively, have been used for analysing the conductance data. Using the appropriate division of the limiting molar conductivity value of [Bu4NBPh4] as a “reference electrolyte”, the limiting ionic conductances (λ±o) for individual ions have been calculated and reported. Dipole–dipole interactions, hydrogen bonding, structural aspects, and configurational theory are the driving forces and have been employed for the discussion of the results. FT-IR spectroscopic studies of variational intensity in the characteristic bands of the studied solvents have been undertaken, and the solvation phenomenon is manifested by the change of these band intensities in the presence of ionic liquids.

 Please wait while we load your content...
Please wait while we load your content...