Tuning the crystal shape of materials by chemical potential: a combined theoretical and experimental study for NiSe2
Wei-Bing
Zhang
*,
Shuguang
Chen
and
Kai
Zeng
School of Physics and Electronic Sciences, Changsha University of Science and Technology, Changsha 410004, People's Republic of China. E-mail: zhangwb@csust.edu.cn; weibingzhangavh@gmail.com; Fax: +86 (0)73185258217; Tel: +86 (0)73185258223
First published on 14th January 2014
Abstract
Understanding and controlling the shape of materials has attracted considerable attention over the past few decades. Taking a typical transition metal chalcogenide NiSe2 as an example, we have figured out the role of chemical potential in the equilibrium shape of materials by a combined theoretical and experimental study. The theoretical equilibrium shape evolution of NiSe2 with chemical potential has been investigated using ab initio atomistic thermodynamics and Wulff construction. Moreover, in order to confirm our theoretical results, a series of NiSe2 crystals with different morphologies were also synthesized via a solvothermal route in mixed solvents of hydrazine hydrate, ethylenediamine and reactant. X-ray powder diffraction (XRD) and field emission scanning electron microscopy (FESEM) were used to analyze the products. Our results indicated that the theoretical equilibrium shapes of NiSe2 change from pyritohedron enclosed by (210) facet, truncated octahedron to perfect octahedron occupied by (111) facet, which agrees with the experimental shapes of NiSe2 synthesized with different volume ratios of mixed solvents. The present theory and experimental work indicates that controlling the chemical potential is a general and efficient way to tailor the shape of materials.
1 Introduction
Tailoring the properties of materials is a central topic of condensed physics and material science, which has attracted considerable attention over the past few decades. The properties of materials are strongly dependent on several important physical parameters such as composition, structure,1,2 size,3 shape2,4 and reactive environments.4 Recent developments in materials science have now made it possible to tailor materials with controllable shape at the nanoscale,5 which has also stimulated an increasing interest for understanding and controlling the shape of materials. Since many critical parameters are responsible for the final shapes which leads to the poor reproducibility of most experiments concerning shape, the underlying formation mechanism of various shapes is still an open question. Clarifying the role of different parameters in morphology evolution is a prerequisite to understanding the underlying mechanism and to design novel materials with better performance.As an illustrative example, we focus on a typical transition metal chalcogenide NiSe2, which is a member of the family NiS2−xSex. Since a metal–insulator transition driven by electron–electron interaction can take place under appropriate conditions of concentration, temperature, or pressure,6,7 NiS2−xSex have attracted much interest over the last few decades.8 Very rich electrical and magnetic properties have been found in this series of compounds. For example, NiS2 is a typical strongly correlated anti-ferromagnetic insulator while NiSe2 which is focused on here is found to be a paramagnetic metal at 0 K respectively. Besides the attention gained in foundational physics, NiSe2 has also shown a wide range of potential applications. For example, Xue et al.9 suggested NiSe2 as a promising cathode material for future rechargeable lithium batteries since the NiSe2 electrode exhibited a high reversible capacity and good cycling ability. In addition, NiSe2 can be also used as an efficient counter electrode (CE) of dye-sensitized solar cells,10 which showed better catalytic activity in the reduction of I3− than the commonly used Pt. Moreover, the device with NiSe2 CE produced a higher power conversion efficiency (8.69%) than that (8.04%) with Pt CE. On the other hand, the synthesis of nickel selenides with special morphologies via a number of routes has also attracted a lot of attention.10–13 Different shapes of NiSe2 particles including symmetrical six-horn nanostars,11 spherical,12 octahedral crystals10,12 and tubular microcrystals13 have been obtained.
The experimental effort has also motivated the increasing interest in theory. Theoretical work attempting to model the effect of different parameters on crystal shape has also been performed recently.14,15 Modern electronic structure method, such as density functional theory (DFT), is known to be one of the most successful approaches in material and surface science. The energetics, structural, and electronic properties of any system and elementary molecular process can be addressed in detail based on DFT calculation. It should be noted that DFT is a theory at zero temperature and pressure, and the results obtained directly in the calculation are also limited to the electronic scale. However, most observable experimental quantities such as shape are meso- and macroscopic properties of materials, which are determined by the statistical interplay of many elementary processes. A multiscan modeling approach combining DFT results with thermodynamic concepts has been developed to address this problem, which is also referred to as an ab initio atomistic thermodynamic approach.16,17 The goal of the thermodynamic approach is to use the data from electronic structure theory to calculate appropriate thermodynamic potential functions such as the Gibbs free energy under different conditions, which can be used to compare the stability of different surface structures in contact with the surrounding gas phase. On the other hand, the equilibrium crystal shape can be obtained using the Wulff construction,18 by minimizing the total surface free energy for a fixed crystal volume, in which the length of a vector drawn normal to a crystal face (hkl) will be proportional to its surface (free) energy γhkl. On the basis of γhkl obtained using an ab initio atomistic thermodynamic approach, the equilibrium shape evolution of materials can be determined by the Wulff construction in principle.
Although NiS2−xSex have been investigated extensively due to their unique electronic correlation and metal–insulator transition,8,19,20 theoretical investigations focusing on the surface of NiSe2 are somewhat scarce. The available results are mainly limited to the electronic structure of bulk NiSe2.19,20 In the present study, we have performed systematic investigations for (111), (001), (110), and (210) surfaces of NiSe2 based on density functional theory, all possible terminations are considered for various surfaces. The equilibrium shapes under different conditions are then determined by the Wulff construction using the Gibbs free energy obtained by an ab initio atomistic thermodynamic approach. In order to confirm our theoretical results, a controllable synthesis with different ratios of mixed solvents has also been constructed. And the products are analyzed by different experimental techniques.
2 Method
2.1 Computational details
The present calculations have been performed using the QUANTUM ESPRESSO package, which is an integrated suite of computer codes for electronic-structure calculations and materials modeling, based on density-functional theory, plane waves, and pseudopotentials.21 General gradient approximations (GGA) in the Perdew–Burke–Ernzerhof (PBE) implementation22 were chosen for the exchange correlation functional and the ultrasoft pseudopotentials were used. Convergence tests have been performed carefully both for plane-wave cutoff energy and k point sampling. A plane-wave basis set with a kinetic energy cutoff of 50 Ry for wave functions and 500 Ry for charge densities were used, and the Brillouin zone sampling with a mesh of 12 × 12 × 12 generated by the scheme of Monkhorst–Pack23 was used for cubic pyrite NiSe2 to ensure a convergence accuracy with a total energy difference less than 0.5 mRy per atom.In order to determine the shape of NiSe2 with a pyrite structure, three low index surfaces (111), (110) and (100) are considered. In addition, a high Miller index (210) surface which was observed in the FeSe2 system24,25 with the same crystal structure was also studied. All possible surface terminations are considered in the calculations and the structural models are also listed in Table. 1. All surfaces were modeled using central symmetric slabs separated by at least 15 Å vacuum space. Since the surfaces involved in the calculations have different geometry and symmetry, it is important to ensure similar numerical accuracy for all the surfaces. During the calculations, the Brillouin zone (BZ) was sampled with a mesh of 4 × 4 × 1 MP points for a (111) surface unit cell. For other surfaces, the k-points were reduced proportionately to maintain a similar sampling of the reciprocal spaces. Specifically, 6 × 6 × 1, 4 × 6 × 1 and 3 × 6 × 1 were used for (100), (110) and (210) surfaces, respectively. All atoms except the central three atomic layers were optimized using the BFGS method26 until the maximum absolute forces of all free atoms converged to 0.001 a.u. The electronic structures for slabs were calculated using the first-order Methfessel–Paxton methods with a width of 0.01 Ry to speed up convergence.
| Label | Area (Å2) | N Ni | N Se | Figure | Label | Area (Å2) | N Ni | N Se | Figure | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 111 | Ni | 61.36 | 24 | 40 | Fig. 2(e) | 210 | Ni | 79.216 | 18 | 32 | Fig. 4(d) |
| 111 | Se1 | 61.36 | 24 | 56 | Fig. 2(c) | 210 | Ni2 | 79.216 | 22 | 40 | Fig. 4(a) |
| 111 | Se2 | 61.36 | 24 | 54 | Fig. 2(a) | 210 | Se1 | 79.216 | 14 | 32 | Fig. 4(e) |
| 111 | Se3 | 61.36 | 24 | 48 | Fig. 2(b) | 210 | Se2 | 79.216 | 14 | 28 | Fig. 4(f) |
| 111 | Se4 | 61.36 | 24 | 42 | Fig. 2(d) | 210 | Se3 | 79.216 | 18 | 40 | Fig. 4(b) |
| 210 | Se4 | 79.216 | 18 | 36 | Fig. 4(c) | ||||||
| 100 | Ni | 35.426 | 14 | 24 | Fig. 1(c) | 110 | Ni | 50.100 | 14 | 26 | Fig.3(c) |
| 100 | Se1 | 35.426 | 14 | 32 | Fig. 1(b) | 110 | Se1 | 50.100 | 14 | 30 | Fig. 3(b) |
| 100 | Se2 | 35.426 | 14 | 28 | Fig. 1(a) | 110 | Se2 | 50.100 | 14 | 28 | Fig. 3(a) |
2.2 Ab initio atomistic thermodynamic approach
Following the approach developed by Reuter and Scheffler,16 the surface free energy γ(T, p) at the given temperature T and pressure p is defined as: | (1) |
The most stable surface composition and geometry is then the one that minimizes the surface free energy at different conditions. On the other hand, the compound should fulfil thermodynamic constraint conditions.
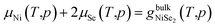 | (2) |
With this constraint, the surface free energy can be rewritten as:
 | (3) |
It should be noticed that the chemical potential μSe can vary only within a limited range. If μSe becomes too low, the formation of Ni crystallites would start at the surface.
 | (4) |
On the other hand, the most Se-rich condition can be defined as the point beyond which solid Se would start to condense on the sample.
| μSe(T,p) ≤ gbulkSe | (5) |
The theoretical range of Se chemical potentials is
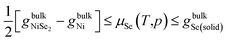 | (6) |
 | (7) |
The most stable form of selenium is known to have a gray color and hexagonal crystal lattice with space group no. 152, in which Se occupied 3a site (x, 0, 1/3). The present calculations predict the crystal lattice a, c and internal degree of freedom x of hexagonal Se to be 4.496 Å, 5.061 Å and 0.2209, respectively, in good agreement with experimental results27 4.38 Å, 4.96 Å, and 0.2254. In addition, the calculations predict the hexagonal Se to be a semiconductor with a band gap at about 1.02 eV, compared with an experimental gap28 at about 1.8 eV. The calculated Gibbs formation energy hexagonal Se is about −0.581 eV. While NiSe2 crystallized in the cubic pyrite structure with a space group no. 205 with Se atoms occupying the 4a (0, 0, 0) site and Ni atoms occupying the 8c (x, x, x) site. The present calculations predict NiSe2 to be metallic, and the Gibbs formation energy was calculated to be −1.854 eV. Thus, the theoretical range of Se chemical potential is −0.927 to −0.581 eV.
2.3 Experimental section
In order to confirm the theoretical results, we also synthesized a series of NiSe2 with different morphologies via a solvothermal route in mixed solvents of hydrazine hydrate and ethylenediamine. A similar experimental technique was used by different groups to synthesize the nickel selenide nanocrystals, which was evidenced to show attractive effects on the shape control.29,30 NiCl2·6H2O (98 wt%), Se powders (99.8 wt%), NH4Cl (99.5 wt%), En (ethylenediamine, 99 wt%) and NH80 (hydrazine hydrate, 80 wt%) were purchased from Tianjin Kermel Chemical Reagent Co., Ltd. All chemicals were of analytical grade and were used without further purification. In a typical experimental procedure, 40 mL of mixed solvent of NH80 and En was prepared, and the volume ratio of NH80 to En varied from 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Then 2 mmol of NiCl2·6H2O and 8 mmol of Se powders were added into the mixed solvent under intensive stirring for 10 min. Subsequently the mixed liquid was transferred into a Teflon-lined stainless steel autoclave with a capacity of 50 mL. After that the autoclave was heated at a certain reaction temperature for a certain time and subsequently cooled naturally to room temperature. Finally the precipitates were washed several times with distilled water and ethanol, dried at 60 °C for 24 h and the products were obtained.
3. Then 2 mmol of NiCl2·6H2O and 8 mmol of Se powders were added into the mixed solvent under intensive stirring for 10 min. Subsequently the mixed liquid was transferred into a Teflon-lined stainless steel autoclave with a capacity of 50 mL. After that the autoclave was heated at a certain reaction temperature for a certain time and subsequently cooled naturally to room temperature. Finally the precipitates were washed several times with distilled water and ethanol, dried at 60 °C for 24 h and the products were obtained.
The products were characterized by X-ray powder diffraction (XRD) on a Rigaku D/max 2200 diffractometer with a graphite monochromator and CuKα radiation (λ = 1.5406 Å) at a scanning speed of 4° min−1. Scanning electron microscopy (SEM) images were observed by a JEOL JSM-6700 F field emission scanning electron microscope (FESEM) with an accelerating voltage of 200 kV.
3 Results and discussion
3.1 Theory calculations
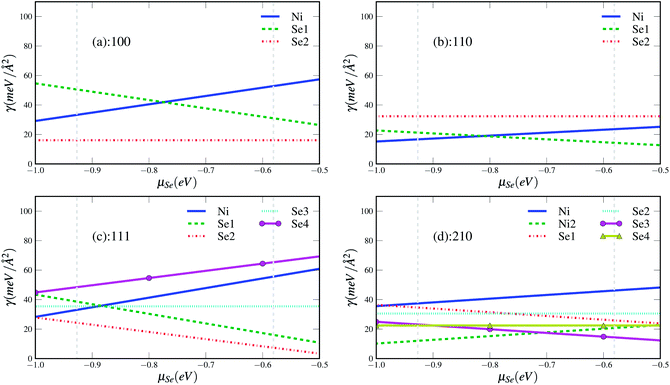
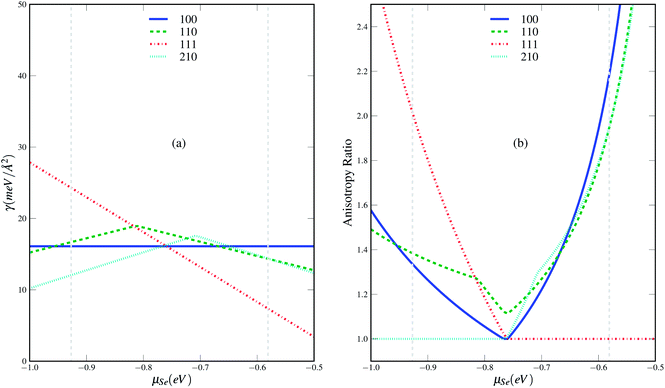
We start our discussion from the stability of the various surfaces. The calculated Gibbs free energies of the possible terminations for four surfaces as a function of Se chemical potential are given in Fig. 5. We can find that the most stable terminations for different surfaces depend on the Se chemical potential. Se-termination surfaces (100Se2, 111Se2) are the most stable phases under the considered range of chemical potential for (100) and (111) surfaces whereas the most stable phases change with increasing chemical potential in the case of (110) and (210) surfaces. The Ni-terminated surface (110Ni, 210Ni2) are the lowest in energy at Se-poor condition whereas the Se-terminated surfaces (110Se1, 210Se3) become the most stable at Se-rich conditions. As shown in Fig. 6, in which only the most stable phase for each surface at different chemical potential is kept, the Ni terminated (210) surface is found to be the most stable at the Se-poor condition. With increasing Se chemical potential, the Se terminated (100) surface is the most thermodynamically favoured phase in the very narrow chemical potential region from −0.767 to −0.759 eV. When the chemical potential is larger than −0.759 eV, the most energetically favored phase becomes Se terminated (111) surface. The lower energy of surface (210) under nickel rich conditions indicates that the high Miller index surfaces should exist and play a very import role in materials, which is also be evidenced in our recent work about the crystal shape of nickel.31 Since the crystal phases are related to the anisotropy ratios of different facets, we also give the anisotropy ratios of different surfaces relative to the lowest-energy surfaces in Fig. 6(b). A quite complex evolution behavior of anisotropy ratios with chemical potential can be found, which also implies that the change of crystal shape with chemical potential should be also very complex. | ||
| Fig. 1 Structural models of different terminations of the NiSe2 (100) surface. The Ni and Se atoms have been represented by white (small) and red (big) balls in the figure. | ||
 | ||
| Fig. 2 Structural models of different terminations of the NiSe2 (111) surface. The Ni and Se atoms have been represented by white (small) and red (big) balls in the figure. | ||
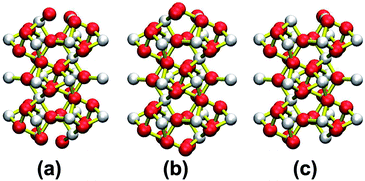 | ||
| Fig. 3 Structural models of different terminations of the NiSe2 (110) surface. The Ni and Se atoms have been represented by white (small) and red (big) balls in the figure. | ||
 | ||
| Fig. 4 Structural models of different terminations of the NiSe2 (210) surface. The Ni and Se atoms have been represented by white (small) and red (big) balls in the figure. | ||
Based on the obtained surface free energies of various surfaces under different conditions, we constructed the equilibrium morphology of NiSe2 as a function of Se chemical potential. Some typical shapes are shown in Fig. 7. We find that the shape is a pyritohedron enclosed by (210) facet at the Se-poor condition. With increasing Se chemical potential, the (100) facet starts to appear, which seems to have a two-fold symmetry. When the chemical potential increases further, the (111) facet is also found in the shape. Meanwhile the portion of (210) facet seems to decrease largely. At the chemical potential around −0.75 eV, a small patch of (110) facet appears in the corner of (111), (210) and (100) surfaces. Since the ratio of (210) surface decreases and (111) surface increases with chemical potential, the (110) facet gets longer and narrower until it disappears. It should be noticed that even as (110) disappears in shape, the (210) surface seems to be still present as shown in Fig. 7(g). When the Se chemical potential is larger than −0.71 eV, a truncated octahedron is found with only the two main low index (100) and (111) facets present. And the portion of (100) surface becomes smaller and smaller while the (111) facet dominates the shape. When the chemical potential approaches the Se-rich condition, the perfect octahedron with only the (111) facet is predicted.
3.2 Experimental results
Three products were synthesized with different ratios of solvents at 180 °C for 20 h, in which the volume ratios of NH80 to En vary from 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (CP1) to 1
1 (CP1) to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (CP3). As shown in Fig. 8, all XRD diffraction peaks of three products match well with the standard pattern of NiSe2 (JCPDS no. 881711, a = 5.962 Å, V = 212.02) with space group name Pa-3, and no other impurities found. The SEM images of single-phase NiSe2 obtained in various solvents are provided in Fig. 9, and the corresponding enlarged FE-SEM images are also provided for clearer visualization. It reveals that NiSe2 particles prepared with the volume ratios of NH80 to En 3
3 (CP3). As shown in Fig. 8, all XRD diffraction peaks of three products match well with the standard pattern of NiSe2 (JCPDS no. 881711, a = 5.962 Å, V = 212.02) with space group name Pa-3, and no other impurities found. The SEM images of single-phase NiSe2 obtained in various solvents are provided in Fig. 9, and the corresponding enlarged FE-SEM images are also provided for clearer visualization. It reveals that NiSe2 particles prepared with the volume ratios of NH80 to En 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are nearly spherical. Whereas the NiSe2 particles produced from NH80 to En 1
1 are nearly spherical. Whereas the NiSe2 particles produced from NH80 to En 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 exhibit a nearly perfect octahedron. When the volume ratio is 1
3 exhibit a nearly perfect octahedron. When the volume ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the obtained shape is a edge- and corner-truncated octahedron.
1, the obtained shape is a edge- and corner-truncated octahedron.
To understand the growth mechanisms of NiSe2 nano crystal, the intermediates synthesized after 1.25 h and 1.5 h were also analyzed. As shown in Fig. 10, most of the diffraction peaks of the products obtained after 1.25 h shown in the figure match well with the standard pattern of trigonal selenium t-Se (JCPDS no. 862246), whereas after 1.5 h, the diffraction peaks of NiSe2 start to appear. This indicates that t-Se is a precursor in the formation of NiSe2. The ethylenediamine is believed to play an important role in formation of selenium nanowires. A previous study32 indicated that ethylenediamine could facilitate the crystal phase transformation from amorphous selenium to trigonal selenium by activating the amorphous selenium ring. In the course of the trigonal selenium formation, ethylenediamine controlled the growth of selenium. Thus, the quantity of ethylenediamine will determine the amount of Se which participates in formation of NiSe2. Specially, when the volume ratio of NH80 and En is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the amount of effective Se in reaction should be small, which corresponds to the Se poor condition. Whereas the mixed solvent with volume ratios of NH80 and En is 1
1, the amount of effective Se in reaction should be small, which corresponds to the Se poor condition. Whereas the mixed solvent with volume ratios of NH80 and En is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, which should correspond to Se-rich condition. While the volume ratio of NH80 and En 1
3, which should correspond to Se-rich condition. While the volume ratio of NH80 and En 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 may correspond to the condition with moderate Se chemical potential.
1 may correspond to the condition with moderate Se chemical potential.
 | ||
Fig. 10 XRD pattern (a) of the products synthesized at 160 °C for 1.5 h and 2.5 h when the volume ratio of NH80 to En is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while (b) and (c) correspond to SEM images of both products. 1, while (b) and (c) correspond to SEM images of both products. | ||
It is very interesting to notice that our present predicted results are in good agreement with the experiment. Under Se-poor condition, our calculation predicts a pyritohedron enclosed by (210) surface. Considering the fact that the high Miller index surface is quite difficult to form due to the kinetic barrier, part of the (210) facet should show as round, which agrees with the near spherical shape observed in the experiment under the mixed solvent with the volume ratios of NH80 and En 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It is also noticed that the pyritohedral form defined by the (210) plane has been found in the FeS2 system with the same structure,25,33 which has been investigated more extensively. When the relative ratio of NH80 and En increases to 1
1. It is also noticed that the pyritohedral form defined by the (210) plane has been found in the FeS2 system with the same structure,25,33 which has been investigated more extensively. When the relative ratio of NH80 and En increases to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, a perfect octahedron is observed in the experiment, which is the same shape predicted in Se-rich conditions. Moreover, the present results are also supported by earlier experiments. Gong et al.10 prepared NiSe2via a simple one-step hydrothermal reaction and found that most of the NiSe2 particles with an average size of about 2–3 mm exhibited an octahedral shape. Han et al.12 have also synthesized selenium-rich NiSe2 particles with nearly perfect octahedrons. When the chemical potential changes from Se-poor to Se-rich conditions, many different shapes are found in theory with an increase of the chemical potential, in which the truncated octahedron is the most likely shape. Whereas at a relative ratio of NH80 and En of 1
3, a perfect octahedron is observed in the experiment, which is the same shape predicted in Se-rich conditions. Moreover, the present results are also supported by earlier experiments. Gong et al.10 prepared NiSe2via a simple one-step hydrothermal reaction and found that most of the NiSe2 particles with an average size of about 2–3 mm exhibited an octahedral shape. Han et al.12 have also synthesized selenium-rich NiSe2 particles with nearly perfect octahedrons. When the chemical potential changes from Se-poor to Se-rich conditions, many different shapes are found in theory with an increase of the chemical potential, in which the truncated octahedron is the most likely shape. Whereas at a relative ratio of NH80 and En of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, an NiSe2 crystal with an edge- and corner-truncated octahedron is synthesized, which can be found clearly in the shapes predicted in the theory calculations. Except for the shapes which have been achieved in experiment, a lot of shapes with various fractions of different facets are also present, which should also be achieved by rational control reaction conditions such as the ratio of NH80 and En. Among these, it should be noticed that some shapes found here consist of all four facets, which agrees with the fact that (100), (210), (111) and (110) cleavages were also observed in the case of pyrite.25,33
1, an NiSe2 crystal with an edge- and corner-truncated octahedron is synthesized, which can be found clearly in the shapes predicted in the theory calculations. Except for the shapes which have been achieved in experiment, a lot of shapes with various fractions of different facets are also present, which should also be achieved by rational control reaction conditions such as the ratio of NH80 and En. Among these, it should be noticed that some shapes found here consist of all four facets, which agrees with the fact that (100), (210), (111) and (110) cleavages were also observed in the case of pyrite.25,33
The agreement between theory and experiment also suggests that controlling the chemical potential is an efficient way to tailor the shape of materials and the Wulff construction using the surface free energy from first principles is predictive. On the other hand, chemical potential is also related to the temperature and pressure of the gas phase in the experiment, the present theoretical results also suggest that the temperature and pressure can also tune the shape of materials. Since the surface free energies of materials are known to depend on chemical potential, the crystal shape tuning by chemical potential thus is expected to be universal for other materials especially for compounds. It should be noticed that the crystal shapes predicted here are determined by Wulff construction on the basis of surface energy in a vacuum, which thus gives the equilibrium thermodynamic shapes of the crystals. Whereas a series of NiSe2 with different morphologies are synthesized via a solvothermal route in mixed solvents of hydrazine hydrate and ethylenediamine, which represents a much more complex environment. During the crystal growth process, kinetics is known to play an important role. As shown above, the present work indicates that the final crystal shapes of materials are dominated by thermodynamics, whereas kinetics can be seen as a perturbation.
4 Conclusion
Based on density functional theory (DFT), ab initio atomistic thermodynamics, Wulff construction, and a solvothermal route in mixed solvents of hydrazine hydrate and ethylenediamine, the shape evolution of NiSe2 crystals with chemical potential has been investigated. Our results indicate that the equilibrium shapes of NiSe2 change from pyritohedron enclosed by (210) facets, truncated octahedron to perfect octahedron occupied by (111) facet, which is in good agreement with experimental shape evolution of NiSe2 by varying the volume ratios of hydrazine hydrate to ethylenediamine. The present theory and experimental work indicates that thermodynamics dominates the crystal shape of materials and controlling the chemical potential is an efficient way to tailor the shape of materials.Acknowledgements
The financial supports from the National Natural Science Foundation of China (no. 11004018) and the Hunan Provincial Natural Science Foundation of China (no. 10JJ4002 and no. 12JJ3039) are appreciated gratefully. Computations were performed partially at the Shanghai Supercomputer Center. This work was also supported by the construct program of the key discipline in Hunan province and the aid program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province.References
- V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Markovi&cacute, Science, 2007, 315, 493–497 CrossRef PubMed.
- R. Narayanan and M. A. El-Sayed, Nano Lett., 2004, 4, 1343–1348 CrossRef.
- C. T. Campbell, S. C. Parker and D. E. Starr, Science, 2002, 298, 811–814 CrossRef PubMed.
- F. Tao and M. Salmeron, Science, 2011, 331, 171–174 CrossRef PubMed.
- W. Niu, L. Zhang and G. Xu, ACS Nano, 2010, 4, 1987–1996 CrossRef PubMed.
- J. M. Honig and J. Spałek, Chem. Mater., 1998, 10, 2910–2929 CrossRef.
- M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039–1263 CrossRef.
- A. Husmann, D. S. Jin, Y. V. Zastavker, T. F. Rosenbaum, X. Yao and J. M. Honig, Science, 1996, 274, 1874–1876 CrossRef.
- M.-Z. Xue and Z.-W. Fu, Electrochem. Commun., 2006, 8, 1855–1862 CrossRef PubMed.
- F. Gong, X. Xu, Z. Li, G. Zhou and Z.-S. Wang, Chem. Commun., 2013, 49, 1437–1439 RSC.
- W. Du, X. Qian, X. Niu and Q. Gong, Cryst. Growth Des., 2007, 7, 2733–2737 Search PubMed.
- Z.-H. Han, S.-H. Yu, Y.-P. Li, H.-Q. Zhao, F.-Q. Li, Y. Xie and Y.-T. Qian, Chem. Mater., 1999, 11, 2302–2304 CrossRef.
- H. Fan, M. Zhang, X. Zhang and Y. Qian, J. Cryst. Growth, 2009, 311, 4530–4534 CrossRef PubMed.
- A. P. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Phys. Rev. Lett., 2013, 111, 015501 CrossRef.
- N. Bonnet and N. Marzari, Phys. Rev. Lett., 2013, 110, 086104 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter, 2001, 65, 035406 CrossRef.
- C. Stampfl, M. Veronica Ganduglia-Pirovano, K. Reuter and M. Scheffler, Surf. Sci., 2002, 500, 368–394 CrossRef.
- G. Wulff, Z. Krystallogr. Mineral., 1901, 34, 449 Search PubMed.
- C. Schuster, M. Gatti and A. Rubio, Eur. Phys. J. B, 2012, 85, 1–10 CrossRef.
- J. Kuneš, L. Baldassarre, B. Schächner, K. Rabia, C. A. Kuntscher, D. M. Korotin, V. I. Anisimov, J. A. McLeod, E. Z. Kurmaev and A. Moewes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035122 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- D. R. Alfonso, J. Phys. Chem. C, 2010, 114, 8971–8980 CAS.
- J. Alonso-Azcrate, M. Rodas, L. Fernndez-Daz, S. Bottrell, J. R. Mas and S. Lpez-Andrs, Geol. J., 2001, 36, 159–170 CrossRef.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- Y. Ohmasa, I. Yamamoto, M. Yao and H. Endo, J. Phys. Soc. Jpn., 1995, 64, 4766–4789 CrossRef CAS.
- A. K. Bhatnagar and S. Subrahmanyam, Solid State Commun., 1982, 42, 281–286 CrossRef CAS.
- S. Chen, K. Zeng, Y. Song, H. Li, P. Liu and F. Li, J. Cryst. Growth, 2012, 358, 57–63 CrossRef CAS PubMed.
- N. Chen, W. Zhang, W. Yu and Y. Qian, Mater. Lett., 2002, 55, 230–233 CrossRef CAS.
- W.-B. Zhang, C. Chen and S.-Y. Zhang, J. Phys. Chem. C, 2013, 117, 21274–21280 CAS.
- Y.-T. Chen, W. Zhang, F.-B. Zhang, Z.-X. Zhang, B.-Z. Zhou and H.-L. Li, Mater. Lett., 2004, 58, 2761–2763 CrossRef CAS PubMed.
- R. Murphy and D. R. Strongin, Surf. Sci. Rep., 2009, 64, 1–45 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |