Time-dependent density functional study of UV-visible absorption spectra of small noble metal clusters (Cun, Agn, Aun, n = 2–9, 20)†
Abstract
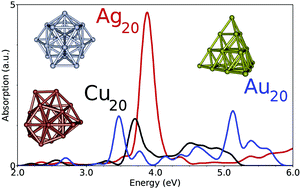
The absorption UV-visible spectra of noble metal clusters Cun, Agn, Aun, n = 2–9 and 20 are investigated in the framework of the time-dependent density functional theory using the long-range corrected density functionals LC-M06L and CAM-B3LYP and high-quality Gaussian basis sets. Some calculations including the spin–orbit coupling are also presented. The contribution of the d electrons to the optical response was found to be lower than it was when a purely local exchange functional was used. Calculated spectra are compared with experimental ones for clusters embedded in a rare-gas matrix.

 Please wait while we load your content...
Please wait while we load your content...