Effect of macrovoids in nano-silica/polyimide mixed matrix membranes for high flux CO2/CH4 gas separation
Xiao Yuan Chenab,
Hoang Vinh-Thanga,
Denis Rodrigue*a and
Serge Kaliaguinea
aDepartment of Chemical Engineering, Université Laval, Québec, Canada G1V 0A6. E-mail: Denis.Rodrigue@gch.ulaval.ca; Fax: +1-418-656-5993; Tel: +1-418-656-2903
bCentre National en Électrochimie et en Technologies Environnementales, Collège Shawinigan, Shawinigan, Canada G9N 6V8
First published on 18th February 2014
Abstract
Macrovoid structured mixed matrix membranes (MMMs) composed of nano-size (200 nm) silica particles and co-polyimide were prepared from 6FDA–ODA–DAM (6FDA = 4,4′-(hexafluoroiso-propylidene)diphthalic anhydride; ODA = 4,4′-oxidianiline; DAM = 1,3,5-trimethyl-2,6-phenylenediamine) with different proportions (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) and tetraethoxysilane (TEOS) via the sol–gel method. The separation performance of MMMs with 6FDA–ODA–DAM treated at high temperature (450 °C) was excellent for CO2/CH4 separation (for 6FOD–ODA–DAM (1
4) and tetraethoxysilane (TEOS) via the sol–gel method. The separation performance of MMMs with 6FDA–ODA–DAM treated at high temperature (450 °C) was excellent for CO2/CH4 separation (for 6FOD–ODA–DAM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1): CO2 permeability ∼265 Barrer and CO2/CH4 selectivity ∼32; for 6FOD–ODA–DAM (1
1): CO2 permeability ∼265 Barrer and CO2/CH4 selectivity ∼32; for 6FOD–ODA–DAM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4): CO2 permeability ∼302 Barrer and CO2/CH4 selectivity ∼25). Remarkably, the best membrane could resist pressure up to 600 psi without any loss of permselectivity. The CO2/CH4 separation performance of a series of silica–6FDA–ODA–DAM(11) MMMs with different SiO2 loadings is theoretically predicted using a modified Maxwell model where both gas permeability and macrovoid shape factor are simultaneously considered as adjustable parameters. Applying the optimized values, the modified Maxwell model predictions were in excellent agreement with experimental permeability data (less than 2% deviation).
4): CO2 permeability ∼302 Barrer and CO2/CH4 selectivity ∼25). Remarkably, the best membrane could resist pressure up to 600 psi without any loss of permselectivity. The CO2/CH4 separation performance of a series of silica–6FDA–ODA–DAM(11) MMMs with different SiO2 loadings is theoretically predicted using a modified Maxwell model where both gas permeability and macrovoid shape factor are simultaneously considered as adjustable parameters. Applying the optimized values, the modified Maxwell model predictions were in excellent agreement with experimental permeability data (less than 2% deviation).
1. Introduction
Membrane-based gas separations are attractive because of their simplicity, low energy costs, and ability to operate in remote locations. Full utilization of the advantages of membrane technology, however, will require new membranes with increased permeabilities and selectivities.1 Today, membrane-based CO2/CH4 gas separation has mainly four important fields of application in petroleum industries,2 natural gas purification,3 bio-gas purification,4 and CO2 capture.5 Mixed matrix membranes (MMMs) combine the potential advantages of inorganic particles and polymer matrix, which are superior permeability or selectivity of the former and good processability and mechanical properties of the latter.6–12 In this regard, the development of these organic–inorganic hybrids focused on structure and composition modification of polyimides to improve their gas selectivity and/or permeability.13–17 In this study, physical and gas transport properties of macroporous hybrid membranes with novel 6FDA–ODA–DAM co-polyimide containing silica were investigated. The hybrid membranes were prepared via a sol–gel technique using this co-polyimide and tetraethoxysilane (TEOS) silica.2. Literature review
Mixed matrix membranes, which are composed of an inorganic nanofiller dispersed in a polymer matrix, have been investigated for gas separation and have the potential to provide a solution to the limiting trade-off between permeability and selectivity of polymeric membranes.18,19 For example, some membranes, in which SiO2 or TiO2 particles are dispersed in polyimide, show much higher gas permeabilities and similar or even improved gas selectivities compared to their corresponding neat polymer membranes.20–26 The sol–gel method is the most widely used preparation technology for nanocomposite membranes. In this method, polymers and inorganic nanoparticle precursors are mixed together in solution. The inorganic precursors then hydrolyze and condense into well-dispersed nanoparticles in the polymer matrix. The advantage of this method is obvious: the reaction conditions are moderate (usually room temperature and ambient pressure) and the concentrations of organic and inorganic components are easy to control in the solution. Additionally, the organic and inorganic ingredients are dispersed at the molecular or nanometer level in the membranes, and thus the membranes are homogeneous.27–30For example, Iwata et al. reported that by using the sol–gel method, a nanocomposite membrane of polyacrylonitrile (PAN) with hydrolyzate of tetraethoxysilane (TEOS) as the inorganic phase showed O2 permeability of 2.2–2.5 Barrer and ideal selectivity of 13–17 (silica contents from 3–20 wt%) in O2/N2 separation.31
Gomes et al. prepared poly(1-trimethylsilyl-1-propyne) (PTMSP)/silica nanocomposite membranes by sol–gel copolymerization of TEOS with different organoalkoxysilanes in tetrahydrofuran solution of PTMSP.32
Joly et al. fabricated polyimide/silica membranes containing 32 wt% silica via the sol–gel method by adding tetramethoxysilane (TMOS) to poly(amic acid) (PAA) solution and subsequently imidizing at 60–300 °C. The nanocomposite membrane had a higher permeability for CO2 (from 0.8 to 2.0 Barrer) and a lower CO2/CH4 selectivity (from 40 to 25) compared to the pure polyimide membrane.21
Kusakabe et al. reported that CO2 permeability of polyimide/SiO2 hybrid nanocomposite membranes was 15 times larger than that of the corresponding polyimide. Permeability also increased with increasing mass fraction of silica, while permselectivity of CO2 to N2 decreased.33
Suzuki et al. reported that hyperbranched polyimide (HBPI)–silica hybrid membranes were prepared via a sol–gel technique using poly(amic acid), water, and tetramethoxysilane.24,34,35 Amine-terminated 6FDA–TAPOB hyperbranched polyimide (HBPI) (HBPI(6FDA-TAPOB)) was prepared by polycondensation of 1,3,5-tris(4-aminophenoxy) benzene (TAPOB) and 6FDA in N,N-dimethylacetamide (DMAc), followed by an addition of a silane coupling agent, 3-aminopropyl-trimethoxysilane (APTrMOS) to modify the end groups.24,34 6FDA-HAB hydroxy polyimide (HPI) (HPI(6FDA-HAB)) was synthesized from 6FDA and 3,3′-dihydroxybenzidine (HAB) in DMAc. Finally, 6FDA-TAPOB hyperbranched polyimide (HBPI(6FDA-TAPOB))/6FDA-HAB hydroxy polyimide (HPI(6FDA-HAB)) blend-silica hybrid membranes were prepared by blending HBPI and HPI polymers, adding of appropriate amounts TMOS and deionized water, followed by imidizing and hybridizing in an oven under N2 flow.35 The results showed that both gas permeabilities and CO2/CH4 selectivities were increased with increasing silica content.
Recently, Suzuki et al. used the same method to obtain hyperbranched polyimide-silica hybrid membranes followed by heat-treatment in nitrogen at 450 °C. These membranes have both excellent gas permeability (134–369 Barrer) and selectivity (32–68), particularly for CO2/CH4 under the tested conditions (76 cm Hg and 25 °C).36
Fardad studied the influence of various catalysts on the structure of silica sol–gel films based on the hydrolysis and condensation of TEOS with 2 moles of water, and in the presence of 2 moles of ethanol. This investigation showed that film thickness, shrinkage, porosity, and optical quality depended on the type of catalysts used in the preparation of the solution precursor.37
Kayser et al.38 prepared amine functionalized nano-spherical silica particles by a modified Stöber method39 and grafted 3-aminopropyl-dimethylmethoxysilane (APDMS) on their surface. These particles were used as inorganic fillers in silica/SPEEK mixed matrix membranes. The results indicated that the main effect of the inorganic filler on proton conductivity is related to changes in the microstructure of the water channels in the wet polymer related to the distribution of nanoparticles in their lattice.
In the above-described investigations, most authors prepared the silica particles in situ in acid conditions (for example, poly(amic acid) (PAA)), with the acid acting as a catalyst in the hydrolysis/condensation reactions. In some cases, silica particles were first produced and then mixed with polymer solution before casting. The polymer morphology changes associated with particle introduction in the MMMs, and their effects on membrane performance in gas separation were seldom discussed. In this work, silica particles were simultaneously generated with membrane fabrication by a simple method. The focus is made on the relationship between morphology, affected by silica particles, and membrane separation performances of the MMMs in CO2/CH4 separation.
3. Experimental
3.1. Materials
Materials for synthesis of co-polyimide compounds: 6FDA = 4,4′-(hexafluoroiso-propylidene)diphthalic anhydride (>99% purity) was provided by Chriskey Company, ODA = 4,4′-oxidianiline (97% purity) was purchased from Sigma-Aldrich, and DAM = 1,3,5-trimethyl-2,6-phenylenediamine (98% purity) was obtained from TCI America. All three compounds were then purified by vacuum sublimation. 1-Methyl-2-pyrrolidone (NMP) was purchased from TCI America and purified by vacuum distillation. Acetic anhydride and triethylamine were obtained from Sigma-Aldrich. Chloroform (CHCl3, 99.8% assay by GC analysis) was obtained from VWR International LLC, and methanol was obtained from Fisher Scientific. Tetraethylorthosilicate (TEOS, 98%) was obtained from Sigma-Aldrich Co. Matrimid® 5218 and Ultem®1000 were purchased from Huntsman Advanced Materials (Switzerland) GmbH and WS Hampshire Inc, respectively.3.2. Co-polyimide synthesis
6FDA-ODA-DAM co-polyimides were synthesized by a two-step method as described elsewhere.40 In the first step, poly(amic acid) (PAA) derived from equimolar amounts of solid 6FDA and DAM diamines (ODA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DAM molar ratios are 1
DAM molar ratios are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) were prepared by solution condensation in NMP. Both reaction mixtures were stirred using a power drill (Mastercraft) connected to a variable autotransformer (The Superior Electric co. Bristol Conn, USA) stirrer under an argon atmosphere and placed in an ice–water mixture for 15 h. In the second step, poly(amic acid) was then imidized to form polyimides by chemical imidization under an argon atmosphere at room temperature for 24 h by adding acetic anhydride (dehydrating agent) and triethylamine (catalyst). The reaction scheme of co-polyimide synthesis is shown in Fig. 1. The polyimide solution was then precipitated with methanol, washed several times with methanol, and dried at 200 °C in a vacuum oven for 24 h.
4) were prepared by solution condensation in NMP. Both reaction mixtures were stirred using a power drill (Mastercraft) connected to a variable autotransformer (The Superior Electric co. Bristol Conn, USA) stirrer under an argon atmosphere and placed in an ice–water mixture for 15 h. In the second step, poly(amic acid) was then imidized to form polyimides by chemical imidization under an argon atmosphere at room temperature for 24 h by adding acetic anhydride (dehydrating agent) and triethylamine (catalyst). The reaction scheme of co-polyimide synthesis is shown in Fig. 1. The polyimide solution was then precipitated with methanol, washed several times with methanol, and dried at 200 °C in a vacuum oven for 24 h.
3.3. Silica/polyimide MMM preparation
The hybrid membranes were prepared by the sol–gel reaction and dense film casting method.35 First, 0.4–0.5 g of polyimide was dissolved in 5–10 ml of chloroform. The obtained solution was then filtered to remove un-dissolved materials and dust particles. Then, appropriate amounts of TEOS (eqn (1), MSiO2 and MTEOS is the molecular weight of SiO2 and TEOS. WTEOS and Wpolyimide are the weight of TEOS and PI used in this experience) and excess water were added in the polymer solution. This hydrolysis reaction is an example of a sol–gel process. The side product is ethanol. The reaction proceeds via a series of condensation reactions that convert the TEOS molecule into a mineral-like solid via the formation of Si–O–Si linkages (eqn (2)). The rate of this conversion is sensitive to the presence of acids and bases, both of which serve as catalysts. The Stöber process allows the formation of mono-dispersed silica particles. The size of silica particles is between 50 and 2000 nanometers depending on type of silicate ester used, type of alcohol used and volume ratios.39 The slurry was agitated for 24 h to obtain a good homogenization and produce macrovoids during this period. A nascent film was cast from the solution onto a clean polyester plate using a small metal container with a cover to delay solvent evaporation from the nascent membrane. The membrane was further dried for 15 h at 200 °C under vacuum. Ethanol evaporated with the high heating temperature. The average thickness of MMMs was 40–85 μm, measured with a micrometer.
 | (1) |
| Si(OC2H5)4 + 2H2O → SiO2 + 4C2H5OH | (2) |
3.4. Thermal treatment of MMMs
The hybrid membranes were further heated under nitrogen at 300 °C and 450 °C for 1 hour each time, thereby obtaining gas separation membranes for further analysis.3.5. Characterization
FT-IR spectra were recorded using a Nicolet Magna 850 Fourier transform infrared spectrometer (Thermo Scientific, Madison, WI) equipped with a liquid-nitrogen-cooled narrow-band MCT detector using Golden-Gate (diamond IRE) ATR accessories (Specac Ltd., London, U.K.). Each spectrum was obtained from the acquisition of 128 scans at 4 cm−1 resolution, from 4000 to 700 cm−1 using Happ-Genzel apodization.The weight loss curves (TGA-DTG) were recorded using a TA Instruments TGA model Q5000IR from 100 to 850 °C at a heating rate of 10 °C min−1 under nitrogen.
The glass transition temperature (Tg) and Young's modulus of MMM were determined using a dynamic mechanical thermal analyzer (TA Instruments, RSA-3, New Castle, DE) on samples having dimensions of 25 × 6 × 0.02 mm3. For Tg measurements, the temperature was increased from 30 to 350 °C at a rate of 10 °C min−1 with a strain of 0.05% and a frequency of 1 Hz.
The membrane density (ρ) is simply defined by the ratio between mass (M) and volume (V). The mass is weighed with an analytical balance Mettler AE200 with a sensitivity of 10−4 g. The volume is then calculated from the diameter (d) (constant at 55 mm) and the average of 8 thicknesses (l) of the membrane.
SEM images were recorded to determine crystal size and to characterize morphology of the dispersed phase, using a JEOL JSM-840A operated at 15–20 kV. From the SEM micrographs, the average diameter of macrovoids, their number and surface were obtained using image analysis software (Image Pro Plus). The average diameter was measured at 2 degree intervals and passing through the centroid giving an average of 90 measurements for each macrovoid.
The cell density is determined from the number of cells per unit section area. It is calculated assuming that the surface distribution is the same in all three dimensions and eqn (3) is the mathematical expression of cell density.41
 | (3) |
3.6. Membrane properties
The pure gas transport properties were measured using the variable pressure (constant volume) method.11,12 In the measurements, the permeate pressure was varied from 10−3 to 30 Torr. For each membrane, gas permeability, CO2/CH4 selectivity, and separation factor were averaged over three replicate permeation tests. The reported data correspond to averages of these results.For the transport of individual components A and B through a membrane, the permeability Pi of penetrant i can be expressed as follows:
 | (4) |
The ideal selectivity can be written as the ratio of permeabilities:
 | (5) |
The separation factor (α*AB) represents the ability of a membrane to separate a binary gas mixture, and is defined as:
| α*AB = (yA/yB)/(xA/xB) | (6) |
4. Results and discussion
4.1. Thermal analysis
Characteristic temperatures from TGA curves were determined as the low temperature peak in the DTG analysis and the values are listed in Table 1. The neat polymer membranes from 6FDA-ODA-DAM co-polyimide are designated 6FOD, whereas the ODA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DAM molar ratio is labelled 11 or 14 (for 1
DAM molar ratio is labelled 11 or 14 (for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively). For example: 6FOD(11)-n%-200, n% is wt% SiO2 loading, and 200 is the treatment temperature. The treatment temperatures are 200, 300 and 450 °C. The temperatures to reach 5% and 10% weight loss of 5–15 wt% SiO2/polyimide MMMs were increased (by about 5–30 °C). Those of MMMs after thermal treatment at 300 and 450 °C were generally lower by about 10–40 °C. DTG peak temperatures also give information on the pyrolysis rates. Thermal stability of the MMM materials prepared via TEOS hydrolysis reaction is believed to be sufficient for gas separation applications, even through the stability value is very close compared to that of the pure polyimide.42 For example, the highest temperature used for hydrogen separation was 300–500 °C. At the natural gas well, the gas pressure is rather high (in excess of 1000 psi) and the gas temperature is on the order of 30–50 °C. All the TGA curves show a plateau, which indicates no remnant hydroxyl groups. There was no residual absorbed solvent or hydroxyl group having low decomposition temperature. At the latter temperature, most chemical decomposition reactions of the material took place. These weight losses are mostly due to the conversion of carbonyl groups (C
4, respectively). For example: 6FOD(11)-n%-200, n% is wt% SiO2 loading, and 200 is the treatment temperature. The treatment temperatures are 200, 300 and 450 °C. The temperatures to reach 5% and 10% weight loss of 5–15 wt% SiO2/polyimide MMMs were increased (by about 5–30 °C). Those of MMMs after thermal treatment at 300 and 450 °C were generally lower by about 10–40 °C. DTG peak temperatures also give information on the pyrolysis rates. Thermal stability of the MMM materials prepared via TEOS hydrolysis reaction is believed to be sufficient for gas separation applications, even through the stability value is very close compared to that of the pure polyimide.42 For example, the highest temperature used for hydrogen separation was 300–500 °C. At the natural gas well, the gas pressure is rather high (in excess of 1000 psi) and the gas temperature is on the order of 30–50 °C. All the TGA curves show a plateau, which indicates no remnant hydroxyl groups. There was no residual absorbed solvent or hydroxyl group having low decomposition temperature. At the latter temperature, most chemical decomposition reactions of the material took place. These weight losses are mostly due to the conversion of carbonyl groups (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) to either CO or CO2.43
O) to either CO or CO2.43
| Membranea | Td5% (°C) | Td10% (°C) | DTG peak (°C) |
|---|---|---|---|
a 6FOD(11), 6FOD(14)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6FDA-ODA-DAM (1 6FDA-ODA-DAM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and 6FDA-ODA-DAM (1 1) and 6FDA-ODA-DAM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4). n%: wt% SiO2 loading, at treatment temperature of 200, 300 and 450 °C. 4). n%: wt% SiO2 loading, at treatment temperature of 200, 300 and 450 °C. |
|||
| 6FOD(11)-0%-200 | 488 | 508 | 529 |
| 6FOD(11)-5%-200 | 495 | 529 | 550 |
| 6FOD(11)-10%-200 | 501 | 531 | 553 |
| 6FOD(11)-15%-200 | 504 | 535 | 554 |
| 6FOD(11)-10%-300 | 450 | 511 | 549 |
| 6FOD(11)-10%-450 | 503 | 532 | 552 |
| 6FOD(14)-0%-200 | 489 | 508 | 523 |
| 6FOD(14)-10%-200 | 447 | 484 | 520 |
| 6FOD(14)-10%-300 | 451 | 484 | 520 |
| 6FOD(14)-10%-450 | 464 | 485 | 520 |
| Matrimid-0%-200 | 474 | 508 | 511 |
| Matrimid-10%-200 | 440 | 486 | 518 |
| Matrimid-10%-450 | 452 | 492 | 523 |
4.2. FTIR analysis and mechanism of reaction
To explore the mechanism of TEOS hydrolysis reaction during MMM casting, FT-IR measurements were used to confirm this reaction. The possible TEOS hydrolysis reaction is displayed in eqn (2).As shown in Fig. 2, the appearance of absorption bands at 1725 cm−1 (asymmetric stretch of the carbonyl group, imide I band) and 1782 cm−1 (symmetric stretch of the carbonyl group, imide II band), 1377 cm−1 (C–N stretch), 1117 cm−1 (imide III band) and 720 cm−1 (deformation of the imide ring or imide IV carbonyl group) confirmed the formation of imides for all membranes.44 Usually, siloxanes show one or more very strong infrared bands in the region 1000–1130 cm−1. Disiloxane and small-ring cyclosiloxanes show a single Si–O–Si band. As the siloxane chains became longer or branches the Si–O–Si absorption becomes broader and more complex showing two or more overlapping band.45 From Fig. 2, carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) peaks were found at 1100 cm−1 in the 6FOD(11) membrane, silica (Si–O) vibrations are found between 1080 and 1060 cm−1 in the others membrane. The 6FOD(11)-20%-ambient has two peaks at 1060–1080 cm−1. Thus these peaks to some extent overlap with the C–O frequencies of polyimides. Other weak vibrations are found in between 2900 and 3000 cm−1 in Fig. 2 for membrane 6FOD(11)-20% at ambient temperature. This membrane is the nascent film and was not heated. These distinctive bands at 2927–2983 cm−1 correspond to the symmetric and asymmetric vibrations of CH2 methylene and CH3 methyl groups. It is thought that these groups belong to the ethanol generated in reaction (2).
O) peaks were found at 1100 cm−1 in the 6FOD(11) membrane, silica (Si–O) vibrations are found between 1080 and 1060 cm−1 in the others membrane. The 6FOD(11)-20%-ambient has two peaks at 1060–1080 cm−1. Thus these peaks to some extent overlap with the C–O frequencies of polyimides. Other weak vibrations are found in between 2900 and 3000 cm−1 in Fig. 2 for membrane 6FOD(11)-20% at ambient temperature. This membrane is the nascent film and was not heated. These distinctive bands at 2927–2983 cm−1 correspond to the symmetric and asymmetric vibrations of CH2 methylene and CH3 methyl groups. It is thought that these groups belong to the ethanol generated in reaction (2).
4.3. Dynamic mechanical testing (DMA) analysis
DMA testing is a versatile and sensitive technique enabling the complete exploration of the relaxation mechanisms in viscoelastic materials.46 The most common use of DMA is for the determination of the glass-transition temperature (Tg), where the maximum loss of applied energy is observed, usually as a peak, in the traces of the loss factor versus temperature.9,11,40 Young's modulus is obtained from the slope of stress–strain curves at low deformation (linear elastic) and represents the rigidity of materials (Fig. 3).Table 2 summarizes the glass transition temperature and Young's modulus of 6FOD(11) polyimide, and 6FOD(11) with TEOS MMM. Compared to the neat 6FOD(11) membrane (Table 2), the Tg values of MMMs decreased with increasing MOF loading (from 5 to 20 wt%). This decrease might be explained by the presence of macrovoids (see below), which can enhance the movement of the polymer chains. In the preparation of polymer foams, carbon dioxide and ethanol (EtOH) mixtures can be used as blowing agents as already proposed.47,48 Gendron at al. studied the effect of blending CO2 with ethanol (EtOH) as a co-blowing agent for polystyrene (PS) foaming.48 The results showed that viscosity and glass transition temperature obviously decreased with increasing amount of foaming agents. The Tg values of treated MMMs are higher than that of the neat polyimide membrane. This may be due to polymer chains becoming more rigid after rearrangement upon high temperature treatment.49 Moreover, Young's modulus of MMM membranes decrease with increasing SiO2 loading (Fig. 3 and Table 2). This behaviour is usually associated with highly reduced densities and low mechanical properties of foamed polymers.50
| Membrane | Tg (°C) | Young's modulus (MPa) (50 °C) |
|---|---|---|
| 6FOD(11)-0%-200 | 319 | 150 |
| 6FOD(11)-5%-200 | 318 | 67 |
| 6FOD(11)-10%-200 | 317 | 66 |
| 6FOD(11)-15%-200 | 305 | 48 |
| 6FOD(11)-20%-200 | 283 | 31 |
| 6FOD(11)-10%-300 | 327 | 56 |
| 6FOD(11)-10%-450 | 353 | 72 |
4.4. Morphology of macrovoid structured MMMs
Typical images of the macrovoid structured MMMs for SiO2 loading varying from 5 to 20 wt% are given in Fig. 4. It is seen that these macrovoids are non-circular and non-uniform until 1–20 micron in diameter; the number of cells and their sizes vary with increasing SiO2 loading. It is thought that the hydrolysis reaction is favoured in the weak acid polyimide solution during membrane casting, but no reaction between PI and TEOS was evidenced (see Section 4.2). The ethanol generated by the hydrolysis reaction was only slightly evaporated during stirring and mostly during dry heating (200 °C) the membrane. The macrovoids were then generated due to ethanol evaporation. | ||
| Fig. 4 SEM micrographs showing the macrovoid structure of 6FOD(11)-200 MMMs with: (a) 5 wt%; (b) 10 wt%; (c) 15 wt%, and (d) 20 wt% SiO2 loading. | ||
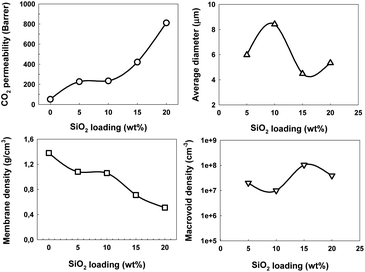
Fig. 5 shows the distribution of macrovoid average diameter in each membrane. Table 3 summarizes the membrane density, average macrovoid diameter and macrovoid density of MMMs. Membrane density was decreased slowly with increasing SiO2 loading compared with the original membrane. The average macrovoid diameter and macrovoid density changed with SiO2 loading. The morphology of macrovoid structure is complex and could be affected by many factors during membrane fabrication such as ambient temperature, pH value of solution, stirring time, etc. These results are consistent with higher void size and lower void number as reported in ref. 48.
 | ||
| Fig. 5 Macrovoid average diameter distribution of MMMs: (a) 6FOD(11)-5%-200; (b) 6FOD(11)-10%-200; (c) 6FOD(11)-15%-200, and (d) 6FOD(11)-20%-200. | ||
| Membrane | Membrane density (g cm−3) | Average diameter (μm) | Macrovoid density (cm−3) |
|---|---|---|---|
| 6FOD(11)-0%-200 | 1.38 | — | — |
| 6FOD(11)-5%-200 | 1.08 | 5.95 | 2.0 × 107 |
| 6FOD(11)-10%-200 | 1.06 | 7.45 | 1.3 × 107 |
| 6FOD(11)-15%-200 | 0.71 | 4.48 | 1.0 × 108 |
| 6FOD(11)-20%-200 | 0.51 | 5.27 | 3.9 × 107 |
| 6FOD(11)-10%-300 | 0.79 | 4.02 | 3.0 × 107 |
| 6FOD(11)-10%-450 | 0.96 | 5.04 | 3.5 × 107 |
The size of silica particles was dependent on the conditions of hydrolysis solution.39 In the present work, 200 nm silica particles were observed for MMM in very weak acid solution. Fig. 6 shows an example for 6FOD(11)-10%-200 membrane. This result is in agreement with ref. 39.
 | ||
Fig. 6 SEM images of SiO2 particles of 6FOD(11)-10%-200 membrane with different magnifications: (a) 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×; and (b) 20 000×; and (b) 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×. 000×. | ||
4.5. Gas transport properties
| Membrane | PCO2 (Barrer) | PCH4 (Barrer) | PCO2/PCH4 | (50/50%) CO2/CH4 mixed gas selectivity |
|---|---|---|---|---|
| 6FOD(14)-0%-200 | 130 | 7.10 | 23.2 | 22.9 |
| 6FOD(14)-10%-200 | 290 | 21.8 | 13.3 | 21.8 |
| 6FOD(14)-10%-450 | 300 | 12.2 | 24.8 | 22.3 |
| Matrimid-0%-200 | 10.0 | 0.28 | 35.3 | 35.0 |
| Matrimid-10%-200 | 41.0 | 1.10 | 38.0 | 38.0 |
| Matrimid-10%-450 | 34.0 | 0.92 | 36.7 | 38.2 |
| Ultem-0%-200 | 1.45 | 0.037 | 38.8 | 36.8 |
| Ultem-10%-200 | 2.78 | 0.15 | 17.5 | 18.2 |
Two co-polyimides with different ODA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DAM (1
DAM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) molar ratios were used as polymer matrices for macrovoid structured MMMs. The CO2/CH4 separation performances of neat and their macrovoid structure membranes are summarized in Tables 4 and 5. The co-polyimide 6FOD(14) with 10 wt% SiO2 has both higher values of CO2 and CH4 permeability compared to those of neat co-polyimide. The macrovoid membranes of 6FOD(14)-10%-450 and 6FOD(11)-10%-450 with heating temperature of 450 °C showed very high CO2 permeability of 302 and 265 Barrer, and their selectivity improved to 24.8 and 32 from 23 and 24, respectively. The separation factor for mixed gas also showed high values from 22 to 34.
4) molar ratios were used as polymer matrices for macrovoid structured MMMs. The CO2/CH4 separation performances of neat and their macrovoid structure membranes are summarized in Tables 4 and 5. The co-polyimide 6FOD(14) with 10 wt% SiO2 has both higher values of CO2 and CH4 permeability compared to those of neat co-polyimide. The macrovoid membranes of 6FOD(14)-10%-450 and 6FOD(11)-10%-450 with heating temperature of 450 °C showed very high CO2 permeability of 302 and 265 Barrer, and their selectivity improved to 24.8 and 32 from 23 and 24, respectively. The separation factor for mixed gas also showed high values from 22 to 34.
| Membrane | PCO2 (Barrer) | PCH4 (Barrer) | PCO2/PCH4 | (50/50%) CO2/CH4 mixed gas selectivity |
|---|---|---|---|---|
| 6FOD(11)-0%-200 | 51.8 | 1.80 | 24.2 | 21.9 |
| 6FOD(11)-5%-200 | 200 | 12.5 | 18.2 | 24.5 |
| 6FOD(11)-10%-200 | 235 | 12.5 | 16.8 | 24.6 |
| 6FOD(11)-15%-200 | 420 | 76.9 | 6.3 | — |
| 6FOD(11)-20%-200 | 810 | 695 | 1.2 | — |
| 6FOD(11)-10%-300 | 245 | 13.1 | 18.7 | 25.7 |
| 6FOD(11)-10%-450 | 265 | 8.6 | 31.8 | 34.2 |
4.6. Modelling of MMM permeation properties
Coupling a theoretical modelling with experimental separation data provides an opportunity to understand the transport properties of these MMMs. As reported in our recent review,52 the particularly useful Maxwell model developed in 1873, originally derived from the estimation of the dielectric properties of particulate composite materials, has been widely accepted as a simple and effective tool for predicting permeation properties of a two-phase ideal MMM as:
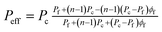 | (7) |
In eqn (7), Peff describes the effective steady-state permeability of a gaseous penetrant through a MMM, Pf and Pc are the effective permeability of pure filler membrane and polymer matrix, respectively, ϕd is the volume fraction of the dispersed filler.52,53 In this equation, Pc and ϕd are often known experimental parameters, while Pf can be considered as either an un-known or a known parameter. The shape factor n depends on the shape of the dispersed filler. Various definitions of n were proposed in the literature. Hamilton and Crosser have, for example, proposed n = 3/ψ, where the sphericity ψ is defined as the ratio between the surface area of a sphere having a volume equal to the particle volume and the particle surface area.54 For near-spherical fillers, the value is therefore taken as n = 3, and eqn (7) reduces to the well-known original Maxwell model.53 Kang et al. reported a shape factor n = 6 for cylindrical or tubular fillers in a polymer matrix.55 In this case, eqn (7) is an expression of the Hamilton-Crosser model.54 For a general case of filler shape, the shape factor n can accept a variety of integer values up to infinity.54
It is clear that in order to mathematically solve eqn (7), both the shape factor n and the filler permeability Pf can be considered as adjustable parameters and optimized by minimizing the differences between experimental data and calculated ones. This difference, namely the average absolute relative error (%AARE), is expressed as follows:
 | (8) |
 | (9) |
Generally, gas permeability in the interfacial void (Pv) of a typical zeolite-polymer MMM is assumed to be the product of Knudsen diffusivity through a pore with the same hydraulic diameter as the void and sorption coefficient of the gas in the void.52,54 In the present case, because of the mean free paths (λ) of penetrant gas (λCO2 = 0.082 μm and λCH4 = 0.062 μm calculated based on ref. 56 at 25 °C and 15 psi) are much smaller than the average macrovoid diameter (Table 3), the gas transport through the macrovoids is assumed to be by molecular or bulk diffusion.57 Thus, coupling with the shape factor n, the macrovoid permeability Pv will be considered as adjustable parameters. First, all the macrovoid MMMs with different SiO2 loadings were assumed to have the same shape factor n and macrovoid permeability Pv. After calculating the membrane permeability PM using eqn (9), the average absolute relative error (%AARE) was then determined using eqn (8). The optimized value of Pv corresponding to the average shape factor navg was obtained for the minimum value of %AARE. Second, owing to a large difference in macrovoid diameter of these silica-6FOD MMMs (see Fig. 4 and Table 3), an optimized shape factor n must be determined for each MMM membrane. This is obtained by using eqn (8) and (9), but only the shape factor n is considered as an adjustable parameter while Pv has the value determined in the previous step. Table 6 summarizes the estimated model parameters obtained from Maxwell model fitting the experimental data of CO2/CH4 separation through the silica-6FOD(11) MMMs with different SiO2 loadings.
| Membrane | ϕv (vol%) | Pv (Barrer) | navg | nop | PCO2 (Barrer) | %AARE | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | n = 3 | n = 6 | nop | n = 3 | n = 6 | nop | |||||
| 6FOD(11)-5%-200 | 24 | 3185 | 11 | 11 | 200 | 98 | 139 | 197 | 53.9 | 29.3 | 1.3 |
| 6FOD(11)-10%-200 | 28 | 12 | 235 | 107 | 156 | 237 | |||||
| 6FOD(11)-15%-200 | 53 | 8 | 420 | 209 | 339 | 414 | |||||
| 6FOD(11)-20%-200 | 67 | 11 | 810 | 326 | 537 | 798 | |||||
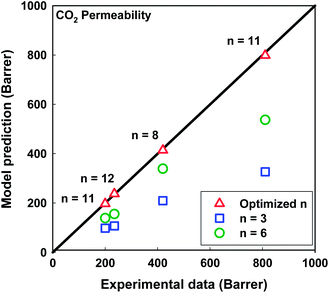
As can be seen in Table 6, the value of the optimized CO2 permeability of macrovoids Pv predicted by the Maxwell model using our MATLAB optimization program is 3815 Barrer. Compared to the CO2 permeability values calculated based on the Knudsen diffusion for a void space with average diameter of 5 nm (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 Barrer) or a pinhole with average diameter of 50 nm (152
200 Barrer) or a pinhole with average diameter of 50 nm (152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Barrer),54 this value is significantly smaller, although the average macrovoid diameters of the studied MMMs are ranging from 4.58 to 7.45 μm (Table 3). This result confirms the above assumption for the gas diffusion mechanism through the macrovoids.
000 Barrer),54 this value is significantly smaller, although the average macrovoid diameters of the studied MMMs are ranging from 4.58 to 7.45 μm (Table 3). This result confirms the above assumption for the gas diffusion mechanism through the macrovoids.
Fig. 10 illustrates a comparison between the CO2 permeability predicted by the Maxwell model with different shape factors n and the experimental data. Both n = 3 (spherical) and n = 6 (cylindrical or tubular) show a significant divergence with the experimental data. Their %AAREs are 53.9 and 29.3%, respectively. Interestingly, better agreement between the Maxwell model predictions and experimental data was observed when applying the optimized shape factors nop (%AARE = 1.3%, see Table 6).
The relation between macrovoid diameter and shape factor n is demonstrated in Fig. 11. The optimized shape factor nop is a linear function of the average macrovoid diameter. This result is remarkably significant for the application of the Maxwell model to predict the gas permeation performance of any kind of MMM morphology.
5. Conclusions
Macrovoid structured mixed matrix membranes with nano-size (200 nm) silica particle and 6FDA-ODA-DAM co-polyimide were produced, which after high temperature treatment showed excellent performance for CO2/CH4 gas separation. These membranes have improved gas permeability (from 52 to 265 Barrer), ideal selectivity (from 24 to 32), and separation factor (from 22 to 34) compared to the original neat polymer membrane. Moreover, 6FOD(11)-10%-450 membrane could withstand pressure up to 600 psi without any loss of permselectivity. CO2 and CH4 permeabilities were found to increase with increasing SiO2 loading (from 5 to 20 wt%), while ideal selectivities decreased due to low compatibility between SiO2 particles and the polymer matrix. It is believed that a compatibilizing agent would be necessary at high loading to solve this problem. Also, membrane density and mechanical properties were found to decrease, while total void area or volume in the MMM increased with increasing SiO2 loading.A special use of shape factor n in the Maxwell equation was developed to predict the gas transport properties through MMMs for this new macrovoid MMM morphology. This work is an additional step to our recent comprehensive computational strategy to fit experimental permeation data of MMMs.58 In this study, the modified Maxwell model predictions were in excellent agreement with experimental data having less than 2% deviation. Both intrinsic gas permeability of the dispersed phase (macrovoid) and shape factor (n) were simultaneously considered. The shape factor (n) was found to be strongly dependent on the foam-like morphology of these MMMs.
Notes and references
- W. J. Koros and G. K. Fleming, J. Membr. Sci., 1993, 83, 1 CrossRef CAS
.
- G. R. Pastor, J. F. Peters, W. K. Larsen and A. C. Iakovakis, U.S. Pat., 4753,666, 1988
.
- http://en.wikipedia.org/wiki/Natural_gas, accessed on 05.04.13.
- S. Basu, A. L. Khan, A. Cano-Odena, C. Liu and I. F. J. Vankelecom, Chem. Soc. Rev., 2010, 39, 750 RSC
.
- W. J. Schell, J. Membr. Sci., 1985, 22, 217 CrossRef CAS
.
- C. Liu and S. Kulprathipanja, Mixed-matrix membranes, in Zeolites in Industrial Separation and Catalysis, Wiley-VCH Verlag GmbH & Co., 2010, p. 329 Search PubMed
.
- A. F. Ismail, P. S. Goh, S. M. Sanip and M. Aziz, Sep. Purif. Technol., 2009, 70, 12 CrossRef CAS PubMed
.
- R. Mahajan and W. J. Koros, Ind. Eng. Chem. Res., 2000, 39, 2692 CrossRef CAS
.
- O. G. Nik, X. Y. Chen and S. Kaliaguine, J. Membr. Sci., 2011, 379, 468 CrossRef CAS PubMed
.
- H. Vinh-Thang, S. Kaliaguine, MOF-based mixed matrix membranes for industrial applications, in Coordination polymers and metal organic frameworks: Properties, types and applications, ed. O. L. Ortiz and L. D. Ramírez, Nova Science Publishers, Hauppauge, N. Y., USA, 2011, pp. 129–168 Search PubMed
.
- X. Y. Chen, H. Vinh-Thang, D. Rodrigue and S. Kaliaguine, Ind. Eng. Chem. Res., 2012, 51, 6895 CrossRef CAS
.
- X. Y. Chen, O. G. Nik, D. Rodrigue and S. Kaliaguine, Polymer, 2012, 53, 3269 CrossRef CAS PubMed
.
- C. Joly, S. Goizet, J. C. Schrotter, J. Sanchez and M. Escoubes, J. Membr. Sci., 1997, 130, 63 CrossRef CAS
.
- C. J. Cornelius and E. Marand, J. Membr. Sci., 2002, 202, 97 CrossRef CAS
.
- C. Hibshman, C. J. Cornelius and E. Marand, J. Membr. Sci., 2003, 211, 25 CrossRef CAS
.
- M. Iwata, T. Adachi, M. Tomidokoro, M. Ohta and T. Kobayashi, J. Appl. Polym. Sci., 2003, 88, 1752 CrossRef CAS
.
- C. Hibshman, M. Mager and E. Marand, J. Membr. Sci., 2004, 229, 73 CrossRef CAS PubMed
.
- F. Peng, L. Lu, H. Sun, Y. Wang, H. Wu and Z. Jiang, J. Membr. Sci., 2006, 275, 97 CrossRef CAS PubMed
.
- F. Peng, L. Lu, H. Sun, Y. Wang, J. Liu and Z. Jiang, Chem. Mater., 2005, 17, 6790 CrossRef CAS
.
- T. C. Merkel, B. D. Freeman, R. J. Spontak, Z. He, I. Pinnau, P. Meakin and A. J. Hill, Science, 2002, 296, 519 CrossRef CAS PubMed
.
- C. Joly, M. Samaihi, L. Porcar and R. D. Noble, Chem. Mater., 1999, 11, 2331 CrossRef CAS
.
- M. Moaddeb and W. J. Koros, J. Membr. Sci., 1997, 125, 143 CrossRef CAS
.
- C. Hibshman, C. J. Cornelius and E. Marand, J. Membr. Sci., 2003, 211, 25 CrossRef CAS
.
- T. Suzuki and Y. Yamada, Polym. Bull., 2005, 53, 139 CrossRef CAS
.
- Y. Kong, H. Du, J. Yang, D. Shi, Y. Wang, Y. Zhang and W. Xin, Desalination, 2002, 146, 49 CrossRef CAS
.
- J. H. Kim and Y. M. Lee, J. Membr. Sci., 2001, 193, 209 CrossRef CAS
.
- R. H. Brzesowsky, G. de With, S. van den Cruijsem, I. J. M. Snijkers-Hendrickx, W. A. M. Wolter and J. G. van Lierop, J. Non-Cryst. Solids, 1998, 241, 27 CrossRef CAS
.
- J. Livage and C. Sanchez, J. Non-Cryst. Solids, 1992, 145, 11 CrossRef CAS
.
- A. Kioul and L. Mascia, J. Non-Cryst. Solids, 1994, 175, 169 CrossRef CAS
.
- M. Smaihi, T. Jermoumi, J. Marignan and R. D. Noble, J. Membr. Sci., 1996, 116, 211 CrossRef CAS
.
- M. Iwata, T. Adachi, M. Tomidokoro, M. Ohta and T. Kobayashi, J. Appl. Polym. Sci., 2003, 88, 1752 CrossRef CAS
.
- D. Gomes, S. P. Nunes and K. V. Peinemann, J. Membr. Sci., 2005, 246, 13 CrossRef CAS PubMed
.
- K. Kusakabe, K. Ichiki, J. Hayashi, H. Maeda and S. Morooka, J. Membr. Sci., 1996, 115, 65 CrossRef CAS
.
- T. Suzuki, M. Miki and Y. Yamada, Eur. Polym. J., 2012, 48, 1504 CrossRef CAS PubMed
.
- M. Miki, T. Suzuki and Y. Yamada, J. Appl. Polym. Sci., 2013, 130, 54 CrossRef CAS
.
- T. Suzuki and Y. Yamada, US Pat., 20120202953, 2012
.
- M. A. Fardad, J. Mater. Sci., 2000, 35, 1835 CrossRef CAS
.
- M. J. Kayser, M. X. Reinholdt and S. Kaliaguine, J. Phys. Chem. B, 2010, 114, 8387 CrossRef CAS PubMed
.
- W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62 CrossRef
.
- X. Y. Chen, D. Rodrigue and S. Kaliaguine, Sep. Purif. Technol., 2012, 86, 221 CrossRef CAS PubMed
.
- R. Gosselin and D. Rodrigue, Polym. Test., 2005, 24, 1027 CrossRef CAS PubMed
.
- Y. Liu, R. Wang and T. S. Chung, J. Membr. Sci., 2001, 189, 231 CrossRef CAS
.
- S. Zhao, Z. Q. Shi, C. Y. Wang and M. M. Chen, J. Appl. Polym. Sci., 2008, 108, 1852 CrossRef CAS
.
- K. P. Pramoda, S. L. Liu and T. S. Chung, Macromol. Mater. Eng., 2002, 287, 931 CrossRef CAS
.
- L. J. Bellamy, The infra-red spectra of complex molecules, 3rd edn, Chapman and Hall, London, ch. 20, 1975 Search PubMed
.
- T. M. Nair, M. G. Kumaran, G. Unnikrishnan and V. B. Pillai, J. Appl. Polym. Sci., 2009, 112, 72 CrossRef CAS
.
- H. Voelker, G. Alicke, H. Schuch, M. Weilbacher and R. Weber, US Pat., 5,182,308, 1993
.
- R. Gendron, M. F. Champagne, Y. Delaviz and M. E. Polasky, J. Cell. Plast., 2006, 42, 127 CrossRef PubMed
.
- H. Kawakami, M. Mikawa and S. Nagaoka, J. Membr. Sci., 1996, 118, 223 CrossRef CAS
.
- X. Y. Chen and D. Rodrigue, J. Cell. Plast., 2009, 45, 405 CrossRef CAS PubMed
.
- H. B. Park, C. H. Jung, Y. M. Lee, A. J. Hill, S. J. Pas, S. T. Mudie, E. van Wagner, B. D. Freeman and D. J. Cookson, Science, 2007, 318, 254 CrossRef CAS PubMed
.
- H. Vinh-Thang and S. Kaliaguine, Chem. Rev., 2013, 113, 4980 CrossRef CAS PubMed
.
- J. C. Maxwell, Treatise on Electricity and
Magnetism, Oxford University Press, London, 1873 Search PubMed
.
- R. L. Hamilton and O. K. Crosser, Ind. Eng. Chem. Fundam., 1962, 1, 187 CAS
.
- D. Y. Kang, C. W. Jones and S. Nair, J. Membr. Sci., 2011, 381, 50 CrossRef CAS PubMed
.
- http://hyperphysics.phy-astr.gsu.edu/hbase/kinetic/menfre.html#c3.
- D. D. Do, Adsorption Analysis: Equilibria and Kinetics, Series on Chemical Engineering, Imperial College Press, London, 1998, vol. 2 Search PubMed
.
- H. Vinh-Thang and S. Kaliaguine, J. Membr. Sci., 2014, 452, 271 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2014 |