Prediction of acidity constants of some important selenium oxoacids in aqueous solution by computational techniques

Abstract

The acidity constants (pK_a) of two important series of selenium oxoacids including H₂SeO_n (n = 1–5) and H₂Se₂O_n (n = 1, 3, 4, 6 and 7) were predicted by using two different computational methods for the first time. The calculations were performed using MP2 level of theory employing a very large basis set, 6-311++G(3df,3pd), and a new density functional method, M06-2X, with the same basis set, separately. A new continuum solvation model, SMD, based on the quantum mechanical charge density of a solute molecule interacting with a continuum description of the solvent, was used to account the solvent effects. The calculated values of pK_a were corrected using the different correlation equations, reported in the literature, to improve the accuracy of results. Also, the calculated results in this work were compared with the corresponding results related to sulfur oxoacids obtained in our previous work. The same trend was observed for the variation of the acidity constants of selenium oxoacids and corresponding sulfur oxoacids (with the number of oxygen atoms). Comparison of the pK_a1 of selenium and sulfur oxoacids showed that the acidity strength of sulfur is higher than selenium while for pK_a2, selenium oxoacids are stronger acids than sulfur oxoacids. The predicted values of pK_a of selenium oxoacids are important and useful in the different chemical aspects of these compounds in chemistry and biochemistry.

---

Introduction

The determination of the protonation states of new compounds in aqueous solution is one of the main goals of computational chemistry. Generally, there are two different standard methods for prediction of the acidity constant (pK_a) of compounds in the literature.¹ The first one is searching a linear correlation between the free energy and the different empirical database. The second method is using ab initio calculations based on the underlying physical chemistry of the process which in principle can provide a better prediction of pK_a. This needs theoretical calculation of the deprotonation reaction, followed by some methods for estimating the solvation free energies of the various species. The problem present in these methods are that the small error (few percent) in the Gibbs free energy changes of gas phase deprotonation and solvation free energy of species lead to errors of a few pK_a units which is inadequate for many of the most interesting practical applications. The reason for this is that the gas-phase deprotonation energy and solvation free energy difference of the protonated and deprotonated species are both large numbers which add together in the pK_a calculation with opposite signs.

It is well-known that the density functional (DFT)² methods, specially the hybrid B3LYP method,^3–5 is capable of reaching average errors of 1–2 kcal mol⁻¹ in calculation of deprotonation energies for small molecule test cases. Recently, two new hybrid meta exchange correlation functional, called M06 and M06-2X were presented by Zhao and Truhlar.⁶ The M06 functional is parameterized including both transition metals and nonmetals, whereas the M06-2X functional is a high nonlocality functional with double the amount of non-local exchange (2X), and it is parameterized only for nonmetals. The M06-2X functional applies for main-group thermochemistry, kinetics, non-covalent interactions, and electronic excitation energies to valence and Rydberg states.⁶

The self-consistent reaction field (SCRF)^7–9 methods have been employed in combination with DFT method to calculate solvation energies in aqueous solution. A new continuum solvation model based on the quantum mechanical charge density of a solute molecule interacting with a continuum description of the solvent known as SMD, (where the “D” stands for “density” to denote that the full solute electron density is used without defining partial atomic charges) is a new recommended option for calculating free energy of solvation which accomplished by performing gas phase and SCRF = SMD calculations for the considered system.¹⁰

Inorganic selenium compounds are widely available in dietary supplements and have been extensively studied for their antioxidant and anticancer properties. Although many in vivo and clinical trials have been conducted using these compounds, their biochemical and chemical mechanisms of efficacy are the focus of much current research. Selenium compounds also have similar abilities to act as both antioxidants and pro-oxidants.¹¹

In our previous work, we predicted the acidity constants (pK_a) of some important sulfur oxoacids using expensive theoretical methods including MP2 and CCSD methods.¹² In this work, the selenium oxoacids were selected for prediction their acidities because of their importance in inorganic chemistry and biochemistry. We were reported the aqueous phase acidities constant (pK_a1 and pK_a2) for some important selenium oxoacids including, H₂SeO_n (n = 1–5) and H₂Se₂O_n (n = 1, 3, 4, 6 and 7) for the first time. The calculations were performed at the second-order Moller–Plesset perturbation (MP2)¹³ and M06-2X methods, separately. Single point calculations on the optimized structures of neutral and related anions were performed according to PCM model and the SMD model was used for calculating the solvation free energies of the species. To the best of author knowledge, there is no experimental report on the values of the pK_as of the considered compounds in the literature except, for H₂SeO₃ and H₂SeO₄. Therefore, it is worthwhile to obtain information about the acidity constants of these compounds, computationally and compare them with the acidity constant of sulfur oxoacids. Among the different considered selenium oxoacids, H₂Se₂O₃ and H₂Se₂O₄ are more well-known than the others. The results obtained in this work are interesting and challenging from the inorganic chemistry and biochemistry aspects and help to better understand of these oxoacids.

Method and theoretical calculations

Thermodynamic cycle

The acidity constant (pK_a) is a measure of a molecule's tendency to become deprotonated in aqueous solution. It is directly related to the standard free energy (ΔG°) of the deprotonation reaction in aqueous solution (1 mol L⁻¹) through the following equation:

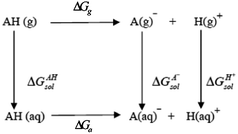
The deprotonation of a compound in aqueous solution can be assumed as a part of the following thermodynamic cycle (Scheme 1):¹⁴

Scheme 1

One part of this cycle, ΔG_g, is the gas-phase deprotonation free energy of the molecule. Three other parts, , are the free energy of solvation of the protonated and deprotonated forms of the molecule and the proton, respectively. The fifth part of the cycle, ΔG_a, is the desired free energy changes of deprotonation in solution. As the sum of free energies around the cycle must add to zero, the fifth term, ΔG_a, can be calculated from the other three terms as:

Computational approach

All the calculations were performed using the Gaussian 09 package.¹⁵ The geometries of the neutral and deprotonated species are fully optimized at the B3LYP/6-311++G(d,p) level of theory in both gas and aqueous phases. All geometry optimizations were followed by frequency calculations to confirm the optimized structures to be the true minima on the potential energy surface. The MP2/6-311++G(3df,3pd) and M06-2X/6-311++G(3df,3pd) levels of theory were used to calculate G^°_gas and ΔG^°_sol values for the selected acids and their corresponding anions. The gas-phase Gibbs free energy change (ΔG^°_gas) is calculated using eqn (3). For G^°_gas(H⁺) the experimental value of −6.28 kcal mol⁻¹ is used.¹⁶

ΔG^°_gas = G^°_gas (A⁻) + G^°_gas (H⁺) – G^°_gas (AH) (3)

Aqueous phase calculations were performed based on the polarizable continuum model (PCM) of Tomasi and co-workers^17–23 employing SMD solvation model for geometry optimization, frequency calculations and also single energy calculations to obtain solvation free energy.

According to the thermodynamic cycle shown in Scheme 1, the total change in Gibbs free energy in solution is equal to the sum of the gas-phase Gibbs free energy (ΔG^°_gas) and the change in solvation energies, ΔΔG^°_sol:

ΔΔG^°_sol = ΔG^°_sol (A⁻) + ΔG^°_sol (H⁺) – ΔG^°_sol (AH) (4)

For G^°_solv(H⁺) the experimental value of −264.61 kcal mol⁻¹ is used.¹⁶

Results and discussion

To the best of author knowledge, there is no information on the geometrical structure of selenium oxoacids in the literature except for H₂SeO₃ and H₂SeO₄ which their geometries are similar to corresponding sulfur oxoacids (H₂SO₃ and H₂SO₄). Base on the valence shell electron pair repulsion (VSEPR) rules it is expected that the other selenium oxoacids have the same structure similar to the corresponding sulfur oxoacids which studied in our previous work.¹² Fig. 1 shows the optimized structures of the selected acids in the gas phase. Also, for more confident the different isomers were selected and searched for the structures with the lowest electronic energies. The optimized structures (Z-matrix) along with the corresponding total electronic energies have been reported in ESI.† The geometries of the selected selenium oxoacids and their mono and dianions were optimized at the B3LYP/6-311++G(d,p) level of theory in both gas and aqueous phases.

Fig. 1 Gas phase optimized structures of studied acids at the B3LYP/6-311++G(d,p) level of theory.

The gas phase optimized structures were used for the frequency calculations, at the MP2/6-311++G(3df,3pd) and M06-2X/6-311++G(3df,3pd) levels of theory which are expensive and reasonable methods, to obtain the Gibbs free energies of the considered species. Tables S2 and S3† tabulated the electronic and Gibbs free energies of the selected species, calculated using MP2 and M06-2X methods, respectively. The gas phase acidity (GA) values, both experimental and theoretical, are widely used to characterize the acidic strength of acids. Table S1† reports the GA of all acids obtained based on eqn (3) for both applied methods.

Tables S4 and S5† show the solvation energies of neutral species and their anions were calculated at the MP2/6-311++G(3df,3pd) and M06-2X/6-311++G(3df,3pd) levels of theory, respectively. To calculate the solvation energy, it is necessary to fully optimize the geometries of oxoacids in the presence of the solvent.

The calculated GA and the solvation free energy of the species can be used to obtain free energy of deprotonation in solution (ΔG_a) through the thermodynamic cycle presented in Scheme 1. It should be mentioned that the calculated gas-phase energies are for a standard state of 1 atm but solvation energies use a standard state of 1 mol L⁻¹, therefore, the value of 1.89 kcal mol⁻¹ which corresponds to RT ln(24.46) must be considered and added to gas-phase energies.^24–26

The values of ΔG_a can be used along with eqn (1) to calculate the pK_a values for acids in aqueous solution. Table S6† reports the values of ΔG^°_gas, ΔΔG^°_sol (eqn (4)), ΔG^°_a and pK_a1 for the first dissociation reactions of the considered acids obtained from the MP2 calculations. As seen, by increasing the number of oxygen atoms in the series of oxoacids containing one selenium atom, the acidity increases (the pK_a1 decreases). It is important to notice this behavior and trend, also, was seen for the acidity of the sulfur oxoacids in our previous work and also the acidity of selenium oxoacids is lower than the corresponding sulfur oxoacids except for H₂SeO (see Fig. 2a). The variation of the acidity of oxoacids containing two selenium atoms is similar to the trend was observed for the corresponding sulfur oxoacids (See Fig. 2b) and with lower acidity strength than the corresponding sulfur oxoacids. For example, H₂Se₂O₄ and H₂Se₂O₇ show the opposite acidity order. The reason for this deviation may be attributed to the intramolecular hydrogen bonding which decreases the tendency for dissociation of proton. As seen in Fig. 2b, it is interesting that this effect is stronger for H₂Se₂O₄ than H₂Se₂O₇ in comparison with that in the sulfur oxoacids. This observation may be attributed to the effect of selenium atom compared to sulfur atom on the intramolecular hydrogen bonding. It is expected that the variation of acidity for sulfur and selenium oxoacids should be the same because they are in the same group in the periodic table but, the calculations show different results in this study. Similar results obtained from M06-2X method, have been reported in Table S7.† Comparison of Tables S6 with S7† shows that, the MP2 level of theory presents the effect of the hydrogen bonding on the acidity much better than the M06-2X method.

Fig. 2 Variation of pK_a1 versus number of oxygen atoms for selenium and sulfur oxoacids. (a) One selenium and sulfur oxoacids (b) two selenium and sulfur oxoacids.

As mentioned before, there are the experimental values only for the pK_a1 and pK_a2 of H₂SeO₄ and H₂SeO₃ in the literature.^27,28 For example, the experimental value of pK_a1 is 2.6 for H₂SeO₃ and has been considered the acidity similar to H₂SO₄ for H₂SeO₄ and classified it as strong acid. It is seen that the corresponding calculated values obtained at two employed theoretical levels have errors from the experimental values. These differences are common in the theoretical calculation of acidity. One of the methods for decreasing this error is finding a linear correlation between the theoretical pK_as and the corresponding experimental data reported in the literature.^29–31 Unfortunately, there are no experimental values for the pK_a of the most of the selected oxoacids in this work to find this correlation. Therefore, the best way for solving this problem is using the different correlation equations reported for the other acids in the literature.

Zimmermann and Tossell²⁹ calculated the acidity of arsenic(III) and arsenic(V) thio- and oxoacids (H₃AsS₃, H₂AsS₃⁻, HAsS₃²⁻, AsS₃³⁻, H₃AsS₄, H₂AsS₄⁻, HAsS₄²⁻, AsS₄³⁻, H₃AsO₃, H₂AsO₃⁻, HAsO₃²⁻, AsO₃³⁻, H₃AsO₄, H₂AsO₄⁻, HAsO₄²⁻, and AsO₄³⁻) using different theoretical methods including CBS-QB3/CPCM, CCSD(T)/6-311G(2d,p), CCSD(T)/aug-cc-pVDZ and CCSD(T)/CEP-121G. They have reported a linear correlation equation for each applied theoretical methods with different r² values. The first reason for using the correlation equations of Zimmermann and Tossell²⁹ is that, the selected acids in their work are similar to selenium oxoacids considered in this work because both series of acids are oxoacids and inorganic acids. The second reason is that these linear correlations were applied to improve the acidity constants of the sulfur oxoacids in previous work and improved our results very well. Therefore, these correlations are used in the present study, too.

Similar to previous work¹² the different linear correlations used to improve the calculated values of pK_as in this work. The predicted pK_a1 values of selenium oxoacids, considered in this work and obtained using different linear correlation equations of Zimmermann and Tossell²⁹ have been reported in Tables 1 and 2 for MP2 and M06-2X methods, respectively. As reported in Tables 1 and 2, the best agreement between the experimental and theory, for the pK_a1 of H₂SeO₃ and H₂SeO₄, is reached using the linear correlation equation obtained based on the CCSD(T)/aug-cc-pVDZ + optimized with CPCM. Comparison of Tables 1 with 2 show that the pK_a1 calculated at the MP2 and M06-2X methods are nearly equivalent and propose that the M06-2X can be applied for the calculation of acidity instead of MP2 method with the low cost of computation.

Table 1 Fitted MP2 pK_a1 based on (y = mx + b) equation

Species	pKa1 (cal.)	(m = 0.444; b = 0.767)^a	(m = 0.429; b = −0.233)^b	(m = 0.273; b = −1.593)^c	(m = 0.428; b = −0.597)^d
		r^2 = 0.952	r^2 = 0.974	r^2 = 0.979	r^2 = 0.944
a CBS-QB3 method; CBS-QB3 CPCM pKa (all structures optimized & energy calculated in PCM) (ref. 29).b CBS-QB3 with explicit salvation; CBS-QB3 CPCM pKa w/H2O (ref. 29).c CCSD(T)/6-311G(2d,p) + CPCM salvation energy (ref. 29).d CCSD(T)/aug-cc-pVDZ + optimized with CPCM (ref. 29).
H2SeO	9.66	5.05	3.91	1.04	3.54
H2SeO2	16.12	7.92	6.68	2.81	6.30
H2SeO3	6.06	3.46	2.36	0.06	2.00
H2SeO4	−6.09	−1.93	−2.84	−3.25	−3.20
H2SeO5	−10.07	−3.70	−4.55	−4.34	−4.90
H2Se2O	5.27	3.10	2.02	−0.15	1.65
H2Se2O3	−9.68	−3.53	−4.38	−4.23	−4.74
H2Se2O4	14.38	7.15	5.93	2.33	5.55
H2Se2O6	−12.42	−4.75	−5.56	−4.98	−5.91
H2Se2O7	−8.72	−3.10	−3.97	−3.97	−4.33

---

Table 2 Fitted M06-2X pK_a1 based on (y = mx + b) equation

Species	pKa1 (cal.)	(m = 0.444; b = 0.767)^a	(m = 0.429; b = −0.233)^b	(m = 0.273; b = −1.593)^c	(m = 0.428; b = −0.597)^d
		r^2 = 0.952	r^2 = 0.974	r^2 = 0.979	r^2 = 0.944
a CBS-QB3 method; CBS-QB3 CPCM pKa (all structures optimized & energy calculated in PCM) (ref. 29).b CBS-QB3 with explicit salvation; CBS-QB3 CPCM pKa w/H2O (ref. 29).c CCSD(T)/6-311G(2d,p) + CPCM salvation energy (ref. 29).d CCSD(T)/aug-cc-pVDZ + optimized with CPCM (ref. 29).
H2SeO	7.34	4.02	2.91	0.41	2.54
H2SeO2	15.96	7.85	6.61	2.76	6.23
H2SeO3	7.11	3.92	2.82	0.35	2.44
H2SeO4	−5.04	−1.47	−2.39	−2.97	−2.75
H2SeO5	−8.95	−3.20	−4.07	−4.03	−4.43
H2Se2O	2.63	1.93	0.89	−0.87	0.53
H2Se2O3	−8.85	−3.16	−4.03	−4.00	−4.38
H2Se2O4	11.21	5.74	4.57	1.46	4.20
H2Se2O6	−10.88	−4.06	−4.90	−4.56	−5.25
H2Se2O7	−6.10	−1.94	−2.85	−3.25	−3.21

---

Tables S8 and S9† report the values of pK_a2 calculated using MP2 and M06-2X levels of theory, respectively. Again, the effect of the intramolecular hydrogen bonding can be seen on the pK_a2 of the acids and the MP2 method shows this effect much better than the M06-2X method. The values of the pK_a2 were improved using the Zimmermann and Tossell's correlation equations and tabulated in Tables 3 and 4. Based on the experimental values of pK_a2 for H₂SeO₃ and H₂SeO₄, the predicted values using the correlated equation of CCSD(T)/aug-cc-pVDZ + optimized with CPCM calculations is more reliable for both applied methods in this work.

Table 3 Fitted MP2 pK_a2 based on (y = mx + b) equation

Species	pKa2 (cal.)	(m = 0.444; b = 0.767)^a	(m = 0.429; b = −0.233)^b	(m = 0.273; b = −1.593)^c	(m = 0.428; b = −0.597)^d
		r^2 = 0.952	r^2 = 0.974	r^2 = 0.979	r^2 = 0.944
a CBS-QB3 method; CBS-QB3 CPCM pKa (all structures optimized & energy calculated in PCM) (ref. 29).b CBS-QB3 with explicit salvation; CBS-QB3 CPCM pKa w/H2O (ref. 29).c CCSD(T)/6-311G(2d,p) + CPCM salvation energy (ref. 29).d CCSD(T)/aug-cc-pVDZ + optimized with CPCM (ref. 29).
H2SeO	31.28	14.65	13.18	6.94	12.79
H2SeO2	22.19	10.62	9.28	4.46	8.90
H2SeO3	14.28	7.11	5.89	2.30	5.51
H2SeO4	6.60	3.70	2.60	0.21	2.23
H2SeO5	19.82	9.57	8.27	3.82	7.88
H2Se2O	41.01	18.97	17.36	9.60	16.95
H2Se2O3	4.15	2.61	1.55	−0.46	1.18
H2Se2O4	8.79	4.67	3.54	0.80	3.16
H2Se2O6	0.49	0.98	−0.02	−1.46	−0.38
H2Se2O7	−3.18	−0.64	−1.60	−2.46	−1.95

---

Table 4 Fitted M06-2X pK_a2 based on (y = mx + b) equation

Species	pKa2 (cal.)	(m = 0.444; b = 0.767)^a	(m = 0.429; b = −0.233)^b	(m = 0.273; b = −1.593)^c	(m = 0.428; b = −0.597)^d
		r^2 = 0.952	r^2 = 0.974	r^2 = 0.979	r^2 = 0.944
a CBS-QB3 method; CBS-QB3 CPCM pKa (all structures optimized & energy calculated in PCM) (ref. 29).b CBS-QB3 with explicit salvation; CBS-QB3 CPCM pKa w/H2O (ref. 29).c CCSD(T)/6-311G(2d,p) + CPCM salvation energy (ref. 29).d CCSD(T)/aug-cc-pVDZ + optimized with CPCM (ref. 29).
H2SeO	29.62	13.92	12.47	6.50	12.08
H2SeO2	20.51	9.87	8.56	4.00	8.18
H2SeO3	12.24	6.20	5.02	1.74	4.64
H2SeO4	6.09	3.47	2.38	0.07	2.00
H2SeO5	19.20	9.30	8.00	3.64	7.62
H2Se2O	38.14	17.70	16.13	8.82	15.72
H2Se2O3	2.30	1.79	0.75	−0.96	0.38
H2Se2O4	11.14	5.71	4.55	1.44	4.17
H2Se2O6	1.64	1.50	0.47	−1.14	0.10
H2Se2O7	−3.07	−0.60	−1.55	−2.43	−1.90

---

Fig. 3a and b show the variation of the pK_a2 of selenium and sulfur oxoacids with the number of oxygen atoms. It is seen in Fig. 3 that the trend of variation of pK_a2 for the selenium and sulfur oxoacids is almost the same. Interestingly, Fig. 3a shows that the pK_a2 of selenium oxoacids are lower than the corresponding sulfur oxoacids which is opposite with what observed for corresponding pK_a1 (Fig. 2a).

Fig. 3 Variation of pK_a2 versus number of oxygen atoms for selenium and sulfur oxoacids. (a) One selenium and sulfur oxoacids (b) two selenium and sulfur oxoacids.

Conclusions

In this work, the pK_a values of some important inorganic selenium oxoacids were calculated at the electron correlated level, MP2/6-311++G(3df,3pd) and a new density functional method, M06-2X/6-311++G(3df,3pd) in both gas and aqueous phases for the first time. The calculated pK_as were corrected by using the different correlation equations of Zimmermann and Tossell.²⁹ The values of pK_a1 and pK_a2, calculated at both levels of theory when used in the correlation equations, give results which are in more agreement with the available experimental data. The results also showed that the M06-2X is comparable with MP2 method in acidity constant calculations. The calculated results also showed the effect of the intramolecular hydrogen bonding on the decreasing of acidity strength. The variation of the acidity constants of the selenium oxoacids are similar to what was seen for sulfur oxoacids in our pervious work. It is interestingly observed that the values of pK_a1 of selenium oxoacids are higher than the corresponding values of sulfur oxoacids while opposite behavior was observed for pK_a2.

Acknowledgements

The authors gratefully acknowledge the financial supports of Isfahan University of Technology.

References

1. K. S. Alongi and G. C. Shields, Annu. Rep. Comput. Chem, 2010, 6, 113.
2. J. K. Labanowski and J. W. Andzelm, Density Functional Methods in Chemistry, Springer-Verlag, New York, 1991, p. 155.
3. A. D. Becke, J. Chem. Phys., 1992, 96, 2155.
4. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
5. A. D. Becke, Int. J. Quantum Chem., 1989, 23, 599.
6. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
7. A. A. Rashin, L. Young and I. A. Topol, Biophys. Chem., 1994, 51, 359.
8. M. Bachs, F. J. Luque and M. Orozco, J. Comput. Chem., 1994, 15, 446.
9. A. Fortuneli and J. Tomasi, Chem. Phys. Lett., 1994, 34, 231.
10. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
11. R. R. Ramoutar and J. L. Brumaghim, Cell Biochem. Biophys., 2010, 58, 1–23.
12. M. Abedi and H. Farrokhpour, Dalton Trans., 2013, 42, 5566.
13. M. Head-Gordon, J. A. Pople and M. Frisch, Chem. Phys. Lett., 1988, 153, 503.
14. C. Lim, D. Bashford and M. Karplus, J. Phys. Chem., 1991, 95, 5610.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford CT, 2009.
16. M. D. Liptak, K. C. Grass, P. G. Seybold, S. Feldgus and G. C. Shields, J. Am. Chem. Soc., 2002, 124, 6421.
17. S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
18. S. Miertus and J. Tomasi, Chem. Phys., 1982, 65, 239–245.
19. M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335.
20. M. T. Cances, V. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
21. V. Barone, M. Cossi, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221.
22. M. T. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253–260.
23. V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417.
24. D. M. Chipman, J. Phys. Chem. A, 2002, 106, 7413.
25. M. D. Liptak and G. C. Shields, J. Am. Chem. Soc., 2001, 123, 7314.
26. M. D. Liptak and G. C. Shields, Int. J. Quantum Chem., 2001, 85, 727.
27. W. L. Jolly, Modern Inorganic Chemistry, McGraw-Hill, New York, 2nd edn, 1991.
28. (a) B. E. Douglas, D. H. McDaniel and J. J. Alexander, Concepts and Models of Inorganic Chemistry, John Wiley & Sons, New York, 3rd edn, 1994; (b) D. F. Shriver, P. W. Atkins and C. H. Langford, Inorganic Chemistry, W.H. Freeman, New York, 1994; (c) I. Kolthoff, Treatise on Analytical Chemistry, Interscience Encyclopedia, New York, 1959.
29. M. D. Zimmermann and J. A. Tossell, J. Phys. Chem. A, 2009, 113, 5105–5111.
30. A. Trummal, A. Rummel, E. Lippmaa, I. Koppel and I. A. Koppel, J. Phys. Chem. A, 2011, 115, 6641–6645.
31. J. R. Rustad, D. A. Dixon, J. D. Kubicki and A. R. Felmy, J. Phys. Chem. A, 2000, 104, 4051–4057.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra47167e

---