The effect of water molecules upon the hydrogen-bonding cooperativity of three-stranded antiparallel β-sheet models

Abstract

The effect of water molecules upon the hydrogen-bonding cooperativity of three-stranded antiparallel β-sheet models has been studied by quantum chemical calculations at the MP2/6-311++G(3df,2p)//MP2/6-31G** level. Our calculation results indicate that the hydrogen-bonding lengths and the atom charge distribution are affected by the H₂O molecules, especially for those in the same amide unit directly bonded. The hydrogen-bonding cooperativity significantly increases the binding energy of the LR or SR hydrogen-bonding ring in the three-stranded β-sheet structures and the influence is also gradually increased as more H₂O molecules are added. We found that the perturbation energies are also affected as the H₂O molecules are added and this supports that the cooperative enhancement is closely related to the orbital interaction. We have also found that the charge transfer among the three diglypeptides is obviously influenced by the H₂O molecules.

---

Introduction

Hydrogen bonds are very important weak interactions in a wide range of chemical and biological systems.^1–3 In the last few decades, there has been an intense research effort to understand the nature and effect of the hydrogen bond and its cooperativity.^4–39 The concept of hydrogen-bonding cooperativity is that one of the individual hydrogen bonds making up a chain of inter-linked hydrogen bonds is more strongly bonded than it would be in the absence of the others. It means that the hydrogen bond cooperativity is mutual enhancement of multiple hydrogen bonds. The additional hydrogen bonds enhance the already formed hydrogen bond and the additional hydrogen bonds are also enhanced by the already formed hydrogen bond.² It is well known that cooperative interactions are important for the stability of many hydrogen-bonded systems. Many physical and chemical properties of biomolecule are influenced by hydrogen-bonding cooperativity.^20–34

The cooperativity of hydrogen bonds has received intensive experimental^18–20 and theoretical^21–38 researches. Both experimental and theoretical studies of amide clusters indicate that there is strong cooperativity in the formation of one-dimensional hydrogen-bonded chains.^28,29,40,41 Dannenberg suggested the unusually large cooperative hydrogen bond in formamide chains due to the electronic effects.^{22,29,30,33,34} Kemp has suggested that hydrogen-bonding cooperativity contributes strongly to the formation of α-helices.³⁶ The studies of Wu et al. indicate there is hydrogen-bonding cooperativity in both α- and 3₁₀-helices and in sheets of unnatural β-polyglycines but little or none in β-sheets of the natural α-polyglycines.^23–25 Dannenberg further suggested the apparent relative absence of cooperativity in β-sheet models of polyglycine derives from the weakening and strengthening of C₅ intrastrand hydrogen bonds.^22,31,32 Liu et al. suggested the charge flow between the hydrogen donor and acceptor groups in the c-NMF molecule is the most important factor inducing the coopterative effect of hydrogen bond.⁴² The studies of Baker and co-workers suggest nonpairwise electronic effects account for half of the total cooperativity in the system of α-helix formation.⁴³ More recently, Greef et al. carried out DFT calculations to understand the origin of the experimentally observed cooperativity in the hydrogen-bond-induced supramolecular polymerization of C₃-symmetrical trialkylbenzene-1,3,5-tricarboxamides (BTAs), and their analysis demonstrated the cooperative growth of these structure is caused by electrostatic interactions and nonadditive effects brought about by redistribution of the electron density with aggregate length.⁴⁴

The hydrogen-bonding cooperativity is still highly challenging especially for that in the peptide-water hydrogen-bonded systems.^45–56 Karplus demonstrated the existence of a cooperative hydration effects for amidic hydrogen bonds, such as those found in peptides.⁵⁵ Tsuzuki et al. demonstrated that the hydrogen-bonding cooperativity significantly increases the binding of the water with the crownophane.⁴⁸ Dannenberg et al. presented density functional theory (DFT) calculations on the solvation of polyalanine α-helices in water. They found that individual water molecules cooperatively hydrogen-bond to both the C- and N-termini of the helix, which results in increases in the dipole moment of the helix/water complex to more than the vector sum of their individual dipole moments.⁵¹ Recently, Ireta has reported studies of β-sheets interactions with individual water molecules suggesting that the strengthening of water–water hydrogen bond along the solvation shell of β-sheets promotes a flat to twist transition.⁵² We have reported the cooperative enhancement of discrete water to the two-stranded antiparallel β-sheet models.⁵⁶ In this paper we further carry out high level ab initio calculations on the discrete water binding to the three-stranded antiparallel diglypeptide β-sheet models for the quantitative evaluation of cooperative enhancement and for the purpose of understanding the origin of the enhancement.

Models and computational details

β-sheets are characteristic structural motifs of proteins and polypeptides. Such motifs consist of two or more parallel or antiparallel hydrogen-bonded peptide strands.⁵⁷ There is a renewed interest in studying β-sheets since it was discovered that its aggregation plays a central role in the mechanism underlying several diseases, including Alzheimer's, Huntington's, Parkinson's, and the prion encephalopathies.^58–62 The diglypeptide molecule provides a good model to study the mechanism involved in the hydrogen-bonding cooperativity effect of β-sheet secondary structures. Two amide groups exist in the diglypeptide molecule and each one can form two hydrogen bonds (its N–H can act as hydrogen bond donor, while its C=O can act as hydrogen bond acceptor) simultaneously, an ability that certainly seems conducive to initiating cooperative hydrogen bond effects. As shown in Fig. 1, three diglypeptide molecules can form three-stranded antiparallel diglypeptide β-sheet models. There is a large hydrogen-bonding ring containing fourteen atoms (LR) between the upper and middle diglypeptide and a small hydrogen-bonding ring containing ten atoms (SR) between the middle and lower diglypeptide. There are also two N–H and two C=O bonds outside of the β-sheet models that can form hydrogen bond with water molecules or amide groups. In this paper, the individual water molecules are gradually bonded to the outside N–H and C=O by the formation of N–H⋯OH₂ and C=O⋯HOH hydrogen bonds.

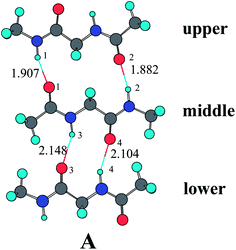Fig. 1 Optimized geometry for the three-stranded antiparallel diglypeptide β-sheet models at the MP2/6-31G** level.

Throughout our studies, the binding energies are calculated by supermolecular approach. For example, the binding energy of LR hydrogen-bonding ring in complex B can be obtained by eqn (1). Where E(BSSE)_{total hydrogen-bonding tetramer} is the binding energy of the total hydrogen-bonding tertamer, E(BSSE)_{upper diglypeptide−H2O hydrogen-bonding dimer} is the binding energy of the hydrogen-bonding dimer formed by the upper diglypeptide and H₂O molecule, and E(BSSE)_{middle-lower diglypeptide hydrogen-bonding dimer} is the binding energy of middle and lower diglypeptide hydrogen-bonding dimer. Both the hydrogen-bonding tetramer and two dimers contain more than one fragment, so all of the binding energies of them are subject to basis set superposition error (BSSE). In this paper, BSSE correction is estimated using the counterpoise (CP) method of Boys and Bernardi.⁶³ The interaction energy calculated by eqn (1) also contains other van der Waals interaction as dispersion or induction as well as possible repulsive interactions, electrostatic contributions and others. Nevertheless, the interaction energy is taken as an estimate of the hydrogen bond energy in this paper.

E_LR = E(BSSE)_{total hydrogen-bonding tetramer} − E(BSSE)_{upper diglypeptide−H2O hydrogen-bonding dimer} − E(BSSE)_{middle-lower diglypeptide hydrogen-bonding dimer} (1)

The geometry optimizations for the antiparallel diglypeptide β-sheet models are carried out at the MP2/6-31G** level. The geometrical structures are optimized with a plane of symmetry (C_s) symmetry restraints.^22,23 All of the electronic energies of the hydrogen-bonding complexes are obtained by performing B3LYP/6-31+G** and MP2/6-311++G(3df,2p) basis sets based on the optimized geometrical structures. The CP correction for basis set superposition error was incorporated using the single point a posteriori method rather than via optimization on the CP-corrected potential energy surfaces (CP-OPT) due to the excessive CPU time required.⁶⁴ The natural bond orbital analysis (NBO) is carried out using the NBO package included in the Gaussian 03 suite of program.^65,66 All the ab initio calculations are carried out in vacuum, thus they correspond to the intrinsic properties.

Results and discussion

Fig. 2, 3, and 4 present the optimized structures of individual water molecules bonding to the three-stranded antiparallel diglypeptide β-sheet models from different positions by the formation of N–H⋯OH₂ and C=O⋯HOH hydrogen bonds. Table 1 lists the hydrogen-bonding lengths and the binding energies of LR and SR hydrogen-bonding ring. The NBO electrostatic charges for the H and O atoms of the hydrogen bonds obtained from MP2/6-31G** calculations are listed in Table 2. The NBO second-order perturbation analysis is applied for the ten hydrogen-bonding complexes at the MP2/6-31G** level. The obtained perturbation energies due to n(O(1)) → σ*(H(1)–N(1)), n(O(2)) → σ*(H(2)–N(2)), n(O(3)) → σ*(H(3)–N(3)), and n(O(4)) → σ*(H(4)–N(4)) orbital interactions are also listed in Table 2.

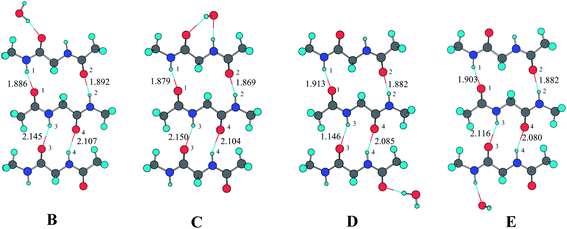Fig. 2 Optimized geometries at the MP2/6-31G** level for the three-stranded sheet structures with one H₂O molecule.

Fig. 3 Optimized geometries at the MP2/6-31G** level for the three-stranded sheet structures with two H₂O molecules.

Fig. 4 Optimized geometry at the MP2/6-31G** level for the three-stranded sheet structures with four H₂O molecules.

Table 1 The hydrogen-bonding lengths (Å) and the bonding energies (kcal mol⁻¹) between up and middle diglypeptides, lower and middle diglypeptides, and the total bonding energies of the three diglypeptide

		A	B	C	D	E	F	G	H	I	J
r(H(1)⋯O(1))		1.907	1.886	1.879	1.913	1.903	1.883	1.885	1.857	1.908	1.858
r(H(2)⋯O(2))		1.882	1.892	1.869	1.882	1.882	1.893	1.870	1.881	1.882	1.881
r(H(3)⋯O(3))		2.148	2.145	2.150	2.146	2.116	2.111	2.147	2.144	2.117	2.112
r(H(4)⋯O(4))		2.104	2.107	2.104	2.085	2.080	2.081	2.084	2.104	2.069	2.067
The binding energy between upper and middle diglypeptides	B3LYP/6-31+G**	−16.66	−17.47	−17.62	−16.61	−16.82	−17.37	−17.53	−18.12	−16.71	−18.20
		0.00	−0.81	−0.96	0.05	−0.16	−0.71	−0.87	−1.46	−0.05	−1.54
	MP2/6-311++G(3df,2p)	−20.36	−20.69	−21.28	−20.30	−20.54	−20.83	−21.20	−21.61	−20.43	−21.70
		0.00	−0.33	−0.92	0.06	−0.18	−0.47	−0.84	−1.25	−0.07	−1.34
The binding energy between lower and middle diglypeptides	B3LYP/6-31+G**	−4.82	−5.34	−4.82	−5.09	−5.31	−5.57	−5.05	−5.10	−5.38	−5.68
		0.00	−0.52	0.00	−0.27	−0.49	−0.75	−0.23	−0.28	−0.56	−0.86
	MP2/6-311++G(3df,2p)	−8.80	−8.88	−8.81	−9.06	−9.35	−9.38	−9.06	−8.88	−9.46	−9.56
		0.00	−0.08	−0.01	−0.26	−0.55	−0.58	−0.26	−0.08	−0.66	−0.76
Total binding energy of the three-stranded sheet structures	B3LYP/6-31+G**	−21.48	−22.82	−22.44	−21.70	−22.13	−22.94	−22.59	−23.22	−22.09	−23.89
		0.00	−1.34	−0.96	−0.22	−0.65	−1.46	−1.11	−1.74	−0.61	−2.41
	MP2/6-311++G(3df,2p)	−29.16	−29.57	−30.09	−29.36	−29.89	−30.22	−30.26	−30.49	−29.88	−31.25
		0.00	−0.41	−0.93	−0.20	−0.73	−1.06	−1.10	−1.33	−0.72	−2.09

---

Table 2 The NBO electrostatic charge of the H and O atoms (e) and the perturbation energies (kcal mol⁻¹) at MP2/6-31G** level

	A	B	C	D	E	F	G	H	I	J
q(H(1))	0.4742	0.4768	0.4775	0.4738	0.4748	0.4773	0.4770	0.4803	0.4744	0.4805
q(O(1))	−0.8384	−0.8416	−0.8415	−0.8373	−0.8403	−0.8436	−0.8404	−0.8450	−0.8392	−0.8460
q(H(2))	0.4761	0.4750	0.4776	0.4762	0.4761	0.4750	0.4776	0.4764	0.4761	0.4764
q(O(2))	−0.8305	−0.8274	−0.8369	−0.8307	−0.8303	−0.8273	−0.8371	−0.8334	−0.8304	−0.8332
q(H3))	0.4834	0.4840	0.4835	0.4824	0.4851	0.4858	0.4826	0.4842	0.4844	0.4852
q(O(3))	−0.7880	−0.7888	−0.7879	−0.7855	−0.8018	−0.8027	−0.7855	−0.7889	−0.7998	−0.8009
q(H(4))	0.4809	0.4805	0.4810	0.4856	0.4826	0.4822	0.4858	0.4807	0.4869	0.4867
q(O(4))	−0.8103	−0.8089	−0.8118	−0.8139	−0.8108	−0.8095	−0.8155	−0.8104	−0.8139	−0.8141
E(n(O(1)) → σ*(H(1)–N(1)))	14.41	15.65	16.02	14.12	14.68	15.89	15.67	17.42	14.44	17.45
E(n(O(2)) → σ*(H(2)–N(2)))	15.32	14.80	16.23	15.34	15.32	14.77	16.18	15.61	15.33	15.57
E(n(O(3)) → σ*(H(3)–N(3)))	6.71	6.80	6.67	6.72	7.51	7.63	6.69	6.82	7.45	7.59
E(n(O(4)) → σ*(H(4)–N(4)))	7.66	7.59	7.68	8.21	8.34	8.29	8.25	7.67	8.70	8.73

---

As shown in Table 1, the hydrogen-bonding lengths of r(H(1)⋯O(1)), r(H(2)⋯O(2)), r(H(3)⋯O(3)), and r(H(4)⋯O(4)) in complex A without water molecule participate are 1.907 Å, 1.882 Å, 2.148 Å, and 2.104 Å, respectively. As one or more H₂O as proton donor or acceptor bond to the outside N–H or C=O, the hydrogen-bonding lengths obviously become shorter, especially those in the same amide unit. For example, the r(H(1)⋯O(1)) in complex B is 1.886 Å, which is shorter by 0.021 Å than that in complex A. The four hydrogen-bonding lengths in complex J are 1.858 Å, 1.881 Å, 2.112 Å, and 2.067 Å, respectively, which are obviously shorter than those in complex A.

It can be seen from Table 1 that the binding energies calculated by B3LYP/6-31+G** are obviously weaker than those from MP2/6-311++G(3df,2p) calculations. However, the relative energies calculated by the two methods are similar. For example, the total binding energies of complex A and J calculated by B3LYP/6-31+G** are −21.48 and −23.89 kcal mol⁻¹. The calculation results by MP2/6-311++G(3df,2p) are −29.16 and −31.25 kcal mol⁻¹, which are obviously stronger than those by B3LYP/6-31+G**. However, the energy difference between complex A and J calculated by MP2/6-311++G(3df,2p) is −2.09 kcal mol⁻¹, which is similar to the value of −2.41 kcal mol⁻¹ by B3LYP/6-31+G**. We also can find that the tendency of energies changes is not influenced by computational methods. So the further discussions are only based on MP2 calculation results.

In complex A, the binding energy of LR hydrogen-bonding ring between the upper and middle diglypeptides is −20.36 kcal mol⁻¹ calculated by MP2/6-311++G(3df,2p) and the SR hydrogen-bonding ring between the lower and middle diglypeptides is −8.80 kcal mol⁻¹. The total binding energy of LR and SR is −29.16 kcal mol⁻¹. When one H₂O molecule acting as proton donor bond to the outer C=O of the upper diglypeptide (complex B), the binding energy of LR is −20.69 kcal mol⁻¹, which is 0.33 kcal mol⁻¹ stronger than that in complex A. It means that the cooperative enhancement is about 0.33 kcal mol⁻¹ as the H₂O molecule added. The binding energy of SR is −8.80 kcal mol⁻¹, which is influenced slightly. In complex C, the O atom of H₂O molecule serves as proton acceptor and bonds to the outside N–H of the upper diglypeptide, while the two H atoms of H₂O molecule serves as proton donor and bonds to the outside C=O simultaneously. The interaction energy of LR is −21.28 kcal mol⁻¹. The cooperative enhancement by the H₂O molecule to the binging energy is about −0.92 kcal mol⁻¹. In complex D and E, one H₂O as proton donor or acceptor bonds to the down diglypeptide. It can be seen from Table 1 that the binding energy of the three-strands β-sheet models is also influenced as the H₂O molecule added, especially for the binding energy of SR.

In complex F, there are two H₂O molecules: one as proton donor bonds to the outer C=O of the upper diglypeptide and the other one as proton acceptor bonds to the outer N–H of the lower diglypeptide. The cooperative enhancement by the two H₂O molecules to the binging energy is as large as −1.06 kcal mol⁻¹ (0.47 kcal mol⁻¹ of LR and 0.58 kcal mol⁻¹ of SR). In complex H, the two H₂O molecules are both bond to the upper diglypeptide. We can find that the cooperative enhancement by the two H₂O molecules to LR is 1.25 kcal mol⁻¹. Similarly, when the two H₂O molecules are both bonded to the lower diglypeptide (complex I), the cooperative enhancement to SR is 0.66 kcal mol⁻¹. In complex J, four H₂O molecules are bonded to the upper diglypeptide and lower diglypeptide simultaneously. It can be seen in Table 1 the cooperative enhancement to LR is 1.34 kcal mol⁻¹, which is slightly stronger than the value of 1.25 kcal mol⁻¹ in complex H. Similarly, the cooperative enhancement to SR 0.76 kcal mol⁻¹ is also slightly stronger than that in complex I. It means that the hydrogen-bonding cooperativity is mutual enhancement by the two H₂O molecules bonding to the upper diglypeptide and the two bonding to the lower diglypeptide.

In the study of two-stranded sheet structures, we have found that the atom charge distributions are obviously affected by the addition of H₂O molecules and the cooperative enhancement is closely related with the orbital interaction. From Table 2, one can see that the electrostatic charges of the H and O atoms in three-stranded sheet structures are also obviously affected by H₂O molecule adding. For example, the q(H(1)) is 0.4742e and the q(O(1)) is −0.8384e in complex A. The values in complex B, F, H, and J which one H₂O molecule bonded to the outer C=O of the upper diglypeptide are 0.4768e and −0.8416e, 0.4773e and −0.8436e, 0.4803e and −0.8450e, 0.4805 and −0.8460. Furthermore, the values of q(H(1)), q(O(1)), q(H(2)), q(O(2)), q(H(3)), q(O(3)), q(H(4)), and q(O(4)) in complex A are 0.4742e, −0.8384e, 0.4761e, −0.8305e, 0.4834e, −0.7880e, 0.4809e, and −0.8103e. The values in complex J are 0.4805e, −0.8460e, 0.4764e, −0.8332e, 0.4852e, −0.8009e, 0.4867e, and −0.8141e, which are obviously more positive and negative charges than those in complex A.

The quantum chemical investigations show that the covalent interaction from a nonbonding orbital of the acceptor atom to the antibonding σ* molecular orbital of the donor group should be a significant ingredient of the hydrogen bonding energies.^67–69 So we applied the NBO second-order perturbation analysis to calculate the second-order stabilization energy of nonbonding orbital of the acceptor O atom to the antibonding σ* molecular orbital of the donor group H–N. The obtained perturbation energies due to n(O(1)) → σ*(H(1)–N(1)), n(O(2)) → σ*(H(2)–N(2)), n(O(3)) → σ*(H(3)–N(3)), and n(O(4)) → σ*(H(4)–N(4)) orbital interactions are listed in Table 2. As shown in Table 2, the perturbation energies are obviously affected as the H₂O molecules bonded, especially for those in the same amide unit directly bonded by the H₂O molecules. For example, the perturbation energies of n(O(1)) → σ*(H(1)–N(1)) in complex B is 15.65 kcal mol⁻¹, which is enhanced by 9% from 14.41 kcal mol⁻¹ of complex A. In complex J, the value of 17.45 kcal mol⁻¹ is increased by 21% from complex A. As listed in Table 2, the perturbation energies due to n(O(1)) → σ*(H(1)–N(1)), n(O(2)) → σ*(H(2)–N(2)), n(O(3)) → σ*(H(3)–N(3)), and n(O(4)) → σ*(H(4)–N(4)) orbital interactions in complex A are 14.41 kcal mol⁻¹, 15.32 kcal mol⁻¹, 6.71 kcal mol⁻¹, and 7.66 kcal mol⁻¹. As four H₂O molecules bonded, the values are changed to 17.45 kcal mol⁻¹, 15.57 kcal mol⁻¹, 7.59 kcal mol⁻¹, and 8.73 kcal mol⁻¹. These results further support the conclusion that the perturbation energies make a certain contribution to the cooperative enhancement of the β-sheet models.

We have also investigated the effect of the charge transfer among the three diglypeptides of the β-sheet structures. The net charges of the upper, middle and lower diglypeptides are listed in Table 3. In complex A, the net charges of the three diglypeptides are −0.0002e, 0.0009e and −0.0007e, respectively. Therefore, the three-stranded sheet structure is electric neutrality. In complex B, one H₂O molecule acting as proton donor bond to β-sheet structure and the net charge of the upper diglypeptide that directly bonded by the H₂O molecule is 0.0118e. The net charge of middle diglypeptide changes from 0.0009e to 0.0027e and the value for the lower diglypeptide changes slightly. The total net charge of the three-stranded sheet structure is 0.0141e. It means that the electronic charge transfer from the three-stranded sheet structure to the H₂O molecule. In complex E, one H₂O molecule acting as proton acceptor bonds to the lower diglypeptide. The total net charge of the three-stranded sheet structure is −0.0193e which means the electronic charge transfer from the H₂O molecule to the three-stranded sheet structure.

Table 3 The individual net charges of upper, middle and lower diglypeptides and the total net charges of the three-stranded diglypeptide sheet structures

	A	B	C	D	E	F	G	H	I	J
Net charges of the upper diglypeptide	−0.0002	0.0118	−0.0191	0.0002	−0.0006	0.0115	−0.0186	−0.0056	−0.0003	−0.0055
Net charges of the middle diglypeptide	0.0009	0.0027	0.0010	0.0016	0.0004	0.0021	0.0018	0.0032	0.0012	0.0036
Net charges of the lower diglypeptide	−0.0007	−0.0004	−0.0007	0.0222	−0.0191	−0.0186	0.0221	−0.0004	0.0041	0.0041
Total net charges of three-stranded sheet structures	0.0000	0.0141	−0.0187	0.0240	−0.0193	−0.0054	0.0053	−0.0028	0.0049	0.0022

---

It is interesting to note that there is an additive property for the total net charge of the three-stranded sheet structure. For example, the total net charge of complex F is −0.0054e, which is close to the summation of complex B and E −0.0052e. The value 0.0053e of complex G is close to the value of C plus D. The sum of D and E is 0.0047e, which is also close to the value 0.0049e of I. However, it is exceptional for H. The total net charge of H is −0.0028e, but the sum of B and C is −0.0046e. In complex H, the two H₂O molecules are both bonded to the same outside C=O. The carbonyl O atom serves as a proton acceptor in three separate hydrogen bonds simultaneously, which would tend to weaken each. So the cooperative effect of the two H₂O molecules in complex H is weaker than the sum of B and C.¹⁷ It is also the reason why the total net charge of complex J is close to the sum of complex H and I but not close to the sum F and G, and neither close to the sum of B, C, D and E.

Conclusion

By employing the method of MP2/6-311++G(3df,2p)//MP2/6-31G**, we performed quantum chemical calculations to investigate the effect of water molecules upon the hydrogen-bonding cooperativity of three-stranded antiparallel β-sheet models. Our calculation results indicate that the hydrogen-bonding lengths and the atom charges distribution are affected by the H₂O molecules, especially those in the same amide unit directly bonded. The hydrogen-bonding cooperativity significantly increases the binding energy of LR or SR hydrogen-bonding ring and the influence is also gradually increased as more H₂O molecules added. The natural bond orbital analyses in this paper further support the cooperative enhancement is closely related to the orbital interaction. We have also found, as the H₂O molecules added, the charge transfer among the three diglypeptides are obviously influenced. Furthermore, there is an additive property for the total net charge of the three-stranded sheet structures. The studies are helpful in understanding the cooperative effect of H₂O molecules in structure and biological activity of proteins and peptides. The results are discussed also with respect to their utility for improving the modeling for peptide structure and protein folding in biological systems.

Acknowledgements

We acknowledge the National Natural Science Foundation of China (grants no. 21201123) for financial support of this research.

References and Notes

1. G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer-Verlag, Berlin, 1991.
2. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, 1997.
3. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, New York, 1999.
4. J. Gsponer, H. Hopearuoho, A. Cavalli, C. M. Dobson and M. Vendruscolo, J. Am. Chem. Soc., 2006, 128, 15127–15135.
5. Z. Cai and J. R. Reimers, J. Phys. Chem. A, 2007, 111, 954–962.
6. T. Rezai, J. E. BocK, M. V. Zhou, C. Kalyanaraman, R. S. Lokey and M. P. Jacobson, J. Am. Chem. Soc., 2006, 128, 14073–14080.
7. X. H. Chen, D. W. Zhang and J. Z. H. Zhang, J. Chem. Phys., 2004, 120, 839–844.
8. D. W. Zhang and J. Z. H. Zhang, J. Chem. Phys., 2003, 119, 3599–3605.
9. D. W. Zhang, Y. Xiang, A. M. Gao and J. Z. H. Zhang, J. Chem. Phys., 2004, 120, 1145–1148.
10. Y. Zhang and C.-S. Wang, J. Comput. Chem., 2009, 30, 1251–1260.
11. C.-S. Wang, Y. Zhang, K. Gao and Z.-Z. Yang, J. Chem. Phys., 2005, 123, 024307.
12. C.-L. Sun, X.-N. Jiang and C.-S. Wang, J. Comput. Chem., 2009, 30, 2567–2575.
13. C.-S. Wang and C.-L. Sun, J. Comput. Chem., 2010, 31, 1036–1044.
14. Y. Zhang and C.-S. Wang, J. Theor. Comput. Chem., 2009, 8, 279–297.
15. Y. Li, X.-N. Jiang and C.-S. Wang, J. Comput. Chem., 2011, 32, 953–966.
16. Y. Li and C.-S. Wang, J. Comput. Chem., 2011, 32, 2765–2772.
17. S. Scheiner, J. Phys. Chem. B, 2006, 110, 18670–18679.
18. J. S. Miller, R. J. Kennedy and D. S. Kemp, J. Am. Chem. Soc., 2002, 124, 945–962.
19. V. A. Jaravine, A. T. Alexandrescu and S. Grzesiek, Protein Sci., 2001, 10, 943–950.
20. N. Juranic, M. C. Moncrieffe, V. A. Likic, F. G. Pendergast and S. Macura, J. Am. Chem. Soc., 2002, 124, 14221–14226.
21. P. Salvador, N. Kobko, R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2004, 126, 14190–14197.
22. R. Viswanathan, A. Asensio and J. J. Dannenberg, J. Phys. Chem. A, 2004, 108, 9205–9212.
23. Y.-L. Zhao and Y.-D. Wu, J. Am. Chem. Soc., 2002, 124, 1570–1571.
24. Y.-D. Wu and Y.-L. Zhao, J. Am. Chem. Soc., 2001, 123, 5313–5319.
25. J.-Q. Lin, S.-W. Luo and Y. D. Wu, J. Comput. Chem., 2002, 23, 1551–1558.
26. R. Viswanathan and J. J. Dannenberg, J. Phys. Chem. B, 2008, 112, 5199–5208.
27. Y. F. Chen, R. Viswanathan and J. J. Dannenberg, J. Phys. Chem. B, 2007, 111, 8329–8334.
28. A. Masunov and J. J. Dannenberg, J. Phys. Chem. B, 2000, 104, 806–810.
29. N. Kobko, L. Paraskevas, E. del Rio and J. J. Dannenberg, J. Am. Chem. Soc., 2001, 123, 4348–4349.
30. N. Kobko and J. J. Dannenberg, J. Phys. Chem. A, 2003, 107, 10389–10395.
31. Y.-F. Chen and J. J. Dannenberg, J. Am. Chem. Soc., 2006, 128, 8100–8101.
32. R. Viswanathan and J. J. Dannenberg, J. Phys. Chem. B, 2008, 112, 5199–5208.
33. R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2003, 125, 8124–8129.
34. R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2003, 125, 14065–14071.
35. Q. Z. Li, X. L. An, B. A. Gong and J. B. Cheng, J. Phys. Chem. A, 2007, 110, 10166–10169.
36. R. J. Kennedy, K.-Y. Tasng and D. S. Kemp, J. Am. Chem. Soc., 2002, 124, 934–944.
37. X.-N. Jiang, C.-L. Sun and C.-S. Wang, J. Comput. Chem., 2010, 31, 1410–1420.
38. X.-N. Jiang and C.-S. Wang, ChemPhysChem, 2009, 10, 3330–3336.
39. H. Dong, W.-J. Hua and S.-H. Li, J. Phys. Chem. A, 2007, 111, 2941–2945.
40. R. Ludwig, O. Reis, R. Winter, F. Weinhold and T. C. Farar, J. Phys. Chem. B, 1998, 102, 9312–9318.
41. R. Ludwig, F. Weinhold and T. C. Farar, J. Phys. Chem. A, 1997, 101, 8861–8870.
42. H.-W. Tan, W.-W. Qu, G.-J. Chen and R.-Z. Liu, J. Phys. Chem. A, 2005, 109, 6303–6308.
43. A. V. Morozov, K. Tsemekhman and D. Baker, J. Phys. Chem. B, 2006, 110, 4503–4505.
44. I. A. W. Filot, A. R. A. Palmans, P. A. J. Hibers, R. A. van Santen, E. A. Pidko and T. F. A. de Greef, J. Phys. Chem. B, 2010, 114, 13667–13674.
45. J. J. Dannenberg, J. Phys. Chem. A, 2008, 110, 5798–5802.
46. P. Salvador, A. Asensio and J. J. Dannenberg, J. Phys. Chem. B, 2007, 111, 7462–7466.
47. J. A. Plumley, M. I.-H. Tsai and J. J. Dannenberg, J. Phys. Chem. B, 2011, 115, 1562–1570.
48. S. Tsuzuki, H. Houjou, Y. Nagawa, M. Goto and K. Hiratani, J. Am. Chem. Soc., 2001, 123, 4255–4258.
49. Q. Johnson, U. Doshi, T. Shen and D. Hamelberg, J. Chem. Theory Comput., 2010, 6, 2591–2597.
50. F. Sterpone, G. Stirnemann, J. T. Hynes and D. Laage, J. Phys. Chem. B, 2010, 114, 2083–2089.
51. M. Marianski and J. J. Dannenberg, J. Phys. Chem. B, 2012, 116, 1437–1445.
52. J. Ireta, J. Chem. Theory Comput., 2011, 7, 2630–2637.
53. O. Lukin and J. Leszczynski, J. Phys. Chem. A, 2002, 106, 6775–6782.
54. C.-L. Sun and C.-S. Wang, J. Mol. Struct., 2010, 856, 38–43.
55. H. Guo and M. Karplus, J. Phys. Chem., 1994, 98, 7104–7105.
56. C.-L. Sun, X.-N. Jiang and C.-S. Wang, Int. J. Quantum Chem., 2013, 113, 1453–1460.
57. A. L. Lehninger, D. L. Nelson and M. M. Cox, Principles of Biochemistry, Worth, New York, 1993, 2nd edn, ch. 4, p. 123.
58. R. Nelson, M. R. Sawaya, M. Balbirnie, A. Ø. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778.
59. M. R. Sawaya, S. Sambashivan, R. Nelson, M. I. Ivanova, S. A. Sievers, M. I. Apostol, M. J. Thompson, M. Balbirnie, J. J. W. Wiltzius, H. T. McFarlane, A. Ø. Madsen, C. Reikel and D. Eisenberg, Nature, 2007, 447, 453–457.
60. M. Sunde, L. C. Serpell, M. Bartlam, P. E. Fraser, M. B. Pepys and C. C. F. Blake, J. Mol. Biol., 1997, 273, 729–739.
61. R. Nelson and D. Eisenberg, Adv. Protein Chem., 2006, 73, 235–282.
62. C. M. Dobson, Nature, 2005, 435, 747–749.
63. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–556.
64. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.
65. E. D. Glendening, A. E. Reed, J. Carpenter and E. F. N. B. O. Weinhold, Version 3.0.
66. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. D. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chem, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 03, Gaussian Inc., Pittsburgh, PA, 2003.
67. T. K. Ghanty, V. N. Staroverov, P. R. Koren and E. R. Davidson, J. Am. Chem. Soc., 2000, 122, 1210–1214.
68. E. D. Isaacs, A. Shukla, P. M. Platzman, D. R. Hamann, B. Barbiellini and C. A. Tulk, Phys. Rev. Lett., 1999, 82, 600.
69. A. M. Pendás, M. A. Blanco and E. Francisco, J. Chem. Phys., 2006, 125, 184112.

---

Footnote

† Electronic supplementary information (ESI) available: The geometrical coordinates of the ten three-stranded antiparallel diglypeptide β-sheet models optimized at the MP2/6-31G** level. See DOI: 10.1039/c3ra45892j

---