17O and 1H relaxometric and DFT study of hyperfine coupling constants in [Mn(H2O)6]2+†
David Esteban-Gómeza,
Claudio Cassinob,
Mauro Bottab and
Carlos Platas-Iglesias*a
aDepartamento de Química Fundamental, Universidade da Coruña, Rúa da Fraga 10, 15008, A Coruña, Spain. E-mail: carlos.platas.iglesias@udc.es; Fax: +34 981 167 065
bDipartimento di Scienze e Innovazione Tecnologica, Università del Piemonte Orientale “Amedeo Avogadro”, Viale T. Michel 11, 15121, Alessandria, Italy
First published on 6th January 2014
Abstract
Nuclear Magnetic Relaxation Dispersion (NMRD) profiles and 17O NMR chemical shifts and transverse relaxation rates of aqueous solutions of [Mn(H2O)6]2+ were recorded to determine the parameters governing the relaxivity in this complex and the 17O and 1H hyperfine coupling constants (HFCCs). The analysis of the NMRD and 17O NMR data provided a water exchange rate of kex298 = 28.2 × 106 s−1, and AO/ħ and AH/ħ hyperfine coupling constants of −34.6 and 5.4 rad s−1, respectively. DFT calculations (TPSSh model) performed on the [Mn(H2O)6]2+ and [Mn(H2O)6]2+·12H2O systems were used to evaluate theoretically the 17O and 1H HFCCs responsible for the 17O NMR chemical shifts and the scalar contributions to 17O and 1H NMR relaxation rates. The use of a mixed cluster–continuum approach with the explicit inclusion of second-sphere water molecules is critical for an accurate calculation of HFCCs of coordinated water molecules. The impact of complex dynamics on the calculated HFCCs was evaluated with the use of molecular dynamics simulations within the atom-centered density matrix propagation (ADMP) approach. These molecular dynamics simulations show that the Aiso values are critically affected by the distance between the oxygen atom of the coordinated water molecule and the MnII ion, as well as by the orientation of the water molecule plane with respect to the Mn–O vector. The substantial scalar contribution to relaxivity observed for [Mn(H2O)6]2+ is related to a combination of a slow water exchange rate and a slow electron spin relaxation.
Introduction
Hyperfine interactions between nuclear spin and electron spin play a key role in the description of NMR relaxation of ligand nuclei in solutions of paramagnetic species.1 Electron spin relaxation in paramagnetic systems provides fluctuating magnetic fields, and therefore causes nuclear relaxation. The observed nucleus however does not see the unpaired electron(s) as localized, but rather as spin density distributed throughout space. The presence of spin density at the resonating nucleus is responsible for the so called Fermi contact mechanism to nuclear relaxation, which depends on the hyperfine coupling constant (HFCC) A/ħ between the electron spin of the metal ion and the nuclear spin.2Recently, we started a research program devoted to the synthesis and physicochemical characterization of MnII complexes with potential application as contrast agents in magnetic resonance imaging (MRI).3–5 Contrast agents are paramagnetic probes that enhance the image contrast by shortening the longitudinal and/or transverse relaxation times of water molecules surrounding the complex.6 Although most commercially available contrast agents are small GdIII chelates, complexes of the d5 metal ion MnII with high-spin configuration represent an alternative to the classical GdIII-based contrast agents. An important potential advantage of MnII-based contrast agents over the classical GdIII-based ones is the lower toxicity of MnII complexes. Furthermore, high-spin MnII complexes present relatively high effective magnetic moments and slow electronic relaxation rates.7
Contrast agents for MRI typically contain one water molecule coordinated to the paramagnetic metal ion that exchanges rapidly with the bulk water. The efficiency of a contrast agent is often evaluated in vitro in terms of its relaxivity, which is defined as the longitudinal relaxation rate enhancement of water proton nuclei per mM concentration of the paramagnetic ion. Relaxivity depends upon a relatively large number of parameters that can hardly be determined by analyzing relaxivity data alone.6 Indeed, variable temperature 17O NMR measurements of chemical shifts and transverse relaxation rates constitute a valuable tool to investigate the parameters influencing relaxivity in MRI CAs.8,9 17O NMR data provide information on the water exchange kinetics of the complex, and depend on the hyperfine coupling constant AO/ħ between the electron spin of the metal ion and the 17O nuclear spin. Additionally, the Nuclear Magnetic Relaxation Dispersion (NMRD) profiles recorded for some MnII complexes such as [Mn(H2O)6]2+ and [Mn2(ENOTA)] show an unusual dispersion at about 0.1 MHz attributed to an important scalar contribution to relaxivity, which depends on the hyperfine coupling constant AH/ħ.9,10 Thus, a detailed study of the AO/ħ and AH/ħ HFCCs in MnII complexes is important for the rational development of MRI contrast agents.
Methods based on Density Functional Theory (DFT) provide a reasonably high accuracy at relatively low computational cost, and therefore represent an attractive tool for the calculation of hyperfine coupling constants (HFCCs) in metal complexes. Different studies have shown that DFT methods provide rather accurate HFCCs of different mononuclear11 and dinuclear12 Mn complexes. However, calculations on the MnII complex with one of the simplest possible ligands, water, have proven rather difficult. For instance, calculations performed within the hybrid-GGA approximation with the B3LYP functional yielded a 55Mn isotropic HFCC Aiso = −164 MHz, which is rather far from the experimental value (−245 MHz).13 The same authors found that the sign of the experimental 17O Aiso value is well reproduced by calculations, but its magnitude is overestimated by 50%. Subsequent studies performed by Kaupp14 and Neese15 with the use of different functionals also provided calculated 17O Aiso values significantly larger than the experimental data.
The 17O relaxation properties of the [Mn(H2O)6]2+ complex were investigated by Merbach et al. at low magnetic field (1.4 T),16 while 1H Nuclear Magnetic Relaxation Dispersion (NMRD) profiles at a single temperature (308 K) were recorded by Bertini and co.10 In this article, we present a combined experimental and computational study that aims at gaining information on the hyperfine coupling constants that govern the scalar contribution to 1H relaxivity and the 17O NMR chemical shifts and relaxation rates in [Mn(H2O)6]2+. For this purpose, 1H NMRD profiles were recorded at three different temperatures, while 17O NMR chemical shifts and transverse relaxation times were measured at high magnetic field (11.7 T). DFT calculations and molecular dynamics studies based on the Atom Centered Density Matrix Propagation (ADMP) model were performed to gain information on the AO/ħ and AH/ħ hyperfine coupling constants and the relation between their values and the solution structure and dynamics of the complex.
Experimental
The proton 1/T1 NMRD profiles were measured on a fast field-cycling Stelar SmartTracer relaxometer (Mede, Pv, Italy) over a continuum of magnetic field strengths from 0.00024 to 0.25 T (corresponding to 0.01–10 MHz proton Larmor frequencies). The relaxometer operates under computer control with an absolute uncertainty in 1/T1 of ±1%. The temperature was controlled with a Stelar VTC-91 airflow heater equipped with a calibrated copper–constantan thermocouple (uncertainty of ±0.1 K). Additional data points in the range 15–70 MHz were obtained on a Stelar Relaxometer equipped with a Bruker WP80 NMR electromagnet adapted to variable-field measurements (15–80 MHz proton Larmor frequency). For these 1H data a 3.2 mM solution of Mn(NO3)2 in non-deuterated water at pH = 1.7 was utilized. The exact complex concentration was determined by the BMS shift method at 11.7 T.17 17O NMR measurements were recorded on a Bruker Avance III spectrometer (11.7 T) equipped with a 5 mm probe and standard temperature control unit. A 8.4 mM aqueous solution of [Mn(H2O)6]2+ containing 2.0% of the 17O isotope (Cambridge Isotope) was used. The observed transverse relaxation rates were calculated from the signal width at half-height.Computational methods
All calculations presented in this work were performed employing the Gaussian 09 package (Revision B.01).18 Full geometry optimizations of the [Mn(H2O)6]2+ system were performed employing DFT within the hybrid meta-GGA approximation with the TPSSh exchange-correlation functional.19 For geometry optimization purposes, we used the standard Ahlrichs' valence double-ξ basis set including polarization functions (SVP).20 Geometry optimizations of the [Mn(H2O)6]2+ system were also performed using the more extended Ahlrichs' valence triple-ξ basis set including polarization functions (TZVP).21 The calculated Mn–O distances calculated at the TPSSh/SVP and TPSSh/TZVP levels differ by only 0.01 Å. Convergence of geometry optimizations of the [Mn(H2O)6]2+ complex in aqueous solution were found to be problematic, while for the [Mn(H2O)6]2+·12H2O system convergence was achieved. No symmetry constraints have been imposed during the optimizations. The highest spin state was considered as the ground state (sextuplet, 3d5). Since these calculations were performed by using an unrestricted model, spin contamination22 was assessed by a comparison of the expected difference between S(S + 1) for the assigned spin state (S(S + 1) = 8.75) and the actual value of 〈S2〉.23 The results obtained indicate that spin contamination is negligible for systems investigated in this work [〈S2〉 − S(S + 1) < 0.0040]. The stationary points found on the potential energy surfaces as a result of geometry optimizations were tested to represent energy minima rather than saddle points via frequency analysis. The default values for the integration grid (75 radial shells and 302 angular points) and the SCF energy convergence criteria (10−8) were used in all calculations.Classical trajectory calculations of [Mn(H2O)6]2+ and [Mn(H2O)6]2+·12H2O were performed in aqueous solution at the TPSSh/SVP level by using the Atom Centered Density Matrix Propagation (ADMP) molecular dynamics model.24 Time steps of 0.2 fs were used during the simulations and a total of 5000 steps were run for the trajectory simulations. The fictitious electron mass was 0.1 amu. All the ADMP calculations were started from the corresponding optimized geometries obtained as described above.
Isotropic 17O, 1H and 55Mn HFCCs in the [Mn(H2O)6]2+ and [Mn(H2O)6]2+·12H2O systems were calculated in aqueous solution with unrestricted DFT methods by employing the TPSSh exchange-correlation functional. For the description of H and O we used the EPR-III basis sets of Barone,25 which is a triple-zeta basis set including diffuse functions, double d-polarizations and a single set of f-polarization functions, together with an improved s-part to better describe the nuclear region. For Mn we used the aug-cc-pVTZ-J basis set developed by Sauer for the calculation of EPR HFCCs, which is described by a (25s17p10d3f2g)/[17s10p7d3f2g] contraction scheme, and contains four tight s-, one tight p-, and one tight d-type function.26 In the case of the [Mn(H2O)6]2+ system, test calculations were also performed employing five additional functionals within the LSDA (SVWN27,28), GGA (BLYP29,30), meta-GGA (TPSS19), hybrid-GGA (B3LYP30,31) and hybrid meta-GGA (M0632) approximations. The CAM-B3LYP hybrid functional, a long range corrected version of B3LYP using the Coulomb-attenuating method, was also tested.33
Throughout this work solvent effects were included by using the polarizable continuum model (PCM), in which the solute cavity is built as an envelope of spheres centered on atoms or atomic groups with appropriate radii. In particular, we used the integral equation formalism (IEFPCM) variant as implemented in Gaussian 09.34
Results and discussion
NMRD and 17O NMR studies
The increase of the water proton R1 value, normalized to a 1 mM concentration of the paramagnetic species, is called relaxivity (r1p) and it represents the efficiency of the paramagnetic solute in catalyzing the solvent relaxation at a given frequency and temperature. The relaxivity observed for [Mn(H2O)6]2+ is the result of both inner- and outer-sphere contributions. The inner sphere term (r1is) is given in eqn (1), where q is the number of inner sphere water molecules (q = 6 for [Mn(H2O)6]2+) and τm is the residence time of water protons in the inner coordination sphere.35
 | (1) |
The longitudinal relaxation rate of inner sphere protons in MnII complexes, 1/TH1m, can be split into the dipolar (1/TDD1m) and scalar or Fermi contact term (1/TSC1m).36 The dipolar contribution is the result of the modulation of the dipolar interaction between the electron (metal-based) and nuclear (of the bound water molecules) magnetic moments. The modulation occurs through rotation of the complex (τR), electron magnetic moment relaxation (T1,2e) and chemical exchange of the coordinated water molecules with bulk water (kex = 1/τM). The enhancement of R1 also depends on the number (q) of bound water molecules and their distance (rMnH) from the metal centre, and on the applied magnetic field strength (eqn (2) and (3)):
 | (2) |
 | (3) |
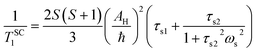 | (4) |
Here AH/ħ represents the 1H hyperfine or scalar coupling constant and 1/τsi is the sum of the exchange rate constant and the longitudinal (1/T1e) or transverse (1/T2e) electron spin relaxation rates:
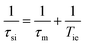 | (5) |
The outer-sphere contribution to relaxivity arises from solvent molecules diffusing in the vicinity of the paramagnetic complex, and depends on additional parameters: the relative diffusion coefficient of solute and solvent molecules, D, and their distance of closest approach, a.37
The temperature dependence of 17O transverse relaxation rates (R2) is given by the Swift–Connick equations,38 which depend primarily on T1,2e, the hyperfine coupling constant AO/ħ, τM and q (eqn (6)–(9)):
 | (6) |
 | (7) |
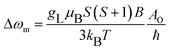 | (8) |
 | (9) |
In these eqn (1)/T2 and ω are the measured 17O NMR transverse relaxation rates and angular frequencies of the paramagnetic solution, 1/T2A and ωA the corresponding values of the acidified water reference, 1/T2r and Δωr represent the reduced relaxation rates and reduced chemical shifts, 1/T2m is the relaxation rate of the bound water, Δωm is the chemical shift difference between bound and bulk water and Pm is the mole fraction of the bound water.
Nuclear magnetic relaxation dispersion (NMRD) profiles of [Mn(H2O)6]2+ were measured at 283, 298 and 310 K in the proton Larmor frequency range 0.01–70 MHz, corresponding to magnetic field strengths varying between 2.343 × 10−4 and 1.645 T (Fig. 1). The relaxivity of [Mn(H2O)6]2+ decreases with increasing temperature in the proton Larmor frequency range 0.1–70 MHz, which shows that the relaxivity is limited by the fast rotation of the complex in solution rather than by a slow water exchange rate. As usually observed for small MnII chelates,3–5 the NMRD profiles show a dispersion between 2 and 20 MHz. In addition, a second dispersion occurs between 0.5 and 0.02 MHz. This has been previously observed by Bertini et al. in the NMRD profile recorded at 308 K,10 and attributed to an important scalar contribution to proton relaxivity.
 | ||
| Fig. 1 1H NMRD profiles recorded at different temperatures for [Mn(H2O)6]2+ at pH 1.7. The lines represent the fit of the data as explained in the text. | ||
The reduced transverse 17O relaxation rates and chemical shifts measured for [Mn(H2O)6]2+ are presented in Fig. 2. Although the full eqn (6) was used to fit the experimental 17O NMR data, it is useful to consider the simplified eqn (10), in which the contribution to 1/T2r of the chemical shift difference between the bound and bulk water (Δωm) has been neglected.
 | (10) |
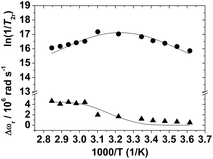 | ||
| Fig. 2 Reduced transverse (●) 17O relaxation rates and 17O chemical shifts (▲) measured at 11.74 T for [Mn(H2O)6]2+ (pH 1.7). The lines represent the fit of the data as explained in the text. | ||
The sign of the temperature dependence of 1/T2r depends on whether the transverse relaxation is dominated by τM, which decreases with increasing temperature, or by the relaxation time of the bound water molecule, T2m, which normally increases with increasing temperature. For [Mn(H2O)6]2+ 1/T2r increases with decreasing temperature below 357 K, reaches a maximum around 312 K, and then decreases in the temperature range 312–275 K. The maximum observed in the temperature dependence of 1/T2r is therefore indicative of a changeover from the fast exchange regime at high temperatures, where T2m is the dominant term in eqn (10), to the low exchange regime at low temperatures, where τM is the dominant term.39 The changeover between fast and slow exchange is also manifested in the temperature dependence of Δωr, which shows an inflection point corresponding to the maximum in 1/T2r. Most of the MnII complexes studied so far do not show a maximum in the temperature dependence of 1/T2r, or this maximum is observed at lower temperatures in comparison with [Mn(H2O)6]2+ (i.e. [Mn(CyDTA)(H2O)]2−).40 These qualitative observations point to a relatively long residence time of the inner-sphere water molecules in the aqua-ion.
A simultaneous analysis of the NMRD and 17O NMR data of [Mn(H2O)6]2+ gave the parameters listed in Table 1, while the curve fits are shown in Fig. 1 and 2. Some parameters were fixed during the fitting procedure: the distance of closest approach for the outer-sphere contribution aMnH was fixed at 3.6 Å, while the distance between the proton nuclei of the coordinated water molecule and the MnII ion (rMnH) was fixed at 2.83 Å. The number of water molecules in the inner coordination sphere of MnII was fixed to q = 6, while the value of the diffusion coefficient, DMnH298, was fixed to the value of the self-diffusion coefficient of water molecules in pure water (DMnH298 = 2.3 × 10−9 m2 s−1).41 The values of aMnH and DMnH298 used in the analysis of the data were taken on the basis of the data reported in the literature for different MnII complexes.3–5 It is worth noting that the outer-sphere contribution to relaxivity is relatively small for [Mn(H2O)6]2+ (Fig. S1, ESI†). As a result, an accurate determination of these parameters from the analysis of the NMRD data was not possible.
| Parameter | [Mn(H2O)6]2+ | [Mn(EDTA)]2− | [Mn(1,4-DO2A)] |
|---|---|---|---|
| a Italicized values were fixed during the fitting procedures.b There is some confusion about the sign of the 17O isotropic HFCC in MnII complexes. In contrast to recent experimental work, the correct sign of AO/ħ = 2πAiso of a water molecule bound to MnII is negative, and corresponds to negative spin densities at the point of nucleus that causes an upfield shift of the 17O resonance. | |||
| kex298/106 s−1 | 28.2 ± 3.5 | 471 | 1134 |
| ΔH‡ kJ mol−1 | 45.6 ± 3.5 | 33.5 | 29.4 |
| τR298/ps | 30.0 ± 0.2 | 57 | 46 |
| Er/kJ mol−1 | 16.7 ± 1.8 | 21.8 | 19.1 |
| τV298/ps | 10.0 ± 10.0 | 27.9 | 4.4 |
| Ev/kJ mol−1 | 14.6 ± 0.7 | 1.0 | 1.0 |
| DMnH298/10−10 m2 s−1 | 23.0 | 23.1 | 23.0 |
| EDMnH/kJ mol−1 | 29.7 ± 9.6 | 18.9 | 17.3 |
| Δ2/1019 s−2 | 0.06 ± 0.06 | 6.9 | 48.1 |
| AO/ħ/106 rad s−1b | −34.6 ± 1.6 | −40.5 | −43.0 |
| AH/ħ/106 rad s−1 | 5.43 ± 0.03 | 0.0 | 0.0 |
| rMnH/Å | 2.83 | 2.83 | 2.83 |
| aMnH/Å | 3.6 | 3.6 | 3.6 |
| q298 | 6 | 1 | 0.87 |
The water exchange rate determined for [Mn(H2O)6]2+ (kex298 = 28.2 × 106 ± 3.5 s−1) is very similar to that determined by Merbach et al. from 17O NMR measurements at 1.4 T.16 The water exchange rates determined for six- and seven-coordinated MnII complexes are faster than that of the fully aquated species (see for instance the data given in Table 1 for [Mn(EDTA)(H2O)]2− and [Mn(1,4-DO2A)(H2O)]). This effect has been attributed to the high-spin d5 configuration, which does not have appreciable angular dependence on ligand field stabilization. Thus, despite the coordination of a ligand, conformational changes during the water substitution process are easily feasible in d5 systems.39
The τR298 value obtained from the analysis of the 1H NMRD profiles (30.0 ps) is somewhat shorter than those determined for small MnII complexes such as [Mn(EDTA)(H2O)]2− and [Mn(1,4-DO2A)(H2O)], in line with the lower molecular weight of the aquated species. The quality of the fits was found to be quite insensitive to the parameters determining the electron spin relaxation Δ2 and τV, and therefore the fitted parameters present rather large errors. However, the activation energy for the modulation of the zero-field-splitting (EV), which was obtained with a very small statistical error, is in very good agreement with the value obtained from EPR measurements (10.5 kJ mol−1).42
The hyperfine coupling constant AO/ħ determined for [Mn(H2O)6]2+ (−34.6 × 106 rad s−1) is in the low part of the range typically observed for MnII complexes (−32 × 106 to −43 × 106 rad s−1).43 A AO/ħ HFCC of −34.6 × 106 rad s−1 corresponds to a Aiso value of −5.5 MHz, which is considerably smaller than that determined with ENDOR spectroscopy from frozen solution (−7.5 MHz).13 The 1H HFCC AH/ħ was found to be 5.5 × 106 rad s−1, which corresponds to a Aiso value of 0.86 MHz. The only MnII complex for which AH/ħ could be determined from 1H relaxation data, [Mn2(ENOTA)(H2O)2], presents a somewhat lower AH/ħ HFCC (2.9 × 106 rad s−1).9
DFT calculations on the [Mn(H2O)6]2+ and [Mn(H2O)6]2+·12H2O systems
As expected, the geometry of [Mn(H2O)6]2+ optimized at the TPSSh/SVP level presents an octahedral geometry according to the Mn–O bonds, with the overall molecule having a Td symmetry (Fig. 3). The calculated Mn–O distance (2.194 Å), is in good agreement with those observed in the solid state with X-ray crystallography,44 and that determined from EXAFS spectra at 25 °C (2.17 Å).45 Different computational studies provided similar geometries with Mn–O bond distances in the range 2.20–2.25 Å.46 | ||
| Fig. 3 Geometries of the [Mn(H2O)6]2+ (top) and [Mn(H2O)6]2+·12H2O (bottom) systems optimized at the TPSSh/SVP level. | ||
The hyperfine coupling tensor for the nucleus N consists of three contributions, namely the isotropic Fermi contact (FC) and the anisotropic spin-dipolar contributions and the spin-orbit contribution. The isotropic FC contribution (Aiso) is given by:47
 | (11) |
Calculations of the 1H, 17O and 55Mn HFCCs in [Mn(H2O)6]2+ were performed using single point calculations in aqueous solution on the optimized geometry described above. The data reported in Table 2 indicate that the SVWN, B3LYP, TPSS, M06, TPSSh and CAM-B3LYP functionals provide 1H and 17O HFCCs in good mutual agreement, while the GGA functional BLYP provides somewhat larger absolute values for both 1H and 17O Aiso. Among all the functionals tested in this work on the [Mn(H2O)6]2+ system the hybrid meta-GGA functional TPSSh provides the best overall agreement with the experimental 1H, 17O and 55Mn Aiso values. Even so, the TPSSh functional gives calculated HFFCs that deviate up to 30% with respect to the values obtained with field ENDOR measurements in frozen solution13 and up to 90% (17O) and 70% (1H) with respect with the values obtained from the analysis of the NMRD and 17O NMR data.
| Functional | 17O | 1H | 55Mn | |
|---|---|---|---|---|
| a Data obtained from the equilibrium geometry.b Calculated values obtained from the analysis of the trajectories of ADMP simulations (see text).c Obtained from high field ENDOR measurements in frozen solutions, ref. 13.d Obtained in this work from a simultaneous fitting of the NMRD and 17O NMR chemical shifts and relaxation rates. | ||||
| [Mn(H2O)6]2+ | SVWN | −10.45 | 1.36 | −141.7 |
| BLYP | −12.57 | 1.83 | −131.1 | |
| B3LYP | −10.73 | 1.39 | −159.8 | |
| TPSS | −10.68 | 1.68 | −175.5 | |
| M06 | −10.04 | 1.16 | −0.81 | |
| CAM-B3LYP | −10.25 | 1.27 | −162.7 | |
| TPSSh | −9.90 | 1.47 | −189.9 | |
| [Mn(H2O)6]2+·12H2O | TPSSha | −6.97 | 0.69 | −173.9 |
| TPSShb | −7.05 | 0.75 | −172.5 | |
| Experimental | −7.5c | −245c | ||
| −5.4d | 0.86d | |||
In previous works we have shown that the explicit inclusion of a few second-sphere water molecules was crucial to obtain accurate 17O and 1H HFCCs in both MnII and GdIII complexes.3,4,48 Thus, we have performed calculations using a cluster–continuum approach explicitly including twelve second-sphere water molecules. This approach may be used to overcome the deficiency of continuum solvent models to account for specific hydrogen-bonding interactions involving inner-sphere and second-sphere water molecules. Twelve is the number of second-sphere water molecules expected to interact by hydrogen bonding to the six coordinated water molecules, and therefore clusters with formula [M(H2O)6]2+·12H2O have been extensively investigated with ab initio and DFT calculations to gain information on the arrangement of first- and second-sphere water molecules in different metal aqua-complexes.49 The structure of the [Mn(H2O)6]2+·12H2O system optimized in aqueous solution at the TPSSh/SVP level possesses a slightly distorted S6 symmetry. In our model six second-sphere water molecules present Mn⋯O distances of 3.734 Å, and are involved in hydrogen-bonding interactions with two coordinated water molecules occupying cis positions in the octahedral coordination polyhedron. These second sphere water molecules are bridged via hydrogen bonds by a second set of second-sphere water molecules with Mn⋯O distances of 5.257 Å. The calculated Mn–O distance (2.215 Å) is in excellent agreement with the experimental values obtained both in the solid state and in solution.44,45
The 1H and 17O values calculated for the [Mn(H2O)6]2+·12H2O system (Table 2) are considerably closer to the experimental values determined by ENDOR spectroscopy,13 as well as to those obtained in this work from NMRD and 17O NMR measurements. This reflects the importance of introducing the most important interactions involving the first and second hydration shells to compute accurate HFCCs in aqueous solution.
ADMP molecular dynamics simulations
Dynamic effects might have an important impact on the 1H, 17O and 55Mn Aiso values, as the HFCCs measured are weighted averages (〈Aiso〉) of individual values for the different configurations present in the sample. Among the different molecular dynamics methods available, we have chosen the atom-centered density matrix propagation (ADMP) approach, which provides O(N) scaling of computational time with system size, N being the number of electrons,50 making it a reasonable choice compared to other computationally more expensive ab initio molecular dynamics methods.ADMP simulations were performed in aqueous solution at the TPSSh/SVP level, and started on the equilibrium geometries of the [Mn(H2O)6]2+ and [Mn(H2O)6]2+·12H2O systems. The overall simulation time was 1 ps. The calculations performed on the [Mn(H2O)6]2+ system resulted in the de-coordination of one of the inner-sphere water molecules during the course of the simulation in the time range 0.4–0.6 ps. The mean residence time of a coordinated water molecule in the [Mn(H2O)6]2+ complex was determined to be ∼4 ns from the analysis of the NMRD and 17O NMR data described above. However, no water exchange events were observed during the simulations performed on the [Mn(H2O)6]2+·12H2O system, which again highlights the importance of treating explicitly the second-sphere solvation shell for an adequate description of the MnII aqua-ion.
The calculations performed on the [Mn(H2O)6]2+·12H2O system (Fig. 4) indicate that the octahedral coordination environment suffers relatively important distortions during the length of the simulations. These distortions affect the individual Mn–O bond distances, which fluctuate between 2.03 and 2.46 Å, and the individual trans O–Mn–O angles of the octahedral coordination polyhedron, which take a value of 180° in the equilibrium geometry and reach values as low as 165.5° during the simulation. The mean distortion of the octahedral coordination polyhedron was assessed by calculating ΔdMn–O and σ defined as:
 | (12) |
 | (13) |
The trajectories obtained from ADMP simulations were used to perform a configurational space sampling by taking 100 snapshots at regular intervals of 10 fs. The 1H, 17O and 55Mn Aiso values were subsequently calculated for each snapshot. The average Aiso values (〈Aiso〉) obtained for the 100 configurations are shown in Table 2. Thus, 〈Aiso〉 were calculated as the average of 100, 600 and 1200 individual Aiso values for 55Mn, 17O and 1H, respectively. Our results indicate that dynamic effects have a negligible effect on the 17O and 55Mn HFCCs (<1.2%), while the mean Aiso value of the lighter 1H nucleus increases by ca. 8% while approaching the experimental value.
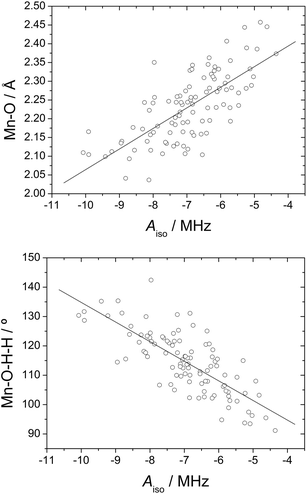
Although the mean Aiso values obtained from ADMP simulations do not differ significantly from those obtained for the equilibrium geometry, the individual 17O and 1H Aiso values for a given water molecule change markedly during the simulation. This allows correlating the calculated HFCCs with geometrical parameters, thereby providing information on the factors that affect the magnitude of the HFCCs. In previous works we have shown that the 17O HFCCs of coordinated water molecules in GdIII and MnII complexes are significantly affected by changes in the M–O bond distances and the orientation of the water molecule plane with respect to the metal–O vector.4,48 Plots of the calculated 17O Aiso values versus the Mn–O distance and the Mn–O–H–H dihedral angle indeed show linear trends (Fig. 5), thereby confirming our previous findings.
The Aiso values obtained from ADMP trajectory calculations were fitted to the following expression:
| Aiso(17O) = a0 + a1(1/rMnO) + a2ϕ | (14) |
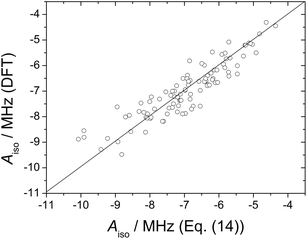 | ||
| Fig. 6 17O isotropic hyperfine coupling constant obtained from DFT calculations on 100 configurations extracted from MD trajectory calculations on the [Mn(H2O)6]2+·12H2O system plotted against those obtained with eqn (14) (R2 = 0.91). | ||
Both the Mn–O distance and the dihedral ϕ angle are expected to change significantly depending upon the MnII coordination environment. For instance, the Mn–Owater distance in different MnII complexes containing inner-sphere water molecules were found to vary in the range 2.19–2.30 Å.9,43g Regarding the tilt angle of the coordinated water molecule, it has been estimated to fall within the range 90–145° for GdIII complexes.52 By constraining the rMnO and ϕ values within these ranges, eqn (14) provides 17O Aiso values in the range −4.8 to −9.2 MHz, which correspond to AO/ħ values of 30–58 × 106 rad s−1. This simple estimate suggests that the 17O HFCCs of coordinated water molecules in MnII complexes may differ significantly depending on the particular structure of the complex.
The 1H HFCCs (Fig. 7) calculated for each of the 100 snapshots extracted from the trajectory calculations correlate reasonably well with the corresponding 17O Aiso values, which indicates that both 1H and 17O HFCCs are affected in a similar way by the Mn–OW distances and Mn–O–H–H dihedral angles. While the 17O Aiso values are negative, 1H Aiso values are positive. However, these different signs correspond to positive spin densities at the point nucleus of both 17O and 1H, due to the different sign of the magnetic moment of these nuclei. This confirms that both the 1H and 17O HFCCs are dominated by the spin delocalization mechanism rather than by spin polarization effects.4
 | ||
| Fig. 7 17O isotropic hyperfine coupling constant plotted as function of the 1H hyperfine coupling constant for 100 configurations extracted from MD trajectories of [Mn(H2O)6]2+·12H2O (R2 = 0.82). | ||
The scalar contribution to 1H relaxivity
As discussed above, the NMRD profiles of [Mn(H2O)6]2+ indicate an important scalar contribution to 1H relaxivity, which is accounted for by eqn (4). However, only one MnII chelate has been reported to date to possess a significant scalar contribution to relaxivity,9 which is generally assumed to be dominated by the dipolar mechanism. To understand the role of the scalar contribution to relaxivity, we have performed simulations in which 1/TSC1 is plotted as a function of the water exchange rate and transverse electron spin relaxation rates (Fig. 8). The longitudinal and transverse electronic relaxation rates, 1/T1e and 1/T2e, are often approximated by using eqn (15) and (16),36 where τv is the electronic correlation time for the modulation of the zero-field-splitting interaction, EV the corresponding activation energy and Δ2 is the mean square zero-field-splitting energy.
 | (15) |
 | (16) |
It has been shown that eqn (15) and (16) provide a rather crude approximation of the electron spin relaxation for GdIII complexes,53 and it is likely that they are neither very accurate for MnII compounds. However, they can still be used to analyze NMRD profiles even at low magnetic fields for small MnII complexes.43
The simulations shown in Fig. 8 were obtained using two different magnetic fields (0.01 and 0.0003 T, corresponding to proton Larmor frequencies of 0.43 and 0.013 MHz, respectively) and eqn (1), (4), (5) and (16). The number of inner-sphere water molecules q was taken as 1.0, as stable MnII-based contrast agents are expected to possess one (or perhaps 2) coordinated water molecules. The 1H hyperfine coupling constant (AH/ħ) was assumed to be equal to the value obtained for [Mn(H2O)6]2+ (5.4 × 106 rad s−1, Table 1). A comparison of the relaxivities calculated at 0.01 and 0.003 T clearly shows that the scalar contribution to relaxivity drops quickly as the magnetic field increases. At low field, the calculated rSC1p values are only significant for particularly slow electron spin relaxation rates (1/T2e < 5 × 108 s−1). A slow electron spin relaxation explains the high scalar contribution to relaxivity observed for [Mn(H2O)6]2+ (the values of τV and Δ2 given in Table 1 give 1/T2e = 3.9 × 108 s−1 with the use of eqn (16)). On the contrary, MnII complexes with poliaminocarboxylate ligands often show much faster electron relaxation (1/T2e = 6 × 109 to 3 × 1010 s−1).3 The slower electronic relaxation of [Mn(H2O)6]2+ in comparison with the MnII complexes investigated so far as potential MRI contrast agents is in line with the hyperfine splitting observed in the EPR spectrum of the aqua-ion,42 which is however not observed for chelates as a result of line-broadening.3 Concerning the effect of water exchange rate, at low field it is clear that the scalar contribution to relaxivity is only significant for small kex values (kex298 < 12 × 108 s−1). Since the water exchange rates determined for MnII chelates are faster than that of the fully aquated species, it is not surprising that MnII complexes lack a significant scalar contribution to relaxivity in most cases. We also notice that the water exchange rate determined for [Mn2(ENOTA)(H2O)] (5.5 × 107 s−1), which presents a sizable scalar contribution, is very close to that of the aqua ion. Increasing the magnetic field results in a broader distribution of kex298 and 1/T2e values that give non-negligible scalar contributions (the observed relaxivity for small MnII complexes at ca. 0.01 T is around 4–5 mM−1 s−1 at 298 K). At this magnetic field the scalar contribution is also favoured by slow electron spin relaxation times and water exchange rates of ca. kex298 = 15 × 108 s−1.
Conclusions
We have performed a 1H and 17O NMR relaxometric study of the [Mn(H2O)6]2+ complex as well as a theoretical analysis of the 1H and 17O HFCCs of the coordinated water molecules in this system. Our DFT calculations show that the explicit inclusion of a second solvation shell is critical to obtain accurate HFCCs. Molecular dynamics simulations show that the 1H and 17O HFCCs on inner-sphere water molecules are very sensitive to the Mn–O distances and the orientation of the coordinated water molecule plane with respect to the Mn–O vector. However, the average HFCCs obtained from up to 100 snapshots extracted from trajectory calculations do not differ significantly from the corresponding Aiso values obtained for the equilibrium geometries, and remain reasonably close to the experimental ones. The important scalar contribution to proton relaxivity in [Mn(H2O)6]2+ is related to a slow electron spin relaxation and a rather slow water exchange rate of the inner-sphere water molecules.Acknowledgements
D. E.-G. thanks Xunta de Galicia (EM2012/088) for generous financial support. C. P.-I. thanks Centro de Supercomputación de Galicia (CESGA) for providing the computer facilities. M. B. thanks the support by the Compagnia di San Paolo (Bando Ateneo-CSP 2012; Project: NANOPROGLY).Notes and references
- I. Bertini and C. Luchinat, Coord. Chem. Rev., 1996, 150, 77 CrossRef.
- F. Rastrelli and A. Bagno, Chem. – Eur. J., 2009, 15, 7990 CrossRef CAS PubMed.
- G. A. Rolla, C. Platas-Iglesias, M. Botta, L. Tei and L. Helm, Inorg. Chem., 2013, 52, 3268 CrossRef CAS PubMed.
- V. Patinec, G. A. Rolla, M. Botta, R. Tripier, D. Esteban-Gómez and C. Platas-Iglesias, Inorg. Chem., 2013, 52, 11173 CrossRef CAS PubMed.
- (a) S. Aime, P. L. Anelli, M. Botta, M. Brochetta, S. Canton, F. Fedeli, E. Gianolio and E. Terreno, J. Biol. Inorg. Chem., 2002, 7, 58 CrossRef CAS PubMed; (b) G. A. Rolla, L. Tei, M. Fekete, F. Arena, E. Gianolio and M. Botta, Bioorg. Med. Chem., 2011, 19, 1115 CrossRef CAS PubMed; (c) L. Tei, G. Gugliotta, M. Fekete, F. K. Kalman and M. Botta, Dalton Trans., 2011, 40, 2025 RSC.
- The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, ed. A. E. Merbach, L. Helm and É. Tóth, Wiley, New York, 2nd edn, 2013 Search PubMed.
- B. Drahos, I. Lukes and E. Toth, Eur. J. Inorg. Chem., 2012, 1975 CrossRef CAS.
- D. H. Powell, O. M. Ni Dhubhghaill, D. Pubanz, L. Helm, Y. S. Lebedev, W. Schlaepfer and A. E. Merbach, J. Am. Chem. Soc., 1996, 118, 9333 CrossRef CAS.
- E. Balogh, Z. He, W. Hsieh, S. Liu and E. Toth, Inorg. Chem., 2007, 46, 238 CrossRef CAS PubMed.
- I. Bertini, F. Briganti, Z. Xia and C. Luchinat, J. Magn. Reson., 1993, 101, 198 CAS.
- O. Schiemann, J. Frischer, N. Kisseleva, S. T. Sigurdsson and T. F. Prisner, ChemBioChem, 2003, 4, 1057 CrossRef CAS PubMed.
- (a) J. Schraut, A. V. Arbuznikov, S. Schinzel and M. Kaupp, ChemPhysChem, 2011, 12, 3170 CrossRef CAS PubMed; (b) N. Cox, W. Ames, B. Epel, L. V. Kulik, L. Rapatskiy, F. Neese, J. Messinger, K. Wieghardt and W. Lubitz, Inorg. Chem., 2011, 50, 8238 CrossRef CAS PubMed.
- D. Baute and D. Goldfarb, J. Phys. Chem. A, 2005, 109, 7865 CrossRef CAS PubMed.
- S. Schinzel, R. Müller and M. Kaupp, Theor. Chem. Acc., 2008, 120, 437 CrossRef CAS PubMed.
- S. Kossmann, B. Kirchner and F. Neese, Mol. Phys., 2007, 105, 2049 CrossRef CAS.
- Y. Ducommun, K. E. Newman and A. E. Merbach, Inorg. Chem., 1980, 19, 3696 CrossRef CAS.
- D. M. Corsi, C. Platas-Iglesias, H. van Bekkum and J. A. Peters, Magn. Reson. Chem., 2001, 39, 723 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef CAS PubMed.
- A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef CAS PubMed.
- J. F. Stanton and J. Gauss, Adv. Chem. Phys., 2003, 125, 101 CAS.
- A. Montoya, T. N. Truong and A. F. Sarofim, J. Phys. Chem. A, 2000, 124, 6108 CrossRef.
- (a) S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291 CrossRef CAS PubMed; (b) H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, G. E. Scuseria, A. D. Daniels and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758 CrossRef CAS PubMed; (c) H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694 CrossRef CAS PubMed.
- N. Rega, M. Cossi and V. Barone, J. Chem. Phys., 1996, 105, 11060 CrossRef CAS PubMed.
- E. D. Hedegard, J. Kongsted and S. P. A. Sauer, J. Chem. Theory Comput., 2011, 7, 4077 CrossRef.
- J. C. Slater, The Self-Consistent Field for Molecular and Solids, Quantum Theory of Molecular and Solids, McGraw-Hill, New York, 1974, vol. 4 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- Z. Luz and S. Meiboom, J. Chem. Phys., 1964, 40, 2686 CrossRef CAS PubMed.
- (a) I. Solomon, Phys. Rev., 1955, 99, 559 CrossRef CAS; (b) I. Solomon and N. Bloembergen, J. Chem. Phys., 1956, 25, 261 CrossRef CAS PubMed; (c) N. Bloembergen, J. Chem. Phys., 1957, 27, 572 CrossRef CAS PubMed; (d) N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842 CrossRef CAS PubMed.
- J. H. Freed, J. Chem. Phys., 1978, 68, 4034 CrossRef CAS PubMed.
- (a) T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307 CrossRef CAS PubMed; (b) T. J. Swift and R. E. Connick, J. Chem. Phys., 1964, 41, 2553 CrossRef CAS PubMed.
- J. Maigut, R. Meier, A. Zahl and R. van Eldik, J. Am. Chem. Soc., 2008, 130, 14556 CrossRef CAS PubMed.
- J. Maigut, R. Meier, A. Zahl and R. van Eldik, Inorg. Chem., 2007, 47, 5702 CrossRef PubMed.
- R. Mills, J. Phys. Chem., 1973, 77, 685 CrossRef CAS.
- A. W. Nolle and L. O. Morgan, J. Chem. Phys., 1962, 36, 378 CrossRef CAS PubMed.
- (a) S. Aime, P. L. Anelli, M. Botta, M. Brochetta, S. Canton, F. Fedeli, E. Gianolio and E. Terreno, J. Biol. Inorg. Chem., 2002, 7, 58 CrossRef CAS PubMed; (b) A. G. Rolla, L. Tei, M. Fekete, F. Arena, E. Gianolio and M. Botta, Bioorg. Med. Chem., 2011, 19, 1115 CrossRef PubMed; (c) B. Drahos, J. Kotek, I. Cisarova, P. Hermann, L. Helm, I. Lukes and E. Toth, Inorg. Chem., 2011, 50, 12785 CrossRef CAS PubMed; (d) B. Drahos, M. Pniok, J. Havlickova, J. Kotek, I. Cisarova, P. Hermann, I. Lukes and E. Toth, Dalton Trans., 2011, 40, 10131 RSC; (e) A. de Sa, C. S. Bonnet, C. F. G. C. Geraldes, E. Toth, P. M. T. Ferreira and J. P. Andre, Dalton Trans., 2013, 43, 4522 RSC; (f) L. Tei, G. Gugliotta, M. Fekete, F. K. Kalman and M. Botta, Dalton Trans., 2011, 40, 2025 RSC; (g) B. Drahos, J. Kotek, P. Hermann, I. Lukes and E. Toth, Inorg. Chem., 2010, 49, 3224 CrossRef CAS PubMed.
- F. A. Cotton, L. M. Daniels, C. A. Murillo and J. F. Quesada, Inorg. Chem., 1993, 32, 4861 CrossRef CAS.
- Y. Chen, J. L. Fulton and W. Partenheimer, J. Am. Chem. Soc., 2005, 127, 14085 CrossRef CAS PubMed.
- (a) H. A. de Abreu, L. Guimaraes and H. A. Duarte, Int. J. Quantum Chem., 2008, 108, 2467 CrossRef; (b) F. P. Rotzinger, J. Phys. Chem. B, 2005, 109, 1510 CrossRef CAS PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526 CrossRef CAS PubMed.
- D. Esteban-Gomez, A. de Blas, T. Rodriguez-Blas, L. Helm and C. Platas-Iglesias, ChemPhysChem, 2012, 13, 3640 CrossRef CAS PubMed.
- (a) G. D. Markham, J. P. Glusker and C. W. Bock, J. Phys. Chem. B, 2002, 106, 5118 CrossRef CAS; (b) W. W. Rudolph and C. C. Pye, J. Phys. Chem. A, 2000, 104, 1627 CrossRef CAS; (c) J. Li, C. L. Fisher, J. L. Chen, D. Bashford and L. Noodleman, Inorg. Chem., 1996, 35, 4694 CrossRef CAS; (d) C. C. Pye and W. W. Rudolph, J. Phys. Chem. A, 1998, 102, 9933 CrossRef CAS; (e) C. W. Bock, G. D. Markham, A. K. Katz and J. P. Glusker, Theor. Chem. Acc., 2006, 115, 100 CrossRef CAS PubMed; (f) M. Pavlov, P. E. M. Siegbahn and M. Sandstrom, J. Phys. Chem. A, 1998, 102, 219 CrossRef CAS.
- S. S. Iyengar, H. B. Schlegel and G. A. Voth, J. Phys. Chem. A, 2003, 107, 7269 CrossRef CAS.
- G. W. Neilson, J. R. Newsome and M. Sandström, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1245 RSC.
- A. M. Raitsimring, A. V. Astashkin, D. Baute, D. Goldfarb and P. Caravan, J. Phys. Chem. A, 2004, 108, 7318 CrossRef CAS.
- (a) A. Borel, S. Laus, A. Ozarowski, C. Gateau, A. Nonat, M. Mazzanti and L. Helm, J. Phys. Chem. A, 2007, 111, 5399 CrossRef CAS PubMed; (b) P. H. Fries, C. Gateau and M. Mazzanti, J. Am. Chem. Soc., 2005, 127, 15801 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Inner-sphere and outer-sphere contributions to relaxivity and optimized Cartesian coordinates obtained with DFT calculations. See DOI: 10.1039/c3ra45721d |
| This journal is © The Royal Society of Chemistry 2014 |