Tailoring strained oxanorbornane headgroups to dimensionally controlled nanostructures through hydrogen bonding

Abstract

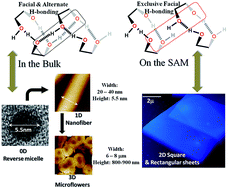
An amphiphilic oxanorbornane skeletal frame has been efficiently organized to direct the formation of dimensionally controllable, geometry-specific nanostructures as diverse as 0-D surface/reverse micelles, 1-D nanofibers, 2-D rectangular/square sheets, and 3-D flowers. The racemate with its precise stereo-projection of the –OH groups and the ring oxygen could be used for Li⁺ ion sensing and aided in the formation of pre-micellar aggregates of conventional surfactants.

---

1. Introduction

Self-assembly schemes are often inspired by the wealth of biological examples present in nature.¹ To exactly mimic the in vitro reassembly (of proteins and lipids) to that of the in vivo counterparts, a thermodynamic equilibrium defined by external conditions such as ionic strength, temperature and pH² is mandatory. During the mimicking process, the kinetics involved in the self assembly processes might typically be very slow or very fast depending on the growth phase, making it difficult to observe the processes under equilibrium. As a result, deciphering the molecular and supramolecular pathways towards complex self-assembly is exceedingly complicated and they have rarely been elucidated by the observation of stable intermediates. Enticed by this challenge, an oxanorbornane based sugar-like amphiphilic scaffold is designed that has a furanose ring and is endowed with multiple hydroxyl groups. These sugars are thermo-dynamically disfavoured compared to pyranose sugars.³ Bacterial polysaccharides and glycoconjugates contain saccharides in the furanose conformation and moreover, furanose sugars are an essential part of extremophiles which live in harsh environments and can endure high salinity, high temperatures and organic solvents. In this context, self assembly of polyhydroxyoxanorbornanes is explored at the air/water interface and in the bulk leading to complex architectures with experimental access to each metastable state simulating the above environments.

2. Experimental

Synthesis of the target molecules started with the cycloaddition of O-benzyl protected furfuryl alcohol with maleic anhydride. Using this method we were able to prepare a compound with one head group and two lipophilic chains as shown in Scheme 1 (ESI†). To achieve this, the anhydride (±)-3 was first reduced using lithium aluminium hydride to obtain the diol (±)-4 and then this was acylated with palmitoyl chloride. Treatment of the resulting diesters (±)-5 with OsO₄ led to the formation of the cis-dihydroxylated product (±)-6, which upon hydrogenolysis in the presence of H₂–Pd/C afforded the amphiphile (±)-7 in a 71% yield.

Monolayer isotherm measurements

The amphiphile monolayers were spread on the surface of ultrapure water (Millipore-Academic) of resistivity 18.2 MΩ cm, from chloroform (Uvasol, Merck India) solutions. The pH of the subphase was altered by adding hydrochloric acid (for acidic pH) or NaOH (for basic pH). Soluble metal chlorides (1 mM) were used for creating saline conditions. Subsequently, surface pressure–area isotherms were obtained using a computer controlled double barrier Langmuir trough, KSV 5000 (Finland) after a thorough clean with alternating rounds of HPLC grade chloroform and methanol (spectroscopic grade, SRL fine chemicals). For isotherm measurements, 100 μL of 1 mM 1a solution was spread using a Hamilton syringe and the surface pressure was measured by the Wilhelmy plate method with a platinum sensor of 0.1 mN m⁻¹ accuracy. After an equilibration period of 20 min with solvent evaporation, isotherms were acquired from the compressed Langmuir films at an optimal speed of 5 mm min⁻¹. Then, Langmuir–Blodgett films on hydrophilized Si(100) substrates were prepared by transferring the monolayers at a desired surface pressure using the vertical dipping method. Hydrophilization was carried out by etching the substrates with hot piranha solution (3 : 1 conc. H₂SO₄–H₂O₂) at 70 °C, followed by rinsing with Millipore water.

Infrared reflection–absorption spectroscopy

Real-time spectral measurements were performed on a Bruker Optic GmbH (Germany) Vertex 70 spectrometer equipped with a mercury cadmium telluride (MCT) detector (spectral resolution 0.1 cm⁻¹), and a home-built optical attachment placed on a vibration isolated Newport I-2000 table (Fountain Valley, CA). The spectrometer was equipped with an external variable-angle reflectance accessory XA 511 coupled to a custom designed Langmuir trough (R & K, Germany). The IR beam was focused onto the water surface with an off-axis parabolic mirror with a focal length of 120 mm, and the desired angle of incidence was obtained when the computer driven stepper motors rotated the mirrors. The angle of incidence was varied between 25 and 65° from the surface normal, the latter being the maximum grazing incidence obtainable. Alternate s- and p-polarized spectra were acquired with a resolution of 4 cm⁻¹ by co-addition of 2048 (for s-polarization) and 4096 (for p-polarization) scans. The entire experimental setup was enclosed and purged with dry N₂ gas. The spectra resulting from this experimental setup were reflectance–absorbance (RA) spectra, where RA = −log(R/R₀), with R being the IR reflectivity of the surface of interest and R₀ being the IR reflectivity of the surface background.

Atomic force microscopy

Sensors fabricated from the layer-by-layer LB transferred films as well as from the solvent-cast films were analyzed with an atomic force microscope (XE-100, Park Systems, Korea) in noncontact and contact modes. The cantilevers (SHOCONA-SS and ACTA, AppNano) were fitted with monolithic, single crystal silicon tips with radii of curvatures <5 nm. Probes used in noncontact mode imaging had a 300 kHz resonance frequency with a spring constant 42 mN m⁻¹. Images were analyzed using XEI image analysis software. To compensate sample tilt, all of the images were subjected to first order plane fitting.

Fabrication of 1a/SAM modified Au electrodes

Gold electrodes (2 mm in diameter) were polished with 0.3 μm alpha alumina powder & 0.05 μm gamma alumina powder on a felt pad for at least 15 min, then rinsed several times with ethanol and water, and finally sonicated in triple-distilled water and absolute alcohol for 10 min, successively. The polished electrodes were further immersed in a 0.5 M H₂SO₄ solution and cleansed electrochemically by applying consecutive cycles of negative potential between −0.4 V and −1.2 V until the obtained voltammograms no longer changed and a characteristic voltammogram of a clean Au electrode was obtained. The clean electrodes were then immersed in ethanol solution containing 2.0 mM C₁₂H₂₅SH for a period of time ranging from 30 min to 5 h at room temperature to form the SAM (self-assembled monolayer) on the surface. The SAM modified Au electrodes were then thoroughly rinsed with ethanol and dried under a stream of N₂. The electrodes were finally soaked in a 1 mM 1a solution in CH₃OH–CHCl₃ mixture (4 : 1) and stored in triple-distilled water.

Electrochemical measurements

A CHI 660B Electrochemical Workstation (CH Instruments, US) was used for all of the electrochemical measurements. A conventional three-electrode setup was employed, with the chemically modified gold electrode as the working electrode, a platinum-wire counter electrode, and a Ag/AgCl electrode as the reference electrode. All of the solutions were prepared in Tris buffer (pH 7.4) with a 1 mM Fe(CN)₆⁴⁻/³⁻ internal standard in 0.1 M KCl electrolyte. Electrochemical impedance measurements for the fabricated sensors were performed using the CHI 660B Electrochemical Workstation with E° = 240 mV. Impedance measurements were performed in a 0.1 M KCl solution containing equal concentrations of oxidized and reduced forms of the Fe(CN)₆ ^3−/4− redox couple. The frequency range used was 100 kHz to 0.01 Hz with an ac amplitude of 5 mV.

Computational methods

Geometry optimization of the individual molecules of interest and the association complexes was done using density functional calculations at the B3LYP/6-31+G(d,p) and B3LYP/6-31G(d) levels of theory respectively, as included in the Gaussian 09 set of programs. All of the optimizations for dimers were carried out with tight convergence criteria without any symmetry constraints. Geometry optimization was followed by frequency calculations for all models to calculate the harmonic vibration modes of the molecule and also to assure the global minimum of the stationary points. To probe the dynamics of lithium ion sensing, we employed an ab initio molecular dynamics (AIMD) approach with Atom-centered Density Matrix Propagation (ADMP) as included in the Gaussian 09 set of programs. The dynamics have been performed at the B3LYP/6-31G(d) level with a minimum trajectory of 300 fs with converged SCF (self-consistent field) results at each point. The fictitious electron mass (EMass) was set to the default 0.1 amu, and the temperature was set to 298 K, similar to the temperature used to acquire IRRAS data, in order to extract the dynamical behavior of the clusters. A velocity scaling thermostat was used to maintain the temperature during the 300 fs equilibration run. The time step employed in each simulation was 0.25 fs. As no thermal and zero-point corrections were applied towards tracing the trajectory, all discussions have been limited to relative self-consistent field energies.

Surface tension measurements

The critical micellar concentration (CMC) of 1b was determined from surface tension measurements using the Wilhelmy method (KSV, Finland) with a platinum plate sensor. The temperature was controlled with a Julabo thermo controller with an accuracy of ±0.5 °C. Surface tension measurements were done at equilibrium at the set temperature until concordance was obtained from three consecutive measurements for each concentration. For binary surfactant systems involving 1b, data were acquired by adding a solution of 1b dissolved in HFIP (hexafluoro-2-propanol) to water and subsequently stirring and purging with dry nitrogen gas to remove the HFIP.

3. Results and discussion

The designed amphiphiles and 2-D molecular organization

Twin-tailed amphiphiles 1a and 1b (Fig. 1a) were designed for the current study, and 1c and 1d (Fig. 1a) were used as controls; their synthetic details are given in Scheme 1 of ESI.† The skeletal framework of these molecules is a highly strained system⁴ (bridgehead bond angle, 96.58°; Fig. 1b and S1†), which has in fact previously provided means to determine the distance dependence of intramolecular charge transfer.⁵ In addition to the usual torsional strain arising due to repulsion between the bond pair of electrons (repulsion due to the eclipsed conformation of the C5–O3 bond with respect to C6–O2), the bridging of carbons C1 and C4 of the boat involved in the construction of the oxanorbornane skeletal framework introduces appreciable angle strain. The strain is physically reflected as a high heat of combustion. The single-crystal X-ray diffraction derived geometrical parameters of a benzyl protected oxanorbornane⁶ skeletal frame are given in Fig. 1b. Until and unless H-bonded functionality is embedded into the oxanorbornane skeleton, disordered crystals are expected. In this context, the air/water interface which restricts the facial and dual/alternate H-bonded interactions between the secondary hydroxyl groups (Fig. 1c), provides an excellent platform to study the disordered packing of these strained systems. 1a (1 mM in CHCl₃) spread at the air/water interface shows an apparent molecular area of 58 Ų per molecule (at pH 6.4) with a collapse pressure of 56 mN m⁻¹ confirming the ability of this molecule to form stable monolayers (Fig. 2b). The stability of a monolayer at the air/water (A/W) interface is often inferred from its collapse surface pressure (Table 1). In Langmuir isotherms it is indicated as the point at which the surface pressure plateaus sharply. It can be seen in Fig. 2a–c that metal ion variation in the subphase did not affect the collapse surface pressures whereas basic pH and low temperatures gave rise to high collapse surface pressures indicating the high stability of monolayers under the respective environmental conditions. A molecular area of 58 Ų is in good agreement with the size of 1a in the cylindrical conformation (Fig. 2g). In the condensed phase, films transferred at 40 mN m⁻¹ showed discontinuous 0-D-surface micelles of sizes in the range 20–50 nm when visualized with HR-TEM (Fig. 2d). The surface micellar orderliness is confirmed by the presence of a diffraction pattern when an electron beam is encountered (Fig. S2†). Real-time Infrared Reflection-Absorption spectral (IRRAS) monitoring (Fig. 2e) of the ν_a(CH₂) stretching confirms an all-trans conformation of the hydrophobic alkyl chains where surface micelles are observed (Fig. 2f). This rules out gauche-confirmation directed disorderliness in the surface micelles and in turn strongly supports the origin of the crystallinity in surface micelles of 1a to be solely induced by alkyl chains and not by the strained oxanorbornane rings. Earlier reports focused on surface micelles made from strongly polar surfactants⁷ and a semi-fluorinated non-polar alkane,⁸ C₈F₁₇C₁₆H₃₃. The feasibility of depositing them over a wide area opens avenues in the applications of surface decoration/template technologies. Both acidic and basic pH subphases (pH 4.0 & pH 11.0) were found to have an expanding effect with high lift-off surface areas (Fig. 2b), whereas low temperatures (Fig. 2c) and metal ion doped subphases (Fig. 2a) have a condensing effect on the monolayers, with Li⁺ affecting them the most. The mean molecular areas at the condensed phases and collapse surface pressures are given for all of the simulated environments in Table 1.

Fig. 1 (a) The molecular structures studied. (b) DFT computed oxanorbornane unit with ring strain angle C1–O1–C4 = 96.58° and total dipole moment μ = 2.3114 D. Molecular coordinates were taken from single-crystal XRD data. (c) Schematic illustration of zig-zag type facial, dual and alternate H-bonding in 1a along with the computed electron density difference (EDD) map confirming the involvement of electron transfer during H-bond formation. Red and blue isosurfaces represent the region in which electron density is increased and decreased respectively after 1a is bound to itself as a dimer. When denoting the hydrogen bonding types, only secondary hydroxyl groups were considered for clarity of presentation.

Fig. 2 (a–c) π–A isotherms of 1a (1 mM in CHCl₃) subjected to saline conditions, and various pH and temperatures, respectively. Arrows indicate the points of collapse surface pressures π_collapse. (d) High resolution-transmission electron microscopy image of the 0-D surface micelles from condensed phase 1a. (e) Surface pressure induced fine structure variations in the p-polarized in situ FT-IRRAS spectra in the –CH₂ stretching vibration region. (f) ν_a(CH₂) frequencies implying enhanced molecular order in the condensed phase (π = 40 mN m⁻¹) of 1a and (g) illustrates the molecular area footprint of the oxanorbornane spherical head complying with the experiment.

Table 1 Mean molecular condensed phase areas and collapse surface pressures from the π–A isotherms

Subphase conditions	Molecular area (Å^2) (condensed phase)	Collapse surface pressure πcollapse (mN m^−1)
a pH.b Temperature of the subphase.
Li^+	51.5	59.3
Ca^+2	57.3	58.3
Zn^+2	56.7	59.4
4.0^a	64.5	54.5
6.4^a	58	56.0
11.0^a	71.5	63.5
10^b	51	59.7
15^b	55	58.7
20^b	57	57

---

3-D molecular organization directed via diverse H-bonding

To test the H-bond effects on the packing efficiency of oxanorbornane skeletons, 2-D restrictions at the air/water interface (A/W) were lifted by allowing the molecule to organize in bulk CHCl₃. Freshly prepared 1a solutions (0.5 mM to 1 mM) gave rise to reverse micelles of 5.5 nm in size and were observed using HR-TEM (Fig. 3a). Time-lapsed mechanistic studies, by incubating pirahna treated Si(100) wafers in CHCl₃ solution, showed directionally elongated nucleation centers comprising 1-D nanofibers (Fig. 3b and d) with a thickness of 5.5 nm (Fig. 3e and A3†) after a day, which subsequently evolved into a 3-D micro-flower geometry analogous to Ostwald ripening. In a binary system of solid solutions or liquid sols, Ostwald ripening is a thermodynamically driven spontaneous process involving growth of larger particles at the expense of smaller ones. For 1a, the large surface area of the 0-D reverse micelles along with the driven facial, dual and alternate H-bonds favor 1-D nanofibers at the expense of reverse micelles. The subsequent transformation of the 1-D nanofibers to 3-D microflowers involves only vertical directional growth. From the force microscopic images it can be observed that the diameter of a 3-D microflower equals the length of a single precursor nanofiber. Ostwald ripening is reported in amphiphilic azobenzene based π-systems where 0-D nanodot transformation to pseudo 1-D nanorods occurred under UV light, inducing the essential requirement of a binary system in the form of cis–trans isomers.⁹ At the solid/liquid interface, Ostwald ripening is reported in two-dimensional crystals of oligothiophenes.¹⁰ The kinetically stable 1-D nanofibers transforming into thermodynamically favoured 3-D microflowers (Fig. 3b and f) involves minimization of the surface free energy of the system within a given volume. In striking contrast, when the two secondary OH groups are chemically protected (ketal, Fig. S3a†) preventing alternative zigzag H-bonds, 1-D nanofibers could not be observed in CHCl₃, suggesting that their assembly involves the strained oxanorbornane skeleton and is H-bond driven. Deprotecting the secondary hydroxyl groups and protecting the primary hydroxyl with a benzyl moiety (Fig. S3b†) gave rise to a structural hierarchy similar to 1a in CHCl₃ (Fig. S4†). This confirms that 1-D nanofiber formation is dictated by the two secondary hydroxyl groups only.

Fig. 3 (a) HR-TEM image of the 0-D reverse micelles of 1a (1 mM) formed in CHCl₃. (b) & (d) NC-AFM images of the 1-D nanofibers of 1a on a Si(100) substrate. (c) & (f) AFM and optical microscopy images of the 3-D microflowers of 1a on Si(100) substrates. (e) Molecular model of ‘bottom-up’ hierarchical assembly in the transformation of anisotropic 1-D nanofibers to 3-D isotropic microflowers.

The alternative zigzag H-bond network (Fig. 4a) was further disrupted by embedding¹¹ 1a into dodecanethiol SAM on the Au(111) surface (Fig. 4b) via hydrophobic interactions (Fig. S5†). Interdigitated bilayers of ∼2.8 nm thickness (Fig. 4c) thus formed in the binary solutions of CHCl₃ and CH₃OH (1 : 4, v/v) as a result of constricting the translational degrees of freedom of the alkyl chains, anticipated to act as templates for 1a. The bilayer deposited Au electrodes when incubated in 1 mM 1a (1 : 1 v/v CHCl₃–CH₃OH) revealed a discrete collection of square nano-sheets with almost similar average lengths and widths irrespective of incubation times. A typical square nano-sheet embedded with a 2-D rectangular sheet could be imaged through non-contact mode AFM, as shown in Fig. 4d. The latter are expected to be precursors to the square nano-sheets, evident from their estimated thicknesses in the line profiles (Fig. S6†) in which the head groups are linked together via H-bonds (Fig. 4e). The two facial hydroxyl groups of embedded 1a enables the freely dispersed 1a to bind through its hydroxyl groups and this growth process propagates along the direction of the H-bond leading to a 3-D network of single-crystalline grains in which several bilayers stack on top of themselves via H-bonds. Fig. 4e dictates the most judicious mechanistic route for sheet formation, where the oxanorbornane heads behave exclusively as single proton donors and acceptors. Additionally, experiments carried out on ITO substrates yielded similar square nano-sheets (Fig. S7†). The shape and sharp edges suggest these sheets to be single-crystalline nano-sheets. Single-crystalline square nano-sheets were earlier reported for porphyrins by adopting a re-precipitation method.¹² Fei Wang et al. reported rectangular 2-D nano-architectures of zinc hydroxydodecylsulfate which were single-crystalline and a product of solution-based synthesis.¹³ The possibility of using SAM surfaces to stabilize thermodynamically metastable structures offers a powerful tool in the development of oriented crystals using bottom-up approach processes.

Fig. 4 (a) H-bonding modes of the frontal secondary hydroxyls in the bulk of CHCl₃ and at the SAM surface where alternate H-bonding is curbed. For clarity, the full oxanorbornane head is not drawn. (b) Graphical illustration of a 1a/SAM modified Au electrode. (c) NC-AFM image of a 1a/SAM/Au surface. Line profile confirms the 1a/SAM vertical projection height to be ∼2.8 nm. (d) Exclusive formation of anisotropic, self-templated 1a nano-sheets (square & rectangular) on a 1a/SAM/Au electrode while restricting alternative H-bonding. (e) H-bonding and growth modes leading to nano-sheets on the SAM surface. (f) Complex impedance plots for a bare gold electrode, (a); SAM/Au electrode, (b); 1a/SAM/Au electrode, (c) in 0.01 M Tris buffer (pH 7.4) containing 1 mM Fe(CN)₆⁴⁻/³⁻ as an internal standard containing 0.1 M KCl as a supporting electrolyte. (g) Impedance response of Fe(CN)₆⁴⁻/³⁻ (0.01 M Tris buffer, pH 7.4; 0.1 M KCl as a supporting electrolyte) at the 1a/SAM/Au electrode in the presence of increasing Li⁺ ion concentration (0.5 mM, (a); 2 mM, (b); 4 mM, (c); 6 mM, (d); 8 mM, (e)).

Li⁺ ion sensing with organized norbornanes – (a) an electrochemical perspective

In view of Li⁺ ions’ superior ability to condense 1a monolayers, over Ca²⁺ and Zn²⁺ ions (Fig. 2a), Li⁺ sensing using embedded 1a was undertaken electrochemically through impedance spectroscopy in the presence of a Fe(CN)₆^4−/3− redox probe. Lithium salts have been extensively used for treating neurological and nervous disorders.¹⁴ In lithium therapy, the slow penetration of lithium ions through the blood brain barrier and other biomembranes owing to its strong hydration, poses a problem. To cater to medical needs, research is mainly focused on increasing the lipophilicity and transport selectivity of the lithium ion carrier in case a competitive interference exists in the form of other alkali metal ions, such as sodium and potassium. Further, sensing lithium in aqueous media using hydroxyl group containing sensors is also difficult as water poses as a potential and competitive binder. Fast electrode reactions at the bare Au surface gave rise to the linear part of the Warburg impedance in Fig. 4f, while SAM/Au and 1a/SAM/Au modified electrodes exhibited blocking (Fig. S8†) of the electron transfer to the redox probe with high R_ct (charge transfer resistance) values of 292 kΩ and 275 kΩ respectively ((b) and (c) in Fig. 4f). Sensitive to the binding characteristics, increasing the concentration of Li⁺ led to a decrease in R_ct from 241 kΩ at 0.5 mM to 90 kΩ at 8 mM Li⁺ concentration (Fig. 4g). Increasingly positive 1a/SAM/Au surfaces, due to Li⁺ binding, increased local concentrations of the negatively charged redox probe, where electrostatic attractions facilitated electron transfer to/from Fe(CN)₆^4−/3− which caused an increase in the current in the CV profiles (Fig. S9†). The same 1a/SAM/Au electrode responded weakly to Ca²⁺ and Zn²⁺ ions (Fig. S10†).

Li⁺ ion sensing with organized norbornanes – (b) a molecular dynamics perspective

An ideal platform for an interfacial 2 : 1 complex with Li⁺ ions (Fig. 5a) was thus created as a strong function of (i) the racemic nature of 1a coupled with precise stereo-projection of the –OH groups and the ring oxygen and (ii) the low dielectric constant¹⁵ of the bilayer 1a/SAM/Au phase. Li⁺ ionophores reported prior to the current work necessitated pre-requisites of high rigidity and structural pre-organization for binding without any conformational change.¹⁶ Accommodating Li⁺ ions introduced extra strain through deformation of the already strained oxanorbornane frame and as a consequence 1a had to adopt a less-than-stable conformation. This deformation energy (Table 2) was calculated to be positive and higher for the bidentate complex (12.96 kcal mol⁻¹) than for the tridentate one (11.83 kcal mol⁻¹). The binding of Li⁺ to 1a is dominated by stabilization interactions mainly arising due to the electrostatic attraction between the ligand and the metal ions. The extent to which these stabilization interactions outweigh the unfavourable interactions due to the deformation energy depends on the number of atoms participating in the complex formation. For the bidentate complex, the ratio of E_{stabilization}/E_deformation is much lower (6.615) when compared to the tridentate complex (7.32). DFT calculations further indicate that the tridentate complex has a higher stabilization energy and lower deformation energy suggesting a higher probability of its formation compared to the bidentate complex, and involves the Li⁺ interacting with three oxygen atoms (two facial and one ring) simultaneously. Interestingly, ab initio molecular dynamics calculations using Atom-centered Density Matrix Propagation¹⁷ (ADMP) indicated time evolutionary transformation (Fig. 5b, c and e and S11†) of the bidentate complex to a tridentate complex, where new O–Li⁺ bond formation occurs at the crucial ethereal bridged oxygen (Fig. 5b). The distances are well under 2.0–2.5 Å, which is similar to natural carbohydrate–Ca²⁺ complexes.¹⁸

Fig. 5 (a) Proposed model of Li⁺ binding with 1a. (b) Ab initio molecular dynamics (AIMD) transformation of the bidentate complex at 0 fs to the tridentate complex at 300 fs. The potential energy values at the respective time intervals are given. (c) O–Li distance evolution trajectories with time, calculated using ADMP-MD at the B3lYP/6-31G(d) level of theory. (d) ADMP potential energy evolution with time for the “1a–lithium” tridentate complex calculated at the B3LYP/6-31G(d) level of theory. (e) The bidentate complex at 0 fs converts into a tridentate complex at 300 fs.

Table 2 Estimated enthalpy of binding, deformation, and stabilization energies for 1a–Li⁺ complexes from density functional calculations performed at the B3LYP/6-31+G(d,p) level of theory

1a–Li^+ complex	ΔHbinding^a (kcal mol^−1)	Edeformation^b (kcal mol^−1)	Estabilization^c (kcal mol^−1)
a Enthalpy of binding, ΔH is defined as: (E^+Li + E1a) − (E^+Li–1a) + (ZPE1a − ZPEE^+Li–1a). The total electronic energy, E is calculated at the B3LYP/6-31+G(d,p) level of theory and ZPE, the zero point energy is calculated at the HF/6-31+G(d,p) level. The vibrational frequencies were scaled by a factor of 0.8929.b Deformation energy is defined as the energy difference between 1a in its complexed form compared to 1a adopting the most stable conformation in its uncomplexed form.c Stabilization energy is defined as the summation of the enthalpy of binding and deformation energy.
Bidentate complex	72.7973	12.9639	85.7612
Tridentate complex	74.5312	11.8346	86.6693

---

We next turned our attention to 1b (Fig. 1a) which can interact with CTAB (cetyltrimethylammonium bromide) and SDS (sodium dodecyl sulfate) in the aqueous phase through C–H⋯O and H-bond interactions, respectively. Prior to this, control experiments executed with pure CTAB and SDS (Fig. S12†) in separate sets under varying conditions of salinity gave critical micellar concentrations that agreed well with previously published results.¹⁹ The so-called “synergetic effect”,²⁰ identified by a decrease in surface tension, was observed (Fig. 6a and b) when water was replaced by 0.5 mM 1b aqueous solution. The initial decrease in the surface tension started much earlier when compared to the titrations of pure CTAB and SDS indicating that 1b enhances the formation of pre-micellar aggregation of both CTAB and SDS. The enhancement is particularly strong in the case of 1b/CTAB due to three C–H⋯O interactions. In the case of 1b/SDS, due to a single hydrogen bond, the CMC values did not show a drastic reduction in the critical micellar concentration values. To further quantitatively estimate the interactions involved between 1b and the conventional surfactants, topology analysis²¹ was used. The relationship between the bond energy E_H-bond and the potential energy density V(r) at the corresponding Bond Critical Points (BCP) could be described as, E_H-bond = V(r)/2. Using this formula²² the interaction energy was evaluated. C_sp³–H is a weak proton donor compared to C_sp–H or C_sp²–H. Therefore, in the case of the 1b/CTAB complex, positively charged nitrogen activates the C_sp³–H bond and gives it sufficient strength to act as a proton donor in the formation of weak C–H⋯O interactions. The computed C_sp³–H⋯O interaction energies (Fig. 6c) and H⋯O distances at the B3LYP/6-31G(d) level of theory are in good agreement with the acceptable²³ range of values. Similarly, the hydrogen bond strength in 1b/SDS was estimated to be −46.97 kJ mol⁻¹ (Fig. 6d). The plots in Fig. 6a and b show sharp break points corresponding to the CMC of the mixtures. Increasing the salinity decreased electrostatic repulsion between the ionic head groups in the pre-micellar aggregates and as a consequence the CMC values further decreased.

Fig. 6 (a & b) CMC determination in binary combinations of 1b with CTAB and SDS respectively under increasing saline conditions. (c) The association complex of 1b with CTAB calculated by DFT at the B3LYP/6-31G(d) level of theory showing C–H⋯O interactions and their energies. Bond critical points are circled for clarity. (d) The association complex of 1b with SDS showing a single O–H⋯O bond and its energy computed by using density functional theory.

4. Conclusions

In summary, methodical access to a wide range of geometrical assemblies encompassing all of the dimensions of a strained structural oxanorbornane framework at the A/W interface as well as in the bulk was demonstrated. A Li⁺ ion sensor was designed by precisely embedding alkyl chains into conventional SAMs. The polyhydroxyl groups of the oxanorbornane framework could be conveniently used to enhance the pre-micellar aggregate formation in conventional surfactants.

Acknowledgements

The authors thank the Department of Science and Technology, New Delhi, India (Grant no. SR/S2 CMP-57/2006). NR and NKS acknowledge the Senior Research Fellowship from IIT Madras. The Computer Centre, IIT Madras is gratefully acknowledged for providing the computational facilities. Financial support of this work by the Department of Science and Technology, INDIA (Grants SR/NM/NS-1034/2012) is also gratefully acknowledged.

References

1. (a) J. Aizenberg, J. C. Weaver, M. S. Thanawala, V. C. Sundar, D. E. Morse and P. Fratzl, Science, 2005, 309, 275–278; (b) M. Hildebrand, Chem. Rev., 2008, 108, 4855–4874.
2. (a) B. Ozbas, J. Kretsinger, K. Rajagopal, J. P. Schneider and D. J. Pochan, Macromolecules, 2004, 37, 7331–7337; (b) D. J. Pochan, J. P. Schneider, J. Kretsinger, B. Ozbas, K. Rajagopal and L. Haines, J. Am. Chem. Soc., 2003, 125, 11802–11803; (c) A. Aggeli, M. Bell, L. M. Carrick, C. W. G. Fishwick, R. Harding, P. J. Mawer, S. E. Radford, A. E. Strong and N. Boden, J. Am. Chem. Soc., 2003, 125, 9619–9628.
3. M. Fukuda, Methods in Enzymology, Glycomics, Elsevier, 2010, vol. 478, 1st edn.
4. (a) M. G. Newton, N. S. Pantaleo, S. Kirbawy and N. L. Allinger, J. Am. Chem. Soc., 1978, 100, 2176–2180; (b) M. Tamres, S. Searles and J. M. Goodenow, J. Am. Chem. Soc., 1964, 86, 3934–3936.
5. H. Oevering, M. N. Paddon-Row, M. Heppener, A. M. Oliver, E. Cotsaris, J. W. Verhoeven and N. S. Hush, J. Am. Chem. Soc., 1987, 109, 3258–3269.
6. M. Ganesan and K. M. Muraleedharan, RSC Adv., 2012, 2, 4048.
7. T. Kato, M. Kameyama, M. Ehara and K.-i. Iimura, Langmuir, 1998, 14, 1786–1798.
8. M. Maaloum, P. Muller and M. P. Krafft, Angew. Chem., Int. Ed., 2002, 41, 4331–4334.
9. S. Mahesh, A. Gopal, R. Thirumalai and A. Ajayaghosh, J. Am. Chem. Soc., 2012, 134, 7227.
10. R. Heinz, A. Stabel, F. C. De Schryver and J. P. Rabe, J. Phys. Chem., 1995, 99, 505.
11. J. Zhu, Y. Qin and Y. Zhang, Anal. Chem., 2009, 82, 436–440.
12. Z. Wang, Z. Li, C. J. Medforth and J. A. Shelnutt, J. Am. Chem. Soc., 2007, 129, 2440–2441.
13. F. Wang, J. E. Jakes, D. Geng and X. Wang, ACS Nano, 2013, 7, 6007–6016.
14. N. E. Rosenthal and F. K. Goodwin, Annu. Rev. Med., 1982, 33, 555.
15. H. Tamagawa, M. Sakurai, Y. Inoue, K. Ariga and T. Kunitake, J. Phys. Chem. B, 1997, 101, 4817–4825.
16. (a) L. A. Paquette and J. Tae, J. Am. Chem. Soc., 2001, 123, 4974–4984; (b) J. Tae, R. D. Rogers and L. A. Paquette, Org. Lett., 2000, 2, 139–142.
17. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
18. C. H. S. Wong, F. M. Siu, N. L. Ma and C. W. Tsang, J. Mol. Struct.: THEOCHEM, 2001, 536, 227–234.
19. H. Nakahara, O. Shibata and Y. Moroi, J. Phys. Chem. B, 2011, 115, 9077–9086.
20. L. Shedlovsky, J. Ross and C. W. Jacob, J. Colloid Sci., 1949, 4, 25.
21. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
22. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
23. (a) U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754; (b) T. Steiner and W. Saenger, J. Am. Chem. Soc., 1992, 114, 10146–10154.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic details, electrochemical experiments, DFT calculations, surface tension measurements, additional AFM, SEM & TEM images. See DOI: 10.1039/c3ra45708g

---