Competition between electron-donor and electron-acceptor substituents in nitrotoluene isomers: a photoelectron spectroscopy and ab initio investigation†
Abstract
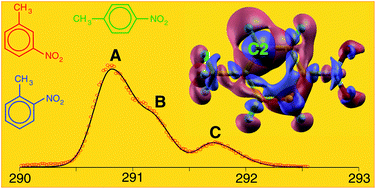
We present an investigation of the close relationship between chemical structure, physical properties and reactivity of the three nitrotoluene isomers: a joint experimental and theoretical study, based on X-ray photoelectron spectroscopy (XPS) measurements and ab initio calculations, addressing the complex interplay between the competing electron-donor and electron-acceptor effects of the nitro- and methyl-substituents on the chemical properties of the nitrotoluene isomers. As the main results of the investigation we: (i) point out that accurate ab initio calculations play a key role in the complete assignment of photoemission measurements, as well as in the estimate of proton affinities in the case of all the eligible sites; (ii) revisit, at a more quantitative level, textbook models based on inductive and resonant effects of different substituents of the aromatic ring, as well as on the hyper-conjugative connection of the methyl group to the π-conjugated system; (iii) provide an accurate analysis of correlation patterns between calculated proton affinities and core-ionization energies, which represent a powerful tool, capable of predicting site-specific reactivities of polysubstituted molecules in the case of electrophilic aromatic substitution reactions.

 Please wait while we load your content...
Please wait while we load your content...