DOI:
10.1039/C3RA45286G
(Paper)
RSC Adv., 2014,
4, 29314-29323
Oxygen defect assisted paramagnetic to ferromagnetic conversion in Fe doped TiO2 nanoparticles
Received
22nd September 2013
, Accepted 13th June 2014
First published on 16th June 2014
Abstract
Here we report the magnetic properties of Fe doped TiO2 nanoparticles annealed in air and vacuum. Fe doped TiO2 nanoparticles display paramagnetism during air annealing and ferromagnetism when the samples are annealed under vacuum. Ferromagnetism in vacuum annealed pure TiO2 nanoparticles is because of the presence of a high density of paramagnetic oxygen vacancy centers. Ferromagnetism in vacuum annealed Fe doped TiO2 is because of the strong exchange interaction of lattice site Fe3+ ions with the nearest paramagnetic oxygen vacancies by forming bound magnetic polarons (BMPs). A collective contribution of the magnetic moment from the bound magnetic polaron on the lattice site and from the paramagnetic oxygen vacancies on the surface and on the grain boundary results in the conversion of paramagnetism to ferromagnetism in vacuum annealed Fe doped TiO2.
1. Introduction
Spintronics studies the utilization of both spin and charge degrees of freedom in order to create an electronic device with enriched functionalities.1 The crucial step in the operation of this device is the efficient injection of spin polarized carriers into non-magnetic semiconductors.2 Diluted magnetic semiconductors (DMS) serve the purpose of a material for spintronics, since this material is being reported to show high spin injection efficiency.2–5 In DMS, a few lattice site atoms are replaced by magnetic ions and thus, exhibit ferromagnetism while preserving the semiconducting properties.2 The initial trials on DMS was concentrated on II–VI or III–V materials such as Mn doped GaAs, InAs, etc. Unfortunately, the low Curie temperature makes these materials unsuitable for most of the practical applications, particularly spintronics, which requires ferromagnetism at room temperature.2,6–8 Ever since the discovery of room temperature ferromagnetism in Co doped TiO2 film by Matsumoto et al., magnetism in TiO2 based DMS have been extensively studied.9–12 In spite of getting room temperature ferromagnetism in different transition metal doped TiO2, debate still persists whether the magnetism is intrinsic or due to the formation of magnetic impurities. Shinde et al. observed superparamagnetism in Co doped TiO2 and ascribed this to the formation of ferromagnetic clusters of cobalt.13 Torres et al. observed paramagnetism on incorporating Fe into TiO2.14 In another study Torres et al. reported that doping of Fe and formation of oxygen vacancies could enhance the paramagnetic moment but might not induce ferromagnetism.15 Bhattacharyya et al. found that TiO2 shows ferromagnetism at low doping concentration of Mn and paramagnetism at high dopant concentration.16 A completely different picture comes to the view when room temperature ferromagnetism is predicted in oxide nanoparticles without adding any magnetic impurities. The magnetism in these nanoparticles is mainly assigned to the presence of oxygen vacancies.17–21 Since only defect induces magnetism in these nanoparticles, the question arises on the necessity of magnetic impurities for observing ferromagnetism. Therefore, in this report we have studied whether oxygen vacancies alone can promote ferromagnetism in TiO2 nanoparticles or doping is necessary to enhance magnetization. To carry out this study we have annealed Fe doped TiO2 nanoparticles under air and vacuum. We have observed that the doped samples do not exhibit any ferromagnetic ordering and pure TiO2 shows only diamagnetism. Ferromagnetism is seen on reheating air annealed pure and doped TiO2 under vacuum. However, magnetization in the vacuum annealed doped sample is enhanced as compared to that in the pure TiO2. This observation clarifies that oxygen vacancy is mostly responsible for ferromagnetism. Doping of Fe assists oxygen vacancies and couple with them to enhance ferromagnetic exchange interaction in the system.
2. Synthesis details
The chemicals used in the present study were of analytical grade. Titanium isopropoxide (Sigma Aldrich, purity 99.9%), 2-propanol (Merck), iron nitrate nonahydrate (Sigma Aldrich, ≥98%) and ethanol (Merck) were purchased from the chemical suppliers without further purification. Fe doped TiO2 nanoparticles with Fe concentration of 2.0 mol%, 3.5 mol% and 5 mol% were prepared by sol–gel method. 5 mL of titanium isopropoxide was mixed with 20 mL of 2-propanol and stirred for 15 min. After 15 min 0.5 mL of water was added to initiate the hydrolysis of the isopropoxide chain. During stirring, iron nitrate nonahydrate solution was added dropwise and the stirring was continued for nearly 6 h. During this period the solution first became sol and then transformed to a thick gel. The gel was first centrifuged in water and then in ethanol for nearly 5 times to make the final product free of any impurities. The centrifuged product was dried in hot air oven to get amorphous doped TiO2, which was further annealed at 450 °C to get crystalline product of Fe doped TiO2 nanoparticles. Diffraction pattern of the prepared nanoparticles was studied with Bruker D8 focus X-ray diffractometer equipped with Cu Kα radiation (λ = 0.154 nm). The scanning range was from 20–80° and the scanning rate was 0.5 s per step with an increment of 0.0057 degree. The high resolution transmission electron microscope (TEM) images of the doped nanoparticles were obtained in a JEOL-JEM-2100 transmission electron microscope at the operating voltage of 200 kV. Energy dispersive X-ray (EDX) spectra of the samples were obtained in JEOL JSM (Model 6390 LV) scanning electron microscope (SEM) with an INCAx-Sight (Oxford instruments) EDX detector. The quantitative elemental analysis of Fe in TiO2 was determined in inductively coupled plasma optical emission spectroscopy (ICP-OES), Perkin Elmer Optima 2100 DV. Raman spectra of the samples were recorded in a Renishaw in-Via Raman spectrometer with Ar ion laser (λ = 514.5 nm) at a resolution of 0.3 cm−1. Electron paramagnetic resonance (EPR) data were obtained in Varian E-112 EPR spectrometer at an applied microwave frequency of 9.0 GHz. Photoluminescence (PL) spectra was obtained in a Perkin Elmer LS-55 spectrometer. The PL instrument contains 2 emission and excitation correction filter wheels with each wheel containing a vertical and horizontal polarizing element. Magnetic measurements were carried out in a superconducting quantum interference device (SQUID) (Evercool SQUID VSM DC magnetometer, Quantum design USA).
3. Results and discussion
Fig. 1a displays the X-ray diffraction pattern of Fe doped TiO2 nanoparticles. The diffraction peaks can be assigned to the tetragonal anatase phase of TiO2 having space group I41/amd (JCPDS file no. 89-4921). Along with anatase, minor brookite phase is also observed at 2θ = 30° and 42° respectively corresponding to the (211) and (221) lattice planes (JCPDS-761934).22 The diffraction spectra do not contain peaks associated with impurity phases. There is small angular displacement in the position of all the diffraction peaks towards higher 2θ when TiO2 is incorporated with 2%, 3.5% and 5 mol% Fe. This signifies that doping of Fe might have decreased the d-spacing of TiO2. To verify this we have determined d-spacing, using WinPlotr software. The changes in the magnitude of d-spacing with Fe concentration is shown in Fig. 1b. As evident from Fig. 1b, d-spacing decreases with the increase of Fe. This is in contrary to the usual expectation that incorporation of large Fe3+ (0.65 Å) on Ti4+ (0.61 Å) would expand the lattice.23 Even though the ionic size of Fe is larger than Ti, the cationic charge (+3) in Fe is lower than that of Ti (+4). Therefore, in order to maintain charge neutrality condition in the lattice oxygen vacancies are expected to be formed nearest to Fe in the lattice. Thus, we may suggest that doping induced formation of oxygen vacancies disturbs the Ti–O bonding and have reduced the coordination of oxygen ions in the TiO2 lattice from octahedral to lower geometry such as tetrahedral.23 These oxygen vacancies have reduced the average numbers of oxygen ions to bind with Fe ions (or with Ti ions) in Fe substituted TiO2 lattice. As a result an overall decrease in d-spacing is encountered in Fe doped TiO2. Transmission electron microscope images of pure and 5.0% Fe doped TiO2 nanoparticles are displayed in Fig. 2a and b. Pure TiO2 nanoparticles have an average size of 10 nm, whereas the doped sample has a particle size of 9 nm. Some amount of agglomeration persists in each sample. Fig. 2c shows the high resolution image of the doped nanoparticle showing the lattice planes with its corresponding selected area electron diffraction (SAED) pattern in the inset of it. The elemental composition is studied with energy dispersive X-ray (EDX) spectroscopy. Fig. 2d shows the EDX pattern of 5% Fe doped TiO2 nanoparticles with the composition of each element in the inset of it. On converting the wt% of Fe to mol% it is found that the corresponding value is 3.04 mol%, which is less than the nominal value of 5 mol% initially added to the host precursor. Actually, EDX is a surface sensitive technique and can determine composition of elements present upto few nm depths from the surface of the sample. Its sensitivity decreases as the analysis depth increases. Moreover, this technique is unable to determine the elemental composition in the core of the nanoparticles. Therefore, in order to determine the actual concentration of Fe in the sample, we carried out ICP-OES for the doped samples. As compared to the nominal concentration of 2%, 3.5% and 5 mol%, the concentration of Fe in the doped samples as determined by ICP-OES are 1.8%, 2.9% and 4.1 mol% respectively. Therefore, the actual concentration of Fe is less than the nominal ones. In the process of dopant incorporation into the lattice the added ions first get attached on the surface of the host semiconductor and during annealing it enters the lattice interior. Few dopant ions are strongly attached to the surface, while few others are weakly interacting with the surface. Since we have centrifuged the as prepared samples, some of the loosely bound Fe ions are easily detached from the surface. Therefore, the calculated concentration is less than the nominal concentration of Fe, initially added during synthesis. X-ray diffraction results indicate modification of the local structure of TiO2 on Fe doping. For further understanding of it, Raman measurement is carried out for the pure and doped samples. Fig. 3 shows the Raman spectra of all the samples. Factor group analysis reveals that the irreducible representation for optical vibrations for anatase and brookite are represented by24,25| | |
Anatase: Γopt = A1g + A2u + 2B1g + B2u + 3Eg + 2Eu
| (1) |
| | |
Brookite: Γopt = 9A1g + 9B1g + 9B2g + 9B3g + 9A1u + 8B1u + 8B2u + 8B3u
| (2) |
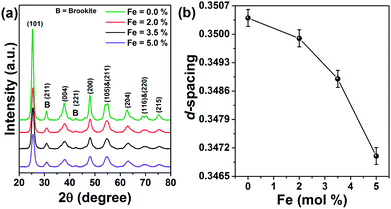 |
| | Fig. 1 X-ray diffraction pattern of (a) pure and Fe doped TiO2 nanoparticles. (b) Variation of d-spacing as a function of dopant concentration. | |
 |
| | Fig. 2 Transmission electron microscope images of (a) TiO2 and (b) 5% Fe doped TiO2 nanoparticles. (c) High resolution image of the doped nanoparticle showing lattice planes with its corresponding SAED pattern in the inset. (d) EDX spectra of 5% Fe doped TiO2 with the composition of each element in the inset. | |
 |
| | Fig. 3 Raman spectroscopy study of pure and Fe doped TiO2 nanoparticles. The inset of the figure shows brookite peaks present in both pure and doped samples. | |
Anatase TiO2 has six Raman active modes. The intense Eg (1) mode appears at 144 cm−1 followed by low intense modes Eg (2) at 200 cm−1 and Eg (3) 639 cm−1.26 B1g peak appears at 398 cm−1 and (A1g + B1g) appears as a single merged peak at 519 cm−1. In the spectra, Raman peaks of brookite appear at 247 cm−1 (A1g), 323 cm−1 (B1g) and 362 cm−1 (B2g).27 The Raman spectra of Fe doped TiO2 is identical to that of anatase TiO2, which indicates that TiO2 retains its structure after incorporation of Fe into the lattice. The changes can be observed in the position and width of the Raman peaks. The width of the Eg (1) and A1g + B1g peak increases and the position is slightly shifted towards higher wavenumber. The Raman vibrational modes of TiO2 are due to the symmetric, asymmetric and bending vibration of Ti–O–Ti bond.28,29 The intense Eg (1) peak is associated with O–Ti–O bending type vibration in which only Ti moves, whereas movement of oxygen remains fixed. The (A1g + B1g) vibration at 519 cm−1 involves movement of only oxygen atoms with Ti movement remains fixed.29 Therefore, any changes in the positioning of Ti or O atoms on introduction of Fe into the lattice framework may affect the Eg (1), (A1g + B1g) Raman peak position, line width, etc. Substitution of high atomic mass Fe on Ti in the TiO2 lattice should increase the d-spacing and increase the lattice volume. However, due to the generation of oxygen vacancies (to compensate charge difference between Fe3+ and Ti4+) in the lattice the average numbers of Fe–O bond is likely to be reduced. This would lead to an overall decrease in d-spacing, resulting in the shifting in the peak position to higher wavenumber. Wu et al. with X-ray absorption fine structure (XAFS) study observed shortening of Ti–O bond length in Fe doped anatase TiO2.23 He stated that shortening of bond length occurred due to oxygen defect induced transformation of coordination geometry from octahedral (TiO6 observed in pure TiO2) to tetrahedral (TiO4) in Fe doped TiO2. He observed that oxygen vacancies could result in the overall shifting of the Raman peak position to higher wavenumber. Naldoni et al. also observed blue shifting of Raman peaks in oxygen deficient nanocrystalline TiO2.30 Apart from peak shifting we have also observed broadening of Raman peak on doping. In stoichiometric TiO2 lattice (with O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti atomic ratio of 2
Ti atomic ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) the basic structural unit consists of ordered TiO6 octahedra with Ti ions surrounded by six O ions. Therefore, Raman scattering from these octahedra can polarize all the Ti–O bonds, resulting in an intense narrow line. Since doping of Fe may generate oxygen vacancies, the average numbers of Ti–O bonds will decrease and the numbers of ordered TiO6 octahedra may reduces to TiO6-n (n is number of oxygen vacancies). Because of the lattice disorder Raman scattering from TiO6-n may polarize few Ti–O bonds and the Raman signal is resulted as broad line. Perker and Siegel studied the effect of oxygen non-stoichiometry on the position and linewidth of Eg (1) Raman signal in oxygen deficient TiO2.31 They reported that decrease in the O/Ti ratio from 2 to 1.89 could result in the broadening of the Eg (1) line. Therefore, decrease in the d-spacing on Fe doping and oxygen defect induced disorder in the lattice, both are possibly resulting in the shifting and broadening of Raman peaks. Electron paramagnetic resonance (EPR) measurement of the doped samples is performed to examine the valence state and local environment of iron in the framework of TiO2. Fig. 4 shows the EPR spectra of Fe doped TiO2 nanoparticles. From the EPR spectra we can calculate the value of g by using the equation
1) the basic structural unit consists of ordered TiO6 octahedra with Ti ions surrounded by six O ions. Therefore, Raman scattering from these octahedra can polarize all the Ti–O bonds, resulting in an intense narrow line. Since doping of Fe may generate oxygen vacancies, the average numbers of Ti–O bonds will decrease and the numbers of ordered TiO6 octahedra may reduces to TiO6-n (n is number of oxygen vacancies). Because of the lattice disorder Raman scattering from TiO6-n may polarize few Ti–O bonds and the Raman signal is resulted as broad line. Perker and Siegel studied the effect of oxygen non-stoichiometry on the position and linewidth of Eg (1) Raman signal in oxygen deficient TiO2.31 They reported that decrease in the O/Ti ratio from 2 to 1.89 could result in the broadening of the Eg (1) line. Therefore, decrease in the d-spacing on Fe doping and oxygen defect induced disorder in the lattice, both are possibly resulting in the shifting and broadening of Raman peaks. Electron paramagnetic resonance (EPR) measurement of the doped samples is performed to examine the valence state and local environment of iron in the framework of TiO2. Fig. 4 shows the EPR spectra of Fe doped TiO2 nanoparticles. From the EPR spectra we can calculate the value of g by using the equation 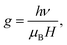 where h is Plank constant, ν is frequency of applied microwave field, μB is Bohr magneton and H is applied magnetic field. We have observed two signals at g = 4.27 and 1.998 respectively. These signals mostly correspond to Fe3+ state in different coordination environment of TiO2.32–34 The spin Hamiltonian associated with these signals is represented by the equation35
where h is Plank constant, ν is frequency of applied microwave field, μB is Bohr magneton and H is applied magnetic field. We have observed two signals at g = 4.27 and 1.998 respectively. These signals mostly correspond to Fe3+ state in different coordination environment of TiO2.32–34 The spin Hamiltonian associated with these signals is represented by the equation35
| |
 | (3) |
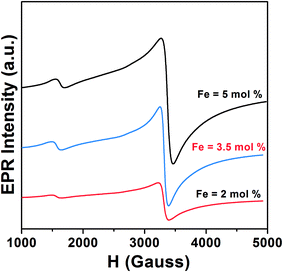 |
| | Fig. 4 Room temperature EPR spectra of 2%, 3.5% and 5% Fe doped TiO2 nanoparticles. | |
First term corresponds to electronic Zeeman and second and third term corresponds to zero field splitting parameter with D and E referred to axial and rhombic splitting components. When Fe3+ ions are incorporated into TiO2, the 6S ground state is splitted into 3 Krammers doublet. The signal at g = 4.27 arise from middle doublet among three Krammers doublet in the case D = 0 and E = 0.35 Thus, this signal arises when Fe3+ remains isolated in low symmetry rhombic field. The signal at g = 1.998 is due to transition from lowest Krammers doublet in case of D ≠ 0 and E = 0.35,36 This signal is for Fe3+ in high symmetry octahedral field of TiO2. In the octahedral coordination Fe3+ interacts with the nearest Fe3+ on the lattice site and undergoes spin–spin coupling resulting in the intense signal at g = 1.998. There is also possibility that Fe3+ interacts with paramagnetic oxygen vacancy (V0) centers forming Fe3+–V0 (with single trapped electron) pair and gives rise to this intense signal.32,33 Therefore, EPR interpretation suggests that Fe3+ ions are located both in low symmetry rhombic field as well as in high symmetry octahedral field. Since the intensity of the line at g = 1.998 is higher than that of g = 4.27 we can say that most of the Fe3+ ions are in octahedral coordination. Room temperature field dependent magnetization (M–H) curves of Fe doped TiO2 nanoparticles are obtained at an applied field of ±20 kOe. Fig. 5a shows the M–H curves of pure and Fe doped TiO2 nanoparticles. It is evident from the figure that the Fe doped TiO2 samples are paramagnetic, whereas pure TiO2 nanoparticles are diamagnetic. We do not completely rule out the possibility of the presence of ferromagnetic clusters or impurities in the doped TiO2 lattice. However, considering the very high bulk magnetization of Fe (218 emu g−1),37 Fe2O3 (84 emu g−1),38 Fe3O4 (90 emu g−1),39 we could expect at least faint ferromagnetic signal in the samples. But from the observed paramagnetism we can infer that the fraction of Fe or its oxides Fe2O3, Fe3O4 are too low and most of the Fe ions are in the lattice interior (this is confirmed by the results of EPR). These dopants in the TiO2 lattice are likely to undergo very weak ferromagnetic exchange interaction (with paramagnetism or antiferromagnetism has dominance over ferromagnetism) and thus, instead of ferromagnetic signal we have observed only paramagnetism in the samples. In order to understand the origin of the paramagnetism in the system we have further carried out temperature dependent magnetization measurement (M–T) for 2% Fe doped TiO2. Fig. 5b shows the zero field cooling (ZFC) and field cooling (FC) magnetization curves for 2% Fe doped TiO2 nanoparticles at an applied field of 500 Oe. The ZFC–FC curves display the typical behavior of paramagnetism. The inverse susceptibility (1/χ) as a function of temperature (T) for the FC curve is shown in the inset of Fig. 5b. The 1/χ vs. T curve deviates from linearity when temperature is progressively lowered from 300 K. The deviation appears when antiferromagnetic interaction prevails at low temperature. In our system paramagnetism appears because of the presence of isolated Fe3+ ions and the antiferromagnetic interaction might be occurring between Fe3+ dimmers or between Fe3+–Fe3+ mediated by lattice site O2− ions. At low temperature paramagnetic Fe3+ ions and antiferromagnetic Fe3+–Fe3+ (or Fe3+–O2−–Fe3+) pair both of these contribute towards magnetization, while at high temperature the anti alignment of the spins in Fe3+ pair is broken and all the spins align randomly showing characteristic of paramagnetism.15,40 We have fitted the high temperature linear part of the 1/χ curve with Curie–Weiss law  where χ is susceptibility, T is temperature and θcw is the Curie–Weiss temperature and C is Curie constant. Extrapolation of the data gives the Curie–Weiss temperature of (−) 235.2 K. Negative θcw indicates presence of antiferromagnetic interaction in the system. Therefore, antiferromagnetic interactions are operating between Fe3+ ions present on neighboring lattice site or between Fe3+ ions via oxygen ions on lattice site. These ions undergo superexchange interaction and results in the anti alignment of the magnetic spins. Many previous results have suggested that the presence of dopant–V0 complex impart ferromagnetic ordering by forming bound magnetic polaron among the spins present on the dopant and the unpaired spin present on the oxygen vacancy.11,12,41 In the discussion on the XRD and Raman spectra of the samples it is understood that doping generates oxygen vacancies on the nearest lattice site to Fe3+. EPR signals at g = 1.99 also signifies the possibility of the presence of Fe3+–V0 center in the doped samples. Hence, the unpaired spins on Fe3+ and the spin on V0 should interact to give ferromagnetism. However, observation of paramagnetism indicates that the density of oxygen vacancies might not be sufficient enough to undergo strong ferromagnetic coupling with the nearest lattice site Fe3+ ions. In order to introduce additional donor carriers or oxygen vacancies, pure and 2% Fe doped TiO2 are vacuum annealed at 200 °C for 3 h. M–H measurement are carried out for the samples and as observed from Fig. 6 initially paramagnetic Fe doped TiO2 and diamagnetic TiO2 both have exhibited ferromagnetism. The coercivity (Hc), remanence (Mr) and saturation magnetization (Ms) values for pure TiO2 are 22 Oe, 0.0015 emu g−1, 0.127 emu g−1 and for doped TiO2 these values are 263 Oe, 0.039 emu g−1 and 1.2 emu g−1 respectively. The slight asymmetry in the coercive field of doped sample is most likely due to the presence of weak antiferromagnetic interaction in the system (by the presence of Fe3+–Fe3+ dimmers or Fe3+–O2−–Fe3+ interaction). Ferromagnetism in pure TiO2 could be ascribed to Ti3+ or oxygen vacancies on the lattice site or on the surface.17,19,28 Although ferromagnetic the saturation magnetization of pure TiO2 is less than that of Fe doped TiO2. The enhanced magnetization in doped sample may be due to the participation of both dopants and defects in the ferromagnetic exchange coupling. The M–H curve of vacuum annealed Fe doped TiO2 at low temperature (20 K) displays slight enhancement in the saturation magnetization (Ms ∼ 1.76 emu g−1) but a large increase in the coercivity (Hc ∼ 592 Oe) as shown in Fig. 6c. We have reheated vacuum annealed Fe doped TiO2 in air at 450 °C and surprisingly, the ferromagnetism is again switched back to paramagnetism (Fig. 6d). These results infer that oxygen vacancies might be playing the driving role on switching the magnetic ordering from paramagnetism to ferromagnetism and then back to paramagnetism in Fe doped TiO2. Simple Fe doping may not induce strong ferromagnetic exchange interaction. It may participate in ferromagnetic exchange interaction only in presence of high density of oxygen vacancies. In order to confirm our assumption that additional oxygen vacancies are generated on vacuum annealing, photoluminescence (PL) measurements are carried out for the air and vacuum annealed pure and 2% Fe doped TiO2 nanoparticles. Fig. 7a shows the PL spectra of air and vacuum annealed TiO2 at an excitation of 320 nm. Excitation at this wavelength generates a UV emission peak at 389 nm associated with indirect band to band transition from edge (X) to the center (X) of Brillouin zone, the emission at 448 nm is due to self trapped exciton bound to oxygen vacancies, the 464 nm is due to F center, 489 nm emission is due to charge transition from Ti3+ to TiO62− linked with oxygen vacancies and the 536 nm emission is due to F+ center (Fig. 7a).42–45 It is seen that vacuum annealing reduces the emission intensity of TiO2 nanoparticles. Decrease in the emission intensity indicates creation of nonradiative oxygen defects on the amorphous grain boundary and on the surface that act as shallow or deep trap centers and prevent carrier recombination. Fig. 7b and c shows the PL spectra of air and vacuum annealed TiO2 nanoparticles doped with 2% Fe. Doped TiO2 also exhibits band edge emission peak as well as defect related emission peaks, similar to that of pure TiO2. However, as compared to pure TiO2 the numbers of defect related emission peaks are higher in doped TiO2. The number of emission peaks in vacuum annealed Fe doped TiO2 are increased many folds than that of its air annealed counterpart. Vacuum annealed Fe doped TiO2 nanoparticles contain several other emission peaks in the range of 530–580 nm. These emission peaks may either be associated with Fe3+ or with other defect center. Literature reports suggest that oxygen vacancies mostly emit in the visible region in the range of 420–530 nm.46,47 In addition, Fe3+ in octahedral coordination is reported to show emission peak at ∼516 nm due to 4T2 (4G) → 6A1(6S) electronic transition.48 In order to understand whether the large number of emission peaks in vacuum annealed Fe doped TiO2 are associated with oxygen vacancies or not, we have reheated the vacuum annealed Fe doped TiO2 in air at 450 °C and observed reduction in the numbers of total number of emission peaks (inset of Fig. 7c). The emission spectrum appears nearly same to that of air annealed Fe doped TiO2 (Fig. 7b). Therefore, from PL measurement it can be speculated that a considerable number of oxygen vacancies are generated in vacuum annealed Fe doped TiO2 and on air annealing these vacancies are again filled up resulting in the disappearance of these defect emission peaks. To support the PL measurement (whether these emissions arise due to d–d transition of Fe3+ or due to oxygen vacancies) we further carried out photoluminescence excitation (PLE) measurement at the emission wavelength of 516 nm. Fig. 7d shows the PLE spectra of vacuum annealed TiO2 and air and vacuum annealed Fe doped TiO2. Interestingly, both doped and undoped samples exhibit similar excitation peaks. Therefore, we can predict that the 516 nm emission is coming from oxygen vacancies. Based on the PL results we can now be nearly certain that vacuum heating generates enough numbers of oxygen vacancies in Fe doped TiO2. These oxygen vacancies could couple with lattice site Fe3+ ions and promote ferromagnetism. Reheating of vacuum annealed Fe doped TiO2 in air reduces the oxygen vacancies and as a consequence the system again reverts back to paramagnetism. The spontaneous magnetization in the sample is determined by the Arrot–Belov–Kouvel (ABK) plot, which measures the variation of M2 (magnetization) vs. H/M.49–51 Fig. 8a displays the ABK plot of vacuum annealed Fe doped TiO2. The high field linear fitting on the Y-axis gives the value of spontaneous magnetization, the value of which is 0.614 ± 0.001 emu g−1. Fig. 8b shows temperature dependent variation of magnetization of vacuum annealed 2% Fe doped TiO2 at an applied field of 500 Oe. Since ZFC curve does not exhibit any peak or hump in the low temperature region, we may discard the possibility of the presence of any spin glass or ferromagnetic oxide phases that may induce the magnetization. A clear difference in the magnetization of the ZFC and FC curves is observed upto 250 K. The point at which ZFC and FC curve bifurcates, i.e. ΔM = ΔMFC − ΔMZFC is defined as the thermomagnetic irreversible temperature.51 The temperature of irreversibility and the difference in the magnetization in the two curves is influenced by the applied magnetic field, magnetic anisotropy present in the system and the approach by which the ZFC and FC measurement is carried out.52–54 In FC mode a magnetic field of 500 Oe is applied at 300 K and then the magnetization is measured while cooling down the sample back to 5 K. The applied magnetic field overcomes the anisotropy present in the system and the spins present in the Fe3+ and in the oxygen vacancies (F+ center) are locked in the direction of the applied magnetic field. Since no magnetic field is applied in the ZFC process, while going down from 300–5 K, the magnetic spins in the dopants and in the defects are randomly oriented. Even though magnetic field is applied at low temperature, this field is not strong enough to overcome the anisotropy barrier and this anisotropy field restricts the domain wall movement in the direction of the applied magnetic field and thus, a lower ZFC magnetization in comparison to FC magnetization is observed.52,53 The inverse susceptibility as a function of temperature is shown in the inset of Fig. 8b. The linear fitting at the high temperature region with the Curie–Weiss law gives the value of Curie–Weiss temperature of 195 K. The positive value of θcw indicates presence of strong ferromagnetic interaction in the system. We have not observed any blocking moment (possibly due to Fe related impurity centers) in the ZFC in the range from low temperature to 300 K. This indicates that magnetic anisotropy of the system is very high which might have prevented blocking of magnetic moment (if we suppose there is any blocking moment due to ferromagnetic clusters) in the low to room temperature range.
where χ is susceptibility, T is temperature and θcw is the Curie–Weiss temperature and C is Curie constant. Extrapolation of the data gives the Curie–Weiss temperature of (−) 235.2 K. Negative θcw indicates presence of antiferromagnetic interaction in the system. Therefore, antiferromagnetic interactions are operating between Fe3+ ions present on neighboring lattice site or between Fe3+ ions via oxygen ions on lattice site. These ions undergo superexchange interaction and results in the anti alignment of the magnetic spins. Many previous results have suggested that the presence of dopant–V0 complex impart ferromagnetic ordering by forming bound magnetic polaron among the spins present on the dopant and the unpaired spin present on the oxygen vacancy.11,12,41 In the discussion on the XRD and Raman spectra of the samples it is understood that doping generates oxygen vacancies on the nearest lattice site to Fe3+. EPR signals at g = 1.99 also signifies the possibility of the presence of Fe3+–V0 center in the doped samples. Hence, the unpaired spins on Fe3+ and the spin on V0 should interact to give ferromagnetism. However, observation of paramagnetism indicates that the density of oxygen vacancies might not be sufficient enough to undergo strong ferromagnetic coupling with the nearest lattice site Fe3+ ions. In order to introduce additional donor carriers or oxygen vacancies, pure and 2% Fe doped TiO2 are vacuum annealed at 200 °C for 3 h. M–H measurement are carried out for the samples and as observed from Fig. 6 initially paramagnetic Fe doped TiO2 and diamagnetic TiO2 both have exhibited ferromagnetism. The coercivity (Hc), remanence (Mr) and saturation magnetization (Ms) values for pure TiO2 are 22 Oe, 0.0015 emu g−1, 0.127 emu g−1 and for doped TiO2 these values are 263 Oe, 0.039 emu g−1 and 1.2 emu g−1 respectively. The slight asymmetry in the coercive field of doped sample is most likely due to the presence of weak antiferromagnetic interaction in the system (by the presence of Fe3+–Fe3+ dimmers or Fe3+–O2−–Fe3+ interaction). Ferromagnetism in pure TiO2 could be ascribed to Ti3+ or oxygen vacancies on the lattice site or on the surface.17,19,28 Although ferromagnetic the saturation magnetization of pure TiO2 is less than that of Fe doped TiO2. The enhanced magnetization in doped sample may be due to the participation of both dopants and defects in the ferromagnetic exchange coupling. The M–H curve of vacuum annealed Fe doped TiO2 at low temperature (20 K) displays slight enhancement in the saturation magnetization (Ms ∼ 1.76 emu g−1) but a large increase in the coercivity (Hc ∼ 592 Oe) as shown in Fig. 6c. We have reheated vacuum annealed Fe doped TiO2 in air at 450 °C and surprisingly, the ferromagnetism is again switched back to paramagnetism (Fig. 6d). These results infer that oxygen vacancies might be playing the driving role on switching the magnetic ordering from paramagnetism to ferromagnetism and then back to paramagnetism in Fe doped TiO2. Simple Fe doping may not induce strong ferromagnetic exchange interaction. It may participate in ferromagnetic exchange interaction only in presence of high density of oxygen vacancies. In order to confirm our assumption that additional oxygen vacancies are generated on vacuum annealing, photoluminescence (PL) measurements are carried out for the air and vacuum annealed pure and 2% Fe doped TiO2 nanoparticles. Fig. 7a shows the PL spectra of air and vacuum annealed TiO2 at an excitation of 320 nm. Excitation at this wavelength generates a UV emission peak at 389 nm associated with indirect band to band transition from edge (X) to the center (X) of Brillouin zone, the emission at 448 nm is due to self trapped exciton bound to oxygen vacancies, the 464 nm is due to F center, 489 nm emission is due to charge transition from Ti3+ to TiO62− linked with oxygen vacancies and the 536 nm emission is due to F+ center (Fig. 7a).42–45 It is seen that vacuum annealing reduces the emission intensity of TiO2 nanoparticles. Decrease in the emission intensity indicates creation of nonradiative oxygen defects on the amorphous grain boundary and on the surface that act as shallow or deep trap centers and prevent carrier recombination. Fig. 7b and c shows the PL spectra of air and vacuum annealed TiO2 nanoparticles doped with 2% Fe. Doped TiO2 also exhibits band edge emission peak as well as defect related emission peaks, similar to that of pure TiO2. However, as compared to pure TiO2 the numbers of defect related emission peaks are higher in doped TiO2. The number of emission peaks in vacuum annealed Fe doped TiO2 are increased many folds than that of its air annealed counterpart. Vacuum annealed Fe doped TiO2 nanoparticles contain several other emission peaks in the range of 530–580 nm. These emission peaks may either be associated with Fe3+ or with other defect center. Literature reports suggest that oxygen vacancies mostly emit in the visible region in the range of 420–530 nm.46,47 In addition, Fe3+ in octahedral coordination is reported to show emission peak at ∼516 nm due to 4T2 (4G) → 6A1(6S) electronic transition.48 In order to understand whether the large number of emission peaks in vacuum annealed Fe doped TiO2 are associated with oxygen vacancies or not, we have reheated the vacuum annealed Fe doped TiO2 in air at 450 °C and observed reduction in the numbers of total number of emission peaks (inset of Fig. 7c). The emission spectrum appears nearly same to that of air annealed Fe doped TiO2 (Fig. 7b). Therefore, from PL measurement it can be speculated that a considerable number of oxygen vacancies are generated in vacuum annealed Fe doped TiO2 and on air annealing these vacancies are again filled up resulting in the disappearance of these defect emission peaks. To support the PL measurement (whether these emissions arise due to d–d transition of Fe3+ or due to oxygen vacancies) we further carried out photoluminescence excitation (PLE) measurement at the emission wavelength of 516 nm. Fig. 7d shows the PLE spectra of vacuum annealed TiO2 and air and vacuum annealed Fe doped TiO2. Interestingly, both doped and undoped samples exhibit similar excitation peaks. Therefore, we can predict that the 516 nm emission is coming from oxygen vacancies. Based on the PL results we can now be nearly certain that vacuum heating generates enough numbers of oxygen vacancies in Fe doped TiO2. These oxygen vacancies could couple with lattice site Fe3+ ions and promote ferromagnetism. Reheating of vacuum annealed Fe doped TiO2 in air reduces the oxygen vacancies and as a consequence the system again reverts back to paramagnetism. The spontaneous magnetization in the sample is determined by the Arrot–Belov–Kouvel (ABK) plot, which measures the variation of M2 (magnetization) vs. H/M.49–51 Fig. 8a displays the ABK plot of vacuum annealed Fe doped TiO2. The high field linear fitting on the Y-axis gives the value of spontaneous magnetization, the value of which is 0.614 ± 0.001 emu g−1. Fig. 8b shows temperature dependent variation of magnetization of vacuum annealed 2% Fe doped TiO2 at an applied field of 500 Oe. Since ZFC curve does not exhibit any peak or hump in the low temperature region, we may discard the possibility of the presence of any spin glass or ferromagnetic oxide phases that may induce the magnetization. A clear difference in the magnetization of the ZFC and FC curves is observed upto 250 K. The point at which ZFC and FC curve bifurcates, i.e. ΔM = ΔMFC − ΔMZFC is defined as the thermomagnetic irreversible temperature.51 The temperature of irreversibility and the difference in the magnetization in the two curves is influenced by the applied magnetic field, magnetic anisotropy present in the system and the approach by which the ZFC and FC measurement is carried out.52–54 In FC mode a magnetic field of 500 Oe is applied at 300 K and then the magnetization is measured while cooling down the sample back to 5 K. The applied magnetic field overcomes the anisotropy present in the system and the spins present in the Fe3+ and in the oxygen vacancies (F+ center) are locked in the direction of the applied magnetic field. Since no magnetic field is applied in the ZFC process, while going down from 300–5 K, the magnetic spins in the dopants and in the defects are randomly oriented. Even though magnetic field is applied at low temperature, this field is not strong enough to overcome the anisotropy barrier and this anisotropy field restricts the domain wall movement in the direction of the applied magnetic field and thus, a lower ZFC magnetization in comparison to FC magnetization is observed.52,53 The inverse susceptibility as a function of temperature is shown in the inset of Fig. 8b. The linear fitting at the high temperature region with the Curie–Weiss law gives the value of Curie–Weiss temperature of 195 K. The positive value of θcw indicates presence of strong ferromagnetic interaction in the system. We have not observed any blocking moment (possibly due to Fe related impurity centers) in the ZFC in the range from low temperature to 300 K. This indicates that magnetic anisotropy of the system is very high which might have prevented blocking of magnetic moment (if we suppose there is any blocking moment due to ferromagnetic clusters) in the low to room temperature range.
 |
| | Fig. 5 Room temperature M–H curves of (a) pure and Fe doped TiO2 nanoparticles. (b) M–T curve of 2% Fe doped TiO2 nanoparticles at an applied field of 500 Oe. The curves show clear paramagnetic behavior with the inset showing the inverse susceptibility curve. The fitting at high temperature is done with Curie–Weiss law. | |
 |
| | Fig. 6 Room temperature M–H curves of vacuum annealed (a) TiO2 and (b) 2.0% Fe doped TiO2 nanoparticles. (c) M–H curve of 2.0% Fe doped TiO2 measured at 20 K. (d) Paramagnetic M–H curve obtained after reheating vacuum annealed 2.0% Fe doped TiO2 in air at 450 °C. | |
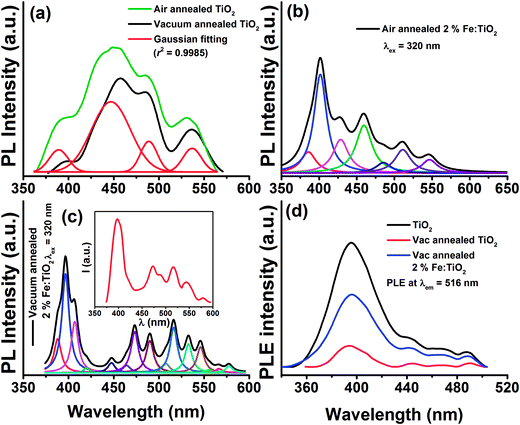 |
| | Fig. 7 Photoluminescence spectra of (a) air and vacuum annealed pure TiO2 at 320 nm excitation. The air annealed TiO2 is fitted with Gaussian showing the presence of 4 different peaks. PL spectra of (b) air and (c) vacuum annealed 2% Fe doped TiO2. Disappearance of few emission peaks on reheating vacuum annealed 2.0% Fe doped TiO2 in air at 450 °C (inset of (c)). (d) PLE spectra of air and vacuum annealed Fe doped TiO2 monitored at the emission wavelength of 516 nm. | |
 |
| | Fig. 8 Arrot–Belov–Kouvel (ABK) plot of (a) Vacuum annealed 2.0% Fe doped TiO2. (b) M–T curve of vacuum annealed 2.0% Fe doped TiO2 nanoparticles. The ZFC and FC curves are bifurcated upto 250 K with no peak in the ZFC curve in the temperature range of 5–300 K. Inset shows 1/χ vs. T curve with high temperature linear fitting gives positive Curie–Weiss temperature indicating ferromagnetic interaction. | |
Mechanism of the ferromagnetic interaction
After having an idea that both oxygen vacancies and impurities are required get enhanced saturation magnetization, a proper mechanism is required to understand the ferromagnetic interaction in the system. The theories which may explain the ferromagnetism in the system are double exchange, indirect Ruderman–Kittel–Kasuya–Yosida (RKKY) and bound magnetic polaron (BMP) percolation theories.41,55–57 Double exchange interaction is applicable at low carrier density and thus, results in low Tc. RKKY interaction, on the other hand, is preferable in metallic system with delocalized carriers or free carriers. BMP theory is suitable in insulating system with localized or immobile carriers.41,56 Due to the wide band gap TiO2 behaves like an insulator with strongly localized carriers in the oxygen vacancies. Therefore, BMP may be a suitable theory to explain the observed magnetism in the system rather than double exchange or RKKY. BMP could be formed by the columbic interaction of F+ center (paramagnetic oxygen vacancy with single electron) electrons with Fe3+. The electron in the F+-center forms a hydrogenic type 1s orbital with radius,  where ε is high frequency dielectric constant, m is electron mass and m* is effective mass of donor electrons and a0 is Bohr radius.56 When the d-orbital of Fe3+ fall within the radius of F+ center the magnetic spins interact with the donor spins and form bound magnetic polaron. Long range ferromagnetism is realized when several such BMPs overlap each other and forms an infinite cluster or when BMP percolation occurs.41 Although air annealed doped samples contain oxygen vacancies nearest to Fe3+, those vacancies may not be sufficient enough to couple with the magnetic impurities to form BMPs. Even if we consider that few BMPs are formed by forming Fe3+–F+, its size do not reach the percolation radius required for ferromagnetic transition. In the air annealed Fe doped TiO2 the number of isolated Fe3+ ions and antiferromagnetic pair (as Fe3+–O2−–Fe3+ on the lattice site) are higher than the number of BMPs and therefore, paramagnetic/antiferromagnetic interaction due to isolated Fe3+/paired Fe3+ is stronger than the ferromagnetic interaction between Fe3+–F+. However, on vacuum annealing sufficient numbers of oxygen vacancies are formed to interact with its nearest Fe3+ ions to form large size BMP. Nevertheless, paramagnetic oxygen vacancies on the surface and at the interface have significant contribution, alongside BMPs, to enhance the magnetization in the vacuum annealed Fe doped TiO2. Fig. 9 shows a pictorial diagram to show the magnetism in vacuum annealed Fe doped TiO2 nanoparticles. In vacuum annealed pure TiO2 the total magnetization is contributed by surface and grain boundary oxygen vacancies i.e. Mtotal = Msurface + Minterface.28 On the other hand in the vacuum annealed Fe doped TiO2 the total magnetization is Mtotal = MBMP + Msurface + Minterface.
where ε is high frequency dielectric constant, m is electron mass and m* is effective mass of donor electrons and a0 is Bohr radius.56 When the d-orbital of Fe3+ fall within the radius of F+ center the magnetic spins interact with the donor spins and form bound magnetic polaron. Long range ferromagnetism is realized when several such BMPs overlap each other and forms an infinite cluster or when BMP percolation occurs.41 Although air annealed doped samples contain oxygen vacancies nearest to Fe3+, those vacancies may not be sufficient enough to couple with the magnetic impurities to form BMPs. Even if we consider that few BMPs are formed by forming Fe3+–F+, its size do not reach the percolation radius required for ferromagnetic transition. In the air annealed Fe doped TiO2 the number of isolated Fe3+ ions and antiferromagnetic pair (as Fe3+–O2−–Fe3+ on the lattice site) are higher than the number of BMPs and therefore, paramagnetic/antiferromagnetic interaction due to isolated Fe3+/paired Fe3+ is stronger than the ferromagnetic interaction between Fe3+–F+. However, on vacuum annealing sufficient numbers of oxygen vacancies are formed to interact with its nearest Fe3+ ions to form large size BMP. Nevertheless, paramagnetic oxygen vacancies on the surface and at the interface have significant contribution, alongside BMPs, to enhance the magnetization in the vacuum annealed Fe doped TiO2. Fig. 9 shows a pictorial diagram to show the magnetism in vacuum annealed Fe doped TiO2 nanoparticles. In vacuum annealed pure TiO2 the total magnetization is contributed by surface and grain boundary oxygen vacancies i.e. Mtotal = Msurface + Minterface.28 On the other hand in the vacuum annealed Fe doped TiO2 the total magnetization is Mtotal = MBMP + Msurface + Minterface.
 |
| | Fig. 9 Schematic diagram showing the presence of possible paramagnetic species, their distribution in the lattice, surface as well as at the interface boundary and the possible ferromagnetic/antiferromagnetic interactions among them. The red sphere inside each nanoparticle represents the magnetic polaron. Overlapping magnetic polaron forms BMPs. Apart from BMPs, coupled F+ centers on the surface and grain boundary also contribute towards ferromagnetism. F center (two trapped electrons) and F2+ (without electrons) are not likely to contribute towards ferromagnetism. | |
4. Conclusion
In summary, we have shown that as prepared air annealed pure TiO2 nanoparticles are diamagnetic, whereas its doped counterpart is paramagnetic in nature. Ferromagnetism occurs only when enough oxygen vacancies are introduced in the system, so that these vacancies can couple with many Fe3+ ions to undergo ferromagnetic exchange interaction. Moreover, oxygen vacancies on the surface and on the interface, produced during vacuum annealing, also contribute to ferromagnetism. Although oxygen deficient TiO2 shows ferromagnetism, the magnetization is tremendously enhanced only when these defects couple with Fe3+ ions. It is observed that reheating of vacuum annealed Fe doped TiO2 in air results in the switching of ferromagnetism back to paramagnetism. Even though oxygen defects may not be the only factor to get ferromagnetism with high magnetization, these defects can surely assist impurities to achieve high magnetization in the ferromagnetic sample.
Acknowledgements
We acknowledge the financial support provided by DST Nanomission through the project SR/NM/NS-98/2010 (G). We are thankful to SAIF IIT Kharagpur for providing us the SQUID facility. We would like to acknowledge SAIF NEHU for carrying out the TEM measurement.
References
- F. Pulizzi, Nat. Mater., 2012, 11, 367 CrossRef CAS PubMed
 .
. - J. K. Furdyna, J. Appl. Phys., 1988, 64, R29 CrossRef CAS PubMed
 .
. - S. J. Pearton, C. R. Abernathy, M. E. Overberg, G. T. Thaler, D. P. Norton, N. Theodoropoulou, A. F. Hebard, Y. D. Park, F. Ren, J. Kim and L. A. Boatner, J. Appl. Phys., 2003, 93, 1 CrossRef CAS PubMed
 .
. - S. A. Chambers, Mater. Today, 2002, 4, 34–39 CrossRef
 .
. - U. Ozgur, Y. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Dogan, V. Avrutin, S. J. Cho and H. Morkoc, J. Appl. Phys., 2005, 98, 041301 CrossRef PubMed
 .
. - H. Ohno, A. Shen, F. Matsukura, A. Oiwa, A. Endo, S. Katsumoto and Y. Iye, Appl. Phys. Lett., 1996, 69, 363–365 CrossRef CAS PubMed
 .
. - S. J. Pearton, C. R. Abernathy, D. P. Norton, A. F. Hebard, Y. D. Park, L. A. Boatner and J. D. Budai, Mater. Sci. Eng., R, 2003, 40, 137–168 CrossRef
 .
. - H. Ohno, Science, 1998, 281, 951–956 CrossRef CAS
 .
. - Y. Matsumoto, M. Murakami, T. Shono, T. Hasegawa, T. Fukumura, M. Kawasaki, P. Ahmet, T. Chikyow, S. Koshihara and H. Koinuma, Science, 2001, 291, 854–856 CrossRef CAS
 .
. - T. Dietl, J. Phys.: Condens. Matter, 2007, 19, 165204 CrossRef
 .
. - R. Janisch, P. Gopal and N. A. Spaldin, J. Phys.: Condens. Matter, 2005, 17, R657–R689 CrossRef CAS
 .
. - B. Choudhury and A. Choudhury, Curr. Appl. Phys., 2013, 13, 1025–1031 CrossRef PubMed
 .
. - S. R. Shinde, S. B. Ogale, J. S. Higgins, H. Zheng, A. J. Millis, V. N. Kulkarni, R. Ramesh, R. L. Greene and T. Venkatesan, Phys. Rev. Lett., 2004, 92, 166601 CrossRef CAS
 .
. - C. E. Rodríguez-Torres, S. J. Stewart, C. Adánb and A. F. Cabrera, J. Alloys Compd., 2010, 495, 485–487 CrossRef PubMed
 .
. - C. E. Rodriguez-Torres, A. F. Cabrera, L. A. Errico, C. Adan, F. G. Requejo, M. Weissmann and S. J. Stewart, J. Phys.: Condens. Matter, 2008, 20, 135210 CrossRef
 .
. - S. Bhattacharyya, A. Pucci, D. Zitoun and A. Gedanken, Nanotechnology, 2008, 19, 495711 CrossRef PubMed
 .
. - N. H. Hong, J. Sakai, N. Poirot and V. Brizé, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 132404 CrossRef
 .
. - J. M. D. Coey, M. Venkatesan, P. Stamenov, C. B. Fitzgerald and L. S. Dorneles, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024450 CrossRef
 .
. - S. D. Yoon, Y. Chen, A. Yang, T. L. Goodrich, X. Zuo, D. A. Arena, K. Ziemer, C. Vittoria and V. G. Harris, J. Phys.: Condens. Matter, 2006, 18, L355 CrossRef CAS
 .
. - J. Hu, Z. Zhang, M. Zhao, H. Qin and M. Jiang, Appl. Phys. Lett., 2008, 93, 192503 CrossRef PubMed
 .
. - S. Zhou, E. Cizmar, K. Potzger, M. Krause, G. Talut, M. Helm, J. Fassbender, S. A. Zvyagin, J. Wosnitza and H. Schimdt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 113202 CrossRef
 .
. - M. Popa, L. Diamandescu, F. Vasiliu, C. M. Teodorescu, V. Cosoveanu, M. Baia, M. Feder, L. Baia and V. Danciu, J. Mater. Sci., 2009, 44, 358–364 CrossRef CAS PubMed
 .
. - Q. Wu, Q. Zheng and R. V. Krol, J. Phys. Chem. C, 2012, 116, 7219–7226 CAS
 .
. - M. Mikami, S. Nakamura, O. Kitao and H. Arakawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155213 CrossRef
 .
. - E. Shojaee, M. Abbasnejad, M. Saeedian and M. R. Mohammadizadeh, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174302 CrossRef
 .
. - B. Choudhury, M. Dey and A. Choudhury, Int. Nano Lett., 2013, 3, 25 CrossRef
 .
. - G. A. Tompsett, G. A. Bowmaker, R. P. Cooney, J. B. Metson, K. A. Rodgers and J. M. Seakins, J. Raman Spectrosc., 1995, 26, 57–62 CrossRef CAS
 .
. - B. Choudhury and A. Choudhury, J. Appl. Phys., 2013, 114, 203906 CrossRef PubMed
 .
. - O. Frank, M. Zukalova, B. Laskova, J. Kurti, J. Koltai and L. Kavan, Phys. Chem. Chem. Phys., 2012, 14, 14567–14572 RSC
 .
. - A. Naldoni, M. Allieta, S. Santangelo, M. Marelli, F. Fabbri, S. Cappelli, C. L. Bianchi, R. Psaro and V. D. Santo, J. Am. Chem. Soc., 2012, 134, 7600 CrossRef CAS PubMed
 .
. - J. C. Parker and R. W. Siegel, Appl. Phys. Lett., 1990, 57, 943–945 CrossRef CAS PubMed
 .
. - C. Fabrega, T. Andreu, A. Cabot and J. R. Morante, J. Photochem. Photobiol., A, 2010, 211, 170–175 CrossRef CAS PubMed
 .
. - G. Pecchi, P. Reyes, T. Lopez, R. Gomez, A. Moreno, J. L. G. Fierro and A. M. Arias, J. Sol-Gel Sci. Technol., 2003, 27, 205–214 CrossRef CAS
 .
. - M. N. Gresu, S. Constantinescu, D. T. Mihaila, D. Ghica and I. Bibicu, Phys. Status Solidi B, 2011, 248, 2927–2931 CrossRef
 .
. - A. S. Rao, R. R. Reddy and T. V. R. Rao, Solid State Commun., 1995, 96, 701–705 CrossRef CAS
 .
. - R. P. S. Charadhar, B. M. Nagabhushana, G. T. Chandrappa, J. L. Rao and K. P. Ramesh, Appl. Magn. Reson., 2008, 33, 137–152 CrossRef
 .
. - M. Kamata, H. Kura, M. Takahashi, T. Ogawa and T. Tanak, IEEE Trans. Magn., 2012, 48, 3944 CrossRef CAS
 .
. - J. Wang, J. Sun, Q. Sun and Q. Chen, Mater. Res. Bull., 2003, 38, 1113 CrossRef CAS
 .
. - K. M. Kant, K. Sethupathi and M. S. R. Rao, J. Appl. Phys., 2008, 103, 07D501 Search PubMed
 .
. - Z. Zhang, Q. Chen, H. D. Lee, Y. Y. Xue, Y. Y. Sun, H. Chen, F. Chen and W. K. Chu, J. Appl. Phys., 2006, 100, 043909 CrossRef PubMed
 .
. - M. J. Calderon and S. D. Sarma, Ann. Phys., 2007, 322, 2618–2634 CAS
 .
. - N. Serpone, D. Lawless and R. Khairutdinov, J. Phys. Chem., 1995, 99, 16646 CrossRef CAS
 .
. - Y. Lei, L. Zhang, G. Meng, G. Li, X. Zhang, C. Liang, W. Chen and S. Wang, Appl. Phys. Lett., 2001, 78, 1125 CrossRef CAS PubMed
 .
. - W. Y. Wu, Y. M. Chang and J. M. Ting, Cryst. Growth Des., 2010, 10, 1646 CAS
 .
. - J. C. Yu, J. Yu, W. Ho, Z. Jiang and L. Zhang, Chem. Mater., 2002, 14, 3808 CrossRef CAS
 .
. - N. D. Abazovic, M. I. Comor, M. D. Dramicanin, D. J. Jovanovic, S. P. Ahrenkiel and J. M. Nedeljkovic, J. Phys. Chem. B, 2006, 110, 25366 CrossRef CAS PubMed
 .
. - A. Roldan, M. Boronat, A. Corma and F. Illas, J. Phys. Chem. C, 2010, 114, 6511 CAS
 .
. - S. S. Pedro, O. Nakamura, R. B. Barthem and L. P. Sosman, J. Fluoresc., 2009, 19, 211–219 CrossRef CAS PubMed
 .
. - D. Kumar and A. Banerjee, J. Phys.: Condens. Matter, 2013, 25, 216005 CrossRef PubMed
 .
. - P. Dutta, P. Dey and T. K. Nath, J. Appl. Phys., 2007, 102, 073906 CrossRef PubMed
 .
. - S. K. Mandal, T. K. Nath, A. K. Das and D. Karmakar, J. Appl. Phys., 2007, 101, 063913 CrossRef PubMed
 .
. - B. Roy and S. Das, J. Appl. Phys., 2008, 104, 103915 CrossRef PubMed
 .
. - D. L. Hou, E. Y. Jiang, S. W. Ren, Z. Q. Li and H. L. Bai, Phys. Status Solidi A, 2002, 191, 597–604 CrossRef CAS
 .
. - P. S. A. Kumar, P. A. Joy and S. K. Date, Bull. Mater. Sci., 2000, 23, 97 CrossRef CAS
 .
. - C. Zener, Phys. Rev., 1951, 82, 403 CrossRef CAS
 .
. - J. M. D. Coey, M. Venkatesan and C. B. Fitzgerald, Nat. Mater., 2005, 4, 173–179 CrossRef CAS PubMed
 .
. - J. M. D. Coey, A. P. Douvalis, C. B. Fitzgerald and M. Venkatesan, Appl. Phys. Lett., 2004, 84, 1332–1334 CrossRef CAS PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. 

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti atomic ratio of 2
Ti atomic ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) the basic structural unit consists of ordered TiO6 octahedra with Ti ions surrounded by six O ions. Therefore, Raman scattering from these octahedra can polarize all the Ti–O bonds, resulting in an intense narrow line. Since doping of Fe may generate oxygen vacancies, the average numbers of Ti–O bonds will decrease and the numbers of ordered TiO6 octahedra may reduces to TiO6-n (n is number of oxygen vacancies). Because of the lattice disorder Raman scattering from TiO6-n may polarize few Ti–O bonds and the Raman signal is resulted as broad line. Perker and Siegel studied the effect of oxygen non-stoichiometry on the position and linewidth of Eg (1) Raman signal in oxygen deficient TiO2.31 They reported that decrease in the O/Ti ratio from 2 to 1.89 could result in the broadening of the Eg (1) line. Therefore, decrease in the d-spacing on Fe doping and oxygen defect induced disorder in the lattice, both are possibly resulting in the shifting and broadening of Raman peaks. Electron paramagnetic resonance (EPR) measurement of the doped samples is performed to examine the valence state and local environment of iron in the framework of TiO2. Fig. 4 shows the EPR spectra of Fe doped TiO2 nanoparticles. From the EPR spectra we can calculate the value of g by using the equation
1) the basic structural unit consists of ordered TiO6 octahedra with Ti ions surrounded by six O ions. Therefore, Raman scattering from these octahedra can polarize all the Ti–O bonds, resulting in an intense narrow line. Since doping of Fe may generate oxygen vacancies, the average numbers of Ti–O bonds will decrease and the numbers of ordered TiO6 octahedra may reduces to TiO6-n (n is number of oxygen vacancies). Because of the lattice disorder Raman scattering from TiO6-n may polarize few Ti–O bonds and the Raman signal is resulted as broad line. Perker and Siegel studied the effect of oxygen non-stoichiometry on the position and linewidth of Eg (1) Raman signal in oxygen deficient TiO2.31 They reported that decrease in the O/Ti ratio from 2 to 1.89 could result in the broadening of the Eg (1) line. Therefore, decrease in the d-spacing on Fe doping and oxygen defect induced disorder in the lattice, both are possibly resulting in the shifting and broadening of Raman peaks. Electron paramagnetic resonance (EPR) measurement of the doped samples is performed to examine the valence state and local environment of iron in the framework of TiO2. Fig. 4 shows the EPR spectra of Fe doped TiO2 nanoparticles. From the EPR spectra we can calculate the value of g by using the equation 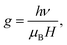 where h is Plank constant, ν is frequency of applied microwave field, μB is Bohr magneton and H is applied magnetic field. We have observed two signals at g = 4.27 and 1.998 respectively. These signals mostly correspond to Fe3+ state in different coordination environment of TiO2.32–34 The spin Hamiltonian associated with these signals is represented by the equation35
where h is Plank constant, ν is frequency of applied microwave field, μB is Bohr magneton and H is applied magnetic field. We have observed two signals at g = 4.27 and 1.998 respectively. These signals mostly correspond to Fe3+ state in different coordination environment of TiO2.32–34 The spin Hamiltonian associated with these signals is represented by the equation35
 where χ is susceptibility, T is temperature and θcw is the Curie–Weiss temperature and C is Curie constant. Extrapolation of the data gives the Curie–Weiss temperature of (−) 235.2 K. Negative θcw indicates presence of antiferromagnetic interaction in the system. Therefore, antiferromagnetic interactions are operating between Fe3+ ions present on neighboring lattice site or between Fe3+ ions via oxygen ions on lattice site. These ions undergo superexchange interaction and results in the anti alignment of the magnetic spins. Many previous results have suggested that the presence of dopant–V0 complex impart ferromagnetic ordering by forming bound magnetic polaron among the spins present on the dopant and the unpaired spin present on the oxygen vacancy.11,12,41 In the discussion on the XRD and Raman spectra of the samples it is understood that doping generates oxygen vacancies on the nearest lattice site to Fe3+. EPR signals at g = 1.99 also signifies the possibility of the presence of Fe3+–V0 center in the doped samples. Hence, the unpaired spins on Fe3+ and the spin on V0 should interact to give ferromagnetism. However, observation of paramagnetism indicates that the density of oxygen vacancies might not be sufficient enough to undergo strong ferromagnetic coupling with the nearest lattice site Fe3+ ions. In order to introduce additional donor carriers or oxygen vacancies, pure and 2% Fe doped TiO2 are vacuum annealed at 200 °C for 3 h. M–H measurement are carried out for the samples and as observed from Fig. 6 initially paramagnetic Fe doped TiO2 and diamagnetic TiO2 both have exhibited ferromagnetism. The coercivity (Hc), remanence (Mr) and saturation magnetization (Ms) values for pure TiO2 are 22 Oe, 0.0015 emu g−1, 0.127 emu g−1 and for doped TiO2 these values are 263 Oe, 0.039 emu g−1 and 1.2 emu g−1 respectively. The slight asymmetry in the coercive field of doped sample is most likely due to the presence of weak antiferromagnetic interaction in the system (by the presence of Fe3+–Fe3+ dimmers or Fe3+–O2−–Fe3+ interaction). Ferromagnetism in pure TiO2 could be ascribed to Ti3+ or oxygen vacancies on the lattice site or on the surface.17,19,28 Although ferromagnetic the saturation magnetization of pure TiO2 is less than that of Fe doped TiO2. The enhanced magnetization in doped sample may be due to the participation of both dopants and defects in the ferromagnetic exchange coupling. The M–H curve of vacuum annealed Fe doped TiO2 at low temperature (20 K) displays slight enhancement in the saturation magnetization (Ms ∼ 1.76 emu g−1) but a large increase in the coercivity (Hc ∼ 592 Oe) as shown in Fig. 6c. We have reheated vacuum annealed Fe doped TiO2 in air at 450 °C and surprisingly, the ferromagnetism is again switched back to paramagnetism (Fig. 6d). These results infer that oxygen vacancies might be playing the driving role on switching the magnetic ordering from paramagnetism to ferromagnetism and then back to paramagnetism in Fe doped TiO2. Simple Fe doping may not induce strong ferromagnetic exchange interaction. It may participate in ferromagnetic exchange interaction only in presence of high density of oxygen vacancies. In order to confirm our assumption that additional oxygen vacancies are generated on vacuum annealing, photoluminescence (PL) measurements are carried out for the air and vacuum annealed pure and 2% Fe doped TiO2 nanoparticles. Fig. 7a shows the PL spectra of air and vacuum annealed TiO2 at an excitation of 320 nm. Excitation at this wavelength generates a UV emission peak at 389 nm associated with indirect band to band transition from edge (X) to the center (X) of Brillouin zone, the emission at 448 nm is due to self trapped exciton bound to oxygen vacancies, the 464 nm is due to F center, 489 nm emission is due to charge transition from Ti3+ to TiO62− linked with oxygen vacancies and the 536 nm emission is due to F+ center (Fig. 7a).42–45 It is seen that vacuum annealing reduces the emission intensity of TiO2 nanoparticles. Decrease in the emission intensity indicates creation of nonradiative oxygen defects on the amorphous grain boundary and on the surface that act as shallow or deep trap centers and prevent carrier recombination. Fig. 7b and c shows the PL spectra of air and vacuum annealed TiO2 nanoparticles doped with 2% Fe. Doped TiO2 also exhibits band edge emission peak as well as defect related emission peaks, similar to that of pure TiO2. However, as compared to pure TiO2 the numbers of defect related emission peaks are higher in doped TiO2. The number of emission peaks in vacuum annealed Fe doped TiO2 are increased many folds than that of its air annealed counterpart. Vacuum annealed Fe doped TiO2 nanoparticles contain several other emission peaks in the range of 530–580 nm. These emission peaks may either be associated with Fe3+ or with other defect center. Literature reports suggest that oxygen vacancies mostly emit in the visible region in the range of 420–530 nm.46,47 In addition, Fe3+ in octahedral coordination is reported to show emission peak at ∼516 nm due to 4T2 (4G) → 6A1(6S) electronic transition.48 In order to understand whether the large number of emission peaks in vacuum annealed Fe doped TiO2 are associated with oxygen vacancies or not, we have reheated the vacuum annealed Fe doped TiO2 in air at 450 °C and observed reduction in the numbers of total number of emission peaks (inset of Fig. 7c). The emission spectrum appears nearly same to that of air annealed Fe doped TiO2 (Fig. 7b). Therefore, from PL measurement it can be speculated that a considerable number of oxygen vacancies are generated in vacuum annealed Fe doped TiO2 and on air annealing these vacancies are again filled up resulting in the disappearance of these defect emission peaks. To support the PL measurement (whether these emissions arise due to d–d transition of Fe3+ or due to oxygen vacancies) we further carried out photoluminescence excitation (PLE) measurement at the emission wavelength of 516 nm. Fig. 7d shows the PLE spectra of vacuum annealed TiO2 and air and vacuum annealed Fe doped TiO2. Interestingly, both doped and undoped samples exhibit similar excitation peaks. Therefore, we can predict that the 516 nm emission is coming from oxygen vacancies. Based on the PL results we can now be nearly certain that vacuum heating generates enough numbers of oxygen vacancies in Fe doped TiO2. These oxygen vacancies could couple with lattice site Fe3+ ions and promote ferromagnetism. Reheating of vacuum annealed Fe doped TiO2 in air reduces the oxygen vacancies and as a consequence the system again reverts back to paramagnetism. The spontaneous magnetization in the sample is determined by the Arrot–Belov–Kouvel (ABK) plot, which measures the variation of M2 (magnetization) vs. H/M.49–51 Fig. 8a displays the ABK plot of vacuum annealed Fe doped TiO2. The high field linear fitting on the Y-axis gives the value of spontaneous magnetization, the value of which is 0.614 ± 0.001 emu g−1. Fig. 8b shows temperature dependent variation of magnetization of vacuum annealed 2% Fe doped TiO2 at an applied field of 500 Oe. Since ZFC curve does not exhibit any peak or hump in the low temperature region, we may discard the possibility of the presence of any spin glass or ferromagnetic oxide phases that may induce the magnetization. A clear difference in the magnetization of the ZFC and FC curves is observed upto 250 K. The point at which ZFC and FC curve bifurcates, i.e. ΔM = ΔMFC − ΔMZFC is defined as the thermomagnetic irreversible temperature.51 The temperature of irreversibility and the difference in the magnetization in the two curves is influenced by the applied magnetic field, magnetic anisotropy present in the system and the approach by which the ZFC and FC measurement is carried out.52–54 In FC mode a magnetic field of 500 Oe is applied at 300 K and then the magnetization is measured while cooling down the sample back to 5 K. The applied magnetic field overcomes the anisotropy present in the system and the spins present in the Fe3+ and in the oxygen vacancies (F+ center) are locked in the direction of the applied magnetic field. Since no magnetic field is applied in the ZFC process, while going down from 300–5 K, the magnetic spins in the dopants and in the defects are randomly oriented. Even though magnetic field is applied at low temperature, this field is not strong enough to overcome the anisotropy barrier and this anisotropy field restricts the domain wall movement in the direction of the applied magnetic field and thus, a lower ZFC magnetization in comparison to FC magnetization is observed.52,53 The inverse susceptibility as a function of temperature is shown in the inset of Fig. 8b. The linear fitting at the high temperature region with the Curie–Weiss law gives the value of Curie–Weiss temperature of 195 K. The positive value of θcw indicates presence of strong ferromagnetic interaction in the system. We have not observed any blocking moment (possibly due to Fe related impurity centers) in the ZFC in the range from low temperature to 300 K. This indicates that magnetic anisotropy of the system is very high which might have prevented blocking of magnetic moment (if we suppose there is any blocking moment due to ferromagnetic clusters) in the low to room temperature range.
where χ is susceptibility, T is temperature and θcw is the Curie–Weiss temperature and C is Curie constant. Extrapolation of the data gives the Curie–Weiss temperature of (−) 235.2 K. Negative θcw indicates presence of antiferromagnetic interaction in the system. Therefore, antiferromagnetic interactions are operating between Fe3+ ions present on neighboring lattice site or between Fe3+ ions via oxygen ions on lattice site. These ions undergo superexchange interaction and results in the anti alignment of the magnetic spins. Many previous results have suggested that the presence of dopant–V0 complex impart ferromagnetic ordering by forming bound magnetic polaron among the spins present on the dopant and the unpaired spin present on the oxygen vacancy.11,12,41 In the discussion on the XRD and Raman spectra of the samples it is understood that doping generates oxygen vacancies on the nearest lattice site to Fe3+. EPR signals at g = 1.99 also signifies the possibility of the presence of Fe3+–V0 center in the doped samples. Hence, the unpaired spins on Fe3+ and the spin on V0 should interact to give ferromagnetism. However, observation of paramagnetism indicates that the density of oxygen vacancies might not be sufficient enough to undergo strong ferromagnetic coupling with the nearest lattice site Fe3+ ions. In order to introduce additional donor carriers or oxygen vacancies, pure and 2% Fe doped TiO2 are vacuum annealed at 200 °C for 3 h. M–H measurement are carried out for the samples and as observed from Fig. 6 initially paramagnetic Fe doped TiO2 and diamagnetic TiO2 both have exhibited ferromagnetism. The coercivity (Hc), remanence (Mr) and saturation magnetization (Ms) values for pure TiO2 are 22 Oe, 0.0015 emu g−1, 0.127 emu g−1 and for doped TiO2 these values are 263 Oe, 0.039 emu g−1 and 1.2 emu g−1 respectively. The slight asymmetry in the coercive field of doped sample is most likely due to the presence of weak antiferromagnetic interaction in the system (by the presence of Fe3+–Fe3+ dimmers or Fe3+–O2−–Fe3+ interaction). Ferromagnetism in pure TiO2 could be ascribed to Ti3+ or oxygen vacancies on the lattice site or on the surface.17,19,28 Although ferromagnetic the saturation magnetization of pure TiO2 is less than that of Fe doped TiO2. The enhanced magnetization in doped sample may be due to the participation of both dopants and defects in the ferromagnetic exchange coupling. The M–H curve of vacuum annealed Fe doped TiO2 at low temperature (20 K) displays slight enhancement in the saturation magnetization (Ms ∼ 1.76 emu g−1) but a large increase in the coercivity (Hc ∼ 592 Oe) as shown in Fig. 6c. We have reheated vacuum annealed Fe doped TiO2 in air at 450 °C and surprisingly, the ferromagnetism is again switched back to paramagnetism (Fig. 6d). These results infer that oxygen vacancies might be playing the driving role on switching the magnetic ordering from paramagnetism to ferromagnetism and then back to paramagnetism in Fe doped TiO2. Simple Fe doping may not induce strong ferromagnetic exchange interaction. It may participate in ferromagnetic exchange interaction only in presence of high density of oxygen vacancies. In order to confirm our assumption that additional oxygen vacancies are generated on vacuum annealing, photoluminescence (PL) measurements are carried out for the air and vacuum annealed pure and 2% Fe doped TiO2 nanoparticles. Fig. 7a shows the PL spectra of air and vacuum annealed TiO2 at an excitation of 320 nm. Excitation at this wavelength generates a UV emission peak at 389 nm associated with indirect band to band transition from edge (X) to the center (X) of Brillouin zone, the emission at 448 nm is due to self trapped exciton bound to oxygen vacancies, the 464 nm is due to F center, 489 nm emission is due to charge transition from Ti3+ to TiO62− linked with oxygen vacancies and the 536 nm emission is due to F+ center (Fig. 7a).42–45 It is seen that vacuum annealing reduces the emission intensity of TiO2 nanoparticles. Decrease in the emission intensity indicates creation of nonradiative oxygen defects on the amorphous grain boundary and on the surface that act as shallow or deep trap centers and prevent carrier recombination. Fig. 7b and c shows the PL spectra of air and vacuum annealed TiO2 nanoparticles doped with 2% Fe. Doped TiO2 also exhibits band edge emission peak as well as defect related emission peaks, similar to that of pure TiO2. However, as compared to pure TiO2 the numbers of defect related emission peaks are higher in doped TiO2. The number of emission peaks in vacuum annealed Fe doped TiO2 are increased many folds than that of its air annealed counterpart. Vacuum annealed Fe doped TiO2 nanoparticles contain several other emission peaks in the range of 530–580 nm. These emission peaks may either be associated with Fe3+ or with other defect center. Literature reports suggest that oxygen vacancies mostly emit in the visible region in the range of 420–530 nm.46,47 In addition, Fe3+ in octahedral coordination is reported to show emission peak at ∼516 nm due to 4T2 (4G) → 6A1(6S) electronic transition.48 In order to understand whether the large number of emission peaks in vacuum annealed Fe doped TiO2 are associated with oxygen vacancies or not, we have reheated the vacuum annealed Fe doped TiO2 in air at 450 °C and observed reduction in the numbers of total number of emission peaks (inset of Fig. 7c). The emission spectrum appears nearly same to that of air annealed Fe doped TiO2 (Fig. 7b). Therefore, from PL measurement it can be speculated that a considerable number of oxygen vacancies are generated in vacuum annealed Fe doped TiO2 and on air annealing these vacancies are again filled up resulting in the disappearance of these defect emission peaks. To support the PL measurement (whether these emissions arise due to d–d transition of Fe3+ or due to oxygen vacancies) we further carried out photoluminescence excitation (PLE) measurement at the emission wavelength of 516 nm. Fig. 7d shows the PLE spectra of vacuum annealed TiO2 and air and vacuum annealed Fe doped TiO2. Interestingly, both doped and undoped samples exhibit similar excitation peaks. Therefore, we can predict that the 516 nm emission is coming from oxygen vacancies. Based on the PL results we can now be nearly certain that vacuum heating generates enough numbers of oxygen vacancies in Fe doped TiO2. These oxygen vacancies could couple with lattice site Fe3+ ions and promote ferromagnetism. Reheating of vacuum annealed Fe doped TiO2 in air reduces the oxygen vacancies and as a consequence the system again reverts back to paramagnetism. The spontaneous magnetization in the sample is determined by the Arrot–Belov–Kouvel (ABK) plot, which measures the variation of M2 (magnetization) vs. H/M.49–51 Fig. 8a displays the ABK plot of vacuum annealed Fe doped TiO2. The high field linear fitting on the Y-axis gives the value of spontaneous magnetization, the value of which is 0.614 ± 0.001 emu g−1. Fig. 8b shows temperature dependent variation of magnetization of vacuum annealed 2% Fe doped TiO2 at an applied field of 500 Oe. Since ZFC curve does not exhibit any peak or hump in the low temperature region, we may discard the possibility of the presence of any spin glass or ferromagnetic oxide phases that may induce the magnetization. A clear difference in the magnetization of the ZFC and FC curves is observed upto 250 K. The point at which ZFC and FC curve bifurcates, i.e. ΔM = ΔMFC − ΔMZFC is defined as the thermomagnetic irreversible temperature.51 The temperature of irreversibility and the difference in the magnetization in the two curves is influenced by the applied magnetic field, magnetic anisotropy present in the system and the approach by which the ZFC and FC measurement is carried out.52–54 In FC mode a magnetic field of 500 Oe is applied at 300 K and then the magnetization is measured while cooling down the sample back to 5 K. The applied magnetic field overcomes the anisotropy present in the system and the spins present in the Fe3+ and in the oxygen vacancies (F+ center) are locked in the direction of the applied magnetic field. Since no magnetic field is applied in the ZFC process, while going down from 300–5 K, the magnetic spins in the dopants and in the defects are randomly oriented. Even though magnetic field is applied at low temperature, this field is not strong enough to overcome the anisotropy barrier and this anisotropy field restricts the domain wall movement in the direction of the applied magnetic field and thus, a lower ZFC magnetization in comparison to FC magnetization is observed.52,53 The inverse susceptibility as a function of temperature is shown in the inset of Fig. 8b. The linear fitting at the high temperature region with the Curie–Weiss law gives the value of Curie–Weiss temperature of 195 K. The positive value of θcw indicates presence of strong ferromagnetic interaction in the system. We have not observed any blocking moment (possibly due to Fe related impurity centers) in the ZFC in the range from low temperature to 300 K. This indicates that magnetic anisotropy of the system is very high which might have prevented blocking of magnetic moment (if we suppose there is any blocking moment due to ferromagnetic clusters) in the low to room temperature range. where ε is high frequency dielectric constant, m is electron mass and m* is effective mass of donor electrons and a0 is Bohr radius.56 When the d-orbital of Fe3+ fall within the radius of F+ center the magnetic spins interact with the donor spins and form bound magnetic polaron. Long range ferromagnetism is realized when several such BMPs overlap each other and forms an infinite cluster or when BMP percolation occurs.41 Although air annealed doped samples contain oxygen vacancies nearest to Fe3+, those vacancies may not be sufficient enough to couple with the magnetic impurities to form BMPs. Even if we consider that few BMPs are formed by forming Fe3+–F+, its size do not reach the percolation radius required for ferromagnetic transition. In the air annealed Fe doped TiO2 the number of isolated Fe3+ ions and antiferromagnetic pair (as Fe3+–O2−–Fe3+ on the lattice site) are higher than the number of BMPs and therefore, paramagnetic/antiferromagnetic interaction due to isolated Fe3+/paired Fe3+ is stronger than the ferromagnetic interaction between Fe3+–F+. However, on vacuum annealing sufficient numbers of oxygen vacancies are formed to interact with its nearest Fe3+ ions to form large size BMP. Nevertheless, paramagnetic oxygen vacancies on the surface and at the interface have significant contribution, alongside BMPs, to enhance the magnetization in the vacuum annealed Fe doped TiO2. Fig. 9 shows a pictorial diagram to show the magnetism in vacuum annealed Fe doped TiO2 nanoparticles. In vacuum annealed pure TiO2 the total magnetization is contributed by surface and grain boundary oxygen vacancies i.e. Mtotal = Msurface + Minterface.28 On the other hand in the vacuum annealed Fe doped TiO2 the total magnetization is Mtotal = MBMP + Msurface + Minterface.
where ε is high frequency dielectric constant, m is electron mass and m* is effective mass of donor electrons and a0 is Bohr radius.56 When the d-orbital of Fe3+ fall within the radius of F+ center the magnetic spins interact with the donor spins and form bound magnetic polaron. Long range ferromagnetism is realized when several such BMPs overlap each other and forms an infinite cluster or when BMP percolation occurs.41 Although air annealed doped samples contain oxygen vacancies nearest to Fe3+, those vacancies may not be sufficient enough to couple with the magnetic impurities to form BMPs. Even if we consider that few BMPs are formed by forming Fe3+–F+, its size do not reach the percolation radius required for ferromagnetic transition. In the air annealed Fe doped TiO2 the number of isolated Fe3+ ions and antiferromagnetic pair (as Fe3+–O2−–Fe3+ on the lattice site) are higher than the number of BMPs and therefore, paramagnetic/antiferromagnetic interaction due to isolated Fe3+/paired Fe3+ is stronger than the ferromagnetic interaction between Fe3+–F+. However, on vacuum annealing sufficient numbers of oxygen vacancies are formed to interact with its nearest Fe3+ ions to form large size BMP. Nevertheless, paramagnetic oxygen vacancies on the surface and at the interface have significant contribution, alongside BMPs, to enhance the magnetization in the vacuum annealed Fe doped TiO2. Fig. 9 shows a pictorial diagram to show the magnetism in vacuum annealed Fe doped TiO2 nanoparticles. In vacuum annealed pure TiO2 the total magnetization is contributed by surface and grain boundary oxygen vacancies i.e. Mtotal = Msurface + Minterface.28 On the other hand in the vacuum annealed Fe doped TiO2 the total magnetization is Mtotal = MBMP + Msurface + Minterface.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.







