Cyclic amine-borane adducts [C_nH_2n+1N·BH₃ (n = 2–6)] as chemical hydrogen storage systems: a computational analysis

Abstract

A detailed theoretical analysis of the cyclic amine-borane adducts has been performed to explore their efficiency towards hydrogen storage. The proton affinities, gas phase basicities and heats of formation of cyclic amines, e.g., aziridine, azetidine, pyrrolidine, piperidine and azepane are calculated at the G4MP2 level. The thermodynamic properties of the borane adducts of these five cyclic aliphatic amines and their associated dehydrogenated products are also investigated. The potential energy surface (PES) associated with the dehydrogenation reaction of all these cyclic amine-borane systems has also been explored. The dehydrogenation reaction enthalpies being close to thermoneutral for all these five ring compounds indicate their potentiality as efficient hydrogen storage materials.

---

1. Introduction

The interest in amine-boranes is growing rapidly because such compounds can act as potential hydrogen storage materials. Among the amine-borane complexes, ammonia-borane (NH₃BH₃) has received considerable attention as an efficient hydrogen storage material due to its high hydrogen content (19.6 wt%).^1,2 To act as an effective hydrogen storage material, a relevant compound should also have favorable thermodynamic properties along with sufficiently rapid kinetics of dehydrogenation reaction. In both gas phase and solid state, thermodynamic properties of the amine-borane adducts have been predicted.^3,4 With the help of accurate ab initio electronic structure theory calculation, it was observed that molecular amine-borane (NH₃BH₃), amine-alane (NH₃AlH₃), and alane-phosphine (AlH₃PH₃) along with [BH₄⁻][PH₄⁺], [AlH₄⁻][NH₄⁺], and [AlH₄⁻][PH₄⁺] salts could serve as potential hydrogen storage materials due to their favorable thermodynamic properties.⁵

Cyclic aliphatic amine-borane adducts can also act as potential hydrogen storage complex.⁶ Although cyclic amine compounds were studied theoretically earlier, their borane adducts are not properly investigated. Many have focused on aziridine as it is the most highly strained compound. They have determined its heats of formation theoretically^7–10 with the help of electronic structure methods. Jursic performed a range of DFT calculations on cyclopropane derivatives, including aziridine.¹¹ Ball and Vayner used ab initio and density functional theory to predict heats of formation and proton affinities of aziridine (C₂H₅N), azetidine (C₃H₇N), pyrrolidine (C₄H₉N) and piperidine (C₅H₁₁N).¹² Vasiliu et al. calculated heats of formation of azole·xBH₃ adducts using composite G3MP2 method with an isodesmic approach.¹³ The experimental proton affinity values have been determined for aziridine, azetidine, pyrrolidine, piperidine and azepane but limited computational works have been performed on those compounds. By using CBS-Q, G3 and B3LYP/6-311+G(3df,2p)//B3LYP/6-31G(d) computational methods, Ohwada et al. performed a thorough analysis of gas phase basicities of the first four cyclic amines and their corresponding N-methyl and N-phenyl derivatives.¹⁴ They observed that basicity increases with increase in ring size, i.e., from three-member ring to six-member ring, but aziridine and its N-substituted derivatives are notably less basic than other compounds. They anticipated that angular strain is not the major source of difference in the strength of basicity of these amines. Later, Radić et al. also affirmed the proposal of Ohwada et al. regarding angular strain, and predicted that the strength of basicity depends on different properties of the initial base, final protonated form and their intermediates.¹⁵

A suitable hydrogen storage material should be stable both with and without hydrogen and must release relatively high amount of H₂ reversibly in a facile process. Recently, Staubitz et al. studied the reversibility of hydrogen uptake of amine-borane adducts¹⁶ and found that electron donating groups on N-site and electron withdrawing groups on B-site increase the endothermicity of ammonia-boranes. They also observed that if the nitrogen is a part of a six-member ring, slightly increase in ring strain of the dehydrogenated product leads to a relative destabilization of product and hence to a more endothermic reaction than is observed for four and five-member rings. In their recent work, Németh et al. carried out a combined experimental and theoretical calculation on aziridine-borane to show that the enthalpy of its hydrogen release reaction is almost thermoneutral, indicating the potential of this complex as recyclable hydrogen storage material.⁶ Motivated by this finding, we have theoretically explored the efficiency of the borane adducts [C_nH_2n+1N·BH₃ (n = 2–6)] of five smallest aliphatic cyclic amines [C_nH_2n+1N (n = 2–6)]: aziridine (n = 2), azetidine (n = 3), pyrrolidine (n = 4), piperidine (n = 5), and azepane (n = 6) as hydrogen storage materials. Though they do not show excellent wt% for hydrogen storage, rather wt% drops with increase in ring size, they may exhibit improved energetics for hydrogen release which is also an important parameter in determining their potentiality toward hydrogen storage. Therefore, our objective of this article is not only to estimate the important thermodynamic properties of the mother cyclic amines accurately but also to analyze the potentiality of the corresponding borane derivatives, which still remain unexplored, toward hydrogen storage.

To accurately quantify the thermochemical parameters of cyclic amine-borane adducts, we have first calculated the heats of formation, proton affinities and gas phase basicities of the mother cyclic amines using the composite G4MP2 method. These estimated thermochemical parameters are in very good agreement with the available experimental results.^17–19 Hence, the thermochemical parameters of the cyclic amine-borane adducts reported here at G4MP2 level is expected to be very accurate, although to the best of our knowledge no experimental results are available. The thermodynamics of the dehydrogenated products of these amine-borane adducts have also been studied. The calculated heats of formation are used to predict the adiabatic bond dissociation energies (BDEs) of the H₃B–N Lewis acid–base dative bonds at both 0 K and 298.15 K. We have also calculated dehydrogenation reaction enthalpies and Gibbs free energy changes associated with the elimination of one hydrogen molecule at 298.15 K. The associated potential energy surface (PES) of the above dehydrogenation reaction is also explored to get an idea about the unimolecular H₂ release pathway in the amine-borane systems.

2. Computational details

All electronic structure calculations are carried out using the Gaussian 09 suite of quantum chemistry program.²⁰ Electronic structures of all the five cyclic amines, the amine-borane adducts, the dehydrogenated products and associated transition states on the PESs are initially optimized by the use of density functional theory (DFT) with the hybrid B3LYP exchange correlation functional^21,22 in conjunction with 6-31G basis set.²³ The geometries are then reoptimized by employing DFT with hybrid meta-GGA functional M06-2X.²⁴ The correlation-consistent aug-cc-pVTZ^25,26 basis set is used with the M06-2X functional. The G4MP2 composite method²⁷ is used to obtain more reliable energies of the species, which can be utilized to calculate thermodynamic parameters very accurately. The G4MP2 method uses geometry optimized at the B3LYP/6-31G(2df,p) level. The zero point vibrational energy is obtained from vibrational frequency calculation at the same level and the frequencies are scaled by a factor of 0.9854. The potential energy surfaces have been constructed using G4MP2 relative energies, while the optimized geometrical parameters are given at M06-2X/aug-cc-pVTZ level (Fig. 1–5). The connecting first order saddle points that are the transition states between the equilibrium geometries are obtained by the synchronous transit-guided quasi-Newton (STQN) method. Normal-mode analysis has been carried out at the same level of theories for equilibrium as well as transition state geometries, which are characterized as minima (number of imaginary frequencies NIMAG = 0) or as a transition state (NIMAG = 1). The intrinsic reaction coordinate (IRC) calculations^28,29 are carried out to confirm the connections between the transition states and local minima.

Fig. 1 Optimized molecular structures with geometrical parameters calculated at M06-2X/aug-cc-pVTZ level for the compounds and TS associated with the three-member ring.

Fig. 2 Optimized molecular structures with geometrical parameters calculated at M06-2X/aug-cc-pVTZ level for the compounds and TS associated with the four-member ring.

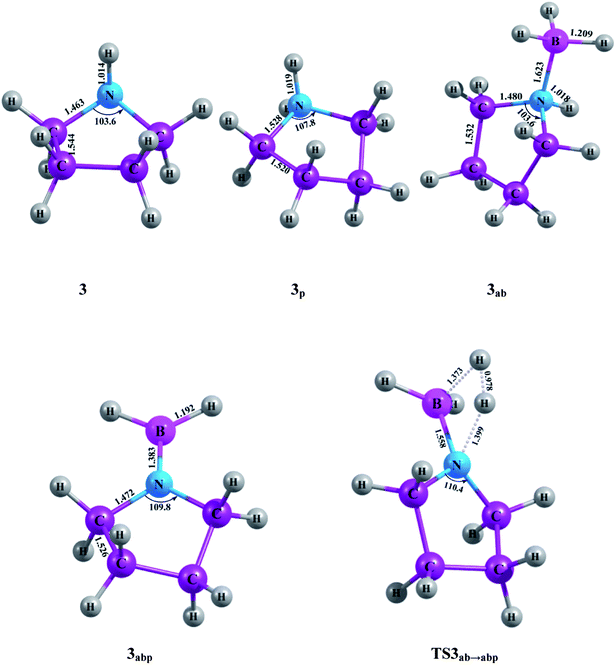Fig. 3 Optimized molecular structures with geometrical parameters calculated at M06-2X/aug-cc-pVTZ level for the compounds and TS associated with the five-member ring.

Fig. 4 Optimized molecular structures with geometrical parameters calculated at M06-2X/aug-cc-pVTZ level for the compounds and TS associated with the six-member ring.

Fig. 5 Optimized molecular structures with geometrical parameters calculated at M06-2X/aug-cc-pVTZ level for the compounds and TS associated with the seven-member ring.

The enthalpies of formation of all the compounds at 0 K and 298.15 K are calculated by the composite G4MP2 method. Total atomization scheme³⁰ is employed for the calculation of heats of formation and for this purpose we have used the literature values of ΔH_f^31,32 for C (169.98 kcal mol⁻¹, 171.29 kcal mol⁻¹), H (51.63 kcal mol⁻¹, 52.10 kcal mol⁻¹), N (112.53 kcal mol⁻¹, 112.97 kcal mol⁻¹) and for B (135.10 kcal mol⁻¹,³³ 133.84 kcal mol⁻¹); the first term in each bracket is the standard heat of formation of the element at 0 K and the second term is the heat of formation of the same element at 298.15 K. Bond dissociation energy (BDE) of the H₃B–N Lewis acid–base dative bond in the amine-borane adduct is calculated at both 0 K and 298.15 K by using the heats of formation of BH₃ and the corresponding cyclic amine.

Proton affinity (PA) is defined as the enthalpy change for the following reaction in gas phase,

A (g) + H⁺ (g) = AH⁺ (g)

The Gibbs free energy change of the above reaction is called the gas phase basicity. Proton affinities of the cyclic amines are calculated by the composite G4MP2 method with the help of the following equation,³⁴

Proton affinity = ΔE_ele + ZPE + 5RT/2,

where ΔE_ele is the energy difference between the cyclic amine and its protonated form and ZPE is the zero point vibrational energy. The term 5RT/2 is the combination of classical estimation of the effect of gaining three translational degrees of freedom (3RT/2) and RT which is actually the PV term for the proton (H⁺). Gas phase basicity of the cyclic amine is also obtained by calculating the Gibbs free energy change of the protonation reaction at the G4MP2 level. It is actually denoted by the negative value of the Gibbs free energy change.

3. Results and discussion

3.1 Heats of formation

The heats of formation of all the five cyclic amines, i.e., aziridine (1), azetidine (2), pyrrolidine (3), piperidine (4), azepane (5) and their borane adducts are given in Table 1 at 0 K and 298.15 K at G4MP2 level. Table 1 also contains available theoretical heats of formation data of the first four cyclic amines at MP2/6-31G* and B3LYP/6-311G** levels.¹² Our calculated heat of formation of 1 at 298.15 K is found to be only 0.4 kcal mol⁻¹ higher compared to the experimental value.¹⁷ As the experimental ΔH_f,298.15K of 2 is not available, we could not compare the calculated value with the experimental one. The calculated heats of formation of 3, 4 and 5 are also in very good agreement with the experimental values.^17,18 The enthalpy of formation of 1 is calculated to be 30.7 kcal mol⁻¹ and this value becomes 24.4 kcal mol⁻¹ in case of the compound 2, which means 2 is 6.3 kcal mol⁻¹ more stable than 1. This enthalpy value further decreases in compound 3 and becomes negative for compound 4. However, a slight increase in the enthalpy is observed on going from 4 to 5. Compound 5 is found to be 1.8 kcal mol⁻¹ less stable than 4. Stability of a ring compound bears an inverse relationship with the ring strain of that compound which is reflected in the calculated heats of formation values of all the cyclic amine systems, 1–5. On going from 1–4 stability increases with decreasing ring strain and attains a maximum value in the six-member ring compound (4) with minimum ring strain. Thereafter, with slight increase in ring strain again in seven-member ring compound (5), the stability falls. Each amine-borane adduct is more stable than the corresponding amine compound, as evident from their heats of formation values, e.g., ΔH_f,298.15K of aziridine-borane adduct (1_ab) is about 10 kcal mol⁻¹ less than aziridine, 1. In other words, 1_ab is about 10.0 kcal mol⁻¹ more stable than 1. This is also true for the other four amine-borane adducts, i.e., azetidine-borane (2_ab), pyrrolidine-borane (3_ab), piperidine-borane (4_ab) and azepane-borane (5_ab) respectively. No experimentally reported heats of formation values are available for the amine-borane adducts. We have also evaluated the heats of formation of the products obtained by the unimolecular dehydrogenation reactions. Except the dehydrogenated product of aziridine-borane, i.e., 1_abp, the dehydrogenated products of azetidine-borane (2_abp), pyrrolidine-borane (3_abp), piperidine-borane (4_abp) and that of azepane-borane (5_abp) are more stable than their corresponding reactants, i.e., the amine-borane adducts. The product 1_abp is observed to be 4.2 kcal mol⁻¹ less stable than the reactant 1_ab. A more clear idea about the stability of the compounds can be obtained from the PES of the dehydrogenation reaction. As the dehydrogenated product 1_abp is less stable than 1_ab, the dehydrogenation reaction is found to take place in an endothermic way (Fig. 7). On the other hand, dehydrogenation reaction of 2_ab shows exothermicity as the dehydrogenated product, 2_abp is more stable than the amine-borane adduct (Fig. 8). The hydrogen elimination from the other three adducts, 3_ab, 4_ab and 5_ab also occurs in an exothermic way (Fig. 9, Fig. 10 and Fig. 11). It should be noted here that due to the lack of any experimentally obtained heats of formation values at 0 K, no comparison can be made with our computed results for ΔH_f,0K. However, we expect that this would enrich the existing literature.

Table 1 Calculated and experimental heats of formation at 0 K (ΔH_f,0K) and at 298.15 K (ΔH_f,298.15K) in kcal mol⁻¹ at G4MP2 level from total atomization energies

Compound	ΔHf,0K	ΔHf,298.15K
	G4MP2	G4MP2	Expt	(MP2/6-31G*)^c	(B3LYP/6-311G**)^c
a Ref. 17. b Ref. 18. c Ref. 12.
1	34.5	30.7	30.3^a	29.2	30.6
2	29.9	24.4	—	36.5	39.7
3	7.3	0.3	−0.8^a	−2.0	2.8
4	−1.9	−10.7	−11.3^a	−12.5	−5.6
5	1.2	−8.9	−10.8^b	—	—
1ab	29.2	20.7	—	—	—
2ab	20.8	10.6	—	—	—
3ab	−1.5	−13.2	—	—	—
4ab	−10.5	−24.0	—	—	—
5ab	−7.2	−22.1	—	—	—
1abp	31.6	24.9	—	—	—
2abp	18.4	10.1	—	—	—
3abp	−5.1	−15.2	—	—	—
4abp	−14.1	−26.0	—	—	—
5abp	−11.4	−24.6	—	—	—

---

Fig. 6 Reaction pathways for the unimolecular release of H₂ from NH₃BH₃ at 298.15 K at the G4MP2 level.

Fig. 7 Reaction pathways for the unimolecular release of H₂ from 1_ab at 298.15 K at the G4MP2 level.

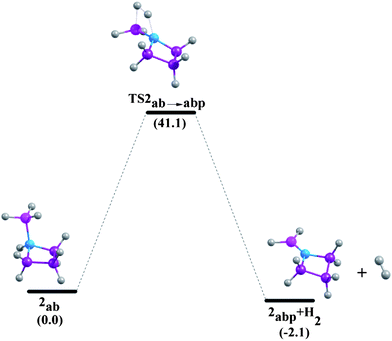Fig. 8 Reaction pathways for the unimolecular release of H₂ from 2_ab at 298.15 K at the G4MP2 level.

Fig. 9 Reaction pathways for the unimolecular release of H₂ from 3_ab at 298.15 K at the G4MP2 level.

Fig. 10 Reaction pathways for the unimolecular release of H₂ from 4_ab at 298.15 K at the G4MP2 level.

Fig. 11 Reaction pathways for the unimolecular release of H₂ from 5_ab at 298.15 K at the G4MP2 level.

3.2 Bond dissociation energies (BDEs)

Table 2 represents the calculated adiabatic BDEs of the H₃B–N dative bonds of all the five cyclic amine-borane adducts at 0 K and at 298.15 K. At 0 K, the B–N BDE of ammonia-borane (25.9 kcal mol⁻¹) obtained at G4MP2 level in this present study exactly reproduces the value obtained at CCSD(T)/CBS level,³⁵ while its value is 26.0 kcal mol⁻¹ at G3MP2 level.¹³ There is about 6.5 kcal mol⁻¹ increase in B–N dative σ-bond energy in aziridine-borane, 1_ab, compared to that of ammonia-borane at 0 K. Subsequent increase in ring size from three-member adduct, 1_ab to four-member adduct, 2_ab leads to an increase in 3.9 kcal mol⁻¹ bond dissociation energy. The B–N bond dissociation energies of 3_ab, 4_ab and 5_ab are 36.0, 35.8 and 35.6 kcal mol⁻¹ respectively, which is of the same order as that of 2_ab. As the ring strain decreases with increasing ring size, it would be easier for a compound to form a stable adduct with borane. This is found to be true for the adduct 2_ab in comparison to the adduct 1_ab. But in case of the adducts 3_ab, 4_ab and 5_ab anomalous behavior is observed as their BDEs deviate from the normal trend.

Table 2 B–N bond dissociation energies (BDEs, ΔE_0K, ΔE_298.15K) in kcal mol⁻¹ for the amine-borane adducts from the heats of formation calculated at the G4MP2 level

Compound	ΔE0K	ΔE298.15K
1ab	32.4	33.7
2ab	36.3	37.6
3ab	36.0	37.2
4ab	35.8	37.1
5ab	35.6	37.0

---

3.3 Proton affinities and gas phase basicities

Table 3 summarizes the calculated proton affinities (PA) of all the five cyclic amines, 1–5 at 298.15 K and also presents a direct comparison with the available experimental data.^18,19 These PA values are obtained by calculating the change of enthalpy of the protonation reaction. The enthalpy of H⁺ is found to be 1.49 kcal mol⁻¹ which is equal to 5/2RT. The PAs calculated by the G4MP2 are in good agreement with the available experimental values. The calculated proton affinity of 1 is the lowest; its value at the G4MP2 level is 216.9 kcal mol⁻¹. The high ring strain in 1 inhibits the formation of quaternary nitrogen and probably this is the reason behind its low protonation energy value (PA value). As the ring strain decreases with the increase of ring size, the proton affinity value consequently increases and becomes 228.0 kcal mol⁻¹ in the compound 4 with minimum ring strain. However, no effect of ring strain is observed on the proton affinity value for seven-member ring compound, 5. The proton affinity value still remains higher in compound 5 although it has a slightly higher ring strain than compound 4, as also supported by available experimental results.

Table 3 Calculated and experimental proton affinities (PA) of the cyclic amines in kcal mol⁻¹ (298.15 K) at G4MP2 level (A + H⁺ → AH⁺)

Compound	PA (cal)	PA (exp)
a Ref. 18. b Ref. 19.
1	216.9 (1 + H^+ → 1p)	215.7^b
2	224.8 (2 + H^+ → 2p)	223.5^b
3	227.6 (3 + H^+ → 3p)	225.2^b
4	228.0 (4 + H^+ → 4p)	226.6^b
5	229.9 (5 + H^+ → 5p)	228.7^a

---

The gas phase basicities are obtained by calculating the Gibbs free energy changes of the gas phase protonation reactions of the mother compounds. Table 4 compares our calculated gas phase basicities of all the five cyclic amines at G4MP2 level with available experimental values.^18,19 The calculated gas phase basicity values at the G4MP2 level are found to be in good agreement with the corresponding experimental values. Similar to the proton affinity values, basicity value also increases with the increase of ring size of the amines.

Table 4 Calculated and experimental gas phase basicities (−ΔG_298.15K) in kcal mol⁻¹ for the cyclic amines at the G4MP2 level

Compound	−ΔG298.15K (cal)	−ΔG298.15K (exp)
a Ref. 18. b Ref. 19.
1	209.3	208.5^b
2	217.5	217.2^b
3	219.8	218.8^b
4	220.5	220.0^b
5	222.2	220.7^a

---

3.4 Dehydrogenation reaction energies

The enthalpy change (ΔH_r) and Gibbs free energy change (ΔG_r) of the dehydrogenation reactions are given in Table 5. The ΔH_r value of NH₃BH₃ is predicted to be −7.0 kcal mol⁻¹ and −6.7 kcal mol⁻¹ at CCSD(T)/CBS³⁶ and G3MP2 levels,¹³ respectively. We have obtained a value of −7.0 kcal mol⁻¹ for the dehydrogenation enthalpy change of ammonia-borane adduct at the composite G4MP2 level, implying that this compound is a potentially good chemical hydrogen storage material as its dehydrogenation reaction is less exothermic.³⁵ On the other hand, phosphine-borane is not an appropriate candidate in this regard as the release of hydrogen in this case is found to be a strongly endothermic process (17.4 kcal mol⁻¹).⁵ In our study, ΔH_r of aziridine-borane, 1_ab, is found to be 3.1 kcal mol⁻¹ which is consistent with the data obtained by Németh et al.⁶ Dehydrogenation reactions of the borane adducts of azetidine (2_ab), pyrrolidine (3_ab), piperidine (4_ab) and azepane (5_ab) are exothermic, their enthalpy changes of dehydrogenation reactions are −1.5 kcal mol⁻¹, −3.0 kcal mol⁻¹, −3.0 kcal mol⁻¹ and −3.5 kcal mol⁻¹ respectively. Therefore, the results for the enthalpy change of H₂ elimination suggest less endothermicity for the compound 1_ab, while suggesting less exothermicity for the compounds 2_ab, 3_ab, 4_ab and 5_ab. The free energy change of the dehydrogenation reaction of compound 1_ab is −5.7 kcal mol⁻¹. This value is close to the ΔG_r value of −5.5 kcal mol⁻¹ for aziridine-borane dehydrogenation reaction at the CBS-QB3 level.⁶ The Gibbs free energy change values of compounds 2_ab, 3_ab, 4_ab and 5_ab are −11.0 kcal mol⁻¹, −10.9 kcal mol⁻¹, −11.5 kcal mol⁻¹ and −12.1 kcal mol⁻¹ respectively, indicating that all the dehydrogenation reactions are spontaneous.

Table 5 Dehydrogenation reaction energies at 298.15 K in kcal mol⁻¹ calculated at the G4MP2 level

Reaction	ΔHr	ΔGr
1ab → 1abp + H2	3.1	−5.7
2ab → 2abp + H2	−1.5	−11.0
3ab → 3abp + H2	−3.0	−10.9
4ab → 4abp + H2	−3.0	−11.5
5ab → 5abp + H2	−3.5	−12.1

---

3.5 Reaction pathways for dehydrogenation reactions

Minh et al. showed that the H₂ release from the NH₃BH₃ has a higher barrier than the dissociation energy of the complex; the reaction energy barrier to release H₂ from it is about 10 kcal mol⁻¹ above the B–N bond dissociation energy.³⁶ As a result, the B–N bond will break before H₂ is eliminated. Therefore, in the present study we have systematically investigated the unimolecular dehydrogenation pathways (shown in Scheme 1) and B–N BDEs of five cyclic amine-borane adducts, i.e., 1_ab, 2_ab, 3_ab, 4_ab and 5_ab along with ammonia-borane. The associated PESs are depicted in Fig. 6–11. The dehydrogenation reaction of 1_ab is found to be endothermic while that of 2_ab, 3_ab, 4_ab and 5_ab are exothermic. The transition state (TS) geometries for all the five adducts are similar to the TS geometry predicted for NH₃BH₃.³⁶ The reaction barrier at 298.15 K for the hydrogen elimination is 42.3 kcal mol⁻¹, 41.1 kcal mol⁻¹, 39.8 kcal mol⁻¹, 40.7 kcal mol⁻¹ and 40.0 kcal mol⁻¹ for 1_ab, 2_ab, 3_ab, 4_ab and 5_ab respectively. For all five cyclic amine-borane adducts BDEs of B–N bond at 298.15 K are found to be less than the dehydrogenation reaction energy barriers. For the adduct 1_ab, the BDE is about 8.6 kcal mol⁻¹ lower than the energy barrier for dehydrogenation reaction. However, for other four adducts this difference between BDE and dehydrogenation energy barrier is substantially less, viz., for 2_ab it is 3.5 kcal mol⁻¹, for 3_ab it is 2.6 kcal mol⁻¹, for 4_ab it is 3.6 kcal mol⁻¹ and for 5_ab it is about 3.0 kcal mol⁻¹. Hence, for cyclic amine-borane adducts, as we move from 1_ab to 5_ab, the unimolecular H₂ release channel becomes more competitive with respect to the B–N bond dissociation energy, indicating the potential of these adducts as effective hydrogen storage systems. These dehydrogenation channels though revealed that hydrogen elimination from 1_ab, 2_ab, 3_ab, 4_ab and 5_ab does not take place unimolecularly as for all these cases B–N bond will break before H₂ is eliminated.

Scheme 1 Reaction pathway presented in five different schemes.

In practice, it is observed that ammonia-borane can behave as a good hydrogen storage system due to the catalytic role of BH₃, generated from B–N bond cleavage, effectively reducing the dehydrogenation barrier.³⁶ The catalytic role of BH₃ is also pronounced in case of aziridine-borane system, as evident from the work of Németh et al., reducing the dehydrogenation barrier height by ∼19 kcal mol⁻¹.⁶ Our calculated B–N bond dissociation energy clearly demonstrates that the dehydrogenation pathway will be preferred over the dissociation of this aziridine-borane adduct (1_ab) in presence of BH₃ as a catalyst. The four, five, six and seven-member ring compounds, i.e., 2_ab, 3_ab, 4_ab and 5_ab are also expected to exhibit similar mechanistic behavior which will be reported in our next work.

4. Conclusion

The heats of formation and BDEs at 0 K and 298.15 K for all the five cyclic amines, their borane adducts and for the dehydrogenated products of the amine-borane adducts are predicted using total atomization scheme. For cyclic amines, good agreement is observed with the available experimental data for the heats of formation, proton affinities and gas phase basicities. With the increase in ring size from three-member ring amine to six-member one, the heats of formation noticeably decrease, indicating that the compounds become more stable with decrease in ring strain. However, on moving further from six-member ring compound to seven-member one heat of formation becomes less negative implying that the latter is less stable than the former one due to slight increase in ring strain. The values of both proton affinities and gas phase basicities support the general conclusion that aziridine is the weakest base while azepane is the strongest one among these five investigated systems. The H₃B–N dative bond of the three-member ring is much weaker compared to the four, five, six and seven-member rings. The calculated dehydrogenation reaction enthalpies are close to thermoneutral for all five ring compounds; it is slightly endothermic for 1_ab and slightly exothermic for 2_ab, 3_ab, 4_ab and 5_ab adducts, indicating their potential as hydrogen storage material. Although it is evident that the wt% drops on moving towards larger ring systems, it is observed that the difference between B–N BDE and the dehydrogenation barrier for 2_ab to 5_ab decreases noticeably compared to 1_ab, indicating improved energetics and facile dehydrogenation process for larger ring compounds. Our work is expected to trigger new experimental investigations on these cyclic amine-borane adducts as potential candidates for hydrogen storage.

Acknowledgements

TB, KS and TD are grateful to the Council of Scientific and Industrial Research (CSIR), Government of India, for providing them research fellowships. AKD is grateful to the Council of Scientific and Industrial Research (CSIR), Govt. of India, for a research grant under scheme number: 03(1168)/10/EMR-II.

References

1. F. H. Stephens, V. Pons and R. T. Baker, Dalton Trans., 2007, 2613.
2. T. B. Marder, Angew. Chem., Int. Ed., 2007, 46, 8116.
3. R. W. Parry, D. R. Schultz and P. R. Girardot, J. Am. Chem. Soc., 1958, 80, 1.
4. V. P. Sorokin, B. I. Vesnina and N. S. Klimova, Russ. J. Inorg. Chem., 1963, 8, 32.
5. D. J. Grant and D. A. Dixon, J. Phys. Chem. A, 2005, 109, 10138.
6. B. Németh, B. Khater, J. C. Guillemin and T. Veszprémi, Inorg. Chem., 2010, 49, 4854.
7. N. Bodor, M. J. S. Dewar, W. B. Jennings and S. D. Worley, Tetrahedron, 1970, 26, 4109.
8. J. A. Boatz and M. S. Gordon, J. Phys. Chem., 1989, 93, 3025.
9. D. J. Berger, P. P. Gaspar and J. F. Liebman, THEOCHEM, 1995, 338, 51.
10. I. M. B. Nielsen, J. Phys. Chem. A, 1998, 102, 3193.
11. B. S. Jursic, THEOCHEM, 1997, 391, 75.
12. E. Vayner and D. W. Ball, THEOCHEM, 2000, 496, 175.
13. M. Vasiliu, A. J. Arduengo and D. A. Dixon, J. Phys. Chem. C, 2012, 116, 22196.
14. T. Ohwada, H. Hirao and A. Ogawa, J. Org. Chem., 2004, 69, 7486.
15. N. Radić, I. Despotović and R. Vianello, Croat. Chem. Acta, 2012, 85, 495.
16. A. Staubitz, M. Besora, J. N. Harvey and I. Manners, Inorg. Chem., 2008, 47, 5910.
17. J. B. Pedley, R. D. Naylor and S. P. Kirby, Thermochemical Data of Organic Compounds, 2, Chapman and Hall, London, 1986.
18. NIST Chemistry Webbook, http://webbook.nist.gov/chemistry.
19. S. G. Lias, J. F. Liebman and R. D. Levin, J. Phys. Chem. Ref. Data, 1984, 13, 695.
20. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al.Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010.
21. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
22. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
23. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215.
25. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
26. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667.
27. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 127, 124105.
28. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.
29. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
30. A. Nicolaides, A. Rauk, M. N. Glukhovtsev and L. Radom, J. Phys. Chem., 1996, 100, 17460.
31. M. W. Chase Jr, C. A. Davies, J. R. Downey Jr, D. J. Frurip, R. A. McDonald and A. N. Syverud, J. Phys. Chem. Ref. Data, 1985, 14(1), 1.
32. S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, J. Phys. Chem. Ref. Data, 1988, 17(1), 1.
33. A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2007, 111, 5936.
34. Z. Wang, I. K. Chu, C. F. Rodriquez, A. C. Hopkinson and K. W. Michael Siu, J. Phys. Chem. A, 1999, 103, 8700.
35. D. A. Dixon and M. J. Gutowski, J. Phys. Chem. A, 2005, 109, 5129.
36. M. T. Nguyen, V. S. Nguyen, M. H. Matus, G. Gopakumar and D. A. Dixon, J. Phys. Chem. A, 2007, 111, 679.

---