Free energy landscapes of the encapsulation mechanism of DNA nucleobases onto carbon nanotubes

Abstract

The confinement mechanism of DNA nucleobases onto single-walled carbon nanotubes is probed at physiological temperature (310 K) using classical molecular dynamics and fully atomistic molecular potentials. The corresponding free energy landscapes are constructed in terms of two order parameters, ξ₁ and ξ₂, for both purine (adenine) and pyrimidine (thymine) moieties, by a metadynamics scheme. Two zig-zag topologies, (16, 0) and (23, 0), are employed as solid models with limiting skeletal diameters, D = 1.25 nm and D = 1.8 nm, respectively, considering hydrophobic and electrically charged nanopores, q = +0.05 e⁻/C. The uncharged nanotubes always exhibit a single free energy minimum located close to the pore center, regardless of individual diameter, whereas the charged nanotubes either inhibit encapsulation or exhibit two energetically distinct confining regions, at the center and close to the pore termini. Very interestingly, the purely hydrophobic solids exhibit a quasi-isotropic free-energy landscape around the nanopore center, F (ξ₁, ξ₂). Independent umbrella sampling calculations show that for the (23, 0) electrically charged nanotubes, the probability maximum at a distance of Ω = 0.54 nm from the pore center is the global one for adenine. These subtle differences are quantified by decomposing the interaction energy between a nucleobase and the solid into its dispersive and electrostatic contributions, and a critical comparison with DFT and experimental data for graphite is discussed. Purine and pyrimidine show similar interaction energies within the hydrophobic nanopores, however, adenine confinement results in slightly more stable hybrids by 0.9–1.4 kJ mol⁻¹; binding affinity increases with the nanotube curvature as a result of enhanced dispersive energy. The detailed thermodynamical analysis reported herein is of paramount importance to study the sequence specific properties of DNA/carbon nanotube hybrids.

---

1. Introduction

Ever since the unravelling of the double-helix structure of DNA,^1,2 the molecule has been considered as the building block of biological organisms. Because DNA is the agent that carries genetic information from one generation to the next, the knowledge of its physical and chemical properties is of paramount importance. Much of that information has to do with the way the nucleobases (NBs)—DNA's own building blocks—interact not only amongst themselves but also with their surrounding environment. Decades later, in the early nineties, single-walled carbon nanotubes (SWCNTs) were first prepared in the laboratory by the groups of Iijima and Bethune.^3–5 Owing to their nanoscale dimensions, carbon nanotubes are able to selectively interact with DNA almost at the atomic level; therefore, the interactions between DNA and carbon nanotubes have been the subject of intense investigation. Amongst other biological applications,^6–9 nanotubes have been proposed as templates for DNA encapsulation and intracellular transport,^10–13 DNA conformation management and analysis,^14,15 ultrafast sequencing of isolated single strands^16,17 and electrochemical sensors for macromolecules.¹⁸ As a result of their geometrical simplicity (1-D symmetry), large elastic modulus, high tensile strength and well-defined physico-chemical properties, carbon nanotubes can be adopted as paradigms of model nanopores for intracellular gene and DNA delivery.^12,19

Many of the aforementioned applications are sequence-dependent, because DNA is an heterogeneous molecule that exhibits hydrophilic (phosphates) but also hydrophobic domains made of four different molecular moieties (NBs). When DNA is hybridized in a double strand (dsDNA), the internally packaged nucleobases are shielded from the outside environment by the phosphate and sugar groups; however, the former can become exposed upon opening of the double helix or they can exist naturally exposed such as in the case of single stranded DNA (ssDNA). Thus, due to the existence of bare hydrophobic sites in the NBs (aromatic rings), homo^20–22 and heteropolymer^16,22–24 ssDNA will readily adsorb onto the external walls of small diameter SWCNTs, according to a π-stacking mechanism of the aromatic rings on the tube walls. The binding affinity of this interaction is markedly influenced by the nucleobase molecular identity. Since NBs have not only intrinsically different π-conjugated systems, but also molecular dipoles, previous theoretical work^20,21 evidenced that a purine-type nucleobase (adenine/A, guanine/G) exhibits a stronger interaction with graphitic-like surfaces when compared to the pyrimidine analogue (thymine/T, cytosine/C). The experimental isotherms obtained by Sowerby et al.²⁵ demonstrate that the adsorption behaviour of aqueous nucleobases onto crystalline graphite follows an elutropic series. Recently,²⁶ the in vacuum energies of individual NBs exoadsorbed onto a D = 0.55 nm SWCNT have been determined and obeyed the general trend, G > A > C ≈ T, in agreement with the results by Sowerby et al.,²⁵ and demonstrating that there is indeed a relationship between binding affinity and molecular identity of the nucleobase. This behaviour was also replicated under aqueous conditions, using thermodynamic integration to calculate the free energy of binding on the outer walls of a narrow (11, 0) nanotube;²⁷ the results obtained showed that binding always leads to favourable thermodynamic states, with free energy values between −43 kJ mol⁻¹ and −28 kJ mol⁻¹, for guanine and cytosine, respectively, due to the π-stacking arrangement of the biomolecule on the solid wall. However, when the nanotube atoms become electrically charged (−0.05 ≤ q (e⁻/C) ≤ +0.05), that stacking behaviour progressively vanishes upon an increase of charge density,²⁸ up to a point where no stable binding can be observed. Xiao et al.²⁹ studied the wrapping of dinucleotides around narrow armchair and chiral nanotubes using replica-exchange molecular dynamics at 300 K and 1 bar. Their simulations indicate that the binding free energy is approximately independent of nanotube topology, but varies with biomolecular identity, spanning a range of −129.6 kJ mol⁻¹ to −117.5 kJ mol⁻¹, for the TT and AA homo-dinucleotides, respectively. The van der Waals energies are the dominant contribution to the binding free energy, and the exoadsorbed nucleobases lie flat on the SWCNT outer walls. When the surface becomes hydrophilic, such as an amine functionalized Si (111) substrate, an opposite trend occurs and the pyrimidines exhibit higher binding affinities than the purine moieties.³⁰

The extreme narrowness of the nanotubes employed in the above studies precludes any possibility of molecular encapsulation. What happens when the diameter is increased, up to the point where the solid's internal volume is large enough to accommodate the nucleobases? We have already characterized the SWCNTs energetic landscape regarding both exo- and endoadsorption using small organic probe molecules, C₁–C₃, and nanopores in the range 1.1 ≤ D (nm) ≤ 1.81.^31,32 Our data revealed that as diameter is increased, the zero-loading heat of endoadsorption decreases, according to a first-order exponential decay, q⁰ ∼ exp(−D), and approaches that for a flat graphene sheet; the opposite was observed for exoadsorption. Wang et al. showed³³ that a similar trend occurs for exoadsorption of adenine dinucleotides onto zig-zag nanotubes beyond D > 0.8 nm. This latter finding can be interpreted in terms of the geometrical features of the nanopore; as the nanotube diameter increases, up to the limit of a flat graphene surface, the binding affinity between a nucleobase and the solid increases as a result of a smaller curvature³⁴ and enhanced π stacking interactions.

While biomolecular exoadsorption on small diameter nanotubes (D < 1 nm) is reasonably understood, confinement driven adsorption is a phenomenon that remains quite unexplored. Pioneering the work in this area were the high temperature (400 K) molecular dynamics simulations of Gao et al.,¹⁰ who employed a D = 1.36 nm armchair nanotube as confining media, and showed that an 8-base long ssDNA could be spontaneously encapsulated in the nanotube within ca. 2 ns. Kamiya and Okada³⁵ performed DFT calculations and determined the encapsulation energy of homopolymer ssDNA as a function of nanotube diameter. However, the system ssDNA/SWCNT was studied under vacuum, thus preventing any extrapolation to aqueous conditions. Nonetheless, their results indicate a rather strong influence of nanotube diameter upon the corresponding encapsulation energy, particularly in the range 1.25 ≤ D (nm) ≤ 1.8.

As far as we know, there are no previous studies of intratubularly confined nucleobases. We shall address this issue using two different diameter nanotubes, both with zig-zag symmetry,³⁶ namely (16, 0) with D = 1.25 nm and (23, 0) with D = 1.8 nm; these two topologies correspond essentially to the narrowest and largest nanopores usually prepared by the electric-arc discharge method.^32,37 Moreover, it is well known that nanotubes can be electrically charged, either using an AFM tip and applying a voltage bias or by chemically doping the solids with p-type dopants to obtain positively charged pores.^14,28 The effect of charge density upon the dynamics and energetics of confinement is probed using purely hydrophobic solids and nanotubes with nominal electric charges of q = +0.05 e⁻/C.

In the present work we report classical molecular dynamics (CMD) simulations of the interactions between nucleobases and zig-zag carbon nanotubes at physiological temperature (310 K); adenine (A) and thymine (T) are chosen as representative models of purine- and pyrimidine-based nucleobases (Fig. 1), and aqueous conditions are mimicked by explicitly including H₂O molecules and Cl⁻ ions in the calculations. The questions that we attempt to answer are: (1) if initially in a bulk solution, will the biomolecules become encapsulated in the nanotubes? (2) What is the influence of nanopore diameter and electrical charge density upon the confinement energetics? (3) How does the confining solid interacts with the nucleobases? To allow an efficient exploration of the thermodynamical phase space two enhanced sampling techniques are independently coupled with CMD, namely well-tempered metadynamics and umbrella sampling. The latter are discussed in Section 2 along with the molecular models and intermolecular potentials employed. The results are presented in Section 3.1 and the confined fluid structure is rationalized in Section 3.2 in terms of the microscopic details involved. Finally, we conclude with a summary and discussion.

Fig. 1 Atomistic representation of the DNA nucleobases studied in this work. The π conjugated system in adenine is represented by a dotted line running through the 6-membered ring, chemical bonds as lines and atoms as spheres: grey (C), blue (N), red (O) and white (H). The arrows indicate the dipole moments^38,39 associated with each isolated molecule.

2. Theoretical methods

2.1. Molecular models

All molecules in this work are described using fully atomistic potentials, which include partial electrostatic charges located in each atom. The dispersive interactions are calculated with the Lennard-Jones (12, 6) potential and cross parameters between unlike particles determined by the classical Lorentz–Berthelot mixing rules.⁴⁰ Nucleobases are modelled as completely flexible entities, and the corresponding potential energies associated with bond stretching, U(r), and angle bending, U(θ), calculated with harmonic potentials (eqn (1)), and the dihedral energies, U(ϕ), via Ryckaert–Bellemans functions (eqn (2)):where r₀ and θ₀ are the equilibrium bond length and angle, respectively. The all-atom OPLS-2001 force-field is employed for the nucleobases⁴¹ and water is described by the 3-site TIP3P model of Jorgensen and co-workers.⁴² According to previous simulation work^43,44 the nanotubes are modelled with the Steele parameterization⁴⁵ for graphitic carbon atoms (σ = 0.34 nm, ε = 28 K) and with a C–C bond length of 1.42 Å.

Two different nanotubes are used, both with zig-zag symmetry,³⁶ corresponding to skeletal diameters of D = 1.25 nm (16, 0) and D = 1.8 nm (23, 0), measured between carbon centers on opposite sides of the wall. In both cases, a length-to-radius ratio of (L/R) ≈ 3.6 was employed, and the positions of all solid atoms constrained throughout the whole simulation length. As previously mentioned, the effect of electrically charging the nanotubes was also addressed by placing a nominal charge of q = +0.05 e⁻ on every carbon atom in the solid, leading to effective charges of q = +5.1136 × 10 ⁻² e⁻/C and q = +5.1152 × 10 ⁻² e⁻/C, for the (16, 0) and (23, 0) topologies, respectively. Charge neutrality on the system was enforced by adding the appropriate integer number of Cl⁻ ions to the simulation box and using the force-field parameterization of Aqvist and Dang.⁴⁶ A total number of 18 and 40 chloride ions were employed for the (16, 0) and (23, 0) nanotubes, respectively.

2.2. Simulation methodology and algorithms

Large simulation cells were built according to a stepwise procedure, with total dimensions 4.02 × 4.02 × 4.22 nm (16, 0) and 4.55 × 4.55 × 5.34 nm (23, 0): (i) initially, the nanotube was placed inside the empty cell, aligned along the z-axis, and the nucleobase with its molecular plane parallel to the pore entrance at a distance of 5 Å, (ii) the cell was solvated with H₂O (and Cl⁻ ions where appropriate), following which, (iii) the whole system was energy-minimized and equilibrated during at least 0.5–0.7 ns, to ensure proper solvent density, first in the canonical ensemble and then finally in the isothermal–isobaric ensemble, resulting in fully equilibrated systems, as observed by the constancy of the main thermodynamical parameters (potential energy, temperature, volume and pressure). During minimization and equilibration the nucleobase position was restrained at a 5 Å distance away from the nanopore terminus. Once this procedure was completed, the nucleobase was unrestrained, production runs were started and data collected during a total time of 0.03–0.1 μs.

Classical molecular dynamics simulations in the isothermal–isobaric ensemble (NPT) were performed using the Gromacs 4.5 simulation package.⁴⁷ Newton's equations of motion were integrated with a timestep of t = 1 fs, while using a Nosé–Hoover thermostat^48,49 and a Parrinello–Rahman barostat⁵⁰ to maintain temperature and pressure at T = 310 K and p = 1 bar. A potential cutoff of 1 nm was employed for both the van der Waals and Coulombic interactions, and the particle-mesh Ewald method^51,52 adopted to calculate the long-range electrostatics using cubic interpolation and a maximum Fourier grid spacing of 0.12 nm. Three-dimensional periodic boundary conditions were applied.

The well-tempered metadynamics scheme of Parrinello and co-workers^53,54 was employed to construct free-energy landscapes using the Plumed 1.2.2 set of routines.⁵⁵ Briefly, the well-tempered algorithm biases Newton dynamics by adding a time-dependent Gaussian potential, V(ζ, t), to the total (unbiased) Hamiltonian, avoiding the system to become permanently trapped in local energy minima and thus leading to a more efficient exploration of the phase space. The potential V(ζ, t) is a function of the so-called collective variables (or order parameters), ζ(q) = [ξ₁(q), ξ₂(q), …, ξ_n(q)], which in turn are related to the microscopic coordinates of the real system, q, according to

where t is the simulation time, W = τ_Gω is the height of a single Gaussian, τ_G is the time interval at which the contribution for the bias potential is added, ω is the initial Gaussian height, ΔT is a parameter with dimensions of temperature, σ_i is the Gaussian width and n is the number of collective variables in the system. In the present work we have used τ_G = 0.1 ps, ω = 0.1 kJ mol⁻¹, ΔT = 310 K and σ = 0.1 nm. It should be noted that the parameter ΔT determines the rate of decay for the height of the added Gaussian potentials; when ΔT → 0 the well-tempered scheme approaches an unbiased simulation.

Considering the quasi one-dimensional symmetry characteristic of SWCNTs, the free-energy landscapes are constructed in terms of two collective variables, ξ₁ and ξ₂:

ξ₁ = r^NB_z(x, y, z) − r_z¹(x, y, z) (4)

ξ₂ = r^NB_z(x, y, z) − r_z²(x, y, z) (5)

In our definition of collective variables, r_z(x, y, z) is the positional vector of the center of mass projected along the z-axis, and the superscripts are relative to the nucleobase (r^NB) and to the SWCNT pore entrance (r¹) and center (r²). At the end of the simulation, the three-dimensional free-energy surface is constructed by summing up the accumulated time-dependent Gaussian potentials according to F(ζ, t) = −[(T + ΔT)/ΔT]V(ζ, t). A discussion on the algorithm's convergence towards the correct free-energy profiles is beyond the scope of this paper and can be found elsewhere;^54,56 suffice it to say that in the long time limit the time derivative of the bias potential tends to zero, [∂V(ζ, t)/∂t]_t→∞ → 0, and the well-tempered method leads to a converged free energy surface. An alternative approach to obtain the latter relies on averaging F(ζ, t) at the final portion of the metadynamics run.⁵⁶ The converged free-energy can thus be mathematically obtained from

where t_tot is the total simulation time and τ is the time window over which averaging is performed. A metadynamics convergence analysis using this second approach is recorded in ESI (Fig. SI1).†

To corroborate the results obtained by the well-tempered metadynamics algorithm, independent calculations were performed using the umbrella sampling technique.^57,58 For a system composed of N particles, the method consists in biasing the classical (unbiased) Hamiltonian that depends on the potential, U(r^N), and kinetic energies, E_kin(p^N), by introducing a time independent harmonic potential, 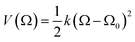, according to H(r^N, Ω, p^N) = U(r^N) + V(Ω) + E_kin(p^N); k is the harmonic force constant, Ω is an order parameter, which in the present case is defined as the absolute three-dimensional distance between the centers of mass of the NB and the SWCNT, Ω = |r^NB(x, y, z) − r^SWCNT(x, y, z)|, and Ω₀ corresponds to the position of the umbrella restrain. We adopted Ω₀ = 0, in direct analogy with the collective variable ξ₂ defined in the well-tempered metadynamics algorithm (eqn (5)). When such a biasing potential is used, the biased probability distribution of the system, P^b(Ω), can be obtained from a Boltzmann weighted average along the Ω order parameter and, therefore, assuming that the system is ergodic:⁵⁸

where β = (1/k_BT), k_B is the Boltzmann constant and δ is the Dirac delta function. Because the biasing potential depends only on the order parameter Ω, and the integration in the numerator is performed over all degrees of freedom except Ω, the unbiased probability of the real system, P^u(Ω), can be evaluated from

P^u(Ω) = P^b(Ω)exp^βV(Ω)Γ (8)

where Γ = −(1/β)ln〈e^−βV(Ω)〉 is independent of Ω and the triangular brackets denote an ensemble average. The reconstruction of the true (unbiased) free energy profile or potential of mean force,⁵⁹ consistent with the Gibbs free energy, F(Ω) = −k_BTlnP^u(Ω), was accomplished using the weighted histogram analysis method (WHAM).^59,60

3. Results and discussion

Results obtained in the calculations are presented in this section, for both the hydrophobic and electrically charged nanotubes, as well as the free-energy landscapes of the corresponding confined systems. The interaction energies between a nucleobase and the hydrophobic solids given in Table 1 were obtained after an initial time window of 2–5 ns, for which the corresponding statistics were discarded. As will be shown, the main features associated with the free-energy landscapes are supported by umbrella sampling calculations. Further on (Section 3.2), the confinement mechanism itself is characterized in terms of the resulting fluid structure and the distances of closest approach between a nucleobase and the solid walls are determined.

Table 1 Interaction energies between the nucleobases and the carbon nanotubes, E^int = E^vdw + E^Coul, where E^vdw is the dispersive energy and E^Coul corresponds to the electrostatic contribution. Subscripts give the uncertainty in the last digit

		E ^vdw (kJ mol^−1)		E ^Coul (kJ mol^−1)		E ^int (kJ mol^−1)
		A	T	A	T	A	T
a Exoadsorbed nucleobases. b Confinement close to the nanopore center. c At the pore termini.
Unch.	(16, 0)	−83.11	−82.21	0.0	0.0	−83.1	−82.2
	(16, 0)^a	−45.79	−43.46	0.0	0.0	−45.7	−43.4
	(23, 0)	−68.61	−67.21	0.0	0.0	−68.6	−67.2
	(23, 0)^a	−48.07	−45.93	0.0	0.0	−48.0	−45.9
Charged	(16, 0)^a	−35.22	−31.83	−19.83	−20.63	−54.9	−52.3
	(23, 0)^b	−67.81	−40.85	−40.53	−28.75	−108.3	−69.5
	(23, 0)^c	−42.21	−43.92	−25.12	−30.72	−67.3	−74.6

---

3.1. Free-energy landscapes and interaction energies

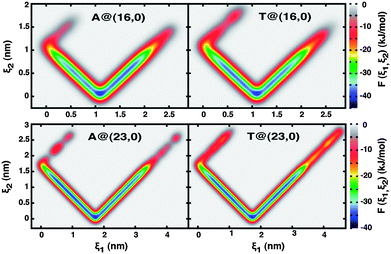
The large-scale well-tempered metadynamics simulations previously described (Section 2.2) were performed with the two different nanotube topologies, (16, 0) and (23, 0), and for each nanotube considering the cases of hydrophobic (uncharged) and electrically charged walls (q = +0.05 e⁻/C). The free-energy landscapes thus obtained are represented in Fig. 2 and 4 as two-dimensional contour maps, where ξ₁ is the distance between the nucleobase c.o.m. and the nanopore entrance projected along the z-axis and ξ₂ is the equivalent distance between the two centres of mass (eqn (4) and (5)).

Fig. 2 Free energy landscapes, F(ξ₁, ξ₂), of adenine (A) and thymine (T) in contact with (16, 0) and (23, 0) hydrophobic nanotubes. The two collective variables, ξ₁ and ξ₂, correspond to the distance between the nucleobase c.o.m. and the nanotube entrance or center, respectively, projected along the z-axis (see text for details). The absolute free energy minima, indicated by the small dark blue regions at [ξ₁, ξ₂]^(16,0) = (1.1, 0.08) nm and [ξ₁, ξ₂]^(23,0) = (1.7, 0.08) nm, coincide almost exactly with the carbon nanotube c.o.m.

The V-shaped and highly symmetrical landscapes of the uncharged solids (Fig. 2) are essentially one dimensionally isotropic regarding the ξ₁ order parameter, in direct relationship to the nanotubes quasi 1-D symmetry about the z-axis. As a result of the strong hydrophobic nature of uncharged nanotubes, it becomes clear from Fig. 2 that confinement of a nucleobase, initially in bulk solution and at a distance of 5 Å away from the nanopore entrance, is an energetically very favourable process; this is particularly true when compared to adsorption of the nucleobases onto the external wall of SWCNTs (exoadsorption). Once trapped inside the nanotube, a nucleobase can explore a region whose boundaries are comprised between the pore termini, 0.15 ≤ ξ₁ (nm) ≤ L_z (where L_z is the SWCNT length), and the inner surface of the solid wall, always avoiding returning back to the bulk solution. Furthermore, it is very interesting to observe that confinement effects are remarkably stronger at the nanopore center, where free energy differences are largest, as indicated by the highly localized dark blue regions of Fig. 2 at ca. [ξ₁, ξ₂]^(16,0) = (1.1, 0.08) nm and [ξ₁, ξ₂]^(23,0) = (1.7, 0.08) nm. The yellow and red domains at ξ₂ > 1.1 nm (16, 0) and ξ₂ > 1.8 nm (23, 0) correspond to remnants of the pre-confinement systems, where the nucleobases are still in the bulk and experiencing strong van der Waals attraction to the hydrophobic nanotube. The confinement process is not only energetically very favourable, but it also seems to be irreversible, at least during the time window spanned. Independent molecular dynamics simulations were performed where the bias potential was turned-off, thus resulting in classical MD calculations. It could be observed that molecular confinement was indeed thermodynamically spontaneous for both nucleobases in either the (16, 0) or (23, 0) hydrophobic topologies, as recorded in ESI (Fig. SI2).†

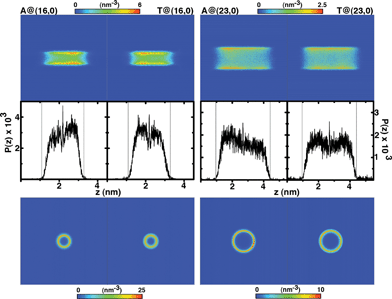
We have calculated the nucleobase number density in the whole simulation box, ρ = (N/V), and plotted the corresponding axial and radial representations as two-dimensional maps in Fig. 3. The well defined annular volume observed in the xy plane, whose thickness essentially corresponds to an atomic layer (σ_LJ ≈ 3–4 Å) and propagates along the z direction, demonstrates that the biomolecule is always in direct contact with the hydrophobic walls, avoiding the H₂O-rich region located about the SWCNT main axis. Increasing the pore diameter drastically enhances this effect, pushing the NBs further away from the pore center and towards the walls.

Fig. 3 Two-dimensional maps of the number density of nucleobases confined onto hydrophobic nanotubes: (top) axial view (xz plane), (bottom) radial representation (xy plane). Normalized probability distribution of the nucleobases c.o.m. position along the z-axis, , where L^(16,0)_z = 4.24 nm and L^(23,0)_z = 5.37 nm. Dashed lines indicate the boundaries of the uncharged nanotubes and the central peaks at 2.19 nm and 2.69 nm coincide almost exactly with the nanopore center. Note that the integral ∫P(z)dz corresponds to 0.996 (A) and 0.993 (T) in the (16, 0) topology and 0.995 (A) and 0.980 (T) for the (23, 0) nanotube, when computed between the solid termini.

Let us now consider that a molecule is confined inside a SWCNT with skeletal diameter D (nm), when its center-of-mass positional vector, r⃑ = r(x, y, z), lies within a cylindrical surface whose cross section in the xy plane is given by

where and are the center coordinates of that cross section in the x and y dimensions, respectively. We have already demonstrated the existence of a non-negligible annular layer adjacent to the solid inner walls that is not accessible to fluid molecules;³¹ this exclusion volume arises essentially from the strong short-ranged repulsive interactions between the fluid and the nanotube. Using a purely isotropic Lennard-Jones sphere model, σ_LJ = 3.7 Å, to study CH₄ confined in SWCNTs, we have determined the thickness of that layer to be δ = 2.8 Å. In the present study, hydrogens are the smallest atoms in any nucleobase molecule, with a Lennard-Jones collision diameter of σ_LJ = 2.5 Å, and therefore δ = 2 Å in eqn (9). We will see later on how this layer thickness is influenced by the existence of partial electrostatic charges on the tube walls, calculating the distance of closest approach between any nucleobase atom and the solid (Section 3.2). In order to evidence the strong and irreversible nature of the confinement process associated with the hydrophobic nanopores, we have computed the number of occurrences over the whole simulation length that fulfil eqn (9). The corresponding frequency histograms along the z-axis were built (Fig. 3) with bin widths of 5 × 10⁻³ nm and then normalized to yield , where L^(16,0)_z = 4.24 nm and L^(23,0)_z = 5.37 nm are the simulation box lengths. When the nanotubes are electrically neutral, the distributions in Fig. 3 show that once a nucleobase is confined, the probability of escaping and returning to the bulk solution is virtually zero, thus resulting in [1 − P(z)] < 0.02 for both topologies. The sharp peaks at z = 2.19 nm (16, 0) and z = 2.69 nm (23, 0) coincide almost exactly with the nanotubes center of mass, in agreement with the existence of a unique free-energy minimum exactly located at the nanotube center (Fig. 2).

The free energy landscapes of the electrostatically charged nanotubes overall bear similarities with the hydrophobic analogues. Nonetheless, the contour maps in Fig. 4 also indicate interesting new features, the most prominent of which is the existence of a second free-energy minimum located at the nanopore entrance, [ξ₁, ξ₂]^(16,0) = (0.08, 1.08) nm and [ξ₁, ξ₂]^(23,0) = (0.08–0.33, 1.41–1.70) nm, that is completely absent for the uncharged nanotubes. It is worth noting that the nanopore termini are symmetrical about the SWCNTs center of mass and thus the sets of collective variables that characterize them are identical, [ξ₁, ξ₂]^(16,0) = (0, 1.1) ⇔ [ξ₁, ξ₂]^(16,0) = (2.2, 1.1) and [ξ₁, ξ₂]^(23,0) = (0, 1.7) ⇔ [ξ₁, ξ₂]^(23,0) = (3.4, 1.7). The quasi one-dimensional symmetry with respect to ξ₁ is still maintained, but breaks up in a much more drastic manner beyond ξ₂ > 1.2 nm (16, 0) and ξ₂ > 1.9 nm (23, 0), corresponding to a region of space outside the nanotubes. This indicates that confinement effects are now weaker and that the encapsulation process itself can be reversed, that is, a confined nucleobase can escape from the internal volume of the nanotube towards the bulk solution. It is also very interesting to observe that in the case of the larger diameter pores (23, 0), confined adenine appears to be kinetically more mobile than thymine (ESI, Fig. SI3†). The almost continuous blue path observed for adenine between 0 < ξ₁ (nm) < 3.4 (Fig. 4), corresponding to the minimum free energy route between opposite nanopore entrances, in the case of thymine becomes almost discretized into three main free energy minima corresponding to the nanopore center and entrances.

Fig. 4 Free energy landscapes, F(ξ₁, ξ₂), of adenine (A) and thymine (T) in contact with (16, 0) and (23, 0) electrically charged nanotubes (q = +0.05 e⁻/C). The two collective variables, ξ₁ and ξ₂, correspond to the distance between the nucleobase c.o.m. and the nanotube entrance or center, respectively, projected along the z-axis (see text for details). Regardless of the particular system, two free energy minima can be observed in each case, corresponding to the nanotube center along the z-axis, [ξ₁, ξ₂]^(16,0) = (1.09, 0.08) nm and [ξ₁, ξ₂]^(23,0) = (1.72, 0.08) nm, and the solids entrance, [ξ₁, ξ₂]^(16,0) = (0.08, 1.08) nm and [ξ₁, ξ₂]^(23,0) = (0.08–0.33, 1.41–1.70) nm. Note that the nanopore termini are symmetrical about the SWCNTs c.o.m. and thus the sets of collective variables are equivalent: [ξ₁, ξ₂]^(16,0) = (0, 1.1) ⇔ [ξ₁, ξ₂]^(16,0) = (2.2, 1.1) and [ ξ₁, ξ₂]^(23,0) = (0, 1.7) ⇔ [ξ₁, ξ₂]^(23,0) = (3.4, 1.7).

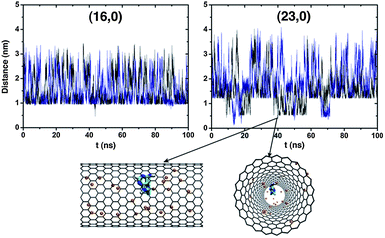
It now becomes clear that the existence of a nonzero charge density on the solid modifies the thermodynamics of confinement. In order to throw some light onto this apparent discrepancy it is necessary to probe the microscopic details. For this purpose, the center-of-mass distances between nucleobase and carbon nanotube have been calculated and are graphically plotted in Fig. 5 as functions of time. A similar plot for the hydrophobic solids can be found in the ESI (Fig. SI4).† When the (16, 0) topology is electrically charged, molecular confinement is inhibited for both nucleobases, at least over the large time window spanned in the simulations. The charge density on the solid now seems to prevent the endohedral adsorption of the biomolecules.

Fig. 5 Center of mass distance between a nucleobase and electrically charged SWCNTs (q = +0.05 e⁻/C): (black) adenine, (blue) thymine. Notice that the almost uniform distance plateaus at ca. 1 nm (16,0) and 1.35 nm (23,0) essentially correspond to the nanopore entrances, (L_z/2)^(16,0) = 1.1 nm and (L_z/2)^(23,0) = 1.7 nm. For the (23, 0) topology, the lower valleys located at distances of 0.3–0.6 nm clearly support the existence of confined nucleobases, as shown by the snapshots obtained at t = 39.97 ns (H₂O molecules have been omitted and the orange spheres correspond to Cl⁻ ions) where adenine is positioned at a distance of 0.38 nm from the SWCNT c.o.m.

A closer inspection of the left graph in Fig. 5 indicates that there is a minimum distance threshold of ca. 1 nm below which neither adenine nor thymine can come closer to the SWCNT center. Bearing in mind that the length of a (16, 0) nanotube is L = 2.2 nm, that threshold can be in fact any of the two (symmetrically opposite) nanopore termini as previously identified by the existence of a second free energy minimum in Fig. 4. The minima located at ξ^(16,0)₂ = 0.08 nm can now be clearly attributed to the adsorption of the nucleobases onto the external walls of the nanotubes, at a site where the NB positional vector projection along the z-axis lies exactly upon the SWCNT c.o.m. It has been previously observed that a similar process of exoadsorption can occur, involving π–π stacking of the nucleobases onto the graphitic mesh, and leading to energetically stable hybrids NB/SWCNT.^22,24 The spike at t ≈ 43.5 ns, in the left graph of Fig. 5, is a spurious one. If the diameter of the nanotube is increased to D = 1.8 nm while maintaining the same charge density a different picture is obtained. The temporal profiles in Fig. 5 for the (23, 0) topology still exhibit a minimum distance threshold, now of ∼1.3 nm; however that threshold can be crossed originating low-lying valleys. These valleys, corresponding to distances of 0.3–0.6 nm between the nucleobases and the SWCNTs center, indicate that molecular confinement is now possible and that the latter can occur multiple times during the whole simulation length, e.g., it is a reversible process.

Because of the manner in which the metadynamics order parameters ξ₁ and ξ₂ were constructed (eqn (4) and (5)), we were able to identify the nanotubes center and/or entrances as the privileged sites to be occupied once molecular confinement occurs. Nonetheless, since ξ₁ and ξ₂ were formulated in terms of one-dimensional distances spanning the nanotube main axis, extra information will be needed to pinpoint the exact location of the encapsulated nucleobases. To this purpose, independent umbrella sampling calculations were conducted using a new order parameter, formulated in terms of the absolute (3D) distance between centres of mass of the nucleobase and the SWCNT, Ω = |r^NB(x, y, z) − r^SWCNT(x, y, z)|. The corresponding potential of mean force (PMF) profiles are recorded in Fig. 6 along with the unbiased probability distributions.

Fig. 6 Potential of mean force (PMF) and probability distribution profiles for the nucleobases in contact with hydrophobic (black) and electrically charged carbon nanotubes (red). The order parameter, Ω, corresponds to the absolute (3D) distance between c.o.m.'s of the nucleobase and the solid. Notice the parallel alignment of the nucleobase with the hydrophobic solid walls and the existence of two maxima in the probability curves for the electrically charged (23, 0) nanotubes. The axial and radial snapshots represent the SWCNT (grey mesh), water oxygen atoms (red dots), Cl⁻ ions (orange) and the nucleobases (N: dark blue, C: light blue, H: white, O: red).

A single, well-defined PMF minimum is observed for the purely hydrophobic solids, to which corresponds a maximum in the probability distribution curve, in good agreement with the findings obtained using the well-tempered metadynamics scheme (Fig. 2). That minimum is located at Ω = 0.26 nm in the case of the narrowest nanotube (16, 0), and is shifted towards larger distances when the SWCNT diameter is increased, Ω = 0.54 nm. Considering the usual definition of skeletal diameter previously described (Section 2.1) and that σ_LJ = 3.4 Å for graphitic carbons, this means that in both topologies the PMF minima denote a configuration where the nucleobase center of mass is at a distance of ca. 0.19 nm away from the graphitic surface, therefore in direct contact with the solid. In terms of the characteristical 1-D symmetry of the nanotubes, it now becomes clear that the nucleobases are indeed confined very close to the pore center, with its molecular plane parallel to the walls thus maximizing the dispersive interactions with the solid. The axial inset in the upper left graph of Fig. 6, obtained at Ω = 0.26 nm for a (16, 0) topology, shows the adenine molecule in direct contact with the nanotube walls, without any H₂O molecules mediating the adsorption process. In a recent study of RNA translocation through hydrophobic and hydroxyl-decorated SWCNTs, Zimmerli and Koumoutsakos⁶¹ observed that the nucleosides experienced multiple stacking/unstacking events within the nanopore, and, while stacked, the volume between the former and the solid was devoid from water. Although not graphically recorded in Fig. 6, a similar conclusion can be established for thymine.

When the charge density on the solids is nonzero the multiplicity and position of the PMF minima become dependent on the particular nanotube diameter (Fig. 6), suggesting a more intricate balance between free energy minima and structural features. The narrowest (16, 0) nanopore exhibits a single probability maximum located at the entrance, Ω = 0.97 nm (A) and Ω = 1.04 nm (T), which rapidly decreases to negligible values once the nucleobase gets further away from the nanotube. On the other hand, if the Ω order parameter is decreased bellow ca. 0.95–0.97 nm, the probability maxima decrease rather abruptly, reaching P(Ω) < 6.5 × 10⁻⁵ almost instantaneously and indicating that molecular confinement in the center of the nanotube is an energetically prohibited process, as the potential of mean force associated rapidly has to surpass a barrier larger than 10 kJ mol⁻¹.

A different picture is obtained when the largest (23, 0) nanotube is employed, for the aforementioned single maxima are split into two contributions. The pore entrance still corresponds to a maximum in the probability distribution, now located at Ω = 1.55 nm (A) and Ω = 1.64 nm (T); however, in the case of adenine, that maximum now becomes a local one. In fact, the new maximum at the pore center (Ω = 0.54 nm) is the absolute one for adenine, whose associated probability P(Ω = 0.54) = 34.322 × 10⁻³, is more than three times larger than that at the pore entrance, P(Ω = 1.55) = 9.845 × 10⁻³; for the pyrimidine molecule, both confinement regions have very similar probabilities of occurrence. Upon confinement, it is preferable for the purine moiety to penetrate deeper into the nanopore center to reach a minimum free energy region; it has already been discussed above that the minimum free energy path between nanopore center and termini is approximately continuous for adenine, but becomes almost discretized into three core domains for thymine (Fig. 4).

These somehow subtle differences between purine and pyrimidine moieties can be numerically addressed by decomposing the total energy of interaction between the confined nucleobase and the solid nanopore, E^int, into the dispersive, E^vdw, and electrostatic, E^Coul, contributions, as recorded in Table 1. It should be noted that the energies calculated for the charged (16, 0) solid correspond to unconfined molecules. When the SWCNTs are purely hydrophobic, the interaction energies increase with the nanotube curvature; due to the strong π conjugated system characteristic of the nucleobases, a diameter decrease enhances the dispersive interactions with the solid thus increasing E^int. Wang and Ceulemans³³ showed that the binding affinity of adenine onto the external walls of zig-zag nanotubes increases as the nanopore opens up and approaches a flat graphene sheet. This is not inconsistent with the results recorded in Table 1. When a nucleobase experiences endohedral confinement, unlike exohedral adsorption, it interacts not only with the wall that is closer but also with the opposite one. Thus, as the nanopore curvature increases, the opposite wall comes closer to the nucleobase and the latter experiences an enhanced interaction with the hydrophobic solid due to the naturally short-ranged dispersive energies. Using small organic probe molecules (C₁–C₃) and Monte Carlo calculations, we have shown that the endohedral isosteric heat of adsorption decreases with the nanotube curvature,³¹ and validated this observation with experimental data.

It has been previously demonstrated that nucleobase adsorption onto the hydrophobic nanotube external walls favoured purine type molecules (adenine, guanine) as opposed to the pyrimidine based moieties (thymine, cytosine).^26–28 The values recorded in Table 1 expand these previous observations for the process of intratubular confinement; whilst energetic differences between adenine and thymine are small (≈0.9–1.4 kJ mol⁻¹), regardless of individual nanotube diameter the purine moiety interacts more strongly with the solid internal walls. Umadevi et al. reported DFT calculations of nucleobase adsorption onto graphene,³⁴ employing a dispersion corrected B3LYP-D/6-31G* functional validated by comparison with experimental calorimetric data.⁶² Their results of binging energy obtained for adenine and thymine, −62.5 kJ mol⁻¹ and −59.7 kJ mol⁻¹, respectively, are in good agreement with our own for the (23, 0) topology, confirming that the energetic differences between the nucleobases, in spite of small, favour the purine molecule. A linear extrapolation of our data towards larger nanotube diameters indicates that confinement enhances the adsorption energetics at least until the nanotube reaches D ≈ 2.05 nm. At this diameter, corresponding to a (26, 0) zig-zag topology, the interaction energies of the nanoconfined nucleobases roughly match those for adsorption onto flat graphene.³⁴ We have also calculated the interaction energies between a nucleobase and the solids external walls, running independent simulations where the nanopore entrances were not accessible to the nucleobases thus effectively preventing molecular encapsulation. The corresponding results (Table 1) indicate that endohedral interactions are stronger by ∼20 kJ mol⁻¹ and ∼40 kJ mol⁻¹ for the (23, 0) and (16, 0) topologies, respectively.

The energies in Table 1 for the (16, 0) electrically charged solids correspond to exoadsorbed nucleobases. It is interesting to observe that the interactions are now weaker than when charge density is null, by ca. 28–30 kJ mol⁻¹. This weakening arises essentially from a marked decrease in the dispersive energies that are diminished by almost 50 kJ mol⁻¹ compared to the hydrophobic solids. A similar observation has been reported before employing a (8, 8) SWCNT with D_eff = 0.75 nm,²⁸ and interpreted in terms of the unstacking of the nucleobases from the solid external walls as a response to a charge density increase. Frishknecht et al.⁶³ studied the exoadsorption of nucleobase monophosphates onto extremely narrow (6, 0) nanopores (D_eff = 0.14 nm) considering only two Na⁺ counterions, and concluded that purines would bind more favourably to the solid, E^int(A) = −43.05 kJ mol⁻¹ and E^int(T) = −22.15 kJ mol⁻¹. These values however do not allow a direct comparison with data in Table 1, for apart the existence of explicit phosphate ions, the (6, 0) solid has a much larger curvature than the (16, 0) considered here, thus preventing π stacking of the nucleotide monophosphates onto the walls.

Increasing the nanopore diameter while maintaining the same charge distribution leads to the occurrence of molecular encapsulation. When a nucleobase is in contact with an electrically charged (23, 0) nanotube, the probability distributions obtained by umbrella sampling exhibit two maxima (Fig. 6), showing that the molecule can be confined in two different regions. The maximum at Ω = 0.54 nm corresponds to a spherical volume located at the nanopore center, whilst the maxima Ω = 1.55 nm (adenine) and Ω = 1.64 nm (thymine) indicate the solid's entrances (Fig. 7). Close to the nanotube center, where a molecule is the furthest away from bulk solution, confinement effects are very strong and the corresponding interaction energies at that location are larger than at the termini (Table 1). The probability distribution maximum at Ω = 0.54 nm is the de facto global maximum for adenine, and, instead, a local one for thymine. Because the purine molecule has a considerably smaller dipole moment,⁶⁴μ (A) = 2.533 D and μ (T) = 4.862 D, its confinement at the nanopore center, where it is in direct contact with both solid walls, stabilizes the molecule by 41 kJ mol⁻¹ compared to the nanotube entrances. Thymine, on the other hand, clearly favours the pore termini, where it is stabilized by ca. 5 kJ mol⁻¹. The existence of a non-zero charge density therefore alters the relative stability of the confined nucleobases at the pore center, forcing a larger separation between the corresponding interaction energies and leading to E^int (A) = −108.3 kJ mol⁻¹ and E^int (T) = −69.5 kJ mol⁻¹.

Fig. 7 Pictorial two-dimensional representation in the xz plane of a (23, 0) electrically charged nanotube, highlighting the two distinct zones where the occurrence of molecular confinement is predominant: (left) at the pore center, Ω = 0.54 nm, and (right) close to the termini, Ω = 1.55–1.64 nm (dimensions are not to scale). The graphitic carbon atoms on the walls have a nominal charge of q = +0.05 e⁻/C.

3.2. Confinement mechanism: structure and dynamics

Initially with the molecular plane perpendicular to the nanotube main axis (z), nucleobases were placed at a distance of 5 Å away from the nanopore entrance (Section 2.2) and immediately started diffusing towards the hydrophobic solids with their molecular plane roughly parallel to the walls; maximizing the dispersive interactions with the graphitic mesh. The confinement kinetics is extremely fast for all systems, and encapsulation is complete at or before 0.02–1.5 ns of initial simulation time (ESI, Fig. SI4†). Postulating that to obtain complete confinement a NB is at a distance of no more than 6 Å (16, 0) or 12 Å (23, 0) away from the SWCNT center, we obtain for the corresponding confinement velocities, 〈v〉 (m s⁻¹): 47.62 (A@16, 0) > 18.87 (T@16, 0) > 7.57 (A@23, 0) > 0.87 (T@23,0). Pei et al.⁶⁵ studied the translocation of a three oligonucleotide single-stranded DNA molecule through bottle-neck (10, 10)–(16, 16) armchair geometries, with diameters D = 1.36 nm and D = 1.89 nm, and observed an average translocation velocity of 〈v〉 = 16.66 m s⁻¹ for the initially confined molecule. Their results are of the same order of magnitude as the average confinement velocities now being reported for the individual nucleobases.

After encapsulation, nucleobases diffuse along the hydrophobic nanopores with the 6-membered ring parallel to the walls (ESI, Animations SI1–SI2†), indicating that dispersive energy dominates molecular interactions. This is particularly surprising, and previously unobserved, for the larger topology where the cylindrical volume centred on the z-axis remains virtually unexplored by the nucleobase during the whole time window.

The number density maps for the electrically charged nanotubes are plotted in Fig. 8. There is no confinement into the (16, 0) solid, and thus the axial number density exhibits a large scattering around the nanotube, evidencing nonetheless a region located immediately outside the walls where exoadsorption can occur. Notice the two z-symmetrical volumes corresponding to the solid carbon atoms, where density approaches zero. This exoadsorption phenomenon has been observed before⁶³ for systems composed of nucleobase monophosphates in contact with (6, 0) nanotubes, either in pure water or under physiological ionic strength, [NaCl] = 134 mM. However, due to the extreme narrowness of a (6, 0) topology, molecular confinement was precluded a priori, and no information could be obtained regarding intratubular encapsulation. In the present case, it is clearly evidenced that the existence of a non-negligible electrical charge distribution in solids of small diameter (D_eff ≤ 0.91 nm) favors exoadsorption and in fact excludes endohedral confinement. The shallow and inner concentric circle observed in the radial representations of (16, 0) nanotubes corresponds to a nucleobase located at the nanopore termini. For the (23, 0) topology, the density maps still indicate the possibility of occurrence of exoadsorption, but because now intratubular encapsulation becomes a competing phenomenon, a second high-density domain exists as indicated by the concentric and internal annular region in the xy plane. The metadynamics calculations and the potential of mean force profiles demonstrated that there are two main regions where confinement is most probable to occur, namely at the pore center and close to the entrances (Fig. 7). This is clearly observable on the axial projections of Fig. 8, where one can identify the existence of those two domains populated with high density, and separated by regions of low density. Furthermore, adenine highly favours the solid walls, whereas thymine can penetrate deeper towards the nanotube main axis; this issue is discussed bellow.

Fig. 8 Two-dimensional maps of the number density of nucleobases confined onto electrically charged nanotubes: (top) axial view (xz plane), (bottom) radial representation (xy plane). Notice the two z-symmetrical volumes corresponding to the solid carbon atoms, where density approaches zero.

To accurately characterize the structure of the confined nucleobases within the hydrophobic pores, we have calculated the radial distribution function^40,66 between the nucleobases surface and the SWCNT graphitic atoms from eqn (10), where V is the volume of the system, V_r is the volume of a spherical shell at distance r from each particle i, N_i is the number of particles i in the system, r_ij is the distance between particles i and j and the triangular brackets denote an ensemble average.

From inspection of Fig. 9 it can be observed that the g(r) curves exhibit two intense peaks, symmetrically located to the z-axis, and extremely close to the solid walls thus indicating direct contact between hydrophobic layers. This result has been discussed above when the density maps were obtained, and the radial distribution functions in Fig. 9 clearly support it. Considering the Lennard-Jones diameter of a graphitic carbon atom, σ_LJ = 0.34 nm, and regardless of the individual nanopore curvature, the radial distribution functions corroborate the absence of any solvent slab between the nanopore walls and a confined nucleobase. This fact arises from the strong π stacking mechanism between hydrophobic molecules, leading to very stable interaction energies as recorded in Table 1. The corresponding g(r) curves for the electrically charged (23, 0) nanotube are similar to the ones recorded in Fig. 9. Nonetheless, they indicate that the approach towards the nanopore main axis occurs more frequently for thymine, as verified by a shift of ∼0.27 nm towards smaller values of r of the less intense peak (ESI, Fig. SI5†).

Fig. 9 Radial distribution functions between the nucleobase surface and the uncharged carbon nanotubes: (black) adenine, (blue) thymine. Curves for thymine have been skewed vertically for illustrative purposes. The diameters indicated in the figure correspond to effective properties, D_eff = D− 3.4 Å, where D is the skeletal diameter of the nanotube, measured between centers of graphitic carbon atoms on opposite sides of the wall.

Whereas the hydrophobic solids always lead to stable confined systems, the (16, 0) electrically charged nanotubes were shown to prevent this process; in the (23, 0) topology the nucleobases can experience multiple confinement/exit events. Nevertheless, we have determined the distances of closest approach between any nucleobase atom and the solid wall, either intratubularly confined or exoadsorbed, as well as the average center-of-mass distances. The results obtained are recorded in Table 2, with statistical uncertainties less than 7 × 10⁻³ nm. It is remarkable to observe that the minimum distance between a NB and the walls is roughly constant and always of the order of 0.26–0.31 nm. The intermolecular pair potentials with the hydrophobic solids seem to be only slightly softer. It has been shown above that the charged (23, 0) topology exhibits two regions where there is maximum probability of confinement, and these have been individually addressed in Table 2. Considering the region at the pore center, it seems that thymine can penetrate deeper into the nanotube (Δ = 0.57 nm) than the purine molecule (Δ = 0.96 nm). The apparent discrepancy between this observation and the energy values in Table 1 is misleading. Because adenine favours direct contact with the walls, the distance towards the nanopore center is larger and therefore the corresponding dispersive energy of interaction is 13.9 kJ mol⁻¹ more favourable than for thymine. Although the latter can penetrate deeper into the pore, because it is further away from the walls, the corresponding binding affinity is smaller (Table 1), and thus both probability distribution maxima are identical. This degree of approach to the wall is clearly dominated by the hydrophobic interactions, for both molecules exhibit similar electrostatic energies, E^Coul = −38.8 kJ mol⁻¹ (A) and E^Coul = −37.6 kJ mol⁻¹ (T). The confinement region at the pore entrances, is located at comparable distances from the center, Δ = 1.52 nm (A) and Δ = 1.70 nm (T). In this domain the hydrophobic effects are smaller, and thus not only the difference between the dispersive interactions with the solid gets blurred but, more importantly, the electrostatic distinction becomes more relevant, E^Coul = −24.2 kJ mol⁻¹ (A) and E^Coul = −31.4 kJ mol⁻¹ (T).

Table 2 Average distances between the centers of mass of the nucleobases and nanotubes, Δ, and minimum distance of closest approach between any individual atom of the NB and of the solid, Δ^min (statistical uncertainties are less than 7 × 10⁻³ nm)

		Δ (nm)		Δ ^min (nm)
		A	T	A	T
a Exoadsorbed nucleobases. b Confinement close to the nanopore center. c At the pore termini.
Unch.	(16, 0)	0.51	0.52	0.26	0.27
	(23, 0)	0.96	0.96	0.27	0.28
Charged	(16, 0)^a	1.56	1.52	0.31	0.30
	(23, 0)^b	0.96	0.57	0.30	0.29
	(23, 0)^c	1.52	1.70	0.31	0.29

---

4. Conclusions

We have demonstrated that the encapsulation mechanism of both purine- and pyrimidine-type nucleobases onto purely hydrophobic SWCNTs is energetically favourable and irreversible during the observed time window; the resulting hybrids exhibit lower free energies (Fig. 2) compared to the unconfined systems. Independent umbrella sampling calculations identified a unique probability distribution maximum as corresponding to a domain comprised between the solid walls and the nanopore center (Fig. 6). Once confined, molecules are in direct contact with the walls at a minimum distance of closest approach of 0.26–0.28 nm. No layer of solvent was observed between hydrophobic slabs. This is due to a robust π-stacking mechanism of the NB onto the graphitic mesh, leading to rather strong dispersive energies of interaction with both the (16, 0) and (23, 0) topologies, −67.2 kJ mol⁻¹ ≤ E^vdw ≤ −83.1 kJ mol⁻¹. These results have been compared with DFT and experimental data for graphite. Contrary to exoadsorption, binding affinity increases with the nanotube curvature, as a result of enhanced interaction with the wall immediately opposite to the adsorptive one. We have estimated a diameter of D ≈ 2.05 nm above which the SWCNT curvature mimics a flat graphene sheet and confinement effects tend to be negligible. Interestingly, adenine and thymine evidence similar interaction energies with the hydrophobic nanopores; however, adenine confinement results in slightly favoured energetics (0.9–1.4 kJ mol⁻¹). This previously unobserved finding extends the exoadsorption studies regarding the binding affinity order of DNA nucleobases towards the nanotubes internal volume: purines > pyrimidines.

Electrically charged nanotubes (q = +0.05 e⁻/C) evidence a completely different behaviour (Fig. 4). In fact, the narrowest nanopore employed, (16, 0), inhibits encapsulation of either the purine or pyrimidine moiety. Instead, that nanotube favours adsorption in a region very close to the pore entrance as indicated by the probability distribution maxima (Fig. 6) located at Ω = 0.97 nm (A) and Ω = 1.04 nm (T). When the diameter increases and the nucleobases are put in contact with the (23, 0) solids, confinement becomes possible once again, although several encapsulation/exit events can occur (Fig. 5). Moreover, the confined systems exhibit lower free energies. In this latter situation, the probability distribution curves indicate two maxima: (i) close to the pore center, and overlapping the one obtained for the corresponding hydrophobic solid, and (ii) at the pore termini. This second region of confinement is energetically less stable than the pore center in the case of adenine (Table 1), where both interaction energies differ by 41 kJ mol⁻¹, the major contribution of which coming from dispersive interactions. The pyrimidine molecule has a larger dipole moment, and thus its withdrawal from the pore center towards the bulk solution leads to a stabilization of 5.1 kJ mol.

The results now being reported are an important contribution for the characterization of the interactions between SWCNTs and DNA strands, because they are sequence dependent. The possibilities are myriads, such as in the case of DNA sequencing and internalization for subsequent cellular delivery, which involves confinement of the biomolecule onto the solid, translocation along the nanopore and finally exit towards the cellular interior. Will there be any specific nucleobase sequence that enhances confinement? If so, what are the energetics between that particular sequence and a carbon nanotube? In face of the detailed thermodynamical characterization performed here, it will be possible to probe long DNA sequences with an understanding at the nucleobase level. These studies are under way and will be reported in the near future.

Acknowledgements

The authors would like to acknowledge Dr Chi-Cheng Chiu for helpful discussions with the Gromacs code and the N.S.E.C. of the Univ. Wisconsin–Madison (USA) for CPU time. This work was partially supported by grant PTDC/CTM/104782/2008 (Portugal). F.J.A.L. Cruz gratefully acknowledges financial support from F.C.T./M.C.T.E.S. (Portugal) through grant SFRH/BPD/45064/2008.

Notes and references

1. J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738.
2. R. E. Franklin and R. G. Gosling, Nature, 1953, 171, 740–741.
3. S. Iijima, Nature, 1991, 354, 56–58.
4. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603–605.
5. D. S. Bethune, C. H. Kiang, M. S. d. Vries, G. Gorman, R. Savoy, J. Vasquez and R. Beyers, Nature, 1993, 363, 605–607.
6. Y. Lin, S. Taylor, H. Li, K. A. S. Fernando, L. Qu, W. Wang, L. Gu, B. Zhou and Y.-P. Sun, J. Mater. Chem., 2004, 14, 527–541.
7. W. Yang, P. Thordarson, J. J. Gooding, S. P. Ringer and F. Braet, Nanotechnology, 2007, 18, 412001.
8. K. Kostarelos, A. Bianco and M. Prato, Nat. Nanotechnol., 2009, 4, 627–633.
9. S. K. Vashist, D. Zheng, G. Pastorin, K. Al-Rubeaan, J. H. T. Luong and F.-S. Sheu, Carbon, 2011, 49, 4077–4097.
10. H. Gao, Y. Kong and D. Cui, Nano Lett., 2003, 3, 471–473.
11. E. Y. Lau, F. C. Lightstone and M. E. Colvin, Chem. Phys. Lett., 2005, 412, 82–87.
12. Y. Wu, J. A. Phillips, H. Liu, R. Yang and W. Tan, ACS Nano, 2008, 2, 2023–2028.
13. S. Ghosh, S. Dutta, E. Gomes, D. Carroll, J. Ralph D'Agostino, J. Olson, M. Guthold and W. H. Gmeiner, ACS Nano, 2009, 3, 2667–2673.
14. X. Zhao and J. K. Johnson, J. Am. Chem. Soc., 2007, 129, 10438–10445.
15. D. Roxbury, J. Mittal and A. Jagota, Nano Lett., 2012, 12, 1464–1469.
16. S. Meng, P. Maragakis, C. Papaloukas and E. Kaxiras, Nano Lett., 2007, 7, 45–50.
17. H. Liu, J. He, J. Tang, H. Liu, P. Pang, D. Cao, P. Krstic, S. Joseph, S. Lindsay and C. Nuckolls, Science, 2010, 327, 64–67.
18. U. Yogeswaran, S. Thiagarajan and S.-M. Chen, Sensors, 2008, 8, 7191–7212.
19. K. Yum, N. Wang and M.-F. Yu, Nanoscale, 2010, 2, 363–372.
20. S. Manohar, T. Tang and A. Jagota, J. Phys. Chem. C, 2007, 111, 17835–17845.
21. A. N. Enyashin, S. Gemming and G. Seifert, Nanotechnology, 2007, 18, 245702–245711.
22. R. R. Johnson, A. T. C. Johnson and M. L. Klein, Nano Lett., 2008, 8, 69–75.
23. D. A. Yarotski, S. V. Kilina, A. A. Talin, S. Tretiak, O. V. Prezhdo, A. V. Balatsky and A. J. Taylor, Nano Lett., 2009, 9, 12–17.
24. A. D. Bobadilla and J. M. Seminario, J. Phys. Chem. C, 2011, 115, 3466–3474.
25. S. J. Sowerby, C. A. Cohn, W. M. Heckl and N. G. Holm, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 820–822.
26. S. G. Stepanian, M. V. Karachevtsev, A. Y. Glamazda, V. A. Karachevtsev and L. Adamowicz, J. Phys. Chem. A, 2009, 113, 3621–3629.
27. R. R. Johnson, A. T. C. Johnson and M. L. Klein, Small, 2010, 6, 31–34.
28. W. Lv, Chem. Phys. Lett., 2011, 514, 311–316.
29. Z. Xiao, X. Wang, X. Xu, H. Zhang, Y. Li and Y. Wang, J. Phys. Chem. C, 2011, 115, 21546–21558.
30. S. Monti, G. Prampolini and V. Barone, J. Phys. Chem. C, 2011, 115, 9146–9156.
31. F. J. A. L. Cruz and J. P. B. Mota, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165426.
32. F. J. A. L. Cruz, I. A. A. C. Esteves, S. Agnihotri and J. P. B. Mota, J. Phys. Chem. C, 2011, 115, 2622–2629.
33. H. Wang and A. Ceulemans, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195419.
34. D. Umadevi and G. N. Sastry, J. Phys. Chem. Lett., 2011, 2, 1572–1576.
35. K. Kamiya and S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155444.
36. R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998.
37. I. A. A. C. Esteves, F. J. A. L. Cruz, E. A. Müller, S. Agnihotri and J. P. B. Mota, Carbon, 2009, 47, 948–956.
38. F. Dong and R. E. Miller, Science, 2002, 298, 1227–1230.
39. J. Ran and P. Hobza, J. Phys. Chem. B, 2009, 113, 2933–2936.
40. J. S. Rowlinson and F. L. Swinton, Liquids and Liquid Mixtures, Butterworths, London, 1982.
41. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
42. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
43. B. Mukherjee, P. K. Maiti, C. Dasgupta and A. K. Sood, J. Chem. Phys., 2007, 126, 124704–124711.
44. F. J. A. L. Cruz, E. A. Müller and J. P. B. Mota, RSC Adv., 2011, 1, 270–281.
45. W. A. Steele, Chem. Rev., 1993, 93, 2355–2378.
46. A. Noy, I. Soteras, F. J. Luque and M. Orozco, Phys. Chem. Chem. Phys., 2009, 11, 10596–10607.
47. B. Hess, C. Kutzner, D. v. d. Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
48. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
49. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
50. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
51. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
52. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8592.
53. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562.
54. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
55. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
56. A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601.
57. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
58. J. Kastner, WIREs Computational Molecular Science, 2011, 1, 932–942.
59. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
60. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
61. U. Zimmerli and P. Koumoutsakos, Biophys. J., 2008, 94, 2546–2557.
62. N. Varghese, U. Mogera, A. Govindaraj, A. Das, P. K. Maiti, A. K. Sood and C. N. R. Rao, ChemPhysChem, 2009, 10, 206–210.
63. A. L. Frischknecht and M. G. Martin, J. Phys. Chem. C, 2008, 112, 6271–6278.
64. C. D. M. Churchill, L. Navarro-Whyte, L. R. Rutledge and S. D. Wetmore, Phys. Chem. Chem. Phys., 2009, 11, 10657–10670.
65. Q. X. Pei, C. G. Lim, Y. Cheng and H. Gao, J. Chem. Phys., 2008, 129, 125101.
66. J. M. Haile, Molecular Dynamics Simulation: Elementary Methods, Wiley, New York, 1992.

---

Footnote

† Electronic supplementary information (ESI) available: Metadynamics convergence analysis (Fig. SI1), plots of c.o.m. distances (Fig. SI2 and Fig. SI4) and mean-squared displacement (Fig. SI3), and radial distribution functions (Fig. SI5) are available as ESI along with graphical animations. See DOI: 10.1039/c3ra45033c

---