Density functional calculations on the distribution of Ti in a Y zeolite and its influence on acidity

Abstract

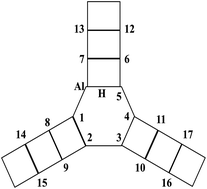
The question of whether Ti replaces Al or Si in the framework of a Y zeolite is studied using a density function theory (DFT) calculation. The distribution properties of Ti in a zeolite are discussed by comparing substitution energies, they show that of the seventeen Si positions investigated the preferred substitution is the one where the Si atoms are located next to the Al, and that the Al is more easily replaced than Si. The framework of the Y zeolite shows a local expansion and deformation after the substitution. The deprotonation energy then reflects the change in Brönsted acidity, demonstrating that the replacement enhances the Brönsted acidity of the zeolite. Further, a detailed illustration of the relationship between the acidity of the zeolite and the location of the Ti is presented.

---

1. Introduction

Since its discovery, the TS-1 zeolite has attracted more and more attention due to its high reactivity under mild conditions, hydrophobicity and excellent stability.^1–3 During the post-synthesis process, some of the framework atoms of the zeolite are substituted by Ti atoms,^4,5 changing the physicochemical properties of the zeolite, especially the acidity.⁶ Therefore influencing the catalytic activity in zeolite-related reactions. The local chemical environments of the Ti atoms and their distribution in the framework of the zeolite should play an important role in influencing the catalytic properties.

In the well-prepared zeolite samples, the Ti atoms are found to be incorporated into the lattice in isolated sites and surrounded by four OSiO₃ tetrahedra.⁷ Recently, the incorporation of Ti into a Y zeolite under acidic conditions by a post-synthesis method has been studied,⁸ and the results show that the Ti species in solution are incorporated into hydroxyl nests generated during the dealumination process in the zeolite framework. Furthermore, the catalytic performance of Ti incorporated into a Y zeolite for the epoxidation of cycloalkenes using aqueous hydrogen peroxide is better than that of a TS-1 zeolite. While the evidence for isomorphous substitution and the improvement of catalytic activity is convincing, the specific details of the siting position of Ti within the framework and the influence of the Ti siting on the properties of zeolites needs further in-depth study.

In zeolites with framework substitution, for example when Ti replaces Si or Al, questions surrounding the location of the substitution and the manner in which the siting affects the chemistry remain largely unanswered experimentally, although some computational approaches have addressed these questions.^9,10 Density functional theory (DFT) can always provide information that is complementary to the multitude of experimental information, such as the distributions of Ti in CHA,¹¹ Beta¹² and MCM-41.¹³ However, there is little in the literature about the distribution of Ti in a Y zeolite. On the other hand, quantum chemical calculations have been frequently applied to the analysis and investigation of the acidity of zeolites.¹⁴ For example, the deprotonation energy¹⁵ represents the strength of a Brönsted acid. The lower the deprotonation energy, the better the ability of a material to provide a proton.

In the present work, we report the results of two sets of calculations by the DFT method. In the first, DFT calculations are used for a detailed study of the question of whether Ti replaces Al or Si in the framework of a Y zeolite by comparing the substitution energies, and the distribution of Ti in a Y zeolite is discussed. Following this, the change of Brönsted acidity is investigated by calculating the deprotonation energies. Finally, the relationship between the distribution of a Ti atom in a Y zeolite and the acidity is investigated.

2. Calculation details

2.1 Cluster models

In this work a 24T cluster model of a Y zeolite has been used to study the substitution of the Ti atom and the change of the acid strength. The 24T cluster represents parts of a supercage that is cut off from a Y zeolite configuration obtained from the Materials Studio library. In the cluster model, the dangling bonds of the Si atoms are terminated by OH and the O–H bonds are oriented along the bond direction towards what would otherwise have been the next Si atom.¹⁶ The terminal H atoms are fixed and other atoms are allowed to relax. The research of Lonsinger¹⁷ et al. shows that the effects of artificial termination do not propagate further than two bonds from the terminating proton. The geometric characterization of the optimized pure Si Y zeolite is shown in Table 1, where a comparison with the neutron diffraction results of a free-Al sample¹⁸ and a DFT calculation result¹⁹ are also included. Although our methodology yields large SiO bonds compared to experiments, the values are almost the same as other DFT calculation results. On the other hand, SiOSi and OSiO angles are calculated with great accuracy. It can be considered that the model that we chose could truly represent the realistic structure of a Y zeolite (Fig. 1).

Table 1 Structure data of the optimized 24T cluster model of a pure Si Y zeolite^a

Labels^b	T–O^c	T–O^19	T–O^18
a Bond lengths are in Å, bond angles are in degrees.b O2, O3 and O4 are shown in Fig. 1.c Optimized values.
Si–O2	1.622	1.622	1.597
Si–O3	1.630	1.632	1.604
Si–O4	1.623	1.622	1.614

---

Labels^b	T–O–T^c	T–O–T^19	T–O–T^18
Si–O2–Si	150	149	149
Si–O3–Si	147	145	146
Si–O4–Si	143	142	141

---

Labels^b	O–T–O^c	O–T–O^19	O–T–O^18
O2–Si–O3	108	108	109
O2–Si–O4	109	109	109
O3–Si–O4	111	111	112

---

Fig. 1 Cluster model location in the supercage of a Y zeolite (a), a pure Si Y zeolite (b) and the optimized 24T cluster model (c). Color code: Si (yellow), O (red), Al (pink), H (white).

A framework Si atom is replaced by an Al atom and the charge is compensated for by a proton, which provided the Brönsted acidity in the 24T cluster model. The calculations of the geometric structure show that the Al–O bond lengths are 1.776 Å, 2.063 Å, 1.791 Å, 1.737 Å respectively, and the Al–O bond connected to H is longer (2.063 Å) than the other three bonds, which agrees with the result of earlier theoretical and experimental studies,²⁰ in that the Al–O distance associated with the acidic proton is significantly longer than the other Al–O distances, by up to 0.2 Å. Meanwhile, the value of the Al–O distance that is connected with the H is consistent with the DFT result of Katada et al.¹⁵ And the O–H distance (0.981 Å) agrees well with the observation of Kalita and co-workers.²¹ Therefore, 18 possible T sites including one Al site and seventeen Si sites are taken into considerations for the substitution.

2.2 DFT calculations

DFT calculations are performed by applying the Dmol³ program in the Materials Studio software package developed by Accelrys, as previously reported.²² Geometry optimization and energy calculations are performed using the double numerical with a polarization (DNP) basis set, BLYP exchange and correlation functional, which give more accurate results for zeolite calculations.²³ The convergence criteria (energy, force, and displacement) are set to 2 × 10⁻⁵ Ha, 4 × 10⁻³ Ha Å⁻¹, and 0.005 Å, respectively. No symmetry constraints are used for any of the cluster models in this study.

The substitution energy is used to measure the energy preference for the substitution by Ti at a certain T site. It is defined as the reaction energy of the virtual reaction, and it is calculated as follows:²⁴

E_Si/Ti = E_{(Si–zeolite)} + E_Ti − E_{(Ti–zeolite)} − E_Si, E_Al/Ti = E_{(Al–zeolite)} + E_Ti − E_{(Ti–zeolite)} − E_Al

The smaller substitution energy means that the replacement of Si or Al by Ti is more likely to occur.

The Brönsted acidity strength of the zeolite is measured by the deprotonation energy (E_DEP). It is defined for the reaction ZH → Z⁻ + H⁺, as follows:

E_DEP = E_Zeo–O⁻ − E_Zeo–OH

Models with high deprotonation energy are poor proton donors and have weak Brönsted acidity.

For convenience, all substitution energies and deprotonation energies are referred to by the corresponding energy, presented as a relative energy.

3. Results and discussion

3.1 Substitution of Si

3.1.1 Configurations. There are seventeen possible positions where Ti can be substituted, these are shown in Fig. 2. The seventeen different configurations are optimized to investigate the structural change of the Y zeolite, and the Si/Ti–O bond lengths and Si/Ti–O–Si bond angles before and after the substitutions are shown in Table 2. The presented T–O bond lengths show that the distances between Ti and O increase by about 0.2 Å after the substitution. Also reported in Table 2 are the enlargements of the Ti–O–Si bond angles by up to 3°–7°, and only a small part among these bond angles varies within about 1°. It can be deduced from the changes of bond lengths and bond angles, that the Ti incorporation in the Y zeolite causes a local expansion and a deformation of the Y zeolite framework, which is related to the atomic radius of the Ti atom. Furthermore, the pore size of the zeolite decreases after the substitution, which corresponds with the findings of Yasunori's research.⁸ The changes in the structure of the channels will definitely influence the catalytic activity of the zeolite, especially for shape-selective reactions.

Fig. 2 Substituted sites of Ti. The intersection of each line represents a T site. Every possible T site with a Ti substitution is numbered. The O atoms of the zeolite are not shown in this figure.

Table 2 Si/Ti–O bond lengths and Si/Ti–O–Si bond angles before and after the substitution as well as the relative E_Si/Ti

T site	Si–O bond length (Å)	Si–O–Si bond angle (°)	Ti–O bond length (Å)	Ti–O–Si bond angle (°)	Relative ESi/Ti (kJ mol^−1)
1	1.691	113.3	1.831	116.2	0
	1.647	108.5	1.877	112.2
	1.679	108.8	1.881	112.7
	1.674		1.847
2	1.651	107.9	1.839	106.6	42.2
	1.690	114.2	1.864	121.9
	1.715	108.3	1.917	112.4
	1.668		1.838
3	1.689	112.6	1.888	118.1	94.1
	1.683	108.8	1.866	108.2
	1.683	112.4	1.874	117.9
	1.664		1.834
4	1.668	110.3	1.853	110.8	28.6
	1.669	110.6	1.857	115.9
	1.701	107.1	1.895	109.7
	1.668		1.833
5	1.648	107.8	1.829	113.1	9.24
	1.669	116.9	1.843	116.9
	1.748	104.4	1.969	109.8
	1.652		1.825
6	1.682	109.4	1.866	107.0	34.6
	1.649	107.4	1.817	105.1
	1.721	111.0	1.902	118.2
	1.670		1.835
7	1.698	106.6	1.901	108.6	18.9
	1.693	113.6	1.872	120.9
	1.644	107.9	1.825	106.0
	1.686		1.843
8	1.711	105.0	1.906	105.2	56.4
	1.677	106.8	1.840	103.5
	1.675	113.2	1.857	120.4
	1.691		1.854
9	1.719	113.9	1.913	121.3	67.7
	1.670	109.2	1.843	110.0
	1.704	108.3	1.891	106.2
	1.683		1.848
10	1.695	113.1	1.883	119.5	33.8
	1.668	107.5	1.846	105.7
	1.668	107.2	1.873	106.3
	1.669		1.833
11	1.693	113.5	1.886	122.7	21.9
	1.663	108.7	1.836	109.3
	1.682	106.6	1.876	104.1
	1.667		1.838
12	1.698	116.4	1.886	122.7	15.2
	1.648	106.7	1.839	106.1
	1.691	108.1	1.874	107.7
	1.664		1.835
13	1.692	114.7	1.878	122.9	22.2
	1.658	107.9	1.842	104.9
	1.679	107.4	1.868	106.4
	1.662		1.835
14	1.695	117.0	1.879	122.7	29.9
	1.658	106.3	1.819	104.4
	1.705	108.9	1.901	110.4
	1.667		1.832
15	1.717	120.3	1.910	125.9	76.1
	1.652	108.9	1.833	107.7
	1.732	103.4	1.909	102.7
	1.674		1.827
16	1.697	116.4	1.882	122.1	21.2
	1.664	107.3	1.845	106.2
	1.693	107.7	1.866	107.3
	1.663		1.836
17	1.696	115.5	1.892	123.0	23.7
	1.662	106.8	1.832	105.4
	1.687	106.8	1.870	106.1
	1.665		1.832

---

Also reported in Table 2 is the relative E_Si/Ti, which takes the corresponding energy of 1 site as a benchmark to represent the difficulty of Si being replaced by Ti, and the relative E_Si/Ti ranges from 0 kJ mol⁻¹ to 94.1 kJ mol⁻¹. The replacement is easiest at the 1, 5 and 7 sites with relative E_Si/Ti of 0 kJ mol⁻¹, 9.24 kJ mol⁻¹ and 18.9 kJ mol⁻¹ respectively, while the replacement is the hardest at the 3 site with a relative E_Si/Ti of 94.1 kJ mol⁻¹. According to the substitution sites shown in Fig. 2, it can be found that the 1, 5 and 7 sites lie in the position nearest to the Al in the six-membered ring of the Y zeolite, and the Al–O–Ti structure is formed. Correspondingly, the most unlikely replaceable position is the position diagonally away from the Al within the same six-membered ring. It can be concluded, on purely energetic grounds, that the probability of a different Si site substituted by a Ti is associated with the position of the Si in the framework of the Y zeolite, and the distributions of the Ti are obtained. That is, Ti is mainly located in positions neighboring Al in the six-membered ring of the Y zeolite, and it is unlikely for it to be distributed in the position diagonally away from Al in the same six-membered ring of the Y zeolite. Therefore, the Brönsted acidity generated from the proton could be influenced.

3.1.2 Acidity. The calculated relative deprotonation energies of the Y zeolite before and after the substitution are shown in Table 3, they take the corresponding energy of the Y zeolite as the benchmark (1244.09 kJ mol⁻¹). All these clusters show a lower deprotonation energy compared with the original Y zeolite, which illustrates that the substitution of Si by Ti enhances the Brönsted acidity of the framework hydroxyl groups. And the relative E_DEP of the Y zeolite with different distributions of Ti ranges from −0.75 kJ mol⁻¹ to −19.9 kJ mol⁻¹. Besides, the Mulliken charge of H increases after the isomorphous substitution, which is consistent with the change of the deprotonation energy that shows the enhanced Brönsted acidity. However, the replacement has a weak influence on the H–O bond length, which is over a narrow range from 0.980 Å to 0.983 Å, compared with the H–O bond length (0.981 Å) of the Y zeolite.

Table 3 The relative E_DEP of the different T sites as well as the H–O bond lengths and the Mulliken charge of H

	Relative EDEP (kJ mol^−1)	H–O bond length (Å)	Mulliken charge of H
Y zeolite	0	0.981	0.349
1	−16.6	0.982	0.365
2	−9.66	0.981	0.355
3	−8.44	0.980	0.352
4	−15.2	0.981	0.357
5	−19.4	0.981	0.360
6	−3.30	0.981	0.358
7	−19.9	0.982	0.362
8	−6.35	0.981	0.359
9	−4.26	0.981	0.361
10	−3.51	0.982	0.359
11	−13.4	0.983	0.361
12	−12.5	0.982	0.358
13	−8.07	0.982	0.361
14	−1.80	0.982	0.361
15	−0.75	0.982	0.359
16	−8.28	0.981	0.358
17	−8.49	0.981	0.359

---

3.2 Substitution of Al

3.2.1 Configuration. Because the number of framework Al atoms decreases during the substitution process, the replacement of Al by Ti is also discussed. After the substitution, the corresponding Ti–O distance is elongated by 0.2 Å to the original Al–O distance and reaches up to 1.923 Å, 2.246 Å, 1.948 Å and 1.900 Å, respectively. The calculated Al–O–Si bond angle increases from 102.0, 99.4 and 124.0 in the non-substituted zeolite to 103.2, 101.0 and 134.8 in the Ti-substituted zeolite. The changes of bond length and bond angle also indicate that Ti incorporation in to the Y zeolite causes a local expansion and a deformation of the Y zeolite framework.

The substitution energy is 83.3 kJ mol⁻¹, whereas the smallest substitution energy in a Si site is 172.8 kJ mol⁻¹ in 1 of the sites. The comparison of the different substitution energies suggests that it is easier to substitute Al than Si. Therefore, it is Al that is the first to be replaced by Ti during the experimental process, and thereby the configuration of the Brönsted acid sites is influenced. The position of the proton provided the Brönsted acidity of the zeolite without changing the structure of the Brönsted acid site, which changes from Al–OH to Ti–OH after the substitution.

3.2.2 Acidity. The deprotonation energy of the Ti substituted zeolite decreases to 1240.7 kJ mol⁻¹, which is between the values of 1240.8 kcal mol⁻¹ (replacement of Si in the 6 site) and 1241.0 kcal mol⁻¹ (replacement of Si in the 10 site) compared with that (1244.1 kJ mol⁻¹) of the Y zeolite, indicating that the Brönsted acidity of the substituted zeolite increases slightly. The influence of replacing Si on Brönsted acidity is greater than that of replacing Al by a comparison of the deprotonation energies.

4. Conclusion

In summary, the question of whether Ti replaces Al or Si in the framework of a Y zeolite, as well as the influence of the substitution on the acidity of the zeolite, is studied using DFT quantum chemical calculations. Si/Ti substitution energies reveal that the probability of substitution is associated with the Si position in the framework of the Y zeolite. And Ti atoms prefer to be located in the position neighboring Al, while the site diagonally away from the Al in the six-membered ring of the zeolite is the least favoured position for the substitution. Meanwhile, Al/Ti substitution is also discussed. By comparing the substitution energies, it is easier to replace Al than Si. According to the change of the bond length and bond angle after the substitution, the incorporation of Ti in the Y zeolite causes a local expansion and deformation of the framework, which may reduce the pore size of the zeolite. Deprotonation energies of different substituted zeolites demonstrate an enhancement in the Brönsted acidity, whereas the replacement of Al shows a weaker influence on the Brönsted acidity of the zeolite. The change in pore size and acidity of a Ti-incorporated Y zeolite will influence the catalytic activity of zeolite-related reactions, especially shape-selective reactions.

References

1. D. Barbera, F. Cavani, T. D. Alessandro, G. Fornasari, S. Guidetti, A. Aloise, G. Giordano, M. Piumetti, B. Bonelli and C. Zanzottera, J. Catal., 2010, 275, 158–169.
2. V. Hulea and E. Dumitriu, Appl. Catal., A, 2004, 227(1–2), 99–106.
3. N. Wilde, C. Worch, W. Suprun and R. Glaser, Microporous Mesoporous Mater., 2012, 164, 182–189.
4. M. Tamura, W. Chaikittisilp, T. Yokoi and T. Okubo, Microporous Mesoporous Mater., 2008, 112, 202–210.
5. V. R. Choudhary and S. K. Jana, Appl. Catal., A, 2002, 224, 51–62.
6. J. Su, G. Xiong, J. Zhou, W. Liu, D. Zhou, G. Wang, X. Wang and H. Guo, J. Catal., 2012, 288, 1–7.
7. A. Gamba, G. Tabacchi and E. Fois, J. Phys. Chem. A, 2009, 113, 15006–15015.
8. Y. Oumi, T. Manabe, H. Sasaki, T. Inuzuka and T. Sano, Appl. Catal., A, 2012, 388, 256–261.
9. C. A. Hijar, R. M. Jacubinas, J. Eckert, N. J. Henson, P. J. Hay and K. C. Ott, J. Phys. Chem. B, 2000, 104, 12157–12164.
10. S. Yuan, H. Si, A. Fu, T. Chu, F. Tian, Y.-B. Duan and J. Wang, J. Phys. Chem. A, 2011, 115, 940–947.
11. A. Damin, S. Bordiga and A. Zecchina, J. Chem. Phys., 2003, 118(22), 10183–10194.
12. G. Sastre and A. Corma, Chem. Phys. Lett., 1999, 302, 447–453.
13. V. Hulea and E. Dumitriu, Appl. Catal., A, 2004, 277, 99–102.
14. T. Noda, K. Suzuki, N. Katada and M. Niwa, J. Catal., 2008, 259, 203–210.
15. N. Katada, K. Suzuki, T. Noda, G. Sastre and M. Niwa, J. Phys. Chem. C, 2009, 113, 19208–19217.
16. A. Simperler, R. G. Bell, M. D. Foster, A. E. Gray, D. W. Lewis and M. W. Anderson, J. Phys. Chem. B, 2004, 108(22), 7152–7161.
17. S. R. Lonsinger, A. K. Chakraborty, D. N. Theodorou and A. T. Bell, Catal. Lett., 1991, 11, 209–217.
18. J. A. Hriljac, M. M. Eddy, A. K. Cheetham, J. A. Donohue and G. J. Ray, J. Solid State Chem., 1993, 106, 66.
19. S. German, K. Naonobu and K. J. Suzuki, J. Phys. Chem. C, 2008, 112, 19293.
20. N. E. Schultz, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 11127–11143.
21. U. Eichler, M. Brandle and J. Sauer, J. Phys. Chem. B, 1997, 101, 10035–10050.
22. B. J. Delley, Chem. Phys., 2000, 113, 7756–7766.
23. B. Kalita and R. C. Deka, J. Phys. Chem. C, 2009, 113, 16070–16076.
24. R. Ch. Deka, V. A. Nasluzov, E. A. Ivanova Shor, A. M. Shor, G. N. Vayssilov and N. Rösch, J. Phys. Chem. B, 2005, 109, 24304–24310.

---