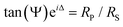Optical and magneto-optical properties of gold core cobalt shell magnetoplasmonic nanowire arrays

Abstract

In this work we present core–shell nanowire arrays of gold coated with a nanometric layer of cobalt. Despite the extremely small Co volume, these core–shell nanowires display large magneto-optical activity and plasmonic resonance determined by the geometry of the structure. Therefore, we are able to tune both the plasmonic and magneto-optical response in the visible range. Through optical and ellipsometric measurements in transmission, and applying a magnetic field to the sample, it is possible to modulate the value of the phase angle (Del {Δ}) between the S and P polarised components. It was found that the core–shell sample produced an order of magnitude larger variation in Del with changing magnetic field direction, compared with hollow cobalt tubes. The enhancement of magneto optical properties through the plasmonic nature of the gold core is complemented with the ability to induce magnetic influence over optical properties via an externally applied field. Moreover, we demonstrate for the first time the ability to use the remanent magnetisation of the Co, in conjunction with the optical properties defined by the Au, to observe remanent optical states in this uniquely designed structure. This new class of magnetoplasmonic metamaterial has great potential in a wide range of applications, from bio-sensing to data storage due to the tuneable nature of multiple resonance modes and dual functionality.

---

Introduction

There is a constant and ever-evolving need for new or enhanced functionality of materials, which cannot always be met by nature. In order to achieve effects different from those naturally occurring in bulk materials, so-called ‘metamaterials’ use functional inclusions, or meta-atoms, of sub wavelength dimensions in order to manipulate incident electromagnetic (EM) radiation in a desired manner. Increasingly we are turning to specifically designed metamaterials to bolster innovation in fields such as superlensing, cloaking devices and photonic circuits.^1,2 This has been achieved due to significant advances in fabrication techniques, which now means one can include multiple materials in a variety of shapes and combinations at the nanoscale to tailor the desired property.^3,4 Noble metals such as gold and silver can be used for advanced optical considerations by exploiting plasmonic resonances with the ability to tailor the response based on the geometric parameters.⁵ Magnetic nanostructures have been studied for enhancements of intrinsic properties including resonant magneto-optic (MO) response,⁶ tuneable magnetic properties and for the study of spin waves.⁷ Although weak plasmonic enhancements have also been observed in purely magnetic nanostructures,⁸ plasmonics is mainly in the domain of noble metals due to high Ohmic losses of ferromagnetic materials.

While plasmonic behaviour has been observed in magnetic materials, perhaps more strikingly, magnetic behaviour can also be found in noble metal nanostructures. It has been shown theoretically that a non-magnetic nanoparticle can be magnetized in a circularly polarized light beam, and the magnetization depends on the direction of rotation of the light wave.⁹ Magnetisation in gold nanodiscs and nanorings has been demonstrated experimentally, with and without externally applied magnetic fields. Owning to virtual current loops or an increase of the magnetic Lorentz force induced by the large collective movement of the conduction electrons in the nanostructures when the resonance is excited, magnetic hot-spots are observed, analogous to localised surface plasmon resonances (LSPRs), resulting in enhanced MO activity.^10,11 Observation of magnetoplasmonic modes on colloidal gold nanoparticles has been achieved by means of magnetic circular dichroism (MCD) spectroscopy confirming the existence of a magnetic component of plasmonic resonance.^12,13 Additionally, the lifetime of these magnetoplasmons has been shown to be dependent on the magnetic field strength.¹⁴

Recently there has been increased interest in combining plasmonic and magnetic materials into hybrid structures for the study of magnetoplasmonics. In essence, magnetoplasmonics aims to use magnetic functionality to allow control of the plasmonic properties with the use of an external magnetic field, and plasmonic functionality to provide enhancement to the local EM field thus enhancing magneto-optic effects.¹⁵ There are a number of ways that this has already been demonstrated, and shown to have great potential application in the fields of gas and biosensing,^16,17 telecommunications¹⁸ and data storage through the inverse Faraday effect.¹⁹ Studies have been carried out ranging from simple thin films of ferromagnetic and noble metal multilayers to nanodiscs and gratings and multi-layered nanoparticles produced via lithographic techniques. The results have demonstrated the ability to modulate the wavevector of a surface plasmon polariton (SPP) with a magnetic field, enhancement of MO activity and resonant plasmonic properties.^20–25 Yttrium-iron-garnets: YIG and bismuth-iron-garnet: BIG, are transparent ferromagnets that have been coupled with plasmonic nanoparticles. Co-sputtering of gold and YIG showed incorporation of Au nanoparticles in the YIG matrix which had a strong influence on the Kerr rotation in the vicinity of the 600 nm plasmon resonance,²⁶ and an anti-dot array of gold on top of a BIG film was demonstrated to provide control over optical transmission with the use of an externally applied magnetic field due to the influence of MO effects on the SPP states at the interface.²⁷

There are also numerous solution based/chemical reduction methods for creating core–shell nanoparticles. Magnetic and plasmonic combinations have been shown to provide enhanced MO as well as use in biological applications, both diagnostic and therapeutic.^28–31 However, surface bound core–shell nanostructures are, as yet, largely unexplored, particularly with high aspect ratios due to difficulty in the fabrication process. Anodised aluminium oxide (AAO) is a well-known, low cost and scalable method of creating large scale arrays of nanostructured metamaterials which also allows for the combination of more than one element. In one approach, high aspect ratio core–shell nano-wires are produced by first depositing the Co-ferrite shell on the walls of the AAO pores by atomic layer deposition, followed by electrodeposition of gold to fill the remainder of the pore.³² An alternative approach is to use a two-step chemical etch to re-widen pores after the initial deposition, and deposit the shell on top of the core material. Initial work on low aspect ratio core–shell, plasmonic/ferromagnetic nanowires made in this way was demonstrated by using gold and nickel, but without exhibiting influence over the plasmonics with magnetic fields, or vice versa.³³ In the present study we examine the never before seen structure of large scale arrays of low aspect ratio nanowires with a gold core and cobalt shell. Further details of the fabrication process can be found in ref. 34.†

Structure of nanowire arrays

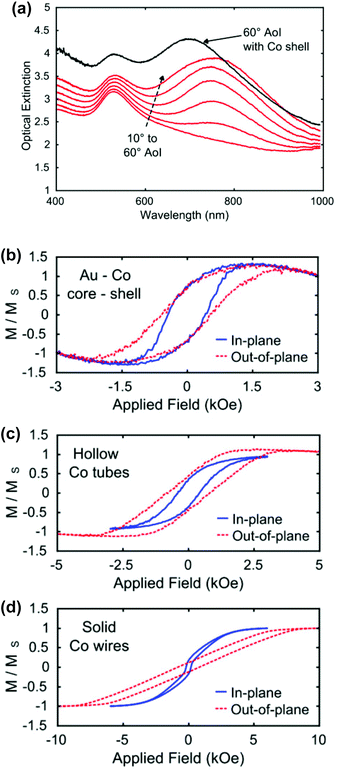
The core–shell nanowires are supported on a glass substrate and are comprised of a gold core approximately 30 nm in diameter and cobalt shell of thickness considerably less than the core diameter, except where it forms a cap on top, Fig. 1a. The spacing of the array is 80 nm and the AAO template in which the nanowires were grown is not removed, and forms a matrix that improves the robustness of the material and influences the optical properties. Scanning transmission electron microscopy (STEM) and electron dispersive X-ray (EDX) analysis were performed on a cross-section sample to confirm the dimensions and map the chemical distribution of the overall structure, Fig. 1b. Fig. 1c displays a colour coded high-angle annular dark-field (HAADF) image from the EDX data. The structures were confirmed to have a Au core of ∼32 nm in diameter and a Co shell ∼4 nm thick, while the cap on top is 15 nm. The Au nanowires were found to be polycrystalline, and no clear epitaxial growth, or diffusion between the Au and Co was observed.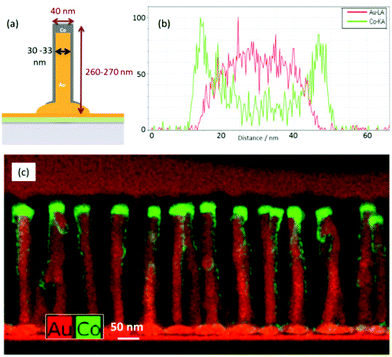

Fig. 1 (a) Core–shell nanowire schematic, (b) EDX line scan profile across one wire, (c) STEM cross-section.

Optical absorption and magnetic properties

Fig. 2a compares the optical absorbance spectra of a gold nanowire array and a Au core–Co shell array, where the array spacing and dimensions of gold cores and gold nanowires are the same. The spectra show absorption peaks relating to two resonances typical of gold nanowire arrays excited by P-polarised light. The smaller peak near 530 nm is a transverse mode due to oscillations across the nanowire, which is insensitive to array parameters. The larger peak is due to a longitudinal mode excited along the wire that changes wavelength depending on nanowire dimensions, array spacing and the refractive index of any material between the nanowires, such as the AAO template.³³ Consequently, the longitudinal resonance is both tuneable and highly sensitive to changes within the array. The Au core–Co shell array differs from the gold nanowire by the few nanometres immediately around the gold being cobalt rather than AAO, and also the cobalt cap on top. The consequence for the Au core–Co shell array is an increase in absorbance across the spectrum and a blue shifting of the longitudinal resonance peak: both these effects increase with cobalt shell thickness up to approximately 10 nm radially. The magnetic properties were studied using vibrating sample magnetometry (VSM), Fig. 2b. These results revealed that the sample has no clear easy axis of magnetisation, with the field required for saturation being approximately 1500 Oe for both in and out of plane directions. This is in stark contrast to pure Co wires in this type of array configuration, Fig. 2d. Competing magnetic energy terms define the overall easy direction of magnetisation. The magnetocrystalline anisotropy and shape anisotropy of cobalt wires tend to align the magnetisation parallel to the wire long axis. However, the magneto-static interactions between neighbouring wires is very strong and more influential therefore changing the overall easy axis to a very clear in-plane setting, perpendicular to the wire long axis.

Fig. 2 (a) Extinction spectra of Au nanowires – aspect ratio 8, at increasing angle of incidence and extinction spectrum with the addition of a Co nano-shell at 60 degrees. (b) VSM measurements of Au-Core Co-Shell nanowire array in and out of plane. (c) VSM measurements of hollow Co nano-tube array in and out of plane. (d) VSM measurements of solid Co wires.

For the core shell sample, and indeed an array of hollow Co tubes, the Co volume was greatly reduced compared to that of solid Co wires, and hence the magneto-static interaction is also reduced resulting in a highly anisotropic array in terms of optics, but with very similar magnetic properties in and out-of-plane. The Co tubes, shown for comparison in Fig. 2c, were made in the same way except that instead of a Au core, a sacrificial polymer is used which can later be removed.†

Effect of the array on polarisation of light

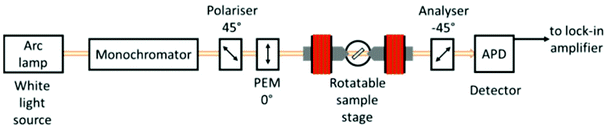
When polarised light is incident on the sample the ellipsometric properties of Psi and Del, which define the polarisation state of the wave, are subject to large changes due to the resonance conditions and the anisotropic properties of the metamaterial. Psi is an amplitude measurement, and Del is an angular measurement of the relative phase difference between P and S components of the transmitted or reflected light from the sample. Standard ellipsometry is measured in reflection, and the equation relating Psi (Ψ) and Del (Δ) is shown below. These values are often incorporated into a model to retrieve information about thin films such as film thickness, optical constants or refractive index. However, here we are only interested in measuring the phase change (Δ) between S and P components in transmission.

The experimental setup for these measurements consists of crossed polarisers and a photoelastic modulator (PEM) linked with two lock-in amplifiers, as shown in Fig. 3. It is based on a setup proposed in ref. 35 but measured in transmission and with the added feature of being able to apply an external magnetic field to the sample. However, an unavoidable limitation of this measurement is that we must apply the field at the same angle of incidence (AOI) as the incoming light due to the requirement of the light to pass through a hole in the centre of the pole pieces. This allows for two spectroscopic scans of amplitude and phase measurements to be made in oppositely orientated magnetic fields, at different angles of incidence to the sample.

Fig. 3 Schematic of experimental setup for ellipsometric measurements with a magnetic field.

The sample was mounted in an opaque holder so that all light incident on the detector had passed through the sample. The pole pieces were adjusted after each increase in AOI to be as close as possible, to maximise the magnetic field strength. At higher AOIs, therefore, the field was weaker; however, hysteresis measurements were taken at every AOI to ensure magnetic saturation.

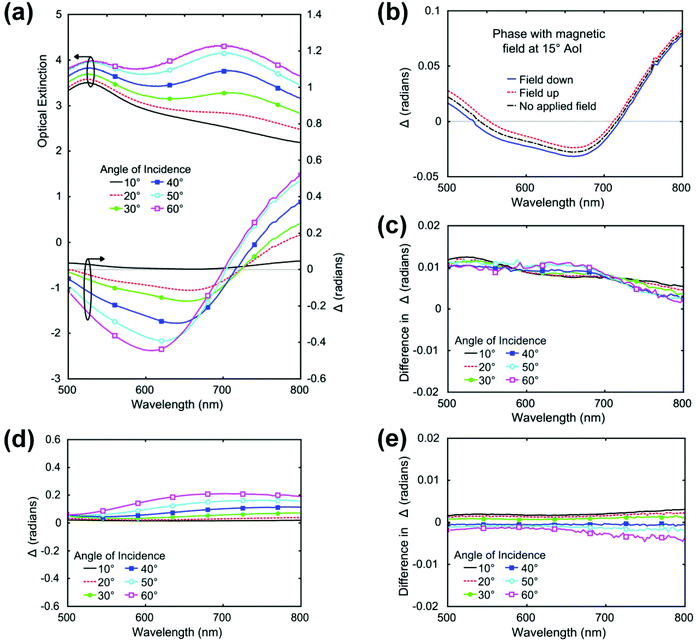
Fig. 4a compares the optical absorption spectra of the Au core–Co shell array to ellipsometric measurements of Δ at varying AOI, with no magnetic field applied. The extinction shows that, at small angles of incidence up to 10 degrees, only the transverse mode is observed in the form of a peak at 530 nm. With the polarisation angle of the incoming light fixed at 45 degrees, the transverse resonance is excited equally by both the S and P components, consistently at all AOI's. As the sample is rotated to higher angles, the P polarised component has greater interaction with the long axis of the nanorods producing the longitudinal mode around 700 nm. Therefore, the polarisation state of the transmitted light changes with wavelength, P-polarised light being preferentially absorbed around the longitudinal resonance peak. The phase difference between P and S polarised components of the transmitted light changes significantly with wavelength near this resonance condition. There is a large transition from negative to positive Δ going from shorter to longer wavelengths across the longitudinal resonance, the zero point being where the P-polarised component of the light is extinguished at the peak of extinction. The effect becomes more pronounced as angle of incidence increases; at 60 degrees the phase difference is roughly 1 radian. Similar behaviour has been noted before for gold nanowire arrays, which showed changes in Δ of 2π or greater.³⁶ The transition point from negative to positive Δ has been shown to be a point of extremely high sensitivity to precisely measure small changes in the surrounding medium for refractive index changes or biosensing.³⁷

Fig. 4 (a) Optical extinction spectra and Δ at varying AOI of Au Core–Co Shell sample with no field applied. (b) Measurements of Δ across the wavelength range, showing the difference for oppositely oriented magnetic fields and the two resonance conditions present at 15 degrees AOI. (c) Difference in measured value of Δ when the direction of magnetic field is reversed for Au Core–Co Shell sample. (d) & (e) Δ with no field applied, and the difference in Δ for opposite fields at varying AOI's for hollow cobalt nanotubes.

When we now apply a magnetic field to the sample in opposite directions we can observe an additional effect. Fig. 4b shows the measured value of Δ across the spectral range when the field is applied in opposite directions in turn at 15 degrees AOI. The angle of incidence of the magnetic field on the sample is also necessarily 15 degrees, the same as the light source, as was described previously. 15 degrees was chosen because at this angle we can see there are two wavelengths at which there is no phase difference. These points represent the two resonance wavelengths accessible at 15 degrees. The resonance around 700 nm is a constant for all AOI's and has been clearly established to correspond to the longitudinal plasmonic resonance of the gold wire. The point around 530–550 nm is highly sensitive to angle of incidence and is not seen at larger angles. Thus it is not caused by the transverse resonance of the gold wires but is believed to be an optical thin film effect, which has also been observed in nickel nanowire arrays embedded in AAO.⁶ This low angle thin film resonance effect does not affect the measured change in Δ with change in field direction. The difference in Δ for all AOI's is roughly 0.01 radians and begins to fall at higher wavelengths, after the plasmon resonance. It is seen that across the wavelength range there is a significant difference in Δ when the direction of the field is reversed. This effect is consistent at all angles of incidence, as shown in Fig. 4c, but is more clearly observable when the overall value of Δ is lower, at lower AOIs. The reduction in the difference in Δ after the resonance wavelength is more evident for higher angles of incidence.

This overlap of magneto-optical activity and plasmonic resonance is a feature that makes magnetoplasmonic structures a new class of tuneable metamaterials. For comparison, hollow Co tubes were measured in the same way. Fig. 4d shows the change in Δ across the wavelength range with increasing angle of incidence. It is clear that, when compared to the gold core cobalt shell sample in Fig. 4a, there is no notable resonance condition, with the largest change in Δ being less than 0.2 radians at 60 degrees AOI. The changes in Δ induced by the application of a magnetic field are less than half of that of the core shell sample, at low AOI's, and at higher AOI's falls further still, to between an order of magnitude less and virtually no measurable change. One might expect that the lack of a gold inner core might bring the magneto optical effects of the cobalt to the fore, the value of Δ is lower overall and so a change might be more easily induced. However, what we see instead is a clear enhancement of the MO activity of the structure due to the amplification of MO by the plasmonic nature of the core, whilst maintaining its optical properties, and vice versa. Δ is an optical measurement that we can more strongly influence when plasmonic and magnetic materials are combined. Solid cobalt wires behave in much the same way as the hollow cobalt tubes with a similarly featureless response across the wavelength range, and only very small changes induced with a magnetic field. Additionally, solid gold wires, while they have a strong optical response, are completely impervious to an external magnetic field.†

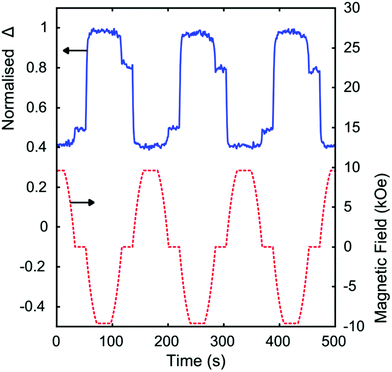
Finally we show for the first time, the ability to maintain a difference in the optical properties based on the remanent magnetisation of the Co layer. The difference in the phase angle between S and P components has been shown to be primarily a feature of the gold nanowires contained in the sample, with the thin Co shell having very little effect on this optical property. However, having shown how an external magnetic field can change the optics, Fig. 4, we now also demonstrate the ability to exploit the feature of ferromagnetic remanence of the Co shell to maintain changes in the optical measurements, even in the absence of a magnetic field. We can observe the remanent states of the sample in terms of optical measurements, as opposed to the purely magnetic measurements shown in Fig. 2b. We select a single wavelength and alternate the direction of the magnetic field while recording Δ, Fig. 5.

Fig. 5 Normalised Δ at 540 nm wavelength and 15 degrees AOI against time varying magnetic field.

From Fig. 5 we can determine that the field required for saturation is less than 3000 Oe at 15 degrees AOI. The same was shown in Fig. 2b, that there is no clear easy axis of magnetisation for the core–shell nanowire array. We see the change in Δ when the magnetic field is reversed, but we also see an optical remanence effect. At zero applied fields the value of Δ is different depending on the magnetic remanence. This result verifies the coupled nature of the magnetic and plasmonic aspects of this core–shell metamaterial. Being ferromagnetic, the cobalt will hold its magnetisation; therefore by changing the direction of the remanent magnetisation, we can both temporarily and permanently change the optical properties.

Conclusion

We have demonstrated the fabrication of a unique architecture for a magnetoplasmonic metamaterial. The Au-core–Co-shell low aspect ratio nanowire array was grown via electro-deposition into an AAO template, which is a scalable, bottom up technique that can be geometrically tuned to a high degree of accuracy. We have demonstrated an order of magnitude enhancement over the control of magneto-optical properties as compared to a hollow Co nanotube array of similar dimensions due to plasmonic enhancement. We have also shown the ability to alter optical properties primarily defined by plasmonic resonance with an external magnetic field, as well as magnetic and optical remanent states. This overlap of magneto-optical activity and plasmonic resonance is a feature that makes magnetoplasmonic structures a new class of tuneable metamaterials with exciting possibilities in sensing or photonic devices.

Acknowledgements

The authors acknowledge the Engineering and Physical Sciences Research Council (EPSRC – UK) for financial support. We also thank Dr Emrah Yücelen from FEI Company for STEM work.

Notes and references

1. J. B. Pendry, D. Schurig and D. R. Smith, Science, 2006, 312, 1780–1782.
2. A. Alù and N. Engheta, Phys. Rev. Lett., 2010, 105, 263906.
3. D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser and S. Schultz, Phys. Rev. Lett., 2000, 84, 4184–4187.
4. P. Evans, W. R. Hendren, R. Atkinson, G. A. Wurtz, W. Dickson, A. V. Zayats and R. J. Pollard, Nanotechnology, 2006, 17, 5746.
5. A. Murphy, J. McPhillips, W. Hendren, C. McClatchey, R. Atkinson, G. Wurtz, A. V. Zayats and R. J. Pollard, Nanotechnology, 2011, 22, 045705.
6. B. Toal, M. McMillen, A. Murphy, W. Hendren, R. Atkinson and R. Pollard, Mater. Res. Express, 2014, 1, 015801.
7. S. M. Chérif, Y. Roussigné, A. A. Stashkevich, M. Darques, K. Bouziane and L. Piraux, J. Appl. Phys., 2011, 109 , 103912.
8. V. Bonanni, S. Bonetti, T. Pakizeh, Z. Pirzadeh, J. Chen, J. Nogués, P. Vavassori, R. Hillenbrand, J. Åkerman and A. Dmitriev, Nano Lett., 2011, 11, 5333–5338.
9. Y. Gu and K. G. Kornev, J. Opt. Soc. Am. B, 2010, 27, 2165–2173.
10. B. Sepúlveda, J. B. González-Díaz, A. García-Martín, L. M. Lechuga and G. Armelles, Phys. Rev. Lett., 2010, 104, 147401.
11. M. Lorente-Crespo, L. Wang, R. Ortuño, C. García-Meca, Y. Ekinci and A. Martínez, Nano Lett., 2013, 13, 2654–2661.
12. F. Pineider, G. Campo, V. Bonanni, C. de Julián Fernández, G. Mattei, A. Caneschi, D. Gatteschi and C. Sangregorio, Nano Lett., 2013, 13, 4785–4789.
13. M. A. Zaitoun, W. R. Mason and C. T. Lin, J. Phys. Chem. B, 2001, 105, 6780–6784.
14. G. Weick and D. Weinmann, Phys. Rev. B: Condens. Matter, 2011, 83, 125405.
15. G. Armelles, A. Cebollada, A. García-Martín and M. U. González, Adv. Opt. Mater., 2013, 1, 10–35.
16. M. G. Manera, G. Montagna, E. Ferreiro-Vila, L. Gonzalez-Garcia, J. R. Sanchez-Valencia, A. R. Gonzalez-Elipe, A. Cebollada, J. M. Garcia-Martin, A. Garcia-Martin, G. Armelles and R. Rella, J. Mater. Chem., 2011, 21, 16049–16056.
17. B. Sepúlveda, A. Calle, L. M. Lechuga and G. Armelles, Opt. Lett., 2006, 31, 1085–1087.
18. B. Sepúlveda, L. M. Lechuga and G. Armelles, J. Lightwave Technol., 2006, 24, 945.
19. A. V. Kimel, A. Kirilyuk, P. A. Usachev, R. V. Pisarev, A. M. Balbashov and T. Rasing, Nature, 2005, 435, 655–657.
20. V. V. Temnov, G. Armelles, U. Woggon, D. Guzatov, A. Cebollada, A. Garcia-Martin, J.-M. Garcia-Martin, T. Thomay, A. Leitenstorfer and R. Bratschitsch, Nat. Photonics, 2010, 4, 107–111.
21. G. Armelles, A. Cebollada, A. García-Martín, J. M. García-Martín, M. U. González, J. B. González-Díaz, E. Ferreiro-Vila and J. F. Torrado, J. Opt. A: Pure Appl. Opt., 2009, 11, 114023.
22. J. B. González-Díaz, A. García-Martín, J. M. García-Martín, A. Cebollada, G. Armelles, B. Sepúlveda, Y. Alaverdyan and M. Käll, Small, 2008, 4, 202–205.
23. J. C. Banthí, D. Meneses-Rodríguez, F. García, M. U. González, A. García-Martín, A. Cebollada and G. Armelles, Adv. Mater., 2012, 24, OP36–OP41.
24. V. I. Belotelov, I. A. Akimov, M. Pohl, V. A. Kotov, S. Kasture, A. S. Vengurlekar, A. V. Gopal, D. R. Yakovlev, A. K. Zvezdin and M. Bayer, Nat. Nanotechnol., 2011, 6, 370–376.
25. M. Rubio-Roy, O. Vlasin, O. Pascu, J. M. Caicedo, M. Schmidt, A. R. Goñi, N. G. Tognalli, A. Fainstein, A. Roig and G. Herranz, Langmuir, 2012, 28, 9010–9020.
26. S. Tomita, T. Kato, S. Tsunashima, S. Iwata, M. Fujii and S. Hayashi, Phys. Rev. Lett., 2006, 96, 167402.
27. G. A. Wurtz, W. Hendren, R. Pollard, R. Atkinson, L. L. Guyader, A. Kirilyuk, T. Rasing, I. I. Smolyaninov and A. V. Zayats, New J. Phys., 2008, 10, 105012.
28. L. Wang, C. Clavero, Z. Huba, K. J. Carroll, E. E. Carpenter, D. Gu and R. A. Lukaszew, Nano Lett., 2011, 11, 1237–1240.
29. Z. Xu, Y. Hou and S. Sun, J. Am. Chem. Soc., 2007, 129, 8698–8699.
30. H.-Y. Park, M. J. Schadt, L. Wang, I.-I. S. Lim, P. N. Njoki, S. H. Kim, M.-Y. Jang, J. Luo and C.-J. Zhong, Langmuir, 2007, 23, 9050–9056.
31. P. K. Jain, Y. Xiao, R. Walsworth and A. E. Cohen, Nano Lett., 2009, 9, 1644–1650.
32. G. Armelles, A. Cebollada, A. Garcia-Martin, J. M. Montero-Moreno, M. Waleczek and K. Nielsch, Langmuir, 2012, 28, 9127–9130.
33. P. R. Evans, W. R. Hendren, R. Atkinson and R. J. Pollard, J. Electrochem. Soc., 2007, 154, K79–K82.
34. A. Murphy, Y. Sonnefraud, A. V. Krasavin, P. Ginzburg, F. Morgan, J. McPhillips, G. Wurtz, S. A. Maier, A. V. Zayats and R. Pollard, Appl. Phys. Lett., 2013, 102, 103103–103105.
35. R. W. Collins, I. An and C. Chen, in Handbook of Ellipsometry, ed. H. G. Tompkins and E. A. Irene, William Andrew Publishing, Norwich, NY, 2005, pp. 329–432.
36. R. Kullock, W. R. Hendren, A. Hille, S. Grafström, P. R. Evans, R. J. Pollard, R. Atkinson and L. M. Eng, Opt. Express, 2008, 16, 21671–21681.
37. W. Yuan, H. P. Ho, S. Y. Wu, Y. K. Suen and S. K. Kong, Sens. Actuators, A, 2009, 151, 23–28.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4nr03792h

---