The search for the most stable structures of silicon–carbon monolayer compounds

Abstract

The most stable structures of two-dimensional (2D) silicon–carbon monolayer compounds with different stoichiometric compositions (i.e., Si : C ratio = 2 : 3, 1 : 3 and 1 : 4) are predicted for the first time based on the particle-swarm optimization (PSO) technique combined with density functional theory optimization. Although the 2D Si–C monolayer compounds considered here are rich in carbon, many of the low-energy metastable and the lowest-energy silicon–carbon structures are not graphene (carbon monolayer) like. Phonon-spectrum calculations and ab initio molecular dynamics simulations were also performed to confirm the dynamical stability of the predicted most stable 2D silicon–carbon structures as well their thermal stability at elevated temperature. The computed electronic band structures show that all three predicted silicon–carbon compounds are semiconductors with direct or indirect bandgaps. Importantly, their bandgaps are predicted to be close to those of bulk silicon or bulk germanium. If confirmed in the laboratory, these 2D silicon–carbon compounds with different stoichiometric compositions may be exploited for future applications in nanoelectronic devices.

---

Introduction

Since the successful isolation of graphene sheets in 2004,^1–5 this honeycomb structured 2D material has inspired intensive research interests largely due to its remarkable electronic, mechanical, and optical properties, including its unconventional quantum Hall effect, superior electronic conductivity, and high mechanical strength. In particular, the unique electronic properties of graphene draw attention to this 2D material as a potential candidate for applications in faster and smaller electronic devices. Like carbon, silicon is another group-IV element and also possesses a 2D allotrope with a honeycomb structure, namely silicene. Unlike the graphene sheet which is flat, the silicene sheet exhibits a weakly-buckled local geometry.^6,7 However, the zero-bandgap characteristics of both graphene and silicene prevent the direct use of both of these 2D sheets in controlled and reliable transistor operation, which hinder their wide applications in future optoelectronic devices. To date, much effort has been devoted to opening a bandgap (in the 1.0–2.0 eV range) in either graphene or silicene sheets,^8–12 although this is still a challenging task as it would require making some major changes to their intrinsic semi-metallic properties originating from the massless Dirac-fermion-like charge carriers.

The desire for the continuous miniaturization of electronic devices calls for the development of new and novel low-dimensional materials. Besides graphene and silicene, a wide range of 2D materials, particularly monolayer sheets with atomic thickness, have been reported in the literature. Coleman et al.¹³ developed a liquid exfoliation technique that can efficiently produce monolayer 2D nanosheets from a variety of inorganic layered materials such as boron nitride (BN), molybdenum disulfide (MoS₂), tungsten disulfide (WS₂), molybdenum diselenide (MoSe₂) and molybdenum telluride (MoTe₂). Using a modified liquid exfoliation technique, Xie et al. successfully fabricated monolayer vanadium disulfide (VS₂) and tin disulfide (SnS₂) in the laboratory.^14–16 On the theoretical side, increasing efforts have been devoted to predicting the structures and functional properties of novel 2D materials, such as monolayer boron sheets with low-buckled configurations,^17,18 monolayer boron–carbon (BC) compounds,^19,20 boron–silicon (BSi) compounds,²¹ aluminum carbon (AlC) compounds,²² carbon nitride (CN),²³ germanene,^24,25 tetragonal TiC,²⁶ SnC²⁷ and other group III–VI compounds.^27,28

2D silicon–carbon (Si–C) monolayers can be viewed as composition-tunable materials between the pure 2D carbon monolayer – graphene – and the pure 2D silicon monolayer – silicene. Efforts have been made towards predicting the most stable structures of the SiC sheet. Recently, Li et al.²⁹ and Zhou et al.³⁰ reported a metallic pt-SiC₂ 2D sheet and semiconducting g-SiC₂ siligraphene, respectively, based on density functional theory (DFT) calculations. Their studies indicate that the electronic properties of 2D silicon–carbon compounds can be strongly dependent on the structure and the stoichiometry. Moreover, few theoretical studies on 2D silicon–carbon compounds with different stoichiometries have been reported in the literature. 2D silicon–carbon sheets with different stoichiometric compositions are expected to possess different electronic properties from SiC and SiC₂ sheets. Thus, it is timely to search for new 2D structures of silicon–carbon compounds with distinct stoichiometries and explore their structure–property relationships. In this study, we perform a comprehensive search for structures of 2D Si–C compounds with stoichiometric compositions (Si : C ratios) of 2 : 3, 1 : 3 and 1 : 4, using particle-swarm optimization (PSO) techniques combined with density functional theory optimization. Our calculations suggest that the 2D Si–C compounds with higher carbon content over silicon are energetically more favored. The predicted lowest-energy structures of Si₂C₃-I, SiC₃-I and SiC₄-I exhibit semiconducting characteristics. Phonon-spectrum calculations and ab initio MD simulations further confirm the dynamic and thermal stability of the lowest-energy 2D structures. Finally, we show that the computed elastic constants of Si–C sheets are between those of graphene and silicene, suggesting that these newly predicted 2D Si–C compounds also possess good elastic properties.

Computational methods

The search for the most stable structures of 2D Si–C compounds was performed using the CALYPSO package³¹ which has been previously used to predict the most stable as well as the low-energy metastable 2D and 3D solid-state structures of various elements and compounds at different pressures.^32–37 Specifically, in the structure search the population size of each generation was set to be 40, and the number of generations was fixed to be 30. A population of 2D Si–C structures in the first generation was generated randomly with the constraint of symmetry. In the ensuing generations, 60% of the population was generated from the best (lowest-energy) structures in the previous generation by using the particle-swarm optimization (PSO) scheme and the other 40% was generated randomly to ensure diversity of the population. Local optimization including the atomic positions and lateral lattice parameters was performed for each of the initial structures.

The structure relaxation and total-energy calculations were performed using the VASP package³⁸ within the generalized gradient approximation (GGA). An energy cutoff of 450 eV and an all-electron plane-wave basis set within the projector augmented wave (PAW) method were used. A dense k-point sampling with the grid spacing less than 2π × 0.04 Å⁻¹ in the Brillouin zone was taken. To prevent interaction between the adjacent solid sheets, a 20 Å vacuum spacing was set along the z⃑ direction (i.e., the direction normal to the monolayer). For the geometric optimization, both the lattice constants and atomic positions were relaxed until the forces on the atoms were less than 0.01 eV Å⁻¹ and the total energy change was less than 1 × 10⁻⁵ eV. Phonon spectra of the low-energy crystalline structures were computed using the VASP package coupled with the PHONOPY program.³⁹ The phonon spectrum calculation was to assure that the obtained 2D sheets entailed no negative phone modes.

Results and discussion

A. Predicted lowest-energy structures of 2D Si–C compounds and their dynamic stability

2D Si–C compounds with three different Si–C stoichiometric compositions are considered, namely, Si₂C₃, SiC₃ and SiC₄. The predicted lowest-energy structure for each stoichiometry is shown in Fig. 1. For comparison, the low-energy metastable structures for each Si : C ratio are also shown in Fig. 1. Here, we use the Roman numerals I, II and III to denote the energy ranking of the low-lying solid structures (for example, Si₂C₃-I and Si₂C₃-II denote the lowest-energy and the second lowest-energy structure, respectively).

Fig. 1 Predicted low-lying solid structures of 2D Si–C compounds based on the PSO simulations. C and Si atoms are represented by brown and blue spheres. The computed relative energy per atom with respect to the lowest-energy structure is given beneath each structure.

To evaluate the relative stabilities among the predicted 2D C–Si compounds, we have computed their cohesive energy. The formula of cohesive energy for the 2D systems is defined as follows:

E_coh = (xE_Si + yE_C − E_SixCy)/(x + y)

where E_coh denotes the cohesive energy of the 2D C–Si compounds, and E_Si, E_C and E_SixCy are the total energy of a single Si atom, a single C atom, and the 2D Si_xC_y compound, respectively. Computed values of E_coh for all the predicted low-energy 2D Si_xC_y structures are listed in Table 1. It can be seen that E_coh increases with increasing carbon composition. SiC₄ has the highest E_coh value, suggesting a higher structural stability compared to the other two C–Si sheets.

Table 1 Computed cohesive energy of all of the predicted low-energy C–Si sheets

2D Structure	Cohesive energy (eV per atom)
Si2C3-I	7.2660
Si2C3-II	7.1712
Si2C3-III	7.1446
SiC3-I	7.8561
SiC3-II	7.8409
SiC3-III	7.8365
SiC4-I	8.0631
SiC4-II	8.0434

---

Next, to ensure that the predicted lowest-energy structure for each Si : C ratio is dynamically stable, phonon spectra of all of the three lowest-energy structures were computed using the supercell frozen phonon theory implemented in the PHONOPY program. The computed phonon spectra of the lowest-energy structures of Si₂C₃, SiC₃ and SiC₄ (Si₂C₃-I, SiC₃-I and SiC₄-I) are plotted in Fig. 2. Clearly, no negative phonon frequencies are present over the entire Brillouin zones for all three of the lowest-energy structures, indicating the inherent dynamical stability of these 2D Si–C sheets.

Fig. 2 Computed phonon band structures of (a) Si₂C₃-I, (b) SiC₃-I and (c) SiC₄-I. Γ(0.0, 0.0, 0.0), X(0.5, 0.0, 0.0), Y(0.0, 0.5, 0.0) and S(0.5, 0.5, 0.0) refer to special points in the first Brillouin zone.

Moreover, the thermal stability of the Si₂C₃-I, SiC₃-I and SiC₄-I structures was examined using ab initio molecular dynamics (AIMD) simulations. In the AIMD simulation, the canonical ensemble (NVT ensemble) is adopted. The AIMD time step was 2 fs and the total simulation time was 15 ps for each given temperature. The structural features of each Si–C sheet prior to and after melting are shown in Fig. 3. It can be seen that the equilibrium structures of the Si₂C₃-I and SiC₃-I sheets at the end of the 15 ps AIMD simulation show no sign of structural disruption at 3500 K, whereas both sheets exhibit disrupted structures at 4000 K. Thus we can conclude that the Si₂C₃-I and SiC₃-I structures can maintain their structure integrity and planar geometry below 3500 K. The SiC₄-I sheet appears to have the highest thermal stability among the three structures, as SiC₄-I can still keep its geometric structure over the 15 ps AIMD simulation with the temperature controlled at 4000 K.

Fig. 3 Snapshots of the three lowest-energy 2D Si–C compounds at the end of two independent 15 ps AIMD simulations: (a) Si₂C₃-I, (b) SiC₃-I and (c) SiC₄-I sheets.

B. Detailed structures of the three 2D Si–C compounds

(a) Si₂C₃ sheets. All three Si–C 2D compounds with different stoichiometric compositions are carbon-rich. As such, it is possible that their most stable structures may resemble the honeycomb structure of graphene. However, as shown in Fig. 1, our global search suggests that many of the structures of these 2D Si–C compounds are quite different from that of graphene. For the Si₂C₃ sheet, the lowest-energy Si₂C₃-I exhibits a planar structure composed of pentagonal, hexagonal and heptagonal rings, where each hexagonal ring is surrounded by four heptagonal and two pentagonal rings (see Fig. 1a). Each hexagonal ring is built upon three Si and three C atoms, where Si and C atoms are located alternately on the vertices. There are two types of pentagonal rings: one is composed of three C and two Si atoms, while the other is composed of four C and one Si atoms. The heptagonal rings are all made of three Si and four C atoms. In all of the polygonal rings, each Si atom is bonded with three C atoms within the same plane, representing a preference for the planar sp²-bonding. No Si–Si bonds exist in the structure of the Si₂C₃-I sheet.

The Si₂C₃-II sheet is 94.8 meV per atom higher in energy than the Si₂C₃-I sheet, although all of the polygonal rings in the Si₂C₃-II sheet are hexagonal. Notably, this Si₂C₃-II sheet can be viewed as silicon-doped graphene. In contrast to the Si₂C₃-I sheet where all of the Si atoms are located separately (no Si–Si bonds were found in the sheet), there are both separately-distributed Si atoms and Si dimers in the Si₂C₃-II sheet. The percentage of Si atoms forming Si dimers is 50%. Since the sp²-hybridization is not favored by silicon Si–Si bonds, a planar structure should be energetically unfavorable, which is possibly a major reason why Si₂C₃-II is less stable than Si₂C₃-I.

The third lowest-energy structure of Si₂C₃, namely the Si₂C₃-III sheet, is 121.4 meV per atom higher in energy than the Si₂C₃-I sheet. Apparently, the Si₂C₃-III sheet is composed of pentagonal, hexagonal and octagonal rings, where each octagonal ring is surrounded by four pentagonal and four hexagonal rings. In this structure, all of the Si atoms form Si dimers so that its energy is much higher than that of the Si₂C₃-I or Si₂C₃-II sheet.

(b) SiC₃ sheets. For SiC₃, three 2D structures are found with close energies. The relative energies of the SiC₃-II and SiC₃-III sheets are 15.2 and 19.6 meV per atom, respectively, with respect to the SiC₃-I sheet. Interestingly, the SiC₃-I sheet presents a graphene-like structure, which contains hexagonal rings only (see Fig. 1d). Similar to the Si₂C₃-I sheet, each Si atom in the SiC₃-I sheet is bonded with three C atoms but not with Si atoms. The Si atoms, along with the C atoms bonded with Si, form armchair Si–C chains, while the other C atoms form armchair C chains. The Si–C chains and the C chains connect with one another, forming the structure of the SiC₃-I sheet. The SiC₃-I sheet can be viewed as silicon-doped graphene. From the viewpoint of doping, it can be said that 50% of the A-site carbon atoms of graphene (in graphene, there are two inequivalent atomic sites, named as site A and site B) are substituted by silicon atoms. Note that our predicted SiC₃-I sheet is indeed the lowest-energy structure as recently predicted by Ding et al.⁴⁰

The structure of the SiC₃-II sheet is also graphene like.⁴¹ The Si atoms in the SiC₃-II sheet are also located separately, as in the SiC₃-I sheet (see Fig. 1e). So, it is surprising that the SiC₃-II sheet is 15.2 meV per atom higher in energy than the SiC₃-I sheet. A closer examination of the structure indicates that the only difference between the structure of the SiC₃-I and SiC₃-II sheets is the location of the two Si atoms in every hexagonal ring. In the SiC₃-I sheet, the two Si atoms are located at the 1 and 3 sites of every hexagonal ring (we denote the six sites of any hexagonal ring as site 1 to site 6), while in the SiC₃-II sheet they are located at the 1 and 4 sites. From the viewpoint of doping, the SiC₃-II sheet can be viewed as having 25% of the A-site and 25% of the B-site carbon atoms of the graphene substituted by Si atoms. The different location distribution of the Si atoms leads to more of the C atoms being connected with one another in the SiC₃-I sheet compared to SiC₃-II, which should be the main reason why the SiC₃-I sheet has a lower energy than the SiC₃-II sheet. Due to the different Si distributions, the structure of the SiC₃-II sheet cannot be decomposed into C chains and Si–C chains, while that of the SiC₃-I sheet can.

The structure of the SiC₃-III sheet is very different from those of the SiC₃-I and SiC₃-II sheets (see Fig. 1f). The SiC₃-III sheet is composed of octagonal, hexagonal, and pentagonal rings, and possesses a much higher symmetry compared to the SiC₃-I and SiC₃-II sheets. The Si atoms in the SiC₃-III sheet form dimers while the C atoms form complete hexagonal rings. It is known that Si dimers in a planar structure are energetically not favored whereas C hexagonal rings are favored. So, even though Si–Si bonds exist, the total energy of the SiC₃-III sheet is only a little higher than that of SiC₃-II sheet.

(c) SiC₄ sheets. The lowest-energy structure of SiC₄, i.e. the SiC₄-I sheet, consists of pentagonal, hexagonal, and heptagonal rings, similar to the structure of the Si₂C₃-I sheet. Each hexagonal ring is surrounded by four heptagonal and two pentagonal rings. As shown in Fig. 1g, the overall structure can be viewed as an alternate arrangement of two different chains: one is formed by heptagonal rings and another is formed by pentagonal and hexagonal rings. The SiC₄-II sheet has a similar structure to the Si₂C₃-III and SiC₃-III sheets, which contain pentagonal, hexagonal, and octagonal rings. However, unlike the other two structures, silicon dimers are not present in the SiC₄-II sheet. The cohesive energy of the SiC₄-II sheet is 19.7 meV per atom higher than that of the SiC₄-I sheet, due to the unfavorable octagonal rings in the 2D carbon systems.

Finally, we make a comparison of the C–C/C–Si bond length in graphene/SiC and the SiC compounds reported here. The C–C bond lengths in Si₂C₃-I, SiC₃-I, and SiC₄-I are 1.438 Å, 1.455 Å, and 1.432 Å respectively, slightly longer than that in graphene (1.42 Å). The C–Si bonds are slightly longer in Si₂C₃-I (1.792 Å) than those either in the SiC sheet (1.786 Å), or in SiC₃-I (1.781 Å) and SiC₄-I (1.770 Å). We have also computed the Si–Si distance between two parallel stacked (in registry) Si₂C₃-I monolayers. As shown in ESI Fig. S1,† the minimum Si–Si distance is about 3.4 Å. Hence, new Si–Si bonds are not expected to form when two Si₂C₃-I monolayers are stacked on top of one another.

In summary, although the 2D Si–C compounds considered here are all C-rich, most of the lowest-energy structures and low-energy metastable structures are not akin to Si-doped graphene. Pentagonal and heptagonal rings are occasionally formed in the lowest-energy structures, and octagonal rings normally appear in the metastable structures. The Si atoms tend to be located separated from one another, i.e. the Si atoms prefer to be bonded with C atoms but not Si atoms, which is a main factor that influences the relative stability of the 2D Si–C structures.

C. Electronic properties of 2D Si–C compounds

The computed electronic band structures of the Si₂C₃-I, SiC₃-I and SiC₄-I sheets, based on GGA calculations, are plotted in Fig. 4. It can be seen that all three of the lowest-energy structures are semiconducting, among which the Si₂C₃-I and SiC₃-I sheets possess a direct bandgap, while the SiC₄-I sheet exhibits an indirect bandgap. The computed bandgaps of the Si₂C₃-I, SiC₃-I and SiC₄-I sheets (at GGA level) are 0.83 eV, 0.86 eV and 0.14 eV, respectively (see Table 2), and all belong to the narrow-gap semiconductors. Note that GGA calculations tend to underestimate the bandgaps of semiconducting materials. To predict the bandgap of each Si–C compound more accurately, we also performed band-structure calculations using the HSE06^42–44 functional which has been proven to be more accurate for bandgap computation. The bandgaps of the Si₂C₃-I, SiC₃-I and SiC₄-I sheets (based on HSE06 calculations) are 1.37 eV, 1.40 eV, and 0.51 eV, respectively. The bandgaps of the Si₂C₃-I and SiC₃-I sheets are very close to that of bulk silicon, while the bandgap of the SiC₄-I sheet is close to that of bulk germanium. Like bulk silicon and germanium, these 2D Si–C compounds may find applications in nanoelectronic devices.

Fig. 4 Computed electronic band structures of (a) Si₂C₃-I, (b) SiC₃-I and (c) SiC₄-I monolayer sheets. The Fermi level is set to 0 eV.

Table 2 Computed bandgaps of Si₂C₃-I, SiC₃-I and SiC₄-I monolayer sheets, based on GGA and HSE06 calculations. Here, D and I denote direct and indirect bandgap, respectively

2D Structure	Bandgap
	GGA	HSE06
Si2C3-I	0.83 eV (D)	1.37 eV (D)
SiC3-I	0.86 eV (D)	1.40 eV (D)
SiC4-I	0.14 eV (I)	0.51 eV (I)

---

The computed partial density of states (PDOSs) of the predicted 2D Si–C compounds was also analyzed. The representative PDOSs for Si₂C₃-I, SiC₃-I and SiC₄-I sheets are plotted in Fig. 5. It is clear that in all three cases the higher valence bands and lower conduction bands (about −2.0 to 2.5 eV of the energy windows) are contributed by the sp² orbitals of Si and C, while the p_z orbitals of Si and C only have contributions to the lower valence bands (below −2.0 eV) and higher conduction bands. So, the electronic properties of these sheets are only determined by the in-plane σ and σ* bonds rather than the π and π* states, in contrast to graphene and graphite where the conjugate π states have a major influence on the electronic properties such as excellent conductivity.

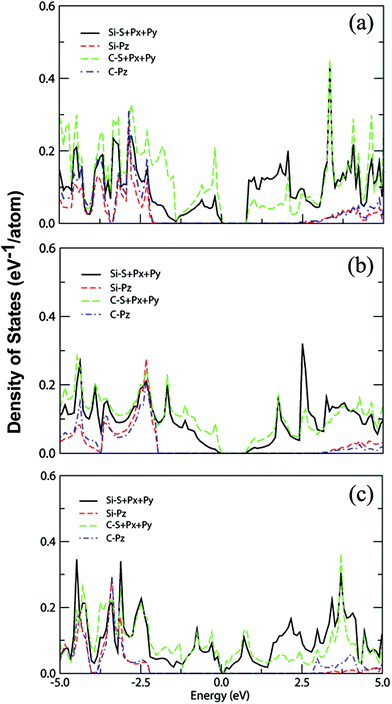Fig. 5 Computed PDOSs for (a) Si₂C₃-I, (b) SiC₃-I and (c) SiC₄-I monolayer sheets. The Fermi level is set at 0 eV.

For the Si₂C₃-I sheet, it is clearly shown that the valence band maximum (VBM) is mainly contributed by the s, p_x and p_y orbitals of the C atoms, while the contribution of Si is about half that of C. On the other hand, the conduction band minimum (CBM) is mainly contributed by Si atoms and the contribution of C atoms is about half that of Si. For the SiC₃-I sheet, both the VBM and CBM are contributed mainly by the sp² hybridization states of C. And for the SiC₄-I sheet, it is obvious that the C and Si atoms contribute to the VBM and CBM nearly equally. It is worth noting that there are such large differences in the contribution to the VBM and CBM states for different 2D Si–C compounds.

To gain a deeper understanding of the nature of the bonding for the predicted 2D Si–C compounds, we applied the electron localization function (ELF) analysis, which can be used to classify chemical bonds rigorously. Due to the more localized characteristic of σ states than π states, a relatively large value of ELF distribution (e.g., 0.725) for the Si–C compounds can mostly characterize the in-plane σ states. The plotted iso-surfaces of ELFs for the lowest-energy Si–C sheets are shown in Fig. 6. It can be seen that in all the cases the ELFs of the C–C bonds are localized just at the center of the bonds and those of the Si–C bonds are localized closer to the C atoms. This is due to the fact that the electronegativity of the C atoms is stronger than that of the Si atoms. For the Si₂C₃-I sheet, apparently there are more Si–C bonds. The incline of ELFs to the C atoms suggests that both the VBM and CBM states mainly originate from the in-plane sp² hybridization states of C and Si, respectively. For the other two cases, most of the C atoms connect with one another, forming C chains. The composition of Si–C bonds in SiC₃-I and SiC₄-I sheets are lower than that in the Si₂C₃-I sheet, hence the charge transfer from Si to C is weaker as reflected by the fact that the contribution of the Si sp² states to the VBM is minor in both cases.

Fig. 6 Iso-surfaces of the ELF with the value of 0.725 for (a) Si₂C₃-I, (b) SiC₃-I and (c) SiC₄-I sheets.

D. Elastic properties of Si–C sheets

As mentioned above, the predicted lowest-energy structures of Si₂C₃, SiC₃ and SiC₄ sheets all possess excellent semiconducting properties that may be exploited for nanoelectronic applications. To this end, the mechanic strengths of the Si–C sheets are also important. It is well known that graphene possesses excellent elastic properties with large elastic constants: c₁₁ = 906.70 GPa and c₁₂ = 244.50 GPa. Previous studies have shown that silicene also has good elastic properties (c₁₁ = 287 GPa and c₁₂ = 127 GPa). We thus speculate that the predicted Si–C sheets may also possess good elastic properties. Based on density functional theory calculations, elastic constants of these 2D Si–C compounds were computed (see Table 3). To evaluate the specific value of elastic constants, we need to define interlayer spacing between two stacked Si_xC_y sheets. Here, we estimate it to be ∼3.80 Å, which can be viewed as the thickness of a corresponding Si_xC_y bilayer. Since the interlayer interaction is van der Waals like, akin to that in graphite, this interlayer distance is just an estimated value due to the limitation of DFT methods in describing weak interactions. Four important elastic constants c₁₁, c₁₂, c₂₂ and c₆₆ of the three lowest-energy Si–C sheets were computed based on GGA. One can see that the computed c₁₁ and c₁₂ of the Si–C sheets are between those of graphene and silicene, and both tend to increase with the concentration of C atoms in the Si–C sheets. Hence, the SiC₄-I sheet possesses the largest value of c₁₁ and c₁₂ among the three Si–C sheets. However, a similar trend is not seen for c₂₂ and c₆₆. The computed c₂₂ and c₆₆ of the SiC₃-I sheet are larger than those of the Si₂C₃-I and SiC₄-I sheets. Overall, the predicted high elastic constants indicate that the 2D Si–C compounds possess reasonably good elastic properties.

Table 3 Computed elastic constants c₁₁, c₁₂, c₂₂ and c₆₆ for the predicted lowest-energy 2D Si–C compounds

2D Structure	Elastic constants (GPa)
	c 11	c 12	c 22	c 66
Si2C3-I	453.8	171.0	473.6	160.2
SiC3-I	594.5	180.8	640.2	231.5
SiC4-I	629.4	192.9	584.6	197.4

---

Conclusion

In conclusion, monolayer silicon–carbon (Si–C) materials can be viewed as composition-tunable materials between the pure 2D carbon monolayer – graphene – and the pure 2D silicon monolayer – silicene. Based on the PSO algorithm combined with density functional theory optimization, we performed an extensive 2D-crystalline search of monolayer structures of silicon–carbon compounds. A number of low-energy structures are predicted for different stoichiometric compositions (i.e., Si₂C₃, SiC₃ and SiC₄). In the most stable structures, each Si atom is bonded with three C atoms, favoring the sp² hybridization. Dynamic and thermal stabilities of the predicted lowest-energy structures were examined through calculations of phonon dispersion and ab initio molecular dynamics simulations. These 2D Si–C compounds possess high thermal stabilities such that the Si₂C₃-I and SiC₃-I sheets can retain their planar geometries below 3500 K while the SiC₄-I sheet can even maintain its planar structure up to 4000 K. Next, the electronic and elastic properties of these three stable sheets were computed. Our calculations suggest that all of the predicted lowest-energy Si–C sheets are semiconductors with a moderate bandgap ranging from 0.5–1.5 eV, comparable to that of bulk silicon or germanium. Lastly, we found that these Si–C sheets possess reasonably high elastic constants whose values are typically between those of graphene and silicene. The composition dependent electronic and mechanical properties of 2D Si–C compounds may find applications in nanoelectronic devices.

Acknowledgements

RLZ thanks the support of the National Natural Science Foundation of China (Grant no. 11104056), the Natural Science Foundation of Anhui Province (Grant no. 11040606Q33). XCZ is supported by ARL (Grant no. W911NF1020099), NSF (Grant no. DMR-0820521), and a grant from USTC for (1000 Talents Program) Qianren-B summer research.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197.
3. K. S. Novoselov, E. McCann, S. V. Morozov, V. I. Falko, M. I. Katsnelson, U. Zeitler, D. Jiang, F. Schedin and A. K. Geim, Nat. Phys., 2006, 2, 177.
4. Y. B. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
5. Q. Tang, Z. Zhou and Z. Chen, Nanoscale, 2013, 5, 4541.
6. A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501.
7. B. Feng, Z. Ding, S. Meng, Y. Yao, X. He, P. Cheng, L. Chen and K. Wu, Nano Lett., 2012, 12, 3507.
8. S. Y. Zhou, G. H. Gweon, A. V. Fedorov, P. N. First, W. A. de Heer, D. H. Lee, F. Guinea, A. H. Castro Neto and A. Lanzara, Nat. Mater., 2007, 6, 770.
9. L. Yang, C. H. Park, Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99, 186801.
10. H. J. Xiang, B. Huang, Z. Y. Li, S. H. Wei, J. L. Yang and X. G. Gong, Phys. Rev. X, 2012, 2, 011003.
11. Z. Ni, Q. Liu, K. Tang, J. Zheng, J. Zhou, R. Qin, Z. Gao, D. Yu and J. Lu, Nano Lett., 2012, 12, 113.
12. S. Lebègue, M. Klintenberg, O. Eriksson and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245117.
13. J. N. Coleman, M. Lotya, A. O. Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568.
14. J. Feng, X. Sun, C. Wu, L. Peng, C. Lin, S. Hu, J. Yang and Y. Xie, J. Am. Chem. Soc., 2011, 133, 17832.
15. J. Feng, L. Peng, C. Wu, X. Sun, S. Hu, C. Lin, J. Dai, J. Yang and Y. Xie, Adv. Mater., 2012, 24, 1969.
16. Y. Sun, H. Cheng, S. Gao, Z. Sun, Q. Liu, F. Lei, T. Yao, J. He and S. Wei, et al. , Angew. Chem., Int. Ed., 2012, 51, 8727.
17. X. Yu, L. Li, X. W. Xu and C. C. Tang, J. Phys. Chem. C, 2012, 116, 20075.
18. X. Wu, J. Dai, Y. Zhao, Z. Zhuo, J. Yang and X. C. Zeng, ACS Nano, 2012, 6, 7443.
19. X. J. Wu, Y. Pei and X. C. Zeng, Nano Lett., 2009, 9, 1577.
20. X. Luo, J. Yang, H. Liu, X. Wu, Y. Wang, Y. Ma, S. H. Wei, X. Gong and H. Xiang, J. Am. Chem. Soc., 2011, 133, 16285.
21. J. Dai, Y. Zhao, X. J. Wu, J. L. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2013, 4, 561.
22. J. Dai, X. J. Wu, J. L. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5, 2058.
23. H. J. Xiang, B. Huang, Z. Y. Li, S. H. Wei, J. L. Yang and X. G. Gong, Phys. Rev. X, 2012, 2, 011003.
24. Z. Ni, Q. Liu, K. Tang, J. Zheng, J. Zhou, R. Qin, Z. Gao, D. Yu and J. Lu, Nano Lett., 2012, 12, 113.
25. A. O'Hare, F. V. Kusmartsev and K. I. Kugel, Nano Lett., 2012, 12, 1045.
26. Z. Zhang, X. Liu, B. I. Yakobson and W. Guo, J. Am. Chem. Soc., 2012, 134, 19326.
27. H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
28. C. Freeman, F. Claeyssens, N. Allan and J. Harding, Phys. Rev. Lett., 2006, 96, 066102.
29. Y. Li, F. Li, Z. Zhou and Z. Chen, J. Am. Chem. Soc., 2011, 133, 900.
30. L. Zhou, Y. Zhang and L. Wu, Nano Lett., 2013, 13, 5431.
31. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
32. Y. Ma, M. I. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182.
33. A. R. Oganov, Y. M. Ma, Y. Xu, I. Errea, A. Bergara and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7646.
34. Y. Xie, A. R. Oganov and Y. Ma, Phys. Rev. Lett., 2010, 104, 177005.
35. R. L. Zhou and X. C. Zeng, J. Am. Chem. Soc., 2012, 134, 7530.
36. R. Zhou, B. Qu, J. Dai and X. C. Zeng, Phys. Rev. X, 2014, 4, 011030.
37. J. Dai, X. J. Wu, J. L. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2013, 4, 3484.
38. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
39. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
40. Y. Ding and Y. Wang, J. Phys. Chem. C, 2014, 118, 4509.
41. Q. Tang and Z. Zhou, Prog. Mater. Sci., 2013, 58, 1244.
42. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
43. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
44. J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4nr03247k

---