Single nickel-related defects in molecular-sized nanodiamonds for multicolor bioimaging: an ab initio study

Abstract

Fluorescent nanodiamonds constitute an outstanding alternative to semiconductor quantum dots and dye molecules for in vivo biomarker applications, where the fluorescence comes from optically active point defects acting as color centers in the nanodiamonds. For practical purposes, these color centers should be photostable as a function of the laser power or the surface termination of nanodiamonds. Furthermore, they should exhibit a sharp and nearly temperature-independent zero-phonon line. In this study, we show by hybrid density functional theory calculations that nickel doped nanodiamonds exhibit the desired properties, thus opening the avenue to practical applications. In particular, harnessing the strong quantum confinement effect in molecule-sized nanodiamonds is very promising for achieving multicolor imaging by single nickel-related defects.

---

1 Introduction

Biologically compatible markers are much sought-after for the study of processes in living cells by means of in vivo multicolor imaging. Their action consists of binding to nanosized objects and tracking their location by emitting light upon excitation. To this end, semiconductor quantum dots and dye molecules have been used in the recent past.^1,2 The former bring the advantages of having small size, high photostability and bright multicolor fluorescence, while on the other hand they are toxic. Reduction of their cytotoxicity is achieved by encapsulation, which leads to a change in their photophysical properties and to a consequent growth in size after surface modification. Dye molecules, on the other hand, lack photostability, presenting blinking and photobleaching at room temperature (see ref. 3 and references therein). This constitutes a major problem when long-term and repetitive monitoring of the bioactive compound is wanted. To solve this problem, a promising strategy is to embed photostable color centers into bioinert nanocrystals,^3,4 such as nanodiamonds.⁵ Small diamond cages or nanodiamonds are obvious choices for in vivo bioimaging as they (i) contain bioinert carbon atoms, (ii) show low chemical reactivity⁶ and (iii) traditional organo-chemistry may be applied for surface functionalization.⁷ However, diamond has an ultraviolet band gap. In ultra-small nanodiamonds the band gap is enlarged due to quantum confinement, thus pure nanodiamonds with clean surfaces are not fluorescent. It is important to mention here that their highest occupied molecular orbital (HOMO) does indeed exhibit the quantum confinement effect, whereas their lowest unoccupied molecular orbital (LUMO) is often surface related and weakly dependent on the size of the nanodiamonds; for instance, it is a weakly bound Rydberg-like state in hydrogenated nanodiamonds.⁸ Visible or longer wavelength emission can only be achieved by introducing color centers into nanodiamonds. The famous nitrogen-vacancy defect (NV) is such a color center in diamond, with unique properties and measurement abilities when its photoluminescence (PL) is combined with magnetic resonance techniques.⁵ The NV-center has a large phonon-side band,⁹ however; it is desirable to embed color centers that have sharp zero-phonon lines in bioimaging applications, in order to achieve sufficient contrast for multicolor imaging. Moreover, according to calculations,¹⁰ the NV center has been shown to be unstable in ultra-small nanodiamonds. Alternative optically active point defects with favorable properties in ultra-small nanodiamonds are urgently required for in vivo bioimaging applications. Recently, it has been demonstrated in meteorite nanodiamonds that the fluorescent Si-V center can be stable in molecule-sized nanodiamonds,¹¹ where we were able to characterize this center with our simulation tools, showing a relatively small quantum confinement effect. Here, we take one step further by characterizing the nickel-related defects in nanodiamonds.

In this paper, we show by advanced hybrid density functional theory (DFT) calculations that fluorescent nickel-related defects with sharp emission are stable in ultra-small nanodiamonds. Their excitations are calculated with time-dependent DFT. In molecule-sized nanodiamonds the wavelength of the emission from the nickel-related color centers shows strong quantum confinement, thus tight control of the size of the nanodiamonds makes it possible to realize multicolor bioimaging with single nickel-related defects, in contrast to the traditional and technologically challenging way of introducing multiple color centers. These color centers are paramagnetic in the ground state, which provides the opportunity to trace these nanoparticles both by light and magnetic fields at the same time.

The nanoparticle geometries were constructed by cutting approximately spherical clusters out of bulk diamond crystal, with varying diameters in the 1.1–2.0 nm range: C₁₄₇ (d = 1.1 nm), C₁₇₅ (d = 1.2 nm), C₃₇₅ (d = 1.55 nm), C₄₅₂ (d = 1.7 nm), and C₆₃₃ (d = 1.9 nm). We applied a standard methodology to terminate the surfaces of the nanodiamonds: the surface dangling bonds were passivated by hydrogen atoms. We note that hydrogenated nanodiamonds may be achieved by hydrogen plasma treatment.^12,13 These nanodiamonds are considered as pristine ones. Pristine nanodiamonds possess excitation energies in the ultraviolet region. In order to introduce redshift into the excitation spectrum of nanodiamonds we introduced nickel-related defects that may act as color centers. In particular, we considered the so-called NE4*,¹⁴ NE4 (ref. 15 and 16) and NE8 (ref. 17) electron paramagnetic resonance (EPR) centers that are associated with the 1.83 eV (678 nm),¹⁴ 1.72 eV (721 nm),¹⁸ and 1.56 eV (794 nm)¹⁷ PL centers in bulk diamond, respectively. Recently, the NE4* and NE4 centers were associated with the different charge states of VNiV defects,^19,20 where VNiV represents a split-vacancy configuration (see Fig. 5). This defect is more stable than the isolated substitutional nickel-defect (W8 EPR center).^19–21 In addition, the W8 defect is rather an absorption than a luminescence center in diamond, according to our recent calculations,²² thus we excluded it in this study. The NE8 defect is associated with a complex of four nitrogen atoms around the split VNiV defect (see Fig. 6), briefly, the N₂VNiVN₂ complex,^17,20 where the defect might be positively charged under typical measurement conditions. As shown above, nickel-related defects with sharp zero-phonon lines in their PL spectra might be the best understood transition metal impurity related defects in bulk diamond. Furthermore, the NE8 PL center can act as a bright single photon source in the NIR region in bulk diamond,^23,24 thus it is particularly attractive as a color center for bioimaging. We note that NE8 defects could be engineered into diamond grains, where their average diameters were between 30 and 100 nm.²⁵ The corresponding PL spectra did not differ from those obtained in bulk diamond because no quantum confinement takes place. However, quantum confinement might provide a sizable effect on the optical properties of nickel-related defects in small nanodiamonds.

We studied the optical properties of the NE4*, NE4 and NE8 color centers in small nanodiamonds by time-dependent density functional theory (TD-DFT) calculations using a hybrid functional in its kernel, where this methodology was proven to provide reliable results for nanodiamonds with different surface terminations,^8,26 including color centers inside hydrogenated nanodiamonds.^11,27 NE4 and NE8 defects may be considered as nickel-related color centers in nitrogen-free and highly nitrogen-contaminated nanodiamonds. We note that the experimental Stokes shift of the considered PL centers is about 30 meV (ref. 17) which is below the expected accuracy of our method, thus we calculated the excitation energies for the ground state geometries of the defects. For the bulk reference calculations we applied a hybrid DFT supercell plane wave methodology that is able to reproduce the experimental defect ionization energies within 0.1 eV in Group-IV semiconductors,^28,29 and is proven to be correct for substitutional Ni impurity (Ni_s) in diamond.²²

2 Results and discussion

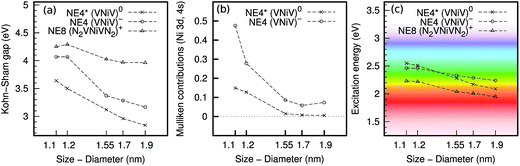
We computed the electronic levels and the lowest excitation energies of the selected nanodiamonds that contained nickel defects. Fig. 1 shows the most important results of our work. We find that:

(i) the introduction of color centers to the nanodiamonds redshifts their excitation energies from the ultraviolet region of the pristine nanodiamonds;

(ii) the quantum confinement effect (QCE) is very strong for the defect levels in the gap of the nanodiamonds, both for the NE4 and NE8 color centers [Fig. 1(a)], and the highest energy occupied defect states significantly hybridized with the host diamond states;

(iii) as a consequence, a strong QCE arises in the luminescence of these color centers [Fig. 1(c)]. We propose that single VNiV defects in nitrogen-free nanodiamonds and single N₂VNiVNi₂ defects in highly nitrogen-contaminated nanodiamonds may be utilized to realize multicolor imaging in the visible toward the infrared region, by finely controlling the size of the nanodiamonds. Small nanodiamonds hosting these nickel color centers would provide an ideal platform for non-invasive in vivo bioimaging. Next, we discuss the stability of the defects in hydrogenated nanodiamonds and bulk diamond, and the photostability of these color centers in hydrogenated nanodiamonds. Finally, we analyze the nature of the excitation and we provide the reason for the strong quantum confinement effect.

Fig. 1 (a) Weighted Kohn–Sham gap of the defects as a function of the size of the hydrogenated nanodiamonds, as calculated by spin-polarized PBE0 hybrid density functional theory. The weights of the pairs of Kohn–Sham states were determined from time-dependent density functional theory calculations as the contribution of these pairs of Kohn–Sham states to the first excitation peak. (b) The contribution of the nickel orbitals in the occupied Kohn–Sham states that participate in the lowest-energy excitation as a function of the size of the hydrogenated nanodiamonds determined by Mulliken analysis. Note the large reduction of this contribution for the NE4 center, which manifests as a smoother slope of the excitation energy as a function of the size of the hydrogenated nanodiamonds. (c) The calculated excitation energies of the corresponding color centers are plotted as a function of the size of the nanodiamonds.

First, we studied the stability of the selected nickel defects by calculating the formation energies of the defects in nanosized and bulk diamonds, as plotted in Fig. 2(a), when the defect is placed in the middle of the nanodiamonds. The VNiV defect is about equally stable in bulk and molecule-sized diamonds. Surprisingly, the N₂VNiVN₂ is even more stable in molecule-sized nanodiamonds than in bulk diamond. These results indicate that once these defects were created in nanodiamonds they will remain there. Next, we considered the relative stability of the corresponding color centers as a function of their position in our largest 1.9 nm nanodiamond [Fig. 2(b)–(d)]. We assumed that the first neighbor shell around the defect should contain carbon atoms when they approach the surface. For both defects, relatively small fluctuations in the calculated formation energies can be observed. Apparently, no thermodynamic force appears to drive these color centers toward the edge of the nanodiamonds. We conclude that these color centers may be found in molecule-sized nanodiamonds once they are formed.

Fig. 2 Stability of nickel-related defects in different diamonds calculated at the DFT PBE level. (a) The calculated formation energies of the selected defects as a function of the size of the diamonds. The defects were placed in the middle of the nanodiamonds. ((b) and (c)) The relative stability of the VNiV and N₂VNiVN₂ color centers within 1.9 nm hydrogenated nanodiamonds as a function of their positions. (d) Shows 1.9 nm hydrogenated nanodiamond with labeling at the positions where we placed the Ni impurity of the selected defects within the nanodiamonds. Because of the lack of inversion symmetry within the nanodiamonds, the depicted 〈110〉_a and 〈110〉_b directions are not equivalent.

Next, we studied the photostability of the Ni-related color centers from the aspect of surface termination. It is well-known from studies of the NV-center, that the NV-center can switch its charge state from negative to neutral when it is close to the hydrogenated diamond surface,^30–32 which is explained by the band bending model between the diamond surface and the environment.³³ Particularly, it is expected that the NV defect can be predominantly found in its neutral charge state in hydrogenated nanodiamond.³⁴ We use the charge transition levels of the NV defect in bulk diamond as a marker to determine whether the selected Ni-related color centers are stable in their given charge states in hydrogenated nanodiamonds. For the sake of completeness, we also include the Ni_s defect in this study²² but we focus on the VNiV and N₂VNiVN₂ complexes. The results are plotted in Fig. 3. There is a window of the Fermi-level positions where the NV defect is stable in its neutral charge state in bulk diamond. In this window the VNiV defect can be neutral, negatively charged and double negatively charged. Its calculated (−|2−) charge transition level is at around E_V +2.0 eV, where E_V is the valence band edge. This is about 0.7 eV below the (0|−) charge transition level of the NV defect. No visible luminescence is expected from the VNiV defect in the (2−) charge state but its (−) and (0) charge states should show luminescence. We conclude that VNiV-related luminescence is expected in hydrogenated nanodiamonds and might not be detected in oxygenated or fluorinated nanodiamonds,^34–36 where the Fermi-level shifts higher with stabilization of the NV⁻ defect. Since the calculated (0|−) charge transition level of VNiV lies relatively deep in the gap at around E_V +1.2 eV, it is more likely that the NE4 center will be active in hydrogenated nanodiamonds. The situation is simpler for the N₂VNiVN₂ complex. The defect is mainly stable in its (+) charge state as a function of the position of the Fermi-level in diamonds, particularly, in the full stability window of NV⁰. We note that neutral N₂VNiVN₂ has an S = 1 ground state. The calculated (+|0) charge transition level is at around E_V +2.9 eV, which is 0.2 eV above the (0|−) charge transition level of the NV defect. This result indicates that the NE8 color center should have a stable luminescence in hydrogenated nanodiamond, and it may emit light even in oxygenated nanodiamonds where NV⁻ is stabilized. Thus, the NE8 color center embedded in hydrogenated nanodiamonds is ideal for ensuring stable luminescence.

Fig. 3 The calculated formation energies and charge transition levels in bulk diamond at the DFT HSE06 level. ((a) and (b)) The formation energies for the VNiV and N₂VNiVN₂ defects, respectively, as a function of the position of the Fermi-level in the band gap of diamond. The calculated valence band edge was aligned with the origin. The valence band (VB) and conduction band (CB) edges are also depicted by shaded areas, where the color of these areas corresponds to the color code of the given defects in (c). The charge transition levels can be read as the crossings between the lines. (c) The charge transition levels in the band gap are depicted for the given defects, where the Ni_s and NV levels were given in ref. 22 and 29.

It is imperative to analyze the electronic structure of the selected Ni-related color centers in order to understand the nature of their optical transitions and the strong effect of quantum confinement on their excitation energies in nanodiamonds. We start the analysis with the split-vacancy VNiV defect, which might be described by substituting a divacancy (two adjacent vacancies in diamond) with a single Ni impurity, where this impurity is placed halfway in between the two vacant sites. Thus, the Ni atom lies in the inversion center of the diamond lattice. The electronic structure of this system was already studied in previous papers,^19,20 thus we only provide a brief description by applying the powerful group theory in combination with the DFT HSE06 calculations in bulk diamond. The full system has D_3d symmetry. Six dangling bonds create a⁽²⁾_2ua⁽²⁾_1ge⁽²⁾_ge⁽⁰⁾_u states. The Ni 3d orbitals split in this crystal field as a⁽²⁾_1ge⁽⁴⁾_ge⁽⁴⁾_g. The a_1g and e_g states can principally hybridize whereas the a_2u and e_u vacancy-like states will be exclusively localized on the carbon dangling bonds of the divacancy (see Fig. 5). The former lies deep in the valence band whereas the latter has higher energy. Between the two levels can be found the e_g and a_1g molecule-like levels except one antibonding combination of the e_g state which is empty and lies high in the band gap of diamond. The resulted states of neutral VNiV defect may be described as a⁽²⁾_2ua⁽²⁾_1ge⁽⁴⁾_ga⁽²⁾_1ge⁽⁴⁾_ge⁽²⁾_ue⁽⁰⁾_g. The a_2u and the empty e_g states do not play a role in the lowest energy excitations. Using spin-polarized DFT HSE06 calculations we found that in bulk diamond the fully occupied spin-up e_u state is resonant with the valence band, whereas the spin-down empty e_u state appears clearly in the band gap building up a high spin S = 1 state (c.f.Fig. 4). This qualitatively agrees with a previous DFT PBE supercell calculation.²⁰ Excitation may occur from the resonant spin-down a_1g or e_g states to the empty e_u state that is optically allowed by parity. In the VNiV⁻ defect, the e_u state is occupied by three electrons, which is principally a Jahn–Teller unstable system. Nevertheless, the Jahn–Teller distortion is small, in agreement with the previous findings.²⁰ The DFT HSE06 method predicts C_2h symmetry of the system which slightly splits the degenerate e_u and e_g states to a_u ⊕ b_u and a_g ⊕ b_g states, respectively. The corresponding defect levels shift up with respect to the defect levels of VNiV⁰ (c.f.Fig. 4), in agreement with the previous finding.²⁰ The excitation may be expected again from the occupied resonant a_g and b_g states to the empty a_u state. In the N₂VNiVN₂ complex, four carbon atoms around the Ni impurity are substituted by nitrogen atoms, so the defect per se has C_2h symmetry. The four nitrogen atoms provide four extra electrons to the system with respect to the VNiV defect. The resulting electronic structures are shown in Fig. 4 and 6. In the positive charge state of the defect, the b_u level is fully occupied, and the unpaired spin will be localized on the b_g level, resulting in the S = 1/2 spin state. The b_u state is resonant with the valence band, whereas the empty a_g state can be found in the band gap of bulk diamond. Excitation may be expected between the b_g and a_g states. The excitations of these defects were investigated in the nanodiamonds.

Fig. 4 Schematic diagram of the DFT HSE06 single particle defect states with symmetry labels in bulk diamond for (a) VNiV⁰ (NE4*), (b) VNiV⁻ (NE4), and (c) N₂VNiVN⁺₂ (NE8). The occupation of defect states in the gap is shown by dots. (d) Resonant defect states of VNiV⁰ and N₂VNiVN⁺₂ in bulk diamond. The absolute value of the isovalues of 0.022 and 0.1 were applied in the VNiV⁰ and N₂VNiVN⁺₂ defects, respectively, where the red and blue lobes represent the negative and positive values of the corresponding wave functions, respectively. Strong hybridization between the e_g and a_1g resonant states and the host crystal states is apparent in the VNiV⁰ defect. The resonant b_u state mixes much less with the host diamond states in the N₂VNiVN⁺₂ defect.

In nanodiamonds, the inversion symmetry is broken, strictly speaking. Thus, D_3d reduces to C_3v, whereas the C_2h symmetry goes to C_1h, going from bulk diamond to nanodiamond. However, the corresponding defect states still resemble the character of such wave functions that have parity (see Fig. 5 and 6). We conclude that it is reasonable to apply the selection rules of assuming the inversion center in the defects and to label the corresponding defect states with the symmetry group associated with the defects in bulk diamond.

Fig. 5 Group theory analysis of VNiV defect states in diamond. The wave functions and the Kohn–Sham levels are the result of the PBE0 calculation in the 1.1 nm nanodiamond. (a) Defect molecule diagram. The yellow background represents the valence band. The nature of the excitation in the neutral charge state (NE4*) is represented by arrows. (b) Single particle orbitals associated with the defect are represented by blue (positive) and red (negative) lobes, with an absolute isovalue of 0.065, where the defect is shown from the view of the symmetry axis.

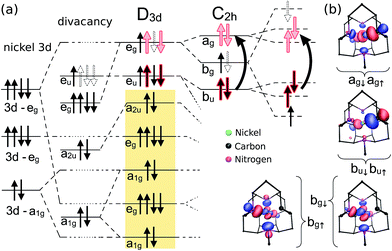Fig. 6 Group theory analysis of the N₂VNiVN₂ defect in the positive charge state, the NE8 center. (a) Defect molecule diagram. The analysis starts, from left to right, with that of the VNiV states (c.f.Fig. 5) but with 4 extra electrons donated by the 4 N-atoms. Next, we take into account that the crystal field is reduced from D_3d to C_2h due to the presence of N-atoms, which splits the corresponding states. The final column shows the large spin-polarization of the b_g state, so the excitation occurs between the b_u and a_g states. According to our time-dependent density functional theory calculations, both spin states contribute to the excitation. (b) The wave functions and the Kohn–Sham levels are the result of the PBE0 calculation in the 1.1 nm nanodiamond. Single particle orbitals associated with the defect are represented by blue (positive) and red (negative) lobes with an absolute isovalue of 0.065, where the defect is shown from the view of the symmetry axis.

In the VNiV⁰ defect, the excitation occurs from the e_g and a_1g states to the e_u state. The e_u state lies in the gap and shows a relatively small quantum confinement effect. However, the e_g and a_1g states appear in the “valence” band of the host nanodiamond. In the smallest nanodiamonds, localization on the Ni-atom can be observed, however, in larger nanodiamonds the contribution becomes weaker and several resonant states appear at deeper energy levels (see Fig. 1(b)). In bulk diamond, these states become almost completely delocalized (see Fig. 4(b and c)). These states show strong quantum confinement (similar to that of the host nanodiamond “valence band maximum” states), which results in relatively strong quantum confinement at the excitation energy.

In the VNiV⁻ defect, the electronic structure is more complex. As mentioned for the bulk case, the double degenerate e_u state is occupied by three electrons, which is the subject of Jahn–Teller distortion resulting in the C_2h symmetry. The e_u state splits to a_u and b_u, where the hole may reside on either the a_u or b_u state, which leads to different types of distortion. According to our calculations, the energy difference between the two possible distortions is within 0.1 eV in nanodiamonds. We always chose the lowest energy configurations in the calculation of the excitation energies. The hole resides on the b_u state in the lowest energy configurations in most of the considered nanodiamonds except the largest one, where the hole is found on the a_u state. Interestingly, in bulk diamond the HSE06 calculations also predict the hole to be on the a_u state. Generally, the defect levels shift up with respect to the case of the neutral defect. As a consequence, the a_1g and the split e_g states get strongly localized on the Ni-atom (and around the defect) in the smallest nanodiamonds of d = 1.1–1.2 nm. In larger nanodiamonds, these states start to smear in the “valence band”, and the character of these wave functions changes significantly (see Fig. 1(b)). This issue has serious consequences for the excitation energies. Despite the Kohn–Sham gaps significantly dropping, going from d = 1.1–1.2 nm to larger nanodiamonds, the excitation energies do not follow this trend. When all the defect states are localized when participating in the excitation, then the electron–hole attractive interaction is about 1.8 eV. This electron–hole interaction is weaker (about 1.0 eV) when the hole part gets delocalized in the excited state. This effect is much less visible for the neutral defect, where the a_1g and e_g states per se are less localized in the smallest nanodiamonds.

Finally, the N₂VNiVN⁺₂ defect is briefly analyzed. In this case, the b_u state can be found in the band gap of the considered nanodiamonds, but its quantum confinement is less pronounced than that of the “valence band maximum” states. As a consequence, this b_u state becomes resonant in bulk diamond. Because both the hole and electron parts of the exciton state are localized, the electron–hole interaction is about 2.0 eV, almost independently of the size of the nanodiamond. The effect of the quantum confinement on the excitation energies of this defect is weaker than for the VNiV defect but still considerable, and allows multi-color imaging from yellow down to infrared as a function of the size of the nanodiamonds.

3 Conclusions

In summary, we have calculated the lowest excitation energy of nickel-related defects in hydrogenated nanodiamonds by assuming large concentrations of nitrogen and no nitrogen. We found that the excitation energy depends very significantly on the size of the nanodiamonds, because the transition occurs between a heavily perturbed valence band like state which is a subject of quantum confinement. We propose that multi-color in vivo bioimaging agents can be fabricated with these single color centers in molecule-sized nanodiamonds, when the size of the nanodiamonds can be finely controlled. All of the considered color centers are paramagnetic, which gives additional freedom for sensing.

4 Computational methods

We modeled the defects in bulk diamond by the supercell method. We used a 512-atom simple cubic supercell, where the Brillouin zone of the supercell was sampled at the Γ-point. This method provides sufficiently convergent charge density and the degeneracy of the defect states can be monitored accordingly. We applied a screened, range-separated, non-local hybrid density functional theory (DFT), called HSE06,^37,38 to calculate the electronic structure and the geometry of the defects. The optimal positions of the atoms are found by minimizing the Hellmann–Feynman forces until the remaining force on each of the atoms is less than 0.02 eV Å⁻¹. The projector-augmented wave (PAW) method³⁹ together with the plane wave basis set was utilized to calculate the charge and spin densities of the system as implemented in the VASP 5.3 code.^40,41 Within this framework, we chose to consider both the 3p and 3d Ni electrons as part of the valence. The energy cut-off for the expansion of the valence wave functions was set to 420 eV, which is convergent for the charge densities of the system. We aligned the valence band edge to the perfect diamond in the defective supercells and applied 2/3 of the monopole term of the Makov–Payne charge correction⁴² in charged defective supercells. This methodology is able to reproduce the experimental ionization energies within 0.1 eV for deep defects in Group-IV semiconductors.^28,29 We note that the presence of d-orbitals in the sp³ electron bath of the host may represent a problem with the validity of the HSE06 functional where extra correction of the functional may be needed.⁴³ By following the method in ref. 43 to check the validity of the applied functional we found that the HSE06 DFT functional gives accurate and trustworthy results for the VNiV and N₂VNiVN₂ defects. This is in line with our previous finding on the Ni_s defect in diamond.²²

The adiabatic charge transition levels (also called occupation levels) of the defects were calculated by the standard methodology (see ref. 28 and references therein) by using the formation energy of the defect (E^Q_form) with a given charge (Q),

where μ_i is the chemical potential of the element i, with number of n_i in the supercell. ΔV and ΔE_corr are the potential alignment and correction of the charged supercell as explained above. We used the total energy of bulk diamond and nickel crystal to obtain the chemical potential of carbon and nickel, whereas the total energy of the nitrogen molecule (simulated in a 10³ ų empty box) was used to obtain the chemical potential of nitrogen. In the symmetry analysis of the single particle defect states, we applied the projected density of the states using the standard projectors of the PAW method.

We carried out ab initio calculations on nanodiamonds with a diameter (d) of 1 to 2 nm. The geometry optimizations were carried out within supercell formalism by using the Perdew–Burke–Ernzerhof (PBE)⁴⁴ functional within DFT. We used 420 eV and 1260 eV cutoffs for the wave function and charge density expansions, respectively. We applied standard PAW-potentials for the ions as implemented in the VASP code. The geometry of the nanodiamonds was optimized until all the forces fell below 0.01 eV Å⁻¹. The distance between any surface atoms of the periodic images was larger than 1 nm, thus the interaction between the nanodiamonds was negligible. We calculated the formation energies of the defects in the nanodiamond at the DFT PBE level by modifying eqn (1).

where E^pristine_tot is the total energy of the pristine nanodiamond, and Δn_i is the number of i-type of atoms in the defective nanodiamond with respect to the number of those atoms in the pristine nanodiamond.

Excitation spectra were calculated by time-dependent density functional theory (TD-DFT) calculations by using TURBOMOLE cluster code,⁴⁵ where the geometry of SiC QDs were taken from VASP calculations. We used a double-ζ polarized basis set with the elimination of the core electrons by effective core potentials, which allowed us to compute the excitation energies even for large nanodiamonds of d = 1.9 nm with 633 carbon atoms and 300 hydrogen atoms. We checked the convergence of the localized basis set by comparing the Kohn–Sham energies obtained with the plane-wave VASP code and the TURBOMOLE cluster code with the PBE functional. The difference between the single particle gaps was smaller than 0.05 eV in each case. We applied the PBE0 hybrid functional⁴⁶ in the TD-DFT kernel that provided reliable excitation energies for similar systems.^8,11,26,27

Acknowledgements

The authors acknowledge the EU FP7 grant DIAMANT (grant no. 270197). AG acknowledges the support from the Lendület program of the Hungarian Academy of Sciences.

References

1. X. Michalet, F. F. Pinaud, L. A. Bentolila, J. M. Tsay, S. Doose, J. J. Li, G. Sundaresan, A. M. Wu, S. S. Gambhir and S. Weiss, Science, 2005, 307, 538–544.
2. J. Lippincott-Schwartz and G. H. Patterson, Science, 2003, 300, 87–91.
3. B. Somogyi and A. Gali, J. Phys.: Condens. Matter, 2014, 26, 143202.
4. B. Somogyi, V. Zólyomi and A. Gali, Nanoscale, 2012, 4, 7720–7726.
5. V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, Nat. Nanotechnol., 2012, 7, 11–23.
6. A. M. Schrand, H. Huang, C. Carlson, J. J. Schlager, E. Osawa, S. M. Hussain and L. Dai, J. Phys. Chem. B, 2007, 111, 2–7.
7. J. Cheng, J. He, C. Li and Y. Yang, Chem. Mater., 2008, 20, 4224–4230.
8. M. Vörös and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 161411.
9. G. Davies and M. Hamer, Proc. R. Soc. London, Ser. A, 1976, 348, 285–298.
10. C. Bradac, T. Gaebel, N. Naidoo, J. R. Rabeau and A. S. Barnard, Nano Lett., 2009, 9, 3555–3564.
11. I. I. Vlasov, A. A. Shiryaev, T. Rendler, S. Steinert, S.-Y. Lee, D. Antonov, M. Vörös, F. Jelezko, A. V. Fisenko, L. F. Semjonova, J. Biskupek, U. Kaiser, O. I. Lebedev, I. Sildos, P. R. Hemmer, V. I. Konov, A. Gali and J. Wrachtrup, Nat. Nanotechnol., 2014, 9, 54–58.
12. H. Girard, J. Arnault, S. Perruchas, S. Saada, T. Gacoin, J.-P. Boilot and P. Bergonzo, Diamond Relat. Mater., 2010, 19, 1117–1123.
13. H. Girard, T. Petit, S. Perruchas, T. Gacoin, C. Gesset, J. Arnault and P. Bergonzo, Phys. Chem. Chem. Phys., 2011, 13, 11517–11523.
14. K. Iakoubovskii, A. Stesmans, B. Nouwen and G. J. Adriaenssens, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 16587–16594.
15. V. Nadolinny and A. Yelisseyev, Diamond Relat. Mater., 1994, 3, 1196–1200.
16. W. Gehlhoff and R. N. Pereira, J. Phys.: Condens. Matter, 2002, 14, 13751.
17. V. A. Nadolinny, A. P. Yelisseyev, J. M. Baker, M. E. Newton, D. J. Twitchen, S. C. Lawson, O. P. Yuryeva and B. N. Feigelson, J. Phys.: Condens. Matter, 1999, 11, 7357.
18. T. Pawlik, C. Noble and J.-M. Spaeth, J. Phys.: Condens. Matter, 1998, 10, 9833.
19. J. Goss, P. Briddon, R. Jones and S. Öberg, J. Phys.: Condens. Matter, 2004, 16, 4567.
20. R. Larico, J. F. Justo, W. V. M. Machado and L. V. C. Assali, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115202.
21. J. Isoya, H. Kanda, J. R. Norris, J. Tang and M. K. Bowman, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 3905–3913.
22. T. Chanier and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245206.
23. J. R. Rabeau, Y. L. Chin, S. Prawer, F. Jelezko, T. Gaebel and J. Wrachtrup, Appl. Phys. Lett., 2005, 86, 131926.
24. M. Wolfer, A. Kriele, O. A. Williams, H. Obloh, C.-C. Leancu and C. E. Nebel, Phys. Status Solidi A, 2009, 206, 2012–2015.
25. E. Wu, J. R. Rabeau, G. Roger, F. Treussart, H. Zeng, P. Grangier, S. Prawer and J.-F. Roch, New J. Phys., 2007, 9, 434.
26. M. Vörös, T. Demjén, T. Szilvási and A. Gali, Phys. Rev. Lett., 2012, 108, 267401.
27. A. Gali, Phys. Status Solidi B, 2011, 248, 1337–1346.
28. P. Deák, B. Aradi, T. Frauenheim, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153203.
29. P. Deák, B. Aradi, M. Kaviani, T. Frauenheim and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075203.
30. K.-M. C. Fu, C. Santori, P. E. Barclay and R. G. Beausoleil, Appl. Phys. Lett., 2010, 96, 121907.
31. L. Rondin, G. Dantelle, A. Slablab, F. Grosshans, F. Treussart, P. Bergonzo, S. Perruchas, T. Gacoin, M. Chaigneau, H.-C. Chang, V. Jacques and J.-F. Roch, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115449.
32. M. V. Hauf, B. Grotz, B. Naydenov, M. Dankerl, S. Pezzagna, J. Meijer, F. Jelezko, J. Wrachtrup, M. Stutzmann, F. Reinhard and J. A. Garrido, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 081304.
33. B. Grotz, M. V. Hauf, M. Dankerl, B. Naydenov, S. Pezzagna, J. Meijer, F. Jelezko, J. Wrachtrup, M. Stutzmann and F. Reinhard, et al. , Nat. Commun., 2012, 3, 729.
34. V. Petráková, A. Taylor, I. Kratochvílová, F. Fendrych, J. Vacík, J. Kučka, J. Štursa, P. Cígler, M. Ledvina, A. Fišerová, P. Kneppo and M. Nesládek, Adv. Funct. Mater., 2012, 22, 812–819.
35. K. J. Rietwyk, S. L. Wong, L. Cao, K. M. O'Donnell, L. Ley, A. T. S. Wee and C. I. Pakes, Appl. Phys. Lett., 2013, 102, 091604.
36. S. Cui and E. L. Hu, Appl. Phys. Lett., 2013, 103, 051603.
37. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
38. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
39. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
41. G. Kresse and J. Furthmüller, Comput. Mat. Sci., 1996, 6, 15.
42. G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022.
43. V. Ivády, I. A. Abrikosov, E. Janzén and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205201.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
46. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985.

---