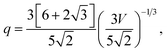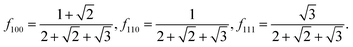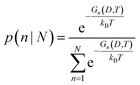DOI:
10.1039/C4NR01504E
(Paper)
Nanoscale, 2014,
6, 9983-9990
Clarifying stability, probability and population in nanoparticle ensembles†
Received
19th March 2014
, Accepted 18th April 2014
First published on 16th May 2014
Abstract
Though theoretical and computational studies typically agree on the low energy, equilibrium structure of metallic nanoparticles, experimental studies report on samples with a distribution of shapes; including high-index, non-equilibrium morphologies. This apparent inconsistency is not due to inaccuracy on either side, nor the result of unquantifiable competition between thermodynamic and kinetic influences, but rather a lack of clarity about what is being inferred. The thermodynamic stability, statistical probability, and the observed population of a given structure are all straightforward to determine, provided an ensemble of possible configurations is included at the outset. To clarify this relationship, a combination of electronic structure simulations and mathematical models will be used to predict the relative stabilities, probability and population of various shapes of Ag, Au, Pd and Pt nanoparticles, and provide some explanation for the observation of high-index, non-equilibrium morphologies. As we will see, a nanoparticle can be in the ground-state, and therefore most thermodynamically stable, but can still be in the minority.
Introduction
Over the past decade our ability to generate, probe and model nanoscale systems has been rapidly improving, and we have seen a convergence in the availability and suitability of research tools.1–7 Thanks to the advent of high performance computing and the increased resolution of characterization methods, we can now observe and simulate on the same scale; working together on the same thing.8,9 This has been a remarkable catalyst for collaboration in nanoscience and nanotechnology. However, this convergence and collaboration has highlighted a number of inconsistencies that can erode confidence.
One such inconsistency that is experienced by many researchers engaged in the study of nanoparticles is the apparent difference between the structures predicted by theory and simulation,10 and the range of structures observed experimentally.11,12 When theory and experiment do not seem to agree it is human nature to seek to discount one or the other approach as being flawed; or worse – irrelevant. However, there are many reasons results may seem to be inconsistent on first inspection. In many cases, these (seemingly contradictory) studies may have been designed to achieve very different objectives, and so the results may not be entirely representative; but this does not mean they are wrong.
To examine this further, let us consider the specific issue of structural monodispersivity versus polydispersivity in ensembles of metallic nanoparticles. One of the aims of most of the theoretical and computational studies of metal nanoparticles (and other nanomaterials) is to identify the most stable structure (size, shape and phase); to establish the ground-state of the system. Traditionally these studies have drawn upon methods used throughout chemistry and solid state physics,13 and are usually based on thermodynamic or kinetic frameworks. In most cases the result is the prediction of the single state (structure); the implication being that alternative (higher energy, non-equilibrium) states will not be observed. This is contrary to experimental observations which typically present as a polydispersed mixture of structures, even if the distribution is narrow, and often contain structures with thermodynamically unfavourable high-index facets.14–21 Examples include trapezohedra,22 tetrahexahedra,23–31 trisoctahedra,32–35 and hexoctahedra.36,37
Although both approaches seek a state of monodispersivity, the perspectives and the objectives here are different. Computational studies are focussed on understanding the stability of metal nanoparticles, and how this can give rise to monodispersivity;38–41 whereas experimental studies seek to moderate the probability of different structures, and measure the population of a specific structure to characterize the monodispersivity.42 This is not the same thing. This issue is exacerbated by the fact that many papers in the literature are imprecise as to whether they are referring to stability or probability; in some cases these terms have been confused. Moreover, both are often used to infer the population of a given state (the fraction of particles that will be in that state) in the system as a whole, but this is rarely quantified. Although it was undoubtedly not the intention of the original authors, this leads to the assumption that most metal nanoparticles will (or should) be in the ground-state, which is misleading, and usually incorrect.
The key is to make sure we are studying the problem from the same perspective, and a good way to bridge this gap is to seek to model ensembles; predicting populations as well as stability. For this we need a more balanced description of the system, which includes a range of possible structures; including those that are high in energy. This is a general problem, but for the purposes of illustration let us continue with the example of ensembles of metal nanoparticles. In the following sections a combination of electronic structure simulations and simple analytical expressions will be used to predict the relative stabilities, probability and population of various shapes of Ag, Au, Pd and Pt nanoparticles, and provide some explanation for the observation of high-index, non-equilibrium morphologies. The results show that even though there is only one ‘ground-state’ morphology in each case, all other possibilities have a non-zero probability of observation, and will have a statistically significant population.
Methods
To study a realistic ensemble of metal nanoparticles (or another type of nano-ensemble) it is necessary to generate a large set of virtual samples that contain considerable variety of shapes and a large range of sizes. Ideally the sizes and shapes should cover the ranges observed experimentally. It is of course possible to model a diverse range of nanostructures, particularly with the advent of high performance computing, but to represent the diversity present in experimental samples we also need to know what sizes and shapes to include, and how many of each type of structure there are likely to be. Without a clear idea of the scope of the problem at the outset, it is more efficient to use an analytical model than to attempt to simulate thousands of explicit structures (many of which may turn out to be largely irrelevant).
Fortunately for metals it is relatively straightforward to rapidly screen the possibilities using an analytical nanomorphology model, designed to compare the thermodynamic stability of isolated (unsupported) nanoparticles. One such model provides the geometric summation of the Gibbs free energy with contributions from the particle bulk, surfaces:
| |  | (1) |
where
M is the molar mass,
ρ is the mass density,
T is the temperature, and
γi(
T) is the specific surface free energy of facet
i.
43 These components converge to the Wulff shape at large sizes. In addition to this, the surface stress
σi(
T) and the external pressure
Pe produce a volume dilation, the magnitude of which depends on the bulk modulus
B0. These components are not present in a Wulff construction, and are significant at small sizes. The weighting factors are fractional areas, so

, and
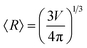
(to be consistent with the Laplace–Young formalism).
The surface-to-volume ratio q and the weighting factors fi provide the size and shape dependence, and can be defined based on the individual geometries, as a function of the total volume, V.44 The simple Platonic (low-index) shapes begin with the octahedron, where f111 = 1, and:
| |  | (2) |
We then have the rhombic dodecahedron, where f110 = 1, and:
| |  | (3) |
and the cube (or regular hexahedron), where
f100 = 1, and:
These shapes occupy the vertices of the standard stereographic triangle for fcc crystals, as illustrated in Fig. 1a, b and c, respectively. When we combine the {100}, {110} or {111} forms we obtain more zonohedrons including other Platonic and Archimedean shapes, among which the truncated octahedron (Fig. 1d) has:
| |  | (5) |
| |  | (6) |
the cuboctahedron (
Fig. 1e) has:
| | 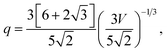 | (7) |
| |  | (8) |
the truncated hexahedron (or truncated cube,
Fig. 1f) has:
| |  | (9) |
| |  | (10) |
the rhombi-octahedron (the Minkowski sum of an octahedron and a rhombic dodecahedron,
Fig. 1g) has:
| |  | (11) |
| |  | (12) |
and the rhombi-hexahedron (the Minkowski sum of a cube and a rhombic dodecahedron,
Fig. 1h) has:
| |  | (13) |
| |  | (14) |
 |
| | Fig. 1 The stereographic triangle with specific zonohedrons, along with additional combination forms: (a) octahedron, (b) rhombic dodecahedron, (c) hexahedron (or cube), (d) truncated octahedron, (e) cuboctahedron, (f) truncated cube, (g) rhombi-octahedron, (h) rhombi-hexahedron, (i) doubly-truncated octahedron, (j) small rhombicuboctahedron, (k) great rhombicuboctahedron, (l) trapezohedron, (m) tetrahexahedron, (n) trisoctahedron, and (o) hexoctahedron. | |
When we combine all of the forms at the vertices of the unit stereographic triangle we obtain more highly-faceted shapes, such as the doubly-truncated octahedron (Fig. 1i), with:
| |  | (15) |
| |  | (16) |
the small rhombicuboctahedron (
Fig. 1j), with:
| |  | (17) |
| |  | (18) |
and the great rhombicuboctahedron (
Fig. 1k), with:
| |  | (19) |
| | 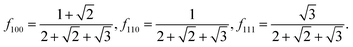 | (20) |
In addition to these morphologies, metal nanoparticles often have high index facets and there have been numerous reports of quasi-spherical particles enclosed entirely by higher index forms, such as {113},22 {210},23,24 {331}32 or {123};37 which are Catalan solids and are also highlighted in the stereographic triangle in Fig. 1. These facets have higher energy surfaces, but yet they often form, and given the opportunity to equilibrate nanoparticles introduce more of these facets.32 These higher index shapes exhibit a higher sphericity (having a q value closer to that of a sphere), which can somewhat counter the higher γi(T) values and increase their relative stability. In the case of the higher-index shapes, the trapezohedron (also known as the deltoidal icositetrahedron, Fig. 1l), where f113 = 1, has:
| |  | (21) |
and the tetrahexahedron (also known as the tetrakis hexahedron,
Fig. 1m), where
f210 = 1, has:
| |  | (22) |
In the case of the trisoctahedron (also known as the small triakis octahedron, Fig. 1n), where f331 = 1:
| |  | (23) |
and in the case of the hexoctahedron (also known as the hexakis octahedron,
Fig. 1o), where
f123 = 1:
| |  | (24) |
By varying V these expressions can be used to model the size-dependent free energy, or by holding V constant the temperature-dependent free energy ΔG(T) may be determined by parameterizing with γi(T) and σi(T). This may be done using any suitable computational method, provided the that it is used consistently (to avoid uncertainties associated with the mixing methods) and has sufficient accuracy to distinguish between different facets and provide the right energetic ordering.
Once parameterized, the models above can be used to compare the relative stability of each shape (n), and predict their probability of observation (p) as a function of the spherically averaged diameter (D = 2〈R〉) and the temperature (T). The latter can be easily obtained using a Boltzmann distribution:
| |  | (25) |
where
kB is Boltzmann's constant. This can in turn be used to used to calculate the population of each
n in an ensemble containing
N shapes (in this case,
N = 15). For the possibilities shown in
Fig. 1, using statistical mechanics:
| | 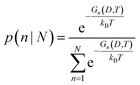 | (26) |
where the denominator is the canonical partition function.
If we calculate each Gn we can compare the relative stability of each shape n, and identify which one is thermodynamically preferred; this will describe the stability. Using the Gn we can compute the probabilities pn∀n ∈ N, to determine how likely each shape is. By combining and comparing the probabilities we can predict the actual populations of all these high-index, non-equilibrium (metastable) geometries. As we will see, the populations are always non-zero, even for the least stable morphology.
Discussion of results
To demonstrate this, let us return to the topic of metallic nanoparticles mentioned above, and investigate the prevalence of high index shapes in typical ensembles (samples) of Ag, Au, Pd and Pt. These materials are relatively well described by density functional theory (DFT) and so parameters have been obtained for the bulk and surface properties using consistent methods and criteria, as described in the ESI.† In general however, provided consistency is preserved, any parametrization method is acceptable (including experiments, if possible).
In the following results, the stability and probability of observation are predicted for all of the shapes in Fig. 1 at a range of different temperatures. For the purposes of demonstration, these include the temperature of liquid helium (4 K), which is consistent with some IGA conditions, and is a good low temperature comparison to standard electronic structure simulations (which are conducted at ∼0 K); liquid nitrogen temperature (77 K); and room temperature (300 K). In principle, any temperature could be used.
In Fig. 2 we can see the size-dependent stability for each of these shapes and materials at low temperature (4 K), plotted in the typical way as a function of the spherically-averaged particle diameter (between 3 nm to 50 nm). As we can see, although there may be a large difference in the specific surface energies (see ESI†) the relative difference in the free energy is very close; in some cases the shapes are almost indistinguishable. Therefore, to establish a thermodynamic ordering it is more convenient to plot the results as a function of the molar surface area (in m2 mol−1), as shown in the upper row of Fig. 3. Due to the different values of q for each shape the energetic order for each set is different to those in Fig. 2, but this treatment is consistent with calorimetry measurements that are often used to establish thermodynamic stability experimentally. Fig. 2 cannot be easily experimentally verified.
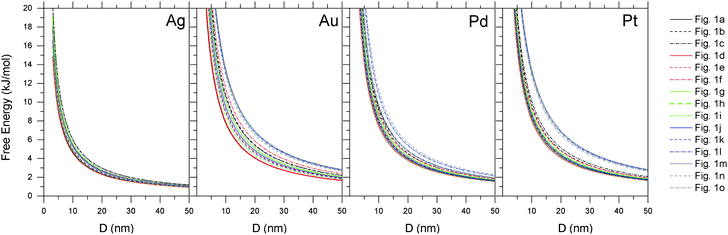 |
| | Fig. 2 Thermodynamic stability for Ag, Au, Pd and Pt nanoparticles of each shape presented in Fig. 1, plotted as a function of the spherically-averaged particle diameter, at low temperature (4 K). | |
 |
| | Fig. 3 The relative stability (upper row) and population (lower row) for Ag, Au, Pd and Pt nanoparticles in each of the shapes presented in Fig. 1, as a function of size, at a temperature of 4 K. | |
Firstly, with respect to bulk metals, the free energy is always positive, indicating that in terms of the absolute stability these nanoparticles are always ‘unstable’. This would be different if we compared to a reservoir of metal clusters or salts. From the upper row of Fig. 3 we can see the relative stability of the different shapes at low temperature is similar. Calorimetry studies would consistently find the octahedron to be the most stable shape (although plotted as a function of the spherically-averaged diameter the lowest energy shape is the truncated octahedron, as has been shown before10); which provides the first source of confusion between observations and computational predictions. Care should always be taken to plot things in a consistent way. The remaining shapes are energetically similar, with the exception of the very high-index shapes (which are clearly less stable, particularly at small sizes). The relative stability (the ‘spread’ between the shapes) varies with material; platinum being more discriminate and silver being more indiscriminate. This of course arises due to the relative bond strength; the cost associated with breaking a Pt bond on a the surface is greater than, for example, Ag. This issue is exacerbated on surfaces with a higher degree of under-coordination, which is why it is most pronounced on high-index Pt nanoparticles.
This discrimination becomes more apparent when we calculate the corresponding probabilities and populations, shown in the lower row of Fig. 3. Here we can see that, although the relative stability of the silver shapes is very close, there is a dramatic difference in the expected population. At small sizes the probability of observing the ground-state (lowest energy) shape is one, and so we could truly expect the population of the most stable shape to be ∼100% at equilibrium. As the size is increased however, the probability of observing alterative shapes increases, and at large sizes the probability of observing the thermodynamically preferred ground-state shape npref is much lower, and the population p(npref|N) ≃ 50 ± 7%. This is entirely the result of thermodynamic and statistical considerations, and has nothing to do with the kinetics of formation.
When we increase the temperature to the liquid nitrogen regime, we can see that the change in populations is far greater than change in stability (Fig. 4). The energy is slightly lowered (as the temperature dependent specific surface energies decrease with increasing temperature), but the energetic ordering appears unchanged. However, in the lower half of this figure the corresponding populations are significantly different to the low temperature case. Already we can see that, in the case of Ag, even the most stable (equilibrium) structure never has a probability of observation of p(n) = 1, and so p(npref|N) < 100%∀D. For each of these metals the probability of observation of many of the non-equilibrium shapes is significant, and a measurable population of the high-index shapes are to be expected down to 10 nm in size in all cases expect Pt. At large sizes, with T = 77 K, p(npref|N) is consistently less than 25%.
 |
| | Fig. 4 The relative stability (upper row) and population (lower row) for Ag, Au, Pd and Pt nanoparticles in each of the shapes presented in Fig. 1, as a function of size, at a temperature of 77 K. | |
And finally, when we reach room temperature (Fig. 5), we see that the while the structure with greatest relative stability will still have the highest probability of observation (in each case) our samples are clearly mixtures. At small sizes the p(npref|N) is typically only marginally higher than other low energy shapes (with the exception of Pt), and at large sizes even the population of high-index shapes (such as the trapezohedron, tetrahexahedron, trisoctahedron and hexoctahedron) is comparable. In the case of Ag and Au there will be almost as many high-energy morphologies as there are low energy ones; and for Pd and Pt, though the trapezohedron, tetrahexahedron, trisoctahedron and hexoctahedron are highly unstable with respect to a transformation to one of the lower energy morphologies, they will be present in significant quantities. Unless there is a driving force to facilitate this transformation, these high energy shapes could represent as much as ∼25% of the sample. Again, this is not a function of the competition between kinetic and thermodynamic influences,45 but merely a consequence of the consideration of an ensemble of particles, rather than an attempt to seek only the ground-state.
 |
| | Fig. 5 The relative stability (upper row) and population (lower row) for Ag, Au, Pd and Pt nanoparticles in each of the shapes presented in Fig. 1, as a function of size, at room temperature. | |
Irrespective of the material, under ambient conditions the population of non-equilibrium shapes will be comparable with population of equilibrium shapes. The probability (like stability) is determined by the properties of individual structures, whereas the population can only be determined when we consider them all. If we included more shape variations, it would not displace the low energy ‘most stable’ shape, which would still be the most ‘probable’, but we would find that the asymptote changes and the population of the low energy shape would decrease. The more possibilities that are included, the lower the total population of each specific possibility, even if it is most stable and highly probable.
The clear message here is that when dealing with large collections of structures, many different configurations are possible, and indeed probable, even if they are thermodynamically unfavorable. Ensuring nanoparticles are thermodynamically controlled and under equilibrium conditions, does not ensure that all of the particles will be in the equilibrium morphology. One does not need to attribute discrepancies in thermodynamic predictions and experimental observations to kinetics to explain the results. This is not to say that kinetic considerations are not important. Certainly they will be influential in determining the morphology; or more correctly the morphologies that can be represented. Careful ministration of kinetic effects will restrict the number of possibilities (the inverse of which defines the asymptote as D → ∞), as can the use of surfactants used in templates assisted growth. However, under realistic thermochemical conditions these measures may not be sufficient to eliminate the polydispersivity entirely, and we should still expect some statistical distribution of shapes.
Conclusions
Dealing with the issue of polydispersivity in ensembles of structures is a general problem in nanoscience, and aside from the explanation of the observation of considerable numbers of high-index shapes in metal nanoparticle samples, there are some lessons here for experimental and computational scientists alike.
When characterizing colloidal samples one should not be overly concerned that the predicted low energy morphology appears to be under-represented (or if the prediction does not appear to describe the entire sample). This does not undermine the validity of the predictions. Even if the population of the ‘ground-state’ structure is quite low, there may not necessarily be a great energetic difference between the shapes that are present, and so the predicted equilibrium structure can still provide a trustworthy representation of the system.
When simulating nanoparticles care should be taken not to overstate the importance of the ground-state structures, or imply that all structures will adopt this configuration. While the greater relative stability does give rise to a greater probability, one cannot assume that this equates to a large population. Furthermore, while there is merit in identifying the most stable morphology (which will be most robust against perturbations), one should not discount the value in simulating non-equilibrium systems and higher-index/energy structures. Including them in virtual samples and quantifying their prevalence does not invalidate the prediction of the ground-state; but only seeking the ground-state will be insufficient to predict the properties of entire ensembles of nanoparticles, irrespective of the accuracy that is achieved.
In general, we should not be too hasty to attribute inconsistencies between thermodynamic models and experimental observations entirely to growth kinetics. Kinetics can be just as selective as thermodynamics in restricting the range of possible morphologies, but in either case the persistent dispersivity can be explained by considering the statistical mechanics as well.
Acknowledgements
Computational resources for this project were supplied by the National Computing Infrastructure (NCI) national facility under Merit Allocation Scheme, Grant p00.
References
- M. K. Nazeeruddin, F. De Angelis, S. Fantacci, A. Selloni, G. Viscardi, P. Liska, S. Ito, B. Takeru and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 16835–16847 CrossRef CAS PubMed.
- R. Agrawal, B. Peng, E. E. Gdoutos and H. D. Espinosa, Nano Lett., 2008, 8, 3668–3674 CrossRef CAS PubMed.
- R. Agrawal, B. Peng and H. D. Espinosa, Nano Lett., 2009, 9, 4177–4183 CrossRef CAS PubMed.
- W. Zhang, Z. Li, B. Wang and J. Yang, Int. J. Quantum Chem., 2013, 113, 89–95 CrossRef CAS.
- L. Mino, A. M. Ferrari, V. Lacivita, G. Spoto, S. Bordiga and A. Zecchina, J. Phys. Chem. C, 2011, 115, 7694–7700 CAS.
- P.-T. Chen, W. W. Pai, S.-W. Chang and M. Hayashi, J. Phys. Chem. C, 2013, 117, 12111–12116 CAS.
- S. Pantelides, T. Pennycook, W. Luo, M. Prang, H. Lee, M. Oxley, J. Garcia-Barriocanal, F. Bruno, C. Leon, J. Santamaria, M. Chisholm, M. Varela and S. Pennycook, Microsc. Microanal., 2011, 17, 1316–1317 CrossRef.
- K. Ø. Hanssen, B. Schuler, A. J. Williams, T. B. Demissie, E. Hansen, J. H. Andersen, J. Svenson, K. Blinov, M. Repisky, F. Mohn, G. Meyer, J.-S. Svendsen, K. Ruud, M. l. Elyashberg, L. Gross, M. Jaspars and J. Isaksson, Angew. Chem., Int. Ed., 2012, 51, 12238–12241 CrossRef CAS PubMed.
- L. Y. Chang, A. S. Barnard, L. C. Gontard and R. Dunin-Borkowski, Nano Lett., 2010, 10, 3073–3076 CrossRef CAS PubMed.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325 CrossRef CAS.
- J. Chen, B. Lim, E. P. Lee and Y. Xia, Nano Today, 2009, 4, 81–95 CrossRef CAS PubMed.
- A. S. Barnard, Rep. Prog. Phys., 2010, 73, 08650 CrossRef.
- N. Tian, Z.-Y. Zhou and S.-G. Sun, J. Phys. Chem. C, 2008, 112, 19801–19817 CAS.
- N. Tian, Z.-Y. Zhou and S.-G. Sun, Chem. Commun., 2009, 1502–1504 RSC.
- A. Mayoral, H. Barron, R. Estrada-Salas, A. Vazquez-Duran and M. José-Yacamán, Nanoscale, 2010, 2, 335–342 RSC.
- Z.-Y. Zhou, Z.-Z. Huang, D.-J. Chen, Q. Wang, N. Tian and S.-G. Sun, Angew. Chem., Int. Ed., 2010, 49, 411–414 CrossRef CAS PubMed.
- F. Wang, C. Li, L.-D. Sun, H. Wu, T. Ming, J. Wang, J. C. Yu and C.-H. Yan, J. Am. Chem. Soc., 2011, 133, 1106–1111 CrossRef CAS PubMed.
- V.-L. Nguyen, M. Ohtaki, V. N. Ngo, M.-T. Cao and M. Nogami, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2012, 3, 025005 CrossRef.
- Z. Quan, Y. Wang and J. Fang, Acc. Chem. Res., 2013, 46, 191–202 CrossRef CAS PubMed.
- X. Wei, R. Zhou, W. Lefebvre, K. He, D. Le Roy, R. Skomski, X. Li, J. E. Shield, M. J. Kramer, S. Chen, X. C. Zeng and D. J. Sellmyer, Nano Lett., 2014, 14, 1362–1368 CrossRef CAS PubMed.
- Y. Li, Y. Jiang, M. Chen, H. Liao, R. Huang, Z. Zhou, N. Tian, S. Chen and S. Sun, Chem. Commun., 2012, 48, 9531–9533 RSC.
- N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Science, 2007, 316, 732–735 CrossRef CAS PubMed.
- Y. Ding, Y. Gao, Z. L. Wang, N. Tian, Z.-Y. Zhou and S.-G. Sun, Appl. Phys. Lett., 2007, 91, 121901 CrossRef PubMed.
- Z.-Y. Zhou, N. Tian, Z.-Z. Huang, D.-J. Chen and S.-G. Sun, Faraday Discuss., 2008, 140, 81–92 RSC.
- J. Li, L. Wang, L. Liu, L. Guo, X. Han and Z. Zhang, Chem. Commun., 2010, 46, 5109–5111 RSC.
- L. Zhang, W. Niu, W. Gao, S. Majeed, Z. Liu, J. Zhao, S. Anjuma and G. Xu, Chem. Commun., 2013, 49, 8836–8838 RSC.
- D. Y. Kim, S. H. Im and O. O. Park, Cryst. Growth Des., 2010, 10, 3321–3323 CAS.
- N. Tian, Z.-Y. Zhou, N.-F. Yu, L.-Y. Wang and S.-G. Sun, J. Am. Chem. Soc., 2010, 132, 7580–7581 CrossRef CAS PubMed.
- T. Ming, W. Feng, Q. Tang, F. Wang, L. Sun, J. Wang and C. Yan, J. Am. Chem. Soc., 2009, 131, 16350–16351 CrossRef CAS PubMed.
- P.-G. Yin, T.-T. You, E.-Z. Tan, J. Li, X.-F. Lang, L. Jiang and L. Guo, J. Phys. Chem. C, 2011, 115, 18061–18069 CAS.
- Y. Ma, Q. Kuang, Z. Jiang, Z. Xie, R. Huang and L. Zheng, Angew. Chem., 2008, 120, 9033–9036 CrossRef.
- J. W. Hong, M. Kim, Y. Kim and S. W. Han, Chem.–Eur. J., 2012, 18, 16626–16630 CrossRef CAS PubMed.
- L. Zhang, W. Niu, Z. Li and G. Xu, Chem. Commun., 2011, 47, 10353–10355 RSC.
- Yu. Yu, Q. Zhang, B. Liu and J. Y. Lee, J. Am. Chem. Soc., 2010, 132, 18258–18265 CrossRef CAS PubMed.
- J. W. Hong, S.-U. Lee, Y. W. Lee and S. W. Han, J. Am. Chem. Soc., 2012, 134, 4565–4568 CrossRef CAS PubMed.
- J. Xiao, S. Liu, N. Tian, Z.-Y. Zhou, H.-X. Liu, B.-B. Xu and S.-G. Sun, J. Am. Chem. Soc., 2013, 135, 18754–18757 CrossRef CAS PubMed.
- A. L. González, C. Noguez, J. Beránek and A. S. Barnard, J. Phys. Chem. C, 2014, 118, 9128–9136 Search PubMed.
- A. S. Barnard, N. Young, A.
I. Kirkland, M. A. van Huis and H. Xu, ACS Nano, 2009, 3, 1431–1436 CrossRef CAS PubMed.
- A. S. Barnard, H. Konishi and H. Xu, Catal. Sci. Technol., 2011, 1, 1440–1488 CAS.
- A. S. Barnard, Catal. Sci. Technol., 2012, 2, 1485–1492 CAS.
- K. Koga and K. P. Sugawara, Surf. Sci., 2003, 529, 23–35 CrossRef CAS.
- A. S. Barnard and P. Zapol, J. Chem. Phys., 2004, 121, 4276–4283 CrossRef CAS PubMed.
- A. S. Barnard, Comput. Phys. Commun., 2011, 182, 11–13 CrossRef CAS PubMed.
- A. S. Barnard, Acc. Chem. Res., 2012, 45, 1688–1697 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available See DOI: 10.1039/c4nr01504e |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
 , and
, and 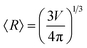 (to be consistent with the Laplace–Young formalism).
(to be consistent with the Laplace–Young formalism).