 Open Access Article
Open Access Article3-Dimensional atomic scale structure of the ionic liquid–graphite interface elucidated by AM-AFM and quantum chemical simulations†
Alister J.
Page
*a,
Aaron
Elbourne
a,
Ryan
Stefanovic
a,
Matthew A.
Addicoat
b,
Gregory G.
Warr
c,
Kislon
Voïtchovsky
d and
Rob
Atkin
*a
aNewcastle Institute for Energy and Resources, The University of Newcastle, Callaghan, NSW 2308, Australia. E-mail: alister.page@newcastle.edu.au; rob.atkin@newcastle.edu.au; Tel: +61-2-4033-9357 Tel: +61-2-4033-9356
bSchool of Engineering and Science, Jacobs University Bremen, Campus Ring 1, 28759 Bremen, Germany
cSchool of Chemistry, The University of Sydney, NSW 2006, Australia
dDepartment of Physics, Durham University, Durham, England, United Kingdom
First published on 5th May 2014
Abstract
In situ amplitude modulated atomic force microscopy (AM-AFM) and quantum chemical simulations are used to resolve the structure of the highly ordered pyrolytic graphite (HOPG)–bulk propylammonium nitrate (PAN) interface with resolution comparable with that achieved for frozen ionic liquid (IL) monolayers using STM. This is the first time that (a) molecular resolution images of bulk IL–solid interfaces have been achieved, (b) the lateral structure of the IL graphite interface has been imaged for any IL, (c) AM-AFM has elucidated molecular level structure immersed in a viscous liquid and (d) it has been demonstrated that the IL structure at solid surfaces is a consequence of both thermodynamic and kinetic effects. The lateral structure of the PAN–graphite interface is highly ordered and consists of remarkably well-defined domains of a rhomboidal superstructure composed of propylammonium cations preferentially aligned along two of the three directions in the underlying graphite lattice. The nanostructure is primarily determined by the cation. Van der Waals interactions between the propylammonium chains and the surface mean that the cation is enriched in the surface layer, and is much less mobile than the anion. The presence of a heterogeneous lateral structure at an ionic liquid–solid interface has wide ranging ramifications for ionic liquid applications, including lubrication, capacitive charge storage and electrodeposition.
Introduction
Ionic Liquids (ILs), which are pure salts with melting points less than 100 °C, have recently generated considerable scientific attention.1–5 This interest is largely a consequence of their (1) useful physicochemical properties,6 including large electrochemical windows,7 negligible vapour pressures,8,9 high thermal stabilities,10etc., and their (2) “designer” characteristics,10 which refer to the ability to tune properties for a given application by varying the ion structure. Due to these properties, and their intrinsic conductivity, ILs have emerged as potential lubricants11–18 and electrochemical solvents.19,20 The two main classes of ILs are protic21 and aprotic,22 classified by the synthesis method.Many ILs exhibit structural heterogeneity over domains of ca. 1 nm, both in the bulk and at interfaces.23–27 This nanostructure arises from electrostatic interactions between charged groups that produce polar domains which solvophobically28 repel uncharged cation alkyl groups, inducing them to cluster together to form apolar regions. These charged and uncharged domains percolate through the liquid producing sponge-like structure.26 The isotropic symmetry of this bulk IL nanostructure is broken near a macroscopic interface. Both atomic force microscopy (AFM) force curves29 and reflectivity experiments30 suggest that discrete ion (or ion pair) layers are present next to the solid surface, and that this layered surface structure decays to the bulk sponge nanostructure over a few nanometers.31 The IL nanostructure in the bulk, as well as that normal to solid interfaces, is relatively well understood.32 The nature and extent of the lateral interfacial nanostructure is less well characterised, especially for bulk IL solid interfaces as opposed to surface monolayers, despite its key role in a wide range of processes including electrodeposition,33 lubrication,14 surface-catalysed reactions and energy applications.32 Capacitance, for example, is a consequence of the relative concentrations of cations and anions at the electrode surface, and hence the lateral interfacial nanostructure.
Much effort has therefore been directed at obtaining high-resolution images of the IL–solid interface. The lateral structure of metal (gold or silver)–aprotic IL interfaces has been extensively studied using in situ scanning tunnel microscopy (STM). For bulk solid–IL interfaces, definitive molecular resolution of the ion layer bound to the surface has not been achieved, as interpretation of the images is complicated by near surface interfacial layers34 and/or coupling of the tunnelling signal from the liquid and the solid substrate.35 Pan et al.35 and Gnahm et al.36 independently identified structures on the scale of the ions at the 1-butyl-3-methylimidazolium hexafluorophosphate–gold interface, but could not clearly distinguish cations from anions. Impurities are also known to be problematic for this IL.37 Similar results were obtained by Su et al.38 for gold surfaces.
Higher resolution images have been realised for IL adsorbed monolayers (adlayers) on gold using ultra high vacuum (UHV) STM;39,40 using a monolayer eliminates the convoluting effect of near surface IL layers. Rows on the surface are clearly evident in these images, but they cannot be unambiguously attributed to cations or anions. Molecular resolution has been achieved in frozen IL monolayers (∼100 K) on gold41 and silver by UHV STM.42 Analysing the STM images in combination with X-ray photoelectron spectroscopy and density functional theory (DFT) calculations42 enabled the surface structure to be correlated with the position of cations and anions, and this represents the state of the art in the field. However, this frozen monolayer is unlikely to be the same as that at bulk IL–solid interfaces at room temperature. Ions confined in a monolayer must accommodate both the solid on one side and the vacuum on the other, have limited capacity to charge separate normal to the surface, and can only reorganise by diffusion within the monolayer itself. At a bulk interface the IL can establish a diffuse layer of charge, and can also exchange dynamically between the surface layer and the bulk liquid.
In this work, in situ AM-AFM43 is used to resolve the highly ordered pyrolytic graphite (HOPG)–bulk propylammonium nitrate (PAN) interface. The ion layer in contact with the graphite is found to be cation rich, and has a highly regular rhomboidal lateral structure. The AM-AFM results are analysed in conjunction with quantum chemical molecular dynamics (QM/MD) simulations to elucidate: (1) the detailed ion arrangements that produce the surface layer nanostructure at the atomic level; (2) the underlying ion-surface interactions that produce this structure; (3) the orientation of ions bound to the surface and (4) the dynamics of ion movements in and out of the layer. This shows definitively that IL (bulk)–solid interfacial morphology differs greatly from IL (monolayer)–solid structures.
Methods
Experimental details
PAN was synthesised as described previously.44 A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar acid–base reaction was conducted by slow addition of concentrated nitric acid (HNO3) (AJAX Finechem Pty. Ltd., 70 w/w%) to a chilled solution (<10 °C) of propylamine (Aldrich 99% w/w%) and Milli-Q water. The resultant solution was rotary evaporated for several hours at a constant temperature of 40 °C. The sample was then thoroughly purged with nitrogen and heated at 105 °C under a nitrogen atmosphere to remove remaining water. The water content of the PAN was undetectable by Karl Fischer titration prior to experimentation (<0.01 v/v%). Highly Ordered Pyrolytic Graphite (HOPG) (NT-MDT, Moscow) was prepared, immediately before experimentation, using adhesive tape to cleave along the basal plane.
1 molar acid–base reaction was conducted by slow addition of concentrated nitric acid (HNO3) (AJAX Finechem Pty. Ltd., 70 w/w%) to a chilled solution (<10 °C) of propylamine (Aldrich 99% w/w%) and Milli-Q water. The resultant solution was rotary evaporated for several hours at a constant temperature of 40 °C. The sample was then thoroughly purged with nitrogen and heated at 105 °C under a nitrogen atmosphere to remove remaining water. The water content of the PAN was undetectable by Karl Fischer titration prior to experimentation (<0.01 v/v%). Highly Ordered Pyrolytic Graphite (HOPG) (NT-MDT, Moscow) was prepared, immediately before experimentation, using adhesive tape to cleave along the basal plane.
The PAN–HOPG interface was studied using an Asylum Research Cypher Atomic Force Microscope (Cypher AFM). All data were obtained at a constant temperature of 25 °C. All images were obtained via amplitude-modulation-AFM (AM-AFM) (“tapping mode” in commercial AFM software) with the cantilevers oscillating at (or close to) resonant frequency which enables sub-nanometer resolution. Stiff cantilevers (ArrowUHFAuD, NanoWorld, Switzerland, nominal spring constant kc = 6 N m−1) were used to image the IL ion layer in contact with the HOPG surface. The cantilevers' free amplitudes (A0) were typically smaller than 1 nm. Imaging amplitude set points (A) were maintained at sub-nanometer oscillations so that the set point ratio was as high as possible (typically A/A0 ≥ 0.7). Using these operational conditions, the AFM tip probes interfacial liquid ions adsorbed to the graphite surface, without directly interacting with the solid itself.43,45 Each cantilever was calibrated using its thermal spectrum prior to imaging and the lever sensitivity is determined using force spectroscopy. The experiments were completed in a droplet of PAN exposed to the atmosphere within the AFM box (a sealed enclosure). As PAN is hygroscopic, the water content of the liquid will increase over the course of an experiment. However, the water content was routinely checked, via Karl Fischer titration, after each experiment. The data presented in this paper were obtained within 30 minutes of the IL droplet being placed on the HOPG. Karl Fischer titration of the ILs collected from the cell after this time period had a value of no more than ∼1 wt% which depended slightly on the ambient humidity; so the water concentration in the data presented will be less than this value.
In AM-AFM, the base of the cantilever is externally oscillated. The tip vibration amplitude is kept constant while travelling laterally across the sample by continually adjusting the tip sample-distance. Topographic images are obtained from corrections imposed by a feedback loop to maintain constant amplitude. The pressure exerted by the tip is progressively increased by lowering the ratio of the working amplitude to free tip vibration amplitude (A/A0). This effectively decreases the imaging set point and the average phase decreases until the tip reaches the ion layer in contact with the surface.
Quantum chemical simulations
Simulations of the PAN–HOPG interface use a model system consisting of 20 ion pairs adsorbed onto a single graphene layer ca. 1.5 × 1.5 nm2 in area. This yields a liquid layer ∼1.5 nm or three ion-pairs deep on the surface, and with a density that corresponds to that of bulk PAN.46 Three-dimensional periodic boundary conditions were employed, and adjacent cells were separated by a vacuum region of 5 nm in the direction normal to the surface. Recent quantum chemical simulations47 have shown that relatively small IL model systems, comparable to that employed here, are capable of accurately reproducing the main features of the bulk structure. As we show below, this model system is sufficiently thick that the different structures at the PAN–vacuum interface48 and PAN–graphene interface, can be distinguished from each other, and from the intervening layer which approximates bulk PAN. The use of a single graphene layer here is appropriate because sub-surface graphitic layers will not appreciably influence the adsorbed IL structure. van der Waals interactions between sub-surface graphene sheet layers and the adsorbed IL are negligible compared to the stronger short-range electrostatic forces present in the liquid, and between the ions and the surface. This is not the case for relatively weakly cohesive molecular liquids (such as water adsorbed on graphite) where sub-surface graphene sheets do affect the structure.49The Kick3 stochastic algorithm47 was used to produce randomly adsorbed ion configurations onto the model graphite surface, after which a 0 K geometry optimization was performed. A total of 2000 initial starting configurations were optimized, producing a total of 1405 unique adsorbed configurations (unique according to energy). Quantum chemical molecular dynamics (MD) simulations were subsequently performed at room temperature (298.15 K) on selected, low energy configurations, in order to establish entropic effects on the interfacial structure. For MD simulations, temperature control was enforced via a Nosé–Hoover chain thermostat (chain length 3), and the system was equilibrated for 20 ps using a 1 fs timestep prior to quantitative analyses. The system was then simulated for a further 80 ps for quantitative analyses.
The quantum chemical method used here is dispersion-corrected 3rd order density functional tight binding theory (DFTB3-D),50 in conjunction with the mio-0-1 DFTB parameter set.51 We have recently validated this approach against full DFT calculations for a series of imidazolium nitrate ILs.47 The DFTB method is a two-centre, extended Hückel approximation to DFT.52 As such, it provides accuracy comparable to full DFT, yet has a computational efficiency ca. 100–1000 times faster than DFT (depending on the size of the system being studied and the level of the DFTB approximation, see below). The DFTB method treats the electron density explicitly and assumes that it can be approximated as a reference density plus a small perturbation. This assumption enables the exchange-correlation energy E to be expanded as a Taylor series,
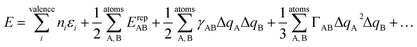 | (1) |
Results and discussion
Fig. 1 presents AM-AFM images of the surface layer of PAN ions bound to a HOPG surface. Contact with the surface layer is achieved through use of a high spring constant cantilever.54 The pressure exerted by the tip is progressively increased until the tip reaches the ion layer in contact with the surface. The raw data is shown in Fig. 1 (left), while Fig. 1 (right) shows the area of the surface bounded by the square after low-pass filtering using the fast Fourier transform algorithm in the Gwyddion software.55 | ||
| Fig. 1 (Left) AM-AFM mode image of the PAN–HOPG interface obtained using a scan amplitude of 1 nm. The inset shows the image 2-dimensional Fourier transform. (Right) filtered image of the area bounded by the square in the raw data. Note the different scales used in the two images. The corresponding phase image and 2-dimensional Fourier transforms are provided as the ESI† (Fig. S1 and S2, respectively). The variation of phase and amplitude of the AFM tip approaching the HOPG substrate is shown in Fig. S3.† | ||
Fig. 1 reveals that the surface-adsorbed layer of PAN has remarkably, and unexpectedly, well-defined symmetry. The Fourier transform confirm that this structure is rhomboidal, comprising one set of four intense spots plus a second, weaker set of four spots rotated by 60°, indicating that two domains are sampled in this image,56 with a lattice dimension of 0.48 ± 0.02 nm and an angle of 60°. The underlying HOPG surface has hexagonal symmetry and a lattice spacing of 0.246 nm.57 Thus, the PAN surface layer has only two symmetry axes and a lattice dimension approximately twice that of the underlying graphite substrate. This suggests that the graphite surface influences, but does not control, the surface layer structure of PAN. While dispersion and solvophobic interactions are expected between cation alkyl chains and HOPG,29 the precise ion arrangements that produce this rhomboidal structure cannot be determined from the images alone.
Fig. 2(a) shows the simulated liquid structure normal to the interface in a single representative ‘side-on’ snapshot of the simulation box. Fig. 2(a) reveals that the same liquid nanostructure, arising from association between polar and non-polar groups throughout the liquid occurs at the PAN–graphite interface, just as it does in the bulk:44 areas rich in charged groups (dark blue nitrogen atoms and red oxygen atoms) are separated by regions rich in apolar carbon (cyan) and hydrogen (white) atoms.
The side-on snapshot also shows that cation alkyl chains are aligned preferentially parallel to the graphene surface. Probability distribution functions for the alkyl chain, the cationic ammonium group and the nitrate anion, determined over the entire simulation, as a function of depth are presented in Fig. 2(e). There is 0 probability below 0.25 nm, reflecting the minimum separation distance between the centres of mass of the graphene carbons and ions (or their fragments). The probability of all groups then rises, but most strongly for the cation alkyl chain, with an intense peak at 0.38 nm. At 0.43 nm the probabilities for the three groups intersect, so this distance is used to define the upper boundary of the surface layer. Integrating the probabilities between 0 and 0.43 nm thus reveals the surface layer composition: for each cation charge group there are 1.2 anions and 2 cation alkyl groups. This shows that the most likely cation conformation in the surface layer has alkyl chains aligned along the HOPG surface with charge groups oriented towards the liquid in order to interact with nearby anions. This conformation maximises the surface area available for alkyl chain adsorption.
Further insight into the orientation of cations in the surface film is derived from the alkyl chain rotational probabilities presented in Fig. 2(d). This was obtained by measuring the angle between the plane formed by the three cation carbon atoms and the graphite surface, for all cations in the equilibrated surface layer averaged over the entire simulation. At 0 K, when the ions are immobile, all cation alkyl chains lie flat along the surface (0°), in order to maximise mutual contact. At 298 K thermal energy permits the rotational and translational motion of these ions, and this gives rise to a distribution of ±30° about the most probable angle of 0°. This distribution is a consequence of alkyl chains rotating (due to thermal motion energy) under the constraint of maximising surface contact and thus interaction energy. Angles of ±90° correspond to the cations “standing” on two of the three carbon atoms on the graphite surface, and are less probable because the weaker adsorption of this conformation means thermal rotation is more influential.
Fig. 2(f) shows how the average minimum vertical displacement of cations and anions (i.e. the shortest distance between any atom in the ion and the surface) that were initially in the surface film changes as the system is equilibrated at room temperature. Anions are mobile and freely move out of the surface layer but, strikingly, the cation vertical displacement is essentially invariant (although individual cations do undergo hindered rotation). Cations initially at the surface remain in the surface layer, due to strong attractions between cation alkyl chains and the graphite surface. Self-diffusion coefficients were determined from the simulation for cations bound to the surface and in the entire simulated film. As anions are not appreciably incorporated into the adsorbed layer (Fig. 2(e)) their self-diffusion coefficient was calculated only for the entire layer. The self-diffusion coefficient for cations and anions in the PAN film above the HPOG sheet can be calculated from the simulation. The self-diffusion coefficient for cations (3.2 × 10−11 m2 s−1) is an order of magnitude lower than that of anions (5.14 × 10−10 m2 s−1). As Fig. 2(b) shows that cations are enriched at the surface, the self-diffusion coefficient for cations in the surface film was also calculated, and found to be another order of magnitude smaller at 7.5 × 10−12 m2 s−1. This calculation reveals that cations are at least an order of magnitude less mobile when in contact with the surface compared to the bulk liquid.
Fig. 2(b) presents a snapshot of the simulation showing the lateral organisation of all ions in the surface layer to a depth of 0.6 nm and, by rendering the anions invisible and just the cations visible in Fig. 2(c). The agreement between simulation and experiment here is near-perfect; Fig. 2(c) shows cations aligned along two out of the three axes of the graphite substrate, as seen in the AM-AFM images. Fig. 2(g) shows a quantitative analysis of this phenomenon, via the lateral orientation probability, defined as the angle formed between the plane through the three cation carbon atoms and the graphite lattice vectors, for all cations in the surface layer, averaged over the entire QM/MD simulation. It is noted that the simulation supercell is large enough to accommodate cations simultaneously packing along all three directions of the HOPG substrate. However, this is not what is observed. Following equilibration at room temperature, the two most probable orientations relative to the graphitic lattice are 0° and 60°, while a third weaker peak is present at −60° and no such peaks are observed during equilibration. The “epitaxial” alignment of cations over the HOPG lattice is the result of attractive van der Waals forces between the HOPG and propyl chain being maximised. However, each peak in Fig. 2(g) exhibits distributions of ±15° that arise from the hindered rotation of the cations in the plane of the surface, enabled by thermal energy. The presence of two dominant peaks in Fig. 2(g) indicates that cations in the equilibrated surface layer pack preferentially along two out of the three directions of the underlying substrate. This reveals the origins of the rhomboidal symmetry observed in Fig. 1.
Inspection of the cation only surface layer (Fig. 2(c)) suggests that (i) cation charge groups tend to be orientated close together and (ii) cation alkyl groups associate with the surface where possible. These results are borne out by the surface layer g(r) data acquired over the course of the simulation (Fig. 3). The strongest correlations occur between cation nitrogens (N1) and anion nitrogens (N2) at 0.25 nm. These atoms are the centres of mass of groups that are electrostatically attracted to each other. The N1–N1 correlation is weaker, but clear, at 0.42 nm. This means that the close association of cation charge groups in the surface layer is facilitated by anion “bridges”. This spacing between cation charge groups is consistent with occupation of every second graphite lattice position. Cation alkyl chains associate on the surface within this framework of electrostatic binding. The g(r)s also reveal that the interactions between carbons bonded to the cation nitrogen (C1–C1) are weaker than those between carbons in the middle of the alkyl chains (C2–C2). This is consistent with cation alkyl chains lying parallel along the surface with an anion between charged groups. The C3 peak is more diffuse as it corresponds to the different “alkyl chain to alkyl chain” configurations across the surface. The C1–C1 correlation is weak due to the distance between the cation charge centres to which they are bound but the C2 carbons can associate more closely.
 | ||
| Fig. 3 Comparison of partial gij(r) distribution functions for important cation–anion (left) and cation–cation (right) interactions in the bulk44 (dotted lines) and in the surface ion layer (solid lines). Atom subscripts refer to the structure inset. Pronounced differences in cation–cation gij(r) data (particularly for the propyl chain carbon atoms and ammonium head group) indicate that cations adopt a significantly different rhomboidal structure at the graphite surface, compared with the bulk sponge structure. This is the result of the reduction in conformational freedom brought about by interaction between the graphitic lattice and the propyl chain. Conversely, bulk/interfacial cation–anion gij(r) are more similar and this is consistent with the fact that anions have minimal interaction with the graphite surface and desorb into the near-surface region as the graphite surface is electrically neutral. | ||
Strong cation alkyl chain–surface (dispersion and solvophobic) interactions lead to cations having limited mobility within the surface layer (as well as normal to it), and align the cation “epitaxially” along a single direction in the HOPG surface layer. Cations are physically separated by the anions that balance the positive charge, and are thus unable to pack close enough on the surface to occupy adjacent positions in the graphite lattice. Hence every second row in the graphite lattice is occupied by cations, accounting for the ∼0.5 nm lattice dimension observed in the AFM image. The packing constraints imparted by dispersion and solvophobic attractions, ion size, and the requirement for neutrality, result in ions arranging on the surface aligned with only two of the three possible directions, producing a rhomboidal structure in the surface layer. Computed self-diffusivities indicate that, on longer time scales, cations will diffuse in and out of the surface layer, but significantly slower than the anions. Furthermore, these self-diffusivities demonstrate that lateral diffusion of cations in the surface layer is relatively limited, and at any given time are most likely to be oriented in one of the two directions defined by the rhomboidal symmetry. Thus, the structure in the AFM image is a consequence of cations that are rendered relatively immobile by the surface in a well-defined rhomboidal configuration.
Conclusions
Combined AM-AFM and QM/MD simulations have elucidated the structure of the PAN–HOPG interface with high resolution. This is the first time the lateral structure of the IL–graphite interface has been imaged for any IL. PAN ions in contact with the graphite surface are highly ordered. AM-AFM reveals a structure with well-defined rhomboidal symmetry and QM/MD shows that this is produced by relatively immobile surface-adsorbed propylammonium cations. This result has important consequences for both IL interfacial systems and, more broadly, AFM imaging. For IL systems, the heterogeneous lateral structure at (carbonaceous) interfaces will influence processes including capacitive charge storage, electrodeposition, heterogeneous catalysis and lubrication,32 and define the design parameters for next generation ILs in these systems. For example, this study shows that for IL based capacitors, short chain length cations should be employed to maximise ion adsorption density on the surface and thus charge storage capacity. Similarly, for electrodeposition and heterogeneous catalysis, cations that interact weakly with the surface will enable easy passage of dissolved solutes to and from the solid surface. For lubrication, ions that interact strongly with the sliding surfaces will form a more robust boundary layer and facilitate smoother sliding. The ion structure required to produce a strong interaction with the substrate depends on the surface. For graphite, a long cation alkyl chain will lead to strong van der Waals interactions and a robust ion layer,58 while for a metal surface an unconstrained charge centre that can pack densely in surface layers will be more effective. For AFM imaging, the correlation between the simulation and the AM-AFM image reveals that the native structure of the liquid in contact with the surface is not significantly affected by forces and confinement effects imparted by the tip during imaging. This clearly demonstrates the capacity of AM-AFM to non-invasively image extremely delicate adsorbed structures.Acknowledgements
This research was supported by an ARC Discovery Project (DP120102708) and ARC Future Fellowship (FT120100313) for RA.References
- R. D. Rogers, Nature, 2007, 447, 917 CrossRef CAS PubMed.
- R. D. Rogers, K. Bica, G. Gurau, M. Smiglak, H. Rodriguez and J. Shamshina, in Congress on Ionic Liquids III, ed. D. R. Macfarlane, Carins, 2009, vol. in preparation Search PubMed.
- R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792 CrossRef PubMed.
- R. D. Rogers, K. R. Seddon and S. Volkov, Green Industrial Applications of Ionic Liquids, Kluwer Academic, Dordrecht, Netherlands, 2003 Search PubMed.
- K. R. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351 CrossRef CAS.
- T. L. Greaves, A. Weerawardena, C. Fong, I. Krodkiewska and C. J. Drummond, J. Phys. Chem. B, 2006, 110, 22479 CrossRef CAS PubMed.
- F. Endres, Chem. Ing. Tech., 2011, 83, 1485 CAS.
- J. S. Wilkes, Green Chem., 2002, 4, 73 RSC.
- M. Freemantle, Chem. Eng. News, 1998, 76, 32 Search PubMed.
- T. Welton, Chem. Rev., 1999, 99, 2071 CrossRef CAS PubMed.
- C. F. Ye, W. M. Liu, Y. X. Chen and L. G. Yu, Chem. Commun., 2001, 2244 RSC.
- B. S. Phillips and J. S. Zabinski, Tribol. Lett., 2004, 17, 533 CrossRef CAS.
- B. Bhushan, M. Palacio and B. Kinzig, J. Colloid Interface Sci., 2008, 317, 275 CrossRef CAS PubMed.
- J. Sweeney, F. Hausen, R. Hayes, G. B. Webber, F. Endres, M. W. Rutland, R. Bennewitz and R. Atkin, Phys. Rev. Lett., 2012, 109, 155502 CrossRef.
- M. D. Bermudez, A. E. Jimenez, J. Sanes and F. J. Carrion, Molecules, 2009, 14, 2888 CrossRef CAS PubMed.
- I. Minami, Molecules, 2009, 14, 2286 CrossRef CAS PubMed.
- A. Elbourne, J. Sweeney, G. B. Webber, E. J. Wanless, G. G. Warr, M. W. Rutland and R. Atkin, Chem. Commun., 2013, 49, 6797 RSC.
- O. Werzer, E. D. Cranston, G. G. Warr, R. Atkin and M. W. Rutland, Phys. Chem. Chem. Phys., 2012, 14, 5147 RSC.
- M. Gorlov and L. Kloo, Dalton Trans., 2008, 2655 RSC.
- S. Z. El Abedin and F. Endres, Accounts of Chemical Research, 2007, 40, 1106 CrossRef CAS PubMed.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206 CrossRef CAS PubMed.
- J. S. Wilkes, Green Chem., 2002, 4, 73 RSC.
- T. L. Greaves, D. F. Kennedy, N. Kirby and C. J. Drummond, Phys. Chem. Chem. Phys., 2011, 13, 13501 RSC.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237 RSC.
- A. Triolo, O. Russina, H. J. Bleif and E. DiCola, J. Phys. Chem. B, 2007, 111, 4641 CrossRef CAS PubMed.
- R. Atkin and G. G. Warr, J. Phys. Chem. B, 2008, 112, 4164 CrossRef CAS PubMed.
- P. Niga, D. Wakeham, A. Nelson, G. G. Warr, M. Rutland and R. Atkin, Langmuir, 2010, 26, 8282 CrossRef CAS PubMed.
- A. Ray, Nature, 1971, 231, 313 CrossRef CAS.
- R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162 CAS.
- M. Mezger, S. Schramm, H. Schroder, H. Reichart, M. Deutsch, E. J. De Souza, J. S. Okasinski, B. M. Ocko, V. Honkimaki and H. Dosch, J. Chem. Phys., 2009, 131, 094701 CrossRef PubMed.
- R. Atkin, N. Borisenko, M. Druschler, S. Z. El Abedin, F. Endres, R. Hayes, B. Huber and B. Roling, Phys. Chem. Chem. Phys., 2011, 13, 6849 RSC.
- R. Hayes, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2010, 12, 1709 RSC.
- R. Atkin, N. Borisenko, M. Drüschler, F. Endres, R. Hayes, B. Huber and B. Roling, J. Mol. Liq., 2014, 192, 44 CrossRef CAS PubMed.
- F. Endres, O. Hofft, N. Borisenko, L. H. Gasparotto, A. Prowald, R. Al-Salman, T. Carstens, R. Atkin, A. Bund and S. Z. El Abedin, Phys. Chem. Chem. Phys., 2010, 12, 1724 RSC.
- G.-B. Pan and W. Freyland, Chem. Phys. Lett., 2006, 427, 96 CrossRef CAS PubMed.
- M. Gnahm, C. Muller, R. Repanszki, T. Pajkossy and D. M. Kolb, Phys. Chem. Chem. Phys., 2011, 13, 11627 RSC.
- R. Atkin, N. Borisenko, M. Druschler, S. Z. El Abedin, F. Endres, R. Hayes, B. Huber and B. Roling, Phys. Chem. Chem. Phys., 2011, 13, 6849 RSC.
- Y. Z. Su, J. W. Yan, M. G. Li, Z. X. Xie, B. W. Mao and Z. Q. Tian, Z. Phys. Chem., 2012, 226, 979 CrossRef CAS.
- R. Foulston, S. Gangopadhyay, C. Chiutu, P. Moriarty and R. G. Jones, Phys. Chem. Chem. Phys., 2012, 14, 6054 RSC.
- T. Waldmann, H.-H. Huang, H. E. Hoster, O. Höfft, F. Endres and R. J. Behm, ChemPhysChem, 2011, 12, 2565 CrossRef CAS PubMed.
- B. Uhl, T. Cremer, M. Roos, F. Maier, H.-P. Steinruck and R. J. Behm, Phys. Chem. Chem. Phys., 2013, 15, 17295 RSC.
- F. Buchner, K. Forster-Tonigold, B. Uhl, D. Alwast, N. Wagner, H. Farkhondeh, A. Groß and R. J. Behm, ACS Nano, 2013, 7, 7773 CrossRef CAS PubMed.
- K. Voitchovsky, J. J. Kuna, S. A. Contera, E. Tosatti and F. Stellacci, Nat. Nanotechnol., 2010, 5, 401 CrossRef CAS PubMed.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 13544 RSC.
- J. J. Kuna, K. Voitchovsky, C. Singh, H. Jiang, S. Mwenifumbo, P. K. Ghorai, M. M. Stevens, S. C. Glotzer and F. Stellacci, Nat. Mater., 2009, 8, 837 CrossRef CAS PubMed.
- T. L. Greaves, A. Weerawardena, I. Krodkiewska and C. J. Drummond, J. Phys. Chem. B, 2008, 112, 896 CrossRef CAS PubMed.
- M. A. Addicoat, S. Fukuoka, A. J. Page and S. Irle, J. Comput. Chem., 2013, 34, 2591 CrossRef CAS PubMed.
- D. Wakeham, A. Nelson, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 12, 20828 RSC.
- C.-J. Shih, M. S. Strano and D. Blankschtein, Nat. Mater., 2013, 12, 866 CrossRef CAS PubMed.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931 CrossRef CAS PubMed.
- T. A. Niehaus, S. Suhai, F. Della Sala, P. Lugli, M. Elstner, G. Seifert and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 085108 CrossRef.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260 CrossRef CAS.
- M. Elstner, P. Hobza, T. Frauenheim, S. Suhai and E. Kaxiras, J. Chem. Phys., 2001, 114, 5149 CrossRef CAS PubMed.
- J. J. Segura, A. Elbourne, E. J. Wanless, G. G. Warr, K. Voitchovsky and R. Atkin, Phys. Chem. Chem. Phys., 2013, 15, 3320 RSC.
- P. Klapetek, Quantitative Data Processing in Scanning Probe Microscopy: SPM Applications for Nanometrology, Elsevier Science, 2012 Search PubMed.
- G. Harburn, C. A. Taylor and T. R. Welberry, Atlas of Optical Transforms, Cornell University Press, 1975 Search PubMed.
- T. R. Albrecht and C. F. Quate, J. Appl. Phys., 1987, 62, 2599 CrossRef CAS PubMed.
- R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4nr01219d |
| This journal is © The Royal Society of Chemistry 2014 |

