Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Softening of phospholipid membranes by the adhesion of silica nanoparticles – as seen by neutron spin-echo (NSE)†
Ingo
Hoffmann
*ab,
Raphael
Michel
a,
Melissa
Sharp
b,
Olaf
Holderer
c,
Marie-Sousai
Appavou
c,
Frank
Polzer
d,
Bela
Farago
b and
Michael
Gradzielski
*a
aStranski-Laboratorium für Physikalische und Theoretische Chemie, Institut für Chemie, Technische Universität Berlin, Straße des 17. Juni 124, Sekr. TC 7, D-10623 Berlin, Germany. E-mail: michael.gradzielski@tu-berlin.de; ingo.hoffmann@tu-berlin.de
bInstitut Max von Laue-Paul Langevin (ILL), F-38042 Grenoble Cedex 9, France
cJülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH, Outstation at MLZ, Lichtenbergstraße 1, D-85747 Garching bei München, Germany
dTEM Group, Institute of Physics, Humboldt Universität zu Berlin, Newtonstraße 15, D-12489 Berlin, Germany
First published on 6th May 2014
Abstract
The interactions between nanoparticles and vesicles are of significant interest both from a fundamental as well as from a practical point of view, as vesicles can serve as a model system for cell membranes. Accordingly the effect of nanoparticles that bind to the vesicle bilayer is very important with respect to understanding their biological impact and also may shed some light on the mechanisms behind the effect of nanotoxicity. In this study we have investigated the influence of small adsorbed silica nanoparticles (SiNPs) on the structure of zwitterionic DOPC vesicles. By a combination of SANS, cryo-TEM, and DLS, we observed that the SiNPs are bound to the outer vesicle surface without significantly affecting the vesicle structure. Most interestingly, by means of neutron spin-echo (NSE) local bilayer fluctuations were studied and one finds a small but marked decrease of the membrane rigidity upon binding of the nanoparticles. This surprising finding may be a relevant aspect for the further understanding of the effects that nanoparticles have on phospholipid bilayers.
1 Introduction
Liposomes are vesicles formed from phospholipids, which constitute the major part of any biological membrane.1 In addition, they have a number of applications such as in cosmetic formulations or as biocompatible carriers for drug delivery2–4 as they are able to load hydrophilic compounds in their aqueous interior as well as hydrophobic molecules within their bilayer.5–7 Upon heating, liposomes undergo a phase transition from a gel phase, in which the hydrophobic chains are frozen and the phospholipid molecules locked in place (Lβ) to a phase, in which the hydrophobic part of the bilayer is fluid and the phospholipids are free to move (Lα).8–10 Phospholipid vesicles (liposomes) are good model systems for biological membranes, where the Lα phase is the most relevant case.Recently, growing attention has been devoted to the study of the interactions in mixed systems of liposomes and inorganic nanoparticles (NPs). This is an important issue in the context of using NPs in nanomedicine but also in the related field of nanotoxicology. Experimental11–15 and theoretical16–24 investigations on those mixed systems have led to the description of different scenarios such as the encapsulation of the NPs within the vesicle or within the phospholipid membrane (for very small and hydrophobic NPs), or simply an attachment to the membrane. Focusing on the latter, the adsorption of NPs has been found to have an important influence on the deformation and poration of lipid membranes25,26 but also to act as stabilizer for liposome dispersions27–29 introducing an electrostatic repulsion between the nanoparticle/vesicle complexes. Further, decoration by nanoparticles may even protect the liposomes against degradation by digestive enzyme,30 leading to an enhanced potential as drug carrier. In recent years the effect of nanoparticles on phospholipid bilayers and in particular their transport through membranes31 has been a topic that received increasing attention due to the fact that it constitutes an essential aspect of nanotoxicity.32–34 In that context it should be noted that the bending elasticity of membranes is central to a number of biologically relevant properties of membrane systems35,36 such as budding37 or the formation of stalks38,39 and also related to the efficiency of gene delivery.40 Of course, additives, such as nanoparticles, may modify the bending rigidity substantially.
However, in order to understand such rather complex systems as nanoparticles interacting with biomembranes, it is first necessary to study simple model systems. As such a simple case we considered phospholipid vesicles to which silica nanoparticles (SiNPs) are admixed, where it is known that the SiNPs possess a high affinity to phospholipid bilayers and therefore one may expect a strong attractive interaction due to van der Waals forces.27,41 Many studies so far dealt with structural changes of the vesicles upon the addition of NPs and their attachment to the lipid bilayer. In contrast, this work aims at examining the influence of the adsorption of silica NPs on the average bending rigidity of zwitterionic unilamellar liposomes in the fluid state, which is a property of crucial importance for the functioning of any membrane, but so far only little is known with respect to the effect of attached nanoparticles on the membrane rigidity. Although membrane fluctuations at the site of adsorption of the NP might be expected to be suppressed, the effect on the surrounding membrane is not yet clear and a systematic understanding of how the molecular ordering in the membrane is affected by the presence of the surface-bound nanoparticles is still largely missing.
There is some experimental evidence, such as a decrease of the phase transition enthalpy and temperatue27,42 upon NP addition, that hints towards an overall softening of the membrane. With the help of neutron spin-echo (NSE) experiments, this question can be appropriately addressed, as it allows to measure rather directly the bending rigidity of mono- and bilayers.43–50 Such investigations are not only important from a fundamental point of view but also of general relevance for understanding the impact of nanoparticles on biological systems, e.g. in the context of nanotoxicity or for applying nanoparticles for drug delivery purposes.
2 Materials and methods
2.1 Materials
DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) with a phase transition temperature (Tm) around −18 °C (ref. 51) was purchased from NOF Corporation (Tokyo, Japan) and used as received. Well-defined unilamellar vesicles (ULV) were obtained by extruding an aqueous phospholipid solution at least 10 times first through a 200 and then another 10 times through a 100 nm pore diameter polycarbonate membrane (Whatman) with a Lipex 10 ml thermobarrel extruder at room temperature (T > Tm). Ludox HS 40 (colloidal silica suspension in water) was purchased from Sigma Aldrich. The nanoparticle suspension was dialysed against water before use using VISKING dialysis tubes (Roth, Karlsruhe, Germany) for 2 days, changing the water at least 5 times. The nanoparticle size was determined by small angle X-ray scattering (SAXS) with a SAXsess Kratky camera system (Anton Paar, Austria). Their average radius was found to be 8.36 nm (see Fig. S1†).For SANS, DLS and NSE experiments, D2O (99.9% isotopic purity, Euriso-top, France) was used as a solvent. Samples for cryo-TEM were prepared in deionized water taken from a Millipore system.
To obtain the final sample, stock solutions with a concentration of 0.2 wt% of DOPC and 0.17 wt% NPs were prepared and mixed 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (w/w) directly before measurements. All measurements were done on 0.1 wt% DOPC vesicle dispersion, i.e., under rather dilute conditions.
1 (w/w) directly before measurements. All measurements were done on 0.1 wt% DOPC vesicle dispersion, i.e., under rather dilute conditions.
SANS, DLS and NSE measurements were performed at 25 °C, which is significantly above the phase transition temperature of DOPC of −18 °C.
2.2 Methods
The form factor of a sphere with core–shell architecture is given by
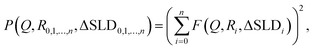 | (1) |
 | (2) |
The static scattering intensity for monodisperse, non-interacting particles is I = 1N·P + Iinc, where Iinc is the incoherent scattering intensity and 1N is the particle number density. For polydisperse particles, the expression changes to
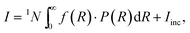 | (3) |
 , where V(R) is the volume of a particle of radius R.
, where V(R) is the volume of a particle of radius R.
A vesicle can be described as a spherical, single shell (the phospholipid bilayer), whereas vesicles decorated with NPs can be described with two shells, the inner shell being the phospholipid bilayer and the outer shell having the thickness of the NPs diameter, as determined by SAXS (see Fig. S1†). The SLD of that shell results from the fraction of NPs and solvent in the shell of the given thickness, which is calculated from the respective volume fractions, assuming complete coverage. Theoretically, if the vesicles are polydisperse, the contrast of the outer shell depends on the size of the vesicle, if we assume a constant number of NPs per area, but as the changes are quite insignificant and the contrast of the outer shell is low anyway, the average value can be used safely (for details see the ESI†).
The log–normal distribution function has been chosen to describe the size distribution. It is defined as:
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σ2/2), the standard deviation is
exp(σ2/2), the standard deviation is  . The thickness of the layers have been chosen to be constant and only the overall size of the vesicles varies.
. The thickness of the layers have been chosen to be constant and only the overall size of the vesicles varies.
| S(Q, t) = s(Q, t)/s(Q, 0) = exp(−DQ2t). | (5) |
The diffusion coefficient of a sphere of radius R is given by the Stokes–Einstein relation:
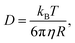 | (6) |
 | (7) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). Zilman and Granek57,58 predicted a stretched exponential decay with a stretch exponent of 2/3:
). Zilman and Granek57,58 predicted a stretched exponential decay with a stretch exponent of 2/3:| S(Q, t) = exp(−(ΓZGQ3t)2/3), | (8) |
 , where κ is the bending modulus of the membrane and for κ/kBT ≫ 1, γ ≈ 1. The absolute values for κ are known to be wrong in many cases59–61 however using an effective viscosity ηeff = η × 3 instead of the bulk viscosity to account for dissipation between membrane and solvent has proven to be successful in the past to correct the values accordingly, mostly on microemulsions60,61 but also on other systems,62 including phospholipid bilayers.63 In a somewhat more elaborate approach Watson and Brown64 adapted a theory by Seifert and Langer,65 in which contributions from lateral flow and interbilayer friction are considered, to the framework of the Zilman–Granek model. The stretched exponential shape of eqn (8) is maintained but instead of the bending modulus κ a renormalized bending modulus κ
, where κ is the bending modulus of the membrane and for κ/kBT ≫ 1, γ ≈ 1. The absolute values for κ are known to be wrong in many cases59–61 however using an effective viscosity ηeff = η × 3 instead of the bulk viscosity to account for dissipation between membrane and solvent has proven to be successful in the past to correct the values accordingly, mostly on microemulsions60,61 but also on other systems,62 including phospholipid bilayers.63 In a somewhat more elaborate approach Watson and Brown64 adapted a theory by Seifert and Langer,65 in which contributions from lateral flow and interbilayer friction are considered, to the framework of the Zilman–Granek model. The stretched exponential shape of eqn (8) is maintained but instead of the bending modulus κ a renormalized bending modulus κ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) is obtained:
is obtained: | (9) |
This quantity is related to the bending modulus through
κ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) = κ + 2d2k, = κ + 2d2k, | (10) |
| k = 24κ/dbilayer2. | (11) |
The complete expression for S(Q, t) for large diffusing particles with a membrane rigidity κ reads
| S(Q, t) = exp(−DQ2t)exp(−(ΓZGQ3t)2/3). | (12) |
In the analysis of NSE data, the diffusion coefficient D obtained from dynamic light scattering is used as an input parameter and ΓZG then remains as the only free parameter.
| g(2) = 1 + B|g(1)|2, | (13) |
3 Results and discussion
3.1 Structure and stability
In order to be able to study the influence of NP adsorption on the liposomes, a system had to be identified where (i) the NPs show (complete) adsorption, (ii) the structure does not change over the timescale of the NSE experiment and to facilitate the analysis (iii) the structure of the liposomes is not changed significantly by the adsorption.Therefore cryo-TEM, SANS and DLS measurements were performed. As can be seen in Fig. 1 and 2 spherical vesicles are formed by the extruded DOPC and the NPs are mostly adsorbed on the vesicles and the size and shape of the vesicles remain unchanged to the situation without NPs. Even though cryo-TEM does not provide 3-dimensional information, it can be inferred from the NPs located at the edge of the vesicles, that the NPs are located on the membrane rather than inside the vesicle. See the ESI† for a more detailed discussion.
 | ||
| Fig. 2 Cryo-TEM image of vesicles decorated with NPs (0.1 wt% DOPC, 0.85 wt% NPs), i.e., with a [NP]/[vesicle] ratio of 12. | ||
The fact that the vesicle structure remains basically unchanged is shown by SANS measurements in which the NPs are hardly visible, due to their rather low contrast in D2O and hardly any change between the spectra with and without added NPs can be seen (Fig. 3). The SANS curves have been fitted using eqn (1), (3) and (4), with the average vesicle size and polydispersity as the only free parameters. Both curves can be described with the same dataset, only adding a second shell with the thickness of the NPs and the contrast calculated as explained in 2.2.1. Fig. S2† shows the ratio of the scattered intensity of the vesicles with and without added NPs. The peak at about 0.06 nm−1 is due to the shift of the form factor minimum (as with the NP decoration the vesicle shell effectively becomes somewhat bigger), whereas the shallow peak at 0.2 nm−1 can be attributed to correlations between NPs on the vesicle surface. With a vesicle surface per NP of 4π × 43.52 nm2/12 = 1982 nm2, this corresponds to a NP spacing of 44.5 nm. Taking into account the fact that the NPs are located on a curved surface, the average distance reduces to 2 × 43.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(44.5/(43.5 × 2)) nm = 42.6 nm, this would result in a peak at 2π/42.61 nm−1 = 0.151 nm−1 which is just a little lower than the observed peak position.
sin(44.5/(43.5 × 2)) nm = 42.6 nm, this would result in a peak at 2π/42.61 nm−1 = 0.151 nm−1 which is just a little lower than the observed peak position.
 | ||
| Fig. 3 SANS curves of pure DOPC vesicles (0.1 wt%) and DOPC vesicles with 0.085 wt% NPs added. Almost no structural change can be seen. Fits have been performed using eqn (3) with eqn (1) and (4), see Table SI† for the parameters. The curve with DOPC and NPs is shifted by a factor of 10. | ||
To obtain translational diffusion coefficients and to check the stability of the NP/vesicle aggregates, DLS measurements were performed (see Fig. 4). The obtained values of 0.36 Å2 ns−1 correspond to a hydrodynamic radius of 53 nm, which is in good agreement with the SANS and cryo-TEM measurements. The fact that the autocorrelation function of the vesicles with added NPs can be well described with a single exponential supports the assumption that the vast majority of the NPs is bound to the vesicles as otherwise a second faster mode would be visible. The blue curve in Fig. 4 is the decay that would result, if the NPs would freely diffuse in the solution and from the comparison with the experimental data such a situation can be largely excluded. The amplitudes of the contribution from NPs and vesicles have been chosen to be equal, in agreement with the intensities obtained from the individual components. The diffusion coefficient of the pure vesicles and the diffusion coefficient of the vesicles with added NPs is quite similar (see Fig. 5), which is in agreement with the SANS and cryo-TEM data. Over the timescale of the NSE experiment the diffusion coefficient does not change significantly and only for much longer times a slight increase is observed (see Fig. 5), which is due to the internalization of the adsorbed particles into the liposome as phospholipid bilayer decorated nanoparticles.69,70 Upon incorporation into the vesicle the NPs take away part of the bilayer, forming a supported lipid bilayer (SLB) around the internalized NPs and hence the vesicle surface is correspondingly reduced. However, it can be concluded that internalization occurs much more slowly than the NSE experiment that was always done with freshly prepared samples (see Fig. 5) and therefore is not relevant for our NSE experiments.
 | ||
| Fig. 5 Development of the diffusion coefficient of DOPC/NP complexes with time as measured by DLS, red triangle: pure DOPC vesicles, vertical line: end of the NSE experiment. | ||
3.2 Changes in the bilayer rigidity
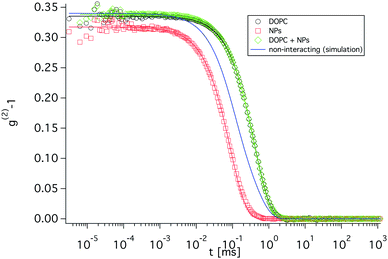
NSE measurements have been performed to investigate the influence of the NPs on the bending modulus of the vesicles.Good fit results of the NSE decay curves are obtained with eqn (12) (see Fig. 6 and S7†) simultaneously fitting all curves with a single set of parameters for all curves but the changes in S(Q, t) upon addition of NPs are in general quite small, yet systematic. Here it should be noted that determining the absolute scale of the bending moduli from NSE data is not a simple task as for that a number of other, not easily accessible parameters has to be known precisely. In contrast, a relative change of the bending modulus can be discerned with rather high precision.
 | ||
| Fig. 6 NSE data of vesicles with added NPs, fits using eqn (12) with a single set of parameters (IN15). | ||
It has been found previously that using a value for d (see eqn (10)) which is close (2d/dbilayer = 1.21) to the half bilayer thickness yields realistic values of κ of about 20 kBT.48,66 This means that the renormalized bending modulus κ![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) = κ + 2κ(dbilayer1.21/2)224/dbilayer2 = 18.6κ (see eqn (10) and (11)). As
= κ + 2κ(dbilayer1.21/2)224/dbilayer2 = 18.6κ (see eqn (10) and (11)). As 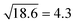 , this corresponds roughly to rescaling the viscosity with a factor of 3 which had been proven successful in the past.
, this corresponds roughly to rescaling the viscosity with a factor of 3 which had been proven successful in the past.
These results were obtained without taking into account translational diffusion and fitting our data in the same way (i.e., using eqn (8) instead of eqn (12)) yields ΓZG of 5.56 Å3 ns−1 which corresponds to a quite realistic value of κ of 26 kBT if ηeff = 3η (cf.eqn (9)) is used or a lower value of 13 kBT if 2d/dbilayer = 1.21 is used. However, at long times, deviations become visible (see Fig. S6†), which have to be attributed to neglecting the translational diffusion.
Given the diffusion coefficient of 0.357 Å2 ns−1 obtained from DLS, only diffusion is responsible for a significant part of the decay, e.g., at 0.9 nm−1S(Q, t) drops to 0.87 after 50 ns only due to translational diffusion, which means it accounts for more than 40% of the decay, assuming the decay of the measured S(Q, t) is to 0.7, as is the case here.
Therefore in order to have a more realistic description of our data, we included translational diffusion determined independently by DLS for the respective samples and good fits (see eqn (12)) were obtained (see Fig. S7† or 6) but ΓZG is reduced to 2.53, which would correspond to a κ of 62 kBT using eqn (10) and 2d/dbilayer = 1.21. However, this value seems unrealistically high when compared to values obtained with other methods.67,71 Accordingly we used d = dbilayer instead of 2d/dbilayer = 1.21, and with shifting the neutral surface to this position a κ value of 23 kBT is obtained, which seems reasonable when compared to other values in the literature.67,71 Therefore this assumption was used to calculate κ in the following, but again it should be noted that this choice of the neutral surface has no effect on the qualitative effects observed in our analysis, i.e., the relative changes of the bending modulus remain the same.
The most relevant parameter to be deduced from the NSE data is the Zilman–Granek relaxation rate ΓZG, which is proportional to κ−1/2 (see eqn (9) to (11)), i.e., allows to deduce directly information about the bending elasticity. Here it should be noted that NSE is rather unique in that respect as it allows to determine this elastic membrane property, which governs the properties of membranes to a large extent,35 in a rather direct fashion. Fitting the data of the NP decorated vesicles using the corresponding diffusion coefficient obtained from DLS, leads to a small but marked increase in ΓZG (and hence a decrease in κ). Varying the translational diffusion coefficient, the numerical value of ΓZG changes, but the general trend, i.e., an increase of ΓZG upon NP addition is preserved regardless of D (see Fig. 7). It might be argued, that the increase in the relaxation rate is due to the translational diffusion of free nanoparticles but this can be safely ruled out, as (i) they have a comparably low contrast and hardly contribute to the scattering signal (see also Fig. S5†) and (ii) it would contradict the results from DLS. Table 1 summarizes the obtained results and shows that the decoration of the phospholipid bilayer with the silica NPs leads to some softening of the bilayer.
 | ||
| Fig. 7 Fit results for ΓZG assuming different translational diffusion coefficients using eqn (12). Regardless of the translational diffusion coefficient the same trend for the change of ΓZG upon NP addition is observed. | ||
| Sample | ϕ DOPC | ϕ NP | D [Å2 ns−1] | Γ ZG [Å3 ns−1] | κ [kBT] |
|---|---|---|---|---|---|
| DOPC | 0.0011 | 0 | 0.357 | 2.53 ± 0.08 | 23 ± 1 |
| DOPC + NP | 0.0011 | 0.00042 | 0.363 | 2.71 ± 0.08 | 20 ± 1 |
Intuitively, it might be assumed that the NPs suppress undulation at their adsorption site and therefore stiffen the membrane. However, at the same time they seem to cause a sufficient degree of disorder in the membrane (as seen for instance in the substantially lowered melting enthalpies) that this effect is more than compensated and the average bending modulus is decreased72 (see Fig. 8). Another argument that could be given here for this softening effect is that the adhesion of the NPs leads to indentations on the vesicle surface, which then lead to an increase of the surface/volume ratio. This then would allow for more pronounced fluctuations and thereby a reduced effective bending modulus.
For a more detailed analysis, it would probably be necessary to implement at least an amplitude parameter for the undulation contribution, which would most likely be decreased due to the suppression of undulation motions at the adsorption sites of the NPs. However, the accuracy of the data (here it should be noted that we performed our experiments on the best performing NSE instrument available, so the data quality we had is state-of-the-art) prohibits the application of a more detailed model and in the approach we chose to use, the two effects (suppression of fluctuations at the adsorption site and softening around the adsorption site) compensate each other to some extent. This also explains, why the net-effect is relatively small. However, our experiments solidly show that the binding of the nanoparticles to the membrane surface leads to some softening of this membrane.
4 Conclusion
With the help of neutron spin-echo (NSE) we have been able to investigate the influence of small silica nanoparticles on the membrane rigidity of phospholipid vesicles. For this purpose we studied a system where no structural changes of the vesicles could be observed upon the addition of silica nanoparticles (where in our case the NP coverage was chosen such that about 40% of the vesicle surface was effectively covered by the silica NPs). The comprehensive analysis of the NSE data shows in general not a very large change but interestingly the addition of the nanoparticles causes a slight softening of the membrane, while in a simple picture one would expect a stiffening of the membrane. Such a stiffening would be expected due to a decrease in membrane fluctuations at the particle location and in addition the repulsive interaction between the negatively charged SiNPs should also lead to a stiffening of the membrane. Hence, this softening occurs, even though the NPs should reduce undulations at their adsorption site and the observed effect most likely stems from the area around the NPs. In general, the arrangement of the phospholipid alkyl chains becomes perturbed by the presence of the bound nanoparticles, thereby leading to a reduction of the elastic properties of the bilayers. These 2 opposing effects explain the small net change in the intermediate scattering function.Our experiments yield the interesting finding that adhesion of silica NPs to phospholipid membranes leads to a softening of the membrane. Furthermore our observations demonstrate the ability of NSE to deliver information on even delicate changes in the dynamics of such systems and show that it is a powerful tool to study processes involved in the interactions between hard nanoparticles and soft membranes, which are relevant to more general topics such as nanotoxicity and the design of innovative hybrid systems for drug delivery.
Acknowledgements
Financial support by the DFG (Deutsche Forschungsgemeinschaft) in the framework of the IGRTG 1524 (SSNI) and the BMBF (Bundesministerium für Bildung und Forschung) through project 05K10KT1 as much as the allocation of beam time by the ILL and the JCNS is gratefully acknowledged. T. Weikl is thanked for fruitful discussions. Dr F. Polzer likes to thank the CRC 951 of the Deutsche Forschungsgemeinschaft and the Joint Lab for Structural Research within IRIS Adlershof for funding.References
- D. D. Lasic, Liposomes: from physics to applications, Elsevier, Amsterdam etc., 1993 Search PubMed.
- D. D. Lasic and D. Papahadjopoulos, Medical applications of liposomes – Foreword, Elsevier Science Bv, 1998, pp. VII–IX Search PubMed.
- D. D. Lasic, Trends Biotechnol., 1998, 16, 307–321 CrossRef CAS.
- G. Cevc, Adv. Drug Delivery Rev., 2004, 56, 675–711 CrossRef CAS PubMed.
- G. Blume and G. Cevc, Biochim. Biophys. Acta, Biomembr., 1990, 1029, 91–97 CrossRef CAS.
- R. Banerjee, J. Biomater. Appl., 2001, 16, 3–21 CrossRef CAS.
- V. P. Torchilin, Nat. Rev. Drug Discovery, 2005, 4, 145–160 CrossRef CAS PubMed.
- S. Mabrey and J. M. Sturtevant, Proc. Natl. Acad. Sci. U. S. A., 1976, 73, 3862–3866 CrossRef CAS.
- M. J. Janiak, D. M. Small and G. G. Shipley, Biochemistry, 1976, 15, 4575–4580 CrossRef CAS.
- P. Y. Bolinger, D. Stamou and H. Vogel, J. Am. Chem. Soc., 2004, 126, 8594–8595 CrossRef CAS PubMed.
- T. K. Sau, A. S. Urban, S. K. Dondapati, M. Fedoruk, M. R. Horton, A. L. Rogach, F. D. Stefani, J. O. Rädler and J. Feldmann, Colloids Surf., A, 2009, 342, 92–96 CrossRef CAS PubMed.
- A. S. Urban, M. Fedoruk, M. R. Horton, J. O. Rädler, F. D. Stefani and J. Feldmann, Nano Lett., 2009, 9, 2903–2908 CrossRef CAS PubMed.
- R. Michel and M. Gradzielski, Int. J. Mol. Sci., 2012, 13, 11610–11642 CrossRef CAS PubMed.
- M. Schulz, A. Olubummo and W. H. Binder, Soft Matter, 2012, 8, 4849–4864 RSC.
- R. C. Van Lehn, P. U. Atukorale, R. P. Carney, Y.-S. Yang, F. Stellacci, D. J. Irvine and A. Alexander-Katz, Nano Lett., 2013, 13, 4060–4067 CrossRef CAS PubMed.
- A. Boulbitch, Europhys. Lett., 2002, 59, 910–915 CrossRef CAS.
- W. T. Góźdź, Langmuir, 2007, 23, 5665–5669 CrossRef PubMed.
- R. Lipowsky and H.-G. Döbereiner, Europhys. Lett., 1998, 43, 219–225 CrossRef CAS.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef.
- U. Seifert and R. Lipowsky, Phys. Rev. A, 1990, 42, 4768–4771 CrossRef CAS.
- R. Golestanian, M. Goulian and M. Kardar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6725–6734 CrossRef CAS.
- H.-K. Lin, R. Zandi, U. Mohideen and L. P. Pryadko, Phys. Rev. Lett., 2011, 107, 228104 CrossRef.
- M. Goulian, R. Bruinsma and P. Pincus, Europhys. Lett., 1993, 22, 145–150 CrossRef CAS.
- T. R. Weikl, Europhys. Lett., 2001, 54, 547–553 CrossRef CAS.
- S. Li and N. Malmstadt, Soft Matter, 2013, 9, 4969–4976 RSC.
- P. R. Leroueil, S. A. Berry, K. Duthie, G. Han, V. M. Rotello, D. Q. McNerny, J. R. Baker, B. G. Orr and M. M. B. Holl, Nano Lett., 2008, 8, 420–424 CrossRef CAS PubMed.
- R. Michel, T. Plostica, L. Abezgauz, D. Danino and M. Gradzielski, Soft Matter, 2013, 9, 4167–4177 RSC.
- S. Savarala, S. Ahmed, M. A. Ilies and S. L. Wunder, ACS Nano, 2011, 5, 2619–2628 CrossRef CAS PubMed.
- L. F. Zhang and S. Granick, Nano Lett., 2006, 6, 694–698 CrossRef CAS PubMed.
- V. J. Mohanraj, T. J. Barnes and C. A. Prestidge, Int. J. Pharm., 2010, 392, 285–293 CrossRef CAS PubMed.
- A. M. Koch, F. Reynolds, H. P. Merkle, R. Weissleder and L. Josephson, ChemBioChem, 2005, 6, 337–345 CrossRef CAS PubMed.
- K. Donaldson, V. Stone, C. L. Tran, W. Kreyling and P. J. A. Borm, Occup. Environ. Med., 2004, 61, 727–728 CrossRef CAS PubMed.
- P. R. Leroueil, S. Hong, A. Mecke, J. R. Baker, B. G. Orr and M. M. Banaszak Holl, Acc. Chem. Res., 2007, 40, 335–342 CrossRef CAS PubMed.
- A. P. Alberola and J. O. Rädler, Biomaterials, 2009, 30, 3766–3770 CrossRef CAS PubMed.
- Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995 Search PubMed.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327–1381 CrossRef CAS.
- R. Lipowsky, J. Phys. II, 1992, 2, 1825–1840 CrossRef CAS.
- Y. Kozlovsky and M. M. Kozlov, Biophys. J., 2002, 82, 882–895 CrossRef CAS.
- B. M. Friedrich, A. Buxboim, D. E. Discher and S. A. Safran, Biophys. J., 2011, 100, 2706–2715 CrossRef CAS PubMed.
- C. R. Safinya, Curr. Opin. Struct. Biol., 2001, 11, 440–448 CrossRef CAS.
- P. S. Cremer and S. G. Boxer, J. Phys. Chem. B, 1999, 103, 2554–2559 CrossRef CAS.
- C. Westerhausen, F. Strobl, R. Herrmann, A. Bauer, S. Schneider, A. Reller, A. Wixforth and M. Schneider, Biophys. J., 2012, 102, 1032–1038 CrossRef CAS PubMed.
- M. Gradzielski, D. Langevin and B. Farago, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3900–3919 CrossRef CAS.
- T. Hellweg, M. Gradzielski, B. Farago and D. Langevin, Colloids Surf., A, 2001, 183, 159–169 CrossRef.
- X. S. Hu, R. Biehl, R. K. Prud'homme, M. Monkenbusch and J. Lal, Phys. B, 2004, 350, 217–219 CrossRef CAS PubMed.
- L. Arriaga, R. Rodríguez-García, I. López-Montero, B. Farago, T. Hellweg and F. Monroy, Eur. Phys. J. E, 2010, 31, 105–113 CrossRef CAS PubMed.
- L. R. Arriaga, I. López-Montero, G. Orts-Gil, B. Farago, T. Hellweg and F. Monroy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031908 CrossRef.
- A. C. Woodka, P. D. Butler, L. Porcar, B. Farago and M. Nagao, Phys. Rev. Lett., 2012, 109, 058102 CrossRef.
- M. Gradzielski, Eur. Phys. J.: Spec. Top., 2012, 213, 267–290 CrossRef CAS.
- M. Mell, L. Moleiro, Y. Hertle, P. Fouquet, R. Schweins, I. López-Montero, T. Hellweg and F. Monroy, Eur. Phys. J. E, 2013, 36, 1–13 CrossRef PubMed.
- I. D. V. Lynch and P. L. Steponkus, Biochim. Biophys. Acta, 1989, 984, 267–272 CrossRef.
- A. Radulescu, V. Pipich, H. Frielinghaus and M.-S. Appavou, J. Phys.: Conf. Ser., 2012, 351, 012026 CrossRef.
- P. Schleger, B. Alefeld, J. Barthelemy, G. Ehlers, B. Farago, P. Giraud, C. Hayes, A. Kollmar, C. Lartigue, F. Mezei and D. Richter, Phys. B, 1997, 241–243, 164–165 CrossRef CAS.
- M. Monkenbusch, R. Schätzler and D. Richter, Nucl. Instrum. Methods Phys. Res., Sect. A, 1997, 399, 301–323 CrossRef CAS.
- F. Mezei, in Neutron Spin Echo, ed. F. Mezei, Springer, Berlin/Heidelberg, 1980, vol. 128, pp. 1–26 Search PubMed.
- W. Helfrich, Z. Naturforsch. C, 1973, 28, 693–703 CAS.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS.
- A. G. Zilman and R. Granek, Chem. Phys., 2002, 284, 195–204 CrossRef CAS.
- M. Monkenbusch, O. Holderer, H. Frielinghaus, D. Byelov, J. Allgaier and D. Richter, J. Phys.: Condens. Matter, 2005, 17, S2903–S2909 CrossRef CAS.
- S. Komura, T. Takeda, Y. Kawabata, S. K. Ghosh, H. Seto and M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041402 CrossRef CAS.
- B. Farago, M. Monkenbusch, K. Goecking, D. Richter and J. Huang, Phys. B, 1995, 213–214, 712–717 CrossRef.
- I. Hoffmann, P. Heunemann, B. Farago, I. Grillo, O. Holderer, M. Päch and M. Gradzielski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061407 CrossRef CAS.
- Z. Yi, M. Nagao and D. P. Bossev, J. Phys.: Condens. Matter, 2009, 21, 155104 CrossRef PubMed.
- M. C. Watson and F. L. H. Brown, Biophys. J., 2010, 98, L9–L11 CrossRef CAS PubMed.
- U. Seifert and S. A. Langer, Europhys. Lett., 1993, 23, 71–76 CrossRef.
- J.-H. Lee, S.-M. Choi, C. Doe, A. Faraone, P. A. Pincus and S. R. Kline, Phys. Rev. Lett., 2010, 105, 038101 CrossRef.
- W. Rawicz, K. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- B. J. Berne and R. Pecora, Dynamic Light Scattering With Applications to Chemistry, Biology and Physics, Dover Publications, reprint edition, 2000 Search PubMed.
- O. Le Bihan, P. Bonnafous, L. Marak, T. Bickel, S. Trépout, S. Mornet, F. de Haas, H. Talbot, J.-C. Taveau and O. Lambert, J. Struct. Biol., 2009, 168, 419–425 CrossRef CAS PubMed.
- A. H. Bahrami, M. Raatz, J. Agudo-Canalejo, R. Michel, E. M. Curtis, C. K. Hall, M. Gradzielski, R. Lipowsky and T. R. Weikl, Adv. Colloid Interface Sci., 2014 DOI:10.1016/j.cis.2014.02.012.
- J. Pan, S. Tristram-Nagle, N. Kučerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS PubMed.
- I. Szleifer, D. Kramer, A. Ben-Shaul, D. Roux and W. M. Gelbart, Phys. Rev. Lett., 1988, 60, 1966–1969 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional SAXS, NSE and TEM measurements and further details concerning SANS and DLS measurements. See DOI: 10.1039/c4nr00774c |
| This journal is © The Royal Society of Chemistry 2014 |