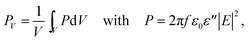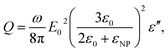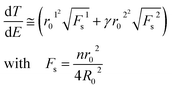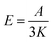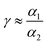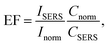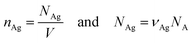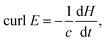Highly effective hot spots for SERS signatures of live fibroblasts

Abstract

Pre-formed silver–boron nanoparticles of 22 nm form pearl-like necklace nanostructures with interparticle junctions of less than 10 nm length in the matrix of polyethylene glycol (8000 Da). The silver necklace nanostructure is stable at 37 °C or 70 °C and also inside a live cell medium. A polyethylene glycol matrix with a shorter chain length (1000 Da) does not protect the nanoparticles against attraction, and random aggregates are formed. Silver necklace nanostructures exhibit strong Raman enhancement by more than ∼10⁹ which is much higher than for silver–citrate or random silver–boron aggregates. The polymeric matrix of 8000 Da contributes strongly to the electromagnetic field enhancement and removes the chemical contribution to the surface Raman scattering increase. The stable interparticle junctions act as local hot spots for strong Raman scattering signals collected from live fibroblasts and allow systematic in situ studies.

---

Introduction

Silver nanoparticles (NPs) are of highest interest in nanotechnology being among the most commercialized products in healthcare and medicine. The reasons for this interest are the unique antibacterial and optical properties of silver among all metals that are strongly dependent on the colloidal geometry and the dielectric function. This dependence is being exploited for the development of novel biosensors,¹ electro-optical devices,² but mostly in biological imaging and surface enhanced Raman scattering (SERS) spectroscopy.³ In nanotechnological development of analytical tools, the SERS application meets technical demands, but it is also dependent on advanced nanoparticle design for strong enhancement.

Compared to conventional Raman spectroscopy, the SERS intensities achieved by silver nanoparticles^4,5 can be as high as 10⁶ to 10¹⁰ or even higher for single molecules^6,7 (three orders of magnitude higher compared to nano-gold) with near infra-red laser excitation.⁸ This increase is due to the dominant influence of the electromagnetic enhancement (∼10⁴) by the local surface plasmon resonance (LSPR) of silver.

Among other metals capable of excitation of surface plasmon oscillations, silver has the lowest imaginary part of the dielectric permittivity, which is responsible for the dissipation of the electric field energy.⁹ Hence the efficiency of surface plasmon excitations is highest for silver NPs. Nanoparticles with a large aspect ratio or those such as periodic arrays and networks exhibit maximum refractive index sensitivity and strongly contribute to the SERS increase. The enhancement of the electromagnetic (EM) field of the silver SPR occurs at the edges of the nanoparticle surface and in the junctions (<10 nm) between the particles.¹⁰

The coupling between two adjacent silver or gold nanoparticles forms an efficient “hot-spot” for SERS. The SERS enhancement factor at such hot spots can be as high as 10¹⁴, which is sufficient for single molecule detection.¹¹ Many efforts have been focused on the design of various hot spots such as silver nanocube dimers,¹² nanoparticle–nanowire couples¹³ or nanorod dimers.¹⁴ The different coupling geometries can be formed by nanofabrication techniques or self-assembly methods to achieve enhanced EM fields for SERS.^15,16 The main drawbacks are (i) the very small number of plasmonic structures, (ii) a single value of EF for each cluster geometry, which is difficult to assess, (iii) the heterogeneity of the colloidal solution and cluster precipitation and (iv) the stability against dissolution.

Alternatively the particle morphology and size distribution can be controlled by a plethora of lithographic approaches.^17–21 However they are time consuming, expensive and inefficient for large scale substrates. The gaps between uniform nanostructures are higher than the range of strong electromagnetic enhancement (i.e. >20 nm), and the biocompatibility is poor.²² The highest SERS EF from the 4 nm silver islands coated with about 6 nm silica film on the glass surface achieved by temperature-programmed desorption²³ does not exceed 10⁸. This value is several orders of magnitude less than from non-ordered elongated colloidal silver.

For live cell studies hot spots of silver NPs can be achieved in the polymeric matrix with a variety of polymers that are nontoxic and biocompatible.^24,25 One thus achieves a high stability of NPs in the cell cytoplasm. However, very little is known about silver ‘hot spots’ optical properties and calculated SERS efficiency. Still, randomly aggregated gold NPs (without junctions) have been widely studied by SERS inside the cells.²⁶ As an initial approach of a long-term study our first aim is to form hot spots of pre-formed silver NPs that enable high SERS efficiency inside live cells (e.g. fibroblasts). In addition, our goal is to define appropriate conditions of this enhancement.

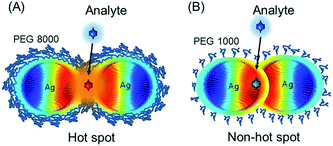
For hot spot formation pre-formed silver NPs are coated with polyethylene glycol (PEG) and the interparticle distance is controlled by the polymer chain length (e.g. 8000 Da or 1000 Da) (Scheme 1).

Scheme 1 (A) Schematic illustration of “hot spot” formation of silver nanoparticles in the matrix of polyethylene glycol (8000 Da). In the interparticle junctions the local increase of the electromagnetic field due to the surface plasmon resonance will contribute to the strong surface Raman scattering enhancement (SERS) from an analyte. (B) “Non hot spots” of silver nanoparticles can be formed in the matrix of polyethylene glycol with a shorter chain length (1000 Da) and in this case Raman signals of an analyte cannot be intensified.

Distinct from previous studies,²⁷ silver NPs assemble into a necklace structure with 8000 Da PEG and can form hot spots. A short PEG chain length is ineffective against particle attraction and hot spots cannot be formed. It is remarkable that hot spots are only of several nm distance and the necklace assembly holds its structure at 37 °C (or even at 70 °C). The SERS enhancement factor (10⁹) at such hot spots is several orders of magnitude higher than from gold or silver aggregates previously reported.^3,28 Because of its strong stability the silver–PEG necklace nanostructure can be used as a flexible SERS platform for a meaningful collection of high quality Raman spectra inside live cells. The unique removal of the chemical contribution to the SERS increase is a prominent advantage of a polymer matrix in a hot spot nanostructure. As another advantage, hot spots can act as secondary sources of the fluorescence increase. This property is highly demanding especially in two photon nonlinear spectroscopy of biomolecules.²⁹

Overall, our challenging work stimulates not only a systematic SERS study of organelles in live fibroblasts but also opens new pathways for hot spot formation in a flexible polymeric system with a specific part of SERS activity.

Results and discussion

(A) Hot-spot formation and stabilization of silver with a necklace nanostructure

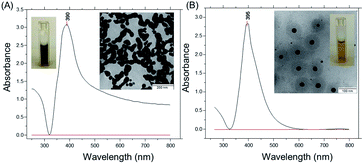
Two types of silver nanoparticles (NPs) were freshly formed by the reduction of silver nitrate aqueous solution with ice-cold sodium borohydride in water (Fig. 1). Large silver NPs appear with a brownish-grey color and form elongated assemblies due to aggregation (TEM image in Fig. 1A). The NPs exhibit a strong absorption near 390 nm with an elevated baseline due to scattering (Fig. 1A). The average size of the NPs is about 100 nm ± 20 nm and the NPs have a negative zeta potential of −36 mV. The other type of silver NPs is formed with an excess of sodium borohydride and exhibits a strong narrow absorbance peak near 395 nm (Fig. 1B).

Fig. 1 (A) UV-vis absorbance spectra of a silver colloidal solution after reduction of 1 × 10⁻³ mol L⁻¹ silver nitrate with 2 × 10⁻³ mol L⁻¹ sodium borohydride aqueous solution. The volume ratio of silver nitrate to sodium borohydride is 3 : 1. The two insets show a snapshot of the final freshly prepared silver colloidal solution and the corresponding TEM image (scale bar is 200 nm). (B) UV-vis absorbance spectra of silver colloidal solution after reduction of 1 × 10⁻³ mol L⁻¹ silver nitrate with 1 × 10⁻³ mol L⁻¹ sodium borohydride aqueous solution at a volume ratio of 1 : 3. The two insets show a snapshot of the final freshly prepared silver colloidal solution and the corresponding TEM image (scale bar is 100 nm).

Silver NPs show a bright yellow color in water and have an average size of 30 nm ± 3 nm (TEM image in Fig. 1B). The negative zeta potential is around −63 mV, and no sediment appeared within several months. To remind, the high stability of smaller silver NPs is due to the hydroborate (BH⁴⁻) and borate (BO₂²⁻ or BO₃³⁻) ions in base-stabilized and partially hydrolyzed sodium borohydride.³³ This provides a substantial electrostatic barrier to aggregation.

Despite the strong Coulombic repulsion the most stable arrangement of silver NPs can be disrupted by a change of the surrounding medium or thermal fluctuations. Without change of the ionic strength silver NPs are added to polyethylene glycol (PEG). The latter acts as a flexible dispersant and easily binds water molecules protecting NPs against attraction. The distance between neighboring NPs can be restricted due to the low configurational freedom and increased local concentration of the polymer chains resulting in the lowering of entropy. Upon heating the electrostatic protective layer of silver nanoparticles may be weakened partially due to the weaker hydroborate or borate ions on the surface of nanoparticles. However, a polymer matrix with a longer chain length may form an additional protective layer effectively contributing to the steric stabilization of nanoparticles. Later polyethylene glycol with long (PEG8, 8000 Da) and short (PEG1, 1000 Da) chains are used to control the distance between NPs resulting in hot spot or non-hot spot formation.

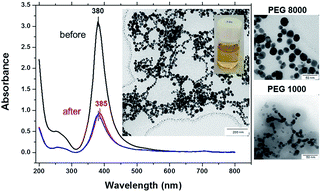
To test the thermal stability silver–PEG solutions were incubated overnight at room temperature followed by 30 min of mild shaking in a thermomixer at 37 °C or 70 °C in a dark room. Before heat treatment bare silver NPs exhibit one distinct absorbance band at 380 nm that is characteristic for absorption of silver NPs of 22 nm ± 3 nm (Fig. 2). The peak at 260 nm appearing shortly after injection of silver into the ice-cold sodium borohydride solution is due to the absorbance of small species at the initial stage of silver(I) reduction by borohydride. To remind, the formation of silver nanoparticles is due to aggregation induced growth, in which initially formed small borohydride-bound silver clusters grow by a mechanism that is largely aggregative in nature.

Fig. 2 UV-vis absorbance spectra of silver colloidal solution (1 × 10⁻³ mol L⁻¹ silver nitrate with 1 × 10⁻³ mol L⁻¹ sodium borohydride) coated by polyethylene glycol of 8000 Da (silver–PEG8 NPs) before and after heating at 37 °C or 70 °C. The two insets show a TEM image (scale bar is 200 nm) and a snapshot of silver–PEG8 NPs after heating at 70 °C. The other two TEM images (scale bar is 50 nm) on the right show silver–PEG8 NPs compared with silver–PEG1 NPs (polyethylene glycol of 1000 Da). Silver–PEG8 NPs form a necklace structure, while PEG1 is inefficient against aggregation of nanoparticles.

At 37 °C the 255 nm peak rapidly grows in, the SPR peak originally centered at 380 nm then red shifts to 385 nm and its intensity decreases threefold. The SPR red shift is due to an increased density of free electrons in the particle,³⁴ because the energy of SPR depends on the dielectric constants of both the nanoparticle and the surrounding medium.³⁵ The full width at half maximum, FWHM, increases from 45 nm to 50 nm (Fig. 2, red curve), indicating formation of larger NPs. The broadening and shift to lower energy occurs due to retardation and excitation of higher order multipoles, when the particles grow beyond a certain diameter.^36–38

At 70 °C the absorbance peak is blue shifted again to 380 nm, its intensity is slightly smaller (Fig. 2, blue curve) and the FWHM value gradually increases up to 55 nm. The TEM image shows spherical silver–PEG8 NPs that assemble into a pearl-necklace structure after heat treatment at 70 °C (inset of Fig. 2). Silver–PEG8 pearl-necklaces have a clear bright yellow color (another inset of Fig. 2) that is distinct from the brown-grey random silver–boron aggregates mentioned above (Fig. 1A). The stability of silver–PEG8 NPs is increased due to PEG. The latter at high molecular weight exhibits increased reactivity of binding water and effectively assembles particles in a necklace structure against attraction.

When silver NPs are coated with polyethylene glycol with a lower molecular weight (PEG1, MW = 1000 Da) a narrow absorbance peak appears at 385 nm and does not shift at 37 °C or 70 °C (Fig. SI1†). Silver–PEG1 colloidal solution is transparent with a clear yellow color and no sediment appears on the bottom after heating. The FWHM value does not change much upon heating being only slightly increased from 43 nm to 46 nm (at 37 °C or 70 °C). However, the intensity of the absorbance peak is decreased by almost threefold after heating of silver–PEG1 solution at 37 °C or 70 °C. The TEM image shows aggregated silver–PEG1 NPs that strongly merge after heating. No assemblies with a necklace-structure are observed (inset of Fig. SI1†). In addition, DLS diagrams of size distribution of colloidal silver solutions are shown in Fig. SI2.†

Overall, silver–boron NPs in the matrix of a longer chain polyethylene glycol (8000 Da) lead to the controlled aggregation of NPs into a pearl-like necklace structure. In this way interparticle junctions are only of several nm size and are stable at 37 °C or even 70 °C. A strong local electromagnetic field enhancement is achieved in the junctions of plasmonic NPs and can be used for Raman scattering enhancement. Later we use this approach to examine the Raman scattering of silver–PEG NPs and their surface enhancement.

(B) Surface-enhanced Raman scattering (SERS) efficiency of silver–PEG NPs

Rhodamine 6G (Rh6G) was used as a test dye to quantify the surface enhanced Raman scattering (SERS) efficiency of silver NPs. Prior to SERS measurements silver NPs were incubated in the presence of Rh6G in MQ water with 10⁻⁴ mol L⁻¹ NaCl for at least 3 hours to ensure the adsorption of dye molecules onto the particle surface. The presence of Cl⁻ anions is necessary in order to assist adsorption of dye molecules, as these anions are specifically adsorbed at Ag surfaces.³⁹ Low concentrations of NaCl promote dye chemisorption via a N–Ag covalent bond.³⁹ It does not induce coagulation of particles (no changes of the UV-vis absorbance spectrum of silver–Cl⁻ solution were observed).

The adsorption of dye molecules onto the silver NP surface is proved by the systematic disappearance of the characteristic Rh6G absorption near 525 nm (Fig. SI3†). As the concentration of Rh6G is decreased to 10⁻⁵ mol L⁻¹ the absorbance peak becomes a shoulder of the main UV-vis band of silver near 393 nm. It disappears when the concentration of the dye is further decreased to 10⁻¹⁰ mol L⁻¹.

Moreover, the Rh6G chemisorption on silver NPs is also proved by the electron transfer quenching of the fluorescence of the silver-dye colloidal solution (Fig. SI4†). As the concentration of the dye decreases from 10⁻⁶ mol L⁻¹ to 10⁻¹⁰ mol L⁻¹, fewer dye molecules contribute to the emission and the fluorescence intensity linearly decreases (Fig. SI4A and B†). However, it is almost quenched in silver–boron colloidal solutions after incubation with 10⁻⁶ mol L⁻¹ Rh6G (Fig. SI4C†). Random aggregates of silver–boron NPs quench the fluorescence by one order of magnitude stronger than monodisperse NPs due to the higher contact surface area. Less effective quenchers of fluorescence are silver–boron NPs that are coated with polyethylene glycol (Fig. SI4D†). Silver–PEG8 pearl-necklaces appear to decrease the dye fluorescence only by ten times, that is two times lower than that of merged silver–PEG1 NPs. Speculatively, this might have several possible reasons.

(a) Silver–PEG1 NPs have a large surface contact area and a thinner polymeric protective layer (eight times less molecular weight than PEG8);

(b) silver–PEG8 NPs form plasmonic hot spots that might serve as secondary sources of fluorescence excitation.

To increase the Raman cross-section, Rh6G aqueous solution was selected at a concentration of 10⁻⁸ mol L⁻¹ in order to ensure the necessary low threshold surface enhancement (10⁶) that is accompanied by a sufficient suppression of fluorescence.⁴⁰ The contribution of water can be neglected, as the Raman scattering from >10⁵ molecules increases by 300–1500 fold. SERS for water is based exclusively on the EM field increase, so that there is no charge-transfer induced surface enhancement. The effective number of the adsorbed dye is about one or two molecules per single silver NP with an average diameter of 22 nm and about four dye molecules per 30 nm NP. Detailed calculation can be found in the Experimental section.

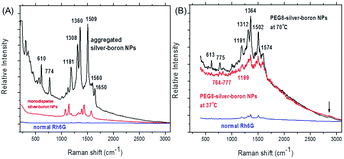
The SERS spectra of bare silver–boron NPs or those coated by PEG8 with adsorbed Rh6G (10⁻⁸ mol L⁻¹ in water) are shown in Fig. 3. In the frequency region below 300 cm⁻¹ small peaks are due to vibrations which involve chemical bonds of silver atoms or aggregates. The Ag–Cl silver–halide vibration occurs at 246 cm⁻¹ and is not influenced by the cations.⁴¹ At a sufficiently negative surface potential the surface Ag–Cl vibration disappears due to the forced desorption of Cl⁻ ions.

Fig. 3 (A) Surface enhanced Raman scattering (SERS) spectra of silver–boron nanoparticles incubated with 10⁻¹⁰ mol L⁻¹ aqueous rhodamine 6G solution compared to a normal Raman spectrum of bulk rhodamine 6G. (B) SERS spectra of a silver–PEG8 colloidal solution after heating at 37 °C or 70 °C. The spectra were collected with 785 nm excitation wavelength at a laser power of 10 mW and an integration time of 1 s with a spectral grating 300 gr mm⁻¹ blazed at 750 nm.

In Fig. 3A the N–H stretch (plane ring deformation) appears near 610 cm⁻¹ and 774 cm⁻¹ (out-of-plane bending motion of the hydrogen atoms of the xanthene skeleton⁴²). On bare silver–boron aggregates the absolute intensity of the 774 cm⁻¹ band is higher due to the conformational distortion by chemisorption of the molecule by the well-known vibronic coupling.⁴³ Moreover, this line is broadened due to the more than one vibration that contributes to this band. Similarly, the C–H in-plane bending coupled to the C–C stretching near 1181 cm⁻¹ is stronger in the aggregates of silver–boron NPs and is in good agreement with the literature.³⁹ In addition, prominent peaks at 1308 cm⁻¹ and 1360 cm⁻¹ from the aromatic C–H stretching might be due to the stronger extinction of aggregated silver NPs (Fig. 1A).

After heating silver–PEG8 NPs preserve their stability, as agglomerates contribute strongly to the elastic Rayleigh scattering, and Raman signals are not superimposed (Fig. 3B). In contrast to bare silver–boron NPs, the N–H stretch vibrations appear with a twofold lower relative intensity with a red shift near 613 cm⁻¹ and 775 cm⁻¹ (or in the region from 774–777 cm⁻¹). This indicates the inhibition of the charge transfer by polyethylene glycol, i.e. weaker chemisorption of the dye that is more pronounced at 37 °C.

In a similar way the carbon–hydrogen vibration is red shifted near 1191 cm⁻¹ at 70 °C and 1199 cm⁻¹ at 37 °C (Fig. 3B). One of the possible reasons could be the stretching ability of polyethylene glycol around silver NPs in water that might be higher at 37 °C. Induced desorption of the C–H aromatic stretching is reflected in red shifted frequencies near 1312 cm⁻¹ and 1364 cm⁻¹ with relative intensities twice smaller than on bare silver–boron NPs (Fig. 3A).

Because of its high sensitivity to molecular distortion the vibrational mode of the carbon skeleton appears on bare silver–boron aggregates as a prominent peak near 1509 cm⁻¹ (Fig. 3A), but it is blue shifted near 1502 cm⁻¹ with PEG8 (Fig. 3B). This indicates that a stronger coupling between the anion and the Ag–Rh6G bonds is achieved on coated silver NPs. However, the C–C aromatic ring stretching near 1560 cm⁻¹ (Fig. 3A) is strongly red shifted to 1574 cm⁻¹ on silver–PEG8 NPs, and the band at 1650 cm⁻¹ is absent.

Overall, on silver NPs the most intense ring and trigonal “breathing” of pyridine at 992 cm⁻¹ and at 1030 cm⁻¹ appear only as small peaks near 1001 cm⁻¹ and 1037 cm⁻¹ (Fig. 3A). The characteristic ring vibrations involving considerable N–O stretching at 1252 cm⁻¹, 835 cm⁻¹ and 541 cm⁻¹ are not observed. Moreover, the pyridinium halide C₅H₅NH⁺Cl⁻ that is located at 2380 cm⁻¹ does not appear as well as the O–H vibrations of water near 2500–2900 cm⁻¹ associated with the EM enhancement. However, on silver–PEG8 NPs the band around 2850 cm⁻¹ appears as a small broad peak, indicating that polymeric matrix promotes the EM enhancement due to the hot spots. To remind, the SERS for water is based exclusively on the EM enhancement so that there is no charge transfer induced surface enhancement.

(C) Laser heating effect versus concentration and SERS factor of silver–PEG NPs

For a meaningful SERS study of live cells reported later the drastic heating effect of silver NPs must be eliminated as a potential drawback because of spectral fluctuations. The local heating of an aqueous drop with silver nanoparticles with 2.55 mm radius due to the laser excitation (λ_exc = 785 nm, power < 6 mW) is less than ΔT = 3 K assuming a laser beam spot with the full width at half maximum (FWHM) of ∼1 μm (Fig. 4). However, the temperature rise depends on the concentration of silver NPs and the laser power.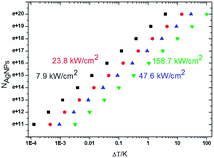

Fig. 4 Plot of the effective number of silver nanoparticles, N_Ag, versus local temperature gradient, ΔT, at different power intensities of a laser beam at the excitation wavelength of 785 nm.

As the typical concentration of silver NPs in a drop is in the order 10¹⁶ per μL the temperature rises up to <0.1 K at 7.9 kW cm⁻² (the lowest value to collect SERS spectra) to <1 K at 23.8–47.6 kW cm⁻². But the heating can reach several K at 158 kW cm⁻² (the highest value for well-resolved SERS lines) comparable to that reported for gold nanoparticles.⁴² The critical concentration of silver NPs, for which the temperature can reach 10–100 K, is in the order of 10¹⁸ to 10²⁰ per μL, and for this SERS spectra exhibit a strongly increased underlying continuum with one or two broad merged spectral lines.

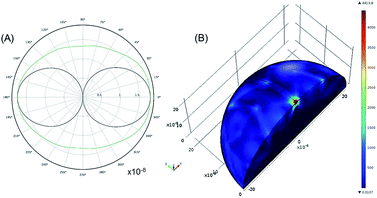
To understand the interaction of the incident near IR light with the silver nanoparticle surface, the 2D far-field scattering diagram and a 3D plot of electromagnetic power loss density (or heat dissipation density) over the volume of an individual silver NP (average diameter 22 nm) are theoretically modelled (Fig. 5). In this model, the scattering of a plane wave with λ_exc = 785 nm is computed for the optical frequency range (7.52 × 10¹⁴ Hz to 4.24 × 10¹⁴ Hz) in which silver as a material has negative complex permittivity.⁹ Due to the symmetry of this model, only one quarter of the sphere is modelled. A region around the silver nanosphere is taken to be half (or 1/20) the wavelength in free space with an outside domain as an absorber of the scattered field that is within the reactive near-field of the scattering sphere (half-wavelength).

Fig. 5 (A) 2D far-field scattering diagram with an E-field-plane (black) and H-field-plane (green) from the silver NP (22 nm) in water. (B) The 3D plot of electromagnetic power loss density (or total power dissipation density), P_V, over a volume of a silver NP. The excitation wavelength is 785 nm.

The far-field scattering pattern shows the E-field-plane (black) and the H-field-plane (green) with a form of a dipole antenna (Fig. 5A). The scattered light has an E-field parallel and an H-field perpendicular to the plane of this pattern. To remind, the angular distribution of the scattered light is determined by the angle with the main polarizability axis. In this way, the scattered intensity is zero in the direction of this vector (forward scattering) and can reach 180° in the backward scattering with the E-far-field values of about 2 × 10⁻⁸ V m⁻¹. It is noticeable that this value is slightly larger for 100 nm NPs being about 40 × 10⁻⁸ V m⁻¹ (Fig. SI5A†).

The electromagnetic power density loss (P_V, W cm⁻³) or resistive losses of total dissipation density over a silver nanosphere (22 nm) are shown as a 3D plot in Fig. 5B. To note, by the heat losses we derive how many electrons are passing through a silver NP, multiplied by the amount of energy each electron loses in the form of heat as it goes, giving an overall rate of heat production. In this way, the resistive heating power is directly proportional to the square of current multiplied by the resistance of silver. The total power dissipation density over silver nanoparticle volume is defined as

where f is the frequency of the incident wave (Hz, near IR), ε₀ is the vacuum permittivity, ε′′ is the imaginary part of the relative permittivity of silver (dissipation factor) and E is the electric field strength (V m⁻¹).

The bright areas show the resonance, where most of the losses take place over the volume of the NP (Fig. 5B). The highest value of this resonance appears as a red spot on the NP and has a value of 4413 W m⁻³. The xyz shows the space distribution of the energy source coming from heat dissipation, i.e. Q(r,t), which is defined as

Q(r,t) = 〈j(r,t)E(r,t)〉_t

where j(r,t) is the current density (A m⁻²) and E(r,t) is the stimulating electric field calculated from a system of Maxwell's equations. An analytical solution of the heat dissipation is introduced as

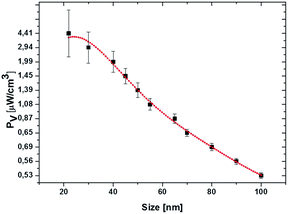
where ω is the frequency of the incident near IR light, E₀ is the electric field amplitude of the incident light (near IR, 785 nm), ε₀ and ε_NP are the dielectric constants of the medium and nanoparticle, and ε′′ is the imaginary part of the dielectric function of silver. The P_V value of an individual silver NP nonlinearly drops from 4.4 μW cm⁻³ to 0.53 μW cm⁻³ with the increase of particle size from 22 nm to 100 nm (Fig. 6). The polynomial fit (red) of the fourth order fits yielded the P_V values rather precise (black) (Fig. 6). The detailed investigation in dependence of the NP concentration (including other conditions) and at different parameters of incident light is our ongoing research activity.

Fig. 6 Dependence of the total power dissipation density, P_V, at resonance over the volume of individual silver NPs on their average diameters from 22 nm to 100 nm. The P_V values (black) are fitted to a polynomial fit (red) of the fourth order (y = 0.6 + 4 × 10⁻²x − 1 × 10³x² + 1.5 × 10⁻⁵x³ − 6.6 × 10⁸x⁴ with adj. R² = 0.99). The excitation wavelength is 785 nm.

In this work the SERS spectra are collected at low power density so that the dynamic fluctuations of particles in the surrounding water are mostly due to the Brownian motion with a negligible laser heating. The number of silver nanoparticles per volume does not exceed the critical value and is in the order of 10¹⁶ per μL. Water is a poor Raman scatterer and its maximum scattering intensity depends on the co-adsorption with the Cl⁻ ions at a relatively high salt concentration (four orders of magnitudes higher than we use here).

The calculated SERS enhancement factors (EFs) are listed in Table 1. The classifications of the main results are ‘VS’ (very strong) with EF ∼ 10⁹, ‘M’ (medium) with EF ∼ 10⁷ and ‘W’ (weak) with EF ∼ 10⁶. The bare silver–boron NPs exhibit SERS signals of Rh6G with moderate enhancement comparable to those reported before. However, silver hot spots protected by polyethylene glycol with a longer chain length (PEG8) increase the SERS EF up to ∼10⁹. This value is higher than from random aggregates of silver–citrate NPs⁴ and comparable with the hot spots on colloidal graphene oxide.⁴⁴ However, the SERS enhancement is still moderate on silver NPs in the polyethylene glycol matrix with shorter polymeric chains (PEG1).

Table 1 Calculated enhancement factors of surface enhanced Raman scattering (SERS) from silver–boron nanoparticles^a

Silver NPs	SERS EF	Result
a W (weak); M (medium), VS (very strong), PEG8 – polyethylene glycol of 8000 Da, PEG1 – polyethylene glycol of 1000 Da.
Mono-silver–boron	3.50 × 10^6	W
Aggreg-silver–boron	9.50 × 10^7	M
Silver—PEG8-37 °C	2.07 × 10^9	VS
Silver—PEG8-70 °C	5.57 × 10^9	VS
Silver–PEG1-37 °C	3.34 × 10^7	M
Silver–PEG1-70 °C	1.67 × 10^7	M

---

Such high EF values with PEG8 can be achieved at the stable interparticle junctions of several nm distance, so-called ‘hot spots’ for local EM increase (Fig. 2). The controlled necklace nanoparticle arrangement and SERS activity are stable under physiological conditions, i.e. 37 °C in aqueous medium of live fibroblasts. However, under equimolar conditions shorter PEG chains might not entirely coat the silver NPs due to their less coiled structure. At a temperature above room temperature, e.g. 37 °C or even higher, at 70 °C, silver–PEG1 NPs form random aggregates that merge at contact (Fig. SI1†).

(D) SERS molecular mapping of live fibroblasts

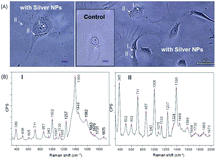
As we have shown that we can achieve unprecedented enhancement of Raman signals, it appears promising to advance this technique for intracellular analysis. Fig. 7A shows optical microscopy phase contrast images of live NIH/3T3 fibroblasts with incubated silver–PEG8 NPs (the inset shows the image of the control cells without NPs). For SERS measurements the culture medium was removed and the Petri dish was rinsed three times with PBS solution.

Fig. 7 (A) Optical phase contrast images of live NIH/3T3 fibroblasts with embedded silver–PEG8 nanoparticles after electroporation of the cellular membranes (scale bar is 50 μm). The inset shows control cells (without nanoparticles). I and II indicate the areas of the collected SERS signals as close to the nucleus and in the cytosol, respectively. (B) SERS spectra from the regions I and II. The underlying continuum of the SERS spectra was subtracted for clarity.

Silver–PEG8 NPs were embedded into the cell interior by incubation^45,46 or by electro-permeabilization based on electroporation⁴⁷ of the cell membrane. Both methods are successful and no visible changes of the cell damage or apoptosis were observed after overnight incubation. However, by the electro-permeabilization approach NPs are more homogeneously distributed mostly in the area close to or surrounding the nucleus leaving the spread tails almost untouched. By the cellular uptake during incubation most NPs were observed throughout the cellular body. About 99% of the control cells and 95% of those with embedded NPs were stretched on the quartz plate of the Petri dish without visible signs of cell damage or apoptosis.

Silver–PEG8 NPs after heating at 37 °C survived the overnight incubation inside the cells. Strong SERS spectra could be collected from 15 cells each in two regions: I (close to the nucleus) and II (throughout the intracellular cytosol) (Fig. 7B).

The SERS bands from I and II are considerably different. Overall, the absolute intensities of the SERS peaks are higher in II region excluding the 1390 cm⁻¹ band. This band was observed in I region and appears due to the DNA/RNA aromatic ring vibrations.⁴⁸ Low frequency SERS peaks (<605 cm⁻¹) appear with higher intensity in the II region than in the I region (Table 2). They are due to the presence of sugar molecules, proteins (S–S stretching disulfide at 502 cm⁻¹) and a minor component in the cytosolic side of the cell membrane (phosphatidylinositol at 602/605 cm⁻¹).⁵⁰

Table 2 Assignment of the surface enhanced Raman scattering (SERS) peaks from live NIH/3T3 fibroblasts with embedded silver nanoparticles

	Peak cm^−1	Assignment
I-cell	498	Polysaccharides, amylose
	605	Phosphatidylinositol
	711	Symmetric stretch vibration of choline group, characteristic for phospholipids
	857	On-plane ring breathing mode in tyrosine C–C
	943	C–C skeletal stretch in protein
	1002	Symmetric ring breathing mode of phenylalanine
	1067	DNA-backbone, nucleic acid band, DNA: O–P–O
	1130	C–N stretch in polypeptide chains
	1165	Aromatic ring vibrations of nucleic acids of DNA/RNA macromolecules, T, G
	1237	Extended amide III region
	1390	Aromatic ring vibrations of nucleic acids of DNA/RNA macromolecules
	1448	Deformation of hydrocarbon chains
	1582	Amide I vibration
	1663
	1670
II-cell	502	S–S disulfide stretching in proteins
	602	Phosphatidylinositol
	711	Symmetric stretch vibration of choline group
	823	Tyr–proteins, DNA: O–P–O backbone stretch/out-of-plane ring breath in tyrosine
	857	On-plane ring breathing mode in tyrosine C–C
	943	C–C skeletal stretch in protein
	1006	Symmetric ring breathing mode of phenylalanine
	1075	DNA-backbone, nucleic acid band, DNA: O–P–O
	1130	C–N stretch in polypeptide chains
	1237	Extended amide III region
	1324	Guanine
	1390	Aromatic ring vibrations of nucleic acids of DNA/RNA macromolecules
	1448	Deformation of hydrocarbon chains
	1586	Amide I vibration

---

Strong SERS peaks at 711 cm⁻¹ and 857 cm⁻¹ arise from phospholipids⁵⁰ and tyrosine⁵¹ (Table 2). The symmetric ring breathing of phenylalanine⁵² with a twice increased intensity was detected at the higher frequency of 1006 cm⁻¹ in II (at 1002 cm⁻¹ close to the nucleus). Additional peaks from the DNA-backbone (DNA: P–O–P)⁵¹ and the most prominent aromatic ring vibrations of nucleic acid DNA/RNA macromolecules⁴⁸ appear close to the nucleus. In the II region the DNA-backbone (DNA: O–P–O) band appearing at 1075 cm⁻¹ and aromatic ring vibrations of DNA (1390 cm⁻¹) with the guanine vibration as a shoulder at 1324 cm⁻¹ can arise from mitochondria or the mitochondrial membrane.^51–53 In both I and II the deformation of hydrocarbon chains appeared at 1448 cm⁻¹ with a series of small peaks due to the amide I vibration (1580–1700 cm⁻¹).^51,54 Overall, the collected SERS signals are much stronger and the spectra are more informative than those reported in the literature.^49,50,54,55

Conclusions

The silver NPs (22 nm) prepared by the reduction of sodium borohydride can assemble into a necklace nanostructure when coated with polyethylene glycol of 8000 Da. The necklace silver–PEG8 NPs can be stable at 37 °C (or 70 °C) necessary for live cell studies by Raman spectroscopy. Such silver NPs can enhance Raman signals of rhodamine 6G up to 10⁹ fold due to the local electromagnetic field enhancement at the interparticle junctions.

By varying the chain length of polyethylene glycol the neighboring silver–boron NPs can be brought into contact (merge with PEG 1000 Da) or kept stably apart at a distance of several nm (with PEG 8000 Da). The polymeric coiled structure can be stretched in a controlled way at 37 °C (or 70 °C) and the chemisorption of dyes can be decreased, the charge transfer thus weakened, leaving only the electromagnetic part for the Raman scattering enhancement. Inside live NIH/3T3 fibroblasts the silver–PEG8 NPs can strongly enhance the characteristic molecular vibrations of the DNA backbone, DNA/RNA aromatic ring vibration, stretching in tyrosine, polypeptides, sugar molecules (amylose), and many others.

Our preliminary results introduce a novel analytical approach towards the engineering of effective SERS substrates with a selectable type of Raman scattering enhancement (electromagnetic or charge transfer). It can be used as an informative analytical tool to examine the mechanisms of interest inside live cells in a systematic manner.

Experimental part

Materials

Silver nitrate (AgNO₃, analytical grade, 99.8%) was purchased from Serva (Germany). Sodium borohydride (NaBH₄, 98%) and polyethylene glycol (PEG-1, biology grade, MW ≈ 1000 Da) were produced by Alfa Aesar (Germany). Polyethylene glycol (PEG-8, biology grade, MW ≈ 8000 Da) was purchased from Aldrich. Sodium chloride (NaCl, ≥99.5%, biology grade, suitable for the cell culture medium) was produced by Sigma (Germany). DMEM, gentamicin, and glucose were purchased from Sigma. Calf serum was purchased from PAA GmbH (Austria).

The water used in all experiments was prepared in a three-stage Millipore Milli-Q Plus 185 purification system and had a resistivity higher than 18.2 MΩ × cm⁻¹. For the experiments with living cells Milli-Q water was autoclaved.

Preparation of silver nanoparticles

Prior to hot spot preparation we formed silver NPs by reduction with sodium borohydride. Small silver nanoparticles (20–30 nm) have been produced by Creighton's procedure,²⁹ while larger particles (60–100 nm) have been formed by a modified Schneider approach.³⁰ This is explained by the relatively high reactivity of borohydride (as compared with citrate^31,32 and carbohydrates), its handiness (as compared with gaseous hydrogen and physical methods) and not too high toxicity (as opposed to hydrazine and hydroxylamine).²⁹

Silver colloidal solution was prepared by chemical reduction of silver nitrate using sodium borohydride as a reducing agent in aqueous solution without organic stabilizers.²⁴ The process was carried out in a 0.25 L Erlenmeyer flask prewashed in concentrated nitric acid. The remains of the acid were removed from the glass walls by abundant amounts of deionized water. A 1 × 10⁻³ mol L⁻¹ concentration of AgNO₃ solution (room temperature) was mixed with fresh, ice-cold 1 × 10⁻³ mol L⁻¹ or 2 × 10⁻³ mol L⁻¹ sodium borohydride aqueous solution under vigorous stirring (300 or 600 rpm) at a nitrogen atmosphere. In the first 20 s, the mixture turned bright yellow. After complete injection (less than 2 min) of silver nitrate solution, stirring was stopped immediately. The final solution of the mixtures changed to brownish-grey (100 nm nanoparticles) or clear yellow color (20–30 nm nanoparticles).

The second part of nanoparticles was formed at the excess volume of sodium borohydride. The silver colloidal solution was kept in darkness to avoid the influence of light and stored at 4 °C. No sediment of silver nanoparticles was observed within several months. The concentration of silver sols was estimated from the UV-vis absorbance spectra by the Beer–Lambert–Bouguer law to be 2.78 × 10⁻³ mol L⁻¹ (pH = 4.7), 2.38 × 10⁻³ mol L⁻¹ (pH = 9.3), 2.1 × 10⁻³ mol L⁻¹ (pH = 9.1), 2.5 × 10⁻³ mol L⁻¹ (pH = 9.2), 2.0 × 10⁻³ mol L⁻¹ (pH = 9.0), and 2.17 × 10⁻³ mol L⁻¹ (pH = 9.2).

Preparation of polyelectrolyte solutions

Polymer aqueous solutions were prepared with a typical concentration of 2 mg mL⁻¹ followed by purification in a sealed semipermeable membrane (cellulose acetate) against MQ water (MW cutoff 20 000 Da) and lyophilized. PEG8 (pH = 6.5) and PEG1 (pH = 6.4) aqueous solutions were obtained under vigorous stirring at room temperature.

Treatment of silver nanoparticles with polyethylene glycol

For every treatment freshly prepared silver colloidal solution was used. To stabilize silver colloidal solution against unavoidable aggregation at 37 °C, silver sols were coated by polyethylene glycol at a volume ratio of 1 : 2. The mixture was incubated during mild shaking in the Eppendorf Thermomixer compact (Hamburg, Germany) overnight, followed by triple washing with MQ water and centrifugation at 14 000 rpm at 4 °C.

To test the colloidal stability, the “poly-silver” mixture was incubated at 37 °C or 70 °C for 60 min and allowed to cool to room temperature before characterization. The color of silver sols with polyethylene glycol was clear yellow without sedimentation at the bottom. The average pH value of silver sols with polyethylene glycol (1000 Da) was between 8 and 9 and for those with a longer chain length (8000 Da) around 9.

Preparation of rhodamine 6G-silver aqueous solutions for Raman measurements

The stock rhodamine 6G solution was prepared at a concentration of 10⁻³ mol L⁻¹ in MQ water (pH = 8.2). Lower concentrations from 10⁻⁴ mol L⁻¹ to 10⁻¹⁰ mol L⁻¹ were obtained by successive dilution of the stock solution by factors of 10 and 100. The dye concentration was monitored via the fluorescence intensity with a calibration curve. For Raman measurements fresh silver colloidal solution was added to a 10⁻⁴ mol L⁻¹ NaCl solution at a volume ratio 1 : 5 of salt to silver followed by the addition of fresh 1 μL rhodamine 6G solution. At electrolyte concentrations higher than 10⁻³ M no reliable data could be obtained due to instability of the silver sol. The mixture was incubated for at least 3 hours at room temperature in darkness before the Raman experiment.

The concentrations of bulk rhodamine 6G solutions were from 10⁻⁶ M to 10⁻¹⁰ M, as at higher concentrations (10⁻³ M to 10⁻⁵ M) the fluorescence is quenched due to the dimerization of dye molecules (i.e. methyl substituents of rhodamine 6G). The fluorescence intensity of bulk rhodamine 6G at 10⁻⁶ M to 10⁻¹⁰ M concentration linearly decreased with the decreased concentration of dye molecules (Fig. SI3B†).

Intensity measurements of rhodamine 6G-silver solutions at very low concentrations

A repeated chemical cleaning with concentrated HNO₃/HCl or concentrated H₂O₂/NH₃ was sufficient to remove adsorbed rhodamine 6G molecules in the dye solutions with concentrations from 10⁻⁸ M to 10⁻¹⁰ M. However, the cuvette required overnight boiling in order to remove dye molecules after the measurements at higher concentrations (10⁻⁶ to 10⁻⁷ M). To get stable and reproducible signals and to avoid unnecessary adsorption and desorption processes at the cuvette walls the clean cuvettes were rinsed several times with portions of the sample solution. This procedure was repeated until equilibrium between the adsorbed and dissolved molecules was established. This was controlled by the fluorescence intensity. In this way a linear relationship between concentration and fluorescence intensity could be established in the range between 10⁻⁶ M and 10⁻¹⁰ M. Reliable data were obtained for each concentration of rhodamine 6G solution by several measurements from independent samples.

Cell culture, co-incubation and electroporation of cells with colloidal silver

Fibroblasts NIH/3T3 (purchased from DMSZ) were cultured in Dulbecco's modified Eagle's medium (DMEM) supplemented with 4.5 g L⁻¹ glucose, 10 v% calf serum, and 10⁻² g L⁻¹ gentamicin (antibiotic). Cells were seeded with 6 × 10³ cells cm⁻² on the glass bottom dish (purchased from Greiner Bio For One) 8.8 cm² culture surface and incubated in an incubator (binder) with 5% CO₂ at 37 °C overnight before Raman measurements.

Silver sols were delivered into the cellular interior by internalization with endocytosis and transported into the late endosomes and lysosomes via overnight incubation of 200 × 10⁻⁶ L (1.3 × 10⁵ cells) in a culture medium suspension with 400 × 10⁻⁶ L particle solution. Alternatively the delivery of silver nanoparticles was achieved by electro-permeabilization of the cell membranes in a BIO-RAD gene-pulser cuvette with 0.4 cm electrode gap inserted inside a home-made electric cell connected to the GHT-Bi500 electroporator (βtech, France). 200 × 10⁻⁶ L (5.34 × 10⁴ cells) in a culture medium were mixed with 400 × 10⁻⁶ L of silver colloidal solution at a sequence of pulse voltages of 250 V for the positive and negative parts with a pulse length 500 ms within the sequence. After the co-incubation and electroporation the colloidal mixture with the cell suspension was mixed with 1 × 10⁻³ L of the culture medium and deposited onto the glass bottom of a Petri dish in the incubator. The inspection of the incubated cells was checked by optical microscopy after 12 hours of aging.

Characterization

A. UV-vis absorption, zeta potential, dynamic light scattering, electron/optical microscopy and fluorescence. To characterize the size distribution of silver NPs a Zeiss EM 912 Omega transmission electron microscope (TEM) and a high-performance particle sizer (Malvern Instruments) for dynamic light-scattering (DLS) measurements were employed. For TEM analysis a drop of the colloidal solution was applied onto the copper grids coated with a carbon film and left to evaporate.

Surface plasmon resonance absorption and concentration of silver nanoparticles were monitored using a Varian CARY50 Conc UV-vis spectrophotometer in the wavelength range from 200 to 900 nm in a quartz cell with 10 mm path length. The ζ-potential of silver colloidal solutions was measured using a zeta sizer (Malvern Instruments). The fluorescence measurements were performed using a FluoroMax-4 spectrofluorometer (Horiba Jobin Yvon). A Nikon Eclipse TS100 routine inverted microscope was employed to collect the refracted light from the transparent live cells through the enhancement of their phase contrast. Observation of the morphology of the cell was conducted using a Leica TCS SP inverted confocal microscope system (Leica, Germany) in transmission mode equipped with a 40× oil immersion objective having 1.25 numerical aperture and 0.1 mm working distance.

B. Calculation of the local temperature gradient dependence on the effective number of silver nanoparticles (plot in Fig. 4). We use the model that accounts for the influence of absorption, size and concentration of nanoparticles in order to understand the temperature gradient increase around a heating sphere of silver nanoparticles.^56,57 For a colloidal drop silver nanoparticle is considered as a heating center with an average radius r₀ and the filling factor F_s for a complete coverage of a drop with metallic nanoparticles (surface filling factor). The temperature gradient can be calculated as follows
where r₀ is the radius of silver nanoparticles, n is the number of silver nanoparticles per droplet S_i, S_c is the surface area of a single drop and R₀ is the radius of a drop (2.55 mm in our experiments). Two surface filling factors are considered, F_s¹ (small nanoparticles, tens of nm) and F_s² (large nanoparticles, hundreds of nm). The absorbed energy, E, can be estimated as
where A is the heating rate per unit volume per unit time and K is the thermal conductivity. Assuming that the surrounding medium is relatively unchanged,
where α₁ and α₂ are absorption coefficients for small and large nanoparticles. The laser power density values were calculated by dividing the applied actual laser power over the surface area of a drop of the colloidal solution. The laser beam width is around one micron.

C. Raman spectroscopy and microscopy. Raman and surface enhanced Raman scattering (SERS) spectra from the silver colloidal solutions and live cells were collected using a confocal Raman microscope (CRM200, WITec, Ulm, Germany) equipped with a piezo-scanner (P-500, Physik Instrumente, Karlsruhe, Germany) at a 785 nm excitation wavelength (Toptica Photonics AG, Graefelfing, Germany). A linearly polarized diode laser beam was focused through the LWD 20×, Nikon Fluor 60× water immersion and Nikon 100× oil immersion objectives with numerical apertures NA = 0.40, 1.00 and 1.25, respectively.

The laser power at the silver colloidal solution was kept no higher than 10 mW, and at the live cell it did not exceed 2 mW as measured using a Newport optical power meter 1830-C. The scattered light was filtered with an analyzer (further polarizer) through the confocal microscope pinhole.

The spectra were collected with a 300 gr mm⁻¹ grating blazed at 750 nm and recorded using a spectrograph (Acton, Princeton Instruments Inc., Trenton, NJ, USA) with a cooled CCD detector (PI-MAX, Princeton Instruments Inc., Trenton, NJ, USA) with an integration time 1 s of fifty accumulations. The signal to noise ratio was high enough to ensure the low value of the root mean square fluctuations averaged in time (typically below 5%). Basic alignment was carried out by the Raman spectrum of a silicon wafer with a characteristic Si line at 520 cm⁻¹ during integration times from 0.3 to 1 s.

The SERS measurements of live cells were conducted in vivo in a μ-dish (35 mm, Ibidi, Munich, Germany) equipped with a heating stage and an external temperature probe (Bioscience Tools, USA) to maintain 37 °C of the cells. The acquired Raman and SERS spectra were corrected for the baseline, background of the μ-dish substrate and the SiO₂ 485 cm⁻¹ band.

Estimation of the SERS enhancement factor

where EF is the average enhancement factor (averaged over all possible positions on the metallic surface and also from molecules randomly adsorbed on the surface as compared to the same number of non-adsorbed molecules), C_norm and C_SERS are concentrations of rhodamine 6G solutions for SERS and normal Raman measurements (i.e. number of molecules on the surface of a single nanoparticle and in bulk solution effectively excited by the laser beam); I_SERS and I_norm are corresponding intensities of the vibrational modes. The Raman peak of rhodamine at 1365 cm⁻¹ was taken for the enhancement factor estimation.

The molecular density of rhodamine 6G adsorbed on the silver nanoparticle surface depends on the average diameter of the particle. For example, let us assume a silver colloidal solution at 1.4 mmol L⁻¹ concentration in a volume 1.2 mL incubated with 10⁻⁸ mol L⁻¹ rhodamine 6G solution.

ν_Ag = C_AgV,

where ν_Ag is the mole number of silver, C_Ag is the concentration of silver nanoparticles (from UV-vis absorbance as estimated above) and V is the volume. ν_Ag = 1.68 10⁻⁶ mol.
where n_Ag is the molecular density of silver, N_Ag is the number of silver atoms in the volume, N_A is Avogadro's number (6.02 × 10²³ mol⁻¹).

The total average density of silver is 8.42 × 10²⁰ L⁻¹ and of rhodamine 6G molecules is 6.02 × 10¹⁵ L⁻¹. Assuming a covalent radius of silver of 145 ± 5 × 10⁻¹² m and an average nanoparticle diameter of 30 × 10⁻⁹ m, the volume of a single nanoparticle is 1.41 × 10⁻²³ m³ and of an atom is 1.27 × 10⁻²⁹ m³, so that one single silver nanoparticle consists of 1 × 10⁶ silver atoms. The silver nanoparticle density is 7 × 10¹⁴ L⁻¹ and when it is divided by dye density, we have about 7 rhodamine 6G molecules adsorbed on one single silver nanoparticle. For bare silver–boron nanoparticles with diameters 22 nm and 100 nm, there are about 3 and 301 rhodamine 6G molecules per single silver nanoparticle, respectively. For silver–PEG nanoparticles with diameters 22 nm and 30 nm (average concentration is about 2 × 10⁻³ mol L⁻¹) there are about one/two and four rhodamine 6G molecules per single nanoparticle, respectively.

Theoretical modelling of the far-field scattering pattern and the total power of heat density dissipation (P_V) by a Comsol Multiphysics software tool

(a) The scattering of a plane wave of light off of a silver nanosphere. In this calculation the far-field scattering pattern of a plane wave of light with 785 nm wavelength is computed over a silver nanosphere of about 22 nm average diameter. Due to the symmetry of the nanosphere only one quarter of it is modelled. The wave vector, k, and the electric field vector, E, are perpendicular to each other as indicated by arrows in Fig. 5B. The E vector is also perpendicular to the surface of the silver nanosphere.

A region of water around the sphere is also modelled. A perfectly matched layer (PML) domain is outside the water domain and acts as an absorber of the scattered field. The PML is not within the reactive near field of the scatterer and it is a half wavelength away. The far-field radiation pattern is plotted in Fig. 5A and shows an electric field, E-plane (black), and a magnetic field, H-plane (green).

For the scattered field, the plane wave travels in the positive x direction, with the electric field (E-field) polarized along the z-axis. The default boundary condition is a perfect electric conductor, which applies to all exterior boundaries including the boundaries perpendicular to the background E-field polarization.

(b) The total power of heat density dissipation (P_V, W m⁻³). This model defines the interaction of the incident electromagnetic plane wave of the wavelength 7.85 × 10⁻⁷ m with the silver sphere of 2.2 × 10⁻⁸ m radius by using specific domain properties described by the classical Maxwell's laws. It also uses the perfectly matched layer that has the equal size of the thickness of a water layer around the modelled silver sphere (3.92 × 10⁻⁷ m).

The electric field strength (V m⁻¹) with xyz spatial components has a shape function of quadratic curl E derived from the classical Maxwell's law as

where H is the magnetic field strength (T).

In the frequency domain of electromagnetic wave equation two interpolation functions are used. The first one includes the real part of permittivity (ε real) and the second one uses its imaginary part (ε imaginary). The table below shows the calculated permittivity values of silver in the range from 397 nm to 705 nm that are used for our model.

Acknowledgements

We thank Rona Pitschke (MPI Colloids) for electron microscopy analysis. We appreciate the allowance to use equipment of the confocal Raman microscope from Admir Masic (MPI Biomaterials) and high voltage electroporator from Ronald Knorr and Rumiana Dimova (MPI Theory). The help with the cell culture assistance by Christine Pilz (MPI Biomaterials) is greatly appreciated. The stipend from the Max-Planck society is acknowledged.

Notes and references

1. Y. Li, C. Jing, L. Zhang and Y.-T. Long, Chem. Soc. Rev., 2012, 41, 632.
2. X. Gong, Y. Bao, C. Qiu and C. Jiang, Chem. Commun., 2012, 48, 7003.
3. J. Kneipp, H. Kneipp, B. Wittig and K. Kneipp, Nanomedicine, 2010, 6, 214.
4. M. Kerker, O. Siiman, L. A. Bumm and D. S. Wang, Appl. Opt., 1980, 19, 3253.
5. R. L. Garrell, K. D. Shaw and S. Krimm, Surf. Sci., 1983, 124, 613.
6. S. Nie and S. R. Emory, Science, 1997, 275, 1102.
7. K. Kneipp, Y. Wang, H. Kneipp, L. T. Perelman, I. Itzkan, R. R. Dasari and M. S. Feld, Phys. Rev. Lett., 1997, 78, 1667.
8. S. R. Emory and S. Nie, Anal. Chem., 1997, 69, 2631.
9. P. B. Johnson and R. W. Christy, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1972, 6, 4370.
10. J. P. Camden, J. A. Dieringer, Y. Wang, D. J. Masiello, L. D. Marks, G. C. Schatz and R. P. Van Duyne, J. Am. Chem. Soc., 2008, 130, 12616.
11. K. Kneipp, Phys. Today, 2007, 60, 40.
12. S. Y. Lee, L. Hung, G. S. Lang, J. E. Cornett, I. D. Mayergoyz and O. Rabin, ACS Nano, 2010, 4, 5763.
13. H. Wei and H. Xu, Nanoscale, 2013, 5, 10794.
14. K. D. Alexander, K. Skinner, S. P. Zhang, H. Wei and R. Lopez, Nano Lett., 2010, 10, 4488.
15. X. J. Liu, L. A. Zhao, H. Shen, H. X. Xu and L. H. Lu, Talanta, 2011, 83, 1023.
16. M. P. Cecchini, V. A. Turek, J. Paget, A. A. Kornyshev and J. B. Edel, Nat. Mater., 2012, 12, 165.
17. D. P. Fromm, A. Sundaramurthy, A. Kinkhabwala, P. J. Schuck, G. S. Kino and W. E. Moerner, J. Chem. Phys., 2006, 124, 061101.
18. W. E. Smith, Chem. Soc. Rev., 2008, 37, 955.
19. A. Mills, G. Hill, M. Stewart, W. E. Smith, S. Hodgen, P. J. Halfpenny, K. Faulds and P. Robertson, Appl. Spectrosc., 2004, 58, 922.
20. P. L. Stiles, J. A. Dieringer, N. C. Shah and R. P. Van Duyne, Annu. Rev. Anal. Chem., 2008, 1, 601.
21. M. J. Banholzer, J. E. Millstone, L. Qin and C. A. Mirkin, Chem. Soc. Rev., 2008, 37, 885.
22. B.-B. Xu, Z.-C. Ma, H. Wang and X.-Q. Liu, et al. , Electrophoresis, 2011, 32, 3378.
23. W. B. Lacy, J. M. Williams, L. A. Wenzler, T. P. Beebe and J. M. Harris, Anal. Chem., 1996, 68, 1003.
24. E. G. Gwinn, O. Neill, A. J. Guerrero, D. Bouwmeester and D. K. Fygenson, Adv. Mater., 2008, 20, 279.
25. S. Ashraf, A. Z. Abbasi, C. Pfeiffer, S. Z. Hussain, Z. M. Khalid, P. R. Gil, W. J. Parak and I. Hussain, Colloids Surf., B, 2013, 102, 511.
26. J. Ando, K. Fujita, N. I. Smith and S. Kawata, Nano Lett., 2011, 11, 5344.
27. A. Shkilnyy, M. Soucé, P. Dubois, F. Warmont, M. L. Saboungi and I. Chourpa, Analyst, 2009, 134, 1868.
28. D. Drescher and J. Kneipp, Chem. Soc. Rev., 2012, 41, 5780.
29. H. Lokstein, A. Betke, M. Krikunova, K. Teuchner and B. Voigt, Photosynth. Res., 2012, 111, 227.
30. J. A. Creighton, C. G. Blatchford and M. G. Albrecht, J. Chem. Soc., Faraday Trans., 1979, 75, 790.
31. S. Schneider, P. Halbig, H. Graen and U. Nickel, Photochem. Photobiol., 1994, 60, 605.
32. J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55.
33. D. L. Van Hyning and C. F. Zukoski, Langmuir, 1998, 14, 7034.
34. K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668.
35. C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley and Sons Inc., Weinheim, Germany, 1983, pp. 7, 31, 33–37, 73, 109, 115, 119.
36. U. Kreibig and M. Volmer, Optical Properties of Metal Clusters, Springer, 1995, p. 29, 30, 37.
37. H. L. Abd El-Mohdy, J. Polym. Res., 2013, 20, 177.
38. Z. H. Mbhele, M. G. Salemane, C. G. van Sittert, J. M. Nedeljkovic, V. Djokovic and A. S. Luyt, Chem. Mater., 2003, 15, 5019.
39. B. Pettinger, K. Krischer and G. Ertl, Chem. Phys. Lett., 1988, 151, 151.
40. F. R. Dollish, W. G. Fateley and F. F. Bentley, Characteristic Raman Frequencies of Organic Compounds, John Wiley & Sons, New York, 1974, p. 266.
41. J. Tang and A. C. Albrecht, Raman Spectroscopy, ed. H. A. Szymanski, Plenum Press, New York, 1970, vol. 2, pp. 33–68.
42. A. G. Skirtach, C. Dejugnat, D. Braun, A. S. Susha, A. L. Rogach, W. J. Parak, H. Moehwald and G. B. Sukhorukov, Nano Lett., 2005, 5, 1371.
43. J. C. Weaver, J. Cell. Biochem., 1993, 51, 426.
44. A. Saha, S. Palmal and N. R. Jana, Nanoscale, 2012, 4, 6649.
45. M. G. Shim, B. C. Wilson, E. Marple and M. Wach, Appl. Spectrosc., 1999, 53, 619.
46. Z. Movasaghi, S. Rehman and I. U. Rehman, Appl. Spectrosc. Rev., 2007, 42, 493.
47. B. P. Gaber and W. L. Peticolas, Biochim. Biophys. Acta, 1977, 465, 260.
48. M. A. Ochsenkuhn, P. R. T. Jess, H. Stoquert, K. Dholakia and C. J. Campbell, ACS Nano, 2009, 3, 3613.
49. K. Kneipp, K. H. Kneipp and J. Kneipp, Acc. Chem. Res., 2006, 39, 443.
50. C. Matthaus, T. Chernenko, J. A. Newmark, C. M. Warner and M. Diem, Biophys. J., 2007, 93, 668.
51. D. Naumann, Proc. SPIE, 1998, 3257, 245.
52. J. W. Chan, D. S. Taylor, T. Zwerdling, S. T. Lane, K. Ihara and T. Huser, J. Biophys., 2006, 90, 648.
53. M. F. Alexeyev, S. P. Ledoux and G. L. Wilson, Clin. Sci., 2004, 107, 355.
54. Y.-S. Huang, T. Karashima, M. Yamamoto and H. Hamaguchi, Biochemistry, 2005, 44, 10009.
55. P. C. Lee and D. Meisel, J. Phys. Chem., 1982, 86, 3391.
56. P. Candeloro, L. Tirinato, N. Malara, A. Fregola, E. Casals and V. Puntes, et al. , Analyst, 2011, 136, 4402.
57. H. Goldenberg and C. J. Tranter, Br. J. Appl. Phys., 1952, 3, 296.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4nr00594e

---