Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A DFT study of oxygen dissociation on platinum based nanoparticles†
Paul C.
Jennings
a,
Hristiyan A.
Aleksandrov
bc,
Konstantin M.
Neyman
bd and
Roy L.
Johnston
*e
aSchool of Chemical Engineering, University of Birmingham, Edgbaston, Birmingham, UK
bDepartament de Química Física & IQTCUB, Universitat de Barcelona, Spain
cFaculty of Chemistry and Pharmacy, University of Sofia, Sofia, Bulgaria
dInstitució Catalana de Recerca i Estudis Avançats (ICREA), Barcelona, Spain
eSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham, UK. E-mail: r.l.johnston@bham.ac.uk; Fax: +44 (0)121 414 4403; Tel: +44 (0) 121 414 7477
First published on 15th November 2013
Abstract
Density functional theory calculations are performed on 38 and 79 metal atom truncated octahedron clusters to study oxygen dissociation as a model for the initial stage of the oxygen reduction reaction. Pure platinum and alloyed platinum–titanium core–shell systems are investigated. It is found that barrierless oxygen dissociation occurs on the (111) facet of the pure platinum clusters. A barrier of ∼0.3 eV is observed on the (100) facet. For the alloyed cluster, dissociation barriers are found on both facets, typically ∼0.6 eV. The differences between the two systems are attributed to the ability of oxygen to distort the (111) surface of the pure platinum clusters. We show that flexibility of the platinum shell is crucial in promotion of fast oxygen dissociation. However, the titanium core stabilises the platinum shell upon alloying, resulting in a less easily distortable surface. Therefore, whilst an alloyed platinum-titanium electrocatalyst has certain advantages over the pure platinum electrocatalyst, we suggest alloying with a more weakly interacting metal will be beneficial for facilitating oxygen dissociation.
1 Introduction
The behaviour of oxygen (O) on platinum (Pt) surfaces has been studied extensively,1–8 although much of the current work is focused on bulk systems, some studies have been performed on smaller cluster systems.9–12 The interest in Pt–O systems is due in part to the relevance of Pt based catalysts in many industrial applications. A good example, is the extensive use of Pt to catalyse the oxygen reduction reaction (ORR) in fuel cells.13–16 However, to develop and successfully market polymer electrolyte fuel cells (PEFCs), it is necessary to reduce the Pt catalyst loading of both anode and cathode electrodes, together with the associated cost, without compromising the performance.The high intrinsic cost of Pt (£843.23 per ounce as of 10/07/13) forms a barrier to the widespread commercialisation of PEFCs. A ten-fold decrease in Pt loading in PEFC stacks is required to make PEFCs a commercially viable option. There are several ways to do this: lower the Pt loading by using a Pt alloy (either binary or ternary);17,18 replace Pt with a non-precious electrocatalyst (inorganic or organic);19,20 maximise the effective surface area of the Pt catalyst i.e. the surface contact between the electrode catalyst layers, the carbonaceous electronic conductor-gas diffusion layer, the polymer electrolyte membrane and the reactants (hydrogen and oxygen).21,22
Another serious problem with PEFCs is that the hydrogen feed usually contains significant amounts of carbon monoxide (CO), which poisons the Pt electrocatalyst. Alloying Pt to reduce loading and improve catalytic characteristics such as performance, durability and reactivity is a promising approach. We previously reported the results of theoretical calculations which suggested that alloying Pt with titanium (Ti), a much cheaper transition metal (£0.28 per ounce as of 10/07/13), to form Ti@Pt core–shell clusters (Ti – core, Pt – shell), results in weaker binding of hydroxyl (OH) and CO with reduced Pt loading.23 Weaker binding of OH can lead to improvements in ORR kinetics, while weakening of CO binding lessens poisoning effects. Weaker adsorption was attributed to changes in the electronic structure attained through alloying; specifically, changes in the d-band centre.24 At the same time the catalyst has to facilitate the initial stage of ORR, namely O2 dissociation.
In our present work, oxygen dissociation is studied on pure Pt clusters as well as core–shell Ti@Pt clusters. Dissociation on the (111) slab model is also included, as this can represent the process on (111) terraces of larger particles. Initially focusing on 38 atom clusters, barrier-free dissociation is observed for the Pt38 cluster on the (111) facet. However, notable dissociation barriers are observed for the (100) facet as well as both (111) and (100) facets on the Pt32Ti6 cluster. This behaviour is explained through an in depth study of cluster stability and is further investigated for 79 atom clusters.
2 Methodology
Calculations are performed using the Vienna Ab initio Simulation Package (VASP) 5.2.25–28 The 5d9 6s1 of Pt, 3d3 4s1 of Ti and 2s2 2p4 of O are treated as valence electrons, while the ionic cores are represented by the projected augmented wave (PAW) method.29,30 Electronic exchange and correlation are described using the generalised gradient approximation (GGA) using the Perdew Wang 91 (PW91) functional.31,32 The Methfessel-Paxton smearing method is used with a width of 0.1 eV (extrapolated for computing final energies to zero smearing) and an energy cutoff of 415 eV is employed. DFT-D calculations were also performed on a number of test cases, although the inclusion of van der Waals forces through the empirical treatment of Grimme results in little change and so was not considered in the following results.The bulk systems were modelled by five layers of repeated 3 × 3 (111) slabs, allowing the top two layers of the Pt(111) slab to relax fully while fixing the bottom 3 layers. A 5 × 5 × 1 k point mesh was used to sample the first Brillouin zone. Approximately 10 Å of vacuum was included between neighbouring systems. For the cluster systems, 38 and 79 atom clusters were considered, these are magic numbers leading to complete Truncated Octahedral (TO) structures. The clusters are placed in the centre of a large enough supercell to ensure sufficient separation (∼10 Å) between periodic images, the Γ point is used to sample the Brillouin zone. All atoms are relaxed according to the calculated atomic forces, with convergence criteria for total energies 1.0 × 10−4 eV and forces required to be less than 0.02 eV Å−1.
In order to assess the (atomic or molecular) oxygen adsorption strength to the Pt surface, the binding energy (Eb) is calculated, as defined in eqn (1).
| Eb = EAB − (EA + EB) | (1) |
E AB is the energy of the cluster with oxygen adsorbed, EA is the energy of the relaxed cluster and EB is the energy of the free oxygen atom or molecule, negative Eb values imply favourable binding. The interaction energy (Eint) is defined in eqn (2).
| Eint = EAB − (E*A + E*B) | (2) |
The single point energies of species distorted upon adsorption are denoted by *, again negative values imply favourable interactions. Distortion energies can be calculated using eqn (3) for Ptn−mTim (where n = 38, 79 and m = 0, 6, 19) and eqn (4) for oxygen distortions.
| ΔE(Ptn−mTim) = E(Ptn−mTim) − E(Ptn−mTim)* | (3) |
| ΔE(O2) = E(O2) − E(O2)* | (4) |
Although specific distortions, brought about by adsorption of oxygen, are discussed in detail, as a more general measure root mean squared displacements (RMSD) of atoms are calculated. RMSD is calculated as defined in eqn (5).
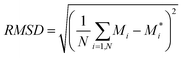 | (5) |
Dissociation pathways were investigated using the VASP Transition State Tools (VTST) implementation by the Henkelman Group, first generating an approximate pathway using the Nudged Elastic Band (NEB) method,33 with further refinements achieved using the Dimer method.34 Bader charge analysis35 was performed using the Bader code36 also from the Henkelman Group.
3 Results and discussion
3.1 Slab model
Large metal nanoparticles are often approximated in computational studies of catalysts by infinite slab models of (111) surface.37 Hence, we start our study investigating O2 dissociation on slabs. There are four non-symmetry equivalent sites on the surface of the infinite (111) slab, the atop, bridge, fcc and hcp sites. It is found that the bridge and fcc sites are energetically competitive, the Eb for O2 at the bridge site being −0.87 eV, while it is −0.86 eV for the fcc position. This is in good agreement with experimental and theoretical studies, which have found both sites favourable for O2 chemisorption.38–42 The hcp site is 0.1 eV higher in energy than the fcc site (at −0.76 eV), while migration occurs when locally minimising O2 at the atop position, resulting in O2 bonding to the more favourable fcc site.For the Pt(111) system, the oxygen molecule is initially adsorbed on a three-fold fcc hollow site, before dissociating resulting in each O atom being bound to fcc hollow sites. The dissociation barrier on the Pt(111) slab is found to be 0.45 eV, in agreement with other calculations, which find a barrier of between 0.4 and 0.6 eV, presented in the literature1,5,43–45 as well as experimental studies.46 An O–O distance of 2.10 Å is found at the transition state (TS) structure, this compares to an O–O distance of 1.40 Å for the initial state (IS) and 1.24 Å in the gas phase O2. Significant elongation of the O–O bond suggests a late transition state. The average Pt–Pt bond lengths in the fcc sites below the adsorbate for the IS, TS and final state (FS) structures are close 2.94, 2.98 and 2.97 Å, respectively. However, the average Pt–Pt bond lengths for the pure Pt(111) surface is found to be 2.82 Å for the fcc hollow. This shows slight elongation of the Pt–Pt bond length when O2 is adsorbed, by ≤0.15 Å. This is reflected in the relatively low RMSD values of 0.03, 0.05 and 0.05 Å, respectively, for IS, TS and FS structures. It is expected that a shortening of the Pt–O bond will be observed, corresponding to increased interactions with the Pt surface as O2 dissociates. Indeed, average Pt–O bond lengths are 2.14, 1.95 and 2.05 Å for the IS, TS and FS, respectively.
The distortion energy of the bulk slab (ΔE(Ptsurf)) is found to be 0.17, 0.25 and 0.39 eV for the IS, TS and FS, respectively. Greater distortion of the surface is generally expected as the system progresses from the IS to the FS due to greater Pt–O interactions and a reduction in O–O interactions. ΔE(O2) values calculated for the IS, TS and FS are 0.64, 5.72 and 6.34 eV, respectively. The average charge on the Pt atoms directly below O2 is +0.18, +0.34 and +0.29 |e| for the IS, TS and FS. While overall average charges on O2 are −0.34, −0.57 and −0.76 |e| for the IS, TS and FS, respectively. For all states, electron density is withdrawn from Pt by O, with increased charge transfer as the system progresses form the IS to the FS. There is greater Pt charge transfer when comparing the TS to the FS, this is due to O2 being bonded to one 3-fold fcc hollow site at the TS and two at the FS.
We also considered PtTi (111) alloyed system, with a model (which has been studied before47) where the second layer of the slab was set as Ti and the top three layers (Pt–Ti–Pt) were allowed to fully relax. During the geometry optimization, however it shows instability and surface and subsurface layers can no longer be identified as (111). In order to study a more realistic model of the PtTi(111) alloyed system, we considered Ti@Pt nanoparticles, with Ti cores, where the effect of edges, larger flexibility, etc. can be taken into account. We studied two model clusters consisting of 38 and 79 metal atoms.
3.2 38 Atom clusters
 | ||
| Fig. 1 Top view of the surface (dark grey) and subsurface (light grey) metal atoms at (111) facet sites on the 38 (left) and 79 (right) atom TO clusters. | ||
| Site | Position | Pt38–O | Pt38–O2 | Pt32Ti6–O | Pt32Ti6–O2 |
|---|---|---|---|---|---|
| a Adsorbate migration to position 4. b Adsorbate migration to position 6. c Adsorbate migration to position 5. | |||||
| 1 | Top | −4.17 | −0.51 | —a | —b |
| 2 | Top | −4.48 | −0.77 | −4.16 | −0.59 |
| 3 | bridge | —b | −1.66 | —a | −0.57 |
| 4 | bridge | −4.72 | −1.67 | −4.39 | −1.02 |
| 5 | bridge | −5.12 | −2.01 | −4.78 | −1.75 |
| 6 | hcp | −5.21 | −1.84 | —c | −0.73 |
| 7 | fcc | −5.12 | −1.80 | —a | −0.37 |
| 8 | 4-fold | −4.79 | —c | −4.25 | —c |
| hollow | |||||
For the pure Pt38 cluster, three-fold hollow positions 6 and 7 on the (111) facets, as well as the edge bridge position 5 between the (111) and (100) facets are the most stable for adsorption of atomic oxygen, −5.21, −5.12 and −5.12 eV, respectively. Interestingly, on Pt32Ti6, three-fold hollow positions are no longer locally stable and move to bridge sites (4 and 5). Position 5 is the most stable site, with an Eb value of −4.78 eV, a decrease of 0.34 eV with respect to the same position on the pure Pt38 cluster.
For O2 adsorption, position 5, the edge-bridge site between (111) and (100) facets is most stable on both Pt38 and Pt32Ti6, Eb values are −2.01 and −1.75 eV, respectively. Hollow positions 6 and 7 are next in stability, −1.84 and −1.80 eV, on Pt38, while on Pt32Ti6 other bridge positions are more favourable. Edge-bridge sites are also found to be positions of favourable O2 bonding in other studies. Step sites on Pt(111) surfaces have been reported to result in particularly stable oxygen bonding.48,49 Furthermore, studies of Pt TO clusters has revealed favourable bonding at the edge-bridge sites.50 Calculations on the Pt(100) surface have favoured bonding to bridge sites, in line with the results presented here.51 As with the previous OH and CO adsorption studies,23,24 weaker bonding for O2 and O is calculated for the bimetallic Ti@Pt cluster when compared with the pure Pt cluster.
It is expected that oxygen dissociation will occur preferentially at sites with higher Eb values, where oxygen is most likely to adsorb to the surface of the cluster. Due to the small size of the cluster, it would be relatively easy for molecular oxygen to dissociate and migrate to any of the other seven sites, or an equivalent site in a different location on the surface. It is therefore assumed that dissociation will also likely result in atomic oxygen being adsorbed on the most energetically favourable sites. The energetic ordering of adsorption for molecular oxygen was similar to that of atomic oxygen, making the proposed dissociation pathways relatively straightforward.
The most stable sites, the edge site 5, as well as hollow sites 6 and 7 are studied. For each pathway, O2 dissociation proceeds from one site to an adjacent position at an equivalent site (e.g. O2 bound to position 5 dissociates to atomic oxygen bound to separate 5 sites). Data for each dissociation pathway is presented in Table 2. In each case, distortion energies of the cluster and O2 at each step of the dissociation pathway are presented.
| ΔE(Ptn−mTim) | RMSD | ΔE(Ptn−mTim)/RMSD | ΔE(O2) | E int | E b | ΔE≠ | |
|---|---|---|---|---|---|---|---|
| a Values for ΔE(Ptsurf). | |||||||
| Initial state | |||||||
| Pt38-5 | 0.42 | 0.09 | 4.67 | 0.58 | −3.02 | −2.01 | |
| Pt32Ti6-5 | 0.37 | 0.07 | 5.29 | 0.49 | −2.62 | −1.76 | |
| Pt38-6 | 0.45 | 0.19 | 2.37 | 1.05 | −3.34 | −1.84 | |
| Pt32Ti6-6 | 0.12 | 0.03 | 4.00 | 0.73 | −1.59 | −0.74 | |
| Pt38-7 | 0.53 | 0.19 | 2.79 | 1.36 | −3.68 | −1.79 | |
| Pt32Ti6-7 | 0.34 | 0.06 | 5.67 | 0.69 | −1.40 | −0.38 | |
| Pt(111) Slab | 0.17a | 0.03 | 5.67a | 0.64 | −1.67 | −0.86 | |
| Transition state | |||||||
| Pt38-5 | 0.39 | 0.08 | 4.88 | 4.64 | −6.72 | −1.68 | 0.32 |
| Pt32Ti6-5 | 0.62 | 0.10 | 6.20 | 4.89 | −6.62 | −1.11 | 0.62 |
| Pt38-6 | 0.48 | 0.19 | 2.53 | 2.75 | −5.03 | −1.80 | 0.04 |
| Pt32Ti6-6 | 0.80 | 0.11 | 7.27 | 2.69 | −3.90 | −0.41 | 0.34 |
| Pt38-7 | 0.54 | 0.19 | 2.84 | 1.83 | −4.16 | −1.79 | 0.00 |
| Pt32Ti6-7 | 0.44 | 0.07 | 6.29 | 5.29 | −5.50 | 0.24 | 0.62 |
| Pt(111) Slab | 0.25a | 0.05 | 5.00a | 5.72 | −6.41 | −0.43 | 0.45 |
| Final state | |||||||
| Pt38-5 | 0.58 | 0.10 | 5.80 | 6.27 | −9.87 | −3.02 | |
| Pt32Ti6-5 | 0.35 | 0.06 | 5.83 | 6.36 | −9.06 | −2.36 | |
| Pt38-6 | 0.65 | 0.11 | 5.91 | 6.29 | −10.32 | −3.39 | |
| Pt32Ti6-6 | 0.38 | 0.06 | 6.33 | 6.79 | −10.13 | −2.95 | |
| Pt38-7 | 0.92 | 0.22 | 4.18 | 6.28 | −10.07 | −2.87 | |
| Pt32Ti6-7 | 0.86 | 0.10 | 8.60 | 6.79 | −10.17 | −2.51 | |
| Pt(111) Slab | 0.39a | 0.05 | 7.80a | 6.34 | −9.12 | −2.39 | |
Distortion energies in the TS structures show, in general, that there is a greater distortion energy associated with the Pt32Ti6 clusters. The one exception is where distortion occurs on site 7 of the Pt32Ti6 cluster, due to different types of TS structures. In this case, a “straight” dissociation pathway is located over the central atop position (site 1) of the Pt32Ti6 cluster. For dissociation on site 6, however, a more curved pathway is preferred, avoiding the atop position and instead progressing over the hollow sites of the alloyed cluster. However, the fact that the distortion energies for the Pt32Ti6 clusters are significantly higher than for the Pt38 clusters suggests that the presence of the Ti core in the alloyed cluster stabilises (makes more rigid) the Pt shell. Nevertheless, the alloyed cluster is still distorted by the adsorbate. In all cases, the cluster distortion energies are greater than that of the slab, suggesting that the slab is significantly harder to distort than both clusters at the TS leading to little change in the slab structure. Similar to IS, data for the FS show the distortion energies associated with the Pt38 clusters are higher than those for the alloyed Pt32Ti6 clusters in all cases. Once again, there is generally greater distortion energies associated with the clusters than the slab. This was found to be the case also for positions 5 and 6.
For the pure Pt clusters, the IS and TS have similar distortion energies, the FS is found to have slightly greater distortion energies. This is consistent with atomic oxygen having a greater effect on the Pt surface than the single O2 molecule. For the Pt32Ti6 clusters, it is found that the TS generally has greater distortion energies than the IS or FS. The exception to this is dissociation occurring at position 7, where a relatively small distortion energy is found at the TS compared to a relatively high energy at the FS. In summary, this energetic ordering suggests that at sites 5 and 6 greater distortions occur at the TS, not the FS as with the pure Pt clusters.
RMSD of the metal atoms are also listed in Table 2, it is important to note that O2 distortions are not accounted for. These indicate the geometric distortion of the metal particle due to adsorption of the O2 molecule. Data on distortions to specific facets of the cluster are described later. For RMSD analysis, the geometry of the distorted cluster, with O2 removed, is compared to the geometry of the relaxed gas phase cluster, with higher values suggesting greater distortion. For the Pt38 clusters, there is a larger RMSD associated with O2 adsorption on the (111) facet, compared to the (100) facet, an average of 0.19 and 0.09 Å, respectively. For the Pt32Ti6 clusters, there is less difference between O2 adsorption on the (111) and (100) facets, 0.03–0.11 Å vs. 0.06–0.10 Å. Furthermore, it is found that smaller RMSD values for the bimetallic clusters can lead to greater distortion energies compared to the pure Pt clusters. This shows that even though there is less overall distortion, there is a greater energetic cost associated with it for the Pt32Ti6 clusters. This is expected, as the Pt2 dimer binding energy is found to be −4.11 eV, which is destabilised over both the PtTi and Ti2 = dimers, −6.08 and −5.34 eV, respectively. Comparing to the values calculated for the bulk system (RMSD < 0.05), there are significantly greater RMSD values associated with the Pt38 clusters and marginally greater values for the Pt32Ti6 cluster.
ΔE(Ptn−mTim)/RMSD has been calculated, showing the energy needed to achieve RMSD of 1.00 Å. An average of 1.71, 3.17 and 1.63 eV Å−1 more energy is required to distort the Pt32Ti6 cluster, than the Pt38 cluster at the IS, TS and FS, respectively. This demonstrates the significant energy barriers that need to be overcome in order to distort the Pt32Ti6 cluster compared to the Pt38 cluster.
A high dissociation barrier (ΔE≠) is found for site 5, on the (100) facet of the Pt32Ti6 cluster, 0.62 eV, this being approximately twice that of the pure Pt38 cluster, 0.32 eV (Table 2). When considering the (111) facet of the Pt32Ti6 cluster, the dissociation barriers for sites 7 and 5 are equal, 0.62 eV, while for site 6 the barrier, 0.34 eV, is about half that of the other two sites. The Pt38 cluster is found to exhibit barrier-free dissociation on the (111) facet, this dramatically differs to the 0.45 eV barrier found on the Pt(111) slab. On the (100) facet of the Pt38 cluster (site 5), comparable dissociation barriers are found to site 6 on the Pt32Ti6 cluster.
| O–O | Pt–O | Pt–Pt | Pt-Xcentre | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | IS | TS | FS | IS | TS | FS | |
| Pt38-5 | 1.39 | 1.92 | 2.89 | 1.95 | 1.82 | 1.95 | 3.24[2] | 3.20[2] | 2.94[2] | — | — | — |
| Pt32Ti6-5 | 1.37 | 1.96 | 3.02 | 1.98 | 1.83 | 1.98 | 3.26[2] | 3.28[2] | 2.93[2] | — | — | — |
| Pt38-6 | 1.45 | 1.66 | 3.32 | 2.07 | 2.00 | 2.07 | 2.64[2] | 2.65[2] | 2.69[2] | 3.27 | 3.26 | 2.95 |
| 3.43[3] | 3.44[3] | 2.93[3] | ||||||||||
| Pt32Ti6-6 | 1.41 | 1.66 | 5.43 | 2.21 | 2.13 | 1.98 | 2.92[2] | 3.02[2] | 2.94[2] | 2.19 | 2.72 | 2.08 |
| 2.74[3] | 3.04[3] | |||||||||||
| Pt38-7 | 1.49 | 1.55 | 3.42 | 2.05 | 2.02 | 1.94 | 2.68[1] | 2.69[1] | 2.95[1] | 3.27 | 3.26 | 3.35 |
| 3.54[3] | 3.55[3] | 2.98[3] | ||||||||||
| Pt32Ti6-7 | 1.40 | 2.03 | 5.47 | 2.19 | 1.99 | 1.95 | 2.78[1] | 2.93[1] | 3.06[1] | 2.12 | 2.23 | 2.11 |
| 2.78[3] | 2.79[3] | |||||||||||
Once oxygen is adsorbed on the (100) facet of the Pt38 cluster, significant elongation of bond type 2 by up to 0.54 Å is observed, although there is less overall distortion of the cluster geometry. Following oxygen adsorption on the (100) facet, the average distortion of the Pt–Pt bonds calculated from the data in Table 3 is 0.43, 0.53 and 0.78 Å for sites 5, 6 and 7 on the Pt38 cluster, respectively. When O2 is adsorbed on the (111) facet, there is a slight elongation of bond type 1 by up to 0.29 Å, although not as much as for bond type 3 by up to 0.85 Å, which is significantly elongated. There is generally a slight contraction in the bond length of type 2 by up to 0.06 Å. This suggests that the majority of the distortion that occurs when O2 is adsorbed on the (111) facet of the Pt38 cluster is due to changes in the bond length of type 3, bonding to the central (111) atom. For the Pt32Ti6 cluster significant elongation is observed of bond type 2 by up to 0.57 Å, when O2 is adsorbed on site 5 of the (100) facet. However, there is considerably less distortion of the other bond types when O2 is adsorbed on the (111) facet, the maximum distortion observed being ≤0.37 Å.
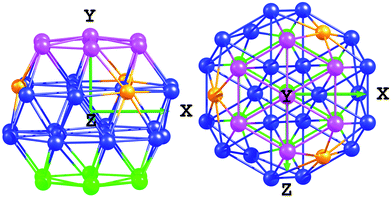
Pt–Xcentre values are only calculated for dissociations on the (111) facet. From the values presented in Table 4, there are few well-defined trends when comparing initial, transition and final states. However, the point of these values is to demonstrate the differences between the Pt38 and Pt32Ti6 clusters. Pt–Xcentre was calculated by defining a plane through the cluster, parallel to the (111) facet on which oxygen is adsorbed and then measuring Pt distortions along the y-axis from that plane. The plane passes through the central atoms of the (111) surfaces surrounding the facet on which the O2 is adsorbed, as shown in Fig. 3.
Following O2 adsorption, Pt–Xcentre distances are presented in Table 4. This reveals small distortions, ≤ 0.14 and ≤ 0.08 Å for the Pt38 and Pt32Ti6 clusters, respectively, measuring distances from the plane to the bottom of the cluster. More significant changes are seen at the top of the cluster, ≤0.91 and ≤0.42 Å for the Pt38 an Pt32Ti6 clusters, respectively. Furthermore, it is found that there is considerably stronger distortion of the Pt38 cluster, with the atop central (111) atom being pulled out of the plane. The relationship between Pt–Xcentre and distortion barriers can be seen in Fig. S1 and S2† for the IS and TS.
| IS | TS | FS | ||||
|---|---|---|---|---|---|---|
| Top | Bottom | Top | Bottom | Top | Bottom | |
| Pt38-6 | 0.83 | 0.13 | 0.82 | 0.14 | 0.51 | 0.14 |
| Pt32Ti6-6 | −0.12 | 0.07 | 0.42 | 0.04 | −0.23 | 0.08 |
| Pt38-7 | 0.83 | 0.00 | 0.82 | 0.00 | 0.91 | 0.00 |
| Pt32Ti6-7 | −0.18 | 0.03 | −0.07 | 0.04 | −0.19 | 0.02 |
| Pt chargesa | Ti chargesb | O charges | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | IS | TS | FS | |
| a Pt atoms interacting directly with O atoms. b Ti atoms interacting directly with O bound Pt atoms. | |||||||||
| Pt38-5 | 0.31 | 0.46 | 0.45 | — | — | — | −0.33 | −0.51 | −0.74 |
| Pt32Ti6-5 | 0.04 | 0.22 | 0.21 | 1.97 | 1.97 | 1.88 | −0.34 | −0.55 | −0.75 |
| Pt38-6 | 0.22 | 0.29 | 0.28 | — | — | — | −0.39 | −0.47 | −0.76 |
| Pt32Ti6-6 | −0.22 | 0.02 | 0.11 | 1.95 | 1.87 | 1.94 | −0.38 | −0.50 | −0.79 |
| Pt38-7 | 0.25 | 0.26 | 0.33 | — | — | — | −0.43 | −0.45 | −0.74 |
| Pt32Ti6-7 | −0.23 | −0.10 | 0.09 | 1.95 | 1.93 | 1.94 | −0.37 | −0.58 | −0.76 |
When O2 is adsorbed on the surface of the pure Pt38 cluster, the Pt atoms on which the oxygen is adsorbed have a positive charge +0.22 to +0.31 |e|. It is generally found on Pt38 and Pt32Ti6 clusters, that the Pt becomes more positively charged as the system moves from the initial to final states, while the O atoms become more negatively charged at the same time. Furthermore, more positive Pt charge values are observed for O2 adsorption on the (100) facet. This charge transfer is found to be comparable between the slab and cluster models. In the case of the Pt32Ti6 cluster Pt has positive and negative charges depending on the state of the system, slightly positive (+0.04 |e|) when O2 is adsorbed on the (100) facet and negative on the (111) facet (−0.22 to −0.23 |e|). At the same time, charges on the Ti atoms, which are remote from the adsorbates, do not change notably. They also do not change when the system progresses from IS to FS. Not surprisingly, the charges on the oxygen atoms get significantly more negative as the system progresses from the initial to the final states. This charge seems unaffected by the site at which oxygen is adsorbed, or whether it is the pure or alloyed cluster. Hence, one can conclude that O atoms have local effects on the withdrawal of electron density from the closest Pt atoms only. When O2 is adsorbed on the (111) facet of the alloyed Pt32Ti6 nanoparticle, Pt is found to have a negative charge at the initial state and a positive charge at the final state, while on the (100) facet, the Pt atoms are positive for all states.
Finally, barrier-free dissociation is observed on the (111) facet of the Pt38 cluster which appears to be due to significant distortions of the facet. There are greater energetic costs associated with distorting the Pt32Ti6 cluster, compared with Pt38 cluster (Table 2). Although according to the cluster geometries there is greater distortion of the Pt38 cluster. This suggests that the presence of the octahedral Ti core in the Pt32Ti6 cluster stabilises the Pt shell and makes the structure more rigid, while Pt38 nanoparticle is more flexible and the surface Pt atoms become more easily distorted, hence more reactive. When compared to the Pt(111) bulk system, the barrier for O2 dissociation is found to be 0.45 eV, however very little distortion of the (111) surface is observed. This supports the suggestion that it is the distortion of the (111) facet on the cluster that leads to barrier-free dissociation.
3.3 79 Atom clusters
| Site | Position | Pt79–O | Pt79–O2 | Pt60Ti19–O | Pt60Ti19–O2 |
|---|---|---|---|---|---|
| a Adsorbate migration to position 9. b Adsorbate migration to position 5. c Adsorbate migration to position 7. d Adsorbate migration to position 8. e Adsorbate migration to position 12. f Adsorbate migration to position 11. g Adsorbate migration to position 10. | |||||
| 1 | Top | —a | —b | −2.69 | —a |
| 2 | Top | —c | −0.41 | —c | −0.41 |
| 3 | Top | −4.36 | −0.71 | −4.24 | —d |
| 4 | Bridge | —e | −1.07 | —f | −0.09 |
| 5 | Bridge | —g | −1.45 | —c | −0.77 |
| 6 | Bridge | —g | −1.21 | —c | −0.68 |
| 7 | Bridge | −5.04 | −1.83 | −4.60 | −1.15 |
| 8 | Bridge | −4.94 | −1.81 | −4.93 | −1.85 |
| 9 | hcp | −4.93 | −1.13 | —d | −0.71 |
| 10 | fcc | −4.98 | −1.39 | —c | −0.69 |
| 11 | hcp | −4.74 | −0.99 | −3.79 | −0.63 |
| 12 | fcc | −4.93 | −0.88 | −3.32 | 0.07 |
| 13 | 4-fold | −4.83 | —d | −4.56 | —d |
| Hollow | |||||
For the pure Pt79 cluster, the hollow site on the (111) facet is no longer as favourable as the edge-bridge sites on the (100) facet for O2 and O adsorption. However, the site resulting in strongest bonding is the edge-bridge site of the (111) facet, labelled as site 7. For the Pt60Ti19 cluster, in all cases, the edge-bridge site on the (100) facet results in strongest bonding. This was also the case for Pt32Ti6.
In a similar fashion to the 38 atom system, O2 dissociation has been investigated at various sites on the (111) and (100) facets of the 79 atom clusters (8, 9, 10 and 11 in Fig. 1). Due to the increased size of the (111) facet, it is no longer beneficial to allow dissociation pathways from a certain site to an identical adjacent site, as this would span the entire facet. Following dissociation, any further barriers observed would be due to migration of the oxygen atoms over the surface, which is not the aim of this study. Therefore, for the 79 atom clusters, the pathways on the (111) facet terminate at the central site 12. As with the 38 atom clusters, dissociation on the edge-bridge site of the (100) facet proceeds from position 8 to two adjacent 8 sites.
The central positions on the (111) facet were also investigated, the hollow site 12 for the Pt79 cluster and site 4 on Pt60Ti19. However, relatively small O2 binding energies, particularly on the Pt60Ti19 cluster, are associated with these sites. Hence, finding TS for O2 dissociation proved difficult on these sites. The terrace site is unlikely to be active for oxygen dissociation due to the weaker Pt–O interactions associated with this position. On the 79 atom clusters, the central three-fold hollow site is surrounded by more favourable edge hollow and bridge sites. This means that it is far more likely that O2 dissociation will occur at the edge sites of the facet, where stronger Pt–O bonding is observed. Furthermore, low-coordinated edge sites are able to distort to a greater extent (see below) than the central three-fold hollow site, hence facilitating lower barriers to O2 dissociation.
| ΔE(Ptn−mTim) | RMSD | ΔE(Ptn−mTim)/RMSD | ΔE(O2) | E int | E b | ΔE≠ | |
|---|---|---|---|---|---|---|---|
| a Values for ΔE(Ptsurf). | |||||||
| Initial state | |||||||
| Pt79-8 | 0.31 | 0.08 | 3.88 | 0.58 | −2.69 | −1.80 | |
| Pt60Ti19-8 | 0.27 | 0.05 | 5.40 | 0.49 | −2.60 | −1.84 | |
| Pt79-9 | 0.13 | 0.06 | 2.17 | 0.80 | −2.05 | −1.12 | |
| Pt60Ti19-9 | 0.12 | 0.02 | 6.00 | 0.71 | −1.51 | −0.68 | |
| Pt79-10 | 0.37 | 0.10 | 7.10 | 0.95 | −2.71 | −1.40 | |
| Pt60Ti19-10 | 0.32 | 0.05 | 6.40 | 0.65 | −1.64 | −0.67 | |
| Pt79-11 | 0.50 | 0.13 | 3.85 | 0.88 | −2.37 | −0.99 | |
| Pt60Ti19-11 | 0.17 | 0.03 | 5.67 | 0.47 | −1.23 | −0.59 | |
| Pt(111) Slab | 0.17a | 0.03 | 5.67a | 0.64 | −1.67 | −0.86 | |
| Transition state | |||||||
| Pt79-8 | 0.22 | 0.10 | 2.20 | 0.78 | −2.46 | −1.46 | 0.34 |
| Pt60Ti19-8 | 0.33 | 0.05 | 6.60 | 5.31 | −6.81 | −1.18 | 0.66 |
| Pt79-9 | 0.22 | 0.08 | 2.75 | 3.69 | −4.81 | −0.91 | 0.21 |
| Pt60Ti19-9 | 0.15 | 0.03 | 5.00 | 5.02 | −5.25 | −0.08 | 0.60 |
| Pt79-10 | 0.73 | 0.18 | 4.06 | 2.23 | −4.45 | −1.49 | 0.00 |
| Pt60Ti19-10 | 0.45 | 0.06 | 7.50 | 5.41 | −5.86 | 0.00 | 0.69 |
| Pt79-11 | 0.45 | 0.15 | 3.00 | 1.14 | −2.54 | −0.95 | 0.05 |
| Pt60Ti19-11 | 0.91 | 0.10 | 9.10 | 3.08 | −3.82 | 0.17 | 0.77 |
| Pt(111) Slab | 0.25a | 0.05 | 5.00a | 5.72 | −6.41 | −0.43 | 0.45 |
| Final state | |||||||
| Pt79-8 | 0.43 | 0.09 | 4.78 | 6.33 | −9.50 | −2.74 | |
| Pt60Ti19-8 | 0.33 | 0.05 | 6.60 | 6.28 | −8.91 | −2.30 | |
| Pt79-9 | 1.38 | 0.16 | 8.63 | 6.28 | −10.57 | −2.91 | |
| Pt60Ti19-9 | 0.40 | 0.05 | 8.00 | 6.79 | −8.69 | −1.50 | |
| Pt79-10 | 1.21 | 0.14 | 8.64 | 6.30 | −10.47 | −2.96 | |
| Pt60Ti19-10 | 0.52 | 0.05 | 10.40 | 6.28 | −7.92 | −1.13 | |
| Pt79-11 | 1.41 | 0.16 | 8.81 | 5.94 | −9.68 | −2.33 | |
| Pt60Ti19-11 | 0.42 | 0.05 | 8.40 | 6.79 | −8.87 | −1.66 | |
| Pt(111) Slab | 0.39a | 0.05 | 7.80a | 6.34 | −9.12 | −2.39 | |
As for Pt38, there are greater distortion energies associated with the FS compared to the IS or TS. This once again suggests that the strongly interacting atomic oxygen has a greater ability to distort the Pt79 surface. For Pt60Ti19, there are greater distortion energies associated with the TS and FS compared to the IS. RMSD analysis demonstrates that for the Pt79 cluster, there is generally least structural distortion when O2 is adsorbed on position 9 on the (111) facet. Although, there is little difference between positions 8 on the (100) facet and 9 on the (111) facet. There is significant distortion of Pt79 when oxygen is adsorbed on sites 10 and 11. As with the 38 atom clusters, there is greater distortion of the pure Pt clusters, compared to the alloyed ones. For Pt60Ti19, there is generally little difference between the RMSD for the cases when O2 is adsorbed on (111) and (100) facets, suggesting again that Ti@Pt structures are more rigid due to the strong interaction between Ti core and Pt shell.
When comparing the (111) and (100) facets, it is found that the Pt79 cluster distortion energy associated with site 8 on the (100) facet is greater than that for site 9 on the (111) facet of the Pt79 IS structure (Table 7). However, the distortion energies become equal at the TS but are 0.95 eV greater on site 9 for the FS structure. For sites 10 and 11 on the (111) facet, the distortion energy is greater than for site 8 in all cases. The ΔE(Pt79) values for sites 9, 10 and 11 correlate with the differences between the dissociation barriers between sites. The smallest ΔE(Pt79) value is for site 9 which also has the largest barrier, whilst site 10 has the largest ΔE(Pt79) value and smallest barrier. There is less correlation between cluster distortion energies, surface sites and dissociation barriers for the Pt60Ti19 system.
ΔE(Ptn−mTim)/RMSD has also been calculated for the 79 atom clusters. An average of 1.62, 4.05 and 0.64 eV Å−1 more energy is required to distort the Pt60Ti19 cluster, than the Pt79 cluster at the IS, TS and FS, respectively. This further demonstrates the significant energy barriers that need to be overcome in order to distort the Pt60Ti19 cluster compared to the Pt79 cluster.
Oxygen distortion values for the IS are greater for the Pt79 system, compared to the Pt60Ti19 system, in all cases. However, at the TS, significantly greater distortion energies are associated with the Pt60Ti19 clusters. This suggests that, initially, when oxygen is adsorbed on the surface of the Pt79 cluster, due to the stronger Pt–O interactions, the O2 molecule is distorted to a greater extent than on the alloyed system, where weaker bonding is observed. However, at the TS, on the more weakly bound Pt60Ti19 system, greater distortion of the O2 molecule is required, compared to the Pt79 system. This greater distortion requires more energy and can rationalise larger dissociation barriers on Ti@Pt compared to the pure Pt nanoparticle. The same discussion is also valid for Pt38 and Pt32Ti6 nanoparticles. O2 distortion energies correlate with the corresponding O–O distances. Furthermore, the smaller difference in the O–O distances between the IS and TS for the Pt79 clusters compared to Pt60Ti19 clusters show that TS are “earlier” on Pt79. Earlier TS are known to have lower barriers, which is found to be the case in this study.
Very similar dissociation barrier on the (100) facet are located for the 79 and 38 atom clusters (Tables 2 and 7). The dissociation barriers are about twice that for the alloyed clusters (0.62 and 0.66 eV for the Pt32Ti6 and Pt60Ti19 clusters, respectively) compared to the pure clusters (0.32 and 0.34 eV for the Pt38 and Pt79 clusters, respectively). However, for the dissociation barriers located on the (111) facet the relationship becomes a little more complicated.
For the Pt38 cluster, barrier-free dissociation was observed on sites 6 and 7 on the (111) facet. For the Pt79 cluster, once again almost barrier-free dissociation is located on sites 10 and 11. However, a dissociation barrier of 0.21 eV is found for dissociation on site 9. When comparing binding energies at sites 9 and 11, there is a small difference of 0.12 eV. Probably this difference is not simply a matter of different Pt–O bonding strengths but is related more to differences in the sites. Sites 9 and 11 are hcp whilst site 10 is fcc. This suggests that the difference in dissociation barriers is probably due to the neighbouring surfaces to which the sites are adjacent. Whilst site 9 is neighbouring a (100) facet, sites 10 and 11 both neighbour (111) facets, implying that the adjacent (100) facet distorts less than an adjacent (111) facet and results in the small dissociation barrier for site 9 on the Pt79 cluster (see Pt–Xcentre values in Table 8). Finally, dissociation barriers on the (111) facet of the Pt60Ti19 clusters are similar to that of the (100) facet. Here again, correlation between barriers and Pt–Xcentre values is found since Pt–Xcentre values are also similar at both types of facets.
| O–O | Pt–O | Pt–Pt | Pt–Xcentre | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | IS | TS | FS | IS | TS | FS | |
| Pt79-8 | 1.39 | 1.42 | 2.98 | 1.96 | 2.01 | 1.95 | 3.18[2] | 3.03[2] | 2.96[2] | — | — | — |
| Pt60Ti19-8 | 1.37 | 2.03 | 3.87 | 1.98 | 1.84 | 1.92 | 3.27[2] | 3.22[2] | 3.04[2] | — | — | — |
| Pt79-9 | 1.42 | 1.79 | 3.94 | 2.14 | 2.00 | 2.02 | 2.77[2] | 2.83[2] | 2.78[2] | 3.21 | 3.30 | 4.22 |
| 2.80[3] | 2.84[3] | 2.93[3] | ||||||||||
| 3.11[5] | ||||||||||||
| Pt60Ti19-9 | 1.41 | 1.98 | 5.03 | 2.22 | 2.02 | 2.10 | 2.91[2] | 2.89[2] | 2.97[2] | 2.96 | 3.00 | 2.95 |
| 2.76[3] | 2.76[3] | 2.77[5] | ||||||||||
| Pt79-10 | 1.44 | 1.60 | 3.17 | 2.08 | 2.00 | 2.04 | 2.72[1] | 2.72[1] | 2.74[1] | 4.01 | 4.01 | 3.93 |
| 3.54[3] | 3.54[3] | 3.12[3] | ||||||||||
| 3.53[4] | 3.54[4] | 3.19[4] | ||||||||||
| 2.98[5] | ||||||||||||
| Pt60Ti19-10 | 1.40 | 2.05 | 3.75 | 2.18 | 1.99 | 2.02 | 2.69[1] | 2.72[1] | 2.70[1] | 2.92 | 2.96 | 2.91 |
| 2.85[3] | 2.77[3] | 2.75[5] | ||||||||||
| 2.90[4] | 2.91[4] | |||||||||||
| Pt79-11 | 1.43 | 1.47 | 2.53 | 2.09 | 2.09 | 2.07 | 3.24[4] | 3.30[4] | 3.08[4] | 3.41 | 3.39 | 3.90 |
| 2.73[5] | 2.76[5] | 3.11[5] | ||||||||||
| Pt60Ti19-11 | 1.37 | 1.71 | 4.89 | 2.33 | 2.13 | 2.09 | 2.90[4] | 2.71[1] | 2.71[1] | 2.94 | 3.11 | 2.91 |
| 2.68[5] | 2.71[3] | 2.85[4] | ||||||||||
| 3.09[4] | ||||||||||||
| 2.76[5] | ||||||||||||
The Pt–Pt bond lengths for the bare Pt79 cluster are 2.66, 2.73, 2.70, 2.75, 2.68 Å for bond types 1 to 5, respectively (Fig. 2). For site 8 on the (100) facet, significant distortion (by an average of 0.33 Å) of bond type 2 is observed. However, for the initial and transition states this is unsurprising as O2 is interacting with the one bond. Therefore, although there is significant elongation of bond type 2, there is less overall distortion of the cluster. Bond types 3 and 4 are distorted (by an average of 0.42 and 0.56 Å, respectively) to the greatest extent for O2 adsorption on the (111) facet. The elongation of bonds surrounding the hollow sites at which oxygen is adsorbed on the (111) facet leads to greater overall distortions of the cluster.
The Pt–Pt bond lengths of the alloyed Pt60Ti19 cluster are 2.68, 2.84, 2.73, 2.75 and 2.73 Å for bond types 1 to 5, respectively. Once again, significant elongation of bond type 2 is observed on the (100) facet when O2 is adsorbed, 0.34 Å, although as with the Pt79 cluster, little overall distortion of the cluster is observed, ≤0.10 Å. There is far less distortion of other bond types when studying dissociation on the (111) facet. This is expected as there appears to be far less distortion of the overall cluster geometries upon adsorbing O2.
Pt–Xcentre values for the bare pure Pt79 cluster are 3.15 and 6.29 Å for the top and bottom of the cluster, respectively. For the bare Pt60Ti19 cluster, these values are found to be 3.02 and 6.05 Å. Once again, there is considerable distortion of the Pt79 cluster when O2 is adsorbed on the (111) facet, with Pt–Xcentre distances elongated by up to 1.07 Å (Table 9). There is less distortion of the IS (111) facet (Pt–Xcentre – 0.06 Å) associated with site 9, where a small dissociation barrier of 0.21 eV is observed. Less distortion is also observed for the Pt60Ti19 clusters, with generally even a slight contraction in the Pt–Xcentre values. More detailed analysis of the changes in Pt–Xcentre can be found in Table 9, once again showing little deviation in distances from the plane to the bottom of the cluster. The relationship between Pt–Xcentre and dissociation barriers can be seen in Fig. S1 and S2† for the IS and TS, again allowing for further comparisons between the 38 and 79 atom clusters.
| IS | TS | FS | ||||
|---|---|---|---|---|---|---|
| Top | Bottom | Top | Bottom | Top | Bottom | |
| Pt79-9 | 0.06 | −0.07 | 0.15 | −0.11 | 1.07 | −0.12 |
| Pt60Ti19-9 | −0.06 | 0.01 | −0.02 | 0.01 | −0.07 | −0.01 |
| Pt79-10 | 0.86 | 0.05 | 0.86 | 0.04 | 0.78 | −0.11 |
| Pt60Ti19-10 | −0.11 | 0.00 | −0.06 | 0.00 | −0.11 | −0.01 |
| Pt79-11 | 0.26 | −0.13 | 0.24 | −0.19 | 0.75 | −0.10 |
| Pt60Ti19-11 | −0.08 | 0.00 | 0.09 | −0.02 | −0.11 | −0.01 |
| Pt chargesa | Ti chargesb | O charges | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | IS | TS | FS | |
| a Pt atoms interacting directly with O atoms. b Ti atoms interacting directly with O bound Pt atoms. | |||||||||
| Pt79-8 | 0.28 | 0.25 | 0.44 | — | — | — | −0.33 | −0.38 | −0.74 |
| Pt60Ti19-8 | −0.03 | 0.19 | 0.11 | 1.87 | 1.86 | 1.83 | −0.33 | −0.59 | −0.74 |
| Pt79-9 | 0.20 | 0.29 | 0.32 | — | — | — | −0.36 | −0.51 | −0.83 |
| Pt60Ti19-9 | −0.28 | −0.16 | −0.16 | 1.59 | 1.62 | 1.47 | −0.37 | −0.58 | −0.74 |
| Pt79-10 | 0.27 | 0.30 | 0.33 | — | — | — | −0.37 | −0.46 | −0.78 |
| Pt60Ti19-10 | −0.26 | −0.12 | −0.14 | 1.38 | 1.50 | 1.49 | −0.36 | −0.60 | −0.78 |
| Pt79-11 | 0.24 | 0.24 | 0.41 | — | — | — | −0.37 | −0.40 | −0.79 |
| Pt60Ti19-11 | −0.39 | −0.22 | −0.15 | 1.25 | 1.35 | 1.47 | −0.34 | −0.50 | −0.78 |
For the Pt60Ti19 clusters, the charges on the Pt atoms bonded to oxygen generally get less negative as the system progresses from the initial to final state. Only for the dissociation on the (100) facet are the Pt atoms positively charged for both the transition and final states. In all cases, the Ti atoms remain positive, generally gaining greater positive charge than Ti atoms in the bare Pt60Ti19 nanoparticle. This is consistent with electron donation from Ti to Pt which in turn donates to O, following the increase in electronegativity. The situation here differs from that on Pt32Ti6 cluster, where the charge on the Ti atoms does not change appreciably when an O2 molecule is adsorbed. This is likely due to the greater Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio when comparing the 79 to the 38 atom clusters. The greater ratio of Ti
Pt ratio when comparing the 79 to the 38 atom clusters. The greater ratio of Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt in the Pt60Ti19 clusters results in similarly negative charges on the Pt atoms, but smaller positive charges on the Ti atoms. This will mean that more charge can be drawn from the Ti core as the system progresses to the FS, which would not be possible for the Pt32Ti6 clusters.
Pt in the Pt60Ti19 clusters results in similarly negative charges on the Pt atoms, but smaller positive charges on the Ti atoms. This will mean that more charge can be drawn from the Ti core as the system progresses to the FS, which would not be possible for the Pt32Ti6 clusters.
3.4 Nanoparticles vs. slab models
We found that the three-fold fcc site on the Pt(111) slab has similar binding energies to the central three-fold fcc site (position 12) on the Pt79 cluster, −0.86 and −0.88 eV, respectively, though, as mentioned previously, position 12 on Pt79 is not favourable for O2 dissociation. It is therefore suggested that the central three-fold fcc site on Pt79 is unlikely to facilitate oxygen dissociation, due to more favourable edge hollow and bridge sites. These sites are absent on the slab Pt(111) model (as no steps or defects are included in the model) it is therefore more likely that dissociation will occur at these three-fold fcc hollow sites, however with a notable barrier of 0.45 eV. The rigidity of the bulk slab leads to generally weaker Pt–O bonding compared to the majority of sites on the Pt clusters. However, Pt–O bonding is found to be generally stronger than on the clusters where alloying leads to changes in electronic effects that results in the weaker boding, as discussed earlier. Hence, the dissociation barrier on the slab model is found to lie in between the Pt clusters, with low dissociation barriers coupled with stronger Pt–O bonding, and the Ti@Pt clusters with higher dissociation barriers and weaker Pt–O bonding.3.5 Surface flexibility
From the discussion in subsections 3.2.3 and 3.3.3, we suggest that surface flexibility has a profound effect on the potential of catalysts to activate O2 dissociation. It is therefore of interest that Pt(111) surface lacks the ability to distort and therefore displays very different properties for oxygen dissociation when compared to pure Pt nanoparticles. We have further shown that surface flexibility is not intrinsic property of nanoparticles. Core–shell interactions stabilise the Pt shell of Ti@Pt clusters reducing flexibility. Calculating ΔE≠/RMSD gives an idea of the dependence of the dissociation barrier on surface flexibility. Values for this ratio are presented in Table 11 for the 38 and 79 atom clusters. The relationship between the RMSD at the TS and dissociation barrier ΔE≠ is plotted in Fig. S3,† while a plot of ΔE≠/RMSD against Eb is presented in Fig. S4.†| 38 Atom Cluster | 79 Atom Cluster | ||
|---|---|---|---|
| Site | ΔE≠/RMSD | Site | ΔE≠/RMSD |
| a ΔE≠/RMSD for the Pt(111) surface is 9.00 eV Å−1. | |||
| Pt38-5 | 4.00 | Pt79-8 | 3.40 |
| Pt32Ti6-5 | 6.20 | Pt60Ti19-8 | 13.20 |
| Pt38-6 | 0.21 | Pt79-9 | 2.63 |
| Pt32Ti6-6 | 3.09 | Pt60Ti19-9 | 20.00 |
| Pt38-7 | 0.00 | Pt79-10 | 0.00 |
| Pt32Ti6-7 | 8.86 | Pt60Ti19-10 | 11.50 |
| Pt79-11 | 0.33 | ||
| Pt60Ti19-11 | 7.70 | ||
Significantly lower ΔE≠/RMSD values are obtained for the 3-fold hollow sites on the Pt38(111) facet, where barrier free dissociation occurs. Higher values are found for all positions on Pt32Ti6 as well as position 5 on Pt38. This shows a strong relationship between the dissociation barrier and cluster distortion. For Pt79, significantly lower values are obtained for the 3-fold hollow sites 10 and 11, where barrier free dissociation occurs. ΔE≠/RMSD for positions 8 and 9 on Pt79 are higher than those for 10 and 11 on Pt79, but lower than all positions on Pt60Ti19. In general, values for Pt79 are comparable with those for Pt38, one more indication that the O2 dissociation barrier and cluster distortion are strongly related.
The ΔE≠/RMSD for the Pt(111) surface is 9.00 eV Å−1. This is greater than for all positions on Pt38 or Pt32Ti6. The ΔE≠/RMSD values for the Pt(111) slab are greater than those for Pt79. This once again demonstrates the very important differences between the Pt clusters and slab. For the Pt60Ti19 cluster, the majority of the ΔE≠/RMSD values are greater than those for the slab (excluding position 11), due to the reduced oxygen adsorption energy, coupled with the lack of flexibility of the Pt shell.
4 Conclusions
We found that when the adsorption strength of the O2 molecule on the cluster surface increases, the dissociation barrier will subsequently decrease. Hence, dissociation barriers on the alloyed Ti@Pt clusters would be found to be greater than those for the pure Pt clusters that exhibit larger Eb values. Further trends, outlined below, were discovered.Pure Pt clusters are easily distorted when O2 is adsorbed on the (111) facet. Furthermore, sites which are relatively easily distorted facilitate barrier-free dissociation of O2, a trend which is not only seen for the small 38 atom clusters but also the larger 79 atom clusters. As for the alloyed Ti@Pt clusters, in all cases significant barriers are observed for all sites, which are greater than the barriers found for the pure Pt clusters.
The presence of the O2 dissociation barriers for the Ti@Pt clusters is attributed to rigidity enhancement of the Pt shell by the Ti core. Significant electron donation is observed from Ti to Pt suggesting strong interactions between the two, which coincides with significantly less distortion of the Ti@Pt clusters, upon binding O2, when compared to the pure Pt clusters.
The presence of the barrierless dissociation on the (111) facet of the pure Pt cluster suggest that small Pt clusters would efficiently activate O2. However, the relatively strong adsorption strength of oxygen to the Pt surface, compared to the alloyed Ti@Pt cluster found in previous studies, means that it would be difficult to remove the resulting oxygen species from the pure Pt cluster surface. Therefore, whilst O2 dissociation would require greater energetic input on the surface of the Ti@Pt clusters, the resulting species (following further transformations to e.g. H2O or H2O2) would be easier to remove from the surface due to the weaker Pt–O interactions compared to the pure Pt cluster.
A very attractive development in the direction of optimal catalyst properties, resulting from findings of the present study, would be substitution of Ti in the core of Pt-based bimetallic particles by another metal (M). The ideal M core would weaken adsorption of atomic oxygen compared to pure Pt, to allow for fast ORR kinetics in the later stages of the reaction (as Ti does), but form weaker Pt–M bonds than Pt–Ti, thus maintaining the kinetic flexibility of the Pt shell which is advantageous for O2 dissociation.
Acknowledgements
This research was funded through the RCUK doctoral training centre in hydrogen, Fuel cells and their applications (EP/G037116/1). Financial support was also provided by the EU (FP7-NMP.2012.1.1-1 project ChipCAT, Ref. No 310191) and the Spanish MICINN (CTQ2012-34969, FIS2008-02238). The authors thank COST Action MP0903: “Nanoalloys as Advanced Materials: From Structure to Properties and Applications”, as well as COST Action CM1104. Much of the work has been performed under the HPC-EUROPA2 project (project number: 228398) with the support of the European Commission – Capacities Area – Research Infrastructures. The computations described in this paper were performed in part using The University of Birmingham's BlueBEAR HPC service, which was purchased through HEFCE SRIF-3 funds, and via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/F067496). This work made use of the facilities of HECToR, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc and NAG Ltd, and funded by the Office of Science and Technology through EPSRC's High End Computing Programme. Computational time granted by the Barcelona Supercomputing Centre on the Marenostrum supercomputers is also gratefully acknowledged. H. A. A. thanks the Ministerio de Educación for a post-doctoral grant (SB2010-0172), Bulgarian Science Fund (grant DCVP 02/1) and FP7 project BeyondEverest for support.References
- Q. Fu, J. Yang and Y. Luo, J. Phys. Chem. C, 2011, 115, 6864–6869 CAS
.
- M. Stamatakis and D. G. Vlachos, ACS Catal., 2012, 2, 2648–2663 CrossRef CAS
.
- D. J. Schmidt, W. Chen, C. Wolverton and W. F. Schneider, J. Chem. Theory Comput., 2012, 8, 264–273 CrossRef CAS
.
- J. M. Bray and W. F. Schneider, Langmuir, 2011, 27, 8177–8186 CrossRef CAS PubMed
.
- A. Smeltz, R. Getman, W. Schneider and F. Ribeiro, Catal. Today, 2008, 136, 84–92 CrossRef CAS PubMed
.
- R. Getman, W. Schneider, A. Smeltz, W. Delgass and F. Ribeiro, Phys. Rev. Lett., 2009, 102, 076101 CrossRef CAS
.
- W. Chen, D. Schmidt, W. F. Schneider and C. Wolverton, J. Phys. Chem. C, 2011, 115, 17915–17924 CAS
.
- R. B. Getman, Y. Xu and W. F. Schneider, J. Phys. Chem. C, 2008, 112, 9559–9572 CAS
.
- D.-H. Lim and J. Wilcox, J. Phys. Chem. C, 2011, 115, 22742–22747 CAS
.
- M. Kettner, W. B. Schneider and A. A. Auer, J. Phys. Chem. C, 2012, 116, 15432–15438 CAS
.
- Y. Xu, W. A. Shelton and W. F. Schneider, J. Phys. Chem. A, 2006, 110, 5839–5846 CrossRef CAS PubMed
.
- D. Cheng and W. Wang, Nanoscale, 2012, 4, 2408–2415 RSC
.
- A. Chandan, M. Hattenberger, A. El-kharouf, S. Du, A. Dhir, V. Self, B. G. Pollet, A. Ingram and W. Bujalski, J. Power Sources, 2013, 231, 264–278 CrossRef CAS PubMed
.
- A. Pollet, J. E. Newton, J. A. Preece and O. J. Curnick, ECS Trans., 2011, 2165–2173 Search PubMed
.
- O. J. Curnick, P. Mendes and B. Pollet, ECS Trans., 2010, 557–561 CAS
.
- O. J. Curnick, P. M. Mendes and B. G. Pollet, Electrochem. Commun., 2010, 12, 1017–1020 CrossRef CAS PubMed
.
- B. Li and S. H. Chan, Int. J. Hydrogen Energy, 2013, 38, 3338–3345 CrossRef CAS PubMed
.
- P. Mani, R. Srivastava and P. Strasser, J. Power Sources, 2011, 196, 666–673 CrossRef CAS PubMed
.
- R. Othman, A. L. Dicks and Z. Zhu, Int. J. Hydrogen Energy, 2012, 37, 357–372 CrossRef CAS PubMed
.
- J.-Y. Choi, R. S. Hsu and Z. Chen, J. Phys. Chem. C, 2010, 114, 8048–8053 CAS
.
- L. Calvillo, M. Gangeri, S. Perathoner, G. Centi, R. Moliner and M. Lázaro, Int. J. Hydrogen Energy, 2011, 36, 9805–9814 CrossRef CAS PubMed
.
- B. Seger and P. V. Kamat, J. Phys. Chem. C, 2009, 113, 7990–7995 CAS
.
- P. C. Jennings, B. G. Pollet and R. L. Johnston, Phys. Chem. Chem. Phys., 2012, 14, 3134–3139 RSC
.
- P. C. Jennings, B. G. Pollet and R. L. Johnston, J. Phys. Chem. C, 2012, 116, 15241–15250 CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS
.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS
.
- J. Perdew, J. Chevary, S. Vosko, K. Jackson, M. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978 CrossRef CAS
.
- D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, J. Chem. Phys., 2012, 136, 074103 CrossRef PubMed
.
- J. Kästner and P. Sherwood, J. Chem. Phys., 2008, 128, 014106 CrossRef PubMed
.
-
R. F. W. Bader, Atoms in Molecules: a Quantum Theory, Oxford University Press, New York, 1994 Search PubMed
.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed
.
- S. M. Kozlov and K. M. Neyman, Top. Catal., 2013, 56, 867–873 CrossRef CAS PubMed
.
- H. Steininger, S. Lehwald and H. Ibach, Surf. Sci., 1982, 123, 1–17 CrossRef CAS
.
- C. Puglia, A. Nilsson, B. Hernnäs, O. Karis, P. Bennich and N. Mårtensson, Surf. Sci., 1995, 342, 119–133 CrossRef CAS
.
- A. Eichler and J. Hafner, Phys. Rev. Lett., 1997, 79, 4481–4484 CrossRef CAS
.
- K. Gustafsson and S. Andersson, J. Chem. Phys., 2004, 120, 7750–7754 CrossRef CAS PubMed
.
- Z. Duan and G. Wang, Phys. Chem. Chem. Phys., 2011, 13, 20178 RSC
.
- D. J. Miller, H. Öberg, L.-A. Näslund, T. Anniyev, H. Ogasawara, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2010, 133, 224701 CrossRef CAS PubMed
.
- L. Qi, J. Yu and J. Li, J. Chem. Phys., 2006, 125, 054701 CrossRef PubMed
.
- V. Šljivančanin and B. Hammer, Surf. Sci., 2002, 515, 235–244 CrossRef
.
- B. Stipe, M. Rezaei, W. Ho, S. Gao, M. Persson and B. Lundqvist, Phys. Rev. Lett., 1997, 78, 4410–4413 CrossRef CAS
.
- J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, J. Chem. Phys., 2004, 120, 10240–10246 CrossRef CAS PubMed
.
- P. Gambardella, V. Šljivančanin, B. Hammer, M. Blanc, K. Kuhnke and K. Kern, Phys. Rev. Lett., 2001, 87, 056103 CrossRef CAS
.
- P. Feibelman, S. Esch and T. Michely, Phys. Rev. Lett., 1996, 77, 2257–2260 CrossRef CAS
.
- M. Shao, A. Peles and K. Shoemaker, Nano Lett., 2011, 11, 3714–3719 CrossRef CAS PubMed
.
- Z. Duan and G. Wang, J. Phys. Chem. C, 2013, 117, 6284–6292 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3nr04750d |
| This journal is © The Royal Society of Chemistry 2014 |