Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stereoselectivity through a network of non-classical CH weak interactions: a prospective study of a bicyclic organocatalytic scaffold†
Jens H.
Aasheim
a,
Heike
Fliegl
b,
Einar
Uggerud
b,
Tore
Bonge-Hansen
*a and
Odile
Eisenstein
*bc
aDepartment of Chemistry, University of Oslo, PO Box 1033, Blindern, 0315 Oslo, Norway. E-mail: tore.hansen@kjemi.uio.no; Fax: +47 228 55441; Tel: +47 228 55446
bCentre for Theoretical and Computational Chemistry (CTCC), Department of Chemistry, University of Oslo, P. O. Box 1033, Blindern, 0315 Oslo, Norway
cInstitut Charles Gerhardt, UMR 5253 CNRS Université Montpellier 2, cc1501, Place E., Bataillon, 34095 Montpellier, France. E-mail: odile.eisenstein@univ-montp2.fr; Fax: +33 467144839; Tel: +33 467143306
First published on 26th September 2014
Abstract
A prospective novel organocatalyst scaffold has been investigated by computational studies for its potential to induce stereoselective reactions. Density functional theory calculations (DFT) of an organocatalysed Diels–Alder reaction between cinnamaldehyde and cyclopentadiene, show that it is possible to induce selectivity by placing appropriate chemical groups on the scaffold. In the present case small substituents with strong electronic effects are found to be more effective in controlling the stereochemical induction than sterically bulky substituents. We show, using noncovalent interaction analysis (NCI plots), that the CF3 group is especially efficient in improving the stereochemical control as well as increasing the reaction rate.
Introduction
Since organocatalysis re-emerged more than 10 years ago, it has established itself as a fast moving field of research as described in several reviews.1 The use of small organic molecules to catalyze reactions has proven to be a practical and efficient way of preserving atom economy and achieving good yields and high enantioselectivity in many catalytic asymmetric transformations. New reactions and novel catalysts are constantly being added to the organocatalytic arsenal, increasing its usefulness and scope. Since the seminal report by MacMillan et al. of the first highly enantioselective Diels–Alder reaction of cyclopentadiene and α,β-unsaturated aldehydes in 2000,2 there has been numerous accounts of organocatalysed cycloaddition reactions.3 Many of them show a preference for the exo product.4 Since then the MacMillan group has developed a series of efficient and useful imidazolidinone organocatalysts, capable of catalyzing a wide range of reactions by means of iminium ion catalysis.5 In addition to MacMillan, Jørgensen–Hayashi diarylprolinol silyl ether catalysts6 and List's proline catalyzed reactions7 have shown the large potential of iminium/enamine organocatalysis.One of the first studies of organocatalysis was carried out by MacMillan who used MM3 Monte Carlo calculations.2 Following this study, computational chemistry, has been considered as a helpful tool in both describing, explaining and also validating organocatalytic structures, selectivity and mechanisms. Additional relevant and notable examples are by the groups of Houk8 and Tomkinson.9 It is thus attractive to consider the possibility of using computational methods to go beyond rationalization and envisage the prediction and rational catalyst design as shown for example by Tomkinson,9 Houk,10 Moitessier11 and also one of us.12 One essential aspect of organocatalysis is the representation of the weak interactions that exist between the various groups of the reactants. This requires the use of a methodology that properly represents dispersion forces. The group of Truhlar has been especially active in this field, and has developed several levels of the Minnesota functional that is appropriate for these kinds of studies.13 Among the various functionals of this family, M06-2X, parameterized for chemical species without metal atoms, is well adapted for applications involving main group thermochemistry, kinetics and non covalent interactions.13b It has been used successfully for studying organocatalytic and cycloaddition reactions.14,15 This functional has been selected for the present study.
The main purpose of this work is to study the possibility of reactivity manipulation, by creating a synthetically viable organocatalytic system that includes adjustable electronic and steric effects. The core of the system is a rigid bicyclic structure, to limit the degrees of freedom and thus provide a better control of the conformational space in addition to significantly simplifying the calculations. Conformational control will also provide a means to shield one side of the reactive site, hence yielding stereochemical control.
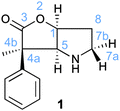
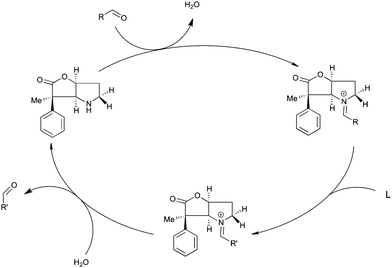
A possibly interesting system is the bicyclic Geissman–Waiss lactone (BL) (Fig. 1) as a candidate for this exploratory study. This lactone provides a bicyclic skeleton with a sp2-hybridised carbonyl,16 providing the needed structural rigidity. The reaction that is considered is shown in Scheme 1. The amine group is transformed into an iminium through a condensation reaction. Then, the reaction between the iminium carrying the reactive group R and the substrate (reaction between R and L giving R′) occurs in a chiral environment that could induce stereocontrol, which can be further influenced by the nature of the group at the 4 position of the lactone. Hydrolysis of the iminium liberates the end product and regenerates the amine form of BL, which re-enters the catalytic cycle.
With these basic structural elements in place we would have a tunable system that could be modified relatively easy by changing the aromatic shielding group. The reaction that we consider is a Diels–Alder reaction in which the iminium is conjugated to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond that serves as a dienophile.
C double bond that serves as a dienophile.
Computational procedure
All structures were computed using the hybrid functional M06-2X13 and the def2-TZVP17 basis set for all atoms. All calculations were performed with the Gaussian 09 computational software package.18 Visualizations were done with the beta version of CYLview.19 Transition states and energy minima were characterized by analytical calculations of harmonic frequencies. IRC-calculations were performed to confirm the connection of transition structures to reactants and products. In these bimolecular reactions, the transition states connects to an adduct between the two reactants. The most stable form of this adduct (obtained from the IRC calculations) serves as origin of energy for calculating the Gibbs energy profiles for each set of reactants. We report Gibbs energies calculated in gas phase for T = 298 K and p = 1 atm. The network of weak interactions was identified using the Non Covalent Interaction (NCI) approach.20 The analysis was carried out with the NCIplot software,21a with VMD21b as visual interface. These methods have been used to identify weak interactions in a wide variety of chemical and biochemical systems, and for discussing asymmetric induction.22Results and discussion
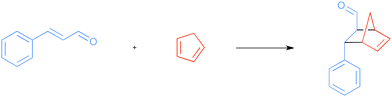
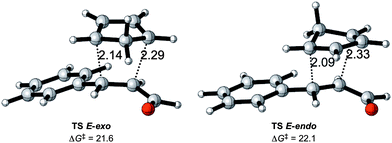
The basic reaction considered is the Diels–Alder reaction between cinnamaldehyde and cyclopentadiene (CP) as shown in Scheme 2, referred to as the uncatalyzed reaction. The lowest set of transition states are shown in Fig. 2, while higher transition states related to other conformations of the cinnamaldehyde are disregarded because they will not contribute significantly to products.In accordance with other theoretical studies of the Diels–Alder reaction,8e,23 all transition states correspond to an asynchronous concerted reaction pathway.
The two new carbon–carbon bond lengths differ by about 0.2 Å for both the endo and the exo reactions, as shown in Fig. 2. The calculations show a slight preference for the exo reaction, in contrast to the normal endo preference usually attributed to secondary orbital interactions between the incoming CP and the carbonyl group.24 A possible reason for this difference is the presence of additional secondary interactions between the incoming CP and the π-system of the phenyl ring in the exo reaction.
The catalysed version of the reaction, following the proposal presented in Scheme 1, is shown in Scheme 3. The condensation of the cinnamaldehyde and the bicyclic lactone (BL) catalyst yields the conjugated iminium ion (Scheme 2), which can serve as an activated dienophile in the Diels–Alder reaction. Hydrolysis recovers the carbonyl group, in the product, and the amine functionality of BL. This study focuses on the cycloaddition step, as it is the rate determining step of the catalytic cycle.9c
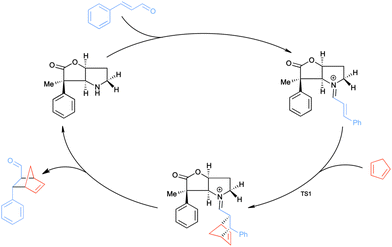 | ||
| Scheme 3 The catalytic cycle of the organocatalysed Diels–Alder reaction between CP and the E-isomer of the iminium ion formed from cinnamaldehyde and BL. | ||
To induce stereoselectivity in Diels–Alder reactions (Scheme 3) one needs to control three aspects: (i) the formation of the E- or Z-iminium ion isomer; (ii) endo- or exo-attack; (iii) attack on either side of the iminium ion, which will be referred to as top and bottom.
The condensation reaction between cinnamaldehyde and the bicyclic lactone (BL) catalyst (1) forms an iminium ion with either an E (H on imine carbon cisoid to the lactone) or a Z conformation. The calculations show a preference of 2 kcal mol−1 for the 1-E over the 1-Z isomer, indicating that the condensation is conformationally controlled at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond period (Fig. 3). The reason for this slight energy preference is likely to come from the close proximity of the phenyl ring at C4 of the lactone (see Fig. 1 for labelling) and the π system of the imimium moiety in the Z-conformation. It remains to be determined if this preference for the E over Z isomer translates into the transition states, and contributes to differentiate the top from bottom faces of the iminium and the endo from the exo pathways.
N double bond period (Fig. 3). The reason for this slight energy preference is likely to come from the close proximity of the phenyl ring at C4 of the lactone (see Fig. 1 for labelling) and the π system of the imimium moiety in the Z-conformation. It remains to be determined if this preference for the E over Z isomer translates into the transition states, and contributes to differentiate the top from bottom faces of the iminium and the endo from the exo pathways.
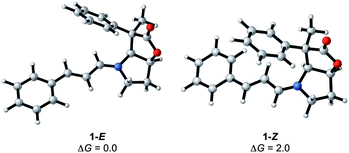 | ||
| Fig. 3 E/Z iminium ions formed by the condensation of 1 and cinnamaldehyde with relative Gibbs energies in kcal mol−1. | ||
Fig. 4 displays the preferred transition states TS1 for the Diels–Alder reaction between the 1-E iminium ion and CP. They all correspond to asynchronous concerted reactions and have activation barriers that are of similar magnitude to that of the uncatalyzed reaction (Fig. 2). The Gibbs energies of activation are the differences in Gibbs energies of the transition state and of the most stable adduct formed between 1-E and CP. The lowest transition state is only 2 kcal mol−1 lower (19.2 versus 21.6 kcal mol−1 for the catalyzed and uncatalyzed systems, respectively). Thus the iminium and the aldehyde forms of the activated dienophile have similar reactivities.
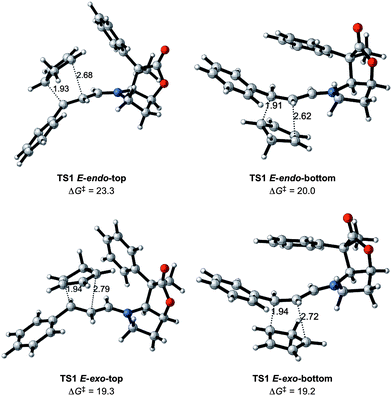 | ||
| Fig. 4 Transition states for the reaction between CP and iminium ion 1-E with Gibbs energies of activation in kcal mol−1 and relevant distances in Å. | ||
The exo attack is slightly preferred over the endo approach by 2 kcal mol−1 on average. The preference for the exo attack is thus somewhat larger in the presence of BL (compare Fig. 2 and 4). Unfortunately, the exo attack is not associated with a significant differentiation for approach on one or another of the two faces. This is illustrated by a negligible difference in energy of only 0.1 kcal mol−1 between the top and bottom transition states. In contrast, the endo attack differentiates between the two faces, and the bottom approach is preferred by 3.3 kcal mol−1 over the top approach (Fig. 4). This indicates that the phenyl group is quite effective in directing the reaction towards one side of the iminium moiety for the endo attack, but unfortunately not for the preferred exo approach. This is due to the inherent flexibility of the iminium chain and some limited flexibility at the C4 phenyl group.
Before considering the effects of further modification of the BL catalysts, the following points have been established: (i) the BL-structure contributes to differentiate addition to the top and bottom faces for the endo transition states, but not sufficiently for the preferred exo transition states; (ii) the energy preference for the E- over Z-iminium ion isomer is conserved in the transition states; (iii) the exo attack of CP on the E isomer is preferred over the endo one. Finally, the catalyst has only a small impact on the rate of reaction since the activation barriers are lowered by only 2 kcal mol−1 compared to the uncatalyzed systems.
The next topic concerns the effect of substituents R1, R2, R3 and R4 (Fig. 5) on the activation energy and selectivity of the reaction (endo vs. exo and top vs. bottom). The Gibbs energies of the eight transition states relative to the most stable adduct formed between CP and each of the relevant iminium ions are given in Table 1. The associated endo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo ratio and ee for both the endo and exo addition, obtained from a Boltzman analysis carried out at 298 K, is given in Table 2.
exo ratio and ee for both the endo and exo addition, obtained from a Boltzman analysis carried out at 298 K, is given in Table 2.
| Entry | TS-endo-top | TS-endo-bottom | TS-exo-top | TS-exo-bottom | |
|---|---|---|---|---|---|
| 1 | TS1-E | 23.3 | 20.0 | 19.3 | 19.2 |
| TS1-Z | 22.5 | 21.9 | 23.2 | 21.2 | |
| 2 | TS2-E | 22.7 | 20.2 | 19.1 | 18.9 |
| TS2-Z | 22.5 | 23.3 | 23.3 | 23.1 | |
| 3 | TS3-E | 18.7 | 19.0 | 17.2 | 17.5 |
| TS3-Z | 20.5 | 19.8 | 19.4 | 18.8 | |
| 4 | TS4-E | 23.4 | 20.6 | 19.7 | 19.9 |
| TS4-Z | 24.2 | 22.8 | 24.5 | 22.6 | |
| 5 | TS5-E | 25.0 | 20.7 | 21.4 | 20.2 |
| TS5-Z | 19.8 | 18.6 | 20.6 | 17.6 | |
| 6 | TS6-E | 23.8 | 19.8 | 19.5 | 18.5 |
| TS6-Z | 23.1 | 21.3 | 23.2 | 20.7 | |
| 7 | TS7-E | 22.1 | 19.5 | 19.1 | 18.5 |
| TS7-Z | 21.8 | 20.9 | 22.0 | 20.5 | |
| 8 | TS8-E | 18.4 | 18.6 | 15.5 | 17.5 |
| TS8-Z | 18.4 | 19.7 | 20.6 | 19.6 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo ratios and ee (%) for the endo and the exo reactions
exo ratios and ee (%) for the endo and the exo reactions
endo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo exo |
ee – endo | ee – exo | |
|---|---|---|---|
| a S and R refer to the absolute configuration at the two carbons of the dienophile. | |||
| 1 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.9 6.9 |
91.5 S,Sa | 2.1 S,S |
| 2 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
96.1 S,S | 16.7 S,S |
| 3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 13 |
26.7 R,R | 23.0 R,R |
| 4 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.9 7.9 |
94.0 S,S | 22.1 R,R |
| 5 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.9 4.9 |
71.2 R,R | 96.4 R,R |
| 6 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9.5 9.5 |
86.7 S,S | 62.6 S,S |
| 7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.3 6.3 |
82.6 S,S | 39.4 S,S |
| 8 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 54 |
22.6 S,S | 93.6 R,R |
The results of Table 1 show that the Gibbs energies of activation for the Diels–Alder reaction vary between 15 and 25 kcal mol−1, which indicates that the nature of the substituents influence the global rate of the reaction. An electron-withdrawing group close to the iminium moiety (R2 = CF3, entry 8) significantly lowers the energy of all transition states. This is consistent with the well-known accelerating effect of electron acceptor groups on the dienophile.2,9,25 Interestingly, changing R3 from Ph to tBu (entry 3) also gives relatively low activation barriers, especially for the addition to the preferred E-isomer. In total, the influence of R3 on the activation energy is relatively modest, indicating that the BL catalyst does not significantly affect the reaction rate.
Table 2 shows that the exo addition is always preferred, but the endo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo ratio varies between 1
exo ratio varies between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.9 (entry 5) to 1
4.9 (entry 5) to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 (entry 8). These two entries giving the lowest and highest endo
54 (entry 8). These two entries giving the lowest and highest endo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo ratio, correspond to a CH3 substituent at R2 for entry 5 and CF3 for entry 8. Since these two groups have similar effective vdW radii,26 this indicates that other factors influence the selectivity. The significant lowering of the activation barriers with CF3, and notably for the exo addition, could be responsible for this result. Changes in positions R3 and R4 have less influence on the endo
exo ratio, correspond to a CH3 substituent at R2 for entry 5 and CF3 for entry 8. Since these two groups have similar effective vdW radii,26 this indicates that other factors influence the selectivity. The significant lowering of the activation barriers with CF3, and notably for the exo addition, could be responsible for this result. Changes in positions R3 and R4 have less influence on the endo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo ratio. Even replacing Me with F at R4 gives similar endo
exo ratio. Even replacing Me with F at R4 gives similar endo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exo ratio (entries 1 and 7). However, increasing the bulk of R4, as for entry 2 with R4 = m-xylene and entry 3 with R4 = tBu, gives larger exo
exo ratio (entries 1 and 7). However, increasing the bulk of R4, as for entry 2 with R4 = m-xylene and entry 3 with R4 = tBu, gives larger exo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) endo ratio than R4 = phenyl.
endo ratio than R4 = phenyl.
Entry 1 is rather unique in giving such a small ee for the exo approach. For all other entries, the ee ratio is larger and can be even very large like for entries 5 and 8. The ee from the endo addition is always very large with the exception of entries 3 and 8. However, we do not need to discuss further the endo addition, as it is not preferred.
The most attractive case appears to be entry 8. The structure of the lowest transition state is given in Fig. 6. As mentioned earlier, this entry is associated with an increase in the reaction rate and a high exo selectivity, in addition to high enantiomeric selectivity. Lowering of the energy barrier is an expected result of the presence of an electron withdrawing group on the dienophile, as known in the Alder rule.2,9,25 This does not however, account for the high selectivity in the exo addition and the significant preference for adding to the top face of the iminium ion. In order to obtain a deeper insight into this issue, an analysis of the noncovalent interactions was performed for the four E iminium ion transition states of entry 8 with NCIplot.21
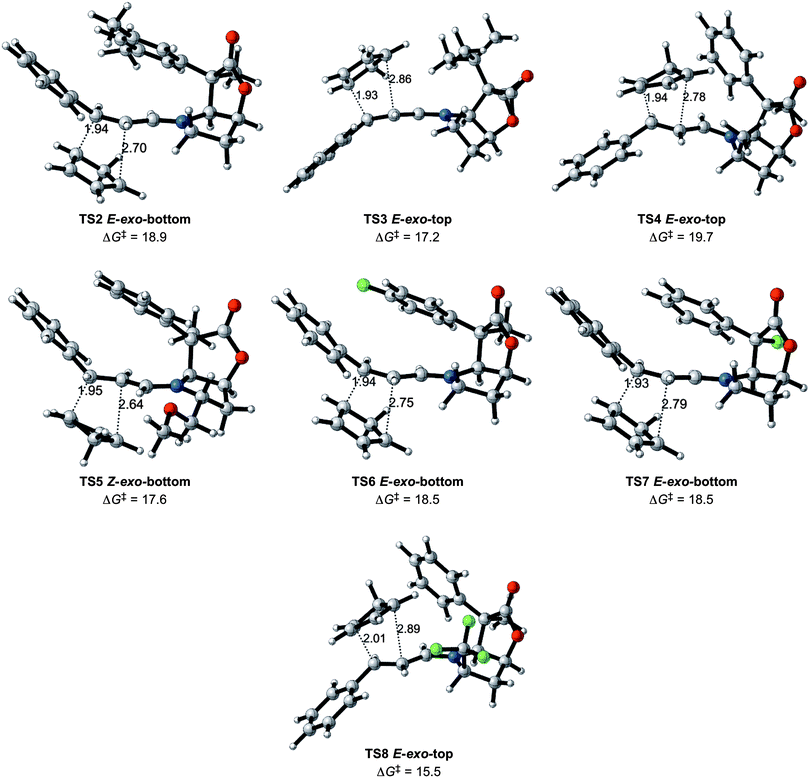 | ||
| Fig. 6 The preferred transition states (TS2 to TS8) for entries 2 to 8 (Table 1) with Gibbs energies of activation in kcal mol−1, and selected distances in Å. | ||
Fig. 7 shows the result of the NCI analysis for the lowest transition state (TS8-E-exo-top) associated with entry 8. The weak interactions revealed by the NCI analysis are color coded from blue, for the strongest attractive weak interactions (hydrogen bonds, for example), to red for repulsive ones (steric clashes). In between, the very weak van der Waals interactions appear in green. Focus is mostly placed on the spaces that define the selectivity of the reaction. Fig. 7 shows that large green surfaces occur in the space between the incoming CP and both the R4 phenyl group and the R2 CF3 group of BL. They are clearly associated with weak interaction between the CH bonds of CP and both the electron density of the phenyl ring and the electron density at the fluorine atoms. These interactions are representative of non-classical CH⋯X interactions, whose importance in determining the structures of large systems have been established.27 Unfortunately, there is not yet any quantitative relation between the size of the surface combined with its colour, and the energy of the interaction. However, a decrease of the size of the surface and a change of colour from darker to lighter green is indicative of a decrease in the magnitude of the weak interactions.
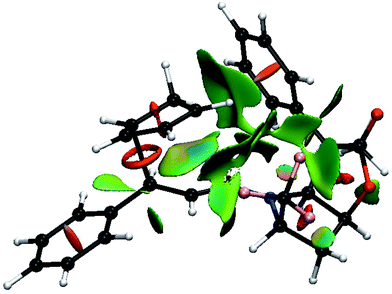 | ||
| Fig. 7 Color-coded noncovalent interactions (NCI) surfaces (attractive decreasing from blue to green, repulsive increasing from yellow to red) for TS8-E-exo-top. | ||
Thus, going to the less preferred transition states for entry 8 is associated with a decrease, or disappearance, of the green surfaces. In particular going from TS8-E-exo-top to TS8-E-endo-top, which corresponds to a raise of 2 kcal mol−1, (Table 1), shows a clear decrease of the green surfaces between CP and the phenyl and CF3 groups (Fig. 8). It seems that in the exo orientation, the CH bonds of CP creates the best network of dispersion interactions with the two electron rich groups. In the case of the bottom attacks, these weak interactions between CP and the phenyl and CF3 groups are lost and the interaction between the R4 phenyl group and the iminium skeleton does not fully compensate (Fig. 9).
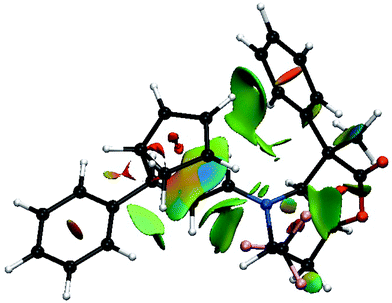 | ||
| Fig. 8 Color-coded noncovalent interactions (NCI) surfaces (attractive decreasing from blue to green, repulsive increasing from yellow to red) for TS8-E-endo-top. | ||
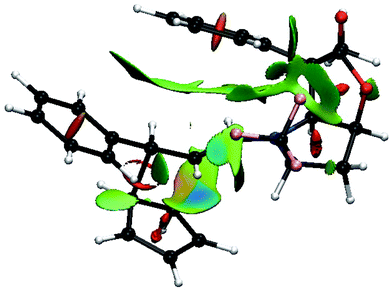 | ||
| Fig. 9 Color-coded noncovalent interactions (NCI) surfaces (attractive decreasing from blue to green, repulsive increasing from yellow to red) for TS8-E-exo-bottom. | ||
The NCI analysis suggests the paradoxical result that it could be preferable to attack the iminium from the most hindered side because approach on this side is in fact dominated by weak interactions. One can thus understand the influence of the CF3 group that modifies the electron distribution and increases the electron density in the appropriate part of the space and enhances the attractive interactions.
Proper substitutions on the BL catalyst (for example by introducing an electron withdrawing group such as CF3) highlight the possibility to direct selectivity by creating an electronic environment that could fit the approaching reagent, an effect somewhat related to enzymatic control. The ideal system may have to be adapted to the reaction and even to the two substrates. This is not surprising in regard of the very high specificity of enzymatic catalysis.
Conclusions
In this prospective study of an organized reaction, DFT calculations have been used to identify the parameters that control the stereocourse of the reaction. A Diels–Alder reaction between cinnamaldehyde and cyclopentadiene was used as a representative case because of the importance of this reaction in organic synthesis. A bicyclic organic scaffold (BL) has been selected based on its relative rigidity, and because it possesses several sites that can be functionalized. DFT calculations and NCI plots for analysis were used to evaluate the steric and electronic effects of a series of modifications on BL, and their influence on the kinetics and stereochemical selectivity. An ideal catalyst should induce a high degree of stereochemical control and appropriately adjust reactivity to maximize the reaction yield without compromising the selectivity. In the presented case, the studies have shown that the shielding effects of appropriately positioned sterically bulky substituents (such as tBu) are surpassed by smaller substituents exerting a strong electron withdrawing effect (such as CF3). This EWG group lowers the energy barrier for all cycloadditions and especially that for the exo cycloaddition. Furthermore, the calculations show that the bicyclic scaffold is not as rigid as initially thought, which is one of the reasons of the limited impact of steric hindrance. This study shows that computations and analysis of the electronic structures along the reaction pathway can guide experiments and save chemical resources.Acknowledgements
J. H. A. thanks the Centre for Theoretical and Computational Chemistry (CTCC) and NOTUR for use of their computational resources. E. U., O. E. and H. F. thank for support by the Norwegian Research Council through the CoE for Theoretical and Computational Chemistry (Grant No. 179568/V30). This work has received support from the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grants No. NN4654K). O. E. thanks the CTCC for an adjunct professorship position and the French CNRS and the MENESR for funding.Notes and references
- (a) P. I. Dalko and L. Moisan, Angew. Chem., Int. Ed., 2001, 40, 3726 CrossRef CAS; (b) P. I. Dalko and L. Moisan, Angew. Chem., Int. Ed., 2004, 43, 5138 CrossRef CAS PubMed; (c) A. Dondoni and A. Massi, Angew. Chem., Int. Ed., 2008, 47, 4638 CrossRef CAS PubMed; (d) P. Melchiorre, M. Marigo, A. Carlone and G. Bartoli, Angew. Chem., Int. Ed., 2008, 47, 6138 CrossRef CAS PubMed; (e) G. Lelais and D. W. C. MacMillan, Aldrichimica Acta, 2006, 39, 78 Search PubMed; (f) B. R. Buckley, M. C. Kimber and N. H. Slater, Annu. Rep. Prog. Chem., Sect. B: Org. Chem., 2012, 108, 98 RSC; (g) U. Scheffler and R. Mahrwald, Chem. – Eur. J., 2013, 19, 14346 CrossRef CAS PubMed.
- K. A. Ahrendt, C. J. Borths and D. W. C. MacMillan, J. Am. Chem. Soc., 2000, 122, 4243 CrossRef CAS.
- (a) B. F. Bonini, E. Capitò, M. Comes-Franchini, M. Fochi, A. Ricci and B. Zwanenburg, Tetrahedron: Asymmetry, 2006, 17, 3135 CrossRef CAS PubMed; (b) R. M. Wilson, W. S. Jen and D. W. C. MacMillan, J. Am. Chem. Soc., 2005, 127, 11616 CrossRef CAS PubMed; (c) M. Lemay and W. W. Ogilvie, Org. Lett., 2005, 7, 4141 CrossRef CAS PubMed; (d) A. Erkkilae, I. Majander and P. M. Pihko, Chem. Rev., 2007, 107, 5416 CrossRef CAS PubMed.
- (a) T. Kano, Y. Tanaka and K. Maruoka, Org. Lett., 2002, 8, 2687 CrossRef PubMed; (b) J. B. Brazier, J. L. Cavill, R. L. Elliot, G. Evans, T. J. K. Gibbs, I. L. Jones, J. A. Platts and N. C. O. Tomkinson, Tetrahedron, 2009, 65, 9961 CrossRef CAS PubMed.
- (a) J. F. Austin and D. W. C. MacMillan, J. Am. Chem. Soc., 2002, 124, 1172 CrossRef CAS PubMed; (b) A. B. Northrup and D. W. C. MacMillan, J. Am. Chem. Soc., 2002, 124, 2458 CrossRef CAS PubMed; (c) S. G. Ouellet, J. B. Tuttle and D. W. C. MacMillan, J. Am. Chem. Soc., 2005, 127, 32 CrossRef CAS PubMed.
- (a) M. Marigo, T. C. Wabnitz, D. Fielenbach and K. A. Jørgensen, Angew. Chem., Int. Ed., 2005, 44, 794 CrossRef CAS PubMed; (b) K. Juhl and K. A. Jørgensen, Angew. Chem., Int. Ed., 2003, 42, 1498 CrossRef CAS PubMed.
- (a) B. List, Acc. Chem. Res., 2004, 37, 548 CrossRef CAS PubMed; (b) B. List, R. A. Lerner and C. F. Barbas III, J. Am. Chem. Soc., 2000, 122, 2395 CrossRef CAS; (c) B. List, J. Am. Chem. Soc., 2000, 122, 9336 CrossRef CAS; (d) B. List, P. Pojarliev and J. Martin, Org. Lett., 2001, 3, 2423 CrossRef CAS PubMed.
- (a) S. Bahmanyar and K. N. Houk, J. Am. Chem. Soc., 2001, 123, 11273 CrossRef CAS PubMed; (b) C. Allemann, R. Gordillo, F. R. Clemente, P. H.-Y. Cheong and K. N. Houk, Acc. Chem. Res., 2004, 37, 558 CrossRef CAS PubMed; (c) F. R. Clemente and K. N. Houk, Angew. Chem., Int. Ed., 2004, 43, 5765 CrossRef PubMed; (d) R. Gordillo, J. Carter and K. N. Houk, Adv. Synth. Catal., 2004, 346, 1175 CrossRef CAS; (e) R. Gordillo and K. N. Houk, J. Am. Chem. Soc., 2006, 128, 3543 CrossRef CAS PubMed; (f) V. Guner, K. S. Khuong, A. G. Leach, P. S. Lee, M. D. Bartberger and K. N. Houk, J. Phys. Chem. A, 2003, 107, 11445 CrossRef CAS.
- (a) J. L. Cavill, R. L. Elliott, G. Evans, I. L. Jones, J. A. Platts, A. M. Ruda and N. C. O. Tomkinson, Tetrahedron, 2006, 62, 410 CrossRef CAS PubMed; (b) G. J. S. Evans, K. White, J. A. Platts and N. C. O. Tomkinson, Org. Biomol. Chem., 2006, 4, 2616 RSC; (c) G. Evans, T. J. K. Gibbs, R. L. Jenkins, S. J. Coles, M. B. Hursthouse, J. A. Platts and N. C. O. Tomkinson, Angew. Chem., Int. Ed., 2008, 47, 2820 CrossRef CAS PubMed.
- K. N. Houk and P. H.-Y. Cheong, Nature, 2008, 455, 309 CrossRef CAS PubMed.
- C. R. Corbeil, S. Thielges, J. A. Schwartzentruber and N. Moitessier, Angew. Chem., Int. Ed., 2008, 47, 2635 CrossRef CAS PubMed.
- M. Bruvoll, T. Hansen and E. Uggerud, J. Phys. Org. Chem., 2007, 206 CrossRef CAS.
- (a) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed; (b) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- T. A. Rokob, A. Hamza and I. Pápai, Org. Lett., 2007, 9, 4279 CrossRef CAS PubMed.
- S. Schenker, C. Schneider, S. B. Tsogoeva and T. Clark, J. Chem. Theory Comput., 2011, 7, 3586 CrossRef CAS.
- (a) A. Barco, N. Baricordi, S. Benetti, C. De Risi, G. P. Pollini and V. Zanirato, Tetrahedron, 2007, 63, 4278 CrossRef CAS PubMed; (b) A. G. H. Wee, J. Org. Chem., 2001, 66, 8513 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision B.04, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- C. Y. Legault, CYLview. version 1.0b, Université de Sherbrooke, Canada, 2008 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- (a) J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625 CrossRef CAS PubMed; (b) W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS , see also http://www.ks.uiuc.edu/Research/vmd/.
- (a) M. Hennum, H. Fliegl, L.-L. Gundersen and O. Eisenstein, J. Org. Chem., 2014, 79, 2514 CrossRef CAS PubMed; (b) B. Castro, R. Chaudret, G. Ricci, M. Kurz, P. Ochsenbein, G. Kretzschmar, V. Kraft, K. Rossen and O. Eisenstein, J. Org. Chem., 2014, 79, 5939 CrossRef CAS PubMed; (c) J.-P. Piquemal, J. Pilmé, O. Parisel, H. Gérard, I. Fourré, J. Bergès, C. Gourlaouen, A. De La Lande, M. C. Van Severen and B. Silvi, Int. J. Quantum Chem., 2008, 108, 1951 CrossRef CAS; (d) R. Chaudret, G. A. Cisneros, O. Parisel and J.-P. Piquemal, Chem. – Eur. J., 2011, 17, 2833 CrossRef CAS PubMed; (e) P. Wu, R. Chaudret, X. Hu and W. T. Yang, J. Chem. Theory Comput., 2013, 9, 2226 CrossRef CAS PubMed; (f) M. Alonso, P. Geerlings and F. De Proft, Chem. – Eur. J., 2013, 19, 1617 CrossRef CAS PubMed.
- L. R. Domingo, J. Org. Chem., 2001, 66, 3211 CrossRef CAS.
- (a) A. Arrieta and F. P. Cossío, J. Org. Chem., 2001, 66, 6178 CrossRef CAS; (b) C. S. Wannere, A. Paul, R. Herges, K. N. Houk, H. F. Schaefer III and P. v. R. Schleyer, J. Comput. Chem., 2007, 28, 344 CrossRef CAS PubMed.
- G. Bott, L. D. Field and S. Sternhell, J. Am. Chem. Soc., 1980, 102, 5618 CrossRef CAS.
- K. Alder, Experientia, Suppl. II, 1955, 86 Search PubMed; J. Sauer, Angew. Chem., Int. Ed. Engl., 1967, 6, 16 CrossRef CAS and references therein. O. Eisenstein and N. T. Anh, Tetrahedron Lett., 1971, 1191 CrossRef; R. Sustmann, Tetrahedron Lett., 1971, 2721 CrossRef; O. Eisenstein and N. T. Anh, Bull. Soc. Chim. Fr., 1973, 2721 Search PubMed; O. Eisenstein and N. T. Anh, Bull. Soc. Chim. Fr., 1973, 2723 Search PubMed; N. T. Anh, E. Canadell and O. Eisenstein, Tetrahedron, 1978, 34, 2283 CrossRef . See also K. N. Houk, J. Gonzàlez and Y. Li, Acc. Chem. Res., 1995, 28, 81 CrossRef; K. N. Houk, Y. Li and J. D. Evanseck, Angew. Chem., Int. Ed. Engl., 1992, 31, 682 CrossRef.
- (a) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48 CrossRef CAS; (b) O. Takahashi, Y. Kohno and M. Nishio, Chem. Rev., 2010, 110, 6049 CrossRef CAS PubMed; (c) M. J. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 1387 RSC; (d) M. J. Nishio, J. Mol. Struct., 2012, 1018, 2 CrossRef CAS PubMed . The web-site http://www.tim.hi-ho.ne.jp/dionisio provides up-to-date information on CH–π interactions.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all reported structures as well as the total electronic and zero-point energies. See DOI: 10.1039/c4nj01460j |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2014 |