The intrinsic view of ionization equilibria of polyprotic molecules

Abstract

The intrinsic approach describing microscopic ionization equilibria is presented. This description massively reduces the number of parameters needed to characterize microequilibria. Particularly, by exploring molecular symmetries and group transferability, this approach is capable of resolving such equilibria even for rather complex molecules. Intrinsic constants are assigned to each ionizable group and interactions between these sites are introduced. These interactions involve pairs or triplets of sites. The strength of these interactions decreases rapidly with the distance between the sites. Once these parameters are known, one can obtain macroconstants, microconstants, microstate mole fractions, and overall or site-specific titration curves. These quantities provide insight into the protonation of the molecules in question. The knowledge of such properties is relevant for a wide range of phenomena, including receptor–ligand interactions, action of drugs, or geochemical processes.

---

Introduction

Binding of ligands to receptors plays a key role not only in chemistry, but also in biology, material sciences, or geochemistry. Prime examples include binding of protons to acids or bases^1–4 and metal ions to ligands, or the formation of multicenter complexes.^5–8 In molecular biology, binding of protons, metal ions, or other species to proteins was investigated in order to facilitate drug design and to explore structure–function relationships.^9–11 Binding of oxygen to hemoglobin as treated by Pauling probably represents one of the best studied systems since.¹ Ion binding is further essential to the performance of novel smart materials, such as self-healing rubber or supramolecular polymers.^12,13 Binding of ions to minerals and natural organic matter determines the interactions between surfaces relevant to geochemical processes in subsurface transport of chemicals, colloidal particles, or microorganisms.¹⁴

The chemical nature of the binding sites where the ligands dock to receptors is primordial. However, this information is often unavailable, and systematic tools to resolve these questions are essential. Here we show how to tackle this problem in the archetypal ionization of polyprotic acids and bases. While monoprotic acids or bases are treated in all introductory chemistry courses, the diprotic case is seldom discussed in textbooks appropriately.^1,9,15 Binding of protons to more complex receptors, such as proteins, polyelectrolytes, or dendrimers is discussed in specialized literature only.^4,16,17 This reluctance might be related to the popularity of macroscopic equilibria in treating polyprotic systems. However, macroconstants only tell us that binding of a proton takes place, but not at which binding site. This information is contained in the microconstants, which specify equilibria between the different microspecies. For molecules with few sites, the number of such microconstants is limited, and their values can be deduced using various tools, for example NMR.^9,18,19 However, the number of microconstants grows very rapidly with the number of sites, and for larger molecules attempts to obtain all these constants may seem hopeless.^20,21

The intrinsic description of ionization equilibria advocated here circumvents this problem by focusing on interactions between sites. This approach drastically reduces the number of parameters involved, and takes molecular symmetries into account. Kirkwood proposed such a framework to deal with proton binding to proteins,²² which was later adapted to polyelectrolytes.^23,24 This approach was refined to treat ionization of proteins and smaller molecules^18,25,26 and currently enjoys rapidly growing interest.^3,21,27–30 The intrinsic description will be presented with examples of increasing complexity, thereby highlighting various strategies to extract the relevant parameters. We address the notion of group transferability, then the central idea of cluster expansion of the free energy, and finally molecular symmetries and homologous series. Concerning the technical background, we refer to the original articles^26,31–33 and reviews.^4,16,27,34

Group transferability

Biochemistry textbooks^1,15 introduce microscopic ionization equilibria by means of glycine. Let us recall with this example the concept of group transferability. This concept assumes that proton affinities of functional groups are influenced by their close chemical environment only.

Glycine has two different ionizable groups, namely an amine and a carboxylic group (Fig. 1a). Depending on the solution pH, this molecule is either deprotonated, which makes it negatively charged, singly protonated and hence neutral, or doubly protonated, which renders it positively charged. This macroscopic description thus invokes three so-called macrospecies. These species are in chemical equilibrium, which can be described with two equilibrium constants called macroconstants. These constants are 2.33 and 9.57 at an ionic strength of 0.1 M and 25 °C as determined by potentiometric titration (Fig. 1c).³⁵ We report common logarithms of formation constants throughout. These macroconstants determine the mole fractions of macrospecies in the prevalence diagram (Fig. 1f). However, the macroscopic description does not tell us which groups ionize. Only the microscopic description provides this information. However, this description involves 4 microspecies and thus 3 independent microconstants have to be determined. Since these microconstants are related to the macroconstants, only one additional constant is needed to complete the microscopic description.

Fig. 1 Ionization of glycine at an ionic strength of 0.1 M and 25 °C. (a) Structural formula and comparison with glycine methyl ester, (b) intrinsic, (c) macroscopic, and (d) microscopic models. Ionization constants are indicated in normal fonts (c, d) and in (b) in bold. Mole fractions with respect to all other microspecies within a macrostate are given in (d) in italic. The interaction parameter is given in (b) in italic bold. The intrinsic model was calibrated with the macroscopic constants and the ionization constant of glycine methyl ester. Calculated (e) site-specific titration curves (f) and the macroscopic prevalence diagram.

The missing constant can be obtained by invoking group transferability. The microscopic ionization constant of the amine group, provided the carboxylic group is neutral, will be very similar to the ionization constant of glycine methyl ester, which is 7.66 under the same conditions (Fig. 1a).³⁶ The perturbation of the amine group through the modification of the distant carboxylic group will be negligible. With this value at hand, the 4 microconstants can be deduced (Fig. 1d). From these constants it follows that the predominant microspecies is the zwitterion, namely where the amine group is protonated and positively charged, while the carboxylic group is deprotonated and negatively charged. The other microspecies, where both groups are neutral, occurs in traces only. One also finds that the mole fraction of each of these microspecies with respect to both singly protonated microspecies is constant. From the microscopic description, the site-specific titration curves can be inferred (Fig. 1e). They reveal that the amine group is fully deprotonated above pH 8, while the carboxylic group protonates only below pH 4.

Since only 3 out of the 4 microconstants are independent, the situation is better summarized with intrinsic (or cluster) parameters. The intrinsic constants correspond to the ionization constants of the neutral molecule, and they are 4.24 for the carboxylic group and 7.66 for the amine group. The mutual influence of these groups can be quantified by a pair interaction parameter, which turns out to be 1.91. This parameter tells us that upon protonation of the carboxylic group the microscopic ionization constant of the amine group decreases by 1.91, and vice versa. This situation is normally referred to as negative or anti-cooperativity.⁵ Microscopic equilibria of glycine can thus be summarized in terms of 3 parameters, namely with 2 intrinsic constants and one interaction parameter (Fig. 1b).

Cluster expansion

The suggested grouping of microscopic parameters in intrinsic constants and interaction parameters is a powerful concept as it reflects the expansion of the free energy in terms of clusters of sites. When all clusters are included, this description is equivalent to classical microscopic equilibria. This grouping suggests, however, that the most important contributions originate from individual sites, less important ones from pairs of sites, while triplets or quadruplets contribute the least. Such an expansion converges rapidly, and when truncated, the parameter space is reduced substantially. Let us now illustrate how this approach can be used to resolve microscopic ionization equilibria of more complex molecules. We will use inositol phosphates as examples since their site-specific titration curves can be directly measured by ³¹P-NMR. To a good approximation, the chemical shift of each phosphorus nucleus is a linear function of the degree of protonation of the respective phosphate group, since cross-coupling between different nuclei is negligible due to the distances involved.^19,26,37

Mernissi-Arifi et al.³⁷ reported site-specific titration of D-myo-inositol 1,2,6-trisphosphate.²⁶ From these data, one obtains the 3 intrinsic ionization constants and the 3 pair interaction parameters from the site-specific titration curves with a least-squares fit (Fig. 2). The intrinsic constants have values of about 6. The most basic phosphate group is situated in position 1, while the most acidic in position 2. The strongest interaction is found between the equatorial groups 1 and 6, while the interaction between the equatorial group 1 and the axial group 2 is weaker. The weakest interaction is between groups 2 and 6, since they are well separated. The pair interaction can be interpreted as the shift of the microconstant of one of these sites due to the protonation of another one. These interactions reflect the mutual configuration of the phosphate groups, and they typically decrease with separation. This distance dependence originates from the electrostatic nature of this interaction, and hence the actual values may also be influenced by conformational degrees of freedom.³⁸

Fig. 2 The ionization process of D-myo-inositol 1,2,6-trisphosphate in 0.1 M (C₂H₅)₄NBr at 25 °C. (a) Structural formula, (b) intrinsic, (c) macroscopic, and (d) microscopic models. The intrinsic model was calibrated on the (e) site-specific titration curves measured using ³¹P-NMR. (f) The macroscopic prevalence diagram.

Once the intrinsic parameters are known, they can be used to calculate other properties of interest (Fig. 2). In particular, one can evaluate all 12 possible microconstants, among which 7 are independent. The missing parameter among the 6 intrinsic parameters is the triplet interaction, which is probably small and can be assumed to vanish.²⁶ Introducing this parameter does not improve the fit. The respective microstate fractions are also presented (Fig. 2d). While the concentration of the macrospecies varies with pH as indicated in the macroscopic prevalence diagram, the respective fractions of microspecies within a given macrospecies remain constant. Very similar results were obtained by direct analysis of the site-specific titration curves in terms of all microscopic ionization equilibria.²⁶

Based on this information, the deprotonation mechanism of the D-myo-inositol 1,2,6-trisphosphate can be deduced. The molecule deprotonates in the 2 position first, as this group is the most acidic one. The second deprotonation step principally involves the group in position 6. However, other microspecies remain significant, and one cannot identify a predominant ionization mechanism, as was the case for glycine.

Triplet interactions become important for D-myo-inositol 1,2,4,5-tetrakisphosphate. The site-specific titration curves obtained by ³¹P-NMR are shown in Fig. 3. By considering pair interactions only, these curves could be described only moderately well.³⁹ A triplet interaction between the groups 1, 4, and 5 improves the description substantially, and the results are summarized in Fig. 3. The pair interaction between the groups 2 and 5 turns out to be negligible due to their substantial separation. A non-vanishing triplet interaction indicates that the shift in the microconstant of a given group due to the protonation of the two neighboring groups is not pair-wise additive. This interaction reflects an additional shift in the microconstant when both neighboring groups are protonated. Triplet interactions originate from averaging of different site–site interactions in various conformers.³⁸ A negative triplet interaction indicates positive cooperativity, which may result from the coupling between ionization and conformational degrees of freedom. This point is discussed in more detail elsewhere.⁵

Fig. 3 The ionization process of D-myo-inositol 1,2,4,5-tetrakisphosphate in 0.2 M KCl at 35 °C. (a) The structural formula, (b) intrinsic, (c) macroscopic, and (d) microscopic models showing prevalent microspecies only. The intrinsic model was calibrated on the (e) site-specific titration curves measured using ³¹P-NMR. (f) Macroscopic prevalence diagram.

The deprotonation mechanism of D-myo-inositol 1,2,4,5-tetrakisphosphate can now be established. Groups 2, 4, and 5 dissociate the first proton almost simultaneously, but the species where group 2 is dissociated dominates. When the second proton dissociates, the prevalent microstate is the one where groups 2 and 5 are dissociated. Within the last deprotonation step, the relevant microspecies feature a deprotonated group 2.

The major simplification introduced by the cluster expansion should be clear now. The D-myo-inositol 1,2,4,5-tetrakisphosphate involves 32 different microconstants, from which 15 are independent, but only 13 of those can be determined from titration curves.²¹ The cluster expansion groups these parameters into 4 intrinsic constants and 11 interaction parameters, whereby 6 involve pairs, 4 triplets, and one quadruplet. For this molecule, the quadruplet contribution corresponds to the highest-order interaction present, and can be neglected. By considering their distance dependence, we identify 6 as the most important ones, namely 5 pair interactions and one triplet. The intrinsic description now involves 10 parameters. For this molecule, a direct analysis in terms of microscopic equilibria would be a daunting task.

Molecular symmetries

The number of independent parameters entering the intrinsic model can be further reduced by invoking molecular symmetries. The reduction in the number of parameters can be so substantial that microequilibria can be fully resolved from the macroconstants of a single molecule in favorable cases.

The simplest example of this situation is realized with symmetric diprotic acids or bases (e.g., aliphatic dicarboxylic acids and diamines).^31,40,41 Since both ionizable groups are equivalent, one has one intrinsic constant and one pair interaction parameter. These two parameters can be obtained from the two macroconstants accessible by potentiometry. One finds that the resulting interaction parameter decreases strongly with increasing separation between the ionizable groups. This dependence reflects the importance of electrostatic interactions and confirms that interactions between more distant groups are negligible.³¹ These interactions depend on the ionic strength only weakly, since the electrostatic interactions are mainly mediated through the molecular backbone of low dielectric permittivity.^40,42

By invoking molecular symmetries and group transferability simultaneously, microscopic equilibria can be resolved from macroconstants even for rather complex molecules. For example, consider linear aliphatic pentamine 2,2,2,2-pent (Fig. 4). Trying to obtain 80 microconstants from 5 macroconstants may seem impossible. However, these microconstants can be obtained by applying the above principles. We first assume that there are only two different intrinsic constants, namely one for the primary amine and one for the secondary amine. The number of interaction parameters can be reduced by exploiting their short ranged nature. When one assumes nearest neighbor pair interactions only, the resulting model fits poorly. The quality of the fit improves substantially when interactions involving three neighboring sites are included, namely triplet interactions and pair interactions between next nearest neighbors. These 5 parameters can be obtained from the 5 known macroconstants, and one finds that the latter pair interaction is negligible. The final intrinsic model thus involves 4 parameters, namely two intrinsic constants, one nearest neighbor pair interaction, and one triplet interaction (Fig. 4). These 4 parameters can be obtained with a least squares fit of the 5 macroconstants, and this model describes these constants within experimental error. Once these parameters are known, one can evaluate all microconstants and other properties of interest. The present results can be confirmed by an analysis of site-specific ¹³C-NMR titration curves of 2,2,2,2-pent, which yields very similar parameters.²⁶ In this case, however, cross-coupling of the chemical shifts between different carbon atoms must be considered.¹⁹ Such coupling is also important in ¹⁵N-NMR titrations.²⁶ These coupling effects may be further complicated by conformational changes, which can be sometimes resolved with multi-dimensional NMR techniques.⁴³

Fig. 4 The ionization process of 1,4,7,10,13-pentaazatridecane (2,2,2,2-pent) at 0.1 M and 25 °C. (a) The structural formula, (b) intrinsic, (c) macroscopic, and (d) microscopic models showing the prevalent microspecies. The intrinsic model was calibrated on the experimental macroconstants. Calculated (e) site-specific titration curves (f) and the macroscopic prevalence diagram.

From this intrinsic model the protonation mechanism of 2,2,2,2-pent can be deduced (Fig. 4). When decreasing the pH, the primary amine group protonates first. In the second protonation step, the other primary amine group is protonated, even though the species with the central amine group protonated is present in small quantities as well. The third protonation step forms the dominant microspecies where the primary amines and the central secondary amine are protonated. The two prevalent microspecies, where one group remains deprotonated, involve the ones with deprotonated secondary amines. This microspecies leads to the pronounced minimum in the site specific titration curve, which has also been observed with ¹³C-NMR.²⁶

Homologous series

Symmetry considerations are sometimes insufficient to constrain the problem such that these parameters can be determined from macroconstants only. In this case, consideration of a homologous series may help. As an example consider the resolution of microequilibria of the biologically relevant 3,4,3-tet or spermine (Fig. 5). Since the amine groups are well separated, one may consider nearest neighbor pair interactions only. There are two such parameters and two different intrinsic constants, which yield 4 unknown parameters. While 4 macroconstants should be sufficient to obtain those unknowns, their values are strongly correlated. This problem can be circumvented by simultaneously considering the homologue 3,3,3-tet or thermine. Supposing that the pair interactions are the same in both molecules, there are 2 additional unknown intrinsic constants. Least-squares fit now yields 6 unknown constants from 8 known macroconstants unanimously. These results can be confirmed by analyzing ¹³C-NMR titration data of spermine, which yield a very similar intrinsic parameter set.²⁷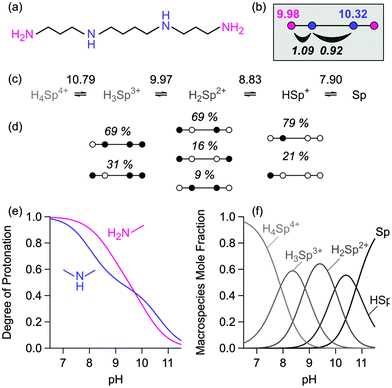

Fig. 5 The ionization process of 1,5,10,14-tetraazatetradecane (3,4,3-tet, spermine) at 0.1 M and 25 °C. (a) Structural formula, (b) intrinsic, (c) macroscopic, and (d) microscopic models showing the prevalent microspecies. The intrinsic model was calibrated on the experimental macroconstants of 3,3,3-tet and 3,4,3-tet (Table 1). Calculated (e) site-specific titration curves (f) and the macroscopic prevalence diagram.

The intrinsic protonation mechanism of spermine can now be deduced (Fig. 5). Under basic conditions, the secondary amine is preferentially protonated due to its somewhat larger basicity. In the next step, the distant primary amine is principally protonated, since in this fashion the molecule can avoid all pair interactions. Subsequently, the other secondary amine is protonated due to the larger basicity of this group.

Our results for 2,2,2,2-pent can also be confirmed with a homologous series. When 2,2-tri and 2,2,2-tet are considered together with 2,2,2,2-pent, one has 12 macroconstants that should be described with the same intrinsic model containing 4 parameters. The best fit results are shown in Table 1, and the resulting parameters turn out to be very similar to the ones obtained from 2,2,2,2-pent only.³¹

Table 1 Macroscopic protonation constants of linear aliphatic polyamines at 0.1 M and 25 °C³⁵ together with calculated values from the intrinsic model

Molecule	n	Macroconstants pKn
		Exp.	Calc.	Diff.
1,5,10,14-Tetraazatetradecane 3,4,3-tet, spermine	1	10.78	10.79	−0.01
	2	9.98	9.97	+0.01
	3	8.85	8.83	+0.02
	4	7.90	7.90	0.00
1,5,9,13-Tetraazatridecane 3,3,3-tet, thermine	1	10.48	10.46	+0.02
	2	9.84	9.83	+0.01
	3	8.51	8.59	−0.08
	4	7.22	7.19	+0.03
1,4,7-Triazaheptane 2,2-tri	1	9.84	9.73	+0.11
	2	9.02	9.10	−0.08
	3	4.25	4.08	+0.17
1,4,7,10-Tetraazadecane 2,2,2-tet	1	9.75	9.74	+0.01
	2	9.07	9.13	−0.06
	3	6.58	6.60	+0.02
	4	3.27	3.34	−0.07
1,4,7,10,13-Pentaazatridecane 2,2,2,2-pent	1	9.76	9.75	+0.01
	2	9.18	9.17	+0.01
	3	8.10	8.09	+0.01
	4	4.65	4.74	−0.09
	5	2.97	2.97	+0.00

---

Polyelectrolytes, dendrimers, and proteins

The intrinsic model can also be used to describe the ionization behavior of molecules with a larger number of sites.^4,16 Linear polyelectrolytes with closely spaced sites ionize in two steps (e.g., linear polyethylene imine and polymaleic acid). Their titration curve features an intermediate plateau at a protonation degree of 1/2. This plateau originates from the stability of the intermediate microstate with alternating protonated and deprotonated sites (Fig. 4d and 6a). Comb-like polyelectrolytes show two intermediate plateaus in the titration curve at 1/2 and 3/4, which can be traced to two stable microstates (Fig. 6b).⁴⁴ The intermediate plateau at 2/3 observed for polypropyleneimine dendrimers is due to a stable even–odd shell microstate (Fig. 6c).³² The ionization mechanism of polyamidoamine dendrimers is different, however. They feature an intermediate plateau at 1/2, which is a consequence of the stability of a microstate where all primary amine groups are protonated (Fig. 6d).⁴⁵ The different structure of the stable microstate results from weak site interactions, but widely different proton affinities of the primary and tertiary amine groups. For polypropyleneimine dendrimers, the site interactions are much stronger, while the affinities of the different amine groups are similar.

Fig. 6 Stable microstates for strongly interacting (a) linear and (b) comb-like polyelectrolytes, and (c) polypropyleneimine or (d) polyamidoamine dendrimers.

When the ionizable groups are situated further apart, the effect of interactions remains weak. When a larger number of neighboring groups are involved, however, their effect may be still important, and usually leads to a diffuse broadening of the titration curve. One observes this situation in more weakly charged polyelectrolytes (e.g., polyvinylamine and polyacrylic acid). Proteins are characterized by a wide distribution in the affinities of the ionizable residues, but by weak site interactions as well.¹⁶

Outlook

The intrinsic approach to fully resolve microscopic ionization equilibria is discussed. Thereby, one assigns an intrinsic constant to each ionizable group, and introduces interactions between these sites. The interactions among pairs of neighboring sites are the most important ones. Their strength decreases rapidly with increasing distance between the sites. While higher order interactions may also be considered, only triplet interactions between neighboring sites seem relevant. By exploring molecular symmetries and group transferability, the intrinsic model can describe even rather complex molecules with a small number of parameters. Once these parameters are known, one can calculate other quantities of interest, including macroconstants, microconstants, and microstate mole fractions. These quantities provide insight into the protonation mechanism of the molecules in question.

The parameters entering the intrinsic model can be obtained by fitting experimental data, but two approaches appear to be most promising. The first approach relies on potentiometric titration data or the corresponding macroconstants. The parameter determination can be simplified by exploiting molecular symmetries, group transferability, or homologous series. The other powerful approach is the analysis of NMR titration curves, from which site-specific titration curves can be extracted. One might be also able to use other spectroscopic techniques, but as a rule, NMR is unsurpassed in terms of selectivity and resolution.^19,27 However, even site-specific titration curves may be insufficient to determine all relevant intrinsic parameters.²¹ In such cases, a combined analysis of homologous series and of group transferability might help to resolve the problem.⁴⁶

While various approaches are now available to determine the intrinsic parameters, their molecular interpretation may be nontrivial. The microconstants often obey the group additivity relationships, but these shifts may be complicated by longer ranged interactions and resonance effects.² For example, secondary amines are more basic than primary ones in spermine, but more acidic in 2,2,2,2-pent. The latter shift is related to the electron withdrawing effect of neighboring amine groups.² The interaction parameters normally decrease with increasing distance between the ionizable groups, mainly due to the important role of Coulombic forces in these interactions. However, these parameters can be strongly influenced through their coupling to conformational degrees of freedom. In some cases, this coupling may even induce negative interactions and cooperative effects, as illustrated with 1,2,4,5-tetrakisphosphate here.

References

1. C. R. Cantor and P. R. Schimmel, Biophysical Chemistry. Part III. The Behavior of Biological Macromolecules, Freeman, New York, 1980.
2. D. D. Perrin, B. Dempsey and E. P. Serjeant, pKa Prediction for Organic Acids and Bases, Chapman and Hall, New York, 1981.
3. A. Onufriev, D. A. Case and G. M. Ullmann, Biochemistry, 2001, 40, 3413–3419.
4. G. J. M. Koper and M. Borkovec, Polymer, 2010, 51, 5649–5662.
5. G. Ercolani and L. Schiaffino, Angew. Chem., Int. Ed., 2011, 50, 1762–1768.
6. I. Szilagyi, I. Labadi, K. Hernadi, I. Palinko, N. V. Nagy, L. Korecz, A. Rockenbauer, Z. Kele and T. Kiss, J. Inorg. Biochem., 2005, 99, 1619–1629.
7. J. Hamacek, J. Alloys Compd., 2008, 451, 347–351.
8. N. Dalla Favera, U. Kiehne, J. Bunzen, S. Hytteballe, A. Lutzen and C. Piguet, Angew. Chem., Int. Ed., 2010, 49, 125–128.
9. B. Noszal, in Biocoordination Chemistry: Coordination Equilibria in Biologically Active Systems, ed. K. Burger, Ellis Horwood, Chichester, 1990, pp. 18–55.
10. T. Kesvatera, B. Jonsson, E. Thulin and S. Linse, Proteins, 1999, 37, 106–115.
11. M. Schaefer, M. Sommer and M. Karplus, J. Phys. Chem. B, 1997, 101, 1663–1683.
12. P. Cordier, F. Tournilhac, C. Soulie-Ziakovic and L. Leibler, Nature, 2008, 451, 977–980.
13. L. Brunsveld, B. J. B. Folmer, E. W. Meijer and R. P. Sijbesma, Chem. Rev., 2001, 101, 4071–4097.
14. M. L. Machesky, M. Predota, D. J. Wesolowski, L. Vlcek, P. T. Cummings, J. Rosenqvist, M. K. Ridley, J. D. Kubicki, A. V. Bandura, N. Kumar and J. O. Sofo, Langmuir, 2008, 24, 12331–12339.
15. J. Wyman and S. J. Gill, Binding and Linkage, University Science Books, Mill Valley, 1990.
16. D. Bashford, Front. Biosci., 2004, 9, 1082–1099.
17. M. Borkovec, G. J. M. Koper and C. Piguet, Curr. Opin. Colloid Interface Sci., 2006, 11, 280–289.
18. K. Mernissi-Arifi, L. Schmitt, G. Schlewer and B. Spiess, Anal. Chem., 1995, 67, 2567–2574.
19. Z. Szakacs, M. Kraszni and B. Noszal, Anal. Bioanal. Chem., 2004, 378, 1428–1448.
20. E. J. King, Acid-Base Equilibria, Pregamon Press, New York, 1965.
21. G. M. Ullmann, J. Phys. Chem. B, 2003, 107, 1263–1271.
22. J. G. Kirkwood and J. B. Shumaker, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 855–862.
23. R. F. Steiner, J. Chem. Phys., 1954, 22, 1458–1459.
24. R. A. Marcus, J. Phys. Chem., 1954, 58, 621–623.
25. D. Bashford and M. Karplus, J. Phys. Chem., 1991, 95, 9556–9561.
26. M. Borkovec and G. J. M. Koper, Anal. Chem., 2000, 72, 3272–3279.
27. C. Frassineti, L. Alderighi, P. Gans, A. Sabatini, A. Vacca and S. Ghelli, Anal. Bioanal. Chem., 2003, 376, 1041–1052.
28. F. A. Plamper, H. Becker, M. Lanzendorfer, M. Patel, A. Wittemann, M. Ballauff and A. H. E. Muller, Macromol. Chem. Phys., 2005, 206, 1813–1825.
29. Y. H. Niu, L. Sun and R. A. Crooks, Macromolecules, 2003, 36, 5725–5731.
30. J. Weisell, J. Vepsalainen and M. Perakyla, J. Phys. Org. Chem., 2013, 26, 360–366.
31. M. Borkovec and G. J. M. Koper, J. Phys. Chem., 1994, 98, 6038–6045.
32. G. J. M. Koper, M. H. P. van Genderen, C. Elissen-Roman, M. W. P. L. Baars, E. W. Meijer and M. Borkovec, J. Am. Chem. Soc., 1997, 119, 6512–6521.
33. M. Borkovec, D. Cakara and G. J. M. Koper, J. Phys. Chem. B, 2012, 116, 4300–4309.
34. M. Borkovec, B. Jonsson and G. J. M. Koper, Surf. Colloid Sci., 2001, 16, 99–339.
35. A. E. Martell, R. M. Smith and R. J. Motekaitis, Critically Selected Stability Constants of Metal Complexes: Version 8.0., National Institute of Standards and Technology, Gainesburg, 2004.
36. R. W. Hay and L. J. Porter, J. Chem. Soc. B, 1967, 1261–1264.
37. K. Mernissi-Arifi, G. Schlewer and B. Spiess, Carbohydr. Res., 1998, 308, 9–17.
38. J. L. Garces, G. J. M. Koper and M. Borkovec, J. Phys. Chem., 2006, 110, 10937–10950.
39. M. Borkovec and B. Spiess, Phys. Chem. Chem. Phys., 2004, 6, 1144–1151.
40. F. H. Westheimer and M. W. Shookhoff, J. Am. Chem. Soc., 1939, 61, 555–560.
41. M. J. Potter, M. K. Gilson and J. A. McCammon, J. Am. Chem. Soc., 1994, 116, 10298–10299.
42. M. Borkovec, J. Daicic and G. J. M. Koper, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 3499–3503.
43. S. J. Baturin, M. Okon and L. P. McIntosh, J. Biomol. NMR, 2011, 51, 379–394.
44. G. J. M. Koper, R. C. van Duijvenbode, D. D. P. W. Stam, U. Steuerle and M. Borkovec, Macromolecules, 2003, 36, 2500–2507.
45. D. Cakara, J. Kleimann and M. Borkovec, Macromolecules, 2003, 36, 4201–4207.
46. G. Orgovan and B. Noszal, J. Pharm. Biomed. Anal., 2011, 54, 965–971.

---