The role of electrostatic induction in secondary isotope effects on acidity: theory and computational confirmation

Abstract

The role of electrostatic induction in secondary isotope effects (SIEs) on acidity is reconsidered. A first order perturbation treatment demonstrates that an electric charge acting on a C–H bond vibrating in its anharmonic potential induces a mass-dependent change in its harmonic force constant and – accordingly – an isotope-dependent shift of its zero-point vibrational energy (ZPVE). Its sense and magnitude are determined by the bond-dipole derivative, dμ/dr. The SIE on the dissociation equilibrium of formic acid was evaluated by gas-phase computations (MP2/311G**) on formic acid and the formate ion, bare and variously hydrated. The CH-stretching frequencies, as well as the IEs on the ZPVE and free energy of ionization (ΔG⁰₂₉₈), are in linear correlation with Δμ/Δr_e, the ratio of the change in the C–H bond moment upon protonation to the corresponding equilibrium bond length difference, suggesting that Δμ/Δr_e is an adequate linear approximation to dμ/dr and confirming the electrostatic origin of the isotope effect. Similar computations on the dissociation of acetic acid and methylammonium ions yield analogous results. In both cases, the mean equilibrium length of the methyl CH bonds, r_m, depends strongly on μ_g, the CH₃ group dipole moment and, when allowance is made for steric effects, the IEs on ZPVE and ΔG⁰₂₉₈ are in linear correlation with μ_g. In each of the three equilibria, the isotopic ΔpK_a value computed for the polyhydrated acid and conjugate base is smaller – in the case of the carboxylic acids much smaller – than that computed with the bare species, reproducing the published experimental values in aqueous solution to within a factor of two.

---

1. Introduction

The inductive effect is defined in the IUPAC Gold Book as “an experimentally observable effect … of the transmission of charge through a chain of atoms by electrostatic induction”. The initial observation that substitution of hydrogen by deuterium in the alkyl group of a carboxylic acid reduces its acidity and that a similar substitution in an alkylamine increases its basicity was attributed to electrostatic induction, in analogy to the very much larger inductive effects of chemically distinct substituent atoms and groups.^1–3 Accordingly, it was concluded that deuterium bound to a carbon atom is effectively more electropositive than protium. The reduced acidity of deuterioformic acid relative to normal formic acid could be attributed to differential polarization of deuterium relative to protium by the negatively charged carboxylate ion, and the reduced acidity of methyl-deuterated acetic acid to transmission of the induced negative charge to the methyl H/D atoms via the C-atom as the one-link “chain”.

Analogous secondary deuterium isotope effects (SIEs) had already been observed on the rates of solvolysis and ascribed to less effective hyperconjugative electron release from deuterium than from protium.^4,5 These SIEs, as well as others that showed up soon thereafter in a variety of reactions, were discussed in similar terms: inductive, hyperconjugative, steric and hybridization-dependent, and were reviewed by this author half a century ago.⁶ While it is universally recognized that isotope effects are vibrational in origin, the practice of discussing secondary deuterium isotope effects in terms that characterize genuine electronic, stereoelectronic and steric substituent effects persists in the current physical organic and biochemical literature.⁷

Charles Perrin and his co-workers carried out an extensive re-investigation of the secondary deuterium isotope effects on the acidity of carboxylic acids,⁸ and the basicity of amines.^9,10 While the authors' experimental data are unexceptionable, Perrin and Flach's conclusion that “[there is] no contribution of an inductive effect to secondary deuterium isotope effects on acidity”,¹¹ which was emphasized in Perrin's review of the field¹² and is already being cited in textbooks as an established fact,¹³ bears scrutiny.

The theoretical justification for assigning a dominant role to electrostatic induction in SIEs on acidity is outlined in the following section; the mathematical proof is relegated to the Appendix (Section 5). In the subsequent sections the results of computations on the secondary deuterium isotope effects on three prototypical acid–base equilibria:

HCO₂H ⇋ HCO₂⁻ + H⁺ (1)

CH₃CO₂H ⇋ CH₃CO₂⁻ + H⁺ (2)

CH₃NH₂ + H⁺ ⇋ CH₃NH₃⁺ (3)

are presented and compared with published experimental data. The computations were carried out on the protio- and deuterio-isotopologs of each acid and its conjugate base, and the isotopic free energy differences (ΔΔG⁰₂₉₈) between them were correlated with their structural and polar parameters. In each case, the computations were carried out first with the bare acid and its conjugate base and then on variously hydrated reactants, in order to gain insight into the factors that modify the IE in aqueous solution. As a compromise between the high accuracy required and the large number of computations that had to be carried out routinely, they were performed using the Gaussian G03W program¹⁴ at the MP2 level with the 6-311G** basis set, which allows for polarization of the hydrogen atoms.

2. Theoretical considerations

Perrin and Flach reject the contribution of electrostatic induction to the SIE on acidity because, in solution, it manifests itself almost entirely in the enthalpy of reaction, whereas they argue that the inductive effect must appear in its entropy.¹⁵ It must be recognized that polarization of an atom within a molecule is an electronic phenomenon. As such, it operates in the gas phase at absolute zero, at which the entropy of reaction necessarily vanishes, except for the possible trivial incursion of a symmetry number. Therefore, in the gas phase reaction at 0 K, IEs due to electrostatic induction cannot appear in the entropy of reaction. The entropy of solvation, as well as the entropy due to the internal motions of the reactants, may indeed contribute to SIEs on acidity in solution at ambient temperature, but it is not a criterion for the presence or absence of an inductive effect.

The second argument raised against assigning a significant role to electrostatic induction deserves consideration in detail. It runs as follows: SIEs, like all isotope effects, can be attributed solely to vibrational frequency shifts, whereas the inductive effect is an electronic phenomenon that – at most – can make a trivial contribution to them. Specifically, electrostatic induction depends on the charge–dipole interaction, whereas the dipole moment differences between the isotopologs, which are due to the anharmonicity of the CH/CD stretching modes, are too small to account for the SIEs on acidity.

Although it is possible to compute isotope effects without separating the energy into its nuclear and electronic components, as for example by the “nuclear-electronic approach” of Hammes–Schiffer,¹⁶ the conventional procedure is to separate them.¹⁷ It is assumed that the reaction occurs on a single adiabatic potential energy surface based on the Born–Oppenheimer approximation, and that the relativistic effects can be neglected. If the vibrations are harmonic and the rotations are regarded as classical, all IEs can be expressed as ratios of the relevant vibrational partition functions, which – for the isotopes of hydrogen at moderate temperatures – are dominated by differences in their zero-point vibrational energy (ZPVE). However, the fact that this approximation constrains isotopologs to have the same electronic energy does not mean that electronic phenomena cannot give rise to isotope effects. It merely requires that these effects, including those that are due to the anharmonicity of vibrational modes, are incorporated in isotope-dependent shifts of their frequencies. This is true for all so-called isotopic substituent effects: inductive, hyperconjugative, steric, hybridization-dependent, etc.

The mechanism by which this occurs in the case of electrostatic polarization was demonstrated with a simple model reaction, developed in discussions with Professors Ruben Pauncz and Max Wolfsberg at the Uppsala University Summer School in Lidingö, Sweden in the summer of 1959, and summarized in ref. 6. An amplified version of the formal proof is given below in the Appendix (Section 5).

First order perturbation theory is applied to an idealized “reaction”, in which an isolated vibrating H–X bond is perturbed by a positive charge placed along its axis towards its X end (Fig. 1). It is postulated that electrical anharmonicity can be neglected, i.e. that the perturbing potential (ax) is effectively linear over the vibrational amplitude. If the one-dimensional potential is purely harmonic, the potential energy curve is shifted upwards or downwards, so that the equilibrium bond length is increased or decreased (Fig. 2), but its curvature remains the same. Thus, the quadratic force constant common to both the H–X bond and the corresponding D–X bond is unchanged, so the frequencies and the isotopic ZPVE difference of the perturbed bonds (the “products”) are the same as those of the unperturbed bonds (the “reactants”); hence no isotope effect. However, if the model's potential well is anharmonic, i.e. includes a cubic term (gx³) in the expression for the potential energy, the harmonic force constant at the displaced minimum changes, resulting in a change in the vibrational frequency and ZPVE of the perturbed bond. Thus, rather than being an additional factor, separate from the vibrational frequency shifts, electric polarization is the driving force for their occurrence.

Fig. 1 Interaction of a charge with a bond vibrating in an anharmonic potential (from ref. 6).

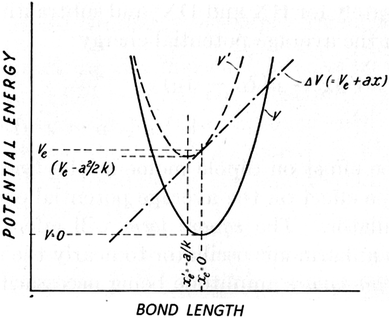Fig. 2 Effect of a linear perturbation on a harmonic potential (from ref. 6).

The direction of the IE depends on the bond's dipole moment derivative (dμ/dr). For example, if X is chlorine, the polarity of the Cl–H bond dipole is Cl^δ−H^δ+, so the interaction of the perturbing positive charge with the bond dipole is attractive. As a result, the equilibrium bond length (r_e) is increased and the potential energy minimum is lowered. (Fig. 2 illustrates the reverse situation: a repulsive interaction that increases with bond extension. The curve is shifted upward and r_e is decreased.)

The dipole moment derivative of HCl is positive,^18,19i.e., μ increases as the bond is stretched and decreases as it contracts. The charge–dipole interaction is attractive, so the potential energy of the vibrating bond decreases during expansion and increases during compression. In a harmonic potential, its average value does not change, as stabilization during bond extension is exactly compensated by destabilization during contraction. In an anharmonic potential, the positive displacement during extension is larger than the negative displacement during contraction. Therefore, the potential energy – averaged over the vibrational cycle – is diminished by reducing the harmonic force constant, lowering the frequency of the vibration and increasing its amplitude.

A conceptual error that has led to a gross underestimate of the role of anharmonicity in the secondary isotope effects is the misidentification of the potential energy of a bond computed at its vibrationally averaged distance r̄₀ with the average value of the potential energy computed over the vibrational cycle.²⁰ The X–H bond length, averaged over its zeroth vibrational level r̄^H₀, is slightly longer than the similarly averaged X–D bond, r̄^D₀, which lies below it in the anharmonic potential well (Fig. 1). The dipole moments of X–H and X–D differ accordingly. The isotope effect on the potential energy computed at these slightly different bond lengths is very small, reflecting the change in the charge–dipole interaction in the shallow region near the minimum of the potential well. In contrast, the average potential energy samples the interaction over the entire vibrational amplitude, from the bond's minimal length at compression to its length at full extension. Thanks to the cubic term, gx³, in the anharmonic potential (see Appendix), the interaction is strongest when the bond is fully extended. Thus, depending on whether the cubic coefficient is positive or negative, the electrostatic perturbation raises or lowers the average potential energy of the X–D bond less than that of the X–H bond, which extends farther during the expansion phase of the vibration. This point is illustrated computationally below in Section 3.1.3 (Digression). It should be noted that the virial theorem requires the average potential energy of the harmonic oscillator to be exactly half of its total vibrational energy. At 0 K this holds in good approximation for the anharmonic oscillator as well, so the average potential energy is very close to half of the ZPVE.

3. Results and discussion

3.1. Deuterium isotope effect on the acidity of formic acid

3.1.1 The gas phase reaction. We consider protonation of a formate ion in terms of the model illustrated in Fig. 1. The perturbation is the positive charge of the proton attached to its carboxylate group. In our model it is entirely electrostatic, due to interaction of the perturbing charge with the dipole of the C–H bond, vibrating in its anharmonic potential. The CH-bond dipole, μ, is:

μ = 1/2 (q_C − q_H) r_CH (4)

i.e., half the difference in atomic charge between the H and C atoms multiplied by the distance between them. In a diatomic molecule, in which the charges are equal and opposite, μ would be the molecular dipole moment. We assume it to be an intrinsic property of the bond that varies monotonically between the anion and the acid, and postulate that dμ/dr is the same in both the acid and anion.²¹ This allows us to regard Δμ/Δr_e, the difference between the values of the C–H bond dipole in the acid and the anion as a linear approximation to dμ/dr.

As shown in Table 1, the long CH-bond of the formate ion is shortened upon protonation and its stretching frequency is increased accordingly. The correlation of the frequency change, and hence of the IE on acidity, with Δμ/Δr_e should go a long way to confirm its electrostatic origin.

Table 1 Charge distribution and CH-bond dipole moment in formic acid and the formate ion at their equilibrium geometries (MP2/6-311G**)

	Atomic charge scale	Charge on H-atom (e)	Charge on C-atom (e)	CH bond moment^a (Debye)	CH bond length (Å)	CH-stretch frequency (cm^−1)
a 1 eÅ = 4.8032 Debye.
HCOOH	Mulliken	0.105	0.446	0.899	1.0972	3120.7
	APT	−0.005	1.041	2.756
HCOO^−	Mulliken	−0.118	0.419	1.482	1.1493	2511.1
	APT	−0.309	1.247	4.293
Δ(HCOOH–HCOO^−)	Mulliken	0.223	0.027	−0.583	−0.0521	609.6
	APT	0.304	−0.206	−1.537

---

The Gaussian program provides two estimates of atomic charge distribution, the familiar Mulliken scale and the APT (Atomic Polar Tensor) scale.²² According to both, the bond is polarized in the sense C^δ+H^δ−, which will henceforth be referred to as positive. The Mulliken and APT charge distributions differ widely in both the acid and anion,²³ but both schemes yield a larger C–H bond dipole in the anion than in the acid (Δμ = −0.583 and −1.537 Debye Å⁻¹ respectively).

Evidently, the bond-moment derivative, dμ/dr, is positive, i.e. the dipole moment increases with the bond length.²⁴ Protonation of the anion interacts repulsively with the C–H dipole, reducing it, shortening the CH-bond and increasing the force constant for the CH-stretching mode of formic acid (6.272 mdyn Å⁻¹) above that of the formate ion (3.930 mdyn Å⁻¹). Consequently, the frequency of the CH/CD-stretching mode is increased for both isotopologs: HCOOH: 3120.7 cm⁻¹ and DCOOH: 2319.9 cm⁻¹vs. HCOO: 2511.1 cm⁻¹ and DCOO⁻: 1828.5 cm⁻¹. Thus, the corresponding increase in ZPVE is less for the deuterated formate ion (Δν = 246 cm⁻¹) than for its protio isotopolog (Δν = 305 cm⁻¹), so it is the stronger base; accordingly, deuterated formic acid is a weaker acid than normal formic acid.

In order to estimate the extent to which isotopic ZPVE differences determine the IE at ambient temperature, we consider the computed thermochemical properties at 1 atm and 298 K, summarized in Table 2. Although thermal excitation of the vibrations and rotations makes a substantial contribution to the enthalpy and entropy of each of the four entities, it is cancelled out almost entirely in the IE. Thus, ΔΔH⁰₂₉₈ and ΔΔG⁰₂₉₈ are both dominated by ΔΔZPVE, approximately 60% of which is due directly to the CH/CD stretching frequency.

Table 2 Thermochemical data (kcal mol⁻¹) for gas phase protonation of the formate ion (MP2/6-311G**)

	G ^0298	ZPVE^a	H ^0298	TS^0298
a In parentheses: contribution of CH/CD-stretching mode.
HCO2H	6.482	21.590 (4.461)	24.160	17.678
DCO2H	4.329	19.567 (3.316)	22.174	17.845
Δ isotopic	2.153	2.023 (1.145)	1.986	−0.167
HCO2^−	−1.819	12.702 (3.590)	15.157	16.976
DCO2^−	−3.723	10.955 (2.614)	13.439	17.162
Δ isotopic	1.904	1.747 (0.976)	1.717	−0.186
ΔΔ acid–anion	0.249	0.276 (0.169)	0.269	0.019

---

The computed value, ΔΔG⁰₂₉₈ = 0.249 kcal mol⁻¹, corresponds to ΔpK_a = −0.183 (K_H/K_D = 1.52) for gas phase deprotonation of formic acid. It is in reasonably good agreement with the values (−ΔpK_a = 0.140–0.164) computed by Perrin and Dong⁸ with a variety of methods, none of which allows for H-atom polarization. Moreover, all of their values are based directly on ΔΔZPVE; i.e., they apply to the gas-phase reaction at 0 K, at which the present computation yields ΔpK_a = −0.202 (K_HK_D = 1.59). All of the computations predict an IE in the gas phase that is much larger than that measured in aqueous solution²⁵ (K_H/K_D = 1.082; ΔpK_a = 0.0342), where solvation evidently has a strong moderating effect.

3.1.2 The effect of hydration. Hydrogen bonding of water molecules to the carboxylate O-atoms would be expected to act in the same direction as protonation, decreasing the bond's dipole moment, shortening it and increasing the frequency of its stretching mode. As a consequence, the isotopic zero point energy differences should decrease as hydration of the anion becomes more efficient. Hydration of the acid molecule is expected to be less significant but cannot be ignored.

Seven hydrates of the formate ion were optimized: a monohydrate (1), two dihydrates (2, 3), two trihydrates (4, 5), and two tetrahydrates (6, 7). Seven hydrates of formic acid were similarly optimized: a monohydrate (8), two dihydrates (9, 10), three trihydrates (11, 12, 13) and a tetrahydrate (14).

Needless to say, these two sets of hydrates do not exhaust the possibilities. Stangret and his collaborators,²⁶ employing IR spectroscopy of HDO and DFT computations, characterized hydrated formate ions containing up to seven water molecules, whereas Chizhik and his coworkers,²⁷ using nuclear magnetic relaxation data, identified hydrated acetate ions with as many as sixteen water molecules. However, computations with the Reference Interaction Site Model (RISM)²⁸ indicate that the average number of H-bonds formed by the carboxylate group of the acetate ion in aqueous solution is 6 and those formed by the carboxyl group of acetic acid average only 2.5.²⁹ Moreover, it can be assumed that the charge density at the C–H bond of the formate ion will be primarily affected by direct bonding to the carboxylate O-atoms, which can accommodate no more than four H-bonds. Thus, at most four water molecules can be H-bonded directly to the ion. The additional water molecules in the hydration shell, being bonded to one another, can presumably have only a secondary effect. Hydration of the acid is less pronounced than that of the anion, so it was taken as a working hypothesis that the anion hydrates (1–7) and acid hydrates (8–14) would suffice to indicate a trend. Their relevant properties are summarized in Tables 3 and 4.

Table 3 Dependence on hydration of the thermochemical properties of the formate ion and the formate-d ion (MP2/6-311G**)

Formate ion hydrates	ΔG^0hydration ^a	ΔZPVE^a	ΔH^0^a	ΔTS^0^a	ΔG^0^a	r e (Å)	μ CH ^b
a kcal mol^−1. b Debye, calculated with Mulliken charges.
H/DCO2^−	—	1.748	1.717	−0.186	1.904	1.1493	1.482
H/DCO2^−⋯H2O (1)	−14.051	1.854	1.795	−0.180	1.975	1.1325	1.311
H/DCO2^−⋯(H2O)2 (2)	−18.438	1.917	1.855	−0.173	2.028	1.1264	1.370
H/DCO2^−⋯(H2O)2 (3)	−22.858	1.885	1.828	−0.180	2.007	1.1255	1.246
H/DCO2^−⋯(H2O)3 (4)	−27.231	1.965	1.897	−0.169	2.056	1.1180	1.251
H/DCO2^−⋯(H2O)3 (5)	−29.334	1.905	1.846	−0.187	2.023	1.1208	1.185
H/DCO2^−⋯(H2O)4 (6)	−34.093	1.916	1.854	−0.179	2.033	1.1189	1.172
H/DCO2^−⋯(H2O)4 (7)	−34.844	1.992	1.923	−0.165	2.089	1.1141	1.256

---

Table 4 Dependence on hydration of the thermochemical properties of formic acid and formic-d acid (MP2/6-311G**)

Formic acid hydrates	ΔG^0hydration ^a	ΔZPVE^a	ΔH^0^a	ΔTS^0 a	ΔG^0^a	r e (Å)	μ CH ^b
a kcal mol^−1. b Debye, calculated with Mulliken charges.
H/DCO2H	—	2.023	1.986	−0.167	2.153	1.0972	0.899
H/DCO2H⋯H2O (8)	−1.832	2.058	1.994	−0.164	2.158	1.0971	0.898
H/DCO2H⋯(H2O)2 (9)	−0.866	2.091	2.024	−0.159	2.183	1.0944	0.794
H/DCO2H⋯(H2O)2 (10)	−4.869	2.065	1.999	−0.163	2.162	1.0978	0.940
H/DCO2H⋯(H2O)3 (11)	−1.824	2.099	2.031	−0.156	2.187	1.0950	0.915
H/DCO2H⋯(H2O)3 (12)	−1.823	2.098	2.030	−0.157	2.187	1.0953	0.888
H/DCO2H⋯(H2O)3 (13)	−5.676	2.068	2.001	−0.163	2.164	1.0977	0.937
H/DCO2H⋯(H2O)4 (14)	+1.079	2.130	2.061	−0.150	2.211	1.0932	0.903

---

Fig. 3 shows an unweighted linear least-squares plot of the dipole moment (Mulliken) of the C–H bond vs. the equilibrium bond length for all of the data points in Tables 3 and 4. The slope of the plot, Δμ/Δr_e = 12.0 Debye Å⁻¹, is quite close to the value derived above for the bare anion and acid, Δμ/Δr_e = 11.2 (thin blue line). This supports the assumption that Δμ/Δr_e is an adequate approximation to the bond dipole moment derivative, dμ/dr, which – within our rather wide limits of precision – is constant over the entire range. The relative values for hydrates with the same n depend on the detailed structure of the hydrate, e.g., how large is the angle between the CH-bond and the molecular dipole moment, whether the water molecules are H-bonded directly to the carboxylate group or to other hydrating water molecules, whether or not they are close enough to the C–H bond to interact with them directly. For example, the three points above the line (2, 4 and 7) refer to hydrates in which the C-bonded H-atom is surrounded by hydrogen atoms of the hydrating water molecules, and can be presumed to be in steric interaction with them, increasing the C–H stretching frequency – and no-doubt the bending frequencies as well – above the increase caused by electrostatic induction.

Fig. 3 Correlation between the C–H bond moment and the bond length in variously hydrated HCO₂⁻ and HCOOH.

All of the points for the acid, including that of the bare molecule, are clustered at the left of the plot, confirming the insensitivity of the C–H bond length – and hence its vibrational frequency – to hydration. Comparing the structures of the monohydrated acid (8) and anion (1), we see that whereas in 1 the water molecule acts as an electrophile, withdrawing negative charge from the carboxylate O-atoms, the interaction in 8 is ambiphilic: withdrawing negative charge from one of the carboxyl group's O-atoms and feeding it to the other via its H-atom.

Fig. 4 shows an unweighted linear least-squares plot, for all of the data points in Tables 3 and 4, of the isotopic free energy difference, ΔG⁰, against the CH-bond dipole moment, μ (Mulliken).³⁰ Although ΔG⁰ and μ are plotted for convenience along the X and Y axis respectively, μ is clearly the independent variable and ΔG⁰ the dependent variable. The plot is reasonably linear; the rather low coefficient of determination (R² = 0.88) is due to the three anomalous formate points: 2, 4 and 7.

Fig. 4 Correlation between ΔG⁰ of H/DCO₂H and H/DCO₂ and the C–H bond dipole moment.

The formic acid points are not clumped together as closely as in Fig. 3. The points for monohydrate (8), dihydrate (10) and trihydrate (13) are very close to one another, but those for dihydrate (9), trihydrates (11) and (12), and tetrahydrate (14) extend to higher values of ΔG⁰ than would be expected on the basis of Δμ alone. Note that in all of the latter four hydrates H-atoms of the bound water molecules are contiguous to the H-atom of the C–H bond. The consequent steric repulsion is evidently responsible for increasing the frequencies of the C–H vibrations. Steric repulsion also appears to be the reason why, unlike 10 and 13, none of the sterically hindered polyhydrates has a significantly larger free energy of hydration than the monohydrate (8).

The linear correlation between Δμ and ΔG⁰ illustrated in Fig. 4 constitutes strong evidence that hydration reduces the magnitude of the SIE by moderating the electron demand of the carboxylate group in the formate ion, thus reducing its C–H stretching frequency. Departures from linearity occur for those hydrates of the formate ion (2, 4 and 7) and formic acid (9, 11, 12 and 14) in which the ZPVE is increased by superposition of a steric isotope effect.

In order to compare the results of gas phase computations on the various hydrates of formic acid and the formate ion with the experimental results, it must be decided which of the specific hydrates of the acid and anion are most likely to be present in dilute aqueous solution. We recognize that hydration of the anion is exergonic, favoring the higher hydrates. However, the standard free energy of hydration for the equilibrium:

HCO₂⁻ + nH₂O ⇋ HCO₂⁻⋯(H₂O)_n (5)

refers to the gas phase reaction at 25 °C and standard pressure, and does not take into account clustering of the n water molecules, as would occur in the liquid phase. Therefore, computations at the same computational level were carried out for a representative water dimer, trimer and tetramer. The respective free energies of dimerization, trimerization and tetramerization of water are: +0.856, −1.323 and −5.091 kcal mol⁻¹. They are much smaller in magnitude than the corresponding free energies of hydration of the anion (Table 3), so they do not upset the sequence favoring the tetrahydrates in aqueous solution. It follows that the dominant anion in solution would be a tetrahydrate. We note that 6 is, in effect, dihydrate 3 externally hydrated by two water molecules, whereas the four water molecules in 7 are H-bonded directly to the carboxylate group, filling its inner hydration shell and leaving room for further hydration. It can thus be assumed that 7 would be a better choice than 6 as the main form of the anion in solution. External hydration of 7 to form a loose hexahydrate, would be expected to increase ΔG⁰ slightly above the computed value, 2.089 kcal mol⁻¹.

It would not be correct to conclude similarly that the main form of the acid in solution would also be the tetrahydrate. In dilute aqueous solution the equilibrium in eqn (1) would indeed be shifted to the right, favouring the higher hydrates, however, from the values in Table 4, the standard free energy difference for the equilibrium:

HCO₂H⋯(H₂O)₃ + H₂O ⇋ HCO₂H⋯(H₂O)₄ (6)

is: ΔG⁰₂₉₈ = 6.75 kcal mol⁻¹. According to the model computations on water clusters mentioned above, the standard free energy difference for the equilibrium:

(H₂O)₃ + H₂O ⇋ (H₂O)₄ (7)

is ca. −3.75 kcal mol⁻¹. Thus, to the extent that extrapolation to the liquid phase is justified, the tetrahydrate (14) would be disfavoured relative to the most stable trihydrate (13) by over 10 kcal mol⁻¹, enough to guarantee that the latter would be the predominant hydrate of formic acid even in dilute solution.

Adopting the values ΔG⁰₂₉₈ = 2.164 kcal mol⁻¹ for the acid (13 in Table 4) and 2.089 kcal mol⁻¹ for the anion (7 in Table 3), we obtain ΔΔG⁰₂₉₈ = 0.075 kcal mol⁻¹ (ΔpK_a = −0.055; K_HK_D = 1.135), only slightly larger than the experimental result for the dissociation of formic acid in water (ΔpK_a = −0.034; K_HK_D = 1.082). As noted above, external hydration of 7 would be expected to bring it even closer.

3.1.3 Digression. As noted above, the average potential energy at the zeroth level of an anharmonic oscillator is close to half of the ZPVE. The Gaussian program provides for computation of the molecular geometry averaged over the ground vibrational level and the potential energy of the molecule frozen in that geometry. Table 5 lists these values for the isotopologs of formic acid and the formate ion. The corresponding bond dipole moments are estimated using the equation:

μ₀ = μ_e + (Δμ/Δr_e) (r̄₀ − r_e) (8)

The vibrationally averaged bond lengths (r̄^H₀ and r̄^D₀) of both the acid and anion are significantly larger than their equilibrium bond lengths (r_e), the difference being 0.0027 Å larger in the anion. The corresponding bond-dipole moment differences differ by 0.03 Debye. The energy difference computed for the anion frozen at r̄^H₀ and r̄^D₀ is larger by a minuscule 0.000034 Hartrees (0.021 kcal mol⁻¹) than the corresponding difference for the acid. This is less than 8% of the ZPVE difference for the bare acid and anion, 0.276 kcal mol⁻¹ (Table 2), or some 16% of the average potential energy. Thus, although the IE is indeed due to the charge–dipole interaction, any estimate of its magnitude based on the difference between the dipole moments of the isotopologs at their vibrationally averaged geometries, such as that attempted by Perrin and Dong,⁸ would be a gross underestimate.

Table 5 Vibrationally averaged CH–CD bond lengths, electronic energies and estimated bond dipoles (MP2/6-311G**)

	r̄ 0 (Å)	E el (Hartrees)	μ 0 (Debye)
a Calculated with eqn (8) (Δμ/Δr = 11.2).
Formic acid	r e = 1.0972	−189.351729	μ e = 0.899
r̄ ^H0 (HCO2H)	1.1065	−189.351585	1.003
r̄ ^D0 (DCO2H)	1.1050	−189.351606	0.986
Δ isotopic	0.0015	0.000021	0.017
Formate ion	r e = 1.1493	−188.769191	μ e = 1.482
r̄ ^CH0 (HCO2^−)	1.1685	−188.769010	1.697
r̄ ^CD0 (DCO2^−)	1.1643	−188.769065	1.650
Δ isotopic	0.0042	0.000055	0.047
ΔΔ (acid–anion)	−0.0027	−0.000034	−0.030

---

3.2. Deuterium isotope effect on the acidity of acetic acid

3.2.1 The gas phase reaction. The alkyl CH bond is normally polarized C^δ−–H^δ+ (negative) and its dipole derivative is negative, i.e., its magnitude increases upon compression.³¹ It is reversed to C^δ+–H^δ− when attached to a sufficiently electronegative substituent, in which case the dipole derivative changes sign – the bond dipole increases with expansion and decreases with compression, as in formic acid. Therefore, whether the C–H dipole is positive or negative, bond extension shifts the negative charge from carbon to hydrogen and contraction shifts it from hydrogen to carbon.

Table 6 lists the values of the projection on the C–C axis of the CH₃-group dipole moment, μ_g, computed with Mulliken and APT charges as the vector sum of the three CH-bond moments. Despite the disparity between the dipole moments computed for each species separately, both scales yield the same difference between the acid and its conjugate base, a reduction of 0.3 Debye. The mean equilibrium bond length of the three methyl bonds, r_m, is some 0.004 Å shorter in the acid than in the anion, so Δμ_g/Δr_m the quantity analogous to the bond dipole moment, Δμ/Δr_e, would be an enormous 75 Debye Å⁻¹.

Table 6 Correlation between the CH₃ dipole, equilibrium CH-bond length and C–H stretching frequency in acetic acid and the acetate ion. (MP2/6-311G**)

	Scale	μ g ^a (Debye)	r m ^b (Å)	ν sym ^c (cm^−1)
a Vector sum of C–H bond moments projected on the C–C axis. b Mean equilibrium C–H bond length. c Frequency of “symmetric” C–H-stretching mode.
CH3COOH	Mulliken	−1.165	1.0914	CH3 3086.7
	APT	−0.307		CD3 2219.4
CH3COO^−	Mulliken	−0.876	1.0961	CH3 3039.4
	APT	−0.004		CD3 2179.7
Δ (acid–anion)	Mulliken	0.289	−0.0041	CH3 47.3
	APT	0.303		CD3 39.7

---

Nevertheless, Δμ_g/Δr_m cannot be regarded as the methyl group's dipole moment derivative, because the variation in the length of the C–H bonds within each methyl group is no smaller than the difference between the two mean values (e.g., in the acid: r_e = 1.0881, 1.0931, 1.0931 Å). Nor does it take their varying angles relative to the C–C axis into account, and moreover, ignores the contribution of the CH-bending modes to μ_g. The latter is difficult to isolate because the bending modes mix with CH-stretching modes of the same symmetry species – particularly in the deuterated isotopologs – as well as with skeletal modes of appropriate symmetry and energy. Early LCAO-MO computations suggest that variation in hybridization due to the change in the CH-bending angle does not shift the electronic charge markedly,³² so the CH-bending modes need not be considered separately in the present context. It should be noted that they achieve crucial importance when there is an empty p-orbital on the adjacent carbon atom, as in CH₃CH₂⁺, in which case they are a major contributor to the hyperconjugative SIE.³³

Protonation of the acetate ion interacts favourably with each of the C–H bonds shortening it and lowering the potential well in which it is vibrating but – if the potential was harmonic – its vibrational force constant would not be affected. Since the well is anharmonic and the dipole derivative is negative, the extension of the bond is disfavoured relative to contraction, the curvature of the potential well increases in order to reduce its amplitude and raises its force constant. The frequency of the methyl stretching modes and their isotopic differences are increased, as illustrated in Table 6 for the “symmetric” stretch.³⁴

The computed thermochemical data for acetic acid and the acetate ion are listed in Table 7. As in formic acid, the IE is dominated by the ZPVE differences, but the direct contribution of the CH₃/CD₃ stretching modes is only about 33%. The entropy of both the isolated acid and its conjugate base increases substantially upon thermal excitation from 0 to 298 K. It is higher for the deuterated isotopologs of both, due to the lower frequencies of their methyl modes, and is only partially canceled by the concomitant increase in enthalpy. Nevertheless, the influence of entropy on the isotope effect is slight.

Table 7 Thermochemical data for the isotope effect on gas phase deprotonation of acetic acid (MP2/6-311G**)

	ZPVE^a	H ^0298 ^a	TS^0298 ^a	G ^0298 ^a
a kcal mol^−1. b Direct contribution of CH3/CD3 stretching modes.
CH3COO^−	30.493	33.866	20.680	13.186
CD3COO^−	24.618	28.171	21.260	6.911
Δ isotopic (acetate ion)	5.875 (3.550)^b	5.695	−0.580	6.275
CH3COOH	39.025	42.513	20.411	22.102
CD3COOH	32.973	36.647	20.961	15.686
Δ isotopic (acetic acid)	6.054 (3.607)^b	5.867	−0.550	6.416
ΔΔ (anion–acid)	−0.179 (−0.057)^b	−0.172	−0.031	−0.140

---

The contribution of the ZPVE to the isotope effect (0.179 kcal mol⁻¹) is somewhat larger than that computed by Perrin and Dong⁸ with B3LYP/6-31G* (0.152 kcal mol⁻¹), from which they obtain ΔpK_a = −0.111. The IE derived from the ΔΔG⁰ value in Table 7 (ΔpK_a = −0.103) is fortuitously close to theirs, but both are much larger than the experimental value, ΔpK_a = −0.0139.²⁵ Evidently, here too solvation reduces the IE on acidity drastically.

3.2.2 The effect of hydration. One monohydrate (15) and two dihydrates (16, 17) of the acetate ion were optimized, as were one monohydrate (18) and two dihydrates (19, 20) of acetic acid. The computation of trihydrates – let alone tetrahydrates – would have been excessively time consuming. Nevertheless, the results listed in Tables 8 and 9 are instructive, especially in view of the similarity of the mono- and dihydrates to those of formic acid and the formate ion: compare: 15 with 1, 16 with 2 and 17 with 3; similarly 18 with 8, 19 with 9, and 20 with 10. The similarity of the corresponding polyhydrates of formate, acetate, and propionate ions has been stressed by Stangret et al.²⁶

Table 8 Dependence on hydration of the thermochemical properties of the acetate ion and the acetate-d₃ ion (MP2/6-311G**)

Acetate ion hydrates	ΔG^0hydration ^a^,^b	ΔZPVE^b	ΔH^0 ^b	ΔTS^0 ^b	ΔG^0 ^b	μ g ^c^,^d
a For: CH3CO2^− + n(H2O) ⇋ CH3CO2^−⋯(OH2)n. b kcal mol^−1. c Debye, calculated with Mulliken charges. d Projection on the CC axis.
CH3/CD3CO2^−	—	5.875	5.695	−0.580	6.275	−0.876
CH3/CD3CO2^−⋯H2O (15)	−24.714	5.923	5.749	−0.548	6.297	−0.832
CH3/CD3CO2^−⋯(H2O)2 (16)	−39.051	6.070	5.864	−0.534	6.398	−1.111
CH3/CD3CO2^−⋯(H2O)2 (17)	−44.573	5.951	5.774	−0.565	6.339	−0.860

---

Table 9 Dependence on hydration of the thermochemical properties of acetic acid and acetic-d₃ acid (MP2/6-311G**)

Acetic acid hydrates	ΔG^0hydration ^a^,^b	ΔZPVE^b	ΔH^0 ^b	ΔTS^0 ^b	ΔG^0 ^b	μ g ^c^,^d
a For: CH3CO2^− + n(H2O) ⇋ CH3CO2^−⋯(OH2)n. b kcal mol^−1. c Debye, calculated with Mulliken charges. d Projection on the CC axis.
CH3/CD3CO2H	—	6.054	5.867	−0.550	6.416	−1.165
CH3/CD3CO2H⋯H2O (18)	−8.087	6.066	5.881	−0.552	6.433	−0.969
CH3/CD3CO2H⋯(H2O)2 (19)	−5.989	6.128	5.924	−0.531	6.464	−0.963
CH3/CD3CO2H⋯(H2O)2 (20)	−11.066	6.064	5.879	−0.552	6.432	−1.031

---

Hydration of both acid and base is exergonic, more strongly so in the latter. Here too, the main factor is the electrophilic interaction of successive water molecules with the anion, a partial protonation that increases the CH-stretching frequencies and increases ΔZPVE and ΔG⁰.

Fig. 5 shows an unweighted linear least-squares plot of the isotopic free energy difference (ΔG⁰) against the methyl-group dipole moment, μ_g (Mulliken), for all of the data points in Tables 8 and 9. The correlation is poor; the worst offender is anion dihydrate 16, in which two of the methyl H-atoms are contiguous (R_HH = 2.227 and 2.247 Å) to H-atoms of two adjacent water molecules and interact with them sterically. If 16 is ignored, the remaining hydrates can be fit to the blue line lying just below the regression line, and – like it – considerably less steep than the blue line connecting the anhydrous anion and acid. The quantitative mismatch is not difficult to rationalize. The quantity listed in the tables as “CH₃-group dipole” is actually its component along the C–C axis, which lies at a different angle to the molecular dipole in the hydrates from those in the bare acid and anion.

Fig. 5 Correlation between ΔG⁰ of CH₃/CD₃CO₂⁻ and CH₃/CD₃CO₂H and the CH₃-group dipole moment.

The striking similarity of the hydrates of acetate to those of formate makes it probable that the predominant species in solution would be a tetrahydrate homologous to 7, in which the inner solvation shell is complete. In order to make an educated guess as to its thermochemistry, we draw a semi-quantitative analogy with formate, as follows: ΔG⁰ of formate increases by 0.103 kcal mol⁻¹ on going from the bare ion to the more stable dihydrate 3. This is 56% of the total increase to tetrahydrate 7 (0.185 kcal mol⁻¹). When the same ratio is adopted for acetate, the increase to dihydrate 17 (0.064 kcal mol⁻¹) suggests that ΔG⁰ of acetate would increase by 0.115 kcal mol⁻¹ to 6.39 kcal mol⁻¹ or thereabouts for the tetrahydrate, perhaps a bit higher due to external hydration.

In 18, as in formic acid monohydrate (8), hydration is ambiphilic. Here too electron attraction is more effective than electron donation, so the C–H stretching frequencies are increased slightly and – with them – the isotopic differences in ZPVE and free energy. The second water molecule in dihydrate 19 acts only as an electrophile, whereas both water molecules in the more stable dihydrate 20 are ambiphilic and are loosely bonded to one another. ΔG⁰ of 18 and 20 is a virtually identical 6.43 kcal mol⁻¹. Turning back to Table 4, we note that the corresponding monohydrate (8) and dihydrate (10) of formic acid also have the same ΔG⁰ value (2.16 kcal mol⁻¹). So does the trihydrate (13), which was recognized above as probably being the prevalent hydrate of formic acid in solution. It can reasonably be assumed that ΔG⁰ of the homologous trihydrate of acetic acid will also be close to that of 18 and 20: 6.43 kcal mol⁻¹. On the assumption that the anion in solution is predominantly a tetrahydrate analogous to 7 and the acid a trihydrate analogous to 13, the estimated value of ΔΔG⁰₂₉₈ for the IE on the ionization of acetic acid in aqueous solution becomes −0.04 kcal mol⁻¹ (ΔpK_a = 0.03; K_H/K_D = 1.07), and would be reduced a bit more by external hydration of the tetrahydrated anion. This is as close to the experimental value (ΔpK_a = −0.0139; K_H/K_D = 1.032) as can be anticipated.

A feature that has not been taken into account is the effect of hydrophobic interaction between the methyl hydrogen atoms and water molecules that are not H-bonded to the carboxylate or carboxyl group. The RISM computations referred to above²⁹ indicate that a large number of water molecules are involved in it – on the average 8.9 in the acid and 10 in the ion. While the internal motions of these molecules may well contribute to the enthalpy and entropy of solvation, they evidently do not make a significant contribution to the isotope effect on the acidity of acetic acid.

3.3. Deuterium isotope effect on the basicity of methylamine

3.3.1 The gas phase reaction. As shown in Table 10, the bond dipole moments computed with the Mulliken and APT charge distributions differ not only quantitatively but in their direction as well. For both the base and the cation the dipole is negative (C^δ−–H^δ+) according to the former and positive (C^δ+–H⁻) according to the latter. We consider the protonation of the amine separately from each of the two points of view:

Table 10 Correlation between the CH₃ dipole, mean equilibrium CH-bond length and C–H stretching frequency in methylamine and the methylammonium ion (MP2/6-311G**)

	Scale	μ g (Debye)	r m ^b (Å)	ν sym ^c (cm^−1)
a Projection the C–C axis. b Mean equilibrium C–H bond length. c Frequency of “symmetric” CH3/CD3 stretching mode.
CH3NH3^+	Mulliken	−0.740	1.0880	CH3 3132.4; CD3 2244.3
	APT	+0.456
CH3NH2	Mulliken	−0.515^a	1.0948	CH3 3032.3; CD3 2185.7
	APT	+1.113^a
Δ (CH3NH3^+–CH3NH2)	Mulliken	−0.225	0.068	CH3 100.1; CD3 58.6
	APT	−0.657

---

(1) Mulliken: the charge–dipole interaction at the methyl carbon upon protonation is attractive. The moderately increased magnitude (0.225 Debye) of the (negative) group dipole moment indicates that electron release from the methyl H-atoms is larger than that from the C-atom, even though they were less negatively charged to begin with. Since Δμ_g is positive and Δμ_g/Δr_m is negative, the CH-bonds become shorter and the methyl stretching frequencies are increased.

(2) APT: the charge–dipole interaction is repulsive. The greatly reduced magnitude (0.657 Debye) of the (positive) group dipole moment indicates substantial electron release from the negatively charged H-atoms to the positively charged C-atom. Since both μ and dμ/dr are positive, the decreased dipole moment is accompanied by shorter CH-bonds and higher methyl stretching frequencies.

Thus, whichever of the two schemes is correct, both produce the same qualitative result: a net shift of the negative charge within the methyl group from hydrogen to carbon, a consequent increase in the CH-stretching frequencies, and an inverse isotope effect. Therefore, in this context, the expression “deuterium is effectively more electron-releasing than protium” is not a solecism.

The computed thermodynamic properties are summarized in Table 11. The three CH-bonds in methylamine are not identical. The antiperiplanar bond, i.e. trans to the nitrogen lone pair, is slightly longer (1.0995 Å) than the two synclinal bonds near 60° and 120° (1.0295 Å), and its bond dipole – computed with Mulliken charges – is lower: −0.440 vs. −0.499 Debye. These results are in qualitative agreement with a model computation by Perrin and his coworkers,¹⁰ according to which the length of an isolated alkyl CH-bond is at a maximum and its stretching frequency is at a minimum in the antiperiplanar conformation, whereas the bond is shortest and its frequency highest in the synclinal conformation. The authors ascribe the effect to varying degrees of negative hyperconjugation. However, the basicities in aqueous solution of all the conformationally constrained amines cited by them (Table 1 of ref. 10) lie in the range: ΔΔG⁰ = 22 ± 5 cal per mol per D-atom. Thus, whatever the steric or stereoelectronic source of the observed conformational variation may be, it is evidently a secondary effect superimposed on electrostatic induction, which they had summarily dismissed.

Table 11 Thermochemical data for the isotope effect on gas phase protonation of methylamine (MP2/6-311G**)

	ZPVE^a^,^b	H ^0298 ^a	TS^0298 ^a	G ^0298 ^a
a kcal mol^−1. b In parentheses: direct contribution of the CH3/CD3 stretching modes.
CH3NH3^+	50.544	53.275	16.602	36.673
CD3NH3^+	44.264	47.118	17.100	30.018
Δ isotope (CH3NH3^+–CD3NH3^+)	6.280 (3.652)	6.157	−0.498	6.655
CH3NH2	40.919	43.620	17.061	26.559
CD3NH2	34.791	37.611	17.576	20.035
Δ isotope (CH3NH2–CD3NH2)	6.128 (3.550)	6.009	−0.515	6.524
ΔΔ (cation–base)	0.152 (0.102)	0.148	0.017	0.131

---

3.3.2 The effect of hydration. Methylammonium ion optimizes to a monohydrate (21), a dihydrate (22) and a trihydrate (23) by successive H-bonding to a water molecule of each of the three N-bonded H-atoms. The trihydrate is threefold symmetric, like the parent anion, but the H-bonded water molecules are tilted away from strict C_3v symmetry into either of two C₃ enantiomers. Methylamine is hydrated to a stable monohydrate (24) and a stable dihydrate (25). A second dihydrate that optimized with one imaginary frequency and a trihydrate with three imaginary frequencies will be disregarded.

The relevant thermochemical properties of the methylammonium ion and its conjugate base are summarized in Tables 12 and 13 respectively.

Table 12 Dependence on hydration of the thermochemical properties of methylammonium- and methyl-d₃-ammonium ions (MP2/6-311G**)

Methylammonium ion hydrates	ΔG^0hydration ^a^,^b	ΔZPVE^b	ΔH^0 ^b	ΔTS^0 ^b	ΔG^0 ^b	μ g ^c
a For: CH3NH3^+ + nH2O ⇋ CH3NH3^+⋯(OH2)n. b kcal mol^−1. c Debye, calculated with Mulliken charges. d Projection on the CN axis.
CH3/CD3NH3^+	—	6.280	6.157	−0.498	6.655	−0.740
CH3/CD3NH3^+⋯H2O (21)	−14.097	6.303	6.146	−0.508	6.654	−0.719^d
CH3/CD3NH3^+⋯(H2O)2 (22)	−25.980	6.307	6.140	−0.502	6.642	−0.688^d
CH3/CD3NH3^+⋯(H2O)3 (23)	−32.158	6.304	6.131	−0.508	6.639	−0.683

---

Table 13 Dependence on hydration of the thermochemical properties of methylamine and methyl-d₃-amine (MP2/6-311G**)

Methylamine hydrates	ΔG^0hydration ^a^,^b	ΔZPVE^b	ΔH^0 ^b	ΔTS^0 ^b	ΔG^0 ^b	μ g ^c^,^d
a For: CH3NH2 + n(H2O) ⇋ CH3NH2⋯(OH2)n. b kcal mol^−1. c Debye, calculated with Mulliken charges. d Projection on the CN axis.
CH3/CD3NH2	—	6.128	6.009	−0.515	6.524	−0.515
CH3/CD3NH2⋯H2O (24)	0.527	6.201	6.049	−0.500	6.548	−0.570
CH3/CD3NH2⋯(H2O)2 (25)	−1.197	6.198	6.037	−0.512	6.550	−0.491

---

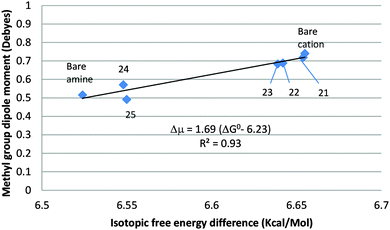
An unweighted linear least-squares plot of the methyl-group dipole moment vs. the isotopic free energy difference is displayed in Fig. 6. Hydration of the methylammonium ion is solely nucleophilic. The H-atoms of the water molecules are not directly involved in the binding and are sufficiently far from the methyl group to preclude a direct steric or stereoelectronic interaction between them. Increasing the number of water molecules H-bonded to the cation causes a slight, monotonic decrease in the magnitude of the CH₃-group dipole, accompanied by a slight but consistent decrease in the isotopic free energy difference. Points 21–23 lie just below the line (not drawn in the figure) connecting the bare cation and amine, confirming that ΔG⁰ is an effectively linear function of μ_g when the hydrated ions are not encumbered by steric interactions and/or gross departures from axial symmetry, such as those noted in the case of the acetate ion. In the amine monohydrate (24), the water molecule acts as an electrophile, increasing ΔG⁰ slightly. It is retained in the dihydrate (25), in which a second water molecule is H-bonded to its O-atom, as well as – loosely (R_HN = 2.27 Å) – to one of the amino H-atoms, leaving ΔG⁰ unchanged.

Fig. 6 Correlation between ΔG⁰ of CH₃/CD₃NH₂ and CH₃/CD₃NH₃⁺ and the CH₃-group dipole moment.

Hydration of the methylammonium ion is strongly exergonic, guaranteeing that the trihydrate, 23, in which the inner hydration shell is complete, will be the dominant species in dilute aqueous solution. It may be assumed that the more highly hydrated amine 25 will predominate in dilute aqueous solution. Therefore, taking 23 to be the principal form of the methylammonium ion in solution and 25 to represent methylamine, we obtain ΔΔG⁰₂₉₈ = 0.090 kcal mol⁻¹, ΔpK_b = 0.066, only 30% larger than the experimental value of the IE on the basicity of methylamine in aqueous solution (ΔΔG⁰₂₉₈ = 0.070 kcal mol⁻¹, ΔpK_b = 0.051).⁹ The contribution of entropy of solvation to the isotope effect is negligible. Thus, gas phase computation of the hydrated species provides a good approximation to the secondary isotope effect on amine basicity in aqueous solution.

These results are consistent with RISM computations³⁵ indicating that, in solution, the methylammonium ion forms three hydrogen bonds to water, and methylamine – on average – forms 2.5. For both the base and cation, these computations also indicate the presence of many water molecules in hydrophobic interaction with the methyl group. Here too, as in the case of acetic acid, its contribution to the isotope effect is evidently negligible.

4. Conclusions

The mechanism by which electrostatic induction alters the frequency of C–H/C–D stretching modes and produces secondary isotope effects is described in terms of a one-dimensional model. Within the constraints of first-order perturbation theory, the interaction between a perturbing charge and the polar bond has two separate effects:

(1) Lengthening or shortening of the equilibrium bond length (r_e) and an upward or downward shift of the potential energy minimum depending on whether the interaction is attractive or repulsive.

(2) In an anharmonic potential, an increase or decrease of the harmonic force constant, according to whether the sign of the bond dipole derivative, dμ/dr, is positive or negative.

This model is applied to the protonation of the formate ion. The computations show that the C–H bond is shorter in formic acid than in the formate ion and its dipole moment is smaller; evidently dμ/dr is positive. Δμ/Δr_e, the difference between the CH-bond dipole moments of the acid and its conjugate base divided by the difference between their equilibrium bond lengths, is thus a linear approximation to dμ/dr. Protonation increases the vibrational frequency of the bond and – in consequence – the isotopic differences in its zero-point energy (ΔΔZPVE) and Gibbs free energy (ΔΔG⁰) increase as well, producing a normal isotope effect on acidity: HCOOH is a stronger acid than DCOOH. The inductive origin of the isotope effect is confirmed by computations on various hydrates of formic acid and the formate ion. The slope of a linear plot of μ vs. r_e is in good agreement with Δμ/Δr_e, and a plot of ΔΔG⁰vs. μ is also adequately linear. In both plots, the linear correlation is improved when the steric interaction between the C–H bond and the H-atoms of hydrating water molecules in several of the hydrates is taken into account.

Similar computations were carried out on the acid–conjugate base pairs: CH₃CO₂H/CH₃CO₂⁻ and CH₃NH₃⁺/CH₃NH₂. In both cases the methyl C–H bonds are shorter in the acid than in its conjugate base and their frequencies higher, leading to a normal SIE on the acidity of acetic acid and an inverse SIE on the basicity of methylamine. Bond shortening is accompanied by a reduction of μ_g, the projection of the methyl-group dipole moment on the C–C axis, representing a shift of the electron density from H to C. The plot of μ_g against ΔΔG⁰ is adequately linear when steric interactions are taken into account.

The SIEs computed with the anhydrous acids and their conjugate bases are larger than the published experimental values in solution; much larger for the carboxylic acids, slightly larger for methylamine. Binding an increasing number of water molecules, especially to the ionic component, reduces the isotope effect. In all three cases: the SIE computed with the polyhydrates in the gas phase at 298 K is reduced to within a factor of two of the experimental value in aqueous solution. The contribution of entropy of solvation to the SIE is negligible. Hydration reduces the SIE primarily by modifying electron release from the carboxylate group in the first case and electron demand from the ammonium group in the second, confirming its inductive origin.

5. Appendix

The essential features of the proof in ref. 6 are as follows:

If a harmonic oscillator (1/2kx², where x = r − r_e) is acted upon by a linear perturbation (V_e + ax), the potential energy function becomes:

V′ = V_e + ax + 1/2kx² (A.1)

We note immediately that the force constant, i.e. the second derivative of the potential energy, is unchanged:

d²V′/dx² = k (A.2)

Eqn (A.1) can be rearranged to

V′ = (V_e − a²/2k) + 1/2k(x + a/k)² (A.3)

The minimum has been shifted upwards or downwards, depending on the sign and magnitude of V_e, and to the right or left, depending on the sign of a, by −a/k (see Fig. 2). Both the original and final potentials are harmonic, with the same force constant, so the linear perturbation cannot give rise to a frequency change or an isotope effect.

If the potential is anharmonic, as in the case of CH-bonds, it contains a cubic term, gx³. The perturbed potential is

V′ = V_e + ax + 1/2kx² + gx³ (A.4)

and its first and second derivatives, respectively, are

dV′/dx = a + kx + 3gx² (A.5)

d²V′/dx² = k + 6gx (A.6)

Equating the quadratic expression in (A.5) to zero, we obtain two solutions for the position of the new extremum,

x_{1,2} = [−k ± (k² − 12ga)^1/2]/6g (A.7)

which is a minimum, i.e. has a positive second derivative, only for the solution with a plus sign before the square root. Rearrangement leads to

x = −k[1 + (1 − 12ga/k²)^1/2]/6g (A.7′)

Since 12ga is much smaller than k², the square root can be expanded in good approximation to (1–6ga/k²), yielding, after substitution and collection of terms, the same displacement to the new minimum derived above for the harmonic potential: x ≅ −a/k. Introducing the new value into eqn (A.6), we obtain

d²V′/dx² ≅ k − 6ag/k (A.8)

The harmonic force constant, vibrational frequency and isotopic zero point energy difference have thus been changed by the linear perturbation, but only because the original potential energy function includes a cubic anharmonic term.

The nature of the perturbation, implied in ref. 6 but not stated there explicitly, is the charge–dipole interaction. For the interaction of a charge q and dipole μ aligned as in Fig. 1, it is expressed by

V = – μq/4πε₀r² (A.9)

Including the charge and the universal constants in a single coefficient, C, it becomes

V = Cμr⁻² (A.9′)

Neglecting electrical anharmonicity, i.e. assuming that the dipole moment varies linearly with distance, the coefficient is

a = C[d(μr⁻²)/dr] (A.10)

a = C[r⁻²dμ/dr + μ d(r⁻²)/dr] (A.10′)

a = C/r² [dμ/dr − μ/2r] (A.10′′)

The minute change in 1/r² between the equilibrium lengths of the perturbed and unperturbed C–H bonds is negligible, so C/r² can be seen as a constant coefficient.

The second term in brackets is of the order of 1 Debye Å⁻¹, whereas dμ/dr is somewhere between 10 and 30 Debye Å⁻¹, depending on the charge distribution scheme used to estimate it. It follows that the coefficient a, which – along with g – is responsible for the isotope effect, can be regarded, for the semi-quantitative purposes of the present paper, as directly proportional to the dipole moment derivative,

a ≅ C′dμ/dr (A.11)

It is an implicit assumption of the model that the bond-dipole moment is an intrinsic function of the bond length that is not affected by the perturbation, i.e. that the charge-induced dipole interaction can be neglected, so that the same value of dμ/dr applies to both the perturbed and unperturbed bonds.

Acknowledgements

The author is indebted to Dr Miri Karni for guidance on computations with the Gaussian program and to Professor Jacob Katriel for ongoing discussions and valuable critical readings of the manuscript. A particularly careful review by one of the referees is gratefully acknowledged.

Notes and references

1. E. A. Halevi and M. Nussim, Bull. Res. Counc. Isr., Sect. A: Math., Phys. Chem., 1956, 5, 263.
2. E. A. Halevi, M. Nussim and A. Ron, J. Chem. Soc., 1963, 866.
3. Y. Bary, H. Gilboa and E. A. Halevi, J. Chem. Soc., Perkin Trans. 2, 1979, 938 , in which several of the early values were revised.
4. E. S. Lewis and C. E. Boozer, J. Am. Chem. Soc., 1952, 74, 6306.
5. V. J. Shiner, J. Am. Chem. Soc., 1953, 75, 292.
6. E. A. Halevi, Prog. Phys. Org. Chem., 1963, 1, 109–184.
7. A. C. Hengge, in Isotope Effects in Chemistry and Biology, ed. A. Kohen and H. Limbach, Taylor and Francis, Boca Raton, 2006, pp. 955–974, and papers cited therein.
8. C. L. Perrin and Y. Dong, J. Am. Chem. Soc., 2007, 129, 4490.
9. C. L. Perrin, B. K. Ohta and J. Kuperman, J. Am. Chem. Soc., 2003, 125, 15008.
10. C. L. Perrin, B. K. Ohta, J. Kuperman, J. Liberman and M. Erdélyi, J. Am. Chem. Soc., 2005, 127, 9641.
11. C. L. Perrin and A. Flach, Angew. Chem., Int. Ed., 2011, 50, 7674.
12. C. L. Perrin, Adv. Phys. Org. Chem., 2010, 44, 123–171.
13. See e.g.F. A. Carroll, Perspectives in Structure and Mechanism in Organic Chemistry, Wiley, Hoboken, 2010, p. 383.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, revision B.04, Gaussian, Inc., Pittsburgh, PA, 2003.
15. The author is partially responsible for this misconception. A poorly worded speculation in ref. 2, intended to suggest that the altered charge distribution may be reflected in the energy and entropy of solvation and erroneously assigned to the inductive effect, was misinterpreted. The idea is expressed more clearly on pp. 129–130 of ref. 6.
16. A. Reyes, M. V. Pak and S. Hammes-Schiffer, J. Chem. Phys., 2005, 123, 64104.
17. J. Bigeleisen and M. G. Mayer, J. Chem. Phys., 1947, 15, 261.
18. E. W. Kaiser, J. Chem. Phys., 1970, 53, 1686.
19. E. A. Halevi, Internat. J. Quantum Chemistry, 1971, Symposium No. 5, 367.
20. Regrettably, this distinction was not brought out clearly in ref. 6.
21. This is an oversimplification, but it is adequate for the present qualitative purposes.
22. J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333.
23. Confidence in the APT scale is reduced by its placement of a larger positive charge on the carbon atom in the anion than in the acid.
24. The corresponding values of Δμ/Δr_e (11.2 and 29.5 respectively), which may seem excessively large at first sight for a bond ca.1 Å long with a dipole moment of a few Debyes, reflect the fact that the magnitude of the C–H bond dipole – and even its sign – vary over a small fraction of the bond length.
25. T. Pehk, E. Kiirend, E. Lippmaa, U. Ragnarsson and L. Grehn, J. Chem. Soc., Perkin Trans. 2, 1997, 445.
26. M. Śmiechowski, E. Goiło and J. Stangret, J. Phys. Chem. B, 2011, 115, 4834 and papers cited therein.
27. M. A. Vovk, M. S. Pavlova, V. I. Chizhik and A. A. Vorontzova, Russ. J. Phys. Chem., 2011, 85, 1597.
28. S. Ten-no, F. Hirata and S. Kato, J. Chem. Phys., 1994, 100, 7443.
29. M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2011, 164, 201.
30. A plot with ΔZPVE as the abscissa would be nearly identical.
31. R. Superfine, J. Y. Huang and Y. R. Shen, Chem. Phys. Lett., 1990, 172, 3.
32. E. A. Halevi and R. Pauncz, J. Chem. Soc., 1959, 1974.
33. A. Ron, E. A. Halevi and R. Pauncz, J. Chem. Soc., 1960, 630.
34. “Symmetric stretch” refers to the lowest of the three CH-stretching frequencies. It is more nearly symmetric (a′) in the anion, which has C_s symmetry, than in the acid.
35. M. V. Fedotova and S. E. Kruchinin, Russ. Chem. Bull., 2012, 61(2), 240.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinate matrices of all optimized structures. See DOI: 10.1039/c4nj00221k

---