Mind the gap!
Jean-Luc
Bredas
ab
aSchool of Chemistry and Biochemistry and Center for Organic Photonics and Electronics, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA. E-mail: jean-luc.bredas@chemistry.gatech.edu
bDepartment of Chemistry, King Abdulaziz University, Jeddah 21589, Saudi Arabia
First published on 19th September 2013
Abstract
The energy gap between the highest occupied and lowest unoccupied electronic levels is a critical parameter determining the electronic, optical, redox, and transport (electrical) properties of a material. However, the energy gap comes in many flavors, such as the band gap, HOMO–LUMO gap, fundamental gap, optical gap, or transport gap, with each of these terms carrying a specific meaning. Failure to appreciate the distinctions among these different energy gaps has caused much confusion in the literature, which is manifested by the frequent use of improper terminology, in particular, in the case of organic molecular or macromolecular materials. Thus, it is our goal here to clarify the meaning of the various energy gaps that can be measured experimentally or evaluated computationally, with a focus on π-conjugated materials of interest for organic electronics and photonics applications.
It is useful to start our discussion at the molecular level. Without losing generality, we will assume the most common, simple case of π-conjugated systems with a closed-shell, singlet electronic ground state. Currently, in the organic materials community, there is widespread use of readily available quantum-chemistry computational codes based on the Hartree–Fock (HF) method or density functional theory (DFT). As a consequence, a large number of manuscripts present the results of molecular orbital (MO) calculations on the neutral molecules. From the outset, it is important to keep in mind that MOs correspond to one-electron wave functions, each associated with a specific energy level; of special interest then are the energies of the highest occupied and lowest unoccupied molecular orbitals, the HOMO and LUMO. Importantly, however, what is measured experimentally upon excitation [or ionization] is the difference in energy between the N-electron ground state of the molecule and its N-electron excited state [or its N ± 1-electron ionized state].
In the context of Hartree–Fock calculations, following Koopmans' theorem, the energy of the HOMO level can be considered as (minus) the vertical ionization potential (IP) while the LUMO energy represents (minus) the vertical electron affinity (EA, where we adopt the IUPAC definition, i.e., the electron affinity is the negative of the energy change when adding an electron to the neutral species; within this definition, most π-conjugated systems have positive EA values since the extra electron is bound). Koopmans' theorem in fact constitutes a rather crude approximation since the ionization potential, from a rigorous standpoint, corresponds to the difference between the total energies of the N − 1-electron and N-electron states while the electron affinity is the difference between the total energies of the N-electron and N + 1-electron states. (It is interesting to realize that the application of Koopmans' theorem somehow works for a number of systems because of a compensation of errors related to neglecting the impact upon vertical ionization of both electron relaxations and electron correlations). In the context of DFT, we note that the exact functional obeys the property that the HOMO energy corresponds exactly to (minus) the vertical ionization potential; the electron affinity is then obtained as (minus) the HOMO energy of the N + 1-electron system. At this point in time, however, finding the exact functional remains the holy grail of DFT practitioners.
In the molecular case, the fundamental gap is defined as the difference between the ionization potential and electron affinity: Efund = IP − EA. Experimentally, it can be determined via a combination of gas-phase ultraviolet photoelectron spectroscopy and electron attachment spectroscopy; at the computational level, it requires the comparison between the total energy of the N-electron ground state and that of the N + 1-electron state (to determine EA) or that of the N − 1-electron state (to determine IP). The calculated HOMO–LUMO gap, i.e., the difference between the calculated HOMO and LUMO energy levels, only provides an approximation to the fundamental gap; the quality of that approximation strongly depends on the specifics of the computational methodology (for instance, in the case of DFT, it very much depends on the nature of the exchange–correlation functional and the amount of Hartree–Fock exchange it includes).
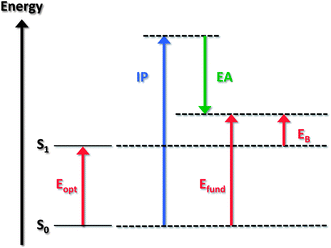
The optical gap of a molecule corresponds to the energy of the lowest electronic transition accessible via absorption of a single photon. (Note that in both molecule and material cases, our discussion will assume that the lowest transition involves the first excited state and neglects the more complex instances where this state is optically forbidden). The optical gap Eopt is generally substantially lower than the fundamental gap; the reason is that, in the excited state (contrary to the ionized state), the electron and hole remain electrostatically bound to one another. The difference between the fundamental gap and the optical gap (when the latter reflects the transition from the ground state to the lowest excited state) is then a measure of the electron–hole pair binding energy, EB. Fig. 1 provides a general illustration of the fundamental and optical gaps when considering molecular state energies.
We now turn our attention from organic molecules to organic molecular (or polymeric) materials. Here, intermolecular interactions broaden the molecular energy levels into electronic bands. The widths of these bands depend on the strengths of these interactions, i.e., on the electronic couplings between adjacent molecules. As in the case of inorganic semiconductors, the upper occupied band can be referred to as the valence band and the lower unoccupied band as the conduction band. In perfectly ordered structures, such as defect-free single crystals, the wave functions delocalize over the whole system. However, in the disordered structures commonly found in organic thin films, the wave functions tend to localize over a few neighboring molecules or even a single molecule. We note that the degree of localization/delocalization is a function of the balance between the strength of the intermolecular electronic couplings, which favors delocalization, and the extent of disorder, which leads to localization.
The band gap is defined as the energy difference between the top of the valence band and the bottom of the conduction band. Thus, rigorously speaking, it corresponds to the energy difference between the ionization potential and electron affinity of the material. The band gap is also referred to as the transport gap since it represents the minimum energy necessary to create a positive charge carrier somewhere in the material (IP) minus the energy gained by adding a negative charge carrier (EA) elsewhere. The band gap or transport gap can be estimated experimentally via a combination of ultraviolet photoelectron spectroscopy (UPS) and inverse photoemission spectroscopy (IPES). Thus, the band gap is the equivalent, at the materials level, of the molecular fundamental gap. It is important to note, however, that the band gap is typically considerably smaller in energy than the molecular fundamental gap; this is due to the fact that, in the solid state, π-conjugated molecules adjacent to the one carrying a charge do strongly polarize, an effect that stabilizes the cationic and anionic states (each generally by about one eV in π-conjugated materials).
Upon photon absorption in a π-conjugated organic material, the lowest optical transition defines the optical gap. It also leads to the formation of a bound electron–hole pair, termed an exciton in the context of condensed-matter physics (the electron–hole pair can indeed be considered as a quasiparticle as it can move from molecule to molecule). Then, the difference between, on the one hand, the band gap or transport gap and, on the other hand, the optical gap between the ground state and the lowest excited state defines the exciton binding energy; in π-conjugated materials, EB is usually on the order of a few tenths of eV (again, a value smaller than the electron–hole pair binding energy in the gas phase due to stabilization of both cations and anions by polarization of surrounding molecules). It is useful to bear in mind that the magnitude of the exciton binding energy is due not only to the small dielectric constant (ε ∼ 3–5) but also to substantial electron–electron and electron–vibration interactions typical of π-conjugated materials. In contrast, in conventional inorganic semiconductor crystals, the exciton binding energy is often so small (a few meV) that at room temperature optical excitation directly leads to the formation of free charge carriers (and thus in these systems Eopt ∼ Etransport).
Finally, it is useful to mention that the solid-state values of ionization potential and electron affinity are, in many instances, approximated experimentally via cyclic voltammetry measurements of the oxidation and reduction potentials carried out in solution. Conversion factors, assessed on a limited set of systems, are then used to translate the redox potentials into solid-state ionization energies. The values of ionization potential and electron affinity determined in this way have thus to be taken with much caution. Moreover, given the use of several approaches to the conversion factors, it is difficult to compare values from different sources; to minimize this issue, it is highly desirable that, in addition to the estimated IP and EA values, the experimental electrode potentials and the approximations and assumptions used in the conversions be reported. (Often, these cyclic-voltammetry-based ionization potentials and electron affinities are inappropriately referred to as “HOMO” and “LUMO” energies).
In a number of instances, either the oxidation potential or the reduction potential is experimentally not accessible. A common procedure is then to use the optical gap to deduce the missing potential. For instance, in the absence of a measurable reduction potential, the electron affinity would be assessed by subtracting the optical gap from the ionization potential. As should be clear from our discussion, this practice is highly misleading since it ignores the exciton binding energy built into the optical gap. Other complications also arise with this practice when the measured lowest optical transition in fact does not correspond to the transition from the ground state to the lowest excited state, which occurs when this transition is either symmetry forbidden or has negligible oscillator strength.
To summarize, in this Focus Article, we have tried to shed light on the concepts behind the various flavors of energy gaps that are relevant for organic materials. We hope that it will contribute to a more consistent use of appropriate terminologies and procedures.
Acknowledgements
The author is indebted to Stephen Barlow, Veaceslav Coropceanu, Antoine Kahn, Thomas Körzdörfer, Seth Marder, and Chad Risko for their critical reading of the manuscript and stimulating discussions. This work has been supported by the Office of Naval Research (Award no. N00014-11-1-0211) and by an Research Collaboration Grant from King Abdulaziz University.| This journal is © The Royal Society of Chemistry 2014 |