Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A fundamental view of enthalpy–entropy compensation
Ulf
Ryde
*
Department of Theoretical Chemistry, Lund University, Chemical Centre, P. O. Box 124, SE-221 00 Lund, Sweden. E-mail: Ulf.Ryde@teokem.lu.se; Fax: +46 46 2228648; Tel: +46 46 2224502
First published on 16th June 2014
Abstract
In this paper, enthalpy–entropy compensation (EEC) during the association of two molecules is studied by minimising model systems with molecular mechanics (MM) or quantum mechanics (QM), calculating translational, rotational, and vibrational contributions to the enthalpy and entropy with standard statistical-mechanics methods, using the rigid-rotor harmonic-oscillator approach. We start with simple two-atom models, for which dispersion and electrostatics can be studied separately, showing that there is no fundamental difference between dispersion, electrostatics, or even covalent interactions. All three types of interactions give rise to EEC and a saturation of TΔS as ΔH becomes strongly negative. Next, homologous series of complexes dominated either by dispersion or hydrogen bonds are studied. We see no qualitative difference between results obtained at the MM or QM level, and for all complexes except two very weak, EEC is observed, owing to the loss of translational and rotational entropy, typically counteracted by the vibrational entropy. Within homologous series, linear relations between TΔS and ΔH with slopes of 0.1–1.7 are obtained with no clear difference between dispersive or hydrogen-bonded systems (but ∼0.01 for ionic and covalent interactions). These relations often reflect the increasing size of the complexes coming from the translational and rotational entropies, but at least for the hydrogen-bonded complexes, it is significantly enhanced also by the vibrational entropy (which depends on the strength of the interaction). Thus, for homologous series of molecules with repeated interactions studied in vacuum, EEC is a rule. However, if water molecules are added, the relation is blurred and it can be predicted that for a real binding reaction in water solution, both enthalpy–entropy compensation and anti-compensation can be observed, depending on the detailed interaction of the two molecules with water before and after binding, further complicated by dynamic effects.
Introduction
The enthalpy–entropy compensation (EEC), i.e. the observation that an increase in the enthalpy during the non-covalent association of two molecules (e.g. the binding of a drug candidate to a protein) is often to a large extent cancelled by a concurrent decrease in the entropy, is a much debated phenomenon. The term has been used with several meanings, but recent reviews have clarified the concept.1–3 Even if the EEC in some cases has been attributed to experimental errors and limitations4,5 or to a natural consequence of thermodynamics,1,6,7 there is now much clear evidence of EEC.8–12 On the other hand, several examples where enthalpy and entropy enforce each other have also been reported.1,13–15 Owing to the importance of EEC for the understanding of molecular recognition and drug design, it has been thoroughly studied by both experimental and theoretical methods.1,16,17In 1981, Jencks pointed out that in the association of two molecules, a favourable binding enthalpy has to overcome an unfavourable loss of translational and rotational entropy when two molecules form a complex, directly leading to EEC.18 Williams and coworkers suggested that residual motion in the complex will partly compensate for the loss in translational and rotational entropy, and that this residual motion will decrease as the strength of the complex is increased.19 Therefore, EEC naturally arises in associations and if the entropy is plotted against enthalpy for interactions with increasing strength, it first rapidly becomes more negative and then saturates and asymptotically approaches a limiting value of complete loss of translational and rotational entropy, as the binding enthalpy becomes more negative (cf.Fig. 1). In a series of articles, they showed that such a curve is supported by experimental measurements and that it can be used to explain and predict binding affinities and cooperativity.16,20–23
Dunitz suggested that the residual motion can be estimated from the vibrational entropy:24 When a complex is formed, the six translational and rotational degrees of freedom of the ligand are converted to six vibrations between the ligand and the receptor, and as the complex becomes stronger, the vibrations become stiffer. The vibrational entropy can be estimated from the entropy of a harmonic oscillator and for many types of interactions, there is a linear relation between the strength of the interaction and the quadratic force constant of the vibration. Interestingly, he made an error of signs, suggesting that the corresponding vibrational entropy opposes the binding enthalpy, although it actually enforces the binding, partly compensating the loss of translational and rotational entropy. However, when correctly performed, this provides a powerful approach to quantify and understand the EEC with theoretical methods.
Recently, Korth used this approach to study EEC in 88 complexes of small molecules in gas phase.25 He argued that quantum mechanical (QM) effects are essential for the understanding of the EEC† and that interactions dominated by hydrogen bonds or by dispersive interactions show a fundamentally different behaviour, giving rise to distinct types of EEC. A problem with such an approach is that for real molecules studied by QM, there are no pure hydrogen-bonded or electrostatic systems without any dispersion, making the distinction problematic. Moreover, QM investigations are limited to the strength of interactions observed for real chemical systems.
In this paper, we explore the opposite viewpoint, i.e. that the EEC can be understood from a molecular mechanics (MM) perspective. The advantage with MM is that we can design systems that are purely dispersive or electrostatic, and continuously modify the strength of the dispersion or the magnitude of the charges, deriving analytical expressions for the enthalpy and entropy of each system. Thereby, we can fully understand what is expected from the two types of systems at any strength of interaction, thereby deciding whether there is any fundamental difference in EEC between dispersive and electrostatic (hydrogen-bonded) systems. We start from simple two-atom models and continue to more complicated systems, involving many interaction sites with or without a combination of dispersive and electrostatic effects. Throughout the investigation, we compare with results obtained at the QM level, to address whether there is any fundamental difference between QM and MM. In agreement with previous theoretical studies,18–25 we observe EEC for essentially all studied systems. The question then naturally arises why EEC is not observed in all experimental studies of ligand binding. We will discuss possible answers to this fundamental question about molecular interactions.
Theory and methods
In this paper, we study several variants of the general binding reaction| M1 + M2 → M1M2 | (1) |
| ΔG = ΔH − TΔS | (2) |
We used either QM or MM to calculate the energies of M1, M2, and M1M2, as well as their vibrational frequencies. From the frequencies, we calculated zero-point vibrational energies, as well as thermal corrections to the enthalpy and entropy of each reactant, based on standard statistical-mechanical expressions,26 using an ideal-gas rigid-rotor harmonic-oscillator (RRHO) approximation. Hence, the enthalpy is given by
| H = Eint + Htrans + Hrot + Hvib, | (3) |
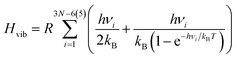 | (4) |
Similarly, the entropy is given by
| S = Strans + Srot + Svib, | (5) |
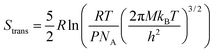 | (6) |
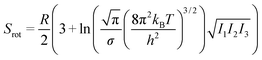 | (7) |
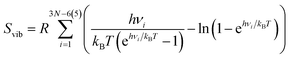 | (8) |
From this, it can be seen that the translational entropy depends on the molar mass of the molecule (M; P is the pressure, assumed to be 1 atm, and h is Planck's constant), the rotation entropy depends on symmetry number (σ = 1 for most molecules, except for those with rotational symmetry) and the moments of inertia (I1, I2, and I3, which depend on the coordinates and masses of the atoms) of the molecule (the formula is somewhat different for linear molecules26), whereas the vibrational entropy depends on the vibrational frequencies.
MM calculations were either performed analytically (diatomic molecules) or with the nmode program in the AMBER 9 software suite,27 using the GAFF force field28 and either zeroed or AM1-BCC charges,29,30 except the β sheet models, which used the Amber ff99SB force field.31 The alkane models with water molecules used a +0.1 e charge on the H atoms and a compensating negative charge on the C atoms, similar to the ff99SB charges on non-polar amino acids. For water, TIP3P parameters were used.32
QM calculations were performed with the Turbomole 6.5 software,33,34 using the TPSS density-functional theory method35 with the def2-TZVPPD basis set36,37 and the empirical DFT-D3 dispersion correction.38 The calculations were sped up by expanding the Coulomb potentials in auxiliary basis sets, the resolution-of-identity approximation.39–41
To obtain more stable results for the vibrational contribution in the MM and QM (but not the analytical) calculations, low-lying vibrational modes were treated by the free-rotor approximation, using the interpolation model suggested by Grimme with the parameter ω0 = 100 cm−1 (ref. 42) (but the term was still assigned to the vibrational contribution). These calculations were performed with the thermo program, kindly provided by Prof. Stefan Grimme. This approximation does not affect the general conclusions of the paper; it only makes the curves smoother.
We will discuss two types of EEC: the first (which we will denote EEC1 in the following) involves a single binding reaction of the type in eqn (1). Then, there is an EEC if ΔH and TΔS have the same signs. This can be characterised by the quotient
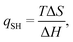 | (9) |
The second type of EEC (which we will denote EEC2 below) involves several binding reactions, typically in some series of homologous molecules. Strictly, EEC2 implies that any difference in ΔH between two reactions in this series (ΔΔH) is counteracted by a difference in TΔS (TΔΔS) with the same sign. This requires that TΔS is a monotonous function of ΔH. In a less stringent, but more useful version, EEC2 implies that there is a significant correlation between ΔH and TΔS with a positive slope for a series of homologous compounds. EEC2 is probably closer to what is normally meant by EEC, but it depends on how the homologous series is defined.
Results
In this paper, we study a number of binding reactions for simple atoms, ions, and molecules at the QM and MM levels, estimating the binding enthalpies and entropies from the standard statistical-mechanics formulae in eqn (3)–(8). Individual reactions will be discussed in separate sections. We aim at answering three questions: is there a fundamental difference in EEC between systems dominated by dispersion or electrostatics (hydrogen bonds)? is there a fundamental difference in EEC when studied by MM or QM? and why is EEC not observed experimentally for all binding reactions?Pure dispersion
We will start with the simple association of two neutral atoms, i.e. a purely dispersive system without electrostatics. At the MM level, this is obtained by assuming that they interact with a Lennard-Jones potential: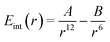 | (10) |
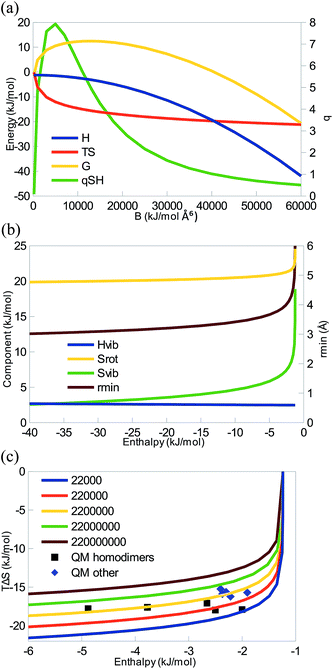
Fig. 1a shows how the enthalpy, entropy, and free energy for the binding reaction depends on the B Lennard-Jones dispersion constant for the interaction of two argon-like atoms. It can be seen that when B > 200 Å6 kJ mol−1 (for smaller B, the RRHO approximation breaks down and the entropy tends towards infinity), the systems shows EEC1 (ΔH and TΔS are both negative), as is illustrated by a positive qSH (eqn (9)). For intermediate values of B, ΔH is small, TΔS is dominating, ΔG is positive (unfavourable binding), and qSH is rather large (qSH ≈ 6 for B = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 Å6 kJ mol−1 which gives the same minimum energy and distance as a QM calculation of Ar2). However, for B > 40
160 Å6 kJ mol−1 which gives the same minimum energy and distance as a QM calculation of Ar2). However, for B > 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å6 kJ mol−1, ΔG becomes negative and qSH decreases below 1.
000 Å6 kJ mol−1, ΔG becomes negative and qSH decreases below 1.
The various enthalpic and entropic contributions are shown in Fig. 1b. In this diatomic system, the three translational degrees of freedom of each of the free atoms are converted to one vibrational, two rotational, and three translational degrees of freedom in the complex. ΔHtrans is constant, −2.5RT (−6 kJ mol−1; the two atoms atom and the complex contribute by 2.5RT each), i.e. favouring the complex formation. ΔHrot is also constant, and for this diatomic system, it is positive, +RT (2 kJ mol−1), because the free atoms do not have any rotational contributions. ΔHvib is also almost constant, ∼3 kJ mol−1; it depends on the single vibrational frequency (ν, cf.eqn (4)), but for the small frequencies typical for non-covalent interactions (for the range shown in Fig. 1b, ν = 0–200 cm−1), the term is small and the dependence on the frequency is weak.
The TΔStrans term is also constant but large and negative, −44 kJ mol−1. It depends on the mass of the atoms (eqn (6)) and reflects the loss of translational entropy when the two atoms form a complex. It is the main cause of EEC1, as suggested by Jencks.18TΔSrot is also rather large. For this diatomic system, it is positive (because the free atoms do not have any rotational contributions, so it compensates for two of the lost translational degrees of freedom). As can be seen in eqn (7), it depends on the moments of inertia, which are functions of the masses and positions of the atoms, but for this diatomic system, it is simply the product of the mass and the distance between the two atoms (rmin, also shown in Fig. 1b). Thus, it decreases somewhat as the diatomic complex becomes more compact. Finally, TΔSvib is positive and shows a strongly decreasing trend. As can be seen in eqn (8), it depends on the vibrational frequency, but, in variance to the Hvib term, it is largest for small frequencies and it becomes insignificant for frequencies above 1000 cm−1. It tends to compensate for the third lost transnational degree of freedom, especially for weak complexes. Consequently, the net enthalpy correction (ΔHtrans + ΔHrot + ΔHvib) is almost constant (−1 kJ mol−1), whereas the total entropy correction becomes more negative as B and therefore ΔH increases, owing to the concerted decrease of both the rotational and vibrational contributions. This gives rise to a strict EEC2, illustrated in Fig. 1c.
Fig. 1c shows that similar results are obtained also for other values of A. In all cases, TΔS first sharply becomes more negative and then saturates as the enthalpy is increased in magnitude, exactly as suggested by Williams.19 In this figure, we have also included QM calculations of a number pairs of noble-gas atoms (it should be noted that the QM results for these weak complexes are very sensitive to the level of theory and details of the calculations and therefore only should be taken as typical, but not particularly accurate results). It can be seen that they follow quite closely the MM results, showing that there is not any major difference between the QM and MM methods for this simple model system. However, it can be seen that the QM results do not give rise to any EEC2 (the MM and QM calculations represent different homologous series – with MM only A is varied, whereas with QM all parameters, including the masses change, because we can only study real systems). In fact, there is essentially no correlation between ΔH and TΔS for the QM calculations (the correlation coefficient r2 is 0.1). If the noble-gas homo- and heterodimers are considered separately, both groups actually show a weak anticorrelation (r2 = −0.1 or −0.2).
Pure electrostatics
Next, we turn to a system without any dispersive interactions but instead with a favourable electrostatic interaction, reminding of a hydrogen bond. With MM, this is obtained by setting B = 0 in eqn (10) and adding an electrostatic term: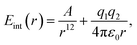 | (11) |
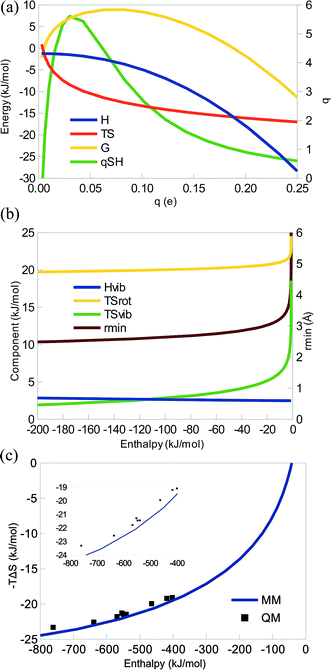
Fig. 2a shows how ΔH, TΔS, and ΔG vary with the charge for some typical parameters. It can be seen that the curves are very similar to those in Fig. 1a: the enthalpy is always negative, TΔS is also negative for all q > 0.004 e (again the harmonic-oscillator approximation breaks down for very weak complexes), therefore counteracting the enthalpy and giving rise to an EEC1 (qSH > 0). There is also a strict EEC2 (the curves are monotonous). The entropy is dominating at small charges, whereas the enthalpy dominates for large charges. Consequently, ΔG changes sign at q = 0.18 e. For a system with unit charges (q = 1 e), the entropy dominates completely (giving ΔH = −559 kJ mol−1 and TΔS = −22 kJ mol−1 with the parameters in Fig. 2a). This illustrates the strength of Coulombic interactions in vacuum. However, in water solvent, it will be scaled down by a factor of 80, giving ΔH = −6 kJ mol−1 and TΔS = −14 kJ mol−1 at the optimum interaction distance.
The various contributions to the enthalpy and entropy are qualitatively identical to those for the dispersive system (Fig. 2b), with only minor quantitative differences: ΔHtrans = −6 kJ mol−1 and ΔHrot = 2 kJ mol−1, as before, ΔHvib is nearly constant (3–4 kJ mol−1), TΔStrans = −42 kJ mol−1, TΔSrot is positive and slowly decreasing with q and E (19–25 kJ mol−1, because rmin decreases), whereas TΔSvib is also positive and more strongly decreasing in magnitude with q and E (1–19 kJ mol−1). Again, the EEC1 is mainly caused by TΔStrans and the EEC2 is caused by the concerted action of the rotational and vibrational entropy. The only major difference compared to the dispersive system is that the interaction energy varies more and may become much more negative.
In Fig. 2c, we show the correlation of the entropy and enthalpies as a function of A with q = 1.0 e. Again, it can be seen that the MM curve predicts a strict EEC2. In the plot, we have also included a number of chemical systems, studied by QM and consisting of pairs of an alkali ion and a halogen ion. It can be seen that they follow the MM curves quite well, although the enthalpy is systematically slightly underestimated (because dispersion is omitted in the MM calculations; cf.eqn (11)). The QM results also show an EEC1 and all QM points, except two pairs (NaCl–RbF and NaCl–CsF) give rise to a strict EEC2. In fact, r2 = 0.95 and the slope of the correlation line is 0.013. The deviation from the perfect correlation comes from the saturation of the entropy, as predicted by the MM theory.
Thus, from a theoretical point of view, there is no fundamental difference between dispersive and electrostatic interactions, although in practice, the latter is often stronger and therefore at a different position on the saturation curve, thereby often giving a smaller slope for the TΔS vs. ΔH correlation line.
Covalent bonds
Next, we consider the formation of a covalent bond. It can be described by a Morse potential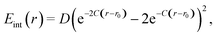 | (12) |
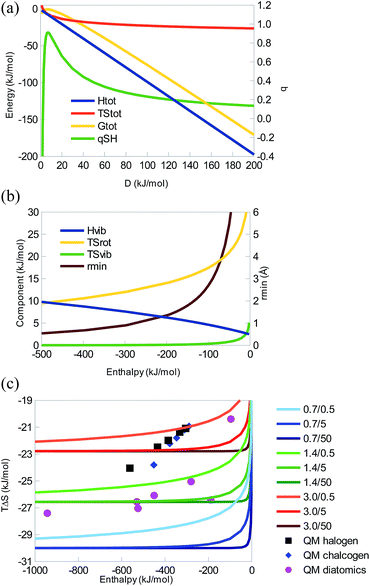
To reduce the number of parameters, we have in a first step set m1 = m2 = 19 Da (F), C = 8.87 Å−1, and assumed an inverse relationship between r and D. Then, we obtain results presented in Fig. 3a, which reproduce the QM results of F2 at D = 192 kJ mol−1. It should be noted that realistic bond lengths (r = 0.7–3.5 Å) are obtained for D = 80–400 kJ mol−1, but we have included larger ranges to show the possible variation of ΔH, TΔS, ΔG, and qSH. For example, qSH and ΔG attain maxima (qSH = 0.9 and ΔG = −1 kJ mol−1) around D = 7 kJ mol−1. However, for realistic parameters, ΔH and TΔS have the same sign, thus exhibiting an EEC1. Moreover, there is a strict EEC2, although qSH < 0.3 and TΔS shows a quite restricted variation, −22 to −35 kJ mol−1. This shows why EEC is normally not discussed for covalent bonds: ΔH is strongly dominating and TΔS is essentially constant.
The various contributions to the enthalpy and entropy are quite different from those of the other two systems (Fig. 3b): ΔHtrans = −6 kJ mol−1 and ΔHrot = 2 kJ mol−1 are still constant, as is TΔStrans = −41 kJ mol−1. However, for reasonable D energies, TΔSvib is insignificant (<1 kJ mol−1), owing to the large vibrational frequency characterising a covalent bond. TΔSrot shows the largest variation, 11–19 kJ mol−1 decreasing when D is increased (owing to changes in the bond length), so this term is the prime cause of the observed EEC2. ΔHvib also shows some variation, owing to the large vibrational frequencies, 4–9 kJ mol−1 (coming almost entirely from the zero-point energy). It provides a positive enthalpy contribution that decreases when D is increased, thereby partly counteracting ΔE, i.e. giving rise to an energy–enthalpy compensation. Thus, for typical covalent bond, the entropy is quite constant, although the small variation (from TΔSrot) is still correlated with that of ΔH, giving an EEC2.
A similar behaviour is seen for other values of r0 and B, as is shown in Fig. 3c. It can be seen that C determines how rapidly the entropy saturates. An EEC would be apparent only for small values of C and D. QM calculations for the homolytic bond dissociation of hydrogen halogenides, hydrogen chalcogenides (with a −1 e net charge), and first-row homo-nuclear diatomics are also included in Fig. 3c. It can be seen that they show a restricted range of TΔS, −20 to −27 kJ mol−1. There is a nearly perfect correlation between ΔH and TΔS for the hydrogen halogenides and hydrogen chalcogenides (r2 = 0.99–1.00), showing a strict EEC2. This linear correlation comes primarily from the TΔSrot term, reinforced by the change in the mass of the heavy atom (the mass is constant for the MM curves in Fig. 3). For the diatomics or all three groups together, the correlation is lower (r2 = 0.48 and 0.36; because there is a mixture of single, double, and triple bonds) and the EEC2 is not strict, but still significant. The slopes of the correlation lines are small, 0.006–0.018.
This exercise shows that even covalent bonds are expected to give a qualitatively similar behaviour. However, owing to the strength of typical covalent interactions, TΔS is essentially always fully saturated and no EEC is normally discussed for such systems.
Water-like systems
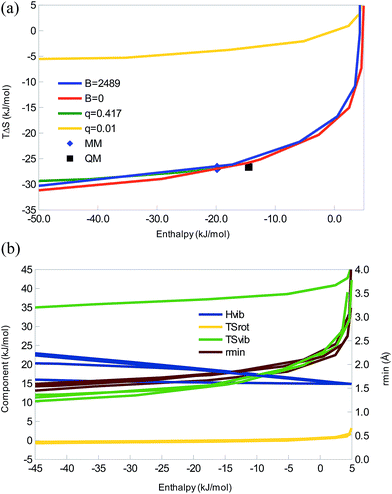
Next, we will study a series of water-like systems, i.e. systems of the form HXH–XH2. We use MM methods and assume that the only significant Lennard-Jones interaction is that between the two heavy atoms (a common assumption in many MM water models, e.g. TIP3P32). Thereby, the system will only involve three parameters (besides the masses, which we fix at the normal masses of hydrogen and oxygen, and the internal geometry of the monomers, which we fix to experimental values): the X–X Lennard-Jones parameters A and B, and the charge on the H atoms, qH (we assume that the two H atoms have the same charge and that the monomers are neutral so that qX = −2qH). In addition, we will keep A constant at the normal value for TIP3P water, 2.435 × 106 Å12 kJ mol−1.32 This system has the advantage that each monomer has three atoms, so that there are rotational contributions to all terms, making it similar to more realistic systems.We studied four cases: we varied qH with constant B, either that of TIP3P water (B = 2489 Å6 kJ mol−1) or B = 0 (no dispersive attraction). Alternatively, we varied B with constant qH, either that of TIP3P water (qH = 0.417 e) or almost zeroed (qH = 0.01 e; if qH is zeroed, the H atoms become non-interacting dummy atoms). Thus we can compare purely dispersive and purely electrostatic variants with a realistic water model.
In all four cases, we obtain enthalpy–entropy curves of the same type as the diatomic systems in Fig. 1c, 2c, and 3c, i.e. with a sharp bend and saturation at large negative enthalpies, as can be seen in Fig. 4. The TIP3P parameters are at the beginning of the saturation plateau and quite close to the QM result. All four curves show strict EEC2, but as the enthalpy (but not the energy) is positive for the weakest interactions, we sometimes do not have EEC1. However, for realistic parameters, qSH ≈ 1.5. It can be seen that dispersion has a minimal effect on this interaction – the curves for B = 0 and B = 2489 Å6 kJ mol−1 are essentially identical, as is the one for q = 0.417 e. It is only the curve for q = 0.01 e that differs and only by a simple translocation of the curve to less negative entropies – the shape is the same.
Looking at the components, ΔHtrans = −6 kJ mol−1 as always and we now have a non-vanishing rotational contributions of the monomers, leading to a negative ΔHrot = −4 kJ mol−1, which will be the same for all large molecules. TΔStrans is constant, −41 kJ mol−1, whereas TΔSrot shows a small variation, depending on the length of the hydrogen bond, 3 to −1 kJ mol−1, most negative for the strongest complexes (cf.Fig. 4b). ΔHvib is positive and quite large, 15–31 kJ mol−1, increasing with the binding energy. Therefore, it again gives rise to some energy–enthalpy compensation. TΔSvib shows the largest variation, 7–45 kJ mol−1, decreasing when the complex becomes stronger. It is the prime cause of the EEC2, compensating for the loss of translational and rotational freedom. It also causes the diverging results for the q = 0.01 e curve, by being ∼25 kJ mol−1 more positive, owing to five very small vibrational frequencies (<20 cm−1; the smallest frequency for the water dimer is 142 cm−1 at the QM level). This is mainly an artefact of the missing dispersion interactions of the hydrogen atoms.
Consequently, this model show that the same type of EEC curves are obtained also for more realistic multi-atom systems and it gives an indication of the sign of the various components in such systems. Dispersion has a minimal influence on the results for the interaction of two water-like molecules, whereas the magnitude of the charges determines the absolute scale of the entropy, without changing the shape of the curves.
Larger dispersive and hydrogen-bonded systems
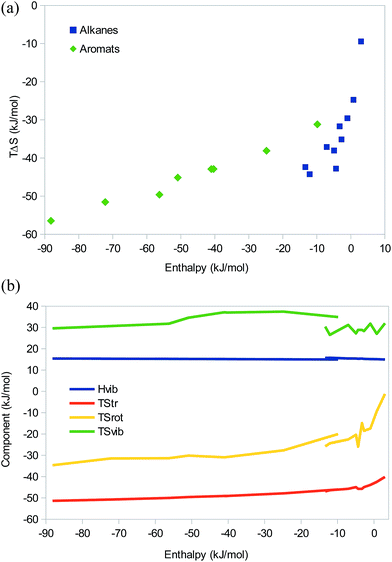
So far, we have seen that there is no significant difference between EEC studied at the QM and MM levels and that there are no fundamental difference between dispersive, electrostatic, hydrogen-bonded, or even covalent systems, only quantitative differences caused by the magnitude of ΔH, i.e. the position on the saturation curve. We will now check that these results are not modified when there are several simultaneous interactions between the two binding molecules. We will continue to study (mainly) dispersive and electrostatic (hydrogen-bonded) interactions separately.As models of dispersive interactions with an increasing strength, we have studied at the MM level dimers of the seven first n-alkanes and the three simplest branched alkanes, as well as eight stacked dimers of simple polyaromatic systems (with 1–6 benzene rings). All had zeroed charges to ensure that the interactions are purely dispersive. The results in Fig. 5 show that for the alkanes, there is an EEC1 (except for the methane and ethane dimers, for which the enthalpy is positive) and a reasonable EEC2 with a correlation r2 = 0.83 and a slope of 1.7. In agreement with Fig. 1b, there is an indication that the points with the least negative entropy show a larger slope than those with more negative enthalpies.
The aromatic systems show a nearly perfect EEC2 (r2 = 0.98). Compared to the alkanes, the slope of the correlation line is appreciably lower, 0.3, reflecting that the complexes are appreciably stronger (ΔE = −15 to −94 kJ mol−1) and therefore lie further to the left on the saturation curve. However, the larger ΔE comes entirely from the increased number of atoms – with the GAFF force field, benzene gives a less favourable interaction energy and enthalpy (−15 and −10 kJ mol−1) than n-hexane (which contains the same number of carbon atom; −18 and −12 kJ mol−1), but the entropy is smaller (TΔS = −31 compared to −44 kJ mol−1), owing mainly to the vibrational term and the higher symmetry of benzene.
Looking at the enthalpy components, the translational and rotational enthalpies are constant at ΔHtrans = −6 kJ mol−1 and ΔHrot = −4 kJ mol−1 as for all larger systems. The vibrational enthalpy is also essentially constant, increasing by less than 1 kJ mol−1 for the largest systems (ΔHvib = 15–16 kJ mol−1; Fig. 5b).
The translational entropy shows a restricted variation, increasing from −40 to −51 kJ mol−1 when the size of the molecules increases (Fig. 5b). TΔSrot shows a similar, but larger variation, increasing from −1 to −35 kJ mol−1 with the size of the molecule. For the alkanes, the EEC2 comes entirely from these two terms, which give correlations of 0.74 and 0.69 to the enthalpy, respectively. Thus, the EEC2 is a pure size effect, which is expected as dispersion is present everywhere and therefore will increase with the size of the molecules. For the aromatic systems, the vibrational entropy also contributes to the EEC2, with a variation of 8 kJ mol−1 and a decent correlation to the enthalpy (r2 = 0.64). Thus, we can conclude that realistic dispersive systems also show pronounced EEC2, but different homologous series can give different slopes, depending on the strength of the interactions.
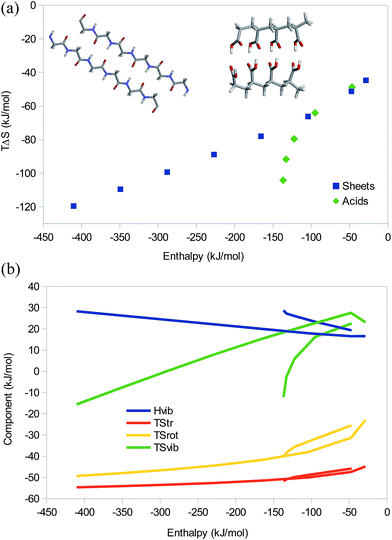
Next, we consider two sets of hydrogen-bonded systems, which are shown in Fig. 6a. The first is dimers of linear glycine oligomers, as a model of a protein β sheet. We studied oligopeptides with 1, 2, 4, 6, 8, 10, 12, and 14 units and no capping groups. The larger systems have n − 2 hydrogen bonds, where n is the number of glycine units, whereas the three smallest systems all have two hydrogen bonds (they were truncated differently). The second was a set of dimers of polycarboxylic acids with 1–5 propionic acid units (i.e. with three carbon atoms between each pair of acid groups). There were two hydrogen bonds between each pair of acidic group in the dimer.
The results in Fig. 6a shows that the β sheets give an almost perfect EEC2 with a correlation between the enthalpy and TΔS of 0.99 and a slope of 0.18. For the polypropionic acid dimers, there is also an EEC2, but it is much less linear, r2 = 0.89 and the slope is 0.56. The reason for this is that the hydrogen bonds become increasingly less favourable at the terminals of the larger dimers, owing to internal strain in the carbon backbone. In fact, with six units, the last hydrogen bond breaks. The three smallest dimers give a better correlation with r2 = 0.97 and a slope of 0.40.
All three entropy components show a good correlation to the total entropy, r2 = 0.89–0.99, with TΔStrans and TΔSvib giving the best correlation and TΔSvib giving the largest contribution to the variation in the total entropy (Fig. 6b). It is notable that TΔSvib changes sign from positive to negative for the largest systems of both models, so that it no longer counteracts the other two terms, but instead contributes to EEC1. Interestingly, for these strong complexes, the vibrational frequencies become so large that also ΔHvib shows a significant variation, 17–28 kJ mol−1, with a good correlation to the total enthalpy (r2 = 0.96–0.98). It therefore gives rise to a significant energy–enthalpy compensation.
It is interesting that the three smallest β-sheet systems follow the same linear EEC2 although they all have two hydrogen bonds. This is caused by both electrostatic and dispersive interactions: the pair-wise difference in binding energy between the n = 1 and 2 complexes (19 kJ mol−1) comes mainly (14 kJ mol−1) from electrostatics, with a contribution of 6 kJ mol−1 from bonded interactions (the smallest complex is strongly distorted by the two hydrogen bonds) and an opposing 1 kJ mol−1 contribution from dispersion. The difference between the n = 2 and 4 complexes (58 kJ mol−1) comes mainly (46 kJ mol−1) from electrostatics, but the dispersion also contributes by 13 kJ mol−1, whereas the bonded contribution is only 1 kJ mol−1 and counteracting. For all the other complexes, adding two Gly residues increases the interaction energy by 63 kJ mol−1, of which 53, 13, and −2 kJ mol−1 come from electrostatics, dispersion, and bonded interactions, respectively.
Thus, we can conclude that for both the dispersive and the hydrogen-bonded systems, a pronounced EEC2 is observed. We do not observe any qualitative difference between the dispersive and hydrogen-bond interactions, besides that the latter are typically stronger. This is in accordance with our results in the previous sections of this article.
Competition with water
So far, all studied systems (except the methane and ethane dimers with positive ΔH) have shown EEC1 and most of them also positive correlation between ΔH and TΔS, indicating EEC2. We have also seen how such EEC arises naturally either from the increase in TΔStrans and TΔSrot with the molecular mass (and therefore with more interactions) or from TΔSvib increasing with the strength of the interactions. Why is then not EEC always observed in all molecular systems? A natural answer to this question is that all the calculations were performed for isolated molecules in vacuum, whereas real interactions take place in water solution. To examine this possibility, we have also performed some tests of how the addition of water molecules may affect the results for some types of interactions. Of course, the present approach cannot properly model the full solvation of the molecules or the dynamics of water, but we believe that it can illustrate some of the expected effects of water.For the series of nine alkane dimers, we added one water molecule to each monomer, ensuring that the two water molecules in the dimer form a hydrogen bond. The results in Fig. 7 shows that the calculations with water give more negative enthalpies than those without water by ∼24 kJ mol−1, i.e. the enthalpy of the new hydrogen bond between the two water molecules. TΔS also becomes more negative by a similar amount. For the nine complexes with water, there is only a faint EEC2 (r2 = 0.16). However, this is mainly caused by a single outlier (isopentane); if it is excluded, r2 = 0.78 and the slope is 1.5. In fact, this is quite close to the EEC correlation line of the alkanes without water, with a slope of 1.0 for the joint systems (r2 = 0.82).
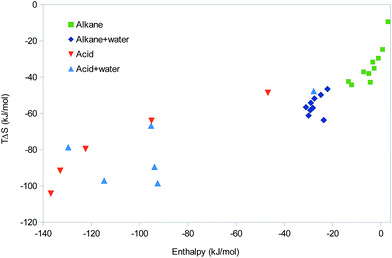 | ||
| Fig. 7 Correlation between the enthalpy and entropy of the ten small alkanes in Fig. 5 and the six dimers of the polypropionic acid oligomers in Fig. 6 without and with water. | ||
We performed also a similar study of the polypropionic-acid systems, for which we added one water molecule to each acidic group, i.e. 1–6 for the various monomers. No attempt was made to add the water molecules at any systematic positions. Instead, they were added more or less random from a pre-equilibrated box of water molecules according to their distance to the acidic molecule. The results of these calculations are also shown in Fig. 7. It can be seen that in this case, the solvated calculations fall in a similar range as those without water. This is expected, because hydrogen bonds with water and neutral carboxylic acids have a similar strength. However, there is a tendency that the calculations with water give a less negative enthalpy and a more negative entropy.
At first, the non-systematic manner in which the water molecules were added may seem to be a disadvantage. It is the reason why the correlation between ΔH and TΔS is modest (r2 = 0.49). However, in practice, this unsystematic study gives more information of the variability of the hydrogen-bond strength and how the enthalpy and entropy terms vary with this strength. The enthalpy and entropy contributions for the six complexes in Table 1 show that TΔStrans and TΔSrot become somewhat more negative as the size of the complex increases (−47 to −53 and −28 to −44 kJ mol−1, respectively). The former term depends only on the molecular mass of the complex, whereas the latter varies also with the geometry (compactness) of the complex. However, only the two vibrational terms show a variation coupled to the strength of the formed hydrogen bonds. ΔHvib show a rather small variation, 17–25 kJ mol−1, slightly increasing with the size of the complexes, but more anticorrelated to the strength of the complex (r2 = 0.79 with respect to ΔE). Thus, it slightly counteracts the binding energy, but the slope of the correlation line is only −0.06, so the effect is quite small. TΔSvib shows a larger variation, 27 to −2 kJ mol−1, but it is more correlated to the size of the complex than to ΔH (r2 = 0.46). This is the reason for the quite poor correlation between the net ΔH and TΔS: the entropy terms show only a weak correlation to the binding energy and the variation of the ΔHvib term is much smaller than the variation in ΔE. This also explains why most points with water lie below the old correlation line between ΔH and TΔS: when the hydrogen bonds formed in the dimer are not ideal, ΔE and therefore also ΔH becomes less negative. However, both TΔStrans and TΔSrot depend mainly on the size of the complex, so they will still become more negative and therefore actually overcompensating the enthalpy.
| n | ΔE | ΔHtrans | ΔHrot | ΔHvib | TΔStrans | TΔSrot | TΔSvib | ΔHtrv | ΔTS | ΔHb |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −34.9 | −6.2 | −3.7 | 17.0 | −46.6 | −27.5 | 26.5 | 7.1 | −47.7 | 0 |
| 2 | −106.1 | −6.2 | −3.7 | 20.7 | −49.2 | −34.1 | 16.5 | 10.8 | −66.8 | 5 |
| 3 | −144.5 | −6.2 | −3.7 | 24.7 | −50.7 | −37.8 | 9.8 | 14.8 | −78.7 | 4 |
| 4 | −106.7 | −6.2 | −3.7 | 22.8 | −51.7 | −39.9 | 2.1 | 12.9 | −89.5 | 4 |
| 5 | −125.7 | −6.2 | −3.7 | 20.9 | −52.6 | −42.4 | −2.0 | 11.0 | −97.0 | 7 |
| 6 | −105.2 | −6.2 | −3.7 | 22.7 | −53.2 | −44.1 | −1.2 | 12.7 | −98.5 | 3 |
The chelate effect
Finally, we will to shortly discuss the chelate effect, which has been discussed in several publications.16,18–21 As already mentioned, the formation of a complex from two free molecules leads to major unfavourable translational and rotational entropy terms. However, this term is paid only once when the complex is formed, i.e. when the first interaction between the two molecules is formed. If there are additional interactions between the two molecules, these should have smaller entropy penalties, coming mainly from the vibrational part.This can be illustrated by N-methylacetamide. In the dimeric complex, it can form either one or two hydrogen bonds, giving ΔE = −32 or −57 kJ mol−1 at our QM level. As the complexes consists of the same molecules, ΔHtrans, ΔHrot, and TΔStrans are all identical for the two complexes. Moreover, ΔHvib agree to within 0.3 kJ mol−1 (Table 2). On the other hand, the complex with two hydrogen bonds is more compact so that TΔSrot is 2 kJ mol−1 more negative for that complex. Likewise that complex is slightly stronger (both NH–O hydrogen bonds are 1.81 Å, compared to 1.90 Å for the single hydrogen bond in the other complex), so TΔSvib is also 2 kJ mol−1 more negative. Consequently, when the first hydrogen bond is formed, the quite favourable energy (ΔE = −32 kJ mol−1) is more than compensated by the unfavourable ΔHvib (16 kJ mol−1) and entropy terms (TΔS = −46 kJ mol−1) so that the net binding free energy is unfavourable (ΔG = 21 kJ mol−1). However, when the second hydrogen bond forms, all these costs have already been paid and the extra energy of the second hydrogen bond (ΔE = −26 kJ mol−1) is only counteracted by a slight increase in the ΔHvib, TΔSrot, and TΔSvib terms, 4 kJ mol−1 in total. Therefore, the free energy becomes favourable (ΔG = −2 kJ mol−1).
| System | r Hb | ΔE | ΔHtrans | ΔHrot | ΔHvib | TΔStrans | TΔSrot | TΔSvib | ΔHtrv | ΔTS | ΔG |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Hb | 1.90 | −31.6 | −6.2 | −3.7 | 15.9 | −45.8 | −25.3 | 24.6 | 6.0 | −46.5 | 20.9 |
| 2 Hb | 1.81 | −57.5 | −6.2 | −3.7 | 15.6 | −45.8 | −27.3 | 23.0 | 5.7 | −50.1 | −1.7 |
| Diff. | −25.9 | 0.0 | 0.0 | −0.3 | 0.0 | −2.0 | −1.6 | −0.3 | −3.6 | −22.6 |
Do we see this effect also in the other systems? In fact, the effect is not qualitatively different from the effects seen in the other homologous series (where we also pay the prime entropic penalty in the first complex and then only add smaller increases in the entropy as the complexes are made larger). Seen in this way, the N-methylacetamide complexes show a 4 kJ mol−1 decrease in TΔSrot + TΔSvib as ΔE or ΔH become more negative by 26 kJ mol−1. This is an EEC2 with a slope of 0.14, i.e. similar to what was found for the β-sheets (0.18). All homologous series will take some advantage of the chelate effect, but they still show an EEC2, as TΔSvib often TΔSrot becomes more negative with the strength of the complex. Moreover, the effect is blurred by the fact that for real molecules in homologous series, the mass increases when more interactions are formed, leading to an increase also in TΔStrans and TΔSvib.
Discussion
In this section, we give a general discussion of all our results (QM or MM results for 89 real molecular systems and MM results for a large number of simplified analytical models). We will first discuss which systems and energy components give rise to the EEC1, then how EEC2 arises. Finally, we will compare our results with those obtained by Korth25 with QM methods for the S22 (ref. 43) and S66 (ref. 44) sets of interacting molecules and discuss whether different types of interactions give rise to different types of EEC.Among our 89 molecular systems, ΔH is negative for all, except two, viz. the methane and ethane dimers, which have slightly positive ΔH (3 and 1 kJ mol−1) owing to the ΔHvib term (ΔE is negative, −2 and −4 kJ mol−1). On the other hand, TΔS is negative for all systems (−9 to −120 kJ mol−1). Thus all systems show an energy–entropy compensation and all except two show EEC1. The same is seen in Korth's data (he also obtained a positive enthalpy for the methane dimer). The quotient qSH shows a large variation, ranging from 29 for the propane dimer (owing to the low ΔH) to 0.3 for the largest β sheets and 0.03 for LiF.
Looking at the enthalpy components, ΔHtrans is always −6 kJ mol−1, favouring the bonding and enhancing the enthalpy. For the diatomic complexes, ΔHrot is positive (+2 kJ mol−1), counteracting the binding, but for all more realistic complexes, it is −4 kJ mol−1, enhancing the enthalpy. On the other hand, ΔHvib is always positive, thereby counteracting the binding. For Korth's complexes of rather similar sizes, it is almost constant, 13–17 kJ mol−1, but in our diatomic complexes it can be as small as 2 kJ mol−1 and for the largest hydrogen-bonded systems it can increase to 29 kJ mol−1. Thus, the net enthalpy correction is in general positive and often ∼5 kJ mol−1, although it is −1 for several of the diatomic complexes, up to 19 kJ mol−1 for the systems with many hydrogen bonds, and 23 kJ mol−1 for H2.
TΔStrans is always negative, −30 kJ mol−1 to −55 kJ mol−1, although it continues to decrease logarithmically (become more negative) with the size of the complex. It is numerically the largest entropy term and therefore always gives the largest contribution to the EEC1. TΔSrot is positive (4–26 kJ mol−1) for the diatomic complexes, counteracting the EEC1. However, for the more typical polyatomic complexes, it is negative and therefore contributing to the EEC1. It increases roughly with the size of the complex, varying between 0 kJ mol−1 (water dimer) and −49 kJ mol−1 for the largest model, thus providing a sizeable contribution to the EEC1. Finally, TΔSvib may have a varying sign. For most complexes, it is positive and 10–40 kJ mol−1. However, for the periodic systems with an increasing number of hydrogen bonds, it decreases with size and eventually becomes negative for the five largest β sheets and acid dimers. Thus, for most complexes, this term compensates the loss of translational and rotational freedom, reducing the EEC1, but for the largest models it may actually contribute to EEC1.
The EEC2 is instead determined by the differences between two complexes in a homologous series. Of course, this somewhat changes the conclusions; for example, both ΔHtrans and ΔHrot are constant and therefore do not contribute to EEC2. However, it also means that the results depend on how you define a homologous series.
If the mass of the complexes do not change, e.g. in the chelate effect or for the toy systems in Fig. 1–4, TΔStrans is also constant and does not contribute to the EEC2. However, in most homologous series (e.g. in all our series of real molecules), the mass increases. Then, both TΔStrans and TΔSrot become more negative, but typically by only a few kJ mol−1 (in our cases, by 0–8 kJ mol−1, often slightly more for TΔSrot than for TΔStrans). Still, it is not evident that this will lead to an EEC2, because it depends on how ΔE changes in the series. For the ionic QM systems in Fig. 2c and the covalent QM systems in Fig. 3c, the strength of the interaction actually decreases with the mass, so that TΔStrans and TΔSrot give rise to a (weak) enthalpy–entropy anti-compensation. For the noble gases and the systems with added water molecules, the trend of ΔE with respect to the mass is varying, so that no conclusion can be reached regarding the EEC2. The same also applies if isomers are included in the alkane and aromatic series (some of the complexes have the same masses, but different ΔE). However, for the pure alkane, polyaromatic, β-sheet, and polypropionic-acid series, the TΔStrans and TΔSrot terms give significant contributions to EEC2. The same actually also applies for TΔSrot in some systems with a constant mass (the model systems in Fig. 1–4 and the chelate complex), because there is direct relation between the strength of the complex and the interaction distance, which contributes to the compactness of the complex (the moment of inertia) and therefore to TΔSrot.
The ΔHvib term gives a varying contribution in the various homologous series. For weak complexes (noble gases, dispersion, alkane, and polyaromatic series), it gives an insignificant contribution. For the ionic and covalent diatomic systems studied by QM, it gives a negative contribution of −1 to −6 kJ mol−1, thereby counteracting ΔE (which becomes more positive in these homologous series). For the large hydrogen-bonded systems, it instead gives a positive contribution of 0–4 kJ mol−1, but again it means that it counteracts ΔE and therefore gives an energy–enthalpy compensation.
Finally, the TΔSvib term is also varying. For the two-atom toy systems, it is always negative and up to 11 kJ mol−1. However, for the real (QM) two-atom systems, it changes very little (less than 1 kJ mol−1). For the alkanes, it gives an alternating sign, ±5 kJ mol−1. However, for the other larger systems, it is in general negative and for the hydrogen-bonded systems rather large, −6 to −10 kJ mol−1, giving rise to a clear EEC2. Thus, this term changes its effect depending on how the EEC is defined: in absolute terms, it typically counteracts the other two entropy components and leads to an anti-EEC1, but for most homologous series it enhances EEC2 and often is the dominant entropy term in that respect.
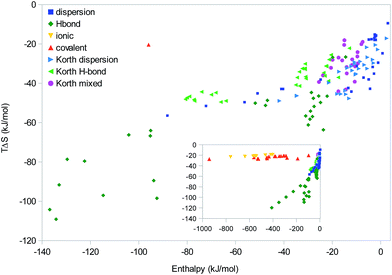
Finally, we consider the data in the same way as Korth,25i.e. looking for linear correlations in a scatter plot of the absolute ΔH and TΔS results of all systems, show in Fig. 8. This is essentially some sort of EEC2, including all molecules in the “homologous” series. However, following Korth, we will group them after the dominant type of interaction. Considering all complexes (inset), a major difference in the correlation of the covalent and ionic complexes on one hand (with a slope of 0.01) and all the other complexes (with an average slope of 0.3) is apparent. However, as we saw in Fig. 1–3, this does not indicate any fundamental difference between the different types of interactions; instead it only reflects that these interactions are stronger and therefore are on the saturation plateau on the ΔH and TΔS curve. The β sheets are also conspicuous owing to the large enthalpies and the nice linear correlation (slope 0.18).
Concentrating on the other complexes with more moderate enthalpies, it is hard to see any clear-cut difference between systems dominated by dispersion or hydrogen bonds. It can be seen that there are a group of hydrogen-bonded systems (with enthalpies around 30 kJ mol−1) that fit quite well into the group and slope of the majority of our and Korth's dispersion-dominated systems. Likewise, our data for the polyaromatic complexes (with a slope of 0.3; dispersion points with ΔH of −40 to −90 kJ mol−1 in Fig. 8) fit quite nicely into both our and Korth's data of hydrogen-bonded complexes. In particular, the slope is lower than for the polypropionic-acid systems (0.56). This confirms our conclusion that there are no clear-cut difference between complexes dominated by dispersive or hydrogen-bond interactions. Instead, individual homologous series have varying slopes and the net slopes obtained from a scatter plot of a large number of complexes mainly depends on the selection of complexes (which series dominate the results).
Conclusions
In this paper we have studied fundamental aspects of enthalpy–entropy compensation based on minimised structures and vibrational frequencies calculated with QM and MM methods and the RRHO approach, in a manner similar to what has been done by Williams, Dunitz, and Korth before.18–25 Our aim has been to decide whether there is any fundamental difference between dispersive and hydrogen-bond interactions, between QM and MM calculations, and to discuss why EEC is observed in some cases, but not all.At the MM level, we can study systems that are purely dispersive or electrostatic. Comparing the curves in Fig. 1 and 2, it is clear that there is no qualitative difference between the two types of interactions: they both show that TΔS first rapidly decreases and then levels out to saturation when ΔH becomes more negative. In fact, also covalent bonds give similar curves (Fig. 3). The only difference is the magnitude of ΔE (and therefore ΔH), which is two orders of magnitude larger for the covalent and ionic bonds.
For homologous series of more realistic molecules dominated by dispersive (alkane or polyaromatic dimers) or hydrogen bonds (polyglycine sheets or polypropionic-acid dimers), nearly linear relations between ΔH and TΔS were obtained, with slopes of 0.2–1.7. There is a tendency that complexes dominated by hydrogen bonds give a smaller slope, but this is mainly caused by the fact that hydrogen bonds typically provide a larger gain in enthalpy for the same number (mass) of added atoms, i.e. that they are further to the left in the saturation plateau in Fig. 1c and 2c. For strong dispersive interactions as in the polyaromatic systems, the slope (0.3) is actually smaller than what is obtained in many hydrogen-bonded systems, as is evident if all studied complexes are included in the same plot (Fig. 8).
We have emphasized the importance to define what is meant by EEC and we have used two different definitions. EEC1 simply states that ΔH and TΔS have the same sign for a certain reaction. In our simple binding reactions, where two molecules form a complex in vacuum, this is the case for all 89 dimers, except the two smallest alkanes (for which ΔH happens to be positive). This EEC1 is caused by the loss of translational and vibrational freedom (entropy), partly counteracted by the gain in vibrational entropy, as has already been suggested by Jencks, Williams, and Dunitz.18–25 However, in real binding reactions, it will be blurred, because both the ligand and the receptor are in water solution, rather than in gas phase, which is expected to reduce the translational and rotational freedom. Moreover, it has to be taken into account that water molecules may be associated with the ligand and the binding site before the binding and that some of these may be displaced upon binding.
We have also discussed EEC2, i.e. how ΔH and TΔS change in homologous series of compounds. This is probably closer to the common meaning of EEC. Such a definition gives the advantage that several terms cancel (ΔΔHtrans, ΔΔHrot, and possibly TΔΔStrans). On the other hand, it must be defined what is meant by a homologous series and the results will depend on that choice. We have shown that for truly homologous series, where the same structural unit and identical interactions are successively added, nearly perfect linear relations between ΔH and TΔS can be obtained. Such an EEC2 is caused by joint effect of all three entropy terms. Thus, for EEC2, TΔΔSvib typically gives a contribution of the same sign as TΔΔStrans and TΔΔSrot and it gives a dominant contribution at least for the hydrogen-bonded systems. For weaker systems, the EEC2 is dominated by the ΔΔStrans and ΔΔSrot terms, i.e. by pure size effect, rather than the strength of the complex (which is correlated with TΔΔSvib).
However, it is apparent from this study that EEC of any kind is not expected to be strict in real binding studies: only for perfect homologous series are nice linear relations obtained. As soon as the interactions change (e.g. as in the larger polypropionic-acid dimers), the relation is blurred and if water molecules are added in a non systematic way, the correlation disappears and anticorrelation can easily be obtained between certain pairs. If the complete dynamic effect of water solvation is included any relation between ΔH and TΔS can be expected.
In conclusion we do not see any fundamental difference between pure dispersive or electrostatic (hydrogen-bonded) interactions, nor between QM or MM calculations. The RRHO model gives a clear indication when and how EEC1 and EEC2 arise during the binding of two molecules in gas phase. However, the real binding reaction between a ligand and a receptor in water solution is much more complicated, with water molecules giving large effects which easily can blur the expected EEC and even giving anticorrelation. Unfortunately, such interactions are determined by the details of the ligand and the receptor45 (and the dynamics of the system) making it hard to reach any general conclusions.
Acknowledgements
This investigation has been supported by grants from the Knut and Alice Wallenberg Foundation (KAW 2013.0022) and the Swedish Research Council (project 2010-5025), as well as by computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc, Lund University.References
- L. Liu and Q.-X. Guo, Chem. Rev., 2001, 101, 673 CrossRef CAS PubMed.
- K. Sharp, Protein Sci., 2001, 10, 661–667 CrossRef CAS PubMed.
- J. D. Chodera and D. A. Mobley, Annu. Rev. Biophys., 2013, 42, 121 CrossRef CAS PubMed.
- O. Exner, Chem. Commun., 2000, 1655 RSC.
- A. Cooper, C. M. Johnson, J. H. Lakey and M. Nöllmann, Biophys. Chem., 2001, 93, 215 CrossRef CAS.
- H. Qian and J. J. Hopfield, J. Chem. Phys., 1996, 105, 9292 CrossRef CAS PubMed.
- E. B. Starikov and B. Nordén, Chem. Phys. Lett., 2012, 538, 118 CrossRef CAS PubMed.
- C.-E. Chang and M. K. Gilson, J. Chem. Theory Comput., 2012, 8, 13156 CrossRef.
- S. Moghaddam, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2009, 131, 4012 CrossRef CAS PubMed.
- C. H. Reynolds and M. K. Holloway, ACS Med. Chem. Lett., 2011, 2, 433 CrossRef CAS PubMed.
- T. S. G. Olsson, J. E. Ladbury, W. R. Pitt and M. A. Williams, Protein Sci., 2011, 20, 1607 CrossRef CAS PubMed.
- C. Forrey, J. F. Douglas and M. K. Gilson, Soft Matter, 2012, 8, 6385 RSC.
- E. Gallicchio, M. M. Kubo and R. M. Levy, J. Am. Chem. Soc., 1998, 120, 4526 CrossRef CAS.
- G. Graziano, J. Chem. Phys., 2004, 120, 4467 CrossRef CAS PubMed.
- D. M. Ford, J. Am. Chem. Soc., 2005, 127, 16167 CrossRef CAS PubMed.
- D. H. Williams, E. Stephens, D. P. O'Brien and M. Zhou, Angew. Chem., Int. Ed., 2004, 43, 6596 CrossRef CAS PubMed.
- S. Moghaddam, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2009, 131, 4012 CrossRef CAS PubMed.
- W. P. Jencks, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 4046 CrossRef CAS.
- M. S. Searle, M. S. Westwell and D. H. Williams, J. Chem. Soc., Perkin Trans. 2, 1995, 141 RSC.
- M. S. Searle and D. H. Williams, J. Am. Chem. Soc., 1992, 114, 10690 CrossRef CAS.
- M. S. Searle and D. H. Williams, Nucleic Acids Res., 1993, 21, 2051 CrossRef CAS PubMed.
- D. H. Williams and M. S. Westwell, Chem. Soc. Rev., 1998, 27, 57 RSC.
- M. S. Westwell, M. S. Searle, J. Klein and D. H. Williams, J. Phys. Chem., 1996, 100, 16000 CrossRef CAS.
- J. Dunitz, Chem. Biol., 1995, 2, 70 CrossRef.
- M. Korth, Med. Chem. Commun, 2013, 4, 1025 RSC.
- F. Jensen, Introduction to Computational Chemistry, J. Wiley & Sons Ltd, Chichester, 1999, pp. 298–306 Search PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, K. M. Merz, D. A. Pearlman, M. Crowley, R. C. Walker, W. Zhang, B. Wang, S. Hayik, A. Roitberg, G. Seabra, K. F. Wong, F. Paesani, X. Wu, S. Brozell, V. Tsui, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, P. Beroza, D. H. Mathews, C. Schafmeister, W. S. Ross and P. A. Kollman, AMBER 9, University of California, San Francisco, 2006 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollamn and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2000, 21, 132–146 CrossRef CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955 CrossRef CAS PubMed.
- P. Jurecka, J. Sponer, J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef PubMed.
- S. Genheden, P. Mikulskis, L. Hu, J. Kongsted, P. Söderhjelm and U. Ryde, J. Am. Chem. Soc., 2011, 133, 13081–13092 CrossRef CAS PubMed.
Footnote |
| † This argument is quite strange, considering that he primarily discussed results obtained at the dispersion-corrected density-functional theory level, i.e. with dispersion estimated with a molecular-mechanics (MM) approach. The fact that he obtains similar results at the MP2 level shows that at least the dispersion interactions are well modelled by MM. |
| This journal is © The Royal Society of Chemistry 2014 |