A comprehensive model of the phototransduction cascade in mouse rod cells

Abstract

Vertebrate visual phototransduction is perhaps the most well-studied G-protein signaling pathway. A wealth of available biochemical and electrophysiological data has resulted in a rich history of mathematical modeling of the system. However, while the most comprehensive models have relied upon amphibian biochemical and electrophysiological data, modern research typically employs mammalian species, particularly mice, which exhibit significantly faster signaling dynamics. In this work, we present an adaptation of a previously published, comprehensive model of amphibian phototransduction that can produce quantitatively accurate simulations of the murine photoresponse. We demonstrate the ability of the model to predict responses to a wide range of stimuli and under a variety of mutant conditions. Finally, we employ the model to highlight a likely unknown mechanism related to the interaction between rhodopsin and rhodopsin kinase.

---

1 Introduction

Visual phototransduction is the biochemical process by which a light stimulus is translated into a neuronal signal. The response is triggered by the absorption of photons of light by visual pigments, which then activate a prototypical G-protein signaling cascade.^1,2 The first steps of phototransduction involve the binding of the heterotrimeric G-protein transducin (G_t) to the activated receptor, rhodopsin (R*). R* catalyzes the exchange of GTP for GDP bound to G_t, which results in the dissociation of the R*·G_t complex and the further dissociation of the G_tα subunit from the G_t heterotrimer.³ G_tα is then free to bind and activate a phosphodiesterase (PDE), resulting in the hydrolysis of intracellular cGMP.^4,5 This leads to the closure of cGMP-gated ion channels, a subsequent drop in the intracellular Ca²⁺ concentration due to its continued extrusion via Na⁺/Ca²⁺, K⁺ ion exchangers,^6,7 and a consequent hyper-polarization of the cell membrane.

Deactivation of the pathway consists of several concurrent mechanisms. Decreasing Ca²⁺ concentrations induce a change in conformation of the protein recoverin (Rec),⁸ causing it to dissociate from rhodopsin kinase (RK).^9,10 The kinase is then free to bind and multiply phosphorylate R*.^11–13 Increasing phosphorylation levels of R* lead to decreased binding affinities of both RK¹⁴ and G_t¹⁵ for it, while the affinity of Arrestin (Arr) for R* increases.^15,16 Arr dissociates from its homo-dimeric and homo-tetrameric storage forms to bind R*, preventing further activation of the pathway and effecting the release and recycling of the light-sensitive chromophore from the receptor.^17–19 Meanwhile, the regulating protein RGS9-1 binds the activated G_tα·PDE complex and stimulates the innate GTPase activity of G_tα, resulting in the deactivation and dissociation of the complex.²⁰ Finally, decreasing Ca²⁺ concentrations trigger the activity of two guanylate cyclase activating proteins (GCAPs), which cause guanylate cyclases (GCs) to synthesize cGMP at higher rates.²¹ This leads to the re-opening of the cGMP-gated ion channels and a return to the dark circulating current.

The rod photoreceptor exhibits the ability to respond to stimuli across several orders of magnitude of intensity, including the detection of single photons. At low light intensities, activation requires efficient and effective signal amplification.²² Saturating stimuli, on the other hand, necessitate rapid recovery to allow the continued detection of light. Overly effective recovery mechanisms, however, would threaten to quench dim-light responses before they are sufficiently amplified. Thus, recovery is tightly controlled by parallel negative-feedback mechanisms, including Ca²⁺-mediated feedback on GCAPs activity^21,23–25 and on Rec regulation of RK.^9,10,26–29 These serve to ramp up signal recovery to more intense stimuli without extinguishing dim-light responses. The result is an exquisitely balanced, but dynamically complex system.

In the past decade, an ongoing effort has been made to produce a comprehensive model of visual phototransduction in rod photoreceptor cells.^30–33 The model to-date has been built to include nearly all of the known mechanisms involved in phototransduction. It has been constructed according to a bottom-up strategy, in which detailed representations of the underlying reactions are implemented according to the law of mass-action, eschewing high-level, empirical kinetic models.³⁴ This model has proven to be very successful in reproducing a variety of mutant conditions in many of the underlying proteins.^32,33 Furthermore, it has been used to make novel predictions of the dynamical role of a homo-oligomerization mechanism of Arr.³³

Although the model parameters were fit using biochemical and electrophysiological data culled from experiments on amphibians, it was found to produce qualitatively accurate simulations of experiments originally performed in mice, despite the approximately ten-fold slower dynamics in amphibians.^32,33 Because modern vision research most commonly employs the mouse visual system, it would be valuable to have a model that can also produce quantitatively accurate simulations of it. To this end, we have adapted the most recent version of the amphibian model by Invergo et al.³³ in order to simulate murine electrophysiological data. This was accomplished both through the integration of previously published parameter values and through the use of informed tuning and estimation techniques for unknown values but, importantly, without modification of the underlying reaction network. The resulting model provides accurate reproductions of the mouse visual response under a range of conditions and stimuli, while pointing to potential gaps in our knowledge of the phototransduction system.

2 Methods

2.1 Model implementation

The unaltered reaction network of Invergo et al.³³ was used to construct the model (Table S1, ESI†). This reaction network is the most recent in a series of iterative improvements to a comprehensive model of amphibian phototransduction.^30–33,35 Each successive iteration of the model has added to or improved the reactions of the previous version according to the latest biochemical knowledge. The current network consists of a system of ordinary differential equations for 96 reactions, deterministically tracking the time evolution of 76 molecular species using 62 parameters. It was implemented using SBTOOLBOX2 for MATLAB (http://www.sbtoolbox2.org).³⁶ Model files in SBTOOLBOX2 or SBML formats are available upon request. All numerical simulations and parameter estimation were carried out in this framework. Deterministic simulations were run from automatically generated and compiled C-code models, based on the CVODE integrator from SUNDIALS.³⁷ Simulated light stimulus intensities in units of R*/s were approximated from published values described in units of photons μm⁻² using a collecting area of 0.43 μm.^2,38

2.2 Parameter determination

Parameters values were retrieved or approximated from the literature when possible. In cases where the true parameter values were unknown, they were either manually tuned to meet experimental expectations or they were estimated through parameter optimization techniques. Manual tuning was performed on individual parameters to reproduce expected behaviors for which experimental data is not available (e.g. changes in concentration of a given protein during a photoresponse). Parameter estimation was done using a combination of the Nelder–Mead Simplex method for local optimization and a particle swarm method for global optimization.³⁹ Optimization was performed against published electrophysiological data of the responses of a three-month-old mouse of the B6D2F1/J strain, which is a F1 hybrid between the C57BL/6J and DBA/2J strains.⁴⁰ After estimation, parameter values were held fixed in all subsequent simulation experiments.

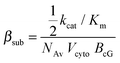2.2.1 Amplification parameters. The model parameters related to the Gt·R* interaction required significant modification to adapt the model to mammalian data (Table S2, ESI†). The parameters controlling the G_tα–PDE interaction, on the other hand, were left unchanged due to their insignificant effect on the model dynamics (see Dell'Orco et al.³² for a global parameter sensitivity analysis). Because the true values of the G_t–R* rate parameters are unknown, they were manually tuned to produce the expected rate of G_tα production per R* per second, as was done in the original formulation of the amphibian iteration of this model.³¹ This rate can be estimated according to the following relationship:¹

A = ν_RG c_GE β_sub n_cG (1)

where A is the amplification constant, estimated to be 5 to 10 s⁻²; ν_RG is the rate of G_tα production per R* per second, to be estimated; c_GE is the coupling efficiency of G_tα to PDE, which, due to the relative insensitivity of the PDE-activation-related parameters, is approximately 1; n_cG is the Hill coefficient of the cGMP channel activation, which was manually tuned to 3.8; and β_sub is the rate constant of cGMP hydrolysis per activated PDE subunit. β_sub may be approximated as follows:⁴¹k_cat is the turnover rate of a doubly-activated PDE holomer, estimated to be 1200 to 3500 s⁻¹;⁴²K_m is the Michaelis constant of cGMP hydrolysis by PDE, estimated to be 17 to 23 μM;⁴²N_Av is Avogadro's constant; V_cyto is the rod outer segment volume, calculated to be approximately 0.03916 pL for the mouse used in the model fitting;⁴⁰ and B_cG is the buffering power of the cytoplasm for cGMP, which is approximately 2.¹

It was determined that an amplification constant (A) of 10 s⁻² was required to fit the electrophysiological data. The ratio k_cat/K_m was maximized according to the reported ranges for the two parameters, resulting in a β_sub of 2.1826 × 10⁻³ s⁻¹ and a v_RG of 1206 s⁻¹. The maximal rate of G_tα production per activated receptor has been reported to be approximately 1290/R*s.⁴³ Therefore, this estimate of v_RG is reasonable. The G_t-related parameters in the model were then manually tuned to approximate this rate of G_tα production (Table S2, ESI†).

2.2.2 Recovery parameters. The basal binding rates of RK and Arr to R* required re-tuning to fit mammalian recovery dynamics (Table S3, ESI†). It was previously reported that a linear decrease in the affinity of RK for R* due to phosphorylation of the receptor provided a better, less sensitive fit to the amphibian electrophysiological data.³³ In the present model, it was found that such a linear relationship resulted in a poor prediction of the signal responses of a Rec-knockout animal. In particular, it resulted in RK out-competing G_t for binding R* and the subsequent full phosphorylation of the receptor before G_t could bind and activate the pathway; this was manifested as a significantly delayed and attenuated peak signal response. By reverting the RK·R* relationship to an exponential one and by setting the exponent to a greater value than was previously used (see Dell'Ocro et al.³²), this problem was alleviated. Note, however, that the true relationship is not known.

The basal rate of RK–R* binding was tuned according to the original estimation by Hamer et al.,³¹ such that RK_darkkRK1₀ = 100 s⁻¹, or 100/R*s, where RK_dark is the quantity of free RK molecules in the dark. According to a steady-state analysis, RK_dark is 580 in the model, thus kRK1₀ was set to 0.1724 s⁻¹. The rates of phosphorylation and the following dissociation of the RK–R* complex were required to be approximately ten-fold faster than in the amphibian model (Table S3, ESI†). Parameters determining the rate of the RK–Rec interaction required no changes.

The Arr–R* interaction required significant re-tuning (Table S3, ESI†). In particular, the binding and dissociation rates were required to be several orders of magnitude faster than in the amphibian model. Hamer et al.³¹ predicted the basal rate of Arr–R* binding to be 0.25/R*s (Arr_totkArr = 0.25 s⁻¹). In the present model, with an initial, steady-state Arr monomer quantity of 1 260 760 molecules, the resulting kArr of 1.9829 × 10⁻⁷ s⁻¹ was much too slow to fit mammalian recovery times. A value of 9.9147 × 10⁻⁶ s⁻¹ (12.5/R*s) was determined to be sufficient through initial estimation and subsequent manual tuning.

The rate of dissociation of the Arr–R* complex prior to R* deactivation was manually tuned to approximate the equilibrium affinity constant of 10 reported by Gibson, et al.¹⁵ Similarly, the increase in the affinity of Arr for R* with each subsequent phosphorylation of R* was manually tuned to approximate the reported slope of this relationship.¹⁵ The equilibrium constants may not accurately represent the physiological rate, however they provided a good fit and were thus retained. The self-association rate of Arr was also found by parameter estimation, while the self-dissociation rate was manually tuned to approximate the measured equilibrium dissociation constant of 60 μm of the reaction.¹⁸

Finally, the rate of binding of RGS9-1 to the G_tα·PDE complex was found to require a significantly faster rate, two orders of magnitude faster than that of the amphibian model (Table S3, ESI†). The rate constant for the hydrolysis and dissociation of G_tα·PDE was set to 98 s⁻¹ according to Skiba et al.⁴⁴

2.2.3 Ca²⁺ and cGMP regulation. The model was modified to accommodate the action of the two distinct GCAPs, as previously implemented.²¹ The rate of cGMP production was changed to:where α_max is the maximal rate of cGMP production by GC, 60 μM s⁻¹ and is assumed to be the same for the activity of both GCAPs;⁴⁵Kc₁ (173 nM; optimized from ref. 25) and Kc₂ (59 nM²⁵) are the Ca²⁺ concentrations at which the GCAPs activity is half maximal, for GCAP₁ and GCAP₂, respectively; and m₁ (3; optimized) and m₂ (1.5; optimized) are Hill coefficients for GCAP₁ and GCAP₂, respectively. β_dark, the dark rate of cGMP hydrolysis, was given a value of 3.19 s⁻¹ according to steady-state analysis and cGMP_dark, the concentration of cGMP in the dark, was manually tuned to be 6.5 μm (Table S4, ESI†).

Ca²⁺ regulation-related parameters were either culled from the literature or estimated by parameter estimation. See Table S4 (ESI†).

3 Results

Model fitting was performed against single-cell recordings of photoresponses to stimuli ranging from 1.7 to 4630 photons μm⁻² in rod photoreceptors of a three-month-old B6D2F1/J mouse.⁴⁰ Photoresponses were measured as the suppression of the dark current in the outer segment of the cell. The resulting model successfully reproduces the primary characteristics of the photoresponse to both dim and saturating light flashes and overall closely corresponds to the experimental data (Fig. 1). In order to test the accuracy of the model in reproducing the mechanisms of light adaptation, we next simulated and compared light flashes in the presence and in the absence of a steady, non-saturating background illumination (Fig. 2A). Consistent with in vivo experiments, we found a shortening of the saturation time in the presence of the steady illumination, however the simulated effect was very moderate compared to experimental observations.⁴⁶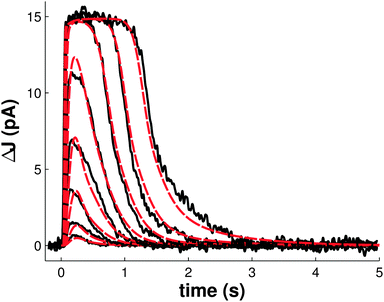

Fig. 1 Simulations of flash responses generated by a three-month-old B6D2F1/J mouse. 20 ms flash stimuli were delivered at time t = 0, with intensities of 1.7, 4.8, 15.2, 39.4, 125, 444, 1406 and 4630 photons μm⁻². Black traces are of experimental data from Kolesnikov et al.⁴⁰ Red traces are of simulations using our model.

Fig. 2 Simulated responses to a saturating flash stimulus in the presence (dashed traces) and the absence (solid traces) of a steady, background stimulus. Background stimuli were 81 photons μm⁻² and resulted in the stable, non-saturating currents indicated by blue, horizontal traces. Flashes of 1590 photons μm⁻² were delivered at t = 100. (A) Wild-type simulations. (B) Simulated GCAPs knock-out, implemented by setting the parameters m₁ and m₂ to zero. The background stimulus results in a slight reduction in saturation time that is more pronounced in the mutant.

To further test the performance of the model, we also simulated a variety of mutant conditions that were previously used for model verification.³³ Overall, simulations produced with the present model correspond well with the experimental data. Decreasing RK activity via underexpression of the protein results in the expected slowing of recovery to a dim flash stimulus (Fig. 3A′) and an increase in saturation time (T_sat, the time spent at at least 90% of the peak amplitude) after a bright stimulus (Fig. 3C′). Overexpression of the kinase did result in a constant decrease in T_sat across all stimulus intensities, which does not occur in experimental measurements with mice (compare Fig. 3C, produced by Sakurai et al.,⁴⁷ with Fig. 3C′), however this phenomenon has previously been observed with this model and the exact reason for this discrepancy remains unclear.³³

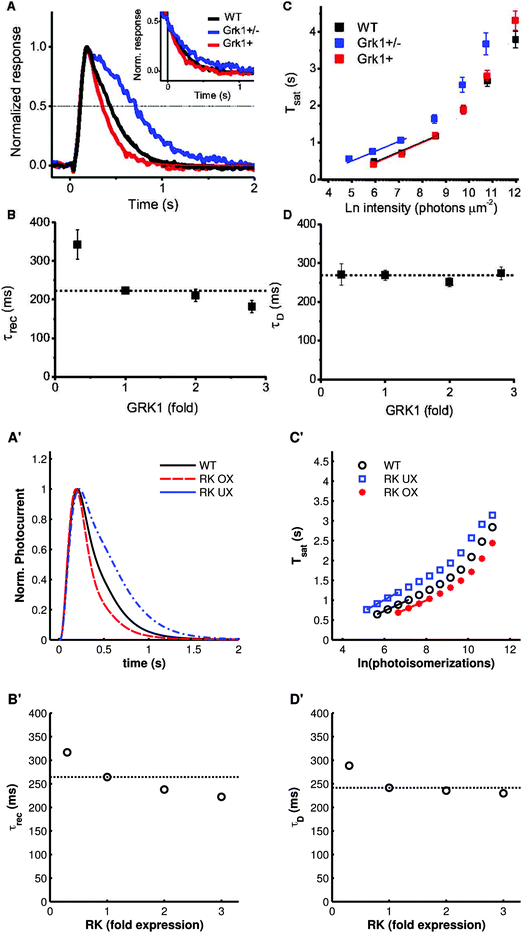Fig. 3 The effects of varying RK expression on the photoresponse. (A–D) Experimental results of Sakurai et al.⁴⁷ (A′–D′) Simulations of the same experiments. (A′) Normalized responses to a non-saturating flash (7R*). 0.3× underexpression (dotted-dashed trace) results in a slowed recovery compared to wild-type (solid trace). 3× overexpression (dashed trace) has a marginal effect. (B′) The time constant of recovery, τ_rec, versus RK expression. (C′) Time spent in saturation (T_sat) as a function of logarithmically increasing stimulus intensities. RK underexpression (open squares) results in an increase in T_sat compared to wild-type (open circles). RK overexpression (stars) leads to a slight decrease in T_sat. The lines show the least-squares best fit of the first four points, used in the determination of τ_D. (D′) τ_D, the slope of the relationship of T_sat with logarithmic stimulus intensity, versus RK expression levels. Underexpression results in a small increase in τ_D, while overexpression has no effect. Notice that τ_rec and τ_D are approximately equivalent for wild-type mice. (Panels A–D copyright 2011 The Association for Research in Vision and Ophthalmology, Inc.) NB: the authors used “Grk1” and “GRK1” interchangeably.

The model also produces excellent predictions of the values of τ_rec (the time constant of an exponential fit to the second half of the recovery from a dim flash stimulus) and the dominant time constant of recovery, τ_D, (the slope of the increase in T_sat with flash stimuli of logarithmically increasing intensities) (Fig. 3B′ and D′). Both values have been measured to be approximately 250 ms for wild-type mice⁴⁷ (Fig. 3B and D). Sakurai et al.⁴⁷ showed that τ_rec is slightly higher when RK is underexpressed and moderately lower with overexpression, which the model accurately captures (Fig. 3B′). τ_D, on the other hand, is not expected to change with increasing RK expression (however, three-fold overexpression may result in a small decrease in τ_rec, as measured by Sakurai et al.⁴⁷ and reproduced by our model; Fig. 3D′). In our simulations, RK underexpression resulted in a minor increase in τ_D (Fig. 3D′).

The removal of Ca²⁺ feedback on RK by simulating a Rec knock-out mouse results in lower peak amplitudes after dim flashes and a strongly reduced T_sat (Fig. 4). A slight decrease in τ_D from 242 in the wild-type to 193 in the simulated knock-out is similar in magnitude to the decrease seen in vivo of 184 ms to 154 ms.²⁸ The model captures well the sharp peak and slowing rate of recovery to non-saturating stimuli exhibited by the knock-out animals (compare Fig. 4B, produced by Makino et al.,²⁸ to Fig. 4E).

Fig. 4 Experimental (A–C²⁸) and simulated (D–F) responses of mice lacking Rec. (A, D) Wild-type responses to flash stimuli. Stimulus intensities were 11.8, 20.6, 42.8, 74.9, 139, 243, 504, 882 and 1690 photons μm⁻². (B, E) Rec knock-out responses. Stimulus intensities were 12.8, 22.4, 46.5, 81.4, 151, 548, 960, 1840, 3230, 6700 and 11 700 photons μm⁻². (C, F) Saturation time as a function logarithmically increasing stimulus intensities. Knocking-out Rec (open circles) results in a distinct shift in saturation time relative to wild-type (stars). (Panels A–C copyright 2004 Makino et al. Panel C was modified to increase the label text size.)

Finally, it is currently understood that RGS9-1-mediated shutdown of the effector PDE is the rate-limiting step in phototransduction recovery, which our previous simulations confirmed,³³ and experimental and modeling results further point to the general importance of RGS proteins in speeding up the kinetics of G-protein signaling. This was most convincingly demonstrated by Burns and Pugh,⁴⁸ who showed that varying the concentration of RGS9-1 has a strong effect on T_sat and τ_D (Fig. 5A). When the experiments of Burns and Pugh⁴⁸ are simulated with our model, we find an excellent correspondence with the published results (Fig. 5B). While some quantitative differences exist between simulations produced with the present model and that of Burns and Pugh, it should be pointed out that the latter model's parameters were specifically fit by maximum likelihood to this data while the simulations were performed with the present model without any specific tuning. In the simulations, underexpression of RGS9-1 leads not only to a strong increase in T_sat but it also results in a notable increase in the slope, τ_D. Conversely, overexpression results in a distinct drop in T_sat and a moderate decrease in τ_D. Thus, RGS9-1 plays a primary role in shaping the dynamics of the murine photoresponse. Furthermore, the estimated rate of binding of RGS9-1 to the G_tα·PDE complex, which is approximately two orders of magnitude faster than that estimated for amphibians, points to this mechanism as a major determinant of the relatively rapid recovery dynamics exhibited by mammalian species.

Fig. 5 The relationship between saturation time and logarithmically increasing stimulus intensity varies strongly with RGS9-1 expression. (A) Experimental (points) and simulated results (lines) presented by Burns and Pugh.⁴⁸ (B) Simulations with the present model; lines represent the least-squares best fit of the points. 0.2× underexpression (X's, dashed line) results in a strong increase in both saturation time and the slope of the relationship compared to wild-type (open circles, solid line). 2× and 4× overexpression (stars, dotted-dashed line; open squares, dotted line, respectively) leads to a moderate drop in saturation time and the slope. (Panel A copyright 2009 the Biophysical Society.)

4 Discussion

4.1 Current challenges in modeling the visual photoresponse

The model presented herein accurately reproduces murine photoresponses to a wide range of stimuli and under a variety of mutant conditions. Notably, this could be accomplished by adapting a model created to reproduce the amphibian photoresponse without any alteration to the underlying reaction network. Given the bottom-up approach used to build the model, this success illustrates the degree to which the true biology of the vertebrate phototransduction system is captured in the modeled reactions. Nevertheless, challenges were encountered during the production of this model, which could point to yet unknown or poorly understood mechanisms. We took advantage of the relative ease of computational simulation in order to investigate some of these short-comings.

The effect of removing Ca²⁺ feedback on RK described above was found to be heavily dependent upon the relationship of the affinities of G_t and RK for R* as a function of the number of phosphates attached to the receptor. While the amphibian model performed better with a linear decrease in affinity of RK for R*,³³ such a linear relationship in the mammalian model led to rapid, maximal phosphorylation of the activated receptor followed by delayed G_t binding at its minimal rate. In effect, RK would entirely out-compete G_t for binding R*. By reverting to the previously implemented exponential relationship of RK affinity for R*,³² this binding competition effect was eliminated. The true relationship between RK–R* affinity and R* phosphorylation level remains unknown and the sensitivity of the model to this relationship indicates that it is an important gap in the present understanding of phototransduction recovery dynamics.

Despite the overall good performance of the model, a notable shortcoming was observed when simulating light-adaptation. In measuring the effect of light adaptation on the photoresponse, we observed an expected shortening of the saturation time in the presence of a steady background illumination. However, the simulated effect was not as strong as expected (Fig. 2A; see, e.g., Fig. 7C in ref. 46). To determine if cGMP regulation was responsible for this behavior, we performed the same simulations with a model of a GCAPs knock-out animal, implemented by setting the GCAPs Hill coefficients (model parameters m₁ and m₂) to zero (Fig. 2B). The effect of the steady background was slightly stronger in the mutant, at least partially implicating the cGMP regulatory dynamics in the discrepancy. It was found through parameter manipulation that the R* deactivation dynamics have a strong effect on this characteristic of light adaptation. Slowing R* deactivation, through decreased RK or Arr activity, results in a larger gap between dark-adapted and light-adapted saturation times for both wild-type and GCAPs knock-out mutants, in line with experimental expectations (data not shown). However, doing so also results in these mechanisms having a stronger influence on the recovery parameters τ_rec and τ_D, disrupting the model's faithful reproduction of the mutant scenarios described in the Results section. On the other hand, simulating the light-adaptation experiments without Ca²⁺ feedback on RK, thereby accelerating R* deactivation, removed any visible effect of light adaptation (data not shown).

Thus, we have found that the RK activity required to fit dark-adapted mammalian flash responses in this model may be too fast to accommodate expected light-adaptation behaviors. Additionally, as previously described, all iterations of this model have also shown inaccurate results of simulating RK overexpression, such that it incorrectly results in a decrease in saturation times.^32,33 The incorporation of a dynamic Arr-oligomerization mechanism partially eliminated this effect by delaying the shutdown of the activated receptor,³³ however some discrepancy with the in vivo results remains (Fig. 3C′). Furthermore, as described above, the model has been also found to be particularly sensitive to the affinity relationship of RK for phosphorylated R*.³³ No realistic, satisfactory combination of parameters could resolve this suite of problems. Because all well-established mechanisms related to receptor deactivation are included in the model, one would speculate that a yet unknown or poorly understood mechanism related to RK activity exists but is absent in the model. It is possible that further clarifying the effects of R* phosphorylation and RK autophosphorylation on the R*–RK interaction may resolve these discrepancies. In particular, our knowledge of the effect of RK autophosphorylation on this interaction is currently limited to only the kinase's unphosphorylated and fully phosphorylated states,¹⁴ leaving the true relationship uncertain in a multi-step phosphorylation paradigm.^13,30

Additionally, it is probable that the cGMP-regulatory mechanisms in the model are insufficient. Only one of the two GC isozymes is present in the model, when in fact both exhibit different properties.²⁵ Unfortunately, we lack mechanistic information on the putative switch between GC₁ and GC₂ functionality in order to properly implement both cyclases in the model.²¹ It is also worth noting that cGMP regulation remains implemented according to an empirical Hill equation rather than the desired, bottom-up representation of the underlying reactions. While a recent detailed model of cGMP kinetics in phototransduction using a similar Hill representation showed excellent performance in predicting local spatio-temporal kinetics, it was only used to simulate single-photon responses⁴⁹ and not a full range of stimuli as we present here. A more complete implementation, capturing the complexities of the interactions of the two GCs and their Ca²⁺-sensitive regulation by the GCAPs, is necessary to improve the dynamics of this important signal recovery mechanism and would likely provide more accurate simulations of light adaptation.

4.2 Future directions

At very dim stimulus intensities, down to a single photon, the probability of two proteins encountering each other as well as the general supramolecular organization become important factors in the phototransduction response,²² as does the local saturation of second messengers such as cGMP.^49,50 Due to its deterministic nature, our model cannot accurately simulate the single photon response (SPR). Furthermore, the representation of the photoreceptor outer segment as a well-mixed volume may omit important localized depletion of the second messengers.^51–53 A series of spatially accurate models of mouse phototransduction have been produced in order to more accurately simulate this scenario.^49,51–54 These models reproduce quite well the SPR and have revealed insights into the mechanisms underlying its variability, however they have not been demonstrated to also faithfully simulate responses to a wider range of stimuli. Additionally, they primarily give focus to the second messengers, while reducing protein activity to high-level, empirical parameters; thus, the intricacies of the inter-protein dynamics are lost. Ideally, the future will see a merging of the two techniques, allowing a detailed, spatially accurate model that can reproduce the full range of responses exhibited by a rod photoreceptor.

4.3 Conclusions

One of the chief aims of systems biology research is the production of quantitatively predictive models from which experimental hypotheses can be derived. It is hoped that our model will be a useful tool in guiding future research on phototransduction. By offering quantitatively accurate predictions across a range of conditions for the primary species used in vision research, it may be used to avoid costly lines of unproductive investigation. Meanwhile, its shortcomings may raise interesting questions regarding gaps in our knowledge of the phototransduction process. Lastly, its modular structure allows for the easy integration of novel features without disrupting the existing network, allowing it to be expanded as research progresses and obviating the need for constructing “one-off” models to explore novel mechanisms.

Acknowledgements

We would like to thank Alexander V. Kolesnikov for kindly providing the electrophysiological data used in the model fitting. This research was funded by grant BFU2010-19443 (subprogram BMC) awarded by the Ministerio de Ciencia y Tecnología (Spain) and by the Direccío General de Recerca, Generalitat de Catalunya (Grup de Recerca Consolidat 2009SGR 1101). BMI was supported by FI-DGR and BE-DGR grants from AGAUR, Generalitat de Catalunya (2011 F1 B1 00275). LM acknowledges funding from the Juan de la Cierva Program of the Spanish Ministry of Science and Innovation (MICINN). DDO acknowledges funding from the Italian Ministry for Research and Education (Fur2013 Dell'Orco).

References

1. E. N. Pugh Jr andT. D. Lamb, Handbook of Biological Physics, Elsevier, North Holland, 2000, vol. 3, pp. 183–255.
2. D.-G. Luo, T. Xue and K.-W. Yau, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9855–9862.
3. Y. Shichida and T. Morizumi, Photochem. Photobiol., 2007, 83, 70–75.
4. N. Bennett and A. Clerc, Biochemistry, 1989, 28, 7418–7424.
5. A. Clerc and N. Bennett, J. Biol. Chem., 1992, 267, 6620–6627.
6. P. Schnetkamp, J. Physiol., 1986, 373, 25–45.
7. P. P. M. Schnetkamp, D. K. Basu and R. T. Szerencsei, Am. J. Physiol., 1989, 257, C153–C157.
8. D. Dell'Orco, M. Müller and K.-W. Koch, Chem. Commun., 2010, 46, 7316–7318.
9. E. N. Gorodovikova, I. I. Senin and P. P. Philippov, FEBS Lett., 1994, 353, 171–172.
10. V. A. Klenchin, P. D. Calvert and M. D. Bownds, J. Biol. Chem., 1995, 270, 16147–16152.
11. M. J. Kennedy, K. A. Lee, G. A. Niemi, K. B. Craven, G. G. Garwin, J. C. Saari and J. B. Hurley, Neuron, 2001, 31, 87–101.
12. T. Maeda, Y. Imanishi and K. Palczewski, Prog. Retinal Eye Res., 2003, 22, 417–434.
13. T. Doan, A. Mendez, P. B. Detwiler, J. Chen and F. Rieke, Science, 2006, 313, 530–533.
14. A. Pulvermüller, K. Palczewski and K. P. Hofmann, Biochemistry, 1993, 32, 14082–14088.
15. S. K. Gibson, J. H. Parkes and P. A. Liebman, Biochemistry, 2000, 39, 5738–5749.
16. S. A. Vishnivetskiy, D. Raman, J. Wei, M. J. Kennedy, J. B. Hurley and V. V. Gurevich, J. Biol. Chem., 2007, 282, 32075–32083.
17. S. M. Hanson, N. Van Eps, D. J. Francis, C. Altenbach, S. A. Vishnivetskiy, V. Y. Arshavsky, C. S. Klug, W. L. Hubbell and V. V. Gurevich, EMBO J., 2007, 26, 1726–1736.
18. M. Kim, S. M. Hanson, S. A. Vishnivetskiy, X. Song, W. M. Cleghorn, W. L. Hubbell and V. V. Gurevich, Biochemistry, 2011, 50, 2235–2242.
19. V. V. Gurevich, S. M. Hanson, X. Song, S. A. Vishnivetskiy and E. V. Gurevich, Prog. Retinal Eye Res., 2011, 30, 405–430.
20. M. Natochin, A. E. Granovsky and N. O. Artemyev, J. Biol. Chem., 1997, 272, 17444–17449.
21. K.-W. Koch and D. Dell'Orco, ACS Chem. Neurosci., 2013, 4, 909–917.
22. L. Cangiano and D. Dell'Orco, FEBS Lett., 2013, 587, 1–4.
23. R. Stephen, S. Filipek, K. Palczewski and M. C. Sousa, Photochem. Photobiol., 2008, 84, 903–910.
24. J.-Y. Hwang and K.-W. Koch, Biochemistry, 2002, 41, 13021–13028.
25. I. V. Peshenko, E. V. Olshevskaya, A. B. Savchenko, S. Karan, K. Palczewski, W. Baehr and A. M. Dizhoor, Biochemistry, 2011, 50, 5590–5600.
26. S. Kawamura, Nature, 1993, 362, 855–857.
27. C.-K. Chen, J. Inglese, R. J. Lefkowitz and J. B. Hurley, J. Biol. Chem., 1995, 270, 18060–18066.
28. C. L. Makino, R. L. Dodd, J. Chen, M. E. Burns, A. Roca, M. I. Simon and D. A. Baylor, J. Gen. Physiol., 2004, 123, 729–741.
29. K. E. Komolov, I. I. Senin, N. A. Kovaleva, M. P. Christoph, V. A. Churumova, I. I. Grigoriev, M. Akhtar, P. P. Philippov and K.-W. Koch, J. Neurochem., 2009, 110, 72–79.
30. R. D. Hamer, S. C. Nicholas, D. Tranchina, P. A. Liebman and T. D. Lamb, J. Gen. Physiol., 2003, 122, 419–444.
31. R. D. Hamer, S. C. Nicholas, D. Tranchina, T. D. Lamb and J. L. P. Jarvinen, Visual Neuroscience, 2005, 22, 417–436.
32. D. Dell'Orco, H. Schmidt, S. Mariani and F. Fanelli, Mol. BioSyst., 2009, 5, 1232–1246.
33. B. M. Invergo, L. Montanucci, K.-W. Koch, J. Bertranpetit and D. Dell'orco, Cell Commun. Signaling, 2013, 11, 36.
34. D. Dell'Orco and K.-W. Koch, Biochem. Soc. Trans., 2010, 38, 1275–1280.
35. D. Dell'Orco and K.-W. Koch, Biochem. J., 2011, 440, 263–271.
36. H. Schmidt and M. Jirstrand, Bioinformatics, 2006, 22, 514–515.
37. A. Hindmarsh, P. Brown and K. Grant, ACM Transactions on Mathematical Software, 2005, 31, 363–396.
38. C. M. Krispel, D. Chen, N. Melling, Y.-J. Chen, K. A. Martemyanov, N. Quillinan, V. Y. Arshavsky, T. G. Wensel, C.-K. Chen and M. E. Burns, Neuron, 2006, 51, 409–416.
39. A. I. F. Vaz and L. N. Vicente, J. Global Optim., 2007, 39, 197–219.
40. A. V. Kolesnikov, J. Fan, R. K. Crouch and V. J. Kefalov, J. Neurosci., 2010, 30, 11222–11231.
41. T. D. Lamb and E. N. Pugh Jr, J. Physiol., 1992, 449, 719–758.
42. H. Muradov, K. K. Boyd and N. O. Artemyev, Vision Res., 2006, 46, 860–868.
43. M. Heck and K. P. Hofmann, J. Biol. Chem., 2001, 276, 10000–10009.
44. N. P. Skiba, J. A. Hopp and V. Y. Arshavsky, J. Biol. Chem., 2000, 275, 32716–32720.
45. K.-W. Koch and L. Stryer, Nature, 1988, 334, 64–66.
46. M. E. Burns, A. Mendez, J. Chen and D. A. Baylor, Neuron, 2002, 36, 81–91.
47. K. Sakurai, J. E. Young, V. J. Kefalov and S. C. Khani, Invest. Ophthalmol. Visual Sci., 2011, 52, 6793–6800.
48. M. E. Burns and E. N. Pugh, Biophys. J., 2009, 97, 1538–1547.
49. O. P. Gross, E. N. Pugh and M. E. Burns, Biophys. J., 2012, 102, 1775–1784.
50. G. Caruso, P. Bisegna, D. Andreucci, L. Lenoci, V. V. Gurevich, H. E. Hamm and E. Dibenedetto, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7804–7807.
51. D. Andreucci, P. Bisegna, G. Caruso, H. E. Hamm and E. DiBenedetto, Biophys. J., 2003, 85, 1358–1376.
52. G. Caruso, H. Khanal, V. Alexiades and F. Rieke, IEE Proc.: Syst. Biol., 2005, 152, 119–137.
53. P. Bisegna, G. Caruso, D. Andreucci, L. Shen, V. V. Gurevich, H. E. Hamm and E. DiBenedetto, Biophys. J., 2008, 94, 3363–3383.
54. G. Caruso, P. Bisegna, L. Lenoci, D. Andreucci, V. V. Gurevich, H. E. Hamm and E. DiBenedetto, PLoS Comput. Biol., 2010, 6, e1001031.

---

Footnotes

† Electronic supplementary information (ESI) available: Tables S1–S4, phototransduction model details. See DOI: 10.1039/c3mb70584f

‡ Present address: European Molecular Biology Laboratory, European Bioinformatics Institute (EMBL-EBI), Wellcome Trust Genome Campus, Hinxton, Cambridge CB10 1SD, UK. E-mail: invergo@ebi.ac.uk; Tel: +44 (0)1223 49 2547.

---