Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic resonant cavities enable acoustophoresis on a disposable superstrate†
C.
Witte
*,
J.
Reboud
,
R.
Wilson
,
J. M.
Cooper
and
S. L.
Neale
*
Biomedical Engineering Research Division, School of Engineering, University of Glasgow, Glasgow, UK. E-mail: c.witte.1@reseach.gla.ac.uk; steven.neale@glasgow.ac.uk
First published on 16th September 2014
Abstract
We demonstrate surface acoustic wave (SAW) induced microparticle manipulation in a microstructured disposable glass-polymer composite superstrate, positioned on a piezoelectric substrate with a single, slanted SAW transducer. An excited SAW was coupled from the piezoelectric substrate into the superstrate, which acted as a transversal resonator structure. We show that the energy transmitted into the superstrate allowed acoustophoretic particle manipulation, while the wide frequency response of the SAW transducer enabled tuneable pressure distributions confined by the microchannel layout. The configuration provides a significant tolerance in positioning – making assembly easy.
Introduction
Microfluidics has enabled a number of new approaches for the manipulation of microscopic biological particles within microchannels. Each of these exploit different forces offering advantages and limitations that make them suitable for different applications (and different particles of interest, be they macromolecules or cells in suspension). Acoustic tweezing is particularly suited to the non-contact handling of microparticles within a microchannel1–5 and can be most readily implemented by attracting particles to acoustic nodes of a standing wave set up within the channel.6,7 This provides 1D to 3D control over the position of the particles depending on the transducer system and microchannel arrangements.8–10 As the pressure gradients generated by the acoustic fields extend throughout the channel, control of the pressure gradients can lead to precise particle manipulation. Ultimately, the magnitude of the forces acting on any particle within a fluid will be governed by the particle's acoustic contrast which, in turn, is a function of the particle's and the fluid's density and compressibility.11In many biological applications, it is desirable to introduce a disposable element into an analytical set-up, which in the case of acoustophoresis will allow separating the piezoelectric acoustic transducer from the liquid/particles to be manipulated. The previously used concept of the ‘superstrate’, onto which the sample is placed, is an example of such a system.12 Acoustic waves generated by a surface acoustic wave (SAW) device have been coupled into a variety of different superstrates (including silicon, glass, PDMS and paper),13–18 while the SAW device itself, usually is fabricated in relatively expensive single crystal piezoelectric wafers (e.g. LiNbO3) which can then be re-used. The transmission of radio frequency radiation into a superstrate to mix and move particles, including droplets, in a microfluidic channel has been reported.12 In such a set-up, despite the fact that the longitudinal wave in the water is reflected between the interfaces of glass/water and lithium niobate/water,12,19 there is still sufficient transmission of acoustic power into the superstrate to generate a Lamb wave. This strategy has been successful in enabling a wide range of droplet manipulations on disposable superstrates,13–15,20–22 including particle enrichment23,24 for lab on a chip applications.
In general, acoustophoretic particle manipulation has been shown for SAW transducers based upon generating standing SAWs using pairs of transducers to create counter propagating surface waves of the same frequency resulting in constructive interference.3,4,25,26 The forces that result from pressure changes in the liquid have been used for different applications such as concentrating,18 trapping,3,9 and the continuous sorting4,27,28 of cells and particles. Usually, these devices have utilized polydimethylsiloxane (PDMS) based microchannel chips, bonded to the piezoelectric substrate, a technology which requires precise alignment of the channel width relative to the pressure nodal planes between two SAW transducers. This may not only be challenging when the dimension of the channel is reduced to tens of micrometers29 but results in a device where the more costly components will need to be discarded following analysis. In addition, it is noteworthy that PDMS has a high acoustic attenuation coefficient, influencing the overall pressure amplitude of the field significantly.29–31 Channels have been etched into the piezoelectric substrate, mitigating against the use of the polymer in creating the microfluidic channel, although alignment and the disposability of the chip (and associated cost) remain as significant issues.32
As an alternative, a complete decoupling of the particle manipulation from the piezoelectric surface into a superstrate with embedded microchannel can be performed (Fig. 1a). The latter maintains all the benefits of a SAW transducer such as a compact planar device structure, broadband response, high frequency, and lead free device,33 with high energies concentrated within the chip.
In this study we show that a acoustophoretic particle manipulation can be achieved using a superstrate (Fig. 1b) with a simple transversal resonator design.34 Uniquely, this is based upon a single SAW transducer (Fig. 1a), where a single exciting planar wave is reflected at the microfluidic wall and in this way superposes with itself.34 Standing acoustic waves form as a result of two counter propagating planar waves, in this case the incident wave and its reflection. By using a broadband interdigitated SAW transducer we show greatly enhanced tolerances to misalignments between the microchannel, which acts a resonance cavity, and the acoustic field. The superstrate is a disposable glass/SU8/glass composite chip (Fig. 1c), which, combined with the simplified platform assembly, enables a quick and easy assembly of SAW devices for particle manipulation.
Materials and methods
Superstrate fabrication
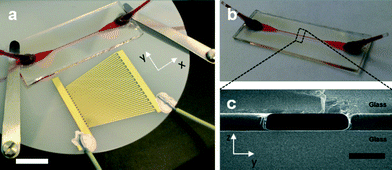
The superstrate with embedded microchannel was designed as a sandwich composite (Fig. 1c) consisting of a standard microscope slide, custom cut (bottom substrate, Menzel Glaser, H: 1 mm × D: 15 mm × L: 40 mm) and a cover slip (top substrate, Menzel Glaser, H: 0.16–0.19 mm × D: 15 mm × L: 40 mm) with the negative photoresist SU8 (MicroChem Corp., USA) in-between. Here, the resist acted as a bonding agent between the substrates and defined the microchannels. SU8 3050 was spin-coated (4000 rpm) onto the substrate and placed on a hotplate at 95 °C. A cover slip containing predrilled holes for inlets and outlets was bonded immediately to the freshly prepared SU8 film by placing it onto the substrate. This was followed by a softbake at 95 °C for 25 minutes. The photoresist was exposed through a polymer-emulsion film mask aligned to the predrilled holes in the cover slip for 60 seconds. A post-exposure bake at 65 °C for 2 minutes and 95 °C for 6 minutes was performed prior to the development of unexposed SU8 through inlet and outlet holes using Microposit EC solvent (Shipley, USA). The resulting channel length, width and height were 15 mm, 173 ± 5 μm and 35 ± 5 μm (obtained from SEM images and Dektak measurements on 3 devices), respectively. Fig. 1 shows the fabricated superstrate (b) and a cross-section of the sandwich composite (c).SAW transducer fabrication and setup assembly
The piezoelectric material used for SAW actuation was a 3 inch diameter, 0.5 mm thick lithium niobate wafer (LiNbO3, Roditi, UK) specified by a 128° Y-cut for wave propagation in the y-direction (3488 m s−1). An interdigitated transducer with slanted electrode design was transferred by standard photolithography, metal deposition and metal lift-off using S1818 resist and evaporation of a 10 nm NiCr adhesion layer and 100 nm Au electrode layer. A broad frequency response was achieved by linearly varying the pitch and the width of 18 electrode pairs from 249 μm to 159 μm with an aperture of 2 cm, resulting in a theoretical bandwidth of 3.5 MHz to 5.5 MHz. The spectrum analysis measuring the S11-parameter (Agilent Technologies E507C ENA series network analyser) showed a frequency response between 3.7 MHz and 5.5 MHz. However, SAW devices are well known for also operating at harmonic frequencies. The slanted IDT used also showed harmonic responses at frequencies up to 21 MHz (Fig. S1, ESI†).A signal generator (TG5011 TTi, UK) combined with an amplifier (Mini Circuits ZHL-5W-1 and a 3 A, ±24 V DC power supply) were used to drive the SAW device. The setup was assembled by placing the composite superstrate onto the piezoelectric transducer and fixing it with metal clamps. Afterwards, 15 μl of deionised water were pipetted along the edge of the superstrate which created a liquid film between the superstrate and the piezoelectric substrate, through capillary action. The water layer was used as coupling layer to enable sufficient acoustic energy transmission into the superstrate.12 Alternative coupling agents have been described in the literature and include glycerol,12 epoxy resin31 and water based gels.20 However, the utilized capillary action provides an easy and consistent route to generate a homogenous coupling layer while the mentioned alternatives may be more difficult to apply (and to remove) and can vary between experiments. It has to be noted that the water layer evaporated during prolonged SAW excitation (>5 min). Therefore, long-term experiments would require regular reapplying of the coupling agent. Bead samples were injected using a syringe pump (NE-1000, New Era Pump Systems, USA). An Olympus microscope (BX52, Japan) with CMOS cameras, (ORCA-Flash4.0, Hamamatsu, Japan and UC30, Olympus, Japan) was used for capturing video sequences of bead manipulations in the microchannel. Polystyrene beads (Bangs Laboratories, USA) of different sizes (3 μm, 6 μm, 8 μm) were suspended in deionised water for acoustophoresis experiments. The frequency of the SAW transducer was varied until a homogenous acoustic focusing effect towards the microchannel centre was observed, signalling the creation of an acoustic standing wave. An infrared camera (Ti 25, Fluke, USA) was used to visualize the excitation of the transducer along the aperture as a function of frequency and to measure the temperature of the surface of the superstrate. Confocal imaging was used to create a z-stack of the microchannel cross-section and obtain insight into the particle alignment upon acoustic actuation.
Estimation of acoustic energy in the microchannel
The experimentally determined resonance frequency was then used to estimate acoustic energy densities based on the method introduced by Barnkob et al.7 Briefly, this method involves temporal tracking of the lateral trajectory of beads, experiencing an acoustic radiation force in a static fluid. For a one-dimensional standing wave, the force acting on a particle with radius a is given by;7Frady = 4πΦka3Eac![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2ky) sin(2ky) | (1) |
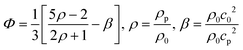 | (2) |
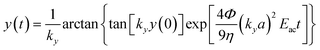 | (3) |
Simulations
Finite element method numerical modelling (COMSOL Multiphysics v3.5, pressure acoustic module, COMSOL, UK) was used to find eigenfrequencies of the superstrate as solutions to the Helmholtz equation, which support lateral modes of the half-wavelength (λ/2) criterion where a pressure nodal plane is defined in the centre of the microchannel.First, a simple 2D model depicting the fluidic domain of the microchannel was used to find resonance modes of the superstrate. The channel outline was approximated to be a solid boundary, assuming a significant difference in acoustic impedance between the water-filled channel (1.45 × 106 kg m−2 s) and the wall (3.45 × 106 kg m−2 s) and hence a strong reflection of the acoustic wave. The centre plane of the fluidic domain was considered only, neglecting a vertical resonance mode (this was justified by the cavity height being several times smaller than the wavelength for the observed frequency range).
Further assumptions were made by considering the channel to be of rectangular shape with straight walls. The width and length of the channel used in the model was 173 μm and 15 mm, respectively. The speed of sound and density used for the fluidic domain was 1450 m s−1 and 1000 kg m−3, respectively.
Results and discussion
Concept
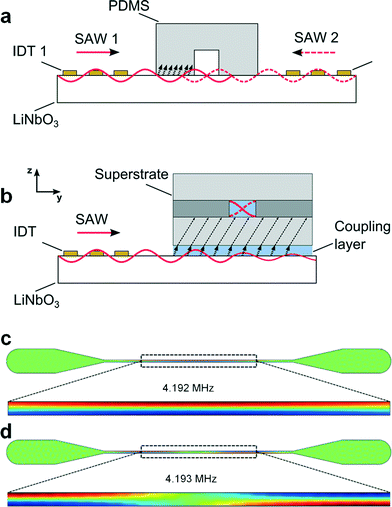
A disposable composite superstrate (Fig. 1b) with embedded microchannel was used as the acoustic cavity for bead manipulation in a standing wave, based on acoustic waves from a SAW device. This contrasts with conventional SAW based particle actuation in PDMS channels which require bonding and careful alignment relative to two SAW transducers. In a conventional SAW based manipulation platform (Fig. 2a), the SAW travels along the piezoelectric substrate and enters the PDMS/LiNbO3 interface where it partially couples as a bulk acoustic wave (BAW) into the PDMS before reaching the microchannel and generating a surface standing wave from interference with a counter-propagating SAW.29 In the concept presented here, the SAW travels along the LiNbO3 substrate followed by coupling of acoustic energy into the fluid of the coupling layer (Fig. 2b).19 Transmission of acoustic radiation as a Lamb-type wave into the glass itself takes place and travels even further into a liquid above it.12,17 Reflections within the channel then superpose and eventually create a standing wave.In particular, in the set-up, a single slanted interdigitated transducer was used for the generation of ultrasound and a disposable glass microfluidic chip was simply placed on the piezoelectric wafer and fixed with metal clamps (Fig. 3a). The channel faced the slanted interdigitated transducer with an orientation perpendicular to the SAW propagation. A thin volume of water, compressed between the piezoelectric substrate and the superstrate helped to couple the incident SAW into the superstrate. Similar to conventional bulk acoustic approaches, a transversal resonator concept can be considered. The propagating Lamb-type wave, formed in the superstrate, radiated acoustic energy into the microchannel. The channel walls acted as near-ideal reflectors resulting in two counter propagating waves, forming a standing wave.
Simulation results
Ideally, the resonance frequency which supports a half-wavelength lateral pressure wave across the width of the resonator-microchannel can be found by considering the width of the cavity and the speed of sound in the fluid. However, in practice, numerical methods can be helpful to predict the resonance modes in more than one dimension, more accurately. To predict these modes, we used 2D models implemented in the finite element analysis tool COMSOL Multiphysics. Fig. 2c–d show several Eigen solutions supporting half a wavelength pressure wave; similar to models shown in previous studies.35 Here, 4.192 MHz and 4.193 MHz were identified in our simulations where the pressure distribution is symmetric across the width of the channel but not homogenous along the channel. This 2D effect, has been described as a “pinching region”. Typically, the number of these regions increases for increasing frequency of the solution of the Helmholtz equation.Finding resonances using broadband transducer
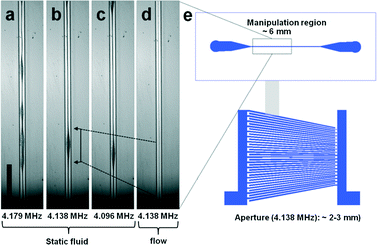
A slanted SAW transducer design was chosen to enable the excitation of a wide range of frequencies (in this case between 3.5 MHz to 5.5 MHz). The design also provides higher harmonic responses of the fundamental frequencies (see ESI† for frequency spectra). This flexible approach permits the identification of the resonance frequency of a superstrate experimentally by scanning through the available range until a strong and homogenous acoustophoretic movement towards a pressure node was observed.The resonance frequency along the aperture of the SAW device was visualised by thermal images (Fig. 3b) and the superstrate position was adjusted accordingly. For the superstrate shown in Fig. 3a, a frequency of 4.138 MHz resulted in a strong focusing effect of beads along a pressure node when injected under continuous flow. Fig. 3a shows 3 μm diameter polystyrene beads approaching the manipulation region (I in Fig. 3a), where the acoustic energy enters the microchannel. There followed a lateral displacement of the beads towards the channel center due to the acoustic radiation force. The alignment of beads was achieved along the channel length (II in Fig. 3a) and confocal images through the height of the channel showed the one-dimensional character of the pressure wave (Fig. 3c).
We identified several frequencies which resulted in a strong lateral mode. This was in close agreement with the simple eigenfrequency analysis which suggested multiple solutions. However, the identified resonance frequencies slightly differed from this simple model in form of a shift towards lower frequencies. In Fig. 4(a–c) bead focusing in a static fluid for 4.179 MHZ, 4.138 MHz and 4.096 MHz are shown. As expected, the pressure distribution was non-uniform resulting in regions where beads were less tightly focused. The variation in the strength of bead focusing along the channel is a common result typically seen in a static fluid in acoustophoretic devices36–38 and related to the complex interaction of the whole chip structure with the microchannel resonance. However, these irregularities were averaged and suppressed by applying a fluidic flow through the channel. Laminar flow kept beads in streamlines once positioned in the pressure node by the acoustic radiation force (Fig. 4d).
When slanted SAW transducers have previously been used to pattern particles,9 the manipulation region has been shown to be limited by the aperture of the SAW device at a particular frequency which varies in position along the width of the device. In comparison, the refraction of the narrow SAW beam into the coupling layer and subsequent refraction into the substrate of the superstrate led to the spreading of the acoustic field further along the channel length. For instance the aperture of the excited frequency of 4.138 MHz was 2–3 mm according to vibrometry measurements (see Fig. S4, ESI†). Once coupled within the chip, we identified a wider manipulation region spanning around 6 mm of the channel length where the particles were manipulated (Fig. 4e).
Acoustic pressure and energy densities
As described in eqn (1), the acoustic radiation force scales with the particle radius and the acoustic energy in the microchannel. In Fig. 5(a–d) it is demonstrated that the time taken for a mixture of beads to move to the acoustic node decreased with increasing bead diameter (3 μm, 6 μm, 8 μm). The lateral path of the bead movement was used to estimate the acoustic transmission into the superstrate using the analytical expression given in eqn (3). Using the method introduced by Barnkorb et al.,7 we estimated the acoustic energy densities and pressure amplitudes coupled from the SAW transducer into the channel. In the case involving the manipulation of 3 μm beads, we calculated energy densities for voltages applied to the SAW transducer in the range of 5 V to 40 V at 4.138 MHz. As shown in Fig. 6e, the acoustic energy density (which is proportional to the pressure amplitude) was a function of the applied voltage. Acoustic energy densities of 12 J m−3 to 1143 J m−3 with corresponding pressure amplitudes of 0.3 MPa to 3.1 MPa were achieved and demonstrated sufficient actuation for rapid bead acoustophoresis (despite decoupling particle handling from the piezoelectric surface into a disposable polymer-glass composite chip).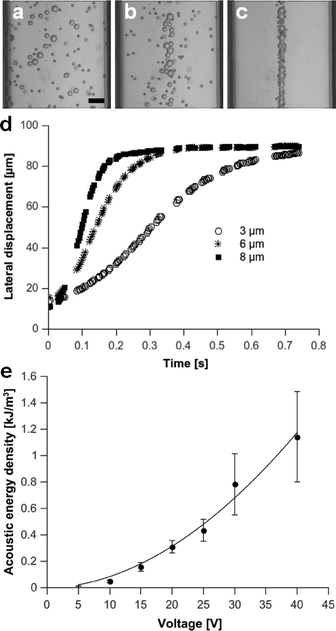 | ||
| Fig. 5 (a–c): Image sequence showing focusing of 3 μm, 6 μm and 8 μm beads at (a) 0 s and after (b) 0.05 s and (c) 1.25 s of acoustic actuation at a frequency of 4.138 MHz and 10 V (static fluid, scale bar: 25 μm). (d) Corresponding lateral displacement of beads over time. (e) Acoustic energy density for various voltages applied to the transducer, calculated after tracking lateral path of 3 μm beads (no flow) and applying analytical expression given in eqn (3). | ||
As the pressure distribution was non-uniform along the channel length, the time taken to focus beads varied and hence the errors in Fig. 5e) were relatively large. It should be noted that a significant temperature change occurred on the surface of the superstrate when applying high voltages (>20 V) to the SAW transducer for prolonged times (~30 min, see Fig. S2, ESI†). Such a change in temperature can alter the resonance response (change in speed of sound) of an acoustophoretic chip39 and should be addressed for long-term experiments with increased input powers. However, for the short term (seconds) focusing experiments, the temperature change (<1 °C) is small.
Benefits of superstrate and broadband SAW transducer
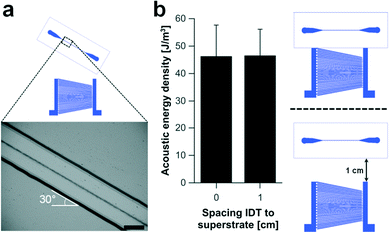
One of the benefits of using a superstrate to decouple the channel from the acoustic actuator is the reduced complexity of the assembly process. Conventional SAW based acoustophoretic systems require a straight and optimally positioned alignment of the channel relative to the SAW transducer to avoid particle/channel wall interactions,40 whereas this approach compensates for any misalignments such as those seen in Fig. 6a. Here, the angle of the superstrate relative to the SAW transducer was increased to 30° while maintaining a stable acoustic focusing effect. This can be best understood by the observation that the acoustic standing wave was not created by opposing SAW devices, but instead by reflections from the microfluidic channel (which maintain their position relative to each other, as the channel is rotated). Furthermore, the distance between the superstrate and the transducer can be varied up to 1 cm without significant loss of acoustic energy coupled into the microchannel (Fig. 6b), where in conventional systems, care must be taken to either move a multiple of wavelengths, or compensate with a phase optimisation of one IDT with respect to the other.41 The results indicated that the coupling of the SAW into the superstrate can take place from an arbitrary point. However, the resonance frequency of the superstrate defines the position of SAW beam within the aperture of the slanted transducer. The position of the travelling SAW for a particular frequency is fixed and the superstrate has to be placed within its path to allow for acoustophoretic manipulations of particles.As discussed above, the slanted broadband SAW transducer design is suitable for finding the resonance point of the superstrate experimentally. The excited frequency can be adjusted until the condition for a stable single pressure node in the centre of the channel is achieved. Any variation in the superstrate geometry can therefore be easily compensated for by changing the frequency. However, beyond the fundamental frequencies (3.7 MHz to 5.5 MHz), the harmonic response of the slanted SAW transducer offered an extended frequency range (see Fig. S1, ESI†). Thus, in addition to a single pressure nodal plane, multinode arrangements creating tuneable pressure distributions in the microchannel can be established.
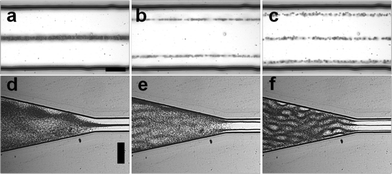
In Fig. 7(a–c), three resonances of the superstrate at 4.138 MHz, 8 MHz and 12.51 MHz are shown, resulting in 1 to 3 pressure nodal planes. Even higher resonance frequencies can be found within the device as shown in Fig. S3 in ESI,† which demonstrates the benefit of using a SAW transducer as a tuneable ultrasound source for acoustophoretic microparticle manipulation.
As mentioned, a spreading of the acoustic wave coupled to the superstrate can be observed which limits the application of the acoustic radiation force to this area unlike in the conventional SAW setup where the SAW is defined by the aperture of the transducer. However, confinement in a static fluid can be achieved when using specific microchannel geometries.38 For instance, a non-uniform channel width alters the pressure distribution and localized force fields can be obtained at particular channel sections using appropriate chip designs. Fig. 7(d–f) shows the confinement of the standing wave in the expanding channel section for the same resonance frequencies. The gradual change in channel width no longer supports the resonance mode but instead produces an intricate pattern of acoustic pressures which are shown by the positions of the beads.
The spatial confinement achievable and the fact that a single transducer per resonance mode is sufficient provides the possibility for segmented acoustophoretic particle manipulation along a channel length to integrate functions including focusing, merging and splitting of samples similar to work shown by Manneberg et al. using bulky BAW transducers.38
Conclusions
We show a new and simple methodology for acoustophoresis of microparticles, which we demonstrated on a disposable chip, known as a superstrate. We show that where a microchannel is embedded in the superstrate, the structure acts as a resonating cavity and particle manipulation can be implemented using a single SAW transducer. The advantages of this technique are found to be the increased tolerance to assembly between the channel and the transducer, making it much more feasible to use the superstrate as a low cost, disposable, element that can be switched between samples. We believe that this concept simplifies SAW mediated cell manipulation and has the potential to enable the trapping, enrichment and separation of microorganism in disposable microfluidic systems.Acknowledgements
Dr Neale acknowledges the support of an Engineering and Physical Sciences Research Council (EPSRC)/Royal Academy of Engineering research fellowship (EP/G058393/1). Professor Cooper is supported by an EPSRC Fellowship (EP/K027611/1) and is an ERC Advanced Investigator. Dr Wilson (Proxomics, EP/I017887/1), Dr Reboud (Lord Kelvin- and Adam Smith Fellowship from the University of Glasgow). The authors thank the James Watt Nanofabrication Centre (Glasgow, UK) for help with device fabrication and characterisation.Notes and references
- M. Kumar, D. L. Feke and J. M. Belovich, Biotechnol. Bioeng., 2005, 89, 129–137 CrossRef CAS PubMed.
- F. Petersson, L. Aberg, A.-M. Swärd-Nilsson and T. Laurell, Anal. Chem., 2007, 79, 5117–5123 CrossRef CAS PubMed.
- J. Shi, D. Ahmed, X. Mao, S.-C. S. Lin, A. Lawit and T. J. Huang, Lab Chip, 2009, 9, 2890–2895 RSC.
- J. Shi, H. Huang, Z. Stratton, Y. Huang and T. J. Huang, Lab Chip, 2009, 9, 3354–3359 RSC.
- M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991 CrossRef CAS PubMed.
- T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506 RSC.
- R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Lab Chip, 2010, 10, 563–570 RSC.
- Y. C. Chen, A. A. Nawaz, Y. H. Zhao, P. H. Huang, J. P. McCoy, S. J. Levine, L. Wang and T. J. Huang, Lab Chip, 2014, 14, 916–923 RSC.
- X. Y. Ding, J. J. Shi, S. C. S. Lin, S. Yazdi, B. Kiraly and T. J. Huang, Lab Chip, 2012, 12, 2491–2497 RSC.
- O. Jakobsson, C. Grenvall, M. Nordin, M. Evander and T. Laurell, Lab Chip, 2014, 14, 1943–1950 RSC.
- H. Bruus, Lab Chip, 2012, 12, 1014–1021 RSC.
- R. P. Hodgson, M. Tan, L. Yeo and J. Friend, Appl. Phys. Lett., 2009, 94, 024102–024103 CrossRef PubMed.
- Y. Bourquin, J. Reboud, R. Wilson and J. M. Cooper, Lab Chip, 2010, 10, 1898–1901 RSC.
- R. Wilson, J. Reboud, Y. Bourquin, S. L. Neale, Y. Zhang and J. M. Cooper, Lab Chip, 2011, 11, 323–328 RSC.
- J. Reboud, Y. Bourquin, R. Wilson, G. S. Pall, M. Jiwaji, A. R. Pitt, A. Graham, A. P. Waters and J. M. Cooper, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15162–15167 CrossRef CAS PubMed.
- A. R. Rezk, A. Qi, J. R. Friend, W. H. Li and L. Y. Yeo, Lab Chip, 2012, 12, 773–779 RSC.
- L. Schmid, A. Wixforth, D. A. Weitz and T. Franke, Microfluid. Nanofluid., 2012, 12, 229–235 CrossRef.
- Y. Chen, S. Li, Y. Gu, P. Li, X. Ding, L. Wang, J. P. McCoy, S. J. Levine and T. J. Huang, Lab Chip, 2014, 14, 924–930 RSC.
- K. M. Seemann, J. Ebbecke and A. Wixfort, Nanotechnology, 2006, 17, 4529–4529 CrossRef CAS.
- Y. Bourquin, J. Reboud, R. Wilson, Y. Zhang and J. M. Cooper, Lab Chip, 2011, 11, 2725–2730 RSC.
- J. Reboud, R. Wilson, Y. Zhang, M. H. Ismail, Y. Bourquin and J. M. Cooper, Lab Chip, 2012, 12, 1268–1273 RSC.
- Y. Bourquin, R. Wilson, Y. Zhang, J. Reboud and J. M. Cooper, Adv. Mater., 2011, 23, 1458–1462 CrossRef CAS PubMed.
- R. J. Shilton, N. R. Glass, P. Chan, L. Y. Yeo and J. R. Friend, Appl. Phys. Lett., 2011, 98, 254103 Search PubMed.
- N. R. Glass, R. J. Shilton, P. P. Y. Chan, J. R. Friend and L. Y. Yeo, Small, 2012, 8, 1881–1888 CrossRef CAS PubMed.
- J. Shi, X. Mao, D. Ahmed, A. Colletti and T. J. Huang, Lab Chip, 2008, 8, 221–223 RSC.
- X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I. K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109 CrossRef CAS PubMed.
- Y. Ai, C. K. Sanders and B. L. Marrone, Anal. Chem., 2013, 85, 9126–9134 CrossRef CAS PubMed.
- J. Nam, H. Lim, D. Kim and S. Shin, Lab Chip, 2011, 11, 3361–3364 RSC.
- L. Johansson, J. Enlund, S. Johansson, I. Katardjiev and V. Yantchev, Biomed. Microdevices, 2012, 14, 279–289 CrossRef PubMed.
- V. Yantchev, J. Micromech. Microeng., 2010, 20, 035031–035031 CrossRef.
- S. M. Langelier, L. Y. Yeo and J. Friend, Lab Chip, 2012, 12, 2970–2976 RSC.
- M. K. Tan, L. Y. Yeo and J. R. Friend, EPL, 2009, 87, 47003 CrossRef.
- P. K. Panda, J. Mater. Sci., 2009, 44, 5049–5062 CrossRef CAS.
- A. Lenshof, M. Evander, T. Laurell and J. Nilsson, Lab Chip, 2012, 12, 684–695 RSC.
- S. M. Hagsater, A. Lenshof, P. Skafte-Pedersen, J. P. Kutter, T. Laurell and H. Bruus, Lab Chip, 2008, 8, 1178–1184 RSC.
- O. Manneberg, B. Vanherberghen, B. Onfelt and M. Wiklund, Lab Chip, 2009, 9, 833–837 RSC.
- O. Manneberg, J. Svennebring, H. M. Hertz and M. Wiklund, J. Micromech. Microeng., 2008, 18, 095025–095025 CrossRef.
- O. Manneberg, S. Melker Hagsater, J. Svennebring, H. M. Hertz, J. P. Kutter, H. Bruus and M. Wiklund, Ultrasonics, 2009, 49, 112–119 CrossRef CAS PubMed.
- P. Augustsson, R. Barnkob, S. T. Wereley, H. Bruus and T. Laurell, Lab Chip, 2011, 11, 4152–4164 RSC.
- L. Johansson, J. Enlund, S. Johansson, I. Katardjiev and V. Yantchev, Biomed. Microdevices, 2011, 14, 279–289 CrossRef PubMed.
- N. D. Orloff, J. R. Dennis, M. Cecchini, E. Schonbrun, E. Rocas, Y. Wang, D. Novotny, R. W. Simmonds, J. Moreland, I. Takeuchi and J. C. Booth, Biomicrofluidics, 2011, 5, 044107 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4lc00749b |
| This journal is © The Royal Society of Chemistry 2014 |